1 Introduction

Landslide disaster of inner dump has always been a hot topic in geotechnical field, which is a massive threat to society and economy in open-pit mine. Among the many factors that may lead to slope failure, groundwater and rainfall are usually the most important and complex factors (Xu et al 2021a, b; Anc et al 2020). For the open-pit mine, due to its large excavation depth, the high dump slope is formed after the waste is filled artificially. The water level of the surrounding groundwater systems is higher than the bottom of the dump slope, and it is easy to form the water level inside the slope (Fig. 1). The redistribution of water within slope results in a breakdown of the mechanical equilibrium because of the replenished groundwater and rainfall infiltration. Landslide-triggering is related to groundwater and rainfall infiltration in the open-pit mine. They increased soil moisture content and pore water pressure, which reduced effective stress and shear strength (Ghiassian et al. 2008). Dong et al. (2012) presented a numerical procedure to explore how hydraulic conductivity anisotropy and strength anisotropy affect the slope stability. The existing slope stability theories cannot explain the complex relationship between stress state and stability of dump slope under the coupling action of diving and rainfall (see Fig. 1).

Fig. 1
figure 1

High dump slope influenced by rainfall and groundwater in the open-pit mine

Full size image

The fluctuation of groundwater level is usually accompanied by the occurrence of seasonal rainfall. Recent studies based on field investigations and monitoring data suggest that landslides are not caused by a single factor, such as rainfall or groundwater, but by the combined action of several factors (Du et al 2013; Shi et al 2021; Wang et al 2016). Moreover, the factors inducing dump slopes instability change constantly as the combinations of rainfall conditions and groundwater change throughout the year. Therefore, it is necessary to discuss slope stability by considering various combinations of rainfall and groundwater in terms of specific characteristics of the dump slopes affected by groundwater and rainfall infiltration in the open-pit mine.

Many studies analyze the influence of a single factor on slope stability, and the main research results are as follows. For single groundwater, Hoek and Bray (1977) first assumed that the hydrostatic pressure presented a triangular distribution on the structural surface. Since then, many experts have carried out research based on this assumption (Wang et al. 2009), while the influence of seepage forces was not considered. Ghiassian (2008) and Kim et al. (2018) deduced the seepage gradient in slopes with uniform flow. Wang et al. (2020) developed the analytical solution of the factor of safety (FoS) to accommodate the effects of groundwater on the stability of the dump slope and suggested that FoS versus groundwater level could be described by an inverse function. Thus, groundwater seepage plays an important role in slope stability. Groundwater penetrates into the structure of the slope through cracks and changes the moisture content of the soil. The deterioration of cohesion and internal friction angle of soil structure eventually lead to slope instability (Padilla et al. 2014; Wang et al 2019).

For a single rainfall factor, previous studies have explored the mechanism of rainfall infiltration into unsaturated soils, which is usually described by Darcy’s law as formulated in Richard’s equation (Van Gaalen et al 2013; Qiu et al 2022; Wang et al 2023). Moreover, the hydraulic properties of the soil in the unsaturated layer are usually described by the van Genuchten equation (Tian et al 2019; Sheikhbaglou et al 2021). More recently, studies have combined mechanical analysis and infiltration methods to assess the slope instability induced by rainfall (Wei et al 2019; Xia et al 2013). Most studies focused on several typical rainfall patterns (e.g., uniform, advanced, and delayed rainfall patterns) (Tsai and Wang 2010; Wu et al 2017a, b). They mainly studied the variation in rainfall parameters, including influence of rainfall (rainfall threshold), rainfall intensity and rainfall time on the stability of unsaturated slope (Pradhan et al 2022; Qiang et al. 2020). The key issues of triggering slope failures by rainfall are the effects of unsaturated soil properties, steady state flow and transient flow in the infiltration and evaporation cases on the stability of various geo-structures (Shahrokhabadi et al 2019; Vo and Russell 2014). More attention was paid to the influence of negative pore pressure or matric suction on retaining structure failure caused by precipitation. A great amount of effort has been devoted to calculating the thrust of earth pressures under unsaturated steady flow conditions and studying the mechanics of partially saturated soil under infiltration condition (Xu et al. 2021a; b; Zhou et al. 2014; Li and Yang 2020; Fathipour et al. 2020, 2023; Hu et al. 2018). Change in backfill saturation has significant influence on active earth pressures (Vahedifard et al 2015; Huang and Jia 2009). Nevertheless, the influences of rainfall and groundwater on the stability of landslides are different. Rainfall is a major factor that causes the deformation of the shallow part of the landslide, while groundwater is the most influential factor for the deep part of the landslide (Zhao et al 2017; Zhou et al 2016). Huang et al. (2016) noted that the mechanism of these influential factors on slope stability is very complex. The mechanism of saturated and unsaturated factors influencing the force of slope in the same slope model needs further study.

Some achievement have also been achieved on slope stability under rainfall and groudwater. In these studies, three main methods are utilized: field investigation and monitoring data analysis, numerical simulation, laboratory experiments and numerous theoretical studies. The relationship between rainfall, groundwater, and landslides is investigated and monitored, and the probability of the landslides is evaluated (Huang et al 2018; Gao and Yin 2007). Numerical simulation studies were carried out to analyze the changes in slope water pressure during the landslide process because these changes have an important impact on the stability of the slope (Wu et al 2017a; b; He 2014; Sun et al 2016). Model tests of slopes under different rainfall and groundwater combinations were conducted, and the precursor information of the slope instability was obtained to assess the slope stability (Xiong et al 2019; Luo et al 2005; Huang and Yuin 2010). Although, some works of slope stability changes under the combined action of rainfall and groundwater have been done from a theoretical perspective (Šimůnek et al. 2016; Wu et al. 2021, Pd et al. 2020). They can describe infiltration and moisture redistribution for different slopes. While, they do not have a general analytical solution and its application in real-world systems requires intensive computation. To date, slope stability under rainfall and groundwater dynamic variation is not taken into account in the slope mechanical model. These models treat all land surfaces as horizontal planes, even though surfaces may be inclining. In the stability analysis, it is generally considered that the wetting front is the potential sliding surface, and the instability possibility in the basement surface in advance is ignored due to the influence of groundwater level variation. Therefore, it is difficult to accurately evaluate the mechanism of landslide disaster in the open-pit coalmine.

Although lots of work has been done by studying the influence of a single rainfall or groundwater factor and combined influence of rainfall and groundwater on slope stability. Using the theoretical model to quantitatively investigate the failure mechanism of real landslides has not been conducted yet under combined influence of rainfall and groundwater. The main aim of this paper is to reveal the correlation between the dynamic variation of rainfall and groudwater and the slope stability from a theoretical perspective. This study develops a stratification slope model to quantitative study slope stability under combined action of rainfall and groundwater, and a theoretical solution of FoS for the inner slopes by affected rainfall and groundwater. In the solving process, the effect of water seepage and the strength reduction of soil in the process of water migration are considered. Saturation theory and unsaturated theory are integrated into the same slope mechanical model. The critical rainfall expression and groundwater expression of the main factors inducing slope instability are determined. The developed model is verified and applied to analyze the stability of an inner dump slope in the Shengli open-pit coalmine under various rainfall and groundwater scenarios.

The study was organized to include several sections, starting with the introduction in Sect. 1, which describes the problem and background. This is followed by a study area of an inner dump slope with the combined influence of rainfall and groundwater in Sect. 2. In Sect. 3, a method was proposed to investigate the landslide problems that are induced by the combined action of rainfall infiltration and groundwater. In the method, a theoretical model for the inner dump slope was established, and an analytical solution of the safety factor (FoS) is then developed for inner dump slopes. Thereafter, according to the methodology, the parametric study was illustrated to study the slope stability changes with the dynamic changes of rainfall and groundwater (Sect. 4). Finally, verification and application are presented with a case study in Sect. 5, which are followed by the conclusions of this study (Sect. 6).

2 Study area

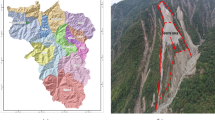
The dump slope of the Shengli open-pit coalmine is employed for the case study in this section, which is located in Xilinhot City, Inner Mongolia, China. The field view of the inner dump slope is shown in Fig. 2. It is a hilly plateau terrain with elevation of 970.00–1326.60 m and its relative elevation is 356.60 m. This inner dump slope was formed in 2010, currently it is discharged to the level of + 975 m and its height is about 165 m. Due to the existence of quaternary porous phreatic aquifers and local rivers on the eastern side, groundwater in the open-pit mine is widely distributed.

Fig. 2
figure 2

Geographical location and contour map in Shengli open-pit coalmine

Full size image

At present, owing to the poor permeability and the difficulty in dredging and lowering water, sidewall seepage had become a serious problem, threatening the safety of the inner dump slope and the safe production of the mine (Wang et al 2020). Actually, the sidewall seepage had already caused some large-scale landslides in the eastern nonworking slope in this mine’s earlier phase. To mitigate sidewall seepage, two sumps are located at the northern and southern ends of the eastern inner dump slope for diversion and drainage, as displayed in Fig. 3. The water sumps are located on the platform of the inner dump, and the mining area is located at the bottom of the benches. Note that the inner dump slope is mainly composed of debris waste. In-situ test shows there is hydraulic relation between groundwater and sump in the inner dump. The groundwater inside the inner dump is replenished from the sumps and quaternary water, which forms the underground water conditions in the inner dump. Driven by the hydraulic gradient, the groundwater in inner dump can flow from the east side of the reservoir to the inner dump. Figure 4 shows the distribution of flow field in the inner dump slope.

Fig. 3
figure 3

Field view of the inner dump slope in Shengli open-pit coalmine

Full size image
Fig. 4
figure 4

Distribution of flow field in the inner dump slope (Wang et al 2020)

Full size image

Figure 5 shows a large amount of water by rainfall on the top of the inner dump and a landslide of slope surface in the inner dump induced by groundwater and rainfall. This work aims to evaluate the influence of groundwater and rainfall on the inner dump in the Shengli open-pit coalmine. On the one hand, during the rainy season, groundwater level changes due to hydraulic recharge from the east side; on the other hand, heavy rainfall causes the water to infiltrate into the slope. The seepage force and the influence depth of rainfall and groundwater are the main factors that threaten the stability of dump slopes in the open-pit coalmine. Determining the major factors of slope instability induced by rainfall and groundwater and illustrating the slope instability mechanism in dump slopes have become urgent problems.

Fig. 5
figure 5

A landslide site induced by groundwater and rainfall in Shengli open-pit coalmine

Full size image

3 Method

3.1 Stratified slope model

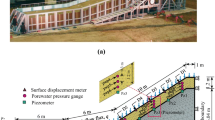
The conventional Green-Ampt infiltration model is used to study shallow water infiltration in initially dry soil. According to the model, there is a sharp wetting front in the infiltration process. Dry soil and wet soil are separated by the wetting front (Green 1911; Ghiassian and Ghareh 2008). In the process of rainfall infiltration, the moisture content of the saturated area above the wet front is θs. Below the wet front is natural soil with initial moisture content θr. The model represents the relationship between infiltration rate and wetting front depth, saturation permeability, suction head at the wetting front and surface water depth. Currently, the stratified soil model is widely used in most cases, and the slope is divided into two layers above the wetting front in the model, including a saturated layer and a transitional layer (Yao et al. 2019). In most cases, stratified soil water content is observed, which can be divided into at least three layers during rainfall, including a saturated layer, a transitional layer, and a natural layer (Yao et al. 2019). However, models of the combined influence of groundwater and rainfall on slopes are rarely studied. The model proposed in this paper unifies the combined influence of groundwater and rainfall on slopes by considering stratified soil. Experiments and theoretical analyses indicate that stratified soil water content should be considered. Meanwhile, the layer below the groundwater level is considered to be saturated. Thus, in the model, the slope affected by rainfall and groundwater can be divided into at least four layers from the top of the slope to the basement surface, including a saturated layer, a transition layer, a natural layer and a groundwater layer, as shown in Fig. 6. The changes in the saturated layer and transition layer are affected by rainfall, and the change in the groundwater layer is affected by groundwater. In Fig. 7, \(h_{{\text{s}}}\) and \(h_{{\text{t}}}\) are the depths of the saturated layer and transitional layer, respectively, m; \(h_{{\text{f}}}\) and \(h_{{\text{d}}}\) are the depths of the wetting front and the natural layer, respectively, m; \(h_{{\text{w}}}\) is the depth of groundwater layer, m; and \(\alpha\) is the slope angle, °.

Fig. 6
figure 6

Stratification model with the combined influence of rainfall and groundwater

Full size image
Fig. 7
figure 7

Distribution of water content of the soil with water infiltration

Full size image

Furthermore, as proposed by Yao et al. (2019), the water content in the transitional layer and saturated layer changes with depth following an ellipse function, and the distribution of the water content during rainfall infiltration is shown in Fig. 7. Therefore, the distribution function of the water content in the unified slope model can be described by:

$$ \theta (h) = \left\{ {\begin{array}{*{20}l} {\theta_{{\text{s}}} } \hfill & {0 \le h \le h_{{\text{s}}} } \hfill & {{\text{Saturated layer}},} \hfill \\ {\theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\sqrt {1 - (\frac{{h - h_{{\text{s}}} }}{{h_{{\text{t}}} }})^{2} } } \hfill & {h_{{\text{s}}} \le h \le h_{{\text{s}}} { + }h_{{\text{t}}} \, } \hfill & {{\text{Transition layer}},} \hfill \\ {\theta_{0} } \hfill & {h_{{\text{s}}} + h_{{\text{t}}} \le h \le h_{{\text{s}}} + h_{{\text{t}}} + h_{{\text{d}}} } \hfill & {\text{Natural layer}} \hfill \\ {\theta_{{\text{s}}} } \hfill & {h_{s} + h_{{\text{t}}} + h_{{\text{d}}} \le h \le h_{{\text{s}}} + h_{{\text{t}}} + h_{{\text{n}}} + h_{{\text{w}}} } \hfill & {\text{Groundwater layer}} \hfill \\ \end{array} } \right. $$
(1)

where \(\theta_{0}\) and \(\theta_{{\text{s}}}\) are the initial and saturated water contents, respectively.

3.2 Model solution

When the rainfall infiltration and groundwater are unified, the study of the slope instability mechanism becomes more complicated. In the unified model, the saturation theory and unsaturated theory are integrated into the same slope mechanical model. The effect of the seepage force on the saturated layer and the variation in the water content due to water migration are considered in the process of solving slope stability (Yao et al 2019; Gavin and Xue 2008; Das et al. 2009; Estabragh et al. 2016).

The following hypotheses are proposed in the solution derivation of the FoS for the unified stratification slope model subjected to rainfall and groundwater:

  1. (i)

    The dump slope is infinitely long and the width of each slice is unity.

  2. (ii)

    The main groundwater level, saturated layer, wetting front and basement surface are parallel to the slope, and the basement is impermeable.

  3. (iii)

    As described by Yao et al. (2019), the soil water content in the transitional layer varies with depth following an ellipse function.

To analyze the influence of groundwater and rainfall on slope stability, the safety factors in the surface of the saturated layer, wetting front and the basement surface are studied in the following sections; their mechanical models are shown in Fig. 8, their angles are all equal to α (see the hypothesis above).\(\sigma_{{{\text{ns}}}}\) and \(\tau_{{{\text{ms}}}}\) are the normal stress and shear stress of saturated layer, respectively, kPa; \(W_{{\text{s}}}\) and \(W_{{\text{f}}}\) are slider gravities above saturated layer and wetting front, respectively, kN;\(W_{{\text{j}}}\) and \(N_{{\text{j}}}\) are slider gravity and slider normal force above the basement, respectively, kN;\(N_{{\text{s}}}\) and \(N_{{\text{f}}}\) are slider normal force above saturated layer and wetting front, respectively, kN;\(\sigma_{{{\text{nf}}}}\) and \(\tau_{{{\text{mf}}}}\) are the normal stress and shear stress of wetting front, respectively, kPa; \(J_{{\text{s}}}\) and \(J_{{\text{w}}}\) are the seepage force of saturated layer and groundwater layer, respectively, kN.\(\sigma_{{{\text{nj}}}}\) and \(\tau_{{{\text{mj}}}}\) are the normal stress and shear stress above basement surface, respectively, kPa. \(u_{{\text{a}}}\) and \(u_{{\text{w}}}\) are the air stress and water stress of the soil, respectively, Pa. \(H\) is the depth from the top of the slope to the basement floor, m.

Fig. 8
figure 8

Calculating diagram of the slope with the combined influence of rainfall and groundwater

Full size image

3.2.1 Safety factor in the saturated surface caused by rainfall

As presented in reference (Cho 2009), the saturated surface of rainfall is taken as the study object, and the mechanical models are shown in Figs.8(a1) and (a2).

The soil gravities (\(W_{{\text{s}}}\)) and normal force (\(N_{{\text{s}}}\)) above the saturated layer surface can be represented as follows:

$$ W_{{\text{s}}} = \gamma^{^{\prime}} V = \gamma^{^{\prime}} h_{{\text{s}}} $$
(2)
$$ N_{{\text{s}}} = \gamma^{^{\prime}} h_{{\text{s}}} \cos \alpha $$
(3)

The seepage force (\(J_{{\text{s}}}\)) of saturated layer should be taken into account (Yao et al 2019; Gavin and Xue 2008), which can be expressed as follows:

$$ J_{{\text{s}}} = \gamma_{{\text{w}}} h_{{\text{s}}} \sin \alpha $$
(4)

The tilt length of slider,\(l\), can be expressed by,

$$ l = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\cos \alpha }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\cos \alpha }$}} $$
(5)

The safety factor on the surface of the saturated layer \(\left( {F_{{{\text{ss}}}} } \right)\) can be expressed as follows:

$$ F_{{{\text{ss}}}} = \frac{{c^{^{\prime}} l + N\tan \varphi^{^{\prime}} }}{{W_{{\text{s}}} \sin \alpha + J_{{\text{s}}} }} $$
(6)

where \(\varphi^{^{\prime}}\) is the effective internal friction angle,°;\(c^{^{\prime}}\) is the effective cohesion, kPa; \(J_{{\text{s}}}\) is the seepage force in the saturation layer caused by rainfall.

Substituting Eqs. (2) ~ (5) into (6), Eq. (7) can be obtained,

$$ F_{{{\text{ss}}}} = \frac{{c^{^{\prime}} l + \gamma^{^{\prime}} h_{{\text{s}}} \cos \alpha \tan \varphi^{^{\prime}} }}{{\gamma^{^{\prime}} h_{{\text{s}}} \sin \alpha + \gamma_{{\text{w}}} h_{{\text{s}}} \sin \alpha }} = \frac{{\tan \varphi^{^{\prime}} }}{{\tan \alpha (1 + \frac{{\gamma_{{\text{w}}} }}{{\gamma^{^{\prime}} }})}} + \frac{{2c^{^{\prime}} }}{{(\gamma^{^{\prime}} + \gamma_{{\text{w}}} )h_{{\text{s}}} \sin 2\alpha }} $$
(7)

where \(\gamma^{^{\prime}}\) and \(\gamma_{{\text{w}}}\) are the buoyant weight and water weight, respectively, kN/m3.

Equation (7) shows that the safety factor in the saturated layer surface is inversely proportional to the saturated layer depth \(\left( {h_{{\text{s}}} } \right)\) caused by rainfall. The first term shows that the decrease of the safety factor is mainly due to the decrease of the internal friction angle caused by rainfall. The second term shows that the increase of the saturated layer depth and the decrease of cohesion can reduce the FoS in the saturated layer. Meanwhile, Eq. (7) also reflects that the seepage force has an important influence on the safety factor of the slope.

3.2.2 Safety factor of wetting front

The wetting front is taken as the study object and the mechanical models are presented in Fig. 8b1, b2.

As described by Eq. (1), the soil water content in the transitional layer varies with depth as an ellipse function,

$$ \theta (h) = \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\sqrt {1 - \left( {\frac{{h - h_{{\text{s}}} }}{{h_{{\text{t}}} }}} \right)^{2} } $$
(8)

Combined with reference (Sun et al 2016), the unit weight of soil in the transitional layer \(\left( {\gamma_{{\text{t}}} } \right)\) can be expressed by:

$$ \gamma_{{\text{t}}} = \gamma_{{\text{d}}} (1 + \theta ) $$
(9)

where \(\gamma_{{\text{t}}}\) and \(\gamma_{{\text{d}}}\) are the unit weight of soil in the transition layer and the drying weight, respectively, kN/m3.

Substituting Eq. (8) into Eq. (9), the soil unit weight in the transition layer can be calculated:

$$ \gamma_{{\text{t}}} = \gamma_{{\text{d}}} [1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\sqrt {1 - (\frac{{h - h_{{\text{s}}} }}{{h_{{\text{t}}} }})^{2} } ] $$
(10)

By using the existing methods of the M-C failure criterion and the limit equilibrium method for unsaturated soils,the normal stress \(\sigma_{{{\text{nf}}}}\) and shear stress \(\tau_{{{\text{mf}}}}\) in the wetting front can be obtained (Yao et al 2019).

$$ \sigma_{{{\text{nf}}}} = (\gamma^{^{\prime}} h_{{\text{s}}} + \int_{{{\text{h}}_{{\text{s}}} }}^{{h_{{\text{f}}} }} {\gamma_{{\text{t}}} dh)\cos^{2} \alpha } = \{ \gamma^{^{\prime}} h_{{\text{s}}} + \gamma_{{\text{d}}} h_{{\text{t}}} [1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}]\} \cos^{2} \alpha $$
(11)
$$ \tau_{{{\text{mf}}}} = (\gamma^{^{\prime}} h_{{\text{s}}} + \int_{{h_{{\text{s}}} }}^{{h_{{\text{f}}} }} {\gamma_{{\text{t}}} dh)} \cos \alpha \sin \alpha = \{ \gamma^{^{\prime}} h_{{\text{s}}} + \gamma_{{\text{d}}} h_{{\text{t}}} [1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}]\} \cos \alpha \sin \alpha $$
(12)

where \(\sigma_{{{\text{nf}}}}\) and \(\tau_{{{\text{mf}}}}\) are the normal stress and shear stress in the wetting front, respectively, kPa.

As proposed in references (Cai et al 2019; Lu 2008; Lu et al 2010), the air pressure \(\left( {u_{{\text{a}}} } \right)\) can usually be neglected in the rainfall infiltration process. The water pressure can be expressed using the pressure head ht in the transitional layer and the water unit weight \(\left( {\gamma_{{\text{w}}} } \right)\). Equation (13) can be obtained,

$$ u_{{\text{a}}} = 0, \, u_{{\text{w}}} = \gamma_{{\text{w}}} h_{{\text{t}}} $$
(13)

where ua and uw are the pore air pressure and pore water pressure, respectively, kPa.

Meanwhile, as proposed by Lu and Godt (2008), Lu et al. (2010), Vanapalli et al. (1996), and Rossi et al. (2013), the change of the internal friction angle caused by matrix suction is related to the change of moisture content. The change of internal friction angle in the the wetting front,\(\varphi^{{\text{b}}}\), can be expressed as:

$$ \tan \varphi^{{\text{b}}} = \frac{{\theta_{0} - \theta_{{\text{r}}} }}{{\theta_{{\text{s}}} - \theta_{{\text{r}}} }}\tan \varphi^{^{\prime}} $$
(14)

The Eqs. (11), (12), (13) and (14) are put together, and the safety factor in the wetting front can be expressed as,

$$ \begin{aligned} F_{{{\text{sf}}}} = & \frac{{\tau_{{\text{f}}} }}{{\tau_{{{\text{mf}}}} }} \\ & = \frac{{c^{^{\prime}} + (\sigma_{{\text{n}}} - u_{{\text{a}}} )\tan \varphi^{^{\prime}} + (u_{{\text{a}}} - u_{{\text{w}}} )\tan \varphi^{{\text{b}}} }}{{\tau_{{\text{m}}} }} \\ & = \frac{{c^{^{\prime}} + \left\{ {\gamma^{^{\prime}} h_{{\text{s}}} + \gamma_{{\text{d}}} h_{{\text{t}}} [1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}]} \right\}\cos^{2} \alpha \tan \varphi^{^{\prime}} - \gamma_{{\text{w}}} h_{{\text{t}}} \frac{{\theta_{0} - \theta_{{\text{r}}} }}{{\theta_{{\text{s}}} - \theta_{{\text{r}}} }}\tan \varphi^{^{\prime}} }}{{\left\{ {\gamma^{^{\prime}} h_{{\text{s}}} + \gamma_{{\text{d}}} h_{{\text{t}}} [1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}]} \right\}\cos \alpha \sin \alpha + \gamma_{{\text{w}}} h_{{\text{s}}} \sin \alpha \cos \alpha }} \\ \end{aligned} $$
(15)

where \(\tau_{{\text{f}}}\) and \(\tau_{{{\text{mf}}}}\) are the shear strength of unsaturated soil and shear stress in the wetting front, kPa.

Based on Eq. (15), the safety factor in the wetting front can be calculated as follows:

$$ \begin{aligned} F_{{{\text{sf}}}} = & \frac{{2c^{^{\prime}} }}{{h_{{\text{s}}} (\gamma^{^{\prime}} { + }\gamma_{{\text{w}}} ) + \gamma_{{\text{d}}} h_{{\text{t}}} \left[ {1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]\sin 2\alpha }} + \frac{{\tan \varphi^{^{\prime}} }}{{\tan \alpha + \frac{{\gamma_{{\text{w}}} \tan \alpha }}{{\{ \gamma^{^{\prime}} + \gamma_{{\text{d}}} \frac{{h_{{\text{t}}} }}{{h_{{\text{s}}} }}\left[ {1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]\cos \alpha }}}} \\ & - \frac{{2\gamma_{{\text{w}}} \frac{{\theta_{0} - \theta_{{\text{r}}} }}{{\theta_{{\text{s}}} - \theta_{{\text{r}}} }}\tan \varphi^{^{\prime}} }}{{(\gamma^{^{\prime}} { + }\gamma_{{\text{w}}} )\frac{{h_{{\text{s}}} }}{{h_{{\text{t}}} }} + \gamma_{d} \left[ {1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]\sin 2\alpha }} \\ \end{aligned} $$
(16)

The safety factor in the wetting front can be divided into three terms according to Eq. (16). The first item shows that the safety factor is inversely proportional to the saturated layer depth (\(h_{{\text{s}}}\)) and the transition layer depth (\(h_{{\text{t}}}\)). Both \(h_{{\text{s}}}\) and \(h_{{\text{t}}}\) are affected by rainfall. It shows that the increase of slipping force and the seepage force in the saturated layer and the reduction of the cohesive force lead to a decrease of the safety factor. The second and third terms show that the ratio of \(h_{{\text{s}}}\) to \(h_{{\text{t}}}\) can reduce the safety factor in the wetting front.

3.2.3 Safety factor of basement surface

The sliding body above the basement surface is taken as the study object, and the mechanical models in the basement surface are shown in Fig. 8c1, c2. The seepage force in the saturated layer and groundwater layer can affect the safety factor of the basement surface.

Based on the above analysis, the soil gravity above the surface of the saturated layer \(W_{{\text{j}}}\) and normal force \(N_{{\text{j}}}\) can be written as follows:

$$ \begin{aligned} W_{{\text{j}}} & = \gamma^{^{\prime}} h_{{\text{s}}} + \int_{{h_{{\text{s}}} }}^{{h_{{\text{f}}} }} {\gamma_{{\text{t}}} dh + \gamma_{{\text{d}}} (1 + \theta_{0} )h_{{\text{d}}} + \gamma^{^{\prime}} h_{{\text{w}}} } \\ & = \gamma^{^{\prime}} (h_{{\text{s}}} + h_{{\text{w}}} ) + \gamma_{{\text{d}}} (1 + \theta_{0} )(h_{{\text{t}}} + h_{{\text{d}}} ) + \gamma_{{\text{d}}} h_{{\text{t}}} (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4} \\ \end{aligned} $$
(17)
$$ \begin{aligned} N_{{\text{j}}} & = [\gamma^{^{\prime}} h_{{\text{s}}} + \int_{{h_{{\text{s}}} }}^{{h_{{\text{f}}} }} {\gamma_{{\text{t}}} dh + \gamma_{{\text{d}}} (1 + \theta_{0} )h_{{\text{d}}} + \gamma^{^{\prime}} h_{{\text{w}}} } ]\cos \alpha \\ & = [\gamma^{^{\prime}} (h_{{\text{s}}} + h_{{\text{w}}} ) + \gamma_{{\text{d}}} (1 + \theta_{0} )(h_{{\text{t}}} + h_{{\text{d}}} ) + \gamma_{{\text{d}}} h_{{\text{t}}} (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}]\cos \alpha \\ \end{aligned} $$
(18)

As displayed in references (Tian et al. 2019; Luo et al. 2005; Huang and Yuin 2010), the seepage force of groundwater \(J_{{\text{w}}}\) can be expressed by:

$$ J_{{\text{w}}} = \gamma_{{\text{w}}} h_{{\text{w}}} \sin \alpha $$
(19)

The safety factor of the basement surface can be expressed as follows:

$$ F_{{{\text{sj}}}} = \frac{{c^{^{\prime}} l + N_{{\text{j}}} \tan \varphi^{^{\prime}} }}{{W_{{\text{j}}} \sin \alpha + J_{{\text{s}}} + J_{{\text{w}}} }} $$
(20)

Substituting Eqs. (4), (17) ~ (19) into Eqs. (20), (21) can be obtained:

$$ F_{{{\text{sj}}}} = \frac{{c^{^{\prime}} l + \left[ {\gamma^{^{\prime}} (h_{{\text{s}}} + h_{{\text{w}}} ) + \gamma_{{\text{d}}} (1 + \theta_{0} )(h_{{\text{t}}} + h_{{\text{d}}} ) + \gamma_{{\text{d}}} h_{{\text{t}}} (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]\cos \alpha \tan \varphi^{^{\prime}} }}{{\left[ {\gamma^{^{\prime}} (h_{{\text{s}}} + h_{{\text{w}}} ) + \gamma_{{\text{d}}} (1 + \theta_{0} )(h_{{\text{t}}} + h_{{\text{d}}} ) + \gamma_{{\text{d}}} h_{{\text{t}}} (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]\sin \alpha + \gamma_{{\text{w}}} h_{{\text{s}}} \sin \alpha + \gamma_{{\text{w}}} h_{{\text{w}}} \sin \alpha }} $$
(21)

where \(h_{{\text{d}}}\) is the natural layer depth, m.

By simplifying Eq. (21), Eq. (22) can be obtained:

$$ \begin{aligned} F_{{{\text{sj}}}} = & \frac{{2c^{'} }}{{\left\{ {(\gamma ^{'} {\text{ + }}\gamma _{{\text{w}}} )(h_{{\text{s}}} + h_{{\text{w}}} ) + \gamma _{{\text{d}}} h_{{\text{t}}} \left[ {\theta _{0} + 1 + (\theta _{{\text{s}}} - \theta _{0} )\frac{\pi }{4}} \right] + \gamma _{{\text{d}}} (1 + \theta _{0} )h_{{\text{d}}} } \right\}\sin 2\alpha }} \\ & + \frac{{\tan \varphi ^{'} }}{{\tan \alpha \left[ {1 + \frac{{\gamma _{{\text{w}}} }}{{\gamma ^{'} + \frac{{\gamma _{{\text{d}}} h_{{\text{t}}} }}{{h_{{\text{s}}} + h_{{\text{w}}} }}[\theta _{0} + 1 + (\theta _{{\text{s}}} - \theta _{0} )\frac{\pi }{4}] + \gamma _{{\text{d}}} (1 + \theta _{0} )\frac{{h_{{\text{d}}} }}{{h_{{\text{s}}} + h_{{\text{w}}} }}}}} \right]}} \\ \end{aligned} $$
(22)

According to Eq. (22), the safety factor in the basement surface can be divided into two terms. The first term shows that the safety factor is inversely proportional to \(h_{{\text{s}}}\),\(h_{{\text{t}}}\) and groundwater depth \(h_{{\text{w}}}\). Meanwhile, the decrease of the cohesion and the increase of seepage force caused by rainfall and groundwater also reduce the safety factor. The second term shows that the ratio of \(h_{{\text{s}}}\) to \(h_{{\text{t}}}\) and the ratio of \(h_{{\text{d}}}\) to \(h_{{\text{s}}}\) influence the safety factor of the basement. In addition, the decrease of the internal friction angle caused by rainfall and groundwater also reduces the safety factor. It is obvious that the safety factor in the basement surface can be affected by the combined action of groundwater and rainfall.

The FoS of the groundwater level surface is considered to be the safety factor for hw = 0.

$$ \begin{aligned} F_{{_{{{\text{sj}}}} }}^{'} = & \frac{{2c^{'} }}{{\left\{ {(\gamma ^{'} {\text{ + }}\gamma _{{\text{w}}} )h_{{\text{s}}} + \gamma _{{\text{d}}} h_{{\text{t}}} \left[ {\theta _{0} + 1 + (\theta _{{\text{s}}} - \theta _{0} )\frac{\pi }{4}} \right] + \gamma _{{\text{d}}} (1 + \theta _{0} )h_{{\text{d}}} } \right\}\sin 2\alpha }} \\ & + \frac{{\tan \varphi ^{'} }}{{\tan \alpha \left[ {1 + \frac{{\gamma _{{\text{w}}} }}{{\gamma ^{'} + \frac{{\gamma _{{\text{d}}} h_{{\text{t}}} }}{{h_{{\text{s}}} }}\left[ {\theta _{0} + 1 + (\theta _{{\text{s}}} - \theta _{0} )\frac{\pi }{4}} \right] + \gamma _{{\text{d}}} (1 + \theta _{0} )\frac{{h_{{\text{d}}} }}{{h_{{\text{s}}} }}}}} \right]}} \\ \end{aligned} $$
(23)

We can obtain,

$$ F_{{{\text{sj}}}} \le F_{{_{{{\text{sj}}}} }}^{^{\prime}} $$
(24)

Combining Eqs. (7), (16), (22) and (24), the safety factor of the slope can be expressed by:

$$ F_{{\text{s}}} = \min \{ F_{{{\text{ss}}}} ,F_{{{\text{sf}}}} ,F_{{{\text{sj}}}} \} $$
(25)

Equation (25) shows that the instability of sliding band is mainly induced by rainfall if the safety factor of the saturated surface caused by rainfall or the wetting front is the smallest. When the safety factor in the basement surface is the smallest, the instability of the sliding band is mainly induced by groundwater.

4 Parametric study

The safety factor functions in the saturated layer surface, wetting front and basement surface are used to analyze the influence mechanism of the parameters including the rainfall and groundwater on the slope instability. In this section, the dump slope of the Shengli open-pit coalmine is employed for the case study in this section. The parameters of the dump slope by tests are as follows: \(\gamma_{{\text{d}}}\) = 18 kPa, \(\gamma^{^{\prime}}\) = 10 kPa, \(\gamma_{{\text{w}}}\) = 9.8 kPa, c = 20 kPa,\(c^{^{\prime}}\) = 13 kPa, \(\theta_{0}\) = 0.13,\(\theta_{{\text{r}}}\) = 0.08, \(\theta_{{\text{s}}}\) = 0.45, \(\varphi\) = 34°, \(\varphi^{^{\prime}}\) = 30° and \(\alpha\) = 30°. Parameter variations in rainfall and groundwater are in the following sections, such as hf, hw, hd and λ. The parameter analysis is carried out in the disscuss below.

4.1 Rainfall and groundwater

In the process of actual rainfall, the saturated layer depth and transitional layer depth do not change independently, but demonstrate a certain proportional relationship affected by rainfall intensity and time. The proportion (\(\lambda\)) of \(h_{{\text{s}}}\) to \(h_{{\text{f}}}\) is expressed as follows:

$$ \lambda { = }\frac{{h_{{\text{s}}} }}{{h_{{\text{f}}} }} $$
(26)

Equations (7), (16), and (22) can be expressed by:

$$ F_{{{\text{ss}}}} = \frac{{\tan \varphi^{^{\prime}} }}{{\tan \alpha (1 + \frac{{\gamma_{{\text{w}}} }}{{\gamma^{^{\prime}} }})}} + \frac{{2c^{^{\prime}} }}{{\lambda h_{{\text{f}}} (\gamma^{^{\prime}} + \gamma_{{\text{w}}} )\sin 2\alpha }} $$
(27)
$$ \begin{aligned} F_{{{\text{sf}}}} = & \frac{{2c^{^{\prime}} }}{{\lambda h_{{\text{f}}} (\gamma^{^{\prime}} + \gamma_{{\text{w}}} ) + \gamma_{{\text{d}}} (1 - \lambda )h_{{\text{f}}} \left[ {1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]\sin 2\alpha }} + \frac{{\tan \varphi^{^{\prime}} }}{{\tan \alpha + \frac{{\gamma_{{\text{w}}} \tan \alpha }}{{\{ \gamma^{^{\prime}} + \gamma_{{\text{d}}} \frac{1 - \lambda }{\lambda }\left[ {1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]}}}} \\ & - \frac{{2\gamma_{{\text{w}}} \frac{{\theta_{0} - \theta_{{\text{r}}} }}{{\theta_{s} - \theta_{{\text{r}}} }}\tan \varphi^{^{\prime}} }}{{(\gamma^{^{\prime}} + \gamma_{{\text{w}}} )\frac{\lambda }{1 - \lambda } + \gamma_{{\text{d}}} \left[ {1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]\sin 2\alpha }} \\ \end{aligned} $$
(28)
$$ \begin{aligned} F_{{{\text{sj}}}} = & \frac{{2c^{'} }}{{(\lambda h_{{\text{f}}} + h_{{\text{w}}} )(\gamma ^{'} \sin 2\alpha + 2\gamma _{{\text{w}}} \sin \alpha ) + \left\{ {\gamma _{{\text{d}}} (1 - \lambda )h_{{\text{f}}} \left[ {\theta _{0} + 1 + (\theta _{{\text{s}}} - \theta _{0} )\frac{\pi }{4}} \right] + \gamma _{{\text{d}}} (1 + \theta _{0} )h_{{\text{d}}} } \right\}\sin 2\alpha }} \\ & + \frac{{\tan \varphi ^{'} }}{{\tan \alpha + \frac{{\tan \alpha }}{{\cos \alpha }}\frac{{\gamma _{{\text{w}}} }}{{\gamma ^{'} + \frac{{\gamma _{d} (1 - \lambda )}}{{\lambda + \frac{{h_{{\text{w}}} }}{{h_{{\text{f}}} }}}}\left[ {\theta _{0} + 1 + (\theta _{{\text{s}}} - \theta _{0} )\frac{\pi }{4}} \right] + \gamma _{{\text{d}}} (1 + \theta _{0} )\frac{{h_{{\text{d}}} }}{{\lambda h_{{\text{f}}} + h_{{\text{w}}} }}}}}} \\ \end{aligned} $$
(29)

Equations (27)–(29) show that the safety factors in the saturated layer surface, wetting front and basement surface are related to \(\lambda\) and the depth (\(h_{{\text{f}}}\)). The changes of safety factor with \(\lambda\) and \(h_{{\text{f}}}\) are shown in Figs.9 and 10, respectively.

Fig. 9
figure 9

Safety factor versus \(\lambda\) when hw = 1 m and hf = 6 m

Full size image
Fig. 10
figure 10

Safety factor versus hf when λ = 0.5 and hw = 1 m

Full size image

Figure 9 shows that the safety factor decreases with increasing ratio (\(\lambda\)). Meanwhile, increasing the wetting front depth (\(h_{{\text{f}}}\)) can also cause the safety factor to decrease as shown in Fig. 10. The influence degrees of \(\lambda\) or \(h_{{\text{f}}}\) on the safety factors on the surface of the saturated layer, the wetting front and basement surface decrease in turn. The change rate of the safety factor in the surface of the saturated layer (\(\lambda\) < 0.1) is much higher than that when \(\lambda\) > 0.1. It shows that the transition zone depth caused by rainfall has great influence on the slope safety factor. Meanwhile, λ = 0.5 is the critical turning point where the primary factor inducing slope instability changes from the groundwater to the rainfall for hw = 1 m and hf = 6 m. The change rates of safety factors in the surface of the saturated layer and wetting front when \(h_{{\text{f}}}\) < 2 m are much higher than those when \(h_{{\text{f}}}\) > 2 m. hf = 6 m is the critical turning point where the primary factor inducing slope instability changes from the groundwater to the rainfall for λ = 0.5 and hw = 1 m. When the groundwater level is unchanged, the main influencing factor of slope stability changes from groundwater to rainfall with the continuous rainfall.

4.2 Depth of natural layer

According to the analysis above, the safety factor of the basement surface in the initial rainfall stage is lower than that in the upper layer affected by rainfall. With the increase of rainfall intensity and rainfall time, the wetting front depth increases. Under the combined action of strength reduction and seepage force, the FoS of different layers continuously decrease. Meanwhile, with increasing groundwater depth, the natural layer depth (\(h_{{\text{d}}}\)) between the wetting front and groundwater level gradually decreases. Thus, it is necessary to analyze the influence of the natural layer on slope stability. \(H\) is the depth from the slope top to the basement floor, m.

The wetting front depth can be expressed by:

$$ h_{{\text{f}}} = H - h_{{\text{d}}} - h_{{\text{w}}} $$
(30)

Substituting Eq. (30) into Eqs. (27), (28) and (29), Eq. (31) can be obtained:

$$ F_{{{\text{ss}}}} = \frac{{\tan \varphi^{^{\prime}} }}{{\tan \alpha (1 + \frac{{\gamma_{{\text{w}}} }}{{\gamma^{^{\prime}} }})}} + \frac{{2c^{^{\prime}} }}{{\lambda (H - h_{{\text{d}}} - h_{{\text{w}}} )(\gamma^{^{\prime}} + \gamma_{{\text{w}}} )\sin 2\alpha }} $$
(31)
$$ \begin{gathered} F_{{{\text{sf}}}} = \frac{{2c^{^{\prime}} }}{{\lambda (H - h_{{\text{d}}} - h_{{\text{w}}} )(\gamma^{^{\prime}} + \gamma_{w} ) + \gamma_{{\text{d}}} (1 - \lambda )(H - h_{{\text{d}}} - h_{{\text{w}}} )\left[ {1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]\sin 2\alpha }} \\ + \frac{{\tan \varphi^{^{\prime}} }}{{\tan \alpha + \frac{{\gamma_{{\text{w}}} \tan \alpha }}{{\{ \gamma^{^{\prime}} + \gamma_{{\text{d}}} \frac{1 - \lambda }{\lambda }\left[ {1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]}}}} - \frac{{2\gamma_{{\text{w}}} \frac{{\theta_{0} - \theta_{{\text{r}}} }}{{\theta_{{\text{s}}} - \theta_{{\text{r}}} }}\tan \varphi^{^{\prime}} }}{{\left\{ {(\gamma^{^{\prime}} + \gamma_{{\text{w}}} )\frac{\lambda }{1 - \lambda } + \gamma_{{\text{d}}} \left[ {1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]} \right\}\sin 2\alpha }} \\ \end{gathered} $$
(32)
$$ \begin{aligned} F_{{{\text{sj}}}} & = \frac{{2c^{^{\prime}} }}{{\left\{ {[\lambda (H - h_{{\text{d}}} - h_{{\text{w}}} ) + h_{{\text{w}}} ](\gamma^{^{\prime}} + \gamma_{{\text{w}}} ) + \gamma_{{\text{d}}} (1 - \lambda )(H - h_{{\text{d}}} - h_{{\text{w}}} )\left[ {\theta_{0} + 1 + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right] + \gamma_{{\text{d}}} (1 + \theta_{0} )h_{{\text{d}}} } \right\}\sin 2\alpha }} \\ & + \frac{{\tan \varphi^{^{\prime}} }}{{\tan \alpha + \frac{{\gamma_{{\text{w}}} \tan \alpha }}{{\gamma^{^{\prime}} + \frac{(1 - \lambda )}{{\lambda + \frac{{h_{{\text{w}}} }}{{H - h_{{\text{d}}} - h_{{\text{w}}} }}}}\left[ {\theta_{0} + 1 + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right] + \gamma_{{\text{d}}} (1 + \theta_{0} )\frac{{h_{{\text{d}}} }}{{\lambda (H - h_{d} - h_{{\text{w}}} ) + h_{{\text{w}}} }}}}}} \\ \end{aligned} $$
(33)

According to Eqs. (31)–(33), the variation of the safety factor with the natural layer depth can be obtained as shown in Fig. 11.

Fig.11
figure 11

Safety factor versus hd when \(\lambda\) = 0.5 and \(h_{w}\) = 5 m

Full size image

Figure 11 shows that both the safety factor and changing rate increase with increasing natural layer depth (\(h_{{\text{d}}}\)). When the groundwater level remains unchanged, the safety factor curves in the saturated layer, wetting front and basement surface gradually intersect, then deviate from each other with the increase of natural layer depth. hd = 15 m is the critical turning point where the primary factor inducing slope instability changes from rainfall to groundwater for λ = 0.5 and hw = 5 m. The above analysis shows that with the increase of rainfall, the main factors affecting the FoS of slope change from the groundwater to the rainfall.

4.3 Critical depths

Based on the above parameters analysis, the primary factors inducing slope instability can change with the changes of \(\lambda\),\(h_{{\text{s}}}\),\(h_{{\text{t}}}\),\(h_{{\text{f}}}\) and \(h_{{\text{w}}}\). There exist the critical depths of groundwater and wetting front that can result in the change of primary factors. Therefore, it is necessary to analyze the critical wetting front depth and critical groundwater depth. The safety factor in the saturated layer is considered as a special case of the safety factor of the wetting front when \(\lambda\) = 1. Thus, a comparative analysis of the safety factors in the wetting front and basement surface are carried out in this section.

4.3.1 Critical depth of wetting front

The groundwater depth will not change in the process of rainfall infiltration. At the beginning of rainfall, the safety factor induced by groundwater is smaller than that caused by rainfall, and groundwater becomes the primary factor threatening slope stability. With increasing rainfall time, the wetting front gradually moves down, and the wetting front depth increases. The safety factor in the wetting front induced by rainfall is equal to the safety factor of the basement surface induced by groundwater. When the wetting front depth reaches the critical value, rainfall will be the primary factor inducing slope instability.

When the depth from the bedrock floor to the top of the slope and the groundwater depth remain unchanged, the natural layer depth can be expressed as follows:

$$ h_{{\text{d}}} = H - h_{{\text{w}}} - h_{{\text{f}}} $$
(34)

Substituting Eq. (32) into Eqs. (30) and (31), Eqs. (33) and (34) can be obtained:

$$ \begin{aligned} F_{{{\text{sf}}}} = \, & \frac{{2c^{^{\prime}} }}{{\left\{ {\lambda h_{{\text{f}}} (\gamma^{^{\prime}} + \gamma_{{\text{w}}} ) + \gamma_{{\text{d}}} (1 - \lambda )h_{{\text{f}}} \left[ {1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]} \right\}\sin 2\alpha }} \\ & + \frac{{\tan \varphi^{^{\prime}} }}{{\tan \alpha + \frac{{\gamma_{{\text{w}}} \tan \alpha }}{{\{ \gamma^{^{\prime}} + \gamma_{{\text{d}}} \frac{1 - \lambda }{\lambda }\left[ {1 + \theta_{0} + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right]}}}} - \frac{{2\gamma_{{\text{w}}} \frac{{\theta_{0} - \theta_{{\text{r}}} }}{{\theta_{{\text{s}}} - \theta_{{\text{r}}} }}\tan \varphi^{^{\prime}} }}{{\left\{ {(\gamma^{^{\prime}} + \gamma_{{\text{w}}} )\frac{\lambda }{1 - \lambda } + \gamma_{{\text{d}}} \left[ {1 + \theta_{0} + (\theta_{s} - \theta_{0} )\frac{\pi }{4}} \right]} \right\}\sin 2\alpha }} \\ \end{aligned} $$
(35)
$$ \begin{aligned} F_{{{\text{sj}}}} = & \frac{{2c^{^{\prime}} }}{{\left\{ {(\lambda h_{{\text{f}}} + h_{{\text{w}}} )(\gamma^{^{\prime}} + \gamma_{{\text{w}}} ) + \{ \gamma_{{\text{d}}} (1 - \lambda )h_{{\text{f}}} \left[ {\theta_{0} + 1 + (\theta_{s} - \theta_{0} )\frac{\pi }{4}} \right] + \gamma_{{\text{d}}} (1 + \theta_{0} )(H - h_{{\text{w}}} - h_{{\text{f}}} )} \right\}\sin 2\alpha }} \\ & + \frac{{\tan \varphi^{^{\prime}} }}{{\tan \alpha + \frac{{\gamma_{{\text{w}}} \tan \alpha }}{{\gamma^{^{\prime}} + \frac{{\gamma_{{\text{d}}} (1 - \lambda )}}{{\lambda + \frac{{h_{{\text{w}}} }}{{h_{{\text{f}}} }}}}\left[ {\theta_{0} + 1 + (\theta_{{\text{s}}} - \theta_{0} )\frac{\pi }{4}} \right] + \gamma_{{\text{d}}} (1 + \theta_{0} )\frac{{H - h_{{\text{w}}} - h_{{\text{f}}} }}{{\lambda h_{{\text{f}}} + h_{w} }}}}}} \\ \end{aligned} $$
(36)

The critical wetting front depth can be set to hfo and obtained from Eq. (35),

$$ F_{{{\text{sf}}}} = F_{{{\text{sj}}}} $$
(37)

Taking the dump slope in the Shengli open-pit coalmine as a case study, the variation curves of the critical wetting front depth (\(h_{{{\text{fo}}}}\)) and critical safety factor (\(F_{{{\text{so}}}}\)) are shown in Figs.12, 13, 14 and 15.

Fig.12
figure 12

Critical wetting front depth hfo versus groundwater depth \(h_{{\text{w}}}\)

Full size image
Fig.13
figure 13

Critical wetting front depth hfo versus ratio λ

Full size image
Fig.14
figure 14

Critical safety factor \(F_{{{\text{so}}}}\) versus \(h_{{\text{w}}}\)

Full size image
Fig.15
figure 15

Critical safety factor Fso versus λ

Full size image

Figures 13, 14 and 15 show that the critical wetting front depth (hfo) showed an increasing trend with the increase of groundwater level (hw), and the increasing rate gradually increased. While, with the increase of λ, the critical wetting front depth (hfo) showed a decreasing trend, and the decreasing rate gradually decreased. This is because, the FoS of slope decreases with the increase of groundwater level, and the greater wetting front depth is required to achieve the same safety factor. Similarly, the increase of λ will also reduces the FoS of slope, and a smaller wetting front depth is required to achieve the same safety factor. When λ is smaller and hw is larger, there is no critical depth of wetting front. Because the FoS of slope is smaller due to the influence of groundwater, and the critical safety factor of slope cannot be reached by the influence of rainfall.

4.3.2 Critical depth of groundwater

Without groundwater, for the slope affected by rainfall, the safety factor in the wetting front caused by upper rainfall is smaller than that induced by groundwater, and rainfall becomes the primary factor threatening slope stability. With increasing groundwater depth, the safety factor in the basement surface induced by the groundwater is equal to the safety factor in the wetting front caused by rainfall. When the groundwater depth reaches the critical value, groundwater will be the primary factor inducing slope instability.

Similarly, the critical groundwater depth can be obtained by Eq. (35), which is set to \(h_{{{\text{wo}}}}\). Taking the dump slope in the Shengli open-pit coalmine as a case, the variation curves of critical groundwater depth (\(h_{{{\text{wo}}}}\))and critical safety factor (\(F_{{{\text{so}}}}\))with the change of \(\lambda\) and \(h_{{\text{f}}}\) are shown in Figs.16, 17, 18 and 19.

Fig.16
figure 16

Critical groundwater depth \(h_{{{\text{wo}}}}\) versus wetting front depth \(h_{{\text{f}}}\)

Full size image
Fig.17
figure 17

Critical groundwater depth \(h_{{{\text{wo}}}}\) versus ratio \(\lambda\)

Full size image
Fig.18
figure 18

Critical safety factor \(F_{{{\text{so}}}}\) versus the wetting front depth \(h_{{\text{f}}}\)

Full size image
Fig.19
figure 19

Critical safety factor \(F_{{{\text{so}}}}\) versus the ratio \(\lambda\)

Full size image

Figures 16, 17, 18 and19 show that the critical groundwater depth (hwo) increases, and the change rate decreases with increasing wetting front depth (hf). In addition, the critical groundwater depth (hwo) also increases with increasing ratio (λ). This is because with increases in wetting front depth, the safety factor will decrease, and the groundwater depth required to reach the same safety factor will increase. Similarly, an increase of λ can also reduce the safety factor of the slope, and the groundwater depth required to reach the same safety factor decreases. The corresponding critical safety factor decreases with increasing wetting front depth. When the ratio (λ) of saturation layer by rainfall and the wetting front depth is larger, there is no critical groundwater depth because the actual safety factor of groundwater cannot be equal to the safety factor in the basement surface.

According to the above analysis, the safety factor changes inversely with the increase of the wetting front depth (hf) and groundwater level (hw). The influence of the ratio coefficient (λ) and the wetting front depth on the safety factors decrease successively in rainfall saturated surface, wetting front and basement surface. The primary factors inducing slope instability change with the variation of groundwater and rainfall parameters. For the inner dump in open-pit mine, we suggest that monitoring the change of groundwater level and rainfall parameters should be appreciated. Critical rainfall parameters and groundwater levels are particularly concerned. The stability of slope is evaluated according to the change of groundwater level and rainfall parameters, and measures are taken in advance to reduce the loss caused by landslide disasters.

5 Verification and application

The inner dump slope in the Shengli open-pit coal-mine was also used to verify the correctness of the above theory. The north end slope displacement was monitored by radar and the FoS in the north end slope was calculated in FLAC-3D software (Liu and Han 2005) to compare with the predictions of the model proposed in this paper for different rainfall parameters and groundwater levels in June 2014. The slope models in FLAC3D was built by directly mapping the slope shown in Fig. 20. The extensions of the slope are 1200 m in x- direction and 200 m in z- direction. Roller boundary condition is enforced at the bottom and lateral boundaries of the model. The calculation and monitoring results are shown in Figs. 21 and 22.

Fig. 20
figure 20

The inner dump slope built in FLAC3D

Full size image
Fig. 21
figure 21

Safety factor during continuous rainfall in June, 2014

Full size image
Fig. 22
figure 22

Displacement variation by radar monitoring during continuous rainfall in June, 2014

Full size image

Figures 21 and 22 showed that the safety factor began to decline during continuous rainfall on June 16 in June 2014. Due to the continuous rainfall and a large number of cracks at the top of the slope, the rainfall accumulates within the slope and the groundwater level showed an upward trend. As a result, continuous rainfall replenished groundwater after June 16. On June 21, the safety factor was approximately 1, and the early warning should be put forward based on the theoretical analysis results. The safety factor was less than 1 and slope failure occurred on June 25. The radar monitoring results showed that the increase rate of displacement was larger after June 16. And the increase rate of displacement is more obvious. Meanwhile, a slope warning appeared and then local slope failure occured. The radar monitoring results were consistent with the results by theoretical and numerical calculation results, which verified the rationality of the model proposed in this paper.

It should be noted that, the model proposed in this paper were used to calculate the FoS and forecast slope stability in this open-pit coal-mine for various rainfall conditions and groundwater elevations in recent years. No landslide disasters occurred in innenr dump of the Shengli open-pit mine. Meanwhile, the observations and monitoring data in the field have been consistent with the predictions of the results of the proposed model in this paper.

The research results are used for the geometry of the existing open-pit dump slope. The calculation result of FoS can be given quantitatively by Eqs. (7), (16) (22) and (23) for different rainfall and groundwater parameters. The primary factors inducing slope instability can be determined by Eq. (23) and the critical parameters can be obtained by Eqs. (7), (16), (22) and (23). Then the stability of the dump slope in the open-pit can be evaluated and preventive measures in advance can be taken to reduce the loss of landslide disaster.

For other slope geometry, with the changing parameters of geometry, the FoS can be calculated and the slope stability can be predicted by the analytical solution of FoS in this paper.

6 Conclusions

To investigate the slope stablity problem affected by the combined action of rainfall infiltration and groundwater, a stratified model of slope affected by rainfall and groundwater is established, and the safety factor functions of different layers are solved. The dump slope in Shengli open-pit coalmine affected by the combined action of rainfall and groundwater is taken as a case, and parametric analysis was carried out to study the instability mechanism of slopes affected by rainfall and groundwater. Important conclusions from this study can be summarized as follows:

  1. 1.

    A stratified model of slopes affected by rainfall and groundwater is established and the theoretical solution of FoS is developed to accommodate the influence of water seepage and the strength reduction of soil caused by water migration on the stability of the dump slope. The correlation characteristics were explored between the mechanical properties and stability of the dump slope and under the coupling action of groundwater and rainfall. The FoS in the saturated layer surface is inversely proportional to e saturated layer depth (\(h_{{\text{s}}}\)) and is affected by rainfall. The FoS in the wetting front is inversely proportional to the saturated layer depth (\(h_{{\text{s}}}\)) and the transition layer depth (\(h_{{\text{t}}}\)). The FoS in the basement surface is affected by the combined action of groundwater and rainfall.

  2. 2.

    The primary factors of inducing slope instability vary with groundwater and rainfall parameters. There exists the critical wetting front and the critical groundwater depth, where the primary inducing factors change. The critical rainfall expression and groundwater expression of the main factors inducing slope instability are determined. The critical wetting front depth increases with the increasing groundwater depth, and the increasing rate gradually increases. As the ratio (\(\lambda\)) increases, the critical wetting front depth decreases, and the decreasing rate continuously reduces. The corresponding critical safety factor decreases with increasing groundwater depth.

  3. 3.

    The critical groundwater depth is affected by rainfall parameters. It increases with the increase of the wetting front depth and ratio (\(\lambda\)), and the increase rate gradually decreases. The corresponding critical safety factor decreases with increasing wetting front depth. When the ratio (\(\lambda\)) and the initial wetting front depth (hf) are larger, there is no critical groundwater depth.

  4. 4.

    The results of this study were applied to a case study in the Shengli open-pit mine. The reliability and accuracy of the proposed mechanical model and theoretical solution were validated by field test data. The application value is that, for the geometry of the existing open-pit dump slope, the change result of FoS can be given quantitatively by the theoretical results according to the rainfall parameters and groundwater hydrological changes.