Introduction

Landslides are the most widespread and serious type of geohazards around the world and are usually associated with rainfall, earthquake, and anthropogenic activities (Keefer et al. 1987; Budimri et al. 2014; Li et al. 2015; Zhang et al. 2018). Research shows that more than 90% of landslides are associated with rainfall (Nilsen 1975; Yu et al. 2014), and thus, rainfall is of great importance to slope stability (Muntohar and Jiao 2010; Li et al. 2011; Saito et al. 2014; Cui et al. 2017b; Kumar et al. 2017). As rainfall infiltration is a persistent process and may last over a wide range of time scales, slope failure may not occur immediately once rainfall starts. Instead, slope failure usually occurs sometime later during the continued rainfall or after rainfall stops. Therefore, studies on the time-dependent slope stability associated with rainfall have gained great attention (Oh and Lu 2015; Sun et al. 2015; Wang et al. 2017; Wu et al. 2017a, b).

During the rainfall infiltration process, there will be an increase in water content and unit weight of soils, which will result in an increase of driving force. On the other hand, the shear strength of soils will decrease, which will weaken the resistance. Therefore, simulating rainfall infiltration into slopes is an important prerequisite to analyze the slope stability associated with rainfall. Analytical approaches, numerical simulation, and model tests are widely used to examine the rainfall infiltration process into slopes. Among these approaches, numerical models usually require a great deal of parameters, which are not always available, and numerical models are sometimes computationally expensive and require considerable preparations before execution (Montrasio and Valentino 2008; Le et al. 2015; Cho 2016; Cui et al. 2017a). Physical model tests also require strict slope models, rainfall conditions, and other monitoring equipment (Huang et al. 2008; Li et al. 2016; Chen et al. 2017). However, analytical approaches, especially the Green-Ampt (GA) model, can provide a quick and straightforward assessment compared to other methods.

The GA model was originally proposed for analysis of the infiltration process on a level ground under ponded water (Green and Ampt 1911) and is also the most widely accepted theory in the analysis of rainfall infiltration into soils (Jia et al. 2015; Liu et al. 2008; Ma et al. 2011). In the GA model, soil above the wetting front is assumed to be fully saturated. However, laboratory and field evidence shows that the water content of soils often exhibits stratified characteristics after infiltration, and thus, some qualitative partitioning and quantitative empirical functions have been developed to depict the actual moisture characteristics of soil above the wetting front (Bodman and Colman 1944; Wang et al. 2003; Chae and Kim 2012; Peng et al. 2012; Mao et al. 2016; Yu and Douglas 2015).

During the infiltration of intense rainfall (or rainstorm) into soil, the infiltration capacity of soil is very great (often assumed to be infinite) at the beginning of rainfall, and all rainwater is absorbed by the soil. Thus during this period, the infiltration rate is equal to the rainfall intensity and will decrease rapidly to the infiltration capacity of the soil once the wetting front forms and the surface soil becomes wet (Gasmo et al. 2000; Zhang et al. 2016a). However, this phenomenon is sometimes ignored when analyzing the rainfall infiltration process into slopes using the GA model (Gavin and Xue 2008; Zhang et al. 2014a, b). In addition, different from infinite slope models (with shallow slope failure) often used to study the influence of rainfall infiltration on slope stability (Kong et al. 2014; Zhang et al. 2014c; Jia et al. 2015), natural slopes mostly show irregular ground surface shapes, and deep slope failures or landslides with irregular sliding surface shapes may also occur (Zhang et al. 2016b). Thus, intense rainfall induced degradation of natural slope stability requires further study.

In this study, a modified GA model, known as the stratified Green-Ampt (SGA) model is proposed, which considers both stratified soil water content above the wetting front and the intense rainfall process into soil. This model is combined with the limit equilibrium method (including the residual thrust method) to estimate the time-dependent stability of slopes during intense rainfall. Firstly, the conventional GA model and concept of stratified soil water content associated with rainfall infiltration are presented. Secondly, the new approach for estimating time-dependent stability of slopes during intense rainfall is proposed. Thereafter, applications including an infinite slope and a finite slope (Majiagou landslide) are illustrated to study the time-dependent slope stability during intense rainfall. Finally, discussions on the rainfall infiltration process and stability of slopes are presented, which are followed by the conclusions of this study.

Theoretical background

GA model

The GA model was proposed by Green and Ampt (1911) to analyze the one-dimensional (1D) vertical infiltration process of thin-layer ponded water into a homogeneous soil with a uniform water content based on Darcy’s Law, which is shown in Fig. 1a. In the context of the GA model, the wetting front is assumed to be a sharp interface during the infiltration, the soil above is fully saturated, while the soil below is in a natural state. The infiltration equation of the GA model is as follows (Green and Ampt 1911):

$$ i={K}_s\frac{h_f+{\psi}_f+H}{h_f} $$
(1)

where i denotes the infiltration rate (m/s), Ks denotes the saturated permeability coefficient or hydraulic conductivity (m/s), hf denotes the depth of the wetting front (m), ψf denotes the suction head at the wetting front (m), and H denotes the thickness of the pounding water layer (m). Because of the simplicity of the GA model, it has been widely used in many research fields such as irrigation, environmental pollution, and natural hazard assessment, etc.

Fig. 1
figure 1

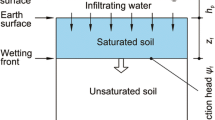
Diagram of rainfall infiltrating into soil. a Infiltration estimated by the GA model (Gavin and Xue 2008). b Layered sketch of soil during infiltration

Full size image

Stratified soil water content above the wetting front

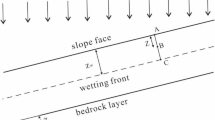
In the GA model, the soil above the wetting front is assumed to be fully saturated. However, in most cases, stratified soil water content is observed, which can be divided into at least three layers, including a saturated layer, a transitional layer, and a natural layer, as shown in Fig. 1b (Bodman and Colman 1945). Experiments and theoretical analyses indicate that the thickness of the saturated layer is approximately half of the depth of the wetting front (Fig. 2) (Wang et al. 2002, 2003; Zhang et al. 2014a). Therefore, the thickness of the saturated zone can be expressed as follows:

$$ {h}_s=\frac{h_f}{2} $$
(2)
Fig. 2
figure 2

Distribution of water content of soil with water infiltration

Full size image

Furthermore, as proposed by Wang et al. (2002, 2003), and validated by Peng et al. (2012) and Zhang et al. (2014a, b), the soil water content in the transitional layer varies with depth as an ellipse function. Therefore, the distribution of the soil water content under infiltration (see Fig. 2) will assume the following function:

$$ \theta (h)=\Big\{{\displaystyle \begin{array}{l}{\theta}_s,0\le h\le {h}_s\\ {}{\theta}_i+\left({\theta}_s-{\theta}_i\right)\sqrt{1-{\left(\frac{h-{h}_s}{h_s}\right)}^2},{h}_s\le h\le {h}_f\\ {}{\theta}_i,h\ge {h}_f\end{array}} $$
(3)

where θi and θs are the initial and saturated water content, respectively, and h is the depth. Therefore, the unit weight of soil in the transitional layer can be expressed as follows:

$$ \gamma (h)=\left(1+\theta \right){\gamma}_d=\left[1+{\theta}_i+\left({\theta}_s-{\theta}_i\right)\sqrt{1-{\left(\frac{h-{h}_s}{h_s}\right)}^2}\right]{\gamma}_d $$
(4)

where γd denotes the dry unit weight of the soil (N/m3).

Methodology

Infiltration process of intense rainfall into slopes based on the SGA model

For a slope with an inclined ground surface (Fig. 3), based on the GA model, the infiltration rate can be expressed as follows (Chen and Young 2006):

$$ i={K}_s\frac{Z_f{\cos}^2\beta +{\psi}_f}{Z_f\cos \beta } $$
(5)

where Zf denotes the vertical depth of the wetting front (m) and β denotes the dip angle of the ground surface (°).

Fig. 3
figure 3

Infiltration process into a slope during intense rainfall

Full size image

At the initial stage of infiltration, with the infiltration capacity greater than the rainfall intensity, rainfall completely infiltrates into soil. During this period, the shallow soil is unsaturated, and the infiltration rate (m/s) is equal to the rain intensity (Gasmo et al. 2000; Wang et al. 2017; Zhang et al. 2016a), which can be expressed as follows:

$$ i=q\cos \beta $$
(6)

where q denotes the rainfall intensity (m/s). During a prolonged infiltration event, when the shallow unsaturated soil eventually becomes saturated and the wetting front forms, the so-called critical time arrives. Therefore, by combining Eqs. (5) and (6), the vertical depth of the wetting front at the critical time, Zc, can be obtained as follows:

$$ {Z}_c=\frac{\psi_f}{\left(q/{K}_s-1\right){\cos}^2\beta } $$
(7)

Based on Eqs. (2) and (3) as well as the mass conservation law, the cumulative rainfall infiltration (m), I, can be written as follows:

$$ {\displaystyle \begin{array}{l}I=\left({\theta}_s-{\theta}_i\right){Z}_s\cos \beta +\underset{Z_s}{\overset{Z_f}{\int }}\left(\theta -{\theta}_i\right)\cos \beta dz\\ {}\kern0.5em =\left({\theta}_s-{\theta}_i\right){Z}_s\cos \beta +\underset{Z_s}{\overset{Z_f}{\int }}\left({\theta}_s-{\theta}_i\right)\cos \beta \sqrt{1-{\left(\frac{z-{Z}_s}{Z_s}\right)}^2} dz\\ {}\kern0.75em =\frac{4+\pi }{8}\left({\theta}_s-{\theta}_i\right)\cos \beta {Z}_f\end{array}} $$
(8)

The cumulative rainfall infiltration at the critical time Ic is as follows:

$$ {I}_c=\frac{4+\pi }{8}\left({\theta}_s-{\theta}_i\right)\cos \beta {Z}_c=\frac{4+\pi }{8}\left({\theta}_s-{\theta}_i\right)\frac{\psi_f}{\left(q/{K}_s-1\right)\cos \beta } $$
(9)

The critical time tc is as follows:

$$ {t}_c=\frac{I_c}{i}=\frac{4+\pi }{8}\left({\theta}_s-{\theta}_i\right)\frac{\psi_f}{q\left(q/{K}_s-1\right){\cos}^2\beta } $$
(10)

The infiltration rate can be expressed as the derivative of the cumulative rainfall infiltration (as expressed in Eq. 8), which is:

$$ i=\frac{dI}{dt}=\frac{4+\pi }{8}\left({\theta}_s-{\theta}_i\right)\cos \beta \frac{d{Z}_f}{dt} $$
(11)

During the initial infiltration stage, the moving speed of the wetting front (m/s),v1, can be obtained by Eqs. (6) and (11):

$$ {v}_1=\frac{d{Z}_f}{dt}=\frac{8q}{\left(4+\pi \right)\left({\theta}_s-{\theta}_i\right)} $$
(12)

Considering Zf = 0 at t = 0, the wetting front depth during the initial infiltration stage before the critical time can be calculated as follows:

$$ {Z}_f=\frac{8q}{\left(4+\pi \right)\left({\theta}_s-{\theta}_i\right)}t,0\le t\le {t}_c $$
(13)

During the steady infiltration stage after the critical time, the moving speed of the wetting front (m/s),v2, can be determined based on Eqs. (5) and (11):

$$ {v}_2=\frac{d{Z}_f}{dt}=\frac{8{K}_s}{4+\pi}\frac{Z_f{\cos}^2\beta +{\psi}_f}{\left({\theta}_s-{\theta}_i\right){Z}_f{\cos}^2\beta } $$
(14)

Integrating Eq. (14) with respect to time under the initial condition where Zf = Zc when t = tc yields the following:

$$ t-{t}_c=a\left({Z}_f-{Z}_c\right)+\frac{a{\psi}_f}{\cos^2\beta}\ln \frac{\psi_f+{Z}_c{\cos}^2\beta }{\psi_f+{Z}_f{\cos}^2\beta },\kern0.5em a=\frac{\left(4+\pi \right)\left({\theta}_s-{\theta}_i\right)}{8{K}_s},t\ge {t}_c $$
(15)

Therefore, the SGA model based on the stratified soil water content above the wetting front is established and can be applied to analyze the infiltration process of intense rainfall into slopes.

New approaches for estimating the time-dependent stability of slopes during intense rainfall

A new approach for estimating the time-dependent stability of an infinite slope

Slope failure induced by rainfall is usually categorized as a shallow failure, and the slip surface is parallel to the slope surface (Cho 2009; Gavin and Xue 2008). Thus, infinite slope models are typically used when studying slope stability during rainfall. Here, an infinite slope model is used to evaluate the time-dependent stability of a slope during intense rainfall, which is shown in Fig. 4a. Zb is the depth of the bedrock (m).

Fig. 4
figure 4

Slope models during intense rainfall. a An infinite slope model during intense rainfall. b A finite slope model during intense rainfall

Full size image

Based on the concept model in Fig. 1b, the soil gravity above the slip surface (kPa), G, can be written as follows:

$$ G={G}_s+{G}_t+{G}_n $$
(16)

where Gs, Gt and Gn represent the gravity of saturated, transitional, and natural layers (kPa), respectively. With the slip surface of the slope set to be parallel to the slope surface, the soil gravity above the bedrock along a unit length perpendicular to the slope profile can be calculated based on Eq. (8), and can be expressed as follows:

$$ {\displaystyle \begin{array}{l}G={G}_s+{G}_t+{G}_n\\ {}\kern1em =\frac{\gamma_d\left(1+{\theta}_s\right){Z}_f\cos \beta }{2}+\cos \beta {\gamma}_d{\int}_{Z_s}^{Z_f}\left[1+{\theta}_i+\left({\theta}_s-{\theta}_i\right)\sqrt{1-{\left(\frac{z-{Z}_s}{Z_s}\right)}^2}\right] dz\\ {}\kern2em +{\gamma}_d\left(1+{\theta}_i\right)\left({Z}_b-{Z}_f\right)\cos \beta \\ {}\kern1em =\frac{\left(4+\pi \right)\left({\theta}_s-{\theta}_i\right)}{8}\cos \beta {\gamma}_d{Z}_f+{\gamma}_d\left(1+{\theta}_i\right)\cos \beta {Z}_b\end{array}} $$
(17)

The safety factor is generally taken as a determinant index in the evaluation of slope stability. Based on the limit equilibrium method (Rahardjo and Fredlund 1984), the safety factor, Fs, for an infinite slope can be obtained as follows:

$$ {F}_s=\frac{G\cos^2\beta \tan \phi +c}{G\sin \beta \cos \beta } $$
(18)

where ϕ denotes the friction angle of the soil (°) and c denotes the cohesion of the soil (kPa).

A new approach for estimating the time-dependent stability of a finite slope

Natural slopes usually have limited ranges, with slope surfaces and slip surfaces showing irregular shapes. A finite slope model shown in Fig. 4b is adopted here to analyze the influence of intense rainfall on slope stability. Referring to the residual thrust method (Zhu 1999), the slope can be divided into n slices with the slope surface and slip surface of each slice as flat planes, and the sides of each slice are vertical. Based on the stratified soil water content concept, the jth soil slice (1 ≤ j ≤ n) can be divided into three layers, which are saturated, transitional, and natural layers (Fig. 5a), and the area of the jth soil slice can be expressed follows:

$$ {A}_j={A}_{sj}+{A}_{tj}+{A}_{nj} $$
(19)

where Asj, Atj, and Anj denote areas of saturated, transitional, and natural layers of the jth soil slice (m2), respectively. Thus, the relevant gravity of the jth soil slice can be written as follows:

$$ {G}_j={G}_{sj}+{G}_{tj}+{G}_{nj} $$
(20)

where Gsj, Gtj, and Gnj are the gravities of saturated, transitional, and natural layers of the jth soil slice (m2), respectively.

Fig. 5
figure 5

Diagram of the jth soil slice. a Geometrical profile of the soil slice. b Forces acting on the soil slice

Full size image

In the calculation of the soil slice gravity, the slices are assumed to be regular polygons. As the unit weight of the soil in the saturated or natural layer is constant, the following equations can be obtained:

$$ {G}_{sj}={\gamma}_s{A}_{sj} $$
(21)
$$ {G}_{nj}={\gamma}_i{A}_{nj} $$
(22)

where γs and γi denote the unit weight of the saturated and natural soils (N/m3), respectively.

The unit weight of the soil in the transitional layer is a function of depth according to Eq. (4), and thus, the calculation of the soil gravity for the transitional layer varies with the geometry of the soil slice. There are three kinds of slices, which are the 1th, nth, and jth slices (1 < j < n) between them, as shown in Fig. 6. The ground surface length of the jth soil slice is denoted as Lj (m), and the soil gravity of the different transitional layers can be calculated as follows:

$$ {\displaystyle \begin{array}{l}{G}_{t1}=\left[{L}_1-{Z}_f\sin {\beta}_1-\frac{Z_f\cos {\beta}_1}{\tan \left({\alpha}_1-{\beta}_1\right)}+\frac{Z_f\sin {\beta}_1}{4}+\frac{Z_f\cos {\beta}_1}{4\tan \left({\alpha}_1-{\beta}_1\right)}\right]\cos \beta {\gamma}_d\\ {}\kern2.25em {\int}_{Z_s}^{Z_f}\left[1+{\theta}_i+\left({\theta}_s-{\theta}_i\right)\sqrt{1-{\left(\frac{z-{Z}_s}{Z_s}\right)}^2}\right] dz\\ {}\kern1em =\left[{L}_1{Z}_f-\frac{3{Z_f}^2\sin {\beta}_1}{4}-\frac{3{Z_f}^2\cos {\beta}_1}{4\tan \left({\alpha}_1-{\beta}_1\right)}\right]\cos {\beta}_1{\gamma}_d\left[\frac{4\left(1+{\theta}_i\right)+\pi \left({\theta}_s-{\theta}_i\right)}{8}\right]\end{array}} $$
(23)
$$ {\displaystyle \begin{array}{l}{G}_{tj}={L}_j\cos {\beta}_i{\gamma}_d{\int}_{Z_s}^{Z_f}\left[1+{\theta}_i+\left({\theta}_s-{\theta}_i\right)\sqrt{1-{\left(\frac{z-{Z}_s}{Z_s}\right)}^2}\right] dz\\ {}\kern1em ={L}_j\cos {\beta}_i{\gamma}_d\left(1+{\theta}_i\right)\left({Z}_f-{Z}_s\right)+{L}_j\cos {\beta}_i{\gamma}_d\left({\theta}_s-{\theta}_i\right)\\ {}\kern2em \left[\frac{Z_s}{2}\arcsin \frac{Z_f-{Z}_s}{Z_s}+\frac{Z_f-{Z}_s}{2{Z_s}^2}\sqrt{1-{\left(\frac{Z_f-{Z}_s}{Z_s}\right)}^2}\right]\\ {}\kern1em ={L}_j\cos {\beta}_i{\gamma}_d{Z}_f\left[\frac{4\left(1+{\theta}_i\right)+\pi \left({\theta}_s-{\theta}_i\right)}{8}\right]\end{array}} $$
(24)
$$ {\displaystyle \begin{array}{l}{G}_{tn}=\left[{L}_n-{Z}_f\sin {\beta}_n-\frac{Z_f\cos {\beta}_n}{\tan \left({\beta}_n-{\alpha}_n\right)}+\frac{Z_f\sin {\beta}_n}{4}+\frac{Z_f\cos {\beta}_n}{4\tan \left({\beta}_n-{\alpha}_n\right)}\right]\cos {\beta}_n{\gamma}_d\\ {}\kern2.25em {\int}_{Z_s}^{Z_f}\left[1+{\theta}_i+\left({\theta}_s-{\theta}_i\right)\sqrt{1-{\left(\frac{z-{Z}_s}{Z_s}\right)}^2}\right] dz\\ {}\kern1em =\left[{L}_n{Z}_f-\frac{3{Z_f}^2\sin {\beta}_n}{4}-\frac{3{Z_f}^2\cos {\beta}_n}{4\tan \left({\beta}_n-{\alpha}_n\right)}\right]\cos {\beta}_n{\gamma}_d\left[\frac{4\left(1+{\theta}_i\right)+\pi \left({\theta}_s-{\theta}_i\right)}{8}\right]\end{array}} $$
(25)

where Gt1, Gtj, and Gtn are the gravities of the 1th, jth, and nth slices of the transitional layer (m2), respectively. The profile of the jth slice is shown in Fig. 5b, and the safety factor is defined as the ratio of the sliding resistance to sliding force, which can be calculated as follows:

$$ {F}_s=\frac{\left[{G}_j\cos {\alpha}_j+{E}_{j-1}\sin \left({\alpha}_{j-1}-{\alpha}_j\right)\right]\tan \phi +{E}_j+c{l}_j}{G_j\sin {\alpha}_j+{E}_{j-1}\cos \left({\alpha}_{j-1}-{\alpha}_j\right)} $$
(26)

where αj denotes the dip angle of the slip surface (°), lj denotes the length of the slip surface of the jth slice (m), and Ej denotes the thrust between the jth slice and the (j + 1)th soil slice (kPa). Reorganizing Eq. (26), the following can be obtained:

$$ {E}_j={F}_s{G}_j\sin {\alpha}_j+{E}_{j-1}\left[{F}_s\cos \left({\alpha}_{j-1}-{\alpha}_j\right)-\sin \left({\alpha}_{j-1}-{\alpha}_j\right)\tan \phi \right]-\left({G}_j\cos {\alpha}_j\tan \phi +c{l}_j\right) $$
(27)
Fig. 6
figure 6

Geometrical profile of soil slices with different types in a finite slope. a the 1th soil slice of a finite slope; b the jth soil slice of a finite slope (1 < j < n); c the nth soil slice of a finite slope

Full size image

In this study, it is assumed that there is no tensile stress between adjacent soil slices, and thus, the effective thrust Ej′ can be expressed as follows:

$$ {E_j}^{\prime }=\Big\{{\displaystyle \begin{array}{l}=0,{E}_j\le 0\\ {}\\ {}={E}_j,{E}_j>0\end{array}} $$
(28)

Thus,

$$ {E}_j={F}_s{G}_j\sin {\alpha}_j+{E_{j-1}}^{\prime}\left[{F}_s\cos \left({\alpha}_{j-1}-{\alpha}_j\right)-\sin \left({\alpha}_{j-1}-{\alpha}_j\right)\tan \phi \right]-\left({G}_j\cos {\alpha}_j\tan \phi +c{l}_j\right) $$
(29)

In the calculation of the safety factor, the equilibrium iteration is conducted under the conditions of E1 = 0 and En = 0.

To obtain the value of Fs, the procedure is as follows. At first, an upper limit value (Fsu) and a lower limit value (Fsl) of Fs are estimated using the conventional limit equilibrium method with conditions of natural and saturated mechanical parameters above the wetting front. Then, the golden ratio method is used to determine the value of Fs. Specifically, with an initial value of Fs0 = 0.618(Fsu − Fsl), one will have Fsu = Fs0 if En > 0 or Fsl = Fs0 if En < 0, and thus, one can obtain Fs1 = 0.618(Fsu − Fsl). Repeating this step, one will have Fsu = Fs1 if En > 0 or Fsl = Fs0 if En < 0, and thus, one can obtain Fs2 = 0.618(Fsu − Fsl). The procedure is repeated until En approaches 0. The value of Fs with a computation result of En = 0 is regarded as the true safety factor.

In summary, the procedure for evaluating the time-dependent slope stability is as follows. First, dividing the slope into multiple soil slices, one can simulate the infiltration process in each soil slice. Second, one can derive equations of the proper gravities for different slope types, i.e., an infinite slope and a landslide with an irregular slope surface. Finally, one can calculate the safety factor of the slope at different times during rainfall infiltration. Based on this approach, the safety factor of the slope is related to the wetting front depth, which is time-dependent. Therefore, the slope stability will eventually show time-dependent characteristics.

Applications of the new approaches for estimating the time-dependent slope stability

Application of the new approach for an infinite slope

The infinite slope case is shown in Fig. 4a, which has a slope angle of 30°. The variables of the case, i.e., cohesion, friction angle, and saturated permeability are listed in Table 1. In particular, the soil is silty clay, which is collected from a Majiagou landslide in the Three Gorges Reservoir (TGR) region of China, and will be explained in detailed in “Application of the new approaches for a finite slope-Majiagou landslide” Section. As mentioned above, the slip surface of an infinite slope is parallel to the slope surface, which is a flat plane. The rainfall infiltration into an infinite slope can be estimated based on Eqs. (10), (13), and (15). With a rainfall intensity of 30 mm/h, and a depth of the slip surface of 5.80 m, which is exactly the infiltration depth at 100 h, the time-dependent stability of the slope can be calculated using Eqs. (16) to (18).

Table 1 Parameters of soil of a sliding body of the Majiagou landslide
Full size table

The safety factors above the sliding surface and wetting front estimated based on the SGA and GA model are shown in Fig. 7. Note that in the estimation using the GA model, the soil above the wetting front is saturated, and thus, the soil at the wetting front has a saturated cohesion and friction angle. The initial safety factor above the sliding surface is 1.06. By using the SGA model, the evolution of the safety factor above the sliding surface can be divided into three phases. For the first phase, which is before the wetting front reaches the sliding surface (< 100 h), there is a natural layer between the wetting front and sliding surface, and the safety factor drops rapidly. For the second phase, when the wetting front exceeds the sliding surface, but the bottom of the saturated layer is above the sliding surface, there is a transitional layer above the sliding surface (100–303 h), and the safety factor keeps dropping. For the third phase, after the bottom of the saturated layer exceeds the sliding surface (> 303 h), the soil above the sliding surface is completely saturated, and the safety factor is constant.

Fig. 7
figure 7

Evolution of the safety factor of an infinite slope under rainfall infiltration with time. tSG: Critical time to unstable state above the sliding surface (GA model); tSS: Critical time to unstable state above the sliding surface (SGA model); tWG: Critical time to unstable state above the wetting front (GA model); tWS: Critical time to unstable state above the wetting front (SGA model)

Full size image

Different from the SGA model, the evolution of the safety factor above the sliding surface using the GA model can be divided into two phases. For the first phase, before the wetting front reaches the sliding surface (< 113 h), there is a natural layer between the wetting front and sliding surface, and the safety factor drops nonlinearly. For the second phase, after the wetting front exceeds the sliding surface (≥ 113 h), the safety factor remains unchanged. Previous studies (Pradel and Raad 1993; Ali et al. 2014; Suradi et al. 2014) indicated that slope failures also occurred along the wetting front during rainfall infiltration, and the safety factor above the wetting front at different infiltration times are studied. Figure 7 shows that the safety factors estimated using both the SGA and GA models decrease nonlinearly with the rainfall time, and the safety factors tend to gradually stabilize. In addition, safety factors above the wetting front are greater than those above the sliding surface at first, but as the former decreases more rapidly, the safety factors become less than the latter with the continuation of rainfall, which agrees with the conclusion of Wang et al. (2017).

For both the safety factors above the sliding surface and wetting front, the results using the GA model are greater than those using the SGA model. This is because with different conceptual models of soil water content distribution above the wetting front, the infiltration estimated by these two models is different, and thus, the gravity of the soil above the same wetting front, and the shear strength parameters of the soil on the slip surface are also different. The results indicate that the GA model can overestimate the slope stability compared to the SGA model.

A safety factor with a value of 1 is a threshold to judge the stability of slopes. With the calculated safety factor above, the critical times for the safety factor reaching 1 (or the slope beginning to become unstable) follow the order of tWS < tWG < tSS < tSG, where tWS, tWG, tSS, and tSG are explained in the caption of Fig. 7.

Application of the new approaches for a finite slope-Majiagou landslide

In this section, the Majiagou landslide is used to illustrate the time-dependent stability of a finite slope with an irregular ground surface. The Majiagou landslide is located on the left bank of the Zhaxi River, a tributary of the Yangtze River, which is 2.1 km from the estuary in Guizhou, Zigui County, Hubei Province of China (Fig. 8a). The landslide is composed of slide masses #1 and #2, and their strike directions are NW, 291° and NW, 310°, respectively. Slide mass #2 has a rear edge with an elevation of 295 m above mean sea level (m.s.l.) and a leading edge with an elevation of 155 m above m.s.l., and the average slope of the landslide is approximately 28°. There are minor-scale shallow landslides and tension cracks in the sliding mass. The landslide body has an approximate average thickness of 22.30 m, and an approximate volume of 1.78 million m3, and it is a typical colluvial landslide mainly consisting of Quaternary diluvium of silty clay with gravels. The bedrock is grey sandstone and purple red mudstone from the Suining Formation of the Late Jurassic (J3S) (Wu et al. 2017a, b; Jiao et al. 2014; Ma et al. 2016), which has a dip direction of 270° to 290° and a dip angle of 25° to 30°. Countermeasures to prevent the Majiagou landslide (landslide mass #1) from further sliding were put into place in 2007 under the TGR Geological Disaster Prevention Project, which consists of anti-slide piles, drainage, and monitoring. Such countermeasures are not implemented for landslide mass #2.

Fig. 8
figure 8

Engineering geological background of slide mass #2 of the Majiagou landslide. a Engineering geology map. b A-A’ Cross section

Full size image

The Majiagou landslide is situated in the torrential rain area of the TGR region with an average annual rainfall of 1066.92 mm and a maximum daily rainfall of 258.70 mm, and the rainfall is mainly concentrated from May to September annually (Li et al. 2017a). Intense rainfall is the main cause of geological hazards such as debris flow and landslides in this region (Jiao et al. 2014; Ma et al. 2016; Li et al. 2017b). In this study, a primary rainfall intensity of 30 mm/h is chosen to study the time-dependent stability of the Majiagou landslide (Ma et al. 2016).

Figure 8b shows the longitudinal A-A’ profile of the Majiagou landslide, with consideration of slope surface and sliding surface shapes. The landslide mass is divided into seven slices, which are sequentially numbered 1# to 7#.

Using the physical and mechanical parameters in Table 1, the method described in “A new approach for estimating the time-dependent stability of an infinite slope” Section is adopted here to analyze the infiltration process and time-dependent stability of the Majiagou landslide. The geometric parameters and infiltration parameters of soil slices are listed in Table 2. With an intensity of 30 mm/h, based on the conditions of E1 = 0 and E7 = 0, the correlation between the safety factor and infiltration time is shown in Fig. 9.

Table 2 Geometric parameters and infiltration parameters of soil slices of the Majiagou landslide
Full size table
Fig. 9
figure 9

Evolution of the safety factor of the Majiagou landslide with time under rainfall infiltration. t'SG: Critical time to less stable state above the sliding surface (GA model), which is inexistent and can not be shown in the figure; t'SS: Critical time to less stable state above the sliding surface (SGA model); t'WG: Critical time to less stable state above the wetting front (GA model); t'WG: Critical time to less stable state above the wetting front (SGA model)

Full size image

Similar to the safety factor of the infinite slope discussed above, the safety factor of the Majiagou landslide above the wetting front is greater than that above the sliding surface at first but becomes less than the latter with the continuation of rainfall. In addition, the safety factor based on the GA model is greater than that based on the SGA model. However, there is no abrupt change in the safety factor above the sliding surface in the first 300 h. This is because the slip surface is very deep, and the ground surface and slip surface have irregular shapes, and thus, an abrupt change in the safety factor can be observed only after a relatively long period of rainfall. The initial safety factor above the sliding surface is 1.07 and the safety factor based on the SGA model decreases to a less stable state (with a safety factor of 1.05) at 220 h and continues to decrease with time, suggesting that countermeasures are required to prevent the occurrence of a disastrous landslide. This finding is quite different from the conclusion drawn from the GA model, in which the safety factor remains greater than 1.05 in the first 300 h, and although the safety factor becomes gradually stable with increasing time, it never reaches 1.05. For the safety factor above the wetting front, the critical times calculated with both the SGA and GA models are approximately 50 h. In addition, the critical times follow the order of t'WS < t'WG < t'SS, where t'WS, t'WG, and t'SS are explained in the caption of Fig. 9 (t'SG is non-existent).

Discussions

Validation of the proposed SGA model

To validate the accuracy of the proposed infiltration model, the rainfall infiltration process of the slope model (as shown in Fig. 10a) is analyzed. The monitored time results of the wetting front arriving at the monitoring sites and those calculated by the SGA and GA models are compared. Lin (2007) conducted a laboratory model test to study the rainfall induced slope failure mechanism using this slope model. The depths of the monitoring sites 1, 2, and 3 are 0.1, 0.2, and 0.4 m, respectively. Several tensiometers are set at the monitoring sites, and the downward process of the wetting front can be monitored during the test. The rainfall intensity is q = 40 mm/h, and the main parameters of the silt are: β = 33.7°, Ks = 0.016 m/h, ψf = 0.11 m, θs = 0.405, θi = 0.1.

Fig. 10
figure 10

Comparison of monitored wetting depth and infiltration process estimated by the SGA model and the GA model. a Slope model and monitoring site of model test by Lin (2007). b Monitored wetting depth and calculated results by the GA model and the SGA model. D-GA: Depth of wetting front calculated by the GA model; D-SGA: Depth of wetting front calculated by the SGA model; D-MV: Monitored value of the depth of wetting front at the monitoring site; R-GA: Moving rate of wetting front calculated by the GA model; R-SGA: Moving rate of wetting front calculated by the SGA model; tCG: Critical time in the infiltration process estimated by the GA model; tCS: Critical time in the infiltration process estimated by the SGA model

Full size image

The depth of monitoring site 1 is 0.1 m, and the ground surface above it is horizontal. The wetting front arrives at this monitoring site at 0.68 h during the test, and the time calculated by the SGA and the GA models is 0.70 h and 0.78 h. In addition, the ground surface above monitoring sites 2 and 3 have a slope angle of 33.7°. The monitored time of the wetting front and that of the detailed infiltration process calculated by the SGA and GA models are shown in Fig. 10b. Similar to the results of monitoring site 1, the time of the wetting front arrival at the monitoring sites 2 and 3 calculated by the SGA model is closer to the monitored value than the time calculated by the GA model. Specifically, the monitored times of sites 2 and 3 are 1.55 h and 3.67 h, while those calculated by the SGA model are 1.5 h and 3.71 h, and the times calculated by the GA model are 1.68 h and 4.15 h. The comparison indicates that the proposed model can accurately depict the rainfall infiltration process into the soil.

The rainfall infiltration process into the soil can be divided into two phases: (1) at the initial infiltration stage, the wetting front moves down at a constant speed. At this stage, the shallow soil is still unsaturated. In regard to the critical time, it is 0.72 h for the SGA model and 0.81 h for the GA model. In the SGA model concept, there is stratification of the soil water content above the wetting front, while the soil above the wetting front is fully saturated in the GA model; (2) after the wetting front is formed, the wetting front continues moving down nonlinearly, the moving rate decreases rapidly and tends to gradually stabilize. Notably, the wetting front depths (Zc) at the critical time using the GA and SGA models are the same, which can be explained by Eq. (7), and the critical time has a relation of tCS < tCG, where tCS and tCG are the critical times in the infiltration process estimated by the SGA and GA models. Figure 10b shows that the wetting front estimated by the SGA model moves faster than that estimated by the GA model, which is also because of the different hypotheses of the water content of soil above the wetting front in the SGA and GA models.

Factors affecting the rainfall infiltration process

The rainfall infiltration process is analyzed in “Infiltration process of intense rainfall into slopes based on the SGA model” Section based on the SGA model. In addition to the soil properties, the infiltration process is affected by two other factors, i.e., slope surface angle and rainfall intensity, which is shown in Eqs. (7) and (15). The infinite slope case mentioned in “Application of the new approach for an infinite slope” Section is selected as an example to analyze the influence of these factors on the rainfall infiltration. As seen in Fig. 11 and Eq. (12), before the critical time, the moving speed of the wetting front remains the same with ground surface angle variation, and such a moving speed is positively correlated with the rainfall intensity. After the critical time, the wetting front depth increases nonlinearly with the infiltration time, and there is a positive relationship between the wetting front depth and slope surface angle, as well as a positive relationship between the wetting front depth and rainfall intensity. After the critical time, a larger slope surface angle will lead to a greater infiltration rate, and consequently, this will lead to a greater wetting front depth.

Fig. 11
figure 11

Influence of the slope surface angle and the rainfall intensity on the wetting front depth. a Influence of the slope surface angle on the wetting front depth. b Influence of the rainfall intensity on the wetting front depth

Full size image

Influence of rainfall intensity on the slope stability

Rainfall is a key factor associated with slope stability, and many studies have pointed out that there is a negative correlation between the rainfall intensity and slope stability. Herein, with the proposed SGA model, the influence of the rainfall intensity on the time-dependent stability of an infinite slope and a finite slope (Majiagou landslide) is analyzed. The variation in the critical time to the unstable state of the infinite slope (Fs = 1) is shown in Fig. 12, and the critical time to the less stable state of the Majiagou landslide (Fs = 1.05) is shown in Fig. 13, which indicates that the slope stability will decrease more quickly if the rainfall intensity is greater. There is a negative exponential correlation between the critical time and rainfall intensity, which can be used to estimate the slope stability under other rainfall conditions.

Fig. 12
figure 12

The critical time to less stable state of an infinite slope as a function of the rainfall intensity

Full size image
Fig. 13
figure 13

The critical time to unstable state of the Majiagou landslide as a function of the rainfall intensity

Full size image

Influence of rainfall on the slope reinforcement design

As slope stability is a public concern, stabilizing piles is one of the effective countermeasures used to reinforce slopes (Li et al. 2015, 2017a, b; Liu et al. 2018). The locations of the stabilizing piles are a key factor influencing the efficiency of slope reinforcement, especially with a fixed project budget and schedule. Herein, the Majiagou landslide is illustrated to analyze the influence of rainfall on the stabilizing piles design. Existing studies indicate that the optimal location of the stabilizing piles is 0.5L (Cai and Ugai 2000; Poulos 1995; Won et al. 2005), where L denotes the horizontal distance from the slope toe to the slope shoulder or the horizontal range of the landslide mass. Thus, the stabilizing piles in this case are between slices 4 and 5, as shown in Fig. 14, which also shows the residual driving force of the Majiagou landslide based on the initial stat, the ultimate state of the Majiagou landslide, and the designed driving force of the stabilizing piles based on both states. The state of the landslide at 0 h is defined as the initial state, and as the safety factor of the landslide decreases and tends to be stable during rainfall, the state of the landslide at 300 h is assumed to be the ultimate state. The designed driving force of the stabilizing piles is required to counter balance the difference between the security state, which can be calculated using a safety factor of Fst = 1.15 and the current state. The designed driving force of the stabilizing piles based on the initial state of the landslide is Fi = 2339.69 kPa, while that based on the ultimate state is Fu = 2628.14 kPa. Notably, persistent intense rainfall has significant influence on the slope reinforcement design.

Fig. 14
figure 14

Residual driving force of the Majiagou landslide. Fi: Designed driving force of stabilizing piles based on initial state of the Majiagou landslide; Fu: Designed driving force of stabilizing piles based on ultimate state of the Majiagou landslide

Full size image

Conclusions

During the rainfall infiltration process into soil, the water content of the soil above the wetting front is assumed to be fully saturated in the GA model concept. However, based on the concept of stratified soil water content above the wetting front, a modified GA model known as the SGA model is developed to evaluate the rainfall infiltration process into soil. Validation of the infiltration process of a slope model during rainfall indicates that, compared to the conventional GA model, the SGA model can more accurately evaluate the infiltration process. By comparing the SGA and GA models, the infiltration process can be divided into two phases according to both calculated results using the SGA model and the GA model. In the first phase, the wetting front moves down at a constant rate, while after the wetting front is formed, the wetting front depth becomes increasing nonlinearly, and the moving rate decreases rapidly and tends to gradually stabilize. In addition, the wetting front estimated by the SGA model moves faster than that estimated by the GA model.

The developed SGA model is applied to estimate the time-dependent stability of an infinite slope and finite slope (Majiagou landslide) during rainfall infiltration. The results reveal that the safety factor calculated based on the GA model is greater than that based on the SGA model. The safety factors calculated from both models decrease nonlinearly with the rainfall time and tend to gradually stabilize. For the infinite slope case, the evolution of the safety factor above the sliding surface can be divided into three phases for the SGA model, while the evolution of the safety factor above the wetting front can be divided into two phases for the GA model. However, the safety factor of the finite slope (Majiagou landslide) does not show such trends.

In addition, the influence of the slope angle and rainfall intensity on the infiltration process and the influence of the rainfall intensity on the time-dependent slope stability are analyzed. The wetting front depth shows a positive correlation with the slope surface angle and rainfall intensity. The difference in the wetting front depth at a given time is more obvious when the slope surface angle is greater, while it is less obvious when the rainfall intensity increases. As the rainfall intensity will reduce the slope stability, the slope will become less stable (with a safety factor equal to or only slightly greater than 1.05) or unstable (with a safety factor less than 1.0) sooner if the rainfall intensity is greater. The critical time of the slope reaching a less stable state or unstable state decreases exponentially with the increase in rainfall intensity. The rainfall also has a significant influence on the designed driving force of the Majiagou landslide.

The primary purpose of this study is to use the stratified soil water concept to analytically estimate the time-dependent slope stability during intense rainfall using a simple SGA model. If a more complex unsaturated flow model needs to be considered, the present work will not be applicable. Similarly, this study is not able to address natural slopes with undulating terrain, uncertain slip surfaces and multiple stratum. To tackle those complex issues, numerical models would likely need to be employed, which will be further pursued in future studies.