Analysis of extreme precipitation and its variability under climate change in a river basin

Abstract

This study investigated the variation of extreme precipitation on a catchment under climate change. Extreme value analysis using generalized extreme value distribution was used to characterize the extreme precipitation. Reliability ensemble average of annual maximum precipitation projections of five global climate model–regional climate model (GCM–RCM) combinations was used to analyse the precipitation extremes under the representative concentration pathways, RCPs 4.5 and 8.5. In order to tackle the nonstationarity present in the bias-corrected ensemble-averaged annual maximum precipitation series under RCPs 4.5 and 8.5, it was split in such a way that the resulting blocks were stationary. Here the analysis was performed for three blocks 2010–2039, 2040–2069 and 2070–2099, each of which were individually stationary. Uncertainty analysis was done to estimate the ranges of extreme precipitation corresponding to return periods of 10, 25 and 50 years. Results of the study indicate that the extreme precipitation corresponding to these return periods in the three time blocks under the RCPs 4.5 and 8.5 exhibit an increasing trend. Extreme precipitation for these return periods are obtained as higher for the RCP scenarios compared to that obtained using observations. Also the extreme precipitation under RCP8.5 is higher compared to that under RCP4.5 scenario.

1 Introduction

If the value of a meteorological variable is extremely high or low, the resulting weather becomes extreme. Analysis of extreme events is important since it can cause significant impacts to different regimes of the society. This study focuses on extreme precipitation and its probable variability due to climate change in a river basin. It has been proved that greenhouse gas emissions are the dominant cause of global warming and its adverse effects have been detected all over the climate system. Natural and human systems are sensitive to the impacts of climate change. Existing risks could be amplified, and also new risks could be created as a result of climate change (IPCC 2014). A changing climate results in unprecedented extreme weather and climate events with changes occurring to its frequency, intensity, spatial extent, duration and timing (IPCC SREX 2012). Climate change impact studies often assess the changes that may happen to the long-term average values of climate variables. In recent times, there is a growing interest to assess changes in the frequency, severity and magnitude of the extreme events.

A substantial increase has been reported in heavy precipitation events in many parts of the world even when there is a reduction in the annual total precipitation (IPCC 2013). Similar observations were reported by Wang et al. (2008) in their investigation on the changes in extreme precipitation in the Dongjiang river basin in Southern China, where significant changes were seen in extreme precipitation on a monthly basis in contrast to a little change in the annual precipitation. An increasing trend of extreme precipitation has been reported from the studies conducted on USA, UK during winter, Australia, South Africa and India (Easterling et al. 2000; Frei and Schär 2001; Goswami et al. 2006), whereas a significant decrease in extreme rainfall events is found in Western Australia, South-East Asia, parts of Central Pacific, northern and eastern New Zealand, etc. (Haylock and Nicholls 2000; Griffiths et al. 2003; Salinger and Griffiths 2001). Some studies reported that extreme precipitation would more probably intensify in dry regions compared to wet regions of the world under the influence of climate change (Donat et al. 2016).

As far as India is concerned, an increasing trend in the extreme rainfall is seen over peninsular, east, north east India and a decreasing trend is seen over major parts of central and north India (Rakhecha and Soman 1994, Guhathakurta et al. 2011). The present study is conducted in the Chaliyar river basin which is located in peninsular India. Few studies have been conducted in this river basin to assess the variability and trends of meteorological variables. The spatial and temporal variability of rainfall at various stations in the river basin on monthly, seasonal and annual scales was studied by Ansari and Chauhan (2017) using parametric (simple regression) and non-parametric (Mann–Kendall test and Sen’s estimator of slope method) trend tests. These tests identified both increases and decreases of precipitation at various stations considered in the study. Chithra and Thampi (2017) analysed downscaled future projections of precipitation at two stations in the Chaliyar river basin and found that there would be an increase in precipitation during the south-west monsoon season under the climate change scenarios SRES A1B, A2 and B1. Extreme precipitation events and their properties are not yet investigated for the river basin. Knowledge of the variation of extreme rainfall would be beneficial since this river basin is a virgin basin and there is a scope to construct many hydraulic structures in the river in future. It would be helpful towards effective planning and management of the watershed as well as in decision-making regarding the selection of design storm for the design of various hydraulic structures proposed in the river basin.

Extreme events can be analysed using descriptive indices and statistical modelling (Data 2009; Monier and Gao 2015). A set of 27 core indices developed by the expert team on climate change detection and indices (ETCCDI) are commonly used to monitor the extremes which are occurring several times within a year. Most of the ETCCDI indices are based on calculating the number of days exceeding a particular percentile threshold (Data 2009; Zhang et al. 2011; Keggenhoff et al. 2014),whereas statistical modelling of the extremes using extreme value theory (EVT) can be used to evaluate the intensity and frequency of extreme events which are rare. The peak-over-threshold (POT) method and the block maxima method are often used for this purpose. In POT, extremes follow a generalized Pareto distribution (GPD), and in the block maxima method extremes follow a generalized extreme value (GEV) distribution (Stedinger 1993). In the present study, statistical modelling of extreme precipitation using the block maxima approach is followed.

Conventionally, hydraulic structures are designed without considering the effect of climate change on the extreme rainfall. Knowledge about the return level and return period under climate change is extremely important for the design of infrastructure and to mitigate the risks associated with extreme climatic events (Madsen and Rosbjerg 1998; Cheng and Agha Kouchak 2014). This is crucial for responsible decision-making even when there are some predictive uncertainties (Halmstad et al. 2013; Notaro et al. 2015; Mirhosseini et al. 2013). In the present study, extreme rainfall events in river basin for the future climate change scenarios were analysed by applying EVT to the projections of global climate model–regional climate model (GCM–RCM) combinations (the driving GCM and the RCM used for downscaling the GCM). This will help in the selection of design values considering the effects of climate change.

2 Materials and methods

2.1 Study area

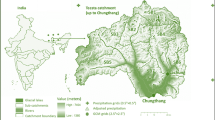
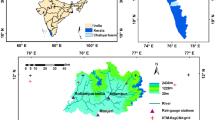
The Chaliyar is the fourth longest river in Kerala with a length of 169 km. The origin of this river is at the Elambalari hills at an altitude of 2067 m above MSL. The river basin spreads over two states, Kerala and Tamil Nadu. The total area of the river basin is 2933 km². Its topography comprises of highland, midland, low land and coastal plains. The predominant land use in this river basin is agriculture (60.04%) and forests (38.74%), the rest being urban areas, pastures, waste lands and rocky areas. The major soil type is loam (42.74%), followed by clay (28.66%), clay loam (24.18%) and sandy loam (4.42%). The climate is tropical humid with hot summer and high monsoon rainfall. March and April are the hottest months, and December and January are the coolest months. Average annual precipitation is 3012.61 mm, and the maximum and minimum temperatures are 34 °C and 24 °C, respectively (Raneesh and Thampi 2013). Digital elevation model (DEM) of the river basin, locations (Table 1) of the gauging stations viz, Kottamparamba, Manjeri and Nilambur and locations of grids of the downscaling RCMs over the river basin are presented in Fig. 1.

Table 1 Location of precipitation gauging stations

Fig. 1

DEM of Chaliyar river basin with the location of precipitation gauging stations and the grids of the downscaling RCMs

2.2 Data

Rainfall data were obtained for three stations in the Chaliyar river basin, namely Kottamparamba, Manjeri and Nilambur. Daily rainfall data at the Kottamparamba (1979–2004) raingauge station was obtained from the Centre for Water Resources Development and Management (CWRDM), Kunnamangalam, Kerala, whereas the data for Nilambur and Manjeri (1974–2004) were collected from the Indian Meteorological Department (IMD).To assess the variation of extreme precipitation at these three stations due to climate change, daily rainfall projections (interpolated using the inverse distance weighting method) of five GCM–RCM combinations under representative concentration pathways, RCPs 4.5 and 8.5, obtained from the website of CORDEX South Asia were used. Details of the GCM–RCM combinations used in this study are presented in Table 2. The resolution of the projections of the GCM–RCM combinations is 0.5^o× 0.5^o.

Table 2 GCM–RCM combinations from CORDEX South Asia used for the study

2.3 Methodology

The methodology used in this study is presented in Fig. 2. Initially, the annual maximum precipitations from observed daily data (1979–2004 for Kottamparamba, 1974–2004 for Manjeri and Nilambur) and annual maximum precipitation projections from the GCM–RCM combinations (2010–2099) were extracted. Reliability ensemble averaging (REA) technique was employed to obtain an ensemble-averaged projection of the GCM–RCM combinations; it was thereafter subjected to bias correction for eliminating systematic errors in the projections. Probabilistic approaches for defining risk, reliability and return periods assume that the time series of extreme events should be stationary with a probability distribution having fixed moments and parameters (Read and Vogel 2015). So to check the nature of the time series, stationarity test was performed on it. To tackle the issue of nonstationarity in the annual maximum time series, it was split into time blocks which were individually stationary. Statistical tests were conducted to identify a suitable distribution which fits the observed series of annual maximum precipitation, and the selected distribution was used for the calculation of extreme precipitation for different return periods in the future too. Extreme precipitation for a return period was estimated along with a confidence interval for each of the stationary blocks and their variations were analysed. The confidence intervals were obtained from the uncertainty quantification using the bootstrap approach.

Fig. 2

Overall methodology

2.3.1 Reliability ensemble averaging

The performances of different climate models may vary for the same region even under a same forcing scenario. So to reduce the uncertainties arising from multiple models, the combined result provided by an ensemble of simulations is the best (Giorgi and Mearns 2003; Das and Umamahesh 2017). Reliability ensemble averaging is one of the widely used ensemble averaging techniques suitable for this purpose. It is a method of calculating the weighted average of climate model simulations based on reliability criteria. Reliability of a model is defined as a measure of its ability to emulate present day climate as well as the convergence of its simulations with the other models in the ensemble under a particular forcing scenario (Giorgi and Mearns 2002). In the present study, reliability factors for different models (GCM–RCM combinations) under the RCP scenarios were calculated based on a methodology followed by Riano (2013). Reliability factor ($\mathop R\nolimits_{i}$) (Eq. 1) for a particular model i is the product of reliability model bias factor ($\mathop R\nolimits_{B,i}$) (Eq. 2) and the reliability model convergence factor ($\mathop R\nolimits_{D,i}$) (Eq. 3).

$$\mathop R\nolimits_{i} =\mathop R\nolimits_{B,i} \times \mathop R\nolimits_{D,i}$$

(1)

$${\text{where}}\,\mathop R\nolimits_{B,i} = \frac{1}{t}\sum\limits_{j = 1}^{t} {\left( {\mathop P\nolimits_{o,j} -\mathop P\nolimits_{i,j} } \right)}^{2}$$

(2)

$$\mathop R\nolimits_{D,i} = \frac{1}{t}\sum\limits_{j = 1}^{t} {\left( {\mathop g\nolimits_{i,j} -\mathop x\nolimits_{j} } \right)}^{2}$$

(3)

$$\mathop x\nolimits_{j} = \frac{{\sum\nolimits_{i = 1}^{N} {\left( {\mathop R\nolimits_{i} \mathop g\nolimits_{i,j} } \right)} }}{{\sum\nolimits_{i = 1}^{N} {\mathop R\nolimits_{i} } }}$$

(4)

$$\mathop w\nolimits_{i} = \frac{{\mathop R\nolimits_{i} }}{{\sum\nolimits_{i}^{N} {\mathop R\nolimits_{i} } }}$$

(5)

where $\mathop P\nolimits_{o,j}$ is the observed maximum precipitation for $j{\text{th}}$ year, $\mathop P\nolimits_{i,j}$ is the historical maximum precipitation for $i{\text{th}}$ model and $j{\text{th}}$ year, t is the time, N is the number of models, $\mathop g\nolimits_{i,j}$ is the maximum precipitation projection under a scenario for $j{\text{th}}$ year and $i{\text{th}}$ model, $\mathop x\nolimits_{j}$ is the REA weighted average of projections of the models (Eq. 4) and $\mathop w\nolimits_{i}$ (Eq. 5) is the weight of each model in the ensemble. The calculation of $\mathop R\nolimits_{B,i}$ is direct since all the terms in Eq. 2 are known. But $\mathop R\nolimits_{D,i}$ requires $\mathop x\nolimits_{j}$ which is dependent on $\mathop R\nolimits_{i}$. So the estimation of $\mathop R\nolimits_{D,i}$ involves iterative calculation. This can be initiated by assuming an initial value for $\mathop R\nolimits_{i}$ (say $\mathop R\nolimits_{i} = \mathop R\nolimits_{B,i}$). The final value of $\mathop R\nolimits_{i}$ can be obtained using $\mathop R\nolimits_{B,i}$ and the converged solution of $\mathop R\nolimits_{D,i}$.

Higher values of $\mathop R\nolimits_{B,i}$ and $\mathop R\nolimits_{D,i}$ indicate less reliable projections since the calculations of these factors are based on mean square errors. $\mathop R\nolimits_{B,i}$ and $\mathop R\nolimits_{D,i}$ can be normalized to obtain a score system where the highest value could represent the most reliable model.

2.3.2 Bias correction

Ensemble projection obtained based on the REA weights should be checked for bias before being used for further analyses. Bias is a systematic deviation of the model results from the expected value due to systematic model errors. Biases are commonly detected by comparing the model output with observations which are truly unbiased. Different bias correction techniques have been developed by various investigators to adjust the systematic errors in climate model simulations (Teutschbein and Seibert 2013). Methods vary in their accuracy by correcting just the mean of the series in the linear scaling approach to more improved statistics in the advanced distribution mapping (Switanek et al. 2017). Mehr and Kahya (2016) developed a methodology to correct the bias in extreme series. In this method, mean of the maximum series of the climate model for a reference period is matched with mean of the maximum series of observations. This method proved to be very helpful since it avoids correction on the whole daily data series. In the present study, to correct the biases of ensemble-averaged annual maximum rainfall series this method was adopted. The corrected ensemble-averaged annual maximum precipitation $\mathop { ( {{AMP}}}\nolimits_{\text{BC}} )$ (Eq. 6) for the reference and future periods was obtained by multiplying a scaling factor to the ensemble-averaged annual maximum precipitation (AMP) series for the respective periods. Scaling factor is the ratio of the long-term mean of the observed annual maximum precipitation ($\mathop {{AMP}}\nolimits_{\text{obs}}$) to the corresponding annual maximum precipitation of the GCM–RCM ensembles over the reference period ($\mathop {{AMP}}\nolimits_{\text{ref}}$). The overbar symbol in Eq. 6 represents the long-term annual mean.

$$\mathop {{AMP}}\nolimits_{\text{BC}} = {{AMP}} \times \frac{{\mathop {\overline{{AMP}} }\nolimits_{\text{obs}} }}{{\mathop {\overline{{AMP}} }\nolimits_{\text{ref}} }}$$

(6)

2.3.3 Test for stationarity

Stationarity of the data is a common assumption in many time series analyses. Stationarity is a property by which statistical properties such as the mean, variance and autocorrelation do not change with time. The concept of stationarity is an important aspect especially when the time series is used for forecasting. Also, the complexity of a model that can be used for an analysis can be reduced with this assumption (Adhikari and Agrawal 2013). A number of recent studies advocate that the hydroclimatic extremes exhibit nonstationarity under anthropogenic climate change (Milly Paul Christopher et al. 2008; Das and Umamahesh 2017). So testing the stationarity of the annual maximum series helps to identify whether there is any likelihood of changes in the pattern of extreme precipitation in the river basin over time. Also it will help to identify the analyses that are suitable with either of the stationary or nonstationary assumptions. Present study uses Kwiatkowski, Phillips, Schmidt and Shin (KPSS) test to check the stationarity of the annual maximum series.

2.3.3.1 Kwiatkowski, Phillips, Schmidt and Shin (KPSS) test

It is used to test the null hypothesis that a univariate time series is stationary against the alternative hypothesis that it is nonstationary (Shin and Schmidt 1992). In this test, the time series ($X_{t} ,t = 1,2, \ldots n$) is decomposed into the sum of a random walk $\mathop R\nolimits_{t}$, deterministic trend $\beta t$ and a stationary error $\mathop \xi \nolimits_{t}$.This test depends on the linear regression model given by Eq. 7.

$$X_{t} = R_{t} + \beta t + \xi_{t}$$

(7)

where the random walk,$\mathop R\nolimits_{t} = \mathop R\nolimits_{{t{ - }1}} + \mathop U\nolimits_{t}$, $\mathop U\nolimits_{t}$ is an identically distributed process with zero mean and variance $\mathop \sigma \nolimits_{u}^{2}$ and $\mathop \xi \nolimits_{t}$ is a stationary error.

If a linear regression model with $\beta = 0$ is used, the test checks whether the series is stationary about a fixed level or not (level stationarity). If the regression model with $\beta$ term is used, the test checks whether the data series is stationary about a deterministic trend or not (trend stationarity).

The KPSS test statistic (K) is given by Eq. 8

$$K = \frac{{\sum\nolimits_{t = 1}^{n} {S_{t}^{2} } }}{{n^{2} s^{2} }}$$

(8)

where $\mathop S\nolimits_{t}$ is the partial sum process of the residuals ($\mathop e\nolimits_{t}$). $\mathop e\nolimits_{t}$ can be obtained from the regression of X on an intercept for level stationarity test and the regression of X on an intercept and a time trend for trend stationarity test. $\mathop s\nolimits^{2}$ is the consistent estimator of long run variance and is dependent on lag length. Selection of lag length is an important aspect in the KPSS test. The criterion given by Schwert (2002) and Kwiatkowski et al. (1992) for selecting the lag length (l) is given by Eq. 9.

$$l = \text{int} \left[ {p \times \left( {\frac{n}{100}} \right)^{0.25} } \right],p = 4,12$$

(9)

where n is the length of the data series.

In the present study, KPSS-level stationarity test was performed on the observed annual maximum series and the bias-corrected ensemble-averaged annual maximum series under the RCPs 4.5 and 8.5 at 10% significance level for two lag lengths given by Eq. 9.

2.3.4 Statistical tests to identify the most suitable distribution

Annual maximum precipitation extracted from the observed daily data was fitted to frequency distributions widely used for the analysis of extreme values (WMO 1989) such as the log-normal (LNII and LNIII), log-Pearson type III and generalized extreme value distribution (GEV). Goodness of fit of the observed data with these distributions was checked using the Kolmogorov–Smirnov (KS) and Anderson–Darling (AD) test. The goodness-of-fit test measures the compatibility of random sample with a theoretical probability distribution.

2.3.4.1 Kolmogorov–Smirnov Test

This test can be used to decide whether the sample follows a specified distribution or not.

The Kolmogorov–Smirnov statistic (D) (Eq. 10) is defined as the largest vertical difference between the theoretical cumulative distribution function ($F(\mathop x\nolimits_{i} )$) and the empirical cumulative distribution function ($F_{n} (x)$) (Eq. 11) (Massey 1951; Chakravarti et al. 1967).

$$D = \hbox{max} (F(x_{i} ) - \frac{i - 1}{n},\frac{i}{n} - F(x_{i} ))$$

(10)

where $\mathop x\nolimits_{i}$ is the random sample, i = 1, 2… n

$$F_{n} (x) = \frac{1}{n}.[{\text{Number }}\,{\text{of }}\,{\text{observations }}\, \le \, \,x]$$

(11)

2.3.4.2 Anderson–Darling test

This test compares the fit of an observed cumulative distribution function to an expected cumulative distribution function (Stephens 1974; Scholz and Stephens 1987). This test gives more weight to the tails than the Kolmogorov–Smirnov test. The Anderson–Darling statistic ($\mathop A\nolimits^{2}$) (Eq. 12) is defined as:

$$\mathop A\nolimits^{2} = - n - \frac{1}{n}\sum\limits_{i}^{n} {(2i - 1).[\ln F(x_{i} ) + \ln (1 - F(x_{n - i + 1} ))]}$$

(12)

where $x_{i}$ is the random sample and i = 1, 2… n

When log-normal (LNII and LN III), log-Pearson type III and generalized extreme value (GEV) distribution were tested for goodness of fit in the observed data, GEV was ranked the first at Manjeri and Nilambur stations, whereas log-Pearson type III was the first at Kottamparamba station (Table 3). Since GEV was the best fit distribution for two out of the three stations, GEV was selected as the most suitable distribution for the river basin.

Table 3 Ranks of distributions in KS and AD tests

2.3.5 Generalized extreme value distribution

Generalized extreme value (GEV) distribution can be used for the maximum series of data when the extreme value distribution to which the data converges is not known (Jenkinson 1955, 1969). GEV distribution is widely used in most of the studies to obtain the extreme precipitation for a particular return period (Ragulina and Reitan 2017; Yin et al. 2016; Shang et al. 2011). The cumulative distribution function (cdf) of the GEV distribution is given by Eq. 13.

$$F(x) = \left\{ {\begin{array}{*{20}l} {{ \exp }\left\{ { - \mathop {\left[ {1 + k\left( {\frac{x - \xi }{\alpha }} \right)} \right]}\nolimits^{{ - \frac{1}{k}}} } \right\},k \ne 0} \\ {{ \exp }\left\{ { - { \exp }\left[ { - \left( {\frac{x - \xi }{\alpha }} \right)} \right]} \right\},k = 0} \\ \end{array} } \right.$$

(13)

where F(x) denotes the cumulative distribution function (cdf), α denotes scale parameter, $\xi$ denotes the location parameter and k is the shape parameter. Depending on the value of k, GEV takes a specific type of extreme value (EV) distribution (when k = 0, type I (EVI) or Gumbel distribution; when k < 0, type II (EVII) or Frechet distribution and when k > 0, type III (EVIII) or Weibull distribution).

The return level $\mathop x\nolimits_{T}$ of a given GEV-distributed random variable associated with a given return period T is given by Eq. 14 (Das and Umamahesh 2017; Cheng and Agha Kouchak 2014).

$$\mathop x\nolimits_{T} = \left\{ {\begin{array}{*{20}c} {\xi + \frac{\alpha }{k}\left\{ {\left[ { - \log \left( {1 - \frac{1}{T}} \right)} \right]^{ - k} - 1} \right\},k \ne 0} \\ {\xi + \alpha \left\{ { - \log \left[ { - \log \left( {1 - \frac{1}{T}} \right)} \right]} \right\},k = 0} \\ \end{array} } \right.$$

(14)

Parameters of the distribution were estimated using the maximum likelihood method (MLE) in the present study. MLE is one of the widely used methods of parameter estimation having many optimal properties such as efficiency, sufficiency, consistency and parameterization invariance (Myung 2003).

2.3.6 Uncertainty in the return levels

Uncertainty of an estimate is the range of values within which the true value is expected to lie (Ramsey and Thompson 2007). Uncertainty creeps in the output from many sources such as the sample chosen for the analysis, model errors, errors in projection, etc. Present study quantifies the uncertainty in a return level from the sample chosen for its estimation. Bootstrapping developed by Efron (1979) can be used to estimate uncertainty that arises from the sample taken for future forecasts. The basic concept behind bootstrapping is resampling of the original sample. The properties of the true estimate can be derived from the properties of bootstrapped samples. Zucchuni and Adamson (1989) used the bootstrap method to find the confidence intervals of the design storms. Hu et al. (2013) used a method based on bootstrapping to estimate the sampling uncertainty in hydrological frequency problem.

Bootstrapping algorithm used in the present study is as follows:

• 1. Original sample is resampled with replacement to N samples (1000).

• 2. Each sample is fitted to a generalized extreme value distribution, and parameters of each sample are estimated using the method of maximum likelihood.

• 3. Based on the N parameter vectors, N estimations of extreme precipitation quantile are obtained.

• 4. This is used to derive the range or distribution of the extreme precipitation quantile.

After doing the KPSS test on the annual maximum series of observations and future projections, the annual maximum series which were not stationary were found out. Then the annual maximum series were divided such that the individual blocks were stationary. Bootstrapping algorithm discussed above was applied on each of the stationary time blocks, and cumulative distribution functions as well as confidence intervals of the return levels were obtained.

3 Results and discussion

3.1 Reliability of the future projections

In the present study, the variation of extreme rainfall for return periods 10, 25 and 50 years under climate change scenarios RCP4.5 and RCP8.5 was assessed. Annual maximum precipitations from five GCM–RCM combinations, viz. ACCESS-CCAM, CNRM-CCAM, CCSM-CCAM, MPI-CCAM and MPI-REMO2009, were extracted. Using the REA technique described in Sect. 2.3.1, weights were assigned to each of the GCM–RCM combinations. The assigned weight indicates the degree of reliability of the projections of a particular GCM–RCM combination.

Table 4 shows the normalized weight of GCM–RCM combinations for the historical and the future RCP scenarios. Higher the weight of GCM–RCM combination, better is the reliability of its projection in the given scenario. Ensemble average of annual maximum precipitation projections can be obtained using these weights. All subsequent analyses are based on the ensemble-averaged projections.

Table 4 REA weights of the GCM–RCM combinations used

3.2 Statistics of bias-corrected annual maximum precipitation

The scaling factor used for bias correction at Kottamparamba was obtained from the ratio between the long-term mean of the observed annual maximum data (1979–2004) and the long-term mean of the ensemble-averaged annual maximum precipitation from the GCM–RCM combinations during the control run (1979–2004). The scaling factors for Manjeri and Nilambur were obtained in the same manner using the data from 1974 to 2004. The scaling factor thus obtained can be multiplied to the historic (1979–2004/1974–2004) and future (2010–2099) ensemble-averaged annual maximum series to get the corrected series for the respective time period.

To check the efficiency of the bias correction method used, the corrected ensemble-averaged annual maximum series during the historic period was compared with the observations. Figure 3 shows the cdfs of the ensemble-averaged annual maximum precipitation series of each station before and after bias correction for the historic period. Compared to the uncorrected series (raw), the cdfs of the bias-corrected series match closely with the cdfs of the observed series at all the stations considered in the study.

Fig. 3

cdfs of annual maximum precipitation series before and after bias correction at a Kottamparamba (1979–2004), b Manjeri (1974–2004) and c Nilambur (1974–2004)

Table 5 presents a comparison of some of the important statistics such as mean, median, 25th percentile and 75th percentile of the observed as well as the bias-corrected annual maximum precipitation (historic) series. The bias correction methodology followed was very efficient and resulted in a reasonably good match between the mean of the corrected series and that of the observations. Other statistics also showed a good match at all the three stations.

Table 5 Comparison of statistics of bias-corrected ensemble-averaged precipitation with that of the observed precipitation

3.3 Nature of annual maximum precipitation

In order to understand the behaviour of the extremes with time, stationarity test (KPSS-level test) was performed on the observed annual maximum series and the corrected ensemble-averaged annual maximum series under RCP scenarios; its results are presented in Table 6. If the test statistic is greater than the critical value at a particular significance level and the p value (probability of obtaining a test statistic) is less than the significance level, the null hypothesis of stationarity is rejected. From Table 6, it can be inferred that the observed annual maximum series at the three stations are stationary. However, the annual maximum series of RCPs 4.5 and 8.5 rejected the stationarity hypothesis. So the annual maximum series of RCP scenarios were split into three time blocks 2010–2039, 2040–2069 and 2070–2099 which were individually stationary. Stationarity of the individual time blocks can be inferred from the results of the KPSS test on each time block presented in Table 7.

Table 6 Results of the KPSS test for the observed and the corrected ensemble-averaged annual maximum precipitation series under RCP scenarios

Table 7 Results of the KPSS test for the various time blocks under RCP scenarios

3.4 Uncertainty ranges of extreme precipitation return levels

Uncertainty analysis using the bootstrapping algorithm discussed in Sect. 2.3.6 was performed on the three time blocks. The empirical frequency distribution curve of extreme precipitation of a particular return period corresponding to each block was obtained from it. Figures 4, 5 and 6 present the empirical frequency distribution curves for return periods 10, 25 and 50 years, at the three stations (Kottamparamba, Manjeri and Nilambur) considered in the study. It can be seen that cdfs of the extreme precipitation for all the return periods for the second time block (2040–2069) is shifted to the right of the first time block. Also, the cdfs of extreme precipitation for all return periods for the third time block (2070–2099) is shifted to the right of the second time block. This indicates that the extreme precipitation for all return periods shows an increasing nature for all the three time blocks, i.e. extreme precipitation for the time block 2040–2069 is higher than the extreme precipitation for the time block 2010–2039 and the extreme precipitation for 2070–2099 is higher than that for the time block 2040–2069.

Fig. 4

Empirical frequency distribution of extreme precipitation at Kottamparamba corresponding to RCP4.5 and RCP8.5 for aT = 10 years, bT = 25 years and cT = 50 years

Fig. 5

Empirical frequency distribution of extreme precipitation at Manjeri corresponding to RCP4.5 and RCP8.5 for aT = 10 years, bT = 25 years and cT = 50 years

Fig. 6

Empirical frequency distribution of extreme precipitation at Nilambur corresponding to RCP4.5 and RCP8.5 for aT = 10 years, bT = 25 years and cT = 50 years

It is important to consider the impacts of climate change into account, while designing a hydraulic structure. Conventional practice of design uses a small percentage in addition to the original design value to account for the climate change impact without studying its real effects in the study area. Extreme precipitation for some specified return periods is often used as the design value while designing the hydraulic structures. To account for the changes that may happen to the extreme precipitation under climate change, projections of climate models can be used. The expected value of the extreme precipitation for different return periods, determined both with the observations and with the future climate change scenarios, and the 90% confidence interval are presented in Tables 8 and 9. These confidence intervals (CI) were derived from the empirical frequency curves. Expectation of the extreme precipitation ($E(\mathop x\nolimits_{T} )$) corresponding to a particular return period can be taken as the design value.

Table 8 Extreme precipitation and 90% confidence intervals for different return periods for the observed period

Table 9 Extreme precipitation and 90% confidence intervals for different return periods under RCP scenarios

4 Conclusions

The present study analysed the variation of extreme precipitation in the Chaliyar river basin under climate change. Extreme precipitation under an intermediate emission scenario, RCP4.5, and the highest emission scenario, RCP8.5, were estimated from the ensemble-averaged projections of five GCM–RCM combinations. The extreme precipitations for return periods 10, 25 and 50 years were estimated for three future time blocks 2010–2039, 2040–2069 and 2070–2099. Results indicate that extreme precipitation for any return period is higher for the block 2040–2069 compared to that for the block 2010–2039; also, the extreme precipitation for 2070–2099 is higher compared to that for 2040–2069. This increase in extreme precipitation over time is an indication of nonstationarity of extremes in the river basin under climate change. When compared to the extreme precipitation estimated from the observations, its values for the future time periods under both the RCP scenarios are significantly higher. Also the extremes projected under RCP8.5 are higher compared to that under RCP4.5. The projected increase in extreme precipitation could affect the engineering design of hydraulic infrastructures. A serious discussion on revising and updating the design criteria must be initiated and appropriate revisions should be implemented so that the likely variations in extreme rainfall due to climate change are taken into account in the design process. Also the results of the study would be beneficial for effective management of the watershed.