1 Introduction

The devastating flooding effects of recent storms (Blake and Gibney 2011; Blake et al. 2013) have emphasized the importance of efficient (fast) and accurate tools that can facilitate real-time predictions of storm surge (Glahn et al. 2009; Das et al. 2010; Smith et al. 2011) or support probabilistic risk assessment (Resio et al. 2009; Toro et al. 2010; Jia and Taflanidis 2013), with the ultimate intention to reduce the economic- and life-loss potential of such events. Computational efficiency is an essential feature for these tools, especially when utilized to guide emergency management decisions (Cheung et al. 2003) made days prior to storm landfall utilizing NOAA National Hurricane Center (NHC) forecasts of hurricane track, size and intensity, including the uncertainty in these forecasts. NHC’s storm surge prediction framework is frequently used for this purpose, utilizing an ensemble of runs of the low-fidelity numerical storm surge model SLOSH (Glahn et al. 2009; Forbes and Rhome 2012). Though computationally efficient, the approach lacks fidelity due to low near-coast resolution and negligence of key processes such as wave forcing (Resio and Westerink 2008; Kerr et al. 2015). Depending on the application of interest, the lower accuracy resulting from this lower fidelity may be an important consideration. On the other hand, recent numerical advances in storm surge prediction (Cheung et al. 2003; Resio and Westerink 2008) have produced high-fidelity simulation models (Luettich et al. 1992; Zijlema 2010), including coupling waves and surge (Dietrich et al. 2011; Kennedy et al. 2012), that permit a detailed representation of the hydrodynamic processes and therefore support high accuracy forecasting (Bunya et al. 2010). Additionally, these high-fidelity model applications facilitate estimation of a variety of enhanced outputs such as inundation depths, waves, winds and currents. Unfortunately, the computational cost associated with their implementation is large, requiring thousands of CPU hours for each simulation (Tanaka et al. 2011), which limits their applicability. For example, during landfalling events they can be utilized, with advanced high-performance computational resources, to provide a small number of high-fidelity, deterministic predictions, but cannot facilitate thousand-run ensembles to examine the impact of forecasting errors in the predicted track or provide a quick updated prediction once new storm track information becomes available. Their implementation for regional hurricane risk assessment, requiring evaluation of response for a large number of scenarios (Toro et al. 2010), faces similar challenges.

This conundrum (fast versus accurate) has provided the incentive for researchers to examine surrogate and interpolation/regression methodologies that can provide fast predictions using a database of high-fidelity, synthetic storms, with the ultimate goal to maintain the accuracy of the numerical model utilized to produce this database while providing greatly enhanced computational efficiency. This is facilitated by providing a fast-to-compute approximation to the input/output relationship of the numerical model, exploiting information within this database. These efforts have been further motivated by the fact that various such databases are constantly created and updated for regional flooding and coastal hazard studies (IPET 2008; Niedoroda et al. 2010; Kennedy et al. 2012; USACE 2015). The underlying foundation of all these methodologies is the parameterization of each synthetic storm through a small number of variables, representing the input for the surrogate/regression model. Surge-response functions have been a popular approach examined within this context (Irish et al. 2009; Song et al. 2012; Taylor et al. 2015). So far, these methods can provide information only for the peak surge and they may impose limitations with respect to the variables that can be utilized for the aforementioned storm parameterization (Irish et al. 2009), stemming from challenges in developing/tuning dimensional response functions for a wide range of input parameters. Another methodology is the interpolation based on the concept of storm similarity index (Das et al. 2010). This approach can exhibit, though, reduced accuracy for storms that deviate from the backside database.

More recently, surrogate modeling concepts (also referenced as metamodels) have been introduced for this purpose. This approach allows a versatile parameterization of storms and supports calculation of a variety of different response outputs (surge, significant wave height, run-up). The first implementation within this family of methods examined the use of moving least squares response surface approximations (Taflanidis et al. 2013). Subsequent enhancements (Jia and Taflanidis 2013) considered kriging metamodeling and examined potential integration with principal component analysis (PCA) to improve computational efficiency when output dimension is large (over a few thousand different responses predicted). The implementation in Jia and Taflanidis (2013) was restricted, though, to only the peak responses and to nearshore nodes, avoiding challenges in predicting the surge for inland locations that might remain dry (“dry nodes”) in some of the storms within the database, and preference for development of multiple metamodels was given to support high accuracy, something that reduces, though, computational efficiency. Additionally, in both these studies (Jia and Taflanidis 2013; Taflanidis et al. 2013) the database adopted was developed with the intention to support the surrogate modeling, something that provided an a priori simple storm parameterization. More recently, artificial neural networks (Kim et al. 2015) were examined for predicting time-dependent surge estimations. This is an important advancement as time-series forecasting is essential for emergency response managers to understand how inundation will develop and recede as the storm passes. A moving averaging was introduced in Kim et al. (2015) to avoid discontinuous oscillations of the predictions in the time series, which might, like any such low-pass filter, reduce accuracy. This application was restricted to a small number of locations on the coast of Louisiana, whereas a limitation of this point-based method is that it does not take advantage of the high degree of spatial continuity in storm surge estimates.

The current paper addresses the research gaps identified in the previous paragraph, offering a surrogate model with high computational efficiency that can support estimation of high-dimensional responses (extending over a large coastal region) while addressing the existence of dry nodes within the utilized database and the time-dependence of the output without the need to adopt moving averaging for facilitating continuous predictions. The foundation of the implementation, as in Jia and Taflanidis (2013), is the integration of kriging metamodeling with PCA, with the latter leveraging the correlation within the database to derive a lower-dimensional output for the development of the surrogate model. To support the intended implementation, and different from (Jia and Taflanidis 2013), the following advancements are provided in this paper: (a.i) The time-series prediction capabilities of the kriging metamodel are examined by (a.ii) leveraging the PCA to facilitate high accuracy and continuity in the forecasts without the need to use time averaging; (a.iii) development over significantly higher output dimension than in Jia and Taflanidis (2013) is considered and (a.iv) the impact of dry nodes is addressed, providing a detailed assessment of the influence of both these features on accuracy/efficiency; (a.v) modifications are examined for the integrated kriging + PCA so that a single metamodel can provide high accuracy; and (a.vi) the implementation for a new database that does not provide an a priori, simple parameterization is considered. These six topics establish the novel contributions of this paper. The performance of the surrogate modeling approach is evaluated through a case study, utilizing a database of 446 storms for the Gulf of Mexico (USACE 2009; Kim et al. 2015). The output includes time histories for 30 locations over a period of 45.5 h with a total of 92 uniform time steps as well as peak responses for 545,635 nearshore nodes.

In the following section, an overview of the kriging metamodeling implementation is provided. In Sect. 3 the database characteristics are presented, and in Sect. 4 the parameterization of the storm scenarios and the modification of the output, corresponding to augmentation of information for dry nodes, are discussed. In Sect. 5 mathematical details for the framework for kriging metamodeling with PCA are reviewed and modifications to facilitate predictions utilizing a single surrogate model are proposed. Section 6 discusses in detail the case study, examining separately the implementation for outputs with temporal and spatial correlation.

2 Overview of surrogate modeling implementation

The surrogate modeling approach considered here provides a simplified, fast-to-compute mathematical approximation to the input/output relationship of a computationally expensive numerical model. This is established by utilizing a database of simulations from this numerical model that ultimately provides implicit information for the input/output relationship. For storm surge forecasting this database corresponds to synthetic storms created through a specific simulation model. The accuracy of the metamodel may be improved if the database is properly designed for this purpose (Sacks et al. 1989), for example through sequential selection of each synthetic storm to maximize the anticipated benefits (Kleijnen and Van Beers 2004). Even when an already established database is utilized, as is the case examined in this paper, the metamodel can be still tuned to provide good accuracy as will be shown later.

An important characteristic of this metamodeling approach is that no explicit information is utilized for the input/output relationship. This means that any chosen, adequate parameterization can be adopted for the synthetic storms, whereas any desired output can be predicted. Therefore, predictions may be established for any output quantity, such as waves, runup or surge, whereas the output vector may even have a large dimension (over a few thousand different responses). The latter will be the case when implementation over a large coastal region is examined that includes a large number of locations we need to know the output for. Each component of the output vector corresponds to the output at a specific location (within the coastal region examined) or specific time instance (when time-series forecasting is established). Ultimately each of these components is separately predicted through the metamodel. Information about spatial distribution of the outputs or temporal relationship between outputs (whether output is a peak response or response at a specific time instance) is not utilized.

The surrogate model ultimately exploits the available database to establish the desired approximation to the input/output relationship. For kriging this is expressed through simple matrix expressions (more details in Sect. 5.2 later), something that facilitates high computational efficiency. Kriging has been also shown in a number of studies (Kleijnen 2009) to be capable of providing accurate predictions even for complex numerical models, i.e., models resulting in highly nonlinear relationships between inputs and outputs, as long as the database informing its formation is sufficiently large. The latter can be evaluated through assessment of its accuracy based on cross-validation criteria (more details in Sect. 5.5). This further supports the transferability of the approach, i.e., its independence of the database utilized; not only is this a data-driven method using no explicit information for the input/output relationship as discussed in the previous paragraph, but also it has the potential to accurately approximate any high-fidelity numerical model.

After the metamodel is developed it may be utilized to provide predictions for the output for any new input, i.e., storm. This can be established for a specific storm or for providing probabilistic forecasts, examining a large number of storm scenarios, for example, by addressing forecasting errors in the predicted storm track (Taflanidis et al. 2013). The computational efficiency of the metamodel can be further exploited to facilitate the development of standalone forecasting tools, as demonstrated in Smith et al. (2011) for the Hawaiian islands, or even support the cyber implementation of rapid risk assessment, as shown in Kijewski-Correa et al. (2014). For such type of applications, especially when implementation over an extended coastal domain is examined, the computational efficiency as well as the memory requirements can be improved through integration of a dimension reduction technique. This approach reduces the dimensionality of the output vector by extracting a smaller number of outputs, frequently called latent outputs, to represent the initial high-dimensional output. Considering the potential strong correlation between responses at different locations or at different time instances, this approach can significantly improve the computational efficiency without compromising accuracy (Chen et al. 2011; Jia and Taflanidis 2013). Principal component analysis (PCA), which is a data-driven dimension reduction technique (Jolliffe 2002), will be adopted here for this purpose (more details in Sect. 5.1). Like the kriging metamodel, this approach does not utilize any spatial/temporal information for the outputs; rather it simply exploits the implicit correlation within the database.

The emphasis in this paper is on the metamodel development utilizing an existing database of synthetic storms. Further details on use of such metamodels as forecasting tools may be found in the aforementioned studies (Smith et al. 2011; Taflanidis et al. 2013; Kijewski-Correa et al. 2014). Next, relevant details of the database used in the case study are provided, before moving on to the remaining aspects of the surrogate model development.

3 Details for synthetic storm database and output

The database utilized in this study is the same as in Kim et al. (2015) and corresponds to the greater New Orleans area and the southeast Louisiana region. This database was initially developed for evaluation of the regional hurricane protection system (IPET 2008; USACE 2009), not with the intention of supporting the formulation of surrogate models. It consists of 304 high-intensity storms and 142 low-intensity storms for a total of 446 storms, simulated by a coupled high-fidelity numerical hydrodynamic model composed of steady-state spectral wave model (STWAVE) (Smith et al. 2001) and advanced circulation model (ADCIRC) (Luettich et al. 1992), with the planetary boundary layer (PBL) model providing wind and pressure input to this coupled hydrodynamic model (Westerink et al. 2008). The computational domain for generating the synthetic storms consists of 2,137,978 nodes. Further details about the atmospheric and hydrodynamic model utilized may be found in (IPET 2008).

The synthetic storms have been generated utilizing the joint probability method (JPM) optimal sampling approach (Niedoroda et al. 2008; Toro et al. 2010), considering the historic characteristics of regional storms. Two separate families of 223 storms each, consisting of 152 high-intensity and 71 low-intensity storms, have been considered with respect to landfall locations in eastern and western Louisiana. These storms correspond to probable combinations of central pressure, radius of maximum winds, forward speed, as well as track for the region. Holland B number (Holland 1980) was kept constant for all storms and a uniform steric water-level adjustment of 0.36576 m from terrestrial datum (NAVD88 2004.65) was applied over the simulation domain to account for seasonal local water-level changes resulting from thermal expansion of the Gulf. With respect to the high-intensity storms, 50 storms are in Category 3, 52 in Category 4 and 50 in Category 5 according to the Saffir-Simpson intensity scale, with return periods ranging from 50 to 3500 years.

For the characterization of each of these storms, the input that is available within the database corresponds to the longitude, x lon, and latitude, x lat, of storm track, the central pressure in mbar, c p, the heading direction, θ, the forward speed in knots (kn), v f, and the radius of the exponential pressure profile for the PBL wind pressure model in nautical miles (nm) R p, which is related to the radius of maximum wind speed. Location of landfall for each synthetic storm is explicitly characterized within the database, whereas the input information extends a few days before and a day after that landfall with a time step of 1 h. Typical input extends over a total of 97 h, and an example is provided in Appendix A. For each storm the central pressure c p decreases as the storm intensifies approaching the coast, then reaches its minimum value which is representative of the storm category and finally increases again as the storm makes landfall, with the exact distance inland from the coast that the latter happens depending upon R p. The minimum value for c p relates to the category of the storm and is 900, 930 or 960 mbar for storms in Category 5, 4 and 3, respectively, and 975 mbar for low-intensity storms. Values for R p and v f remain practically constant before landfall but exhibit strong variation after storm makes landfall.

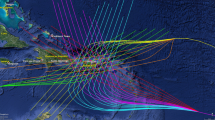
The different tracks and landfall locations for the storms within the database for eastern and western Louisiana are shown in Fig. 1. Three track groups can be distinguished in each region, reported in the figure with different line types and with identifiers T1, T2 and T3. For eastern Louisiana, two secondary track groups can also be distinguished, corresponding to storms with different forward speeds within the T2 family. Table 1 provides details for each of the track groups: the total number of storms as well as the combination of parameters examined for each track.

Fig. 1
figure 1

Storm track groups for eastern (black) and western (gray) Louisiana

Full size image
Table 1 Characteristics for the different synthetic storms in the database
Full size table

Two different outputs are examined here. The first output corresponds to the peak storm surge over 545,635 output points, corresponding to nearshore nodes for the computational grid (IPET 2008) within the region between 87.5 W and 93.5 W longitude and latitude greater than 28.5 N (Louisiana coast). The second output corresponds to time histories for 30 selected nodes, corresponding to critical points for the regional flood protection system as well as points in identified vulnerable areas. The location of these points is reported in Kim et al. (2015). At these 30 nodes, the time-series information for each of these inputs is provided with a time step of 30 min for a total of 92 steps (46.5 h), extending 21.5 h before and 24 h after the landfall (times when significant surge is expected). This leads to an additional 2760 different outputs (92 outputs for each of the 30 nodes).

4 Parameterization of database and augmentation of output

4.1 Parameterization of storms

For establishing a surrogate model, the appropriate parameterization of the database of synthetic storms is required to provide the model input. This parameterization needs to capture all important features that distinguish the different storms from one another but also avoid over-parameterization, since this can lead to reduction in computational accuracy as well as numerical problems when input parameters exhibit high correlation within the available database (Lophaven et al. 2002). Characteristics of storms at or close to landfall are commonly selected for this purpose, considering their strong correlation to peak surge responses (Resio et al. 2009; Taflanidis et al. 2013). Of course, track/strength variability prior to landfall can also be important, depending on the output examined (for example, higher importance is anticipated when examining time-series forecasting). The underlying assumption is that this variability is addressed by appropriate selection of each track history when creating the initial database. Since the synthetic storms considered here have been generated utilizing the JPM approach, they satisfy this criterion. Therefore, a parameterization through a small number of parameters is justifiable.

Two separate families of inputs may be distinguished in this parameterization, intensity/size/speed related and track related. For the former, the values of c p, v f and R p at peak hurricane intensity prior to landfall (which are the ones reported in Table 1) are chosen since these were the ones also utilized within the JPM approach for creating the synthetic storms. Because the intention for developing such surrogate models is to eventually use them in forecasting mode, the radius of maximum wind speed R m is chosen over R p since the former is the one provided by the NHC during landfalling events. Following the recommendations in Kim et al. (2015), the relationship between R p and R m is obtained as

$$R_{\text{m}} = 0.5387 + 0.9524R_{\text{p}} - 0.00575R_{\text{p}}^{2} + 1.17 \times 10^{ - 5} R_{\text{p}}^{3}$$
(1)

where both radii are in nautical miles.

For the track characterization, it is evident from Fig. 1 that an adequate parameterization can be established based on a reference location and angle of approach (heading direction). These two inputs uniquely define each track as also shown in Fig. 2 for family T1 in eastern and western Louisiana. Two different parameterizations will be examined here, both also demonstrated in the latter figure. The first adopts the suggestions by Taflanidis et al. (2013); the reference landfall is determined at a specific reference latitude, in this case when each storm crosses 29.5 N. This leads then to the longitude for the reference landfall, x lon, and the heading direction θ at that time step as inputs. The second parameterization utilizes the conventional landfall location (instead of the reference landfall), which as discussed earlier is explicitly defined within the storm input provided. Only the landfall longitude (and not additionally the latitude) is adopted as input, as this is sufficient for a unique definition of each storm based on the shape of the coast in the examined region. As evident in Fig. 2, additionally adopting the landfall latitude in the characterization of each storm would lead to an over-parameterization of the storm input (landfall latitude and longitude are correlated for a specific coastal region).

Fig. 2
figure 2

Illustration of track characterization for the T1 track groups in western (left) and eastern (right) Louisiana

Full size image

Therefore, the n x  = 5 dimensional input vector for parameterization of each synthetic storm corresponds to the (i) reference landfall location x lon, (ii) heading direction θ at that location, (iii) central pressure c p, (iv) forward speed v f and (v) radius of maximum winds R m when each storm reaches its maximum intensity.

$${\mathbf{x}} = [\begin{array}{*{20}c} {x_{\text{lon}} } & \theta & {c_{\text{p}} } & {v_{\text{f}} } & {R_{\text{m}} } \\ \end{array} ]^{\text{T}}$$
(2)

Based on the characteristics of the database discussed in Sect. 3, the following variability exists for these input parameters: c p has four different values [900, 930, 960, 975] mbar, forward speeds v f has three different values [6, 11, 17] kn, radius of max winds R m takes thirteen values [6.05, 7.80, 10.33, 11.57, 13.50, 15.65, 16.04, 16.19, 18.11, 18.69, 20.66, 21.48, 27.69] nm and 50 different values are considered for the reference location and heading, with landfall locations spanning from 94.5° to 88.5° west and heading direction ranging from 120° to 223° (north = 180°).

A final important issue to note is that since no tide variation has been considered in the generation of the synthetic storms, the tide cannot be considered as an explicit input. Its influence can be approximated in forecasting applications by first subtracting the excess steric adjustments used for the synthetic storms from the predicted storm surge and then adding the actual tide over a specific area (Resio et al. 2009; Kim et al. 2015). Here, the subtraction of the steric adjustments, used to account for seasonal local water-level changes resulting from thermal expansion of the Gulf, is because all synthetic storms already include the influence of this thermal expansion.

4.2 Adjustment for dry nodes

Before developing the surrogate model, an adjustment is required for inland locations. The challenge with these locations is that they do not always get inundated; in other words dry locations might remain dry for some storms. For example, in the implementation considered here, 59,867 nodes, corresponding to 11 % of the total output, have only been inundated in 10 % or fewer of the synthetic storms. For such cases the only information available is that the location remained dry.

One approach to address this challenge would be to develop a separate surrogate model (Burges 1998) for the binary output representing the condition of the location, i.e., either wet or dry. If we prefer to avoid this, or if we additionally need to know exactly the storm surge, the initial database can be augmented to show an approximate storm water elevation at each node without regard to whether that water elevation is above or below ground level. To facilitate this, the approach proposed in Taflanidis et al. (2012) is adopted. The storm water elevation is described with respect to the mean sea level as reference point. When a location remains dry, the storm water elevation corresponding to the nearest location (nearest node in the high-fidelity numerical model) that was inundated is used as an approximation. The database is adjusted for the scenarios for which each location remained dry, and the updated response database is used as the basis data for the surrogate model. Comparison of the predicted storm water elevation to the ground elevation of the location indicates whether the location was inundated or not, whereas the storm surge is calculated by subtracting these two quantities. The latter is defined here as the height of inundation with respect to the ground. Thus, this approach allows us to gather simultaneous information about both the inundation (binary answer; yes or no) and the storm surge, although it does involve the aforementioned approximation for enhancing the database with complete information for the surge elevation for all nodes/storms.

5 Kriging surrogate modeling with principal component analysis

After appropriate parameterization of the input and modification of the output, each synthetic storm is characterized by the n x dimensional input vector \({\mathbf{x}} = [x_{1} \, \, \ldots \,x_{i} \, \, \ldots \,x_{{n_{x} }} ]\) (n x  = 5 for the application considered here) and provides n y dimensional output vector y(x). As discussed in Sect. 3, each component of y(x), denoted y k (x) herein, pertains to a specific response output at a specific coastal location or specific instant in time, whereas n y can be high. For the specific applications examined here, n y  = 545,635 for the peak storm surge response and n y  = 2760 for the time-series forecasting. A database of n (n = 446 for the application considered here) high-fidelity simulations (observations) is available with evaluations of the response vector {y h; h = 1, …, n} for different storm scenarios {x h; h = 1, …, n}. We will denote by \({\mathbf{X}} = [{\mathbf{x}}^{1} \; \ldots \,{\mathbf{x}}^{n} ]^{T} \in {\mathbb{R}}^{{n \times n_{x} }}\) and \({\mathbf{Y}} = [{\mathbf{y}}^{1} \, \ldots \,{\mathbf{y}}^{n} ]^{T} \in {\mathbb{R}}^{{n \times n_{y} }}\) the corresponding input and output matrices, respectively. These observations are frequently referenced as the training set or support points.

Various formulations can be considered for the surrogate model for prediction over the different output components: A separate metamodel can be trained for each of the outputs, a single metamodel can be considered for all of them, or a small number of metamodels can be established, each representing a sub-group of outputs (based on some desired classification for definition of the sub-groups). The first choice might be impractical if the number of outputs is large, and it additionally provides non-smooth predictions, as will be also demonstrated later, for time-series forecasting since it does not explicitly incorporate information about the relationship for each response output at different times. For a large dimensional output, as is the case examined here, the development of a single metamodel (or of a relatively small number of metamodels) is preferable to facilitate computational efficiency. To further improve this efficiency, integration with PCA is adopted, as discussed in Sect. 2, for reduction in the dimension of the output. This is established simply by exploiting the correlation within the observation matrix Y. PCA provides a low-dimensional space of outputs (latent outputs), and the surrogate model can then be developed in this space, with the metamodel predictions first established in the latent space and then transformed back to the initial, high-dimensional output space. An overview of the overall approach is summarized in Fig. 3. In the following three sub-sections the mathematical framework is briefly reviewed, with sufficient details to facilitate the discussions around the novel aspects of the paper. Some details related to the tuning/optimization of the kriging metamodel are also discussed in Sect. 5.4. Then, specifics for the kriging and PCA integration are examined, and the validation framework for the metamodel accuracy is presented.

Fig. 3
figure 3

Schematic for kriging with PCA implementation

Full size image

5.1 Output dimension reduction by PCA

PCA is implemented by first converting output into zero mean and unit variance under the statistics of the observation set through the linear transformation

$${\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y}}_{k} = \frac{{y_{k} - \mu_{k}^{y} }}{{\sigma_{k}^{y} }},{\text{ with }}\mu_{k}^{y} = \frac{1}{n}\sum\limits_{h = 1}^{n} {y_{k}^{h} } ,\sigma_{k}^{y} = \sqrt {\frac{1}{n}\sum\limits_{h = 1}^{n} {\left( {y_{k}^{h} - \mu_{k}^{y} } \right)}^{2} }$$
(3)

The corresponding (normalized) vector for the output is denoted by \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} }}\) and the observation matrix by \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Y} }}\). The eigenvalue problem for the covariance matrix \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Y} }}^{T} {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Y} }}\) is then considered and only the m c largest eigenvalues, along with associated eigenvectors, are retained. These correspond to the principal directions that represent the components with largest variability within the initial database (Jolliffe 2002), and each equivalently defines a latent output z j , j = 1, …, m c . The relationship between the initial output vector and the vector of the latent outputs z \({=}\, [z_{1} \, \ldots \,z_{{m_{c} }} ]\), facilitating the transformation back to the original space, is

$${\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} }} = {\mathbf{Pz}}$$
(4)

where P is the \(n_{y} \times m_{c}\) projection matrix containing the eigenvectors corresponding to the \(m_{c}\) largest eigenvalues. The \(n \times m_{c}\) observation matrix Z for z, needed for the surrogate model development, is \({\mathbf{Z}}^{T} = {\mathbf{P}}^{ - 1} {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Y} }}^{T}\), whereas m c can be chosen so that latent outputs account at least for r o [say 99 %] of the total variance of the data (Tipping and Bishop 1999). If λ j is the jth largest eigenvalue, then this is facilitated by selecting \(m_{c}\) so that the ratio

$$r_{c} = \sum\nolimits_{j = 1}^{{m_{c} }} {\lambda_{j} } \left/\sum\nolimits_{j = 1}^{{n_{y} }} {\lambda_{j} } \right.$$
(5)

is greater than r o . It is then m c  < min(n, n y ), with m c being usually a small fraction of min(n, n y ). For n ≪ n y , obviously, m c  ≪ n y , leading to a significant reduction in the dimension of the output.

5.2 Kriging surrogate model

The kriging metamodel is established for vector z with observation matrix Z. If PCA is not adopted, then these would have been replaced by y and Y, respectively. Kriging provides a metamodel approximation to z, denoted \({\hat{\mathbf{z}}}({\mathbf{x}})\), as well as the variance of the approximation error for each component z j , denoted \(\sigma_{j}^{2} ({\mathbf{x}})\). This error follows a Gaussian distribution, stemming from the fact that kriging is a Gaussian process metamodel (Sacks et al. 1989). The fundamental building blocks of kriging are the n p dimensional basis vector, f(x) [for example, linear or quadratic polynomial], and the correlation function R(x j,x k) with tuning parameters s. An example for the latter (the one used in the case study here) is the generalized exponential correlation,

$$R({\mathbf{x}}^{l} ,{\mathbf{x}}^{m} ) = \prod\nolimits_{i = 1}^{{n_{x} }} {\exp [ - s_{i} |{\mathbf{x}}_{i}^{l} - {\mathbf{x}}_{i}^{m} |^{{s_{{n_{x} + 1}} }} ]} { ; }\,{\mathbf{s}} = [s_{1} \, \cdots {\text{ s}}_{{n_{x} + 1}} ].$$
(6)

For the set of n observations with input matrix X and corresponding latent output matrix Z, we then define the \(n \times n_{p}\) basis matrix \({\mathbf{F}} = [{\mathbf{f}}({\mathbf{x}}^{1} )\, \ldots \,{\mathbf{f}}({\mathbf{x}}^{n} )]^{\text{T}}\) and the correlation matrix \({\mathbf{R}}\) with the j, k elements defined as R(x j , x k), j, k = 1, …, n. Also for every new input x we define the n-dimensional correlation vector r(x) = [R(x, x 1) … R(x, x n)]T between the input and each of the elements of X. The kriging prediction is finally (Sacks et al. 1989)

$${\hat{\mathbf{z}}}({\mathbf{x}}) = {\mathbf{f}}({\mathbf{x}})^{\text{T}} {\varvec{\upalpha}}_{{}}^{*} + {\mathbf{r}}({\mathbf{x}})^{\text{T}} {\varvec{\upbeta}}_{{}}^{*}$$
(7)

where \({\varvec{\upalpha}}_{{}}^{*} = ({\mathbf{F}}_{{}}^{\text{T}} {\mathbf{R}}_{{}}^{ - 1} {\mathbf{F}}_{{}} )^{ - 1} {\mathbf{F}}_{{}}^{T} {\mathbf{R}}_{{}}^{ - 1} {\mathbf{Z}}\) and \({\varvec{\upbeta}}_{{}}^{*} = {\mathbf{R}}_{{}}^{ - 1} ({\mathbf{Z}} - {\mathbf{F\varvec{\upalpha} }}_{{}}^{*} )\) are the \(n_{p} \times m_{c}\) dimensional and \(n \times m_{c}\) dimensional, respectively, coefficient matrices.

Through the proper tuning of the parameters s of the correlation function, kriging can efficiently approximate very complex functions. The optimal selection of s is typically based on the maximum likelihood estimation (MLE) principle (Lophaven et al. 2002), leading to optimization problem

$${\mathbf{s}}^{ * } = \mathop {\arg \hbox{min} }\limits_{{\mathbf{s}}} \left[ {\left| {\mathbf{R}} \right|^{{\tfrac{1}{n}}} \sum\nolimits_{j = 1}^{{m_{c} }} {\frac{1}{{\gamma_{j} }}\tilde{\sigma }_{j}^{2} } } \right]$$
(8)

where |.| stands for determinant of a matrix, γ j is a weight for each output quantity, equivalently representing scaling for the output and typically chosen as the variance over the observations Z, and \(\tilde{\sigma }_{j}^{2}\) corresponds to the process variance (mean square error) and is given by the diagonal elements of the matrix \(({\mathbf{Z}} - {\mathbf{F\varvec{\upalpha} }}_{{}}^{*} )^{\text{T}} {\mathbf{R}}^{ - 1} ({\mathbf{Z}} - {\mathbf{F\varvec{\upalpha} }}_{{}}^{*} )/n\). Standard approaches for solving this optimization are given in Lophaven et al. (2002) and involve in general small computational effort. Note that Eq. (8) supports tuning of the kriging metamodel to maximize accuracy in the latent output space. Though this is evidently correlated to establishing high accuracy for the original output y, it is not guaranteed to provide optimal accuracy for y. In other words, there might be a different selection for s that provides higher accuracy when specifically examining error statistics over y. Identifying this, though, will entail a very challenging optimization (involving transformation of the predictions for each s examined back to the high-dimensional space y and optimization over some error measure there) and should be avoided since the approach in Eq. (8) can facilitate high accuracy and is very efficiently performed.

If multiple metamodels are established for the different output components, then this process needs to be separately implemented for each one of them, leading to vectors \({\varvec{\upalpha}}_{j}^{*}\)(with dimension n p ) and \({\varvec{\upbeta}}_{j}^{*}\) (with dimension n) and tuning parameters s j that are different for each output (Jia and Taflanidis 2013). The metamodel predictions, expressed through Eq. (7), are then established for each output separately, with the correlation vector r j (x) being also different for each output (stemming from the differences in s j ).

Beyond the approximation Eq. (7), kriging also provides an estimate for the approximation error variance \(\sigma_{j}^{2} ({\mathbf{x}})\). This is a local estimate, meaning that it is a function of the input x and not constant over the entire domain X, and for output z j is given by

$$\sigma_{j}^{2} ({\mathbf{x}}) = \tilde{\sigma }_{j}^{2} [1 + {\mathbf{u}}({\mathbf{x}})^{\text{T}} ({\mathbf{F}}_{{}}^{\text{T}} {\mathbf{R}}_{{}}^{ - 1} {\mathbf{F}}_{{}} )^{ - 1} {\mathbf{u}}({\mathbf{x}}) - {\mathbf{r}}({\mathbf{x}})^{\text{T}} {\mathbf{R}}_{{}}^{ - 1} {\mathbf{r}}({\mathbf{x}})]$$
(9)

where \({\mathbf{u}}({\mathbf{x}}) = {\mathbf{F}}_{{}}^{\text{T}} {\mathbf{R}}_{{}}^{ - 1} {\mathbf{r}}({\mathbf{x}}) - {\mathbf{f}}({\mathbf{x}})\). This statistical information about the kriging error can be utilized when predictions for the different outputs are established, as will be also demonstrated later, while it additionally can be incorporated in risk assessment applications (Jia and Taflanidis 2013).

5.3 Transformation to the original space

The predictions provided by the surrogate model need to be transformed from the latent space to the original space. Utilizing Eqs. (4) and (3) leads to the following prediction for y(x), \({\hat{\mathbf{y}}}({\mathbf{x}}) = {\varvec{\Sigma}}^{y} \left({\mathbf{P}}{\hat{\mathbf{z}}}({\mathbf{x}}) \right) + {\varvec{\upmu}}^{y}\), where Σ y is the diagonal matrix with elements \(\sigma_{k}^{y}\) and μ y is the vector with elements \(\mu_{k}^{y}\) k = 1, …, n y . The variance \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{k}^{2} ({\mathbf{x}})\) of the approximation error for y k (x) corresponds to the diagonal elements of the matrix \({\varvec{\Sigma}}^{y} [{\mathbf{P}}{\varvec{\upsigma}}({\mathbf{x}}){\mathbf{P}}^{T} + \upsilon^{2} {\mathbf{I}}]{\varvec{\Sigma}}^{y}\) (Jia and Taflanidis 2013), where σ(x) is the diagonal matrix with elements \(\sigma_{j}^{2} ({\mathbf{x}})\), j = 1, …, m c , and \(\upsilon^{2} {\mathbf{I}}\) stems from truncation errors in PCA. An estimate for the latter is given by \(\upsilon^{2} = \sum\nolimits_{{j = m_{c} + 1}}^{{n_{y} }} {\lambda_{j} /(n_{y} - m_{c} )}\), corresponding to the average variance of the discarded dimensions when formulating the latent output space. Since PCA is a linear projection, the prediction error for y also follows a Gaussian distribution (same as z).

5.4 Characteristics for kriging and for its integration with PCA

Kriging offers as a metamodel a few important advantages for the implementation examined here (storm surge prediction with potential high-dimensional output). Firstly, the kriging predictions are efficiently performed through the matrix manipulations in Eq. (7); this requires keeping in memory only matrices \({\varvec{\upalpha}}^{*}\) and \({\varvec{\upbeta}}^{*}\) and calculating for each new x of vectors f(x) and r(x). Implementation involves no matrix inversions, which provides high computational efficiency when compared to other metamodels with similar accuracy, such as moving least squares response surface approximation. Furthermore, when the initial database is sufficiently large, kriging provides better behavior than such metamodels when used for extrapolation (Noon and Winer 2009), that is, when providing predictions for inputs that are outside the range covered by the initial database (though this practice should be, in general, avoided). Additionally, training of kriging through optimization of Eq. (8) for identification of the optimal vector s can be very efficiently performed, and kriging facilitates an estimate for the prediction accuracy through Eq. (9). Finally kriging is an exact interpolation, which means that when the new input is the same as one of the initial support points, the prediction will match the actual response, or equivalently variance \(\sigma_{j}^{2} ({\mathbf{x}})\) for each output will be zero at support points.

Integration, now, of PCA with kriging reduces the dimension of matrices \({\varvec{\upalpha}}^{*}\) and \({\varvec{\upbeta}}^{*}\) from n y to m c (\(n_{p} \times m_{c}\) rather than \(n_{p} \times n_{y}\) for \({\varvec{\upalpha}}^{*}\) and \(n \times m_{c}\) rather than \(n \times n_{y}\) for \({\varvec{\upbeta}}^{*}\)), reducing significantly the memory requirements and facilitating higher computational efficiency in establishing the kriging predictions through Eq. (7). This also contributes to matrix manipulation that, due to the low dimension of the involved matrices, can be very easily vectorized (more details discussed in Jia and Taflanidis 2013). The latter is important when the surrogate model is utilized to provide forecasts, examining a large number of storm scenarios resulting from the NHC estimation errors for track/intensity. The ability to vectorize the matrix manipulations allows estimation for all these scenarios with only a very small additional computational burden compared to predictions for a single storm/scenario. Furthermore, the significantly reduced memory requirements are essential for supporting real-time forecasting tools that can be easily distributed and even implemented within cyber platforms (Smith et al. 2011; Kijewski-Correa et al. 2014). With respect to the cyber implementation, this allows platforms that can simultaneously support multiple users within a collaborative environment.

Additionally, the correlation between responses at different locations or different time instances are directly captured through PCA, and for predictions at new inputs this correlation is automatically recovered when the predictions in the latent space are transformed back to the original space. This means, for example, that continuity for the output in time-series forecasting can be automatically established, without the need to introduce remedies such as the time averaging discussed earlier. Furthermore, since the number of latent outputs is typically small, development of metamodels for each of them separately can be considered. The more efficient application is, though, to consider a single metamodel. Of particular importance in this case is the fact that the components of z have an associated relevance, represented by their variance, which is proportional to eigenvalue λ j , the portion of the variability within the initial database represented from each latent output. This means that, contrary to common approaches for normalizing vector z within the surrogate model optimization of Eq. (8) through the introduction of weights γ j , in this case no normalization should be established, i.e., γ j  = 1. This equivalently corresponds to latent outputs with larger values of λ j being given higher priority in the surrogate model optimization.

Of course the incorporation of PCA and consideration of only a smaller number of latent outputs introduce an additional source of error (truncation error). However, a proper selection of the number of latent outputs, so that a large portion of the total variance of the initial observation matrix Y is retained, can lead to small errors stemming from this truncation. In addition, PCA requires that transformation matrix P with dimension \(n_{y} \times m_{c}\) is kept in memory. Since this can be a large dimensional matrix, maintaining a smaller value for m c (but large enough to minimize PCA errors) offers significant advantages. It should be stressed here that despite the requirement to additionally keep P in memory, PCA still supports great computational savings, as will be demonstrated in the example later.

5.5 Assessment of metamodel accuracy

The accuracy of the metamodel can be evaluated directly by the process variance \(\tilde{\sigma }_{j}^{2}\) which assesses, though, the performance with respect to the latent outputs, not the actual outputs. An alternative is to calculate different error statistics for the components of the actual output vector y using some validation method (Kohavi 1995), the common ones being test sample or cross-validation approaches. The first one compares the metamodel predictions on storms not used in the metamodel development process and requires new observations (storm simulations), or, equivalently, splitting of the initial database to a training set and a validation set. Only the training set is used in the metamodel formulation discussed in Sects. 5.1 and 5.2. The second approach, which is the popular one, repeats comparisons of the accuracy over different divisions of the entire database to a learning sample and a test sample and has the benefit that it requires no new observations, though it might provide pessimistic predictions of accuracy if the database is small (Iooss 2009). Here a leave-one-out cross validation is adopted, which is the recommended practice for efficient assessment of metamodel accuracy (Meckesheimer et al. 2002). This cross-validation approach is performed as follows: Each of the observations from the database is sequentially removed, then the remaining support points are used to predict the output for it, and the error between the predicted and real responses is evaluated. The validation statistics are obtained by averaging the errors established over all observations. It should be stressed that this validation approach assesses the metamodel accuracy against the simulation model used for generating the database of synthetic storms, but addresses no other modeling errors. Further details on this issue, which falls out of the scope of this study, are provided in (Resio et al. 2009).

The remaining question is then what statistics to adopt in this validation. For scalar outputs, two commonly used measures to assess the accuracy are the coefficient of determination \({\text{RD}}_{k}^{2}\) and the mean error \({\text{ME}}_{k}\) given, respectively, by

$$\begin{aligned} {\text{RD}}_{k}^{2} = & \,1 - \frac{{\sum\nolimits_{h = 1}^{n} {\left( {y_{k} ({\mathbf{x}}^{h} ) - \hat{y}_{k} ({\mathbf{x}}^{h} )} \right)^{2} } }}{{\sum\nolimits_{h = 1}^{n} {\left( {y_{k} ({\mathbf{x}}^{h} ) - \sum\nolimits_{j = 1}^{n} {y_{k} ({\mathbf{x}}^{h} )} /n} \right)^{2} } }} \\ {\text{ME}}_{k} = & \,\frac{{\sum\nolimits_{h = 1}^{n} {|y_{k} ({\mathbf{x}}^{h} ) - \hat{y}_{k} ({\mathbf{x}}^{h} )|} }}{{\sum\nolimits_{h = 1}^{n} {|y_{k} ({\mathbf{x}}^{h} )|} }} \\ \end{aligned}$$
(10)

Larger value of \({\text{RD}}_{k}^{2}\) (closer to 1) and smaller values for \({\text{ME}}_{k}\) (closer to zero) indicate a good fit. In addition the mean square error can be used as an error statistic

$${\text{MSE}}_{k} = \frac{1}{n}\sum\nolimits_{h = 1}^{n} {\left( {y_{k} ({\mathbf{x}}^{h} ) - \hat{y}_{k} ({\mathbf{x}}^{h} )} \right)^{2} }$$
(11)

which, contrary to the aforementioned two others, is not a normalized measure (follows units of surge). For evaluating the efficiency across multiple outputs, the average versions of these expressions can be used. This then provides the average coefficient of determination, ARD2, and average mean error, AME, and the average mean square error, AMSE, given respectively by

$$\begin{aligned} {\text{ARD}}^{2} = & \,\frac{1}{{n_{y} }}\sum\nolimits_{k = 1}^{{n_{y} }} {{\text{RD}}_{k}^{2} } \\ {\text{AME}} = & \,\frac{1}{{n_{y} }}\sum\nolimits_{k = 1}^{{n_{y} }} {{\text{ME}}_{k} } \\ {\text{AMSE}} = & \,\frac{1}{{n_{y} }}\sum\nolimits_{k = 1}^{{n_{y} }} {{\text{MSE}}_{k} } \\ \end{aligned}$$
(12)

For the peak surge response another accuracy measure is the mean misclassification, representing the percentage of nodes that have been classified erroneously with respect to their wet/dry conditions, i.e., dry nodes predicted as wet and vice versa. This is given by

$${\text{AMC}} = \frac{1}{{nn_{y} }}\sum\nolimits_{k = 1}^{{n_{y} }} {\sum\nolimits_{h = 1}^{n} {I_{kh} } }$$
(13)

where I kh is an indicator function for misclassification (one if misclassified and zero if not) of the kth output for the hth storm.

6 Case study for Louisiana coast

This section discusses the implementation of the surrogate model framework to the Louisiana coast, utilizing the database presented in Sect. 3. The implementation for peak surge response and time-series forecasting is separately discussed to better illustrate the advantages of PCA for nodes that have spatial or temporal correlation. For each case, a range of different settings will be examined with respect to the kriging implementation to illustrate the key points/novelties discussed in the previous sections.

6.1 Peak surge response over an extended coastal region

For the peak surge, as discussed earlier, a total of n y  = 545,635 outputs are considered. In addition, results are reported for subsets of this group, corresponding to nodes that were inundated in at least 5, 10, 30, 50 and 100 % of the storms in the initial database, to examine how the percentage of dry nodes impacts the predictive capabilities of the surrogate model. The number of nodes within the subsets mentioned above is, respectively, 510,011, 485,768, 447,347, 433,561 and 354,070. It is immediately evident, as also discussed earlier, that a large portion of the outputs considered correspond to nodes that have remained dry for a large portion of the available database.

PCA is first implemented to reduce the dimension of the output. For the n y  = 545,635 dimensional output and the database of 446 storms, PCA is efficiently performed within only 160 s in a workstation with 4 core 3.2 GHz Xeon CPU and 8 GB of Ram (same machine is used in all results reported herein). m c  = 50 latent outputs are retained which accounts for r c  = 98 % of the total variability in the initial outputs and facilitates a significant reduction in the size of matrices that need to be stored in memory by 89 %. The choice to only keep 50 latent outputs was made since it was observed that further increase in m c facilitated a very slow increase of r c . Further insights for this challenge will be provided later.

A metamodel is then established, and different approaches (all mentioned within Sect. 5.2) are examined with respect to kriging implementation: (i) a single kriging for all latent outputs, (ii) a separate kriging for each latent output and (iii) a single kriging for the initial high-dimensional output without integrating PCA. These cases will be denoted herein as (k.i) pca-single, (k.ii) pca-separate and (k.iii) single, respectively. The average time for the optimization of the kriging characteristics, described in Eq. (8), is less than 20 s for pca-single adopting standard kriging tuning techniques (Lophaven et al. 2002). The pca-separate requires 20 s for each of the latent outputs (same optimization implemented every time), whereas the required time for single is very high, close to 50 min, stemming from the high dimension of the matrices involved, which reduces computational efficiency for the matrix manipulations required (Lophaven et al. 2002). Note that the latter computational burden is similar (probably a conservative estimate) to the one that would be required even for pca-single if an optimization for the error statistics of the actual output was adopted, as discussed in Sect. 5.2, instead of the approach in Eq. (8).

With respect to implementation efficiency, single prediction through pca-single takes close to 0.08 s (this includes metamodel predictions and transformation back to the original space). For pca-separate the implementation time is 0.2 s and for single around 0.3 s. For predictions over 1000 different storms the numbers are 8, 8.1 and 22 s. This demonstrates the advantages that lower-dimensional matrix manipulations, facilitated through PCA, can provide in estimating outputs over different storm scenarios (vectorized matrix calculations). Overall, these comparisons demonstrate the high computational efficiency established through integrating PCA in the approach; significant memory reduction is established and times for training and implementation of the metamodel are also reduced.

Moving now to accuracy assessment, the two different landfall characterizations provided very similar results with the reference landfall approach providing slightly improved performance (not sufficiently different to justify a clear preference, though). This is the case presented herein; due to space limitation the alternative input characterization is not discussed further. Results for the three examined surrogate models over the entire output are presented in Table 2, utilizing the error statistics (performance measures) discussed in Sect. 5.5.

Table 2 Prediction accuracy of three different surrogate modeling approaches for peak surge considering average statistics over the entire output
Full size table

All three approaches yield a similar level of high accuracy (differences are fairly small from a statistical perspective), as demonstrated by the high values of the coefficient of determination (values close to 0.95 are always considered as very accurate results) and smaller than 7–8 % error with additionally, very small misclassification percentage. These results clearly show that the metamodel replicates the results of the high-fidelity simulations with high accuracy and therefore can be considered as an adequate surrogate for the high-fidelity model. An important feature to stress is that pca-single provides comparable results to single and slightly better than pca-separate. The latter is opposite to the trends reported in Jia and Taflanidis (2013) and should be attributed to the normalization that was proposed here in the tuning of pca-single through Eq. (8), i.e., recommendation to use γ j  = 1, that equivalently provided higher importance to latent outputs that represent the larger variability of the initial database. The overall comparisons justify the preference toward pca-single as it facilitates higher computational efficiency and high accuracy (no significant reduction in accuracy by incorporating PCA or considering a single metamodel rather than a seperate metamodel for each output).

The impact of dry nodes is further examined considering the pca-single metamodeling implementation. This impact is examined by considering the error statistics averaged over nodes that have been inundated at least in 5, 10, 30, 50 and 100 % of the storms in the initial database. This is performed by changing the summation within Eqs. (10) and (12) to consider just those nodes and not the entire output. The comparison allows us to examine how the quality of information in the initial database (larger portions of storms providing complete information for the storm surge and therefore not augmented with neighboring storm water level as described in Sect. 4.2) influences prediction accuracy. Results are reported in Table 3 for the error statistics discussed in Sect.  5.5. Two additional statistics are reported in this table (last two rows) that will be discussed later. It is evident from this table that there is a strong influence of the quality of initial information within the database on the kriging accuracy, with error statistics significantly improving (coefficient of determination over 0.96) even when the evaluation is restricted within the nodes that were inundated in 10 % of the available storms. Note that this comparison corresponds to the metamodel that has been optimized considering all outputs, simply the prediction accuracy is evaluated over different output cases.

Table 3 Prediction accuracy of pca-single metamodel when evaluated over all nodes (All) or over nodes that have been inundated at least for certain percentage (%) of storms in the database
Full size table

Another interesting comparison is whether a metamodel that is tuned for such a specific output case could offer any further advantages in the performance for that specific output case. For this reason another implementation is examined and presented in parenthesis in Table 3, for which the metamodel is formulated specifically for the output that corresponds to nodes that were inundated in at least 30 % of the storms (therefore n y  = 447,347 in this case). For the PCA to account for r o  = 98 % of the total variability, only m c  = 19 latent outputs are needed, compared to 50 required previously, when all nodes are examined. If m c  = 50 latent outputs were adopted for this implementation, then r c  = 99.32 %. This demonstrates that the challenges discussed earlier in establishing a high value of r c stem from the dry nodes within the initial observation matrices. Results for pca-single and m c  = 19 are reported in Table 3 in parenthesis. For the case with m c  = 50 (not reported in Table 3), the error statistics are calculated as ARD2 = 0.972, AME = 4.68 %, AMSE = 0.0253 and AMC = 0.58 %. The comparison illustrates that for the same PCA accuracy, the metamodel explicitly optimized for the output corresponding to nodes inundated in at least 30 % of the storms offers negligible advantages over the metamodel established considering all outputs. On the other hand, increasing the number of latent outputs and therefore reducing the errors coming from the PCA truncation can have a considerable effect on accuracy (compare the results in parenthesis in Table 3 with the statistics provided above for increased m c ). Of course a larger value of m c decreases computational efficiency in terms of memory requirements, although the result is dependent on the case examined. For example, for a new metamodel implementation that examines the entire output and increases m c for PCA to 103 (representing in this case r c  = 99 % of total variability), the performance will show very small improvement; the error statistics for this case are calculated as ARD2 = 0.942, AME = 6.47 %, AMSE = 0.0430 and AMC = 1.12 % (compare these results to first column in Table 3).

The overall discussion demonstrates that the m c value should be selected with care, examining the benefits between accuracy and computational efficiency. This can be established, as suggested by Jia and Taflanidis (2013), by gradually increasing m c and evaluating its impact on ARD2 and AME, and judging if the benefits are justifiable against the decreased computational efficiency, depending also upon the implementation examined for the metamodel. For example, for standalone tools usually there is no concern about memory requirements, while for applications within a cyber platform these requirements become critical.

Finally, a demonstration for the utilization of the kriging approximation error is provided. This error can be used to perform probabilistic assessment for storm surge risk (Resio et al. 2009; Jia and Taflanidis 2013) or for facilitating conservative estimates. The latter is demonstrated here by focusing on the false-negative misclassifications, i.e., when a node is predicted dry but it was supposed to be wet. This error measure is denoted by AMC-FN and is calculated through Eq. (13), but with the indicator function being one only if the condition as stated above is satisfied (node predicted dry when it is actually wet). The unbiased prediction for AMC-FN is established by utilizing the kriging approximation, \(\hat{y}_{k} ({\mathbf{x}})\). A conservative estimation for AMC-FN, denoted AMCe-FN, may be established by utilizing a prediction \(\hat{y}_{k} ({\mathbf{x}}) + b \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{k} ({\mathbf{x}})\) that incorporates the approximation error, where b is some chosen coefficient (some portion of the standard deviation is added to the kriging prediction in this case). AMC-FN and AMCe-FN are reported in Table 3 earlier for a value of b = 1. Considering that the approximation error is Gaussian, this approach is equivalent to declaring a node is wet if the probability of the storm elevation exceeding the ground elevation is over 84 %. The comparison between AMC-FN and AMCe-FN demonstrates that including the error facilitates the desired conservativeness as the rate for AMCe-FN significantly reduces.

6.2 Time-series forecasting

For the time-series forecasting, examining the metamodel performance for time-dependent outputs, the 30 different locations discussed in Sect. 3 are examined, and for each location 92 different time steps (with time interval of 30 min) are considered with conventional landfall corresponding to the 44th step. Two different applications are examined with respect to the definition of the output: (o.i) establishing a metamodel for each location (n y  = 92 for each of the 30 locations) and (o.ii) establishing a metamodel for all locations together (n y  = 2760). The terms each-location and all-locations will be utilized herein to distinguish these two output cases. With respect to the kriging formulation, for each of these output cases, the three metamodel implementations discussed in Sect. 6.1 are examined, (k.i) pca-single, (k.ii) pca-separate and (k.iii) single, as well as a fourth one, (k.iv) considering a separate kriging for each output without integrating PCA, referenced as seperate. This latter implementation is only examined for the each-location output case since this is the only case that the dimension of output (n y  = 92) would practically allow development of a separate kriging metamodel for each initial output. Note that the PCA for all-locations simultaneously addresses the temporal (92 time steps) and spatial (30 locations) correlation of the total 2760 outputs.

The overall performance of the metamodel (across all points) as well as the performance of four specific critical locations in eastern Louisiana are discussed. The same points as in Kim et al. (2015) are chosen and are identified, following the terminology in that paper, as 3, 4, 9 and 18. The longitude and latitude for these points are [−90.3680° 30.0503°], [−89.4067° 28.9317°], [−89.6730° 29.8702°] and [−90.1131° 30.0262°], respectively.

For the PCA, the number of latent outputs is selected so that r c is greater than 99.9 %, yielding m c equal to 9, 14, 8 and 9 for locations 3, 4, 9 and 18, respectively. For the all-locations output case, this yields m c  = 113. Note that due to the lower dimension n y of the initial output, reducing the value of m c is not so critical in this case as it was when examining the peak surge in Sect. 6.1 (matrix P, which depends on both n y and m c , is still relatively small even for larger m c value). This is the reason why a higher value of r c has been allowed here.

Results for computational burden for training and implementation of the metamodel follow exactly the same trends as in Sect. 6.1, simply with higher efficiency in this case due to the smaller value of n y . For example, for the all-locations output case, the evaluation times for 1000 storms are below 0.5 s for all kriging implementations. This computational burden is not further discussed here. The focus is on accuracy of the metamodel, and results are reported in Table 4 where the performance is assessed for each of the four identified locations. For this assessment the summations in Eq. (10) are established with respect to only the 92 outputs for the specific location. Results are reported for the two different output cases as well as the four different kriging implementations examined. Following the recommendation by Kim et al. (2015) for time-dependent outputs, in addition to the error statistics from Sect. 5.5, the correlation coefficient, defined as the normalized covariance between the actual and predicted storm surge forecast, is also utilized here. This is defined for each separate location considered and for the hth storm is given by

$$ \begin{aligned} cc_{h} &= \frac{{\sum\nolimits_{k = 1}^{{n_{y}}} {\left( {y_{k}^{h} - \bar{y}^{h} } \right)\left( {\hat{y}_{k}({\mathbf{x}}^{h} ) - \bar{\hat{y}}({\mathbf{x}}^{h} )} \right)}}}{{\sqrt {\sum\nolimits_{k = 1}^{{n_{y} }} {\left( {y_{k}^{h} - \bar{y}^{h} } \right)^{2} \sum\nolimits_{k = 1}^{{n_{y} }} {\left({\hat{y}_{k} ({\mathbf{x}}^{h} ) - \bar{\hat{y}}({\mathbf{x}}^{h})} \right)^{2} } } } }}; \\ \bar{y}^{h} &= \frac{1}{{n_{y}}}\sum\nolimits_{k = 1}^{{n_{y} }} {y_{k}^{h} } , \, \bar{\hat{y}}({\mathbf{x}}^{h} ) = \frac{1}{{n_{y}}}\sum\nolimits_{k = 1}^{{n_{y} }} {\hat{y}_{k} ({\mathbf{x}}^{h})} \end{aligned}$$
(14)

where summations are expressed with respect to the 92 time steps for each location. The average correlation coefficient is then provided by averaging over all storms as

$$\mathop {cc}\limits^{\_} = \frac{1}{n}\sum\nolimits_{h = 1}^{n} {cc_{h} }$$
(15)
Table 4 Prediction accuracy for time-series forecasting, assessed for four different locations, for the different output definitions and kriging approaches
Full size table

Overall all implementations yield very high accuracy, with coefficient of determination close to or over 0.97, average error below 3 %, small mean square error and correlation coefficient over 0.95. The accuracy level is similar to the ones reported in Kim et al. (2015). Again this demonstrates the potential of the kriging metamodel to become a surrogate for the high-fidelity model. With respect to the output cases, as expected, implementation separately for each-location provides better performance over all-locations, but with a very small margin of improvement. This shows that the spatial correlation of the outputs does allow for tuning of metamodels for all locations (all-locations implementation) without sacrificing accuracy. With respect to the kriging approaches examined, separate and pca-separate yield better performance, but with very small differences over the pca-single. Since the latter can offer substantial computational savings (especially for larger n y ), it establishes a very good compromise between accuracy and efficiency. Note that if output had even higher dimension, for example more locations or larger time span examined, then there would have been a stronger preference for pca-single.

To verify the performance of the metamodeling for the entire output, the accuracy assessment over all outputs is evaluated and results are presented in Table 5 for each-location output (i.e., kriging is tuned for each specific output but performance averaged over all locations) and for all locations (i.e., kriging tuned over all outputs to start with). This further demonstrates the efficiency of a single kriging metamodel trained over all the outputs, since no substantial difference is shown between the two different applications.

Table 5 Prediction accuracy for time-series forecasting averaged over all 30 examined locations
Full size table

Further assessment of the metamodel performance is illustrated in Figs. 4 and 5, for locations 4 and 9, respectively. These figures show the time-series forecasting by different kriging implementations for 8 different storms (sub-plots in each figure) with characteristics shown in Table 6 (input vector for each of them is provided). Note that the scale in each subplot is different, so that differences are better demonstrated, whereas the x-axis in each figure corresponds to the time step (44th step represents conventional landfall).

Fig. 4
figure 4

Time-series forecasting at location 4 for different storms. Subplots (a)-(h) correspond to the different storms (reported in Table 6)

Full size image
Fig. 5
figure 5

Time-series forecasting at location 9 for different storms. Subplots (a)-(h) correspond to the different storms (reported in Table 6)

Full size image
Table 6 Input characteristics for the storms used in Figs. 4, 5 and 6
Full size table

All sub-plots in Figs. 4 and 5 verify the accuracy of the metamodel that has been already demonstrated in the results in Table 4: Close agreement between the surrogate and high-fidelity predictions is reported, whereas cases that are characterized by larger discrepancies correspond to lower values for the surge. It should be noted that the latter instances have small contribution toward the overall error and therefore are given lower priority in the surrogate model optimization. More importantly, the results in these figures demonstrate the capabilities of the framework in seamlessly facilitating smooth time-series predictions. When a separate metamodel is developed for each actual output (separate implementation), then the resultant predictions contribute to a time-series forecast that is non-smooth (but still provides good accuracy). This stems from the fact that correlation information between the inputs at different time steps is not considered (either explicitly or implicitly) in the development of the metamodel. This is the same challenge encountered in Kim et al. (2015) in a similar context (considering neural network metamodel implementation for each output). In that study a low-pass filtering in the form of time averaging (with a carefully selected window size) was suggested to facilitate smooth predictions. This is not necessary, though, if single or even if pca-separate approaches are adopted; smooth predictions are automatically provided. For single, since a single metamodel is utilized to provide simultaneous information for all outputs, smoothness of the predictions is facilitated by implicitly addressing the correlation. The case of pca-separate is more interesting; in this case separate metamodels are utilized for each latent output, so one could expect similar challenges as in the separate approach, but when transformed into the original space the smoothness of the predictions is maintained. This should be attributed to the fact that PCA explicitly considers the correlation of the output and demonstrates the advantages argued earlier that PCA automatically captures and recovers any correlation features of the high-fidelity model predictions.

Finally, and similar to the last investigation considered in Sect. 6.1, a demonstration for the utilization of the kriging approximation error is provided in Fig. 6. This figure shows results for location 9 in a similar format as Figs. 4 and 5. As in the previous figures, the scale in each subplot is also different, so that differences are better demonstrated, whereas the x-axis in each figure corresponds to the time step (44th step represents conventional landfall). The results shown in this figure correspond to the pca-single implementation without (\(\hat{y}_{k} ({\mathbf{x}})\) is plotted) and with consideration of the approximation error (\(\hat{y}_{k} ({\mathbf{x}}) \pm b \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{k} ({\mathbf{x}})\) for b = 1 is plotted). First note that \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }_{k} ({\mathbf{x}})\) is not constant over the different storms (corresponding to different input values x); rather it is larger for storms for which the difference from the target is larger. This demonstrates the benefits of kriging in providing a local estimation error and the fact that this error is well aligned with the actual accuracy of the metamodel. Furthermore, considering one standard deviation around the mean predictions (b = 1), the error band envelopes the actual storm surge. This demonstrates, again, that conservative results can be facilitated by introducing the approximation error in the metamodel predictions.

Fig. 6
figure 6

Time-series forecasting at location 9 for different storms through pca-single approach with and without considering kriging prediction error. Subplots (a)-(h) correspond to the different storms (reported in Table 6)

Full size image

7 Conclusions

The development of surrogate models for prediction of storm surge utilizing an existing database of high-fidelity synthetic storms was discussed in this paper. The outputs corresponded to peak response over an extended coastal region as well as time series for the surge over selected, critical, coastal locations. These settings create a high-dimensional output with significant temporal or spatial correlation. The motivation for establishing the metamodels is to ultimately facilitate fast predictions during landfalling storms to support development of real-time tools (and potential implementation in cyber platforms) and guide the decisions of emergency response managers, as well as to support regional risk assessment studies. Therefore, both accuracy and computational efficiency are important aspects for the surrogate modeling, and both of them were extensively discussed. As a case study, the development of a metamodel utilizing a database of 446 synthetic storms for the Gulf of Mexico (Louisiana coast) was examined.

The metamodeling implementation requires appropriate parameterization of the existing database of the synthetic storms, to provide the input vector for the surrogate model, and guidelines were provided to establish this, examining the characteristics of these storms with respect to two groups of parameters (i) track and (ii) intensity/speed/size of the storm. For the storm output, a modification was also discussed for nodes that for some storms remained dry within the database. Kriging was considered as the surrogate model, due to its potential in approximating complex responses and its numerical efficiency, while for addressing the high dimensionality of the output principal component analysis (PCA) was adopted as a data-driven dimension reduction technique. The integration of PCA was shown to provide significant improvements in computational efficiency as well as in reduction of memory requirements. The surrogate model is built with respect to the low-dimensional latent outputs provided by PCA, with predictions ultimately transformed back to the original output space. Beyond the computational savings, this approach captures the correlation between responses at different locations or different time instances, and for predictions at new inputs this correlation is automatically recovered. This allows, for example, the continuity for the output in time-series forecasting to be automatically established, without the need to introduce additional remedies, such as time averaging.

The case study for the Louisiana coast showed that the kriging metamodel can support high accuracy estimation of all quantities examined (peak storm surge, time-series surge forecasting), with coefficient of determination close to 95 % or better, while the integration of PCA improves significantly computational efficiency and captures well the spatial/temporal correlations of responses. For peak surge predictions, the accuracy of kriging significantly improved when looking at nodes for which higher-quality information was available, i.e., for nodes that were inundated for a larger number of the storms. For time-series surge prediction, surrogate modeling combined with PCA provided much smoother predictions, compared to applying a separate surrogate model for responses at each time step, which led to jagged predictions. PCA was demonstrated to very effectively capture and recover the spatial and temporal correlation of the outputs. Also, explicitly considering the approximation error stemming from the metamodel was shown to seamlessly facilitate reasonably conservative estimates, with actual surge consistently lower than the conservative estimates.

Overall, the study demonstrated that integration of surrogate modeling with PCA can facilitate high efficiency and accuracy; the predictions are provided fast and have a very good match to the high-fidelity database. The kriging metamodel framework developed here should be considered an appropriate surrogate model for the high-fidelity model that provided the synthetic storms, which can, therefore, support the development of accurate/efficient forecasting tools. These tools could be of great value for guiding emergency responses, especially since the approach can be further leveraged to provide approximations for a range of different outputs.