Pseudo-Almost Periodic Solution on Time-Space Scales for a Novel Class of Competitive Neutral-Type Neural Networks with Mixed Time-Varying Delays and Leakage Delays

Abstract

A competitive neural network model was proposed to describe the dynamics of cortical maps in which, there exist two memories: long-term and short-term. In this paper, we investigate the existence and the exponential stability of the pseudo-almost periodic solution of a system of equations modeling the dynamics of neutral-type competitive neural networks with mixed delays in the time-space scales for the first time. The mixed delays include time-varying delays and continuously distributed ones. Based on contraction principle and the theory of calculus on time-space scales, some new criteria proving the convergence of all solutions of the networks toward the unique pseudo-almost periodic solution are derived by using the ad-hoc Lyapunov–Krasovskii functional. Finally, numerical example with graphical illustration is given to confirm our main results.

1 Introduction

The human brain is made up of a large number of cells called neurons and their synapses. An artificial neural network is an information processing system that has certain characteristics in common with biological neural networks. Recently, many researchers have been devoted to the stability analyses, periodic oscillations and pseudo-almost periodic solutions of different class of neutral-type neural networks (see [1, 3, 15, 16]) due to their wide range of applications, such as associative memory, pattern recognition, signal processing, image processing, fault diagnosis, automatic control engineering, combinatorial optimization, and so on (see [7, 10, 12, 14]). Furthermore, over the last twenty years, Anke Meyer-Baese et al. proposed the so-called competitive neural networks with different time scales in [2], which is used to model the dynamics of cortical cognitive maps with unsupervised synaptic modifications. Different from the traditional neural networks with first-order interactions, in this paper, we consider a target model with two different state variables: the short-term memory (STM) variable, describing the fast neural activity and the long-term memory (LTM) variable, describing the slow unsupervised synaptic modifications. In addition, it has been reported that if the parameters and time delays are appropriately chosen, the delayed competitive neural networks in leakage term can exhibit complicated behaviors even with strange chaotic attractors (see [13]). Based on the aforementioned arguments, the study of delayed competitive neural networks and its analogous equations have attracted worldwide interest (see [3, 5, 15]). In fact, it is natural and important that systems contain some information about the derivative of the past state to further describe and model the dynamics for such complex neural reactions. Many researchers have studied the dynamics of various classes of neutral-type neural networks (see [1, 3, 15]). In real world, the mixed time-varying delays and leakage delay should be taken into account when modeling realistic neural networks.

Recently, the concept of pseudo-almost periodic on time-space scales have been introduced in [8], which generalizes the one of the almost periodicity on time-space scales, and the author gave some properties of the space of pseudo-almost periodic functions on time-space scales. Before moving on, the meaning of this notion will be explained firstly, we say that a ld-continuous function f is pseudo-almost periodic on time-space scales if

$$\begin{aligned} f=g+\phi , \end{aligned}$$

where g is almost periodic on time-space scales and $\phi$ is ergodic function, in the sense that, for $r\in {\varPi }$ with $r>0$

$$\begin{aligned} \lim \limits _{r\longrightarrow +\infty }\frac{1}{2r}\int _{t_{0}-r}^{t_{0}+r}\Vert \phi (s)\Vert \nabla s=0, \end{aligned}$$

(where $t_{0}\in \mathbb {T}$ and ${\varPi }:=\left\{ \tau \in \mathbb {R}{:}\, t\pm \tau \in \mathbb {T}, \forall t\in \mathbb {T}\right\} \ne 0.$). It is known that the existence and stability of almost periodic solutions play an important role in characterizing the behavior of a dynamical system. To the author’s best knowledge, there are few works on the existence of almost periodic solutions and the periodic solutions for neutral-type competitive neural networks (CNNs) [5, 15], especially, for discrete time CNNs. Besides, little has been done about the pseudo-almost periodic solutions on time-space scales for the competitive neural networks with mixed time-varying and leakage delays. Therefore, it is a challenging and important problem both in theories and applications.

On the other hand, controversial opinions arise from the possibility of equal roles displayed by both continuous time and discrete time neural networks in various implementations and applications. However, it is troublesome to study the dynamical properties for continuous and discrete time systems, respectively. We should mention that, in many references, the networks are described either by difference equations or by differential equations, that is, dynamical systems are defines as $\mathbb {Z}$ or $\mathbb {R}$. Stefan Hilger in his PhD thesis in 1988, proposed the famous theory of dynamics equations on time-space scales which has been extensively studied and developed, in recent years. In addition, pseudo almost periodicity is more universal than periodicity. Moreover, pseudo-almost periodic solutions on time scales were introduced in [8]. This theory represents a powerful tool for applications in economics, biological models, quantum physics, neural networks, Lotka volterra and among others.

However, from the time scales angle, it is known that $\mathbb {R}$ and $\mathbb {Z}$ are classical periodic time scales that can be unified well by the following periodic time scale:

$$\begin{aligned} \mathbb {T}=\bigcup \limits _{k=-\infty }^{+\infty }[k(a+b),k(a+b)+a], \,\ a,b\in \mathbb {R}, \,\ k\in \mathbb {Z}. \end{aligned}$$

(1)

We can obtain ${\varPi }_{0}=\{n(a+b), n\in \mathbb {Z}\}$ as the periodicity set for the time scale (1). Obviously, if $a=b=0$, then $\mathbb {T}=\mathbb {R}$; if $a=0$, $b=1$, then $\mathbb {T}=\mathbb {Z}$.

The remainder of this paper is organized as follows: In Sect. 2, we will present the model of CNNs. In Sect. 3, we will introduce some necessary notations, definitions and fundamental properties of the space $PAP(\mathbb {T},\mathbb {R}^{n})$ (which will be used in the paper). In Sect. 4, some sufficient conditions are derived ensuring the existence of the pseudo-almost periodic solution on time-space scales. Section 5 is devoted to the exponential stability of the pseudo-almost periodic solution on time-space scales of a CNNs model, and the convergence of all solutions to its unique pseudo almost periodic solution. At last, one illustrative numerical example is given.

2 Model Description

In this paper, we consider a new n-neuron neutral-type competitive neural networks with mixed time-varying delays and leakage delays on time-space scales which is defined in the following lines:

(2)

where $j=1,\ldots ,n$; $\mathbb {T}$ is an almost periodic time scale; $x_{i}(t)$ is the neuron current activity level ($i=1,\ldots ,n$); $\alpha _{i}(t), c_{i}(t)$ are the time variable of the neuron i (where $i=1,\ldots ,n$); $f_{j}(x_{j}(t))$ is the output of neurons; $m_{ij}(t)$ is the synaptic efficiency; $y_{i}$ is the constant external stimulus; $D_{ij}(t)$, $D_{ij}^{\tau }(t)$, $\overline{D}_{ij}(t)$, $\widetilde{D}_{ij}(t)$ represent the connection weight and the synaptic weight of delayed feedback between the ith neuron and the jth neuron respectively; $B_{i}(t)$ is the strength of the external stimulus; $E_{i}(t)$ denotes disposable scale; $I_{i}(t)$, $J_{i}(t)$ denote the external inputs on the ith neuron at time t; $\eta _{i}(t)$ and $\varsigma _{i}(t)$ are leakage delays and satisfy $t-\eta _{i}(t)\in \mathbb {T}$, $t-\varsigma _{i}(t)\in \mathbb {T}$ for $t\in \mathbb {T}$; $\tau _{ij}(t)$, $\sigma _{ij}(t)$ and $\xi _{ij}(t)$ are transmission delays and satisfy $t-\tau _{ij}(t)\in \mathbb {T}$, $t-\sigma _{ij}(t)\in \mathbb {T}$ and $t-\xi _{ij}(t)\in \mathbb {T}$ for $t\in \mathbb {T}$.

The neural network is modeled by a system of deterministic equations with a time-dependent input vector rather than a source emitting input signal with a prescribed probability distribution. By setting $S_{i}=\sum \nolimits _{j=1}^{n}m_{ij}(t)y_{i}=Y^{T}m_{i}(t)$, where $y=(y_{1},y_{2},\ldots ,y_{n})^{T}$, $m_{i}=(m_{i1},m_{i2},\ldots ,m_{in})^{T}$ and, without loss of generality, the input stimulus Y is assumed to be normalized with unit magnitude $|y|^{2}=1$, summing up the LTM over j, then the above networks are simplified and we obtain a state-space representation of the LTM and STM equations of the networks:

$$\begin{aligned} \left\{ \begin{array}{lll} STM{:}\,x^{\nabla }_{i}\left( t\right) = -\alpha _{i}(t)x_{i}\left( t-\eta _{i}(t)\right) +\sum \limits _{j=1}^{n}D_{ij}\left( t\right) f_{j}\left( x_{j}\left( t\right) \right) \\ \quad +\sum \limits _{j=1}^{n}D_{ij}^{\tau }\left( t\right) f_{j}\left( x_{j}\left( t -\tau _{ij}(t)\right) \right) \quad +\sum \limits _{j=1}^{n}\overline{D}_{ij}\left( t\right) \displaystyle {\int }_{t-\sigma _{ij}(t)} ^{t}f_{j}\left( x_{j}\left( s\right) \right) \nabla s\\ +\sum \limits _{j=1}^{n}\widetilde{D}_{ij}\left( t\right) \displaystyle {\int }_{t-\xi _{ij}(t)} ^{t}f_{j}\left( x_{j}^{\nabla }\left( s\right) \right) \nabla s+B_{i}(t)S_{i}(t)+I_{i}\left( t\right) ,\\ LTM{:}\,S_{i}^{\nabla }(t)=-c_{i}(t)S_{i}(t-\varsigma _{i}(t))+E_{i}(t)f_{i}(x_{i}(t))+J_{i}(t),\quad t\in \mathbb {T}, \end{array} \right. \end{aligned}$$

(3)

For convenience, we introduce the following notations:

$$\begin{aligned}&\displaystyle \alpha _{i}^{+}=\sup \limits _{t\in \mathbb {T}}|\alpha _{i}(t)|, \,\ \alpha _{i}^{-}=\inf \limits _{t\in \mathbb {T}}|\alpha _{i}(t)|>0,\,\ c_{i}^{+}=\sup \limits _{t\in \mathbb {T}}|c_{i}(t)|,\,\ c_{i}^{-}=\inf \limits _{t\in \mathbb {T}}|c_{i}(t)|>0,&\\&\displaystyle \eta _{i}^{+}=\sup \limits _{t\in \mathbb {T}}|\eta _{i}(t)|, \,\ \varsigma _{i}^{+}=\sup \limits _{t\in \mathbb {T}}|\varsigma _{i}(t)|,\,\ B_{i}^{+}=\sup \limits _{t\in \mathbb {T}}|B_{i}(t)|,\,\ E_{i}^{+}=\sup \limits _{t\in \mathbb {T}}|E_{i}(t)|,&\\&\displaystyle D_{i}^{+}=\sup \limits _{t\in \mathbb {T}}|D_{i}(t)|,\,\ (D_{i}^{\tau })^{+}=\sup \limits _{t\in \mathbb {T}}|D_{i}^{\tau }(t)|,\,\ D_{ij}^{+}=\sup \limits _{t\in \mathbb {T}}|D_{ij}(t)|,&\\&\displaystyle (D_{ij}^{\tau })^{+}=\sup \limits _{t\in \mathbb {T}}|D_{ij}^{\tau }(t)|,\,\ \overline{D}_{ij}^{+}=\sup \limits _{t\in \mathbb {T}}|\overline{D}_{ij}(t)|,\,\ (\widetilde{D}_{ij})^{+}=\sup \limits _{t\in \mathbb {T}}|\widetilde{D}_{ij}(t)|,&\\&\displaystyle \tau _{ij}^{+}=\sup \limits _{t\in \mathbb {T}}|\tau _{ij}(t)|,\,\ \sigma _{ij}^{+}=\sup \limits _{t\in \mathbb {T}}|\sigma _{ij}(t)|,\,\ \xi _{ij}^{+}=\sup \limits _{t\in \mathbb {T}}|\xi _{ij}(t)|,\quad i,j=1,\ldots ,n.&\end{aligned}$$

We denote $[a,b]_{\mathbb {T}}=\{t, t\in [a,b]\cap \mathbb {T}\}$. The initial conditions associated with system (2), are of the form:

$$\begin{aligned} x_{i}\left( s\right) = \varphi _{i}\left( s\right) ,\,\ S_{i}\left( s\right) = \phi _{i}\left( s\right) ,\,\ s\in [-\theta ,0]_{\mathbb {T}} ,1\le i\le n, \end{aligned}$$

where $\varphi _{i}(.)$ and $\phi _{i}(.)$ are the real-valued bounded $\nabla$-differentiable functions defined on $[-\theta ,0]_{\mathbb {T}}$, $\theta =\max \{\eta ,\tau ,\sigma ,\xi ,\varsigma \}$, $\eta =\max \limits _{1\le i\le n}\eta _{i}^{+}$, $\tau =\max \limits _{1\le i,j\le n}\tau _{ij}^{+}$,

$\sigma =\max \limits _{1\le i,j\le n}\sigma _{ij}^{+}$, $\xi =\max \limits _{1\le i,j\le n}\xi _{ij}^{+}$ and $\varsigma =\max \limits _{1\le i,j\le n}\varsigma _{ij}^{+},\quad i,j=1,\ldots ,n$.

Remark 1

This is the first time to study the pseudo-almost periodic solutions of system (2) for the both cases: continuous and discrete. Besides, since it studies almost periodic problem, although paper [15] deals with $\nabla$-dynamic systems on time scales, its results also cannot be applied to (2).

Remark 2

In [13], the authors only consider the constant delay and the constant leakage term:

$$\begin{aligned} \left\{ \begin{array}{l} STM{:} x_{i}^{\nabla }\left( t\right) = -\alpha _{i}(t)x_{i}\left( t-\delta _{i}\right) +\sum \limits _{j=1}^{n}D_{ij}(t) f_{j}\left( x_{j}\left( t \right) \right) +\sum \limits _{j=1}^{n}D_{ij}^{\tau }(t) f_{j}\left( x_{j}\left( t-\tau _{ij} \right) \right) \\ \qquad \quad \qquad \qquad \qquad +\,B_{i}(t)S_{i}(t)+I_{i}(t),\\ LTM{:} S_{i}^{\nabla }(t)=-c_{i}(t)S_{i}(t-\varsigma _{i}))+E_{i}(t)f_{i}(x_{i}(t))+J_{i}(t),\quad i=1,\ldots ,n,\,\ t\in \mathbb {T}. \end{array} \right. \end{aligned}$$

If the leakage delays are constants and the coefficients $\overline{D}_{ij}(t)=\widetilde{D}_{ij}(t)\equiv 0$, it is clear that the model in Liu et al. (2014) is a special case of the system investigated in this work. Furthermore, model (2) is more general than model in [13].

3 Preliminaries and Function Spaces

In this section, we will introduce some basic definitions of time scales which will be used as the proof of our relative results.

A time scale $\mathbb {T}$ is a closed subset of $\mathbb {R}$. It follows that the jump operators $\sigma ,\rho :\mathbb {T}\longrightarrow \mathbb {T}$ defined by $\sigma (t)=\inf \{s\in \mathbb {T}{:}s>t\}$ and $\rho (t)=\sup \{s\in \mathbb {T}{:}s<t\}$ for all $t\in \mathbb {T}$. A point $t\in \mathbb {T}$ is called left-dense if $t>\inf \mathbb {T}$ and $\rho (t)=t$, left-scattered if $\rho (t)<t$, right-dense if $t<\sup \mathbb {T}$ and $\sigma (t)=t$, and right-scattered if $\sigma (t)>t$. If $\mathbb {T}$ has a right scatter minimum m, define $\mathbb {T}_{k}{:}=\mathbb {T}\backslash {m}$; otherwise, set $\mathbb {T}^{k}=\mathbb {T}$. The notations $[a,b]_{\mathbb {T}}$, $[a,b)_{\mathbb {T}}$ and so on, we will denote time scale intervals

$$\begin{aligned}{}[a,b]_{\mathbb {T}}=\{t\in \mathbb {T}{:} a\le t\le b\}, \end{aligned}$$

where $a,b\in \mathbb {T}$ with $a<\rho (b)$.

Finally, the graininess function $\nu {:}\mathbb {T}\longrightarrow +\infty$ is defined by $\nu (t)=t-\rho (t)$, for all $t\in \mathbb {T}$.

Definition 1

([4]). The function $f{:}\mathbb {T}\longrightarrow \mathbb {R}$ is called ld-continuous provided that it is continuous at each left-dense point and has a right-sided limit at each point, write $f\in C_{ld}(\mathbb {T})=C_{ld}(\mathbb {T},\mathbb {R})$. Let $t\in \mathbb {T}^{k}$ the Nabla derivative of f at t to be the number (provided it exists) with the property that given any $\epsilon >0$, there is a neighborhood U of t (i.e., $U=(t-\delta ,t+\delta )\cap \mathbb {T}$ for some $\delta >0$) such that

$$\begin{aligned} \left| f(\rho (t))-f(s)-f^{\nabla }[\rho (t)-s]\right| \le \epsilon |\rho (t)-s|, \,\ \text {for all}\,\ s\in U. \end{aligned}$$

Let F be a function, it is called the antiderivative of $f{:}\mathbb {T}\longrightarrow \mathbb {R}$ provided $F^{\nabla }(t)=f(t)$ for each $t\in \mathbb {T}_{k}$. If $F^{\nabla }(t)=f(t)$ then we define the nabla integral by

$$\begin{aligned} \int _{a}^{t}f(s)\nabla s = F(t)-F(a). \end{aligned}$$

A function $p{:}\mathbb {T}\longrightarrow \mathbb {R}$ is called $\nu$-regressive if $1-\nu (t)p(t)\ne 0$ for all $t\in \mathbb {T}_{k}$. The set of all $\nu$-regressive and left-dense continuous functions $p{:}\mathbb {T}\longrightarrow \mathbb {R}$ will be denoted by $\mathcal {R}_{\nu }= \mathcal {R}_{\nu }(\mathbb {T})=\mathcal {R}_{\nu }(\mathbb {T},\mathbb {R})$. We define the set

$$\begin{aligned} \mathcal {R}_{\nu }^{+}=\mathcal {R}_{\nu }^{+}(\mathbb {T},\mathbb {R})=\left\{ p\in \mathcal {R}_{\nu }: 1-\nu (t)p(t)>0, \,\ \forall t\in \mathbb {T}\right\} . \end{aligned}$$

If $p\in \mathcal {R}_{\nu }$ then we define the nabla exponential function by

$$\begin{aligned} \hat{e}(t,s)=\exp \left( \int _{s}^{t}\hat{\xi }_{\nu (\tau )}(p(\tau ))\nabla \tau \right) , \,\ \text {for all} \,\ t,s\in \mathbb {T}, \end{aligned}$$

where $\mu$-cylinder transformation is as in

$$\begin{aligned} \hat{\xi }_{h}(z):=\left\{ \begin{array}{ll}-\frac{1}{h}\log (1+zh), &{} \quad \text {if} \,\ h\ne 0\\ z &{} \quad \text {if}\,\ h=0. \end{array} \right. \end{aligned}$$

Definition 2

([4]). Let $p,q:\mathbb {T}\longrightarrow \mathbb {R}$ are two regressive functions; define

$$\begin{aligned} (p\oplus _{\nu } q)(t)=p(t)+q(t)-\nu p(t)q(t), \,\ \ominus _{\nu } p(t)=-\frac{p(t)}{1-\nu p(t)}, \,\ p\ominus _{\nu } q=p\oplus _{\nu } (\ominus _{\nu } q). \end{aligned}$$

Lemma 1

([4]). Assume that $p,q:\mathbb {T}\longrightarrow \mathbb {R}$ are two $\nu$-regressive functions, then

• (i) $\hat{e}_{0}(t,s)\equiv 1$ and $\hat{e}_{p}(t,t)\equiv 1$;

• (ii) $\hat{e}_{p}(\rho (t),s)=(1-\nu (t)p(t))\hat{e}_{p}(t,s)$;

• (iii) $\hat{e}_{p}(t,s)=\frac{1}{\hat{e}(s,t)}=\hat{e}_{\ominus \nu }(s,t)$;

• (iv) $\hat{e}_{p}(t,s)\hat{e}_{p}(s,r)=\hat{e}_{p}(t,r)$;

• (v) $(\hat{e}_{ p}(t,s))^{\nabla }=( p)(t)\hat{e}_{p}(t,s)$.

Lemma 2

([6]). For each $t_{0}\in \mathbb {T}$ in $\mathbb {T}\backslash \mathbb {T}_{k}$ the single-point set $\{t_{0}\}$ is $\nabla$-measurable and its $\nabla$-measure is given by $\nu _{\nabla }(\{t_{0}\})=\nu (t_{0})-t_{0}$.

For more details of time scales and $\nabla$-measurability, one is referred to read the excellent books ([4, 6]).

Lemma 3

([9]) Let f, g be nabla differentiable functions on $\mathbb {T}$, then:

• (i) $(\lambda _{1}f+\lambda _{2}g)^{\nabla }=\lambda _{1}f^{\nabla }+\lambda _{2}g^{\nabla }$, for any constants $\lambda _{1},\lambda _{2}$;

• (ii) $(fg)^{\nabla }(t)=f^{\nabla }(t)g(t)+f(\rho (t))g(t)^{\nabla }=f(t)g^{\nabla }(t)+f^{\nabla }(t)g(\rho (t))$;

• (iii) If f and $f^{\nabla }$ are continuous, then $\left( \int _{a}^{t}f(t,s)\nabla s\right) ^{\nabla }=f(\rho (t),t)+\int _{a}^{t}f(t,s)\nabla s$.

Lemma 4

([9]) Assume $p\in \mathcal {R}_{\nu }$ and $t_{0}\in \mathbb {T}$. If $1-\nu (t)p(t)>0$ for $t\in \mathbb {T}$, then $\hat{e}_{p}(t,t_{0})>0$ for all $t\in \mathbb {T}$.

Lemma 5

Suppose that f(t) is an ld-continuous function and c(t) is a positive ld-continuous function which satisfies that $c(t)\in \mathcal {R}_{\nu }^{+}$. Let

$$\begin{aligned} g(t)=\int _{t_{0}}^{t}\hat{e}_{-c}(t,\rho (s))f(s)\nabla s, \end{aligned}$$

where $t_{0}\in \mathbb {T}$, then

$$\begin{aligned} g^{\nabla }(t)=f(t)-c(t)\int _{t_{0}}^{t}\hat{e}_{-c}(t,\rho (s)) f(s) \nabla s. \end{aligned}$$

Proof

$$\begin{aligned} g^{\nabla }(t)= & {} \left( \int _{t_{0}}^{t}\hat{e}_{-c}(t,\rho (s))f(s)\nabla s\right) ^{\nabla }\\= & {} \left( \hat{e}_{-c}(t,t_{0})\int _{t_{0}}^{t}\hat{e}_{-c}(t_{0},\rho (s))f(s)\nabla s\right) ^{\nabla }\\= & {} \hat{e}_{-c}(\rho (t),t_{0})\hat{e}_{-c}(t_{0},\rho (t))f(t)-c(t)\hat{e}_{-c}(t,t_{0})\int _{t_{0}}^{t}\hat{e}_{-c}(t_{0},\rho (s))f(s)\nabla s\\= & {} f(t)-c(t)\int _{t_{0}}^{t}\hat{e}_{-c}(t_{0},\rho (s))f(s)\nabla s. \end{aligned}$$

Definition 3

([9]) A time scale $\mathbb {T}$ is called an almost periodic time scale if

$$\begin{aligned} {\varPi }{:}=\left\{ \tau \in \mathbb {R}{:} t\pm \tau \in \mathbb {T}, \forall t\in \mathbb {T}\right\} \ne 0. \end{aligned}$$

Definition 4

([9]) Let $\mathbb {T}$ be an almost periodic time scale. A function $f\in C_{ld}(\mathbb {T},\mathbb {R}^{n})$ is called an almost periodic on $\mathbb {T}$, if for any $\epsilon >0$, the set

$$\begin{aligned} E(\epsilon ,f)=\left\{ \tau \in {\varPi }{:} |f(t+\tau )-f(t)|<\epsilon , \forall t\in \mathbb {T}\right\} , \end{aligned}$$

is relatively dense; that is, for any given $\epsilon >0$, there exists a constant $l(\epsilon )>0$ such that each interval of length $l(\epsilon )$ contains at least one $\tau =\tau (\epsilon )\in E(\epsilon ,f)$ such that

$$\begin{aligned} |f(t+\tau )-f(t)|<\epsilon , \forall t\in \mathbb {T}. \end{aligned}$$

The set $E(\epsilon ,f)$ is called the $\epsilon$-translation set of f(t), $\tau$ is called the $\epsilon$-translation number of f(t) and $l(\epsilon )$ is called the contain interval length of $E(\epsilon ,f)$.

Let $AP(\mathbb {T})=\left\{ f\in C_{ld}(\mathbb {T},\mathbb {R}){:} f \,\ \text {is almost periodic}\right\}$ and $BC(\mathbb {T},\mathbb {R}^{n})$ denote the space of all bounded continuous functions from $\mathbb {T}$ to $\mathbb {R}^{n}$. Define the class of functions $PAP_{0}(\mathbb {T})$ as follows:

$$\begin{aligned} PAP_{0}(\mathbb {T})=\left\{ f\in BC(\mathbb {T},\mathbb {R}^{n}){:} f \,\ \text {is nabla measurable such that}\right. \\ \left. \lim \limits _{r\longrightarrow +\infty }\frac{1}{2r}\int _{t_{0}-r}^{t_{0}+r}|f(s)|\nabla s=0, \,\ \text {where}\,\ t_{0}\in \mathbb {T}, r\in {\varPi }\right\} . \end{aligned}$$

Definition 5

([9]) A function $f\in C_{ld}(\mathbb {T},\mathbb {R}^{n})$ is called pseudo almost periodic if $f=g+\phi$, where $g\in AP(\mathbb {T})$ and $\phi \in PAP_{0}(\mathbb {T})$. Denote by $PAP(\mathbb {T})$, the set of pseudo-almost periodic functions.

By Definition 5, one can easily show that

Lemma 6

([9]) If $f,g\in PAP(\mathbb {T})$, then $f+g, fg\in PAP(\mathbb {T})$; if $f\in PAP(\mathbb {T})$, $g\in AP(\mathbb {T})$, then $fg\in PAP(\mathbb {T})$.

Lemma 7

([9]) If $f\in C_{ld}(\mathbb {R},\mathbb {R})$ satisfies the Lipschitz condition, $\varphi \in PAP(\mathbb {T})$, $\theta \in C_{ld}^{1}(\mathbb {T},{\varPi })$ and $\eta :=\inf \limits _{t\in \mathbb {T}}\left( 1-\theta ^{\nabla }(t)\right) >0$, then $f(\varphi (t-\theta (t)))\in PAP(\mathbb {T})$.

4 The Existence of Pseudo-Almost Periodic on Time-Space Scales Solutions

In this section, we will present a new condition for the uniqueness, global exponential stability for pseudo-almost periodic solutions of (2) and the convergence are also derived. The existence and uniqueness of pseudo-almost periodic solution are given based on Banach’s fixed point theorem and the theory of calculus on time-space scales.

Let

$$\begin{aligned} \mathbb {B}=\{(\varphi _{1},\varphi _{2},\ldots ,\varphi _{n},\phi _{1},\phi _{2},\ldots ,\phi _{n})^{T}:\varphi _{i},\phi _{i}\in C^{1}(\mathbb {T},\mathbb {R}), i=1,\ldots ,n\}. \end{aligned}$$

with the norm $\Vert \psi \Vert _{\mathbb {B}}=\sup \limits _{t\in \mathbb {T}}\max \limits _{i=1,\ldots ,n}\{|\varphi _{i}(t)|,|\phi _{i}(t)|,|\varphi ^{\nabla }_{i}(t)|,|\phi ^{\nabla }_{i}(t)|\},$ then $(\mathbb {B},\Vert \psi \Vert _{\mathbb {B}})$ is a Banach space.

For every $\psi =(\varphi _{1},\ldots \varphi _{n},\phi _{1},\ldots ,\phi _{n})\in \mathbb {B}$, we consider the following system

$$\begin{aligned} x_{i}^{\nabla }(t)=-\alpha _{i}(t)x_{i}(t)+F_{i}(t,\varphi _{i}),\,\ S_{i}^{\nabla }(t)=-c_{i}(t)x_{i}(t)+G_{i}(t,\phi _{i}), \,\ t\in \mathbb {T}, \end{aligned}$$

(4)

where, for $i=1,\ldots ,n$

$$\begin{aligned} F_{i}(t,\varphi _{i}(t))= & {} \alpha _{i}(t)\int _{t-\eta _{i}(t)}^{t}\varphi _{i}^{\nabla }(s)\nabla s +\sum \limits _{j=1}^{n}D_{ij}\left( t\right) f_{j}\left( \varphi _{j}\left( t\right) \right) \\&+\sum \limits _{j=1}^{n}D_{ij}^{\tau }\left( t\right) f_{j}\left( \varphi _{j}\left( t -\tau _{ij}(t)\right) \right) +\sum \limits _{j=1}^{n}\overline{D}_{ij}\left( t\right) \int _{t-\sigma _{ij}(t)} ^{t}f_{j}\left( \varphi _{j}\left( s\right) \right) \nabla s\\&+\sum \limits _{j=1}^{n}\widetilde{D}_{ij}\left( t\right) \int _{t-\xi _{ij}(t)} ^{t}f_{j}\left( \varphi _{j}^{\nabla }\left( s\right) \right) \nabla s+B_{i}(t)\phi _{i}(t)+I_{i}\left( t\right) ,\\ G_{i}(t,\phi _{i}(t))= & {} c_{i}(t)\int _{t-\varsigma _{i}(t)}^{t}\phi _{i}^{\nabla }(s)\nabla s+E_{i}(t)f_{i}(\varphi _{i}(t))+J_{i}(t). \end{aligned}$$

Let $y_{\psi }(t)=\left( x_{\varphi _{1}}(t),\ldots ,x_{\varphi _{n}}(t),S_{\phi _{1}}(t),\ldots ,S_{\phi _{n}}(t)\right) ^{T}$, where

$$\begin{aligned} x_{\varphi _{i}}(t)=\int _{-\infty }^{t}\hat{e}_{-\alpha _{i}}(t,\rho (s))F_{i}(t,\varphi _{i}(s))\nabla s,\\ S_{\phi _{i}}(t)=\int _{-\infty }^{t}\hat{e}_{-c_{i}}(t,\rho (s))G_{i}(t,\phi _{i}(s))\nabla s, \end{aligned}$$

Let us list some assumptions which will be used throughout the rest of this paper.

($\mathbf{H_{1}}$):

For all $1\le i,j\le n,$, the functions $\alpha _{i}\left( \cdot \right) , c_{i}\left( \cdot \right) \in \mathcal {R}_{\nu }^{+}$ and $D_{ij}(.)$, $D^{\tau }_{ij}(.)$ $\overline{D}_{ij}(.)$, $\widetilde{D}_{ij}(.)$, $B_{i}(.)$, $E_{i}(.)$, $\eta _{i}(.)$, $\varsigma _{i}(.)$, $\tau _{ij}(.)$, $\sigma _{ij}(.)$, $\xi _{ij}(.)$, $I_{i}(.)$, $J_{i}(.)$ are ld-continuous pseudo-almost periodic functions for $i,j=1,\ldots ,n$.

$\inf \limits _{t\in \mathbb {T}}\left( 1-\tau _{ij}^{\nabla }(t)\right) >0$, $\inf \limits _{t\in \mathbb {T}}\left( 1-\sigma _{ij}^{\nabla }(t)\right) >0$ and $\inf \limits _{t\in \mathbb {T}}\left( 1-\xi _{ij}^{\nabla }(t)\right) >0$.

($\mathbf{H_{2}}$):

The functions $f_{j}\left( \cdot \right)$, are $\nabla$-differential and satisfy the Lipschitz condition, i.e., there are constants $L_{j}>0$ such that for all $x,y\in \mathbb {R}$, and for all $1\le j\le n,$ one has $\left| f_{j}\left( x\right) -f_{j}\left( y\right) \right| \le L_{j}\left| x-y\right| .$

($\mathbf{H_{3}}$):

$$\begin{aligned}&\max \limits _{1\le i\le n}\left\{ \frac{M_{i}}{\alpha _{i}^{-}},\left( 1+\frac{\alpha _{i}^{+}}{\alpha _{i}^{-}}\right) M_{i},\frac{N_{i}}{c_{i}^{-}},\left( 1+\frac{c_{i}^{+}}{c_{i}^{-}}\right) N_{i}\right\} \le r,\\&\quad \max \limits _{1\le i\le n}\left\{ \frac{\overline{M}_{i}}{\alpha _{i}^{-}},\left( 1+\frac{\alpha _{i}^{+}}{\alpha _{i}^{-}}\right) \overline{M}_{i},\frac{\overline{N}_{i}}{c_{i}^{-}},\left( 1+\frac{c_{i}^{+}}{c_{i}^{-}}\right) \overline{N}_{i}\right\} \le 1, \end{aligned}$$

where r is a constant, and for $i=1,\ldots ,n$

$$\begin{aligned} M_{i}= & {} \alpha _{i}^{+}\eta _{i}^{+}r\!+\!\sum \limits _{j=1}^{n}\left( D_{ij}^{+}\!+\!(D_{ij}^{\tau })^{+}\!+\!\overline{D}_{ij}^{+}\sigma _{ij}^{+} +\widetilde{D}_{ij}^{+}\xi _{ij}^{+}\right) (L_{j}r+|f_{j}(0)|)+B_{i}^{+}r+I_{i}^{+},\\ \overline{M}_{i}= & {} \alpha _{i}^{+}\eta _{i}^{+}+\sum \limits _{j=1}^{n}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}+\overline{D}_{ij}^{+}\sigma _{ij}^{+}+\widetilde{D}_{ij}^{+}\xi _{ij}^{+}\right) L_{j} +B_{i}^{+},\\ N_{i}= & {} c_{i}^{+}\varsigma _{i}^{+}r+E_{i}^{+}(L_{i}r+|f_{i}(0)|)+J_{i}^{+}, \overline{N}_{i}=c_{i}^{+}\varsigma _{i}^{+}+E_{i}^{+}L_{i}. \end{aligned}$$

Lemma 8

Suppose that assumptions $(H_{1})-(H_{3})$ hold. Let $\mathbb {F}=\{\psi \in \mathbb {B}: \Vert \psi \Vert _{\mathbb {B}}\le r\}$ and define the nonlinear operator ${\varGamma }:\mathbb {F}\longrightarrow \mathbb {F}$ by for each $\psi \in PAP(\mathbb {T},\mathbb {R}^{n})$

$$\begin{aligned} ({\varGamma }\psi )(t)=y_{\psi }(t), \quad \psi \in \mathbb {F}. \end{aligned}$$

Then ${\varGamma }$ maps $PAP(\mathbb {T},\mathbb {R}^{n})$ into itself.

Proof

We show that for any $\psi \in \mathbb {F}$, ${\varGamma }\psi \in \mathbb {F}$.

$$\begin{aligned} \left| F_{i}(s,\varphi _{i}(s))\right|= & {} \left| \alpha _{i}(s)\int _{s-\eta _{i}(s)}^{s}\varphi _{i}^{\nabla }(u)\nabla u +\sum \limits _{j=1}^{n}D_{ij}\left( s\right) f_{j}\left( x_{j}\left( s \right) \right) \right. \\&+\sum \limits _{j=1}^{n}D_{ij}^{\tau }(s) f_{j}\left( x_{j}\left( s-\tau _{ij} (s)\right) \right) +\sum \limits _{j=1}^{n}\overline{D}_{ij}\left( s\right) \int _{s-\sigma _{ij}(s)} ^{s}f_{j}\left( x_{j}\left( u\right) \right) \nabla u\\&+\left. \sum \limits _{j=1}^{n}\widetilde{D}_{ij}^{\tau }\left( s\right) \int _{s-\xi _{ij}(s)} ^{t}f_{j}\left( x_{j}^{\nabla }\left( u\right) \right) \nabla u+B_{i}(s)S_{i}(s)+I_{i}\left( s\right) \right| \\\le & {} \alpha _{i}^{+}\int _{s-\eta _{i}(s)}^{s}\left| \varphi _{i}^{\nabla }(u)\right| \nabla u+\sum \limits _{j=1}^{n}D_{ij}^{+}\left| f_{j}\left( \varphi _{j}\left( s \right) \right) \right| \\&+ \sum \limits _{j=1}^{n}(D_{ij}^{\tau })^{+}\left| f_{j}\left( \varphi _{j}\left( s -\tau _{ij}(s)\right) \right) \right| +\sum \limits _{j=1}^{n}\overline{D}_{ij}^{+}\int _{s-\sigma _{ij}(s)}^{s}\left| f_{j}\left( \varphi _{j}\left( u \right) \right) \right| \nabla u \\&+ \sum \limits _{j=1}^{n}\widetilde{D}_{ij}^{+}\int _{s-\xi _{ij}(s)}^{s}\left| f_{j}\left( \varphi _{j}^{\nabla }\left( u \right) \right) \right| \nabla u+B_{i}^{+}\left| \phi _{i}(s)\right| +I_{i}^{+}\\\le & {} \alpha _{i}^{+}\eta _{i}^{+}r+\sum \limits _{j=1}^{n}D_{ij}^{+}\left( L_{j}\left| \varphi _{j}\left( s\right) \right| +\left| f_{j}(0)\right| \right) \\&+ \sum \limits _{j=1}^{n}(D_{ij}^{\tau })^{+}\left( L_{j}\left| \varphi _{j}\left( s-\tau _{ij}(s)\right) \right| +\left| f_{j}(0)\right| \right) \\&+ \sum \limits _{j=1}^{n}\overline{D}_{ij}^{+}\sigma _{ij}^{+}\left( L_{j}r+\left| f_{j}(0)\right| \right) \\&+ \sum \limits _{j=1}^{n}\widetilde{D}_{ij}^{+}\xi _{ij}^{+}\left( L_{j}r+\left| f_{j}(0)\right| \right) +B_{i}^{+}\left| \phi _{i}\left( s\right) \right| + I_{i}^{+}\\\le & {} M_{i}. \end{aligned}$$

In a similar way, we have

$$\begin{aligned} \left| G_{i}(s,\phi _{i}(s))\right| \le N_{i}. \end{aligned}$$

Which leads to, for $i=1,\ldots ,n$

$$\begin{aligned} \sup \limits _{t\in \mathbb {T}}\left| x_{\varphi _{i}}(t)\right|= & {} \sup \limits _{t\in \mathbb {T}}\left| \int _{-\infty }^{t}\hat{e}_{-\alpha _{i}^{-}}(t,\rho (s))F_{i}(t,\varphi _{i}(s))\nabla s\right| \\\le & {} \sup \limits _{t\in \mathbb {T}}\int _{-\infty }^{t}\hat{e}_{-\alpha _{i}^{-}}(t,\rho (s))\left| F_{i}(s,\varphi _{i}(s))\right| \nabla s\\\le & {} \frac{M_{i}}{\alpha _{i}^{-}}, \end{aligned}$$

and,

$$\begin{aligned} \sup \limits _{t\in \mathbb {T}}\left| S_{\phi _{i}}(t)\right| =\sup \limits _{t\in \mathbb {T}}\left| \int _{-\infty }^{t}\hat{e}_{-c_{i}}(t,\rho (s))G_{i}(t,\phi _{i}(s))\nabla s\right| \le \frac{N_{i}}{c_{i}^{-}}. \end{aligned}$$

Otherwise, for $i=1,\ldots ,n$, we have

$$\begin{aligned} \sup \limits _{t\in \mathbb {T}}\left| x_{\varphi _{i}}^{\nabla }(t)\right|= & {} \sup \limits _{t\in \mathbb {T}}\left| \left( \int _{-\infty }^{t}\hat{e}_{-\alpha _{i}}(t,\rho (s))F_{i}(t,\varphi _{i}(s))\nabla s\right) ^{\nabla } \right| \\= & {} \sup \limits _{t\in \mathbb {T}}\left| F_{i}(t,\varphi _{i}(t))-\alpha _{i}(t)\int _{-\infty }^{t}\hat{e}_{-\alpha _{i}}(t,\rho (s))F_{i}(t,\varphi _{i}(s))\nabla s\right| \\\le & {} \alpha _{i}^{+}\eta _{i}^{+}r+\sum \limits _{j=1}^{n}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}+(\overline{D}_{ij})^{+}\sigma _{ij}^{+} +(\widetilde{D}_{ij})^{+}\xi _{ij}^{+}\right) (L_{j}r+\left| f_{j}(0)\right| )\\&+\,B_{i}^{+}r+I_{i}^{+}+\frac{\alpha _{i}^{+}}{\alpha _{i}^{-}}\left( \alpha _{i}^{+}\eta _{i}^{+}r+\sum \limits _{j=1}^{n}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}+(\overline{D}_{ij})^{+}\sigma _{ij}^{+}\right. \right. \\&+ \left. \left. (\widetilde{D}_{ij})^{+}\xi _{ij}^{+}\right) (L_{j}r+\left| f_{j}(0)\right| )+ B_{i}^{+}r+I_{i}^{+}\right) \\= & {} \left( 1+\frac{\alpha _{i}^{+}}{\alpha _{i}^{-}}\right) M_{i}. \end{aligned}$$

Similarly,

$$\begin{aligned} \sup \limits _{t\in \mathbb {T}}\left| S_{\phi _{i}}^{\nabla }(t)\right| \le \left( 1+\frac{c_{i}^{+}}{c_{i}^{-}}\right) N_{i}. \end{aligned}$$

From hypothesis $(H_{3})$, we can obtain

$$\begin{aligned} \Vert {\varGamma }\psi \Vert _{\mathbb {B}}\le r, \end{aligned}$$

which implies that operator ${\varGamma }$ is a self-mapping from $\mathbb {F}$ to $\mathbb {F}$.

Theorem 1

Let $(H_{1})-(H_{3})$ hold. The system (2) has a unique pseudo-almost-periodic solution in the region $\mathbb {F}=\{\psi \in \mathbb {B}: \Vert \psi \Vert _{\mathbb {B}}\le r\}$.

Proof

It suffices to show that the operator ${\varGamma }$ is a contraction mapping.

First, for $\psi =\left( \varphi _{1},\ldots ,\varphi _{n},\phi _{1},\ldots ,\phi _{n}\right) ^{T}$, ${\varOmega }=\left( u_{1},\ldots ,u_{n}, v_{1},\ldots ,v_{n}\right) ^{T}\in \mathbb {F}$, we have

$$\begin{aligned} \sup \limits _{s\in \mathbb {T}}\left\| x_{\varphi _{i}}(s)-x_{u_{i}}(s) \right\|\le & {} \frac{1}{\alpha _{i}^{-}}\sup \limits _{s\in \mathbb {T}} \left( \alpha _{i}^{+}\eta _{i}^{+}\left\| \varphi _{i}^{\nabla }(s)-u_{i}^{\nabla }(s)\right\| +\sum \limits _{j=1}^{n} D_{ij}^{+}\left\| \varphi _{i}(t)-u_{i}(t)\right\| \right. \\&+\sum \limits _{j=1}^{n} (D_{ij}^{\tau })^{+}L_{j}\left\| \varphi _{j}(s-\tau _{ij}(s))-u_{j}(s-\tau _{ij}(s))\right\| \\&+\sum \limits _{j=1}^{n} (\overline{D}_{ij})^{+}L_{j}\sigma _{ij}^{+}\left\| \varphi _{j}(s)-u_{j}(s)\right\| \\&+\left. \sum \limits _{j=1}^{n} (\widetilde{D}_{ij})^{+}L_{j}\xi _{ij}^{+}\left\| \varphi _{j}^{\nabla }(s)-u^{\nabla }_{j}(s)\right\| +B_{i}^{+}\left\| \phi _{j}(s)-v_{j}(s)\right\| \right) \\\le & {} \frac{1}{\alpha _{i}^{-}}\left( \alpha _{i}^{+}\eta _{i}^{+}+\sum \limits _{j=1}^{n}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}+(\overline{D}_{ij})^{+}\sigma _{ij}^{+}+(\widetilde{D}_{ij})^{+}\xi _{ij}^{+}\right) L_{j}\right. \\&+\left. B_{i}^{+}\right) \Vert \psi -{\varOmega }\Vert _{\mathbb {B}}\\= & {} \frac{\overline{M}_{i}}{\alpha _{i}^{-}}\Vert \psi -{\varOmega }\Vert _{\mathbb {B}}. \end{aligned}$$

Besides,

$$\begin{aligned} \sup \limits _{s\in \mathbb {T}}\left\| x^{\nabla }_{\varphi _{i}}(s)-x^{\nabla }_{u_{i}}(s) \right\|\le & {} \frac{1}{\alpha _{i}^{-}}\sup \limits _{s\in \mathbb {T}} \left( \alpha _{i}^{+}\eta _{i}^{+}\left\| \varphi _{i}^{\nabla }(s)-u_{i}^{\nabla }(s)\right\| +\sum \limits _{j=1}^{n} D_{ij}^{+}\left\| \varphi _{i}(t)-u_{i}(t)\right\| \right. \\&+\sum \limits _{j=1}^{n} (D_{ij}^{\tau })^{+}L_{j}\left\| \varphi _{j}(s-\tau _{ij}(s))-u_{j}(s-\tau _{ij}(s))\right\| \\&+\sum \limits _{j=1}^{n} (\overline{D}_{ij})^{+}L_{j}\sigma _{ij}^{+}\left\| \varphi _{j}(s)-u_{j}(s)\right\| \\&+\left. \sum \limits _{j=1}^{n} (\widetilde{D}_{ij})^{+}L_{j}\xi _{ij}^{+}\left\| \varphi _{j}^{\nabla }(s)-u^{\nabla }_{j}(s)\right\| +B_{i}^{+}\left\| \phi _{j}(s)-v_{j}(s)\right\| \right) \\\le & {} \frac{1}{\alpha _{i}^{-}}\left( \alpha _{i}^{+}\eta _{i}^{+}+\sum \limits _{j=1}^{n}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}+(\overline{D}_{ij})^{+}\sigma _{ij}^{+}+(\widetilde{D}_{ij})^{+}\xi _{ij}^{+}\right) L_{j}\right. \\&+\left. B_{i}^{+}\right) \Vert \psi -{\varOmega }\Vert _{\mathbb {B}}\\= & {} \frac{\alpha _{i}^{+}}{\alpha _{i}^{-}}\left( \alpha _{i}^{+}\eta _{i}^{+}\left\| \varphi _{i}^{\nabla }(s)-u_{i}^{\nabla }(s)\right\| +\sum \limits _{j=1}^{n} D_{ij}^{+}\left\| \varphi _{i}(t)-u_{i}(t)\right\| \right. \\&+\sum \limits _{j=1}^{n} (D_{ij}^{\tau })^{+}L_{j}\left\| \varphi _{j}(s-\tau _{ij}(s))-u_{j}(s-\tau _{ij}(s))\right\| \\&+\sum \limits _{j=1}^{n} (\overline{D}_{ij})^{+}L_{j}\sigma _{ij}^{+}\left\| \varphi _{j}(s)-u_{j}(s)\right\| \\&+\left. \sum \limits _{j=1}^{n} (\widetilde{D}_{ij})^{+}L_{j}\xi _{ij}^{+}\left\| \varphi _{j}^{\nabla }(s)-u^{\nabla }_{j}(s)\right\| +B_{i}^{+}\left\| \phi _{j}(s)-v_{j}(s)\right\| \right) \\\le & {} \frac{1}{\alpha _{i}^{-}}\left( \alpha _{i}^{+}\eta _{i}^{+}+\sum \limits _{j=1}^{n}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}+(\overline{D}_{ij})^{+}\sigma _{ij}^{+}+(\widetilde{D}_{ij})^{+}\xi _{ij}^{+}\right) L_{j}\right. \\&+\left. B_{i}^{+}\right) \Vert \psi -{\varOmega }\Vert _{\mathbb {B}}\\\le & {} \left( 1+\frac{\alpha _{i}^{+}}{\alpha _{i}^{-}}\right) \overline{M}_{i}\Vert \psi -{\varOmega }\Vert _{\mathbb {B}}. \end{aligned}$$

Similarly,

$$\begin{aligned} \sup \limits _{s\in \mathbb {T}}\left\| S_{\phi _{i}}(s)-S_{v_{i}}(s) \right\|\le & {} \left( \frac{\overline{N}_{i}}{c_{i}^{-}}\right) \Vert \psi -{\varOmega }\Vert _{\mathbb {B}}, \end{aligned}$$

and

$$\begin{aligned} \sup \limits _{s\in \mathbb {T}}\left\| S^{\nabla }_{\phi _{i}}(s)-S^{\nabla }_{v_{i}}(s) \right\|\le & {} \left( 1+\frac{c_{i}^{+}}{c_{i}^{-}}\right) \overline{N}_{i}\Vert \psi -{\varOmega }\Vert _{\mathbb {B}}, \end{aligned}$$

therefore,

$$\begin{aligned} \Vert {\varGamma }\psi -{\varGamma }{\varOmega }\Vert\le & {} \kappa \Vert \psi -{\varOmega }\Vert _{\mathbb {B}}, \,\ \text {where}\,\ \kappa <1. \end{aligned}$$

According to the well-known contraction principle there exists a unique fixed point $y^{*}\left( \cdot \right)$ such that ${\varGamma }y^{*}=y^{*}$. So, $y^{*}$ is a pseudo almost periodic solution of the model (2) in $\mathbb {F}=\{\psi \in \mathbb {B}{:} \,\ \Vert \psi \Vert _{\mathbb {B}}\le r\}$. This completes the proof.

Remark 3

To the best of our knowledge, there have been no results on the pseudo almost periodic solutions on time-space scale for competitive neural networks with time varying coefficients, mixed delays and leakage until now. Hence, the obtained results are essentially new and the investigation methods used in this paper can also be applied to study pseudo-almost periodic solutions on time-space scale for some other types of neural networks, such as Cohen–Grossberg neural networks.

Remark 4

In practice, time delays, leakage delay and parameter perturbations are unavoidably encountered in the implementation of competitive neural networks. They may destroy the stability of pseudo-almost periodic solution of competitive neural networks, thus it is crucial to study the dynamic behaviors of pseudo-almost periodic solution of competitive neural networks with time delays, leakage term and parameter perturbations.

5 Global Exponential Stability of Pseudo-Almost Periodic Solution and the Convergence of All Solutions to Its Unique Pseudo Almost Periodic Solution

In this section, we will study the exponential stability of pseudo-almost periodic solutions of (2):

Definition 6

Let $Z^{*}\left( t\right) =\left( x_{1}^{*}\left( t\right) , x_{2}^{*}\left( t\right) , \ldots ,x_{n}^{*}\left( t\right) ,S_{1}^{*}\left( t\right) ,S_{2}^{*}\left( t\right) ,\ldots ,S_{n}^{*}\left( t\right) \right) ^{T}$ be a pseudo-almost periodic solution on time-space scales of system (3) with initial value $\psi ^{*}\left( t\right) =\left( \varphi _{1}^{*}\left( t\right) ,\varphi _{2}^{*}\left( t\right) ,\ldots , \varphi _{n}^{*}\left( t\right) ,\phi _{1}^{*}\left( t\right) ,\phi _{2}^{*}\left( t\right) ,\ldots , \phi _{n}^{*}\left( t\right) \right) ^{T}$. If there exist constants $\gamma >0$, $\ominus _{\nu }\gamma \in \mathcal {R}_{+}$ and $M>1$ such that for every solution $Z\left( t\right) =\left( x_{1}\left( t\right) , x_{2}^{*}\left( t\right) , \ldots ,x_{n}\left( t\right) ,S_{1}\left( t\right) ,S_{2}\left( t\right) ,\ldots ,S_{n}\left( t\right) \right) ^{T}$ of system (3) with any initial value $\psi \left( t\right) =\left( \varphi _{1}\left( t\right) ,\varphi _{2}\left( t\right) ,\cdots , \varphi _{n}\left( t\right) ,\phi _{1}\left( t\right) ,\phi _{2}\left( t\right) ,\cdots , \phi _{n}\left( t\right) \right) ^{T}$, $\,\ \forall t\in (0,+\infty )_{\mathbb {T}}$, $t\ge t_{0}$,

$$\begin{aligned} \left\| Z\left( t\right) -Z^{*}\left( t\right) \right\| _{0}= & {} \max \left\{ \left\| x\left( t\right) -x^{*}\left( t\right) \right\| _{\infty } ,\Vert x^{\nabla }\left( t\right) -x^{*\nabla }\left( t\right) \Vert _{\infty },\right. \\&\left. \left\| S\left( t\right) -S^{*}\left( t\right) \right\| _{\infty } ,\Vert S^{\nabla }\left( t\right) -S^{*\nabla }\left( t\right) \Vert _{\infty }\right\} \\\le & {} M e_{\ominus \gamma }(t,t_{0})\Vert \psi \Vert _{1} \\= & {} M e_{\ominus \gamma }(t,t_{0})\sup \limits _{t\in [-\gamma ,0]_{\mathbb {T}}}\max \left\{ \left\| \varphi \left( t\right) -\varphi ^{*}\left( t\right) \right\| _{\infty } ,\left\| \varphi ^{\nabla }\left( t\right) -\varphi ^{*\nabla }\left( t\right) \right\| _{\infty },\right. \\&\left. \left\| \phi \left( t\right) -\phi ^{*}\left( t\right) \right\| _{\infty } ,\left\| \phi ^{\nabla }\left( t\right) -\phi ^{*\nabla }\left( t\right) \right\| _{\infty } \right\} , \end{aligned}$$

where $t_{0}=\max \{[-\theta ,0]_{\mathbb {T}}\}$. Then $Z^{*}\left( \cdot \right)$ is said to be globally exponential stable.

Theorem 2

Let $(H_{1}){-}(H_{3})$ hold. The unique pseudo-almost periodic solution of system (2) is globally exponentially stable.

Proof

From Theorem 1 the system (2) has one and only one pseudo-almost periodic solution on time scales $Z^{*}(t)=(x^{*}_{1}(t),\ldots x^{*}_{n}(t),S^{*}_{1}(t),\ldots ,S^{*}_{n}(t))^{T}\in \mathbb {R}^{n}$ with the initial condition $\psi ^{*}(t)=(\varphi ^{*}_{1}(t),\ldots ,\varphi ^{*}_{n}(t),\phi ^{*}_{1}(t),\ldots ,\phi ^{*}_{n}(t))^{T}$.

Let $Z(t)=(x_{1}(t),\ldots ,x_{n}(t),S_{1}(t),\ldots ,S_{n}(t))$ one arbitrary solution of (2) with initial condition $\psi (t)=(\varphi _{1}(t),\ldots ,\varphi _{n}(t),\phi _{1}(t),\ldots ,\phi _{n}(t))^{T}$.

From system (2) we obtain:

$$\begin{aligned} \left\{ \begin{array}{ccc} u^{\nabla }_{i}\left( t\right) = -\alpha _{i}(t)u_{i}\left( t\right) +\alpha _{i}(t)\displaystyle {\int }_{t-\eta _{i}(t)}^{t}u^{\nabla }_{i}(s)\nabla s+\sum \limits _{j=1}^{n}D_{ij}\left( t\right) p_{j}\left( u_{j}(t)\right) \\ +\sum \limits _{j=1}^{n}D^{\tau }_{ij}\left( t\right) p_{j}(u_{j}\left( \left( t-\tau _{ij}(t)\right) \right) +\sum \limits _{j=1}^{n}\overline{D}_{ij}\left( t\right) \displaystyle {\int }_{t-\sigma _{ij}(t)} ^{t}p_{j}\left( u_{j}\left( s\right) \right) \nabla s\\ \sum \limits _{j=1}^{n}\widetilde{D}_{ij}\left( t\right) \displaystyle \int _{t-\xi _{ij}(t)} ^{t}h_{j}\left( u_{j}^{\nabla }\left( s\right) \right) \nabla s+B_{i}(t)v_{i}(t),\\ v_{i}^{\nabla }(t)=-c_{i}(t)v_{i}(t)+c_{i}(t)\displaystyle {\int }_{t-\varsigma _{i}(t)}^{t}u_{i}^{\nabla }(s)\nabla s+E_{i}(t)p_{i}(u_{i}(t))\,\ t\in \mathbb {T}, \end{array} \right. \end{aligned}$$

(5)

where $u_{i}(t)=x_{i}(t)-x^{*}_{i}(t), v_{i}(t)=S_{i}(t)-S_{i}^{*}(t)$, $p_{j}(u_{j}(t))=f_{j}(x_{j}(t))-f_{j}(x_{j}^{*}(t))$, $h_{j}(x_{j}^{\nabla }(t))=f_{j}(x_{j}^{\nabla }(t))-f_{j}({x_{j}^{*}}^{\nabla }(t))$, for $i,j=1,\ldots ,n$, the initial condition of (5) is $u_{i}(s)=\varphi _{i}(s)-\varphi _{i}^{*}(s), \,\ s\in [-\theta ,0]_{\mathbb {T}}$, $v_{i}(s)=\phi _{i}(s)-\phi _{i}^{*}(s), \,\ s\in [-\theta ,0]_{\mathbb {T}}$, where $i=1,\ldots ,n$.

Multiplying the first equation in system (5) by $\hat{e}_{-\alpha _{i}}(t_{0},\rho (s))$ and the second equation by $\hat{e}_{-c_{i}}(t_{0},\rho (s))$, and integrating over $[t_{0},t]_{\mathbb {T}}$, where $t_{0}\in [-\theta ,0]_{\mathbb {T}}$, we obtain

$$\begin{aligned} \left\{ \begin{array}{ccc} u_{i}\left( t\right) = u_{i}\left( t_{0}\right) \hat{e}_{-\alpha _{i}}(t,t_{0})+\displaystyle {\int }_{t_{0}}^{t}\hat{e}_{-\alpha _{i}}(t,\rho (s))\left( \alpha _{i}(s)\int _{s-\eta _{i}(s)}^{t}u^{\nabla }_{i}(u)\nabla u\right. \\ ~~~~~~~~+\sum \limits _{j=1}^{n}D_{ij}\left( s\right) p_{j}\left( u_{j}(s)\right) +\sum \limits _{j=1}^{n}D^{\tau }_{ij}\left( s\right) p_{j}(u_{j}\left( \left( s-\tau _{ij}(s)\right) \right) \\ \left. \quad +\sum \limits _{j=1}^{n}\overline{D}_{ij}\left( s\right) \int _{s-\sigma _{ij}(s)} ^{s}p_{j}\left( u_{j}\left( u\right) \right) \nabla u\right. \\ \left. +\sum \limits _{j=1}^{n}\widetilde{D}_{ij}\left( s\right) \displaystyle \int _{s-\xi _{ij}(s)} ^{t}h_{j}\left( u_{j}^{\nabla }\left( u\right) \right) \nabla u+B_{i}(s)v_{i}(s)\right) \nabla s,\\ v_{i}(t)=v_{i}(t_{0})\hat{e}_{-c_{i}}(t,t_{0})+\int _{t_{0}}^{t}\hat{e}_{-c_{i}}(t,\rho (s))\left( c_{i}(s)\int _{s-\varsigma _{i}(s)}^{s} v_{i}^{\nabla }(u)\nabla u\right. \\ \left. +\,E_{i}(s)p_{i}(u_{i}(s))\right) \nabla s,\,\ t\in \mathbb {T}, \end{array} \right. \end{aligned}$$

(6)

Now, we define $G_{i}$, $\overline{G}_{i}$, $H_{i}$ and $\overline{H}_{i}$ as follows:

$$\begin{aligned} G_{i}(w)= & {} \alpha _{i}^{-}-w-\left( \exp \left( w \sup \limits _{s\in \mathbb {T}}\nu (s)\right) \left( \alpha _{i}^{+}\eta _{i}^{+} \exp \left( w\eta _{i}^{+}\right) \right. \right. +\sum \limits _{j=1}^{n}D_{ij}^{+}L_{j}\\&+\sum \limits _{j=1}^{n}(D_{ij}^{\tau })^{+}L_{j}\exp \left( w\tau _{ij}^{+}\right) +\sum \limits _{j=1}^{n}\overline{D}_{ij}^{+}L_{j}\sigma _{ij}^{+}\exp \left( w\sigma _{ij}^{+}\right) \\&\left. +\sum \limits _{j=1}^{n}\widetilde{D}_{ij}^{+}L_{j}\xi _{ij}^{+}\exp \left( w\xi _{ij}^{+}\right) +B_{i}^{+}\right) ,\\&\overline{G}_{i}(w)=c_{i}^{-}-w-\left( \exp \left( w\sup \limits _{s\in \mathbb {T}}\nu (s)\right) c_{i}^{+}\varsigma _{i}^{+}\exp \left( w\varsigma _{i}^{+}\right) +E_{i}^{+}L_{i}\right) ,\\ H_{i}(w)= & {} \alpha _{i}^{-}-w-\left( \alpha _{i}^{+}\exp \left( w \sup \limits _{s\in \mathbb {T}}\nu (s)+\alpha _{i}^{-}-\beta \right) \left( \alpha _{i}^{+}\eta _{i}^{+} \exp \left( w\eta _{i}^{+}\right) \right. \right. \\&+\sum \limits _{j=1}^{n}D_{ij}^{+}L_{j}+\sum \limits _{j=1}^{n}(D_{ij}^{\tau })^{+}L_{j}\exp \left( w\tau _{ij}^{+}\right) +\sum \limits _{j=1}^{n}\overline{D}_{ij}^{+}L_{j}\sigma _{ij}^{+}\exp \left( w\sigma _{ij}^{+}\right) \\&\left. +\sum \limits _{j=1}^{n}\widetilde{D}_{ij}^{+}L_{j}\xi _{ij}^{+}\exp \left( w\xi _{ij}^{+}\right) +B_{i}^{+}\right) ,\\ \overline{H}_{i}(w)= & {} c_{i}^{-}-w-\left( c_{i}^{+}\exp \left( w\sup \limits _{s\in \mathbb {T}}\nu (s)+c_{i}^{-}-w\right) c_{i}^{+}\varsigma _{i}^{+}\exp \left( w\varsigma _{i}^{+}\right) +E_{i}^{+}L_{i}\right) , \end{aligned}$$

where $i=1,\ldots ,n$, $w\in ]0,+\infty [$.

From $\left( H_{3} \right)$, we have

$$\begin{aligned} G_{i}(0)= & {} \alpha _{i}^{-}-\left( \alpha _{i}^{+}\eta _{i}^{+}+\sum \limits _{j=1}^{n}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}+\overline{D}_{ij}^{+}\sigma _{ij}^{+} +\widetilde{D}_{ij}^{+}\xi _{ij}^{+}\right) L_{j}+B_{i}^{+}\right)>0,\\ \overline{G}_{i}(0)= & {} c_{i}^{-}-(c_{i}^{+}\varsigma _{i}^{+}+E_{i}^{+}L_{i})>0,\\ H_{i}(0)= & {} \alpha _{i}^{-}\!-\!\left( \alpha _{i}^{+}\!+\!\alpha _{i}^{-}\right) \left( \alpha _{i}^{+}\eta _{i}^{+}\!+\!\sum \limits _{j=1}^{n}\left( D_{ij}^{+}\!+\! (D_{ij}^{\tau })^{+}\!+\!\overline{D}_{ij}^{+}\sigma _{ij}^{+} \!+\!\widetilde{D}_{ij}^{+}\xi _{ij}^{+}\right) L_{j}\!+\!B_{i}^{+}\right) \!>\!0,\\ \overline{H}_{i}(0)= & {} c_{i}^{-}-(c_{i}^{+}+c_{i}^{-})(c_{i}^{+}\varsigma _{i}^{+}+E_{i}^{+}L_{i})>0, i=1,\ldots ,n. \end{aligned}$$

Since the functions $G_{i}(.)$, $\overline{G}_{i}(.)$, $H_{i}(.)$ and $\overline{H}_{i}(.)$ are continuous on $[0,+\infty )$ and $G_{i}(w)$, $\overline{G}_{i}(w)$, $H_{i}(w)$, $\overline{H}_{i}(w)\longrightarrow -\infty$ when $w\longrightarrow +\infty$, it exist $\eta _{i}, \bar{\eta }_{i}, \epsilon _{i}, \bar{\epsilon }_{i}>0$ such as $H_{i}(\eta _{i})=\overline{H}_{i}(\bar{\eta }_{i})=G_{i}(\epsilon _{i})=\overline{G}_{i}(\bar{\epsilon }_{i})=0$ and $G_{i}(w)>0$ for $w\in (0,\eta _{i})$, $\overline{G}_{i}(w)>0$ for $w\in (0,\bar{\eta }_{i})$, $H_{i}(w)>0$ for $w\in (0,\epsilon _{i})$, $\bar{H}_{i}(w)>0$ for $w\in (0,\bar{\epsilon }_{i})$. Let $a=\min \limits _{1\le i\le n}\left\{ \eta _{i}, \bar{\eta }_{i}, \epsilon _{i}, \bar{\epsilon }_{i}\right\}$, we obtain

$$\begin{aligned} H_{i}(a)\ge 0,\,\ \overline{H}_{i}(a)\ge 0, \,\ G_{i}(a)\ge 0,\,\ \text {and} \,\ \overline{G}_{i}(a)\ge 0,\,\ i=1,\ldots ,n. \end{aligned}$$

So, we can choose the positive constant $0<\gamma <\min \limits _{1\le i \le n}\{a,\alpha _{i}^{-},c_{i}^{-}\},$

$\text {such that}\,\ H_{i}(\gamma )>0,\,\ \overline{H}_{i}(\gamma )>0, \,\ G_{i}(\gamma )>0\,\ \text {and} \,\ \overline{G}_{i}(\gamma )>0, \,\ i=1,\ldots ,n.$ which imply that, for $i=1,\ldots ,n$

$$\begin{aligned}&\frac{1}{\alpha _{i}^{-}-\gamma }\sum \limits _{j=1}^{n}\left( \exp (\gamma \sup \limits _{s\in \mathbb {T}}\nu (s))\left( \alpha _{i}^{+}\eta _{i}^{+}+\sum \limits _{j=1}^{n}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}\,+\overline{D}_{ij}^{+}\sigma _{ij}^{+}\right. \right. \right. \\&\quad \left. \left. \left. +\,\widetilde{D}_{ij}^{+}\xi _{ij}^{+}\right) L_{j}+B_{i}^{+}\right) \right)<1,\\&\quad \frac{1}{c_{i}^{-}-\gamma }\left( \exp (\gamma \sup \limits _{s\in \mathbb {T}}\nu (s))c_{i}^{+}\varsigma _{i}^{+}+E_{i}^{+}L_{i}\right)<1,\\&\quad \left( 1+\frac{\alpha _{i}^{+}\exp (\gamma \sup \limits _{s\in \mathbb {T}}\nu (s))}{\alpha _{i}^{-}-\gamma }\right) \sum \limits _{j=1}^{n}\left( \exp (\gamma \sup \limits _{s\in \mathbb {T}}\nu (s))\left( \alpha _{i}^{+}\eta _{i}^{+}+\sum \limits _{j=1}^{n}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}\right. \right. \right. \\&\quad \left. \left. \left. +\,\overline{D}_{ij}^{+}\sigma _{ij}^{+}+\widetilde{D}_{ij}^{+}\xi _{ij}^{+}\right) L_{j}+B_{i}^{+}\right) \right)<1,\\&\quad \left( 1+\frac{c_{i}^{+}\exp (\gamma \sup \limits _{s\in \mathbb {T}}\nu (s))}{c_{i}^{-}-\gamma }\right) \left( c_{i}^{+}\varsigma _{i}^{+}+E_{i}^{+}L_{i}\right) <1, \end{aligned}$$

Let

$$\begin{aligned} K= & {} \max \limits _{1\le i\le n}\left\{ \frac{\alpha _{i}^{-}}{\alpha _{i}^{+}\eta _{i}^{+}+\sum \limits _{j=1}^{n}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}+\overline{D}_{ij}^{+}\sigma _{ij}^{+} +\widetilde{D}_{ij}^{+}\xi _{ij}^{+}\right) L_{j}+B_{i}^{+}},\right. \nonumber \\&\left. \frac{c_{i}^{-}}{c_{i}^{+}\varsigma _{i}^{+}+E_{i}^{+}L_{i}}\right\} . \end{aligned}$$

(7)

By hypothesis ($H_{3}$), we have $K>1$, therefore,

$$\begin{aligned} \Vert Z(t)-Z^{*}(t)\Vert \le K \hat{e}_{\ominus _{\nu } \gamma }(t,t_{0})\Vert \psi \Vert _{0},\,\ \forall t\in [t_{0},0]_{\mathbb {T}}, \end{aligned}$$

(8)

where $\ominus _{\nu }\gamma \in \mathcal {R}_{\nu }^{+}$. We claim that

$$\begin{aligned} \Vert Z(t)-Z^{*}(t)\Vert \le K \hat{e}_{\ominus _{\nu } \gamma }(t,t_{0})\Vert \psi \Vert _{0},\,\ \forall t\in [t_{0},+\infty )_{\mathbb {T}}. \end{aligned}$$

(9)

To prove (9), we show that for any $\varpi >1$, the following inequality holds:

$$\begin{aligned} \Vert Z(t)-Z^{*}(t)\Vert \le \varpi K \hat{e}_{\ominus _{\nu } \gamma }(t,t_{0})\Vert \psi \Vert _{0},\,\ \forall t\in [t_{0},+\infty )_{\mathbb {T}}. \end{aligned}$$

(10)

If (10) is not true, then there must be some $t_{1}\in (0,+\infty )_{\mathbb {T}}$, $d\ge 1$ such that

$$\begin{aligned} \Vert Z(t_{1})-Z^{*}(t_{1})\Vert =d \varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}, \end{aligned}$$

(11)

and

$$\begin{aligned} \Vert Z(t)-Z^{*}(t)\Vert \le d \varpi K \hat{e}_{\ominus _{\nu } \gamma }(t,t_{0})\Vert \psi \Vert _{0}, \,\ t\in [t_{0},t_{1}]_{\mathbb {T}}. \end{aligned}$$

(12)

By (6), (11), (12) and $(H_{1}){-}(H_{3})$, we have for $i=1,\ldots ,n$

$$\begin{aligned} |u_{i}(t_{1})|\le & {} \hat{e}_{-\alpha _{i}}(t_{1},t_{0})\Vert \psi \Vert _{0}+d \varpi K \hat{e}_{\ominus _{\nu }\gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}\int _{t_{0}}^{t_{1}} \hat{e}_{-\alpha _{i}}(t_{1},\rho (s))\hat{e}_{\gamma }(t_{1},\rho (s))\\&\times \left( \alpha _{i}^{+}\int _{s-\eta _{i}(s)}^{s}\hat{e}_{\lambda }(\rho (u),u)\nabla u+\sum \limits _{j=1}^{n} D_{ij}^{+}L_{j}\hat{e}_{\gamma }(\rho (s),s)\right. \\&+\, (D_{ij}^{\tau })^{+}L_{j}\hat{e}_{\gamma }(\rho (s),s-\tau _{ij}(s))+\sum \limits _{j=1}^{n} \overline{D}_{ij}^{+}L_{j}\int _{s-\sigma _{ij}(s)}^{s}\hat{e}_{\gamma }(\rho (u),u)\nabla u\\&+\,\left. \sum \limits _{j=1}^{n} \widetilde{D}_{ij}^{+}L_{j}\int _{s-\xi _{ij}(s)}^{s}\hat{e}_{\gamma }(\rho (u),u)\nabla u+ B_{i}^{+}\right) \nabla s\\\le & {} \hat{e}_{-\alpha _{i}}(t_{1},t_{0})\Vert \psi \Vert _{0}+d \varpi K \hat{e}_{\ominus _{\nu }\gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}\int _{t_{0}}^{t_{1}} \hat{e}_{-\alpha _{i}}(t_{1},\rho (s))\hat{e}_{\gamma }(t_{1},\rho (s))\\&\times \,\left( \alpha _{i}^{+}\hat{e}_{\lambda }(\rho (s),s-\eta _{i}(s))+\sum \limits _{j=1}^{n} D_{ij}^{+}L_{j}\hat{e}_{\gamma }(\rho (s),s)\right. \\&+ (D_{ij}^{\tau })^{+}L_{j}\hat{e}_{\gamma }(\rho (s),s-\tau _{ij}(s))+\sum \limits _{j=1}^{n} \overline{D}_{ij}^{+}L_{j}\int _{s-\sigma _{ij}(s)}^{s}\hat{e}_{\gamma }(\rho (u),u)\nabla u\\&+\,\left. \sum \limits _{j=1}^{n} \widetilde{D}_{ij}^{+}L_{j}\int _{s-\xi _{ij}(s)}^{s}\hat{e}_{\gamma }(\rho (u),u)\nabla u+ B_{i}^{+}\right) \nabla s\\\le & {} \hat{e}_{-\alpha _{i}}(t_{1},t_{0})\Vert \psi \Vert _{0}+d \varpi K \hat{e}_{\ominus _{\nu }\gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}\int _{t_{0}}^{t_{1}} \hat{e}_{-\alpha _{i}}(t_{1},\rho (s))\hat{e}_{\gamma }(t_{1},\rho (s))\\&\times \left( \alpha _{i}^{+}\eta _{i}^{+}\exp \left[ \gamma \left( \eta _{i}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s)\right) \right] +\sum \limits _{j=1}^{n} D_{ij}^{+}L_{j}\exp \left( \gamma \sup \limits _{s\in \mathbb {T}}\nu (s)\right) \right. \\&+\, (D_{ij}^{\tau })^{+}L_{j}\exp \left[ \gamma \left( \tau _{ij}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s)\right) \right] +\sum \limits _{j=1}^{n} \overline{D}_{ij}^{+}L_{j}\exp \left[ \gamma \left( \sigma _{ij}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s)\right) \right] \\&+\,\left. \sum \limits _{j=1}^{n} \widetilde{D}_{ij}^{+}L_{j}\exp \left[ \gamma \left( \xi _{ij}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s)\right) \right] + B_{i}^{+}\right) \nabla s \end{aligned}$$

$$\begin{aligned}\le & {} d\varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}\left\{ \frac{1}{K}\hat{e}_{-\alpha _{i}\oplus _{\nu }\gamma }(t_{1},t_{0})+ \left[ \exp \left( \gamma \sup \limits _{s\in \mathbb {T}}\nu (s)\right) \right. \right. \nonumber \\&\times \, \left( \alpha _{i}^{+}\eta _{i}^{+}\exp (\gamma \eta _{i}^{+})+ \sum \limits _{j=1}^{n}D_{ij}^{+}L_{j}+\sum \limits _{j=1}^{n}(D_{ij}^{\tau })^{+}L_{j}\exp (\gamma \tau _{ij}^{+})\right. \nonumber \\&+\left. \sum \limits _{j=1}^{n}\overline{D}_{ij}^{+}\sigma _{ij}^{+}L_{j}\exp (\gamma \sigma _{ij}^{+})+ \sum \limits _{j=1}^{n}\widetilde{D}_{ij}^{+}L_{j}\xi _{ij}^{+}\exp (\gamma \xi _{ij}^{+})\right) \nonumber \\&+\left. \left. B_{i}^{+}\right] \frac{1-\hat{e}_{-\alpha _{i}\oplus _{\nu }\gamma }(t_{1},t_{0})}{\alpha _{i}^{-}-\gamma }\right\} \nonumber \\\le & {} d\varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}\left\{ \frac{1}{K}-\frac{1}{\alpha _{i}^{-}-\gamma }\left( \exp \left( \gamma \sup \limits _{s\in \mathbb {T}}\nu (s)\right) \left( \alpha _{i}^{+}\eta _{i}^{+}\exp (\gamma \eta _{i}^{+})\right. \right. \right. \nonumber \\&+\sum \limits _{j=1}^{n}D_{ij}^{+}L_{j}+\sum \limits _{j=1}^{n}(D_{ij}^{\tau })^{+}L_{j}\exp (\gamma \tau _{ij}^{+})\nonumber \\&+\left. \sum \limits _{j=1}^{n}\overline{D}_{ij}^{+}\sigma _{ij}^{+}L_{j}\exp (\gamma \sigma _{ij}^{+})+ \sum \limits _{j=1}^{n}\widetilde{D}_{ij}^{+}L_{j}\xi _{ij}^{+}\exp (\gamma \xi _{ij}^{+})\right) \nonumber \\&+ \left. B_{i}^{+}\right] \hat{e}_{-\alpha _{i}\oplus _{\nu }\gamma }(t_{1},t_{0}) +\frac{1}{\alpha _{i}^{-}-\gamma }\left( \exp \left( \gamma \sup \limits _{s\in \mathbb {T}}\nu (s) \left( \alpha _{i}^{+}\eta _{i}^{+}\exp (\gamma \eta _{i}^{+})\right. \right. \right. \nonumber \\&+\sum \limits _{j=1}^{n}D_{ij}^{+}L_{j}+\sum \limits _{j=1}^{n}(D_{ij}^{\tau })^{+}L_{j}\exp (\gamma \tau _{ij}^{+})\nonumber \\&+\left. \left. \left. \sum \limits _{j=1}^{n}\overline{D}_{ij}^{+}\sigma _{ij}^{+}L_{j}\exp (\gamma \sigma _{ij}^{+})+ \sum \limits _{j=1}^{n}\widetilde{D}_{ij}^{+}L_{j}\xi _{ij}^{+}\exp (\gamma \xi _{ij}^{+})\right) +B_{i}^{+}\right) \right\} \nonumber \\\le & {} d\varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}. \end{aligned}$$

(13)

In addition, we have

$$\begin{aligned} |v_{i}(t_{1})|\le & {} \hat{e}_{-c_{i}}(t_{1},t_{0})\Vert \psi \Vert _{0}+ d\varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}\int _{t_{0}}^{t_{1}}\hat{e}_{-c_{i}}(t_{1},\rho (s))\hat{e}_{\gamma }(t_{1},\rho (s))\nonumber \\&\quad \times \left( c_{i}^{+}\int _{s-\varsigma _{i}(s)}^{s}\hat{e}_{\gamma }(\rho (u),u)\nabla u+E_{i}^{+}L_{i}\right) \nabla s\nonumber \\\le & {} \hat{e}_{-c_{i}}(t_{1},t_{0})\Vert \psi \Vert _{0}+ d\varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}\int _{t_{0}}^{t_{1}}\hat{e}_{-c_{i}\oplus _{\nu }\gamma }(t_{1},\rho (s))\nonumber \\&\quad \times \left( c_{i}^{+}\varsigma _{i}^{+}\hat{e}_{\gamma }(\rho (s),s-\varsigma _{i}(s))+E_{i}^{+}L_{i}\right) \nabla s\nonumber \\\le & {} \hat{e}_{-c_{i}}(t_{1},t_{0})\Vert \psi \Vert _{0}+ d\varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}\int _{t_{0}}^{t_{1}}\hat{e}_{-c_{i}\oplus _{\nu }\gamma }(t_{1},\rho (s))\nonumber \\&\quad \times \left( c_{i}^{+}\varsigma _{i}^{+}\exp \left[ \gamma \left( \varsigma _{i}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s)\right) \right] +E_{i}^{+}L_{i}\right) \nabla s\\\le & {} d\varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}\left\{ \left[ \frac{1}{K}-\frac{1}{c_{i}^{-}-\gamma }\left( \exp \left[ \gamma \left( \varsigma _{i}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s)\right) \right] \right. \right. \right. \nonumber \\&\quad +\left. \left. \left. E_{i}^{+}L_{i}\right) \right] \hat{e}_{-c_{i}\oplus _{\nu }\gamma }(t_{1},t_{0})+\frac{1}{c_{i}^{-}-\gamma }\left( \exp \left[ \gamma \left( \varsigma _{i}^{+}+\sup \limits _{s\in \mathbb {T}}\nu (s)\right) \right] +E_{i}^{+}L_{i}\right) \right\} \nonumber \\\le & {} d\varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}. \end{aligned}$$

We can easily obtain some upper bound of the derivative $|u_{i}^{\nabla }(t_{1})|$ and $|u_{i}^{\nabla }(t_{1})|$ as follow:

$$\begin{aligned} |u_{i}^{\nabla }(t_{1})|\le d\varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}, \end{aligned}$$

(14)

and

$$\begin{aligned} |v_{i}^{\nabla }(t_{1})|\le d\varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}. \end{aligned}$$

(15)

From (13) to (15), we obtain

$$\begin{aligned} \Vert Z(t_{1})-Z^{*}(t_{1})\Vert < d\varpi K \hat{e}_{\ominus _{\nu } \gamma }(t_{1},t_{0})\Vert \psi \Vert _{0}. \end{aligned}$$

(16)

which contradicts (11), therefore (10) holds. Letting $\varpi \longrightarrow 1$, then (9) holds. This implies that only pseudo-almost periodic solution of system (2) is globally exponentially stable.

Theorem 3

Suppose that assumptions ($H_{1}){-}(H_{3}$) hold.

Let $y^{*}\left( \cdot \right) =\left( x_{1}^{*}\left( \cdot \right) ,\ldots ,x_{n}^{*}\left( \cdot \right) ,,S_{1}^{*}\left( \cdot \right) ,\ldots ,,S_{n}^{*}\left( \cdot \right) \right) ^{T}$ be a pseudo-almost periodic solution of system (2). If

$$\begin{aligned}&\min \left\{ \alpha _{i}^{-}-\sum \limits _{j=1}^{n}L_{j}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}+(\overline{D}_{ij})^{+}\sigma _{ij}^{+}+(\widetilde{D}_{ij})^{+}\xi _{ij}^{+}\right) -E_{i}^{+}L_{i},\right. \\&\quad \left. c_{i}^{-}-B_{i}^{+}\right\} >0, \end{aligned}$$

then all solutions $\psi =(\varphi _{1},\ldots ,\varphi _{n},\phi _{1},\ldots ,\phi _{n})$ of (2) satisfying

$$\begin{aligned} x_{i}^{*}\left( 0\right) =\varphi _{i}\left( 0\right) , \,\ S_{i}^{*}\left( 0\right) =\phi _{i}\left( 0\right) , 1\le i\le n, \end{aligned}$$

converge to its unique pseudo-almost periodic solution $y^{*}$.

Proof

Let $y^{*}\left( \cdot \right) =\left( x_{1}^{*}\left( \cdot \right) ,\ldots ,x_{n}^{*}\left( \cdot \right) , S_{1}^{*}\left( \cdot \right) ,\ldots ,S_{n}^{*}\left( \cdot \right) \right)$ be a solution of (2) and $\psi \left( \cdot \right) =\left( \varphi _{1}\left( \cdot \right) ,\ldots ,\varphi _{n}\left( \cdot \right) , \phi _{1}\left( \cdot \right) ,\ldots ,\phi _{n}\left( \cdot \right) \right)$ be a pseudo almost periodic solution of (2). First, one verifies without difficulty that

$$\begin{aligned}&\left( x_{i}^{*}\left( t\right) -\alpha _{i}(t)\int _{t-\eta _{i}(t)}^{t}x_{i}(u)\nabla u\right) ^{\nabla } -\left( \varphi _{i}^{*}\left( t\right) -\alpha _{i}(t)\int _{t-\eta _{i}(t)}^{t}\varphi _{i}(u)\nabla u\right) ^{\nabla }\\&\quad =-\alpha _{i}(t)\left( x_{i}^{*}\left( t-\eta _{i}(t)\right) -\varphi _{i}\left( t-\eta _{i}(t)\right) \right) +\sum \limits _{j=1}^{n}D_{ij}\left( t\right) \left[ f_{j}(x_{j}^{*}\left( t \right) )-f_{j}(\varphi _{j}\left( t \right) )\right] \\&\qquad + \sum \limits _{j=1}^{n}D_{ij}^{\tau }\left( t\right) \left[ f_{j}(x_{j}^{*}\left( t-\tau _{ij}(t) \right) )-f_{j}(\varphi _{j}\left( t-\tau _{ij}(t) \right) )\right] \\&\qquad +\sum \limits _{j=1}^{n}\overline{D}_{ij}\left( t\right) \int \limits _{t-\sigma _{ij}(t)}^{t}\left[ f_{j}(x_{j}^{*}\left( t-u\right) )-f_{j}(\varphi _{j}\left( t-u\right) )\right] \nabla u \\&\qquad +\sum \limits _{j=1}^{n}\widetilde{D}_{ij}\left( t\right) \int \limits _{t-\xi _{ij}(t)}^{t} \left( f_{j}\left( (x_{j}^{*})^{\nabla }\left( u\right) \right) -f_{j}\left( \varphi _{j}^{\nabla }\left( u\right) \right) \right) \nabla u, \end{aligned}$$

and

$$\begin{aligned} S_{i}^{\nabla }(t)-\phi _{i}^{\nabla }(t)=-c_{i}(t)\left( S_{i}(t-\varsigma _{i})-\phi _{i}(t-\varsigma _{i})\right) +E_{i}(t)\left( f_{i}(x_{i}(t))-f_{i}(\varphi _{i}(t))\right) . \end{aligned}$$

then,

$$\begin{aligned} S_{i}^{\nabla }(t)-\phi _{i}^{\nabla }(t)=-c_{i}(t)\left( S_{i}(t-\varsigma _{i})-\phi _{i}(t-\varsigma _{i})\right) +E_{i}(t)\left( f_{i}(x_{i}(t))-f_{i}(\varphi _{i}(t))\right) . \end{aligned}$$

then

$$\begin{aligned}&\left( S_{i}^{*}\left( t\right) -c_{i}(t)\int _{t-\eta _{i}(t)}^{t}S_{i}(u)\nabla u\right) ^{\nabla } -\left( \phi _{i}^{*}\left( t\right) -c_{i}(t)\int _{t-\eta _{i}(t)}^{t}\phi _{i}(u)\nabla u\right) ^{\nabla }\\&\quad =-c_{i}(t)\left( S_{i}(t)-\phi _{i}(t)\right) +E_{i}(t)\left( f_{i}(x_{i}(t))-f_{i}(\varphi _{i}(t))\right) . \end{aligned}$$

Now, consider the following (ad-hoc) Lyapunov–Krasovskii functional

$$\begin{aligned} \begin{array}{cccc} V: &{} \mathbb {R} &{} \longrightarrow &{} PAP\left( \mathbb {T},\mathbb {R}^{n}\right) \\ &{} t &{} \longmapsto &{} V_{1}(t)+V_{2}(t)+V_{3}(t)+V_{4}(t)+V_{5}(t), \end{array} \end{aligned}$$

where

$$\begin{aligned} V_{1}(t)= & {} \sum \limits _{i=1}^{n}\left| \left( x_{i}^{*}\left( t\right) -\alpha _{i}(t)\int _{t-\eta _{i}(t)}^{t}x_{i}(u)\nabla u\right) -\left( \varphi _{i}^{*}\left( t\right) -\alpha _{i}(t)\int _{t-\eta _{i}(t)}^{t}\varphi _{i}(u)\nabla u\right) \right| ,\\ V_{2}\left( t\right)= & {} \sum \limits _{j=1}^{n}\sum \limits _{i=1}^{n}\int \limits _{t-\tau _{j}(t) }^{t}L_{j}\left( D_{ij}^{+}+(D_{ij}^{\tau })^{+}\right) \left| x_{i}^{*}\left( s\right) -\varphi _{i}\left( s\right) \right| \nabla s,\\ V_{3}\left( t\right)= & {} \sum \limits _{j=1}^{n}\sum \limits _{i=1}^{n}\int \limits _{t-\sigma _{ij}(t)}^{t }\int \limits _{t-s}^{t}L_{j}\overline{D}_{ij}^{+}\left| x_{i}^{*}\left( u\right) -\varphi _{i}\left( u\right) \right| \nabla u\,\ \nabla s,\\ V_{4}\left( t\right)= & {} \sum \limits _{j=1}^{n}\sum \limits _{i=1}^{n}\int \limits _{t-\xi _{ij}(t)}^{t }\int \limits _{s}^{0}L_{j}\widetilde{D}_{ij}^{+}\left| (x_{i}^{*})^{\nabla }\left( u\right) -(\varphi _{i})^{\nabla }\left( u\right) \right| \nabla u\,\ \nabla s. \end{aligned}$$

and

$$\begin{aligned} V_{5}(t)=\sum \limits _{i=1}^{n}\left| \left( S_{i}^{*}\left( t\right) -c_{i}(t)\int _{t-\eta _{i}(t)}^{t}S_{i}(u)\nabla u\right) -\left( \phi _{i}^{*}\left( t\right) -c_{i}(t)\int _{t-\eta _{i}(t)}^{t}\phi _{i}(u)\nabla u\right) \right| . \end{aligned}$$

Let us calculate the upper right Dini derivative $D^{+}V\left( t\right)$ of V along the solution of the equation above. Then one has

$$\begin{aligned} DV_{1}^{+}(t)\le & {} -\sum \limits _{i=1}^{n}\alpha _{i}^{-}\left| x_{i}^{*}\left( t\right) -\varphi _{i}\left( t\right) \right| +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}D_{ij}^{+} \left| f_{j}(x_{j}^{*}\left( t \right) )-f_{j}(\varphi _{j}\left( t \right) )\right| \\&+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}(D_{ij}^{\tau })^{+} \left| f_{j}(x_{j}^{*}\left( t-\tau _{j}(t) \right) )-f_{j}(\varphi _{j}\left( t-\tau _{j}(t) \right) )\right| \\&+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n} \overline{D}_{ij}^{+} \int \limits _{t-\sigma _{ij}(t)}^{t} \left| f_{j}(x_{j}^{*}\left( t-u\right) )-f_{j}(\varphi _{j}\left( t-u\right) )\right| \nabla u\\&+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n} \widetilde{D}_{ij}^{+} \int \limits _{t-\xi _{ij}(t)}^{t} \left| f_{j}\left( (x_{j}^{*}) {\nabla }\left( u\right) \right) -f_{j}\left( \varphi _{j}^{\nabla }\left( u\right) \right) \right| \nabla u\\ \end{aligned}$$

$$\begin{aligned}\le & {} -\sum \limits _{i=1}^{n}\alpha _{i}^{-}\left| x_{i}^{*}\left( t\right) -\varphi _{i}\left( t\right) \right| +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}D_{ij}^{+} L_{j}\left| x_{j}^{*}\left( t \right) -\varphi _{j}\left( t \right) \right| \\&+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}(D_{ij}^{\tau })^{+}L_{j} \left| x_{j}^{*}\left( t-\tau _{j}(t) \right) -\varphi _{j}\left( t-\tau _{j}(t) \right) \right| \\&+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n} \overline{D}_{ij}^{+} \int \limits _{t-\sigma _{ij}(t)}^{t} L_{j}\left| (x_{j}^{*}\left( t-u\right) -\varphi _{j}\left( t-u\right) \right| \nabla u\\&+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n} \widetilde{D}_{ij}^{+} \int \limits _{t-\xi _{ij}(t)}^{t} L_{j}\left| (x_{j}^{*})^{\nabla }\left( u\right) -\varphi _{j}^{\nabla }\left( u\right) \right| \nabla u+B_{i}^{+}\left| S_{i}(t)-\phi _{i}(t)\right| \end{aligned}$$

Obviously,

$$\begin{aligned} DV_{2}^{+}(t)\le & {} \sum \limits _{j=1}^{n}\sum \limits _{i=1}^{n}L_{j}(D_{ij}^{+}+(D_{ij}^{\tau })^{+})\left[ \left| x_{i}^{*}\left( t\right) -\varphi _{i}\left( t\right) \right| -\left| x_{i}^{*}\left( t-\tau _{ij}(t) \right) -\varphi _{i}\left( t-\tau _{ij}(t) \right) \right| \right] \\\le & {} \sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}L_{j}(D_{ij}^{+}+(D_{ij}^{\tau })^{+})\left| x_{i}^{*}\left( t\right) -\varphi _{i}\left( t\right) \right| \\&-\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}L_{j}(D_{ij}^{+}+(D_{ij}^{\tau })^{+})\left| x_{i}^{*}\left( t-\tau _{j}(t) \right) -\varphi _{i}\left( t-\tau _{j}(t) \right) \right| \end{aligned}$$

and

$$\begin{aligned} DV_{3}^{+}(t)\le & {} \sum \limits _{j=1}^{n}\sum \limits _{i=1}^{n}L_{j}\overline{D}_{ij}^{+}\int _{t-\sigma _{ij}(t)}^{t} \left[ \left| x_{i}^{*}\left( t\right) -\varphi _{i}\left( t\right) \right| -\left| x_{i}^{*}\left( t-s\right) -\varphi _{i}\left( t-s\right) \right| \right] \nabla s \\\le & {} \sum \limits _{j=1}^{n}\sum \limits _{i=1}^{n}L_{j}\overline{D}_{ij}^{+}\int _{t-\sigma _{ij}(t)}^{t}\left| x_{i}^{*}\left( t\right) -\varphi _{i}\left( t\right) \right| \nabla s\\&-\sum \limits _{j=1}^{n}\sum \limits _{i=1}^{n}L_{j}\overline{D}_{ij}^{+}\int _{t-\sigma _{ij}(t)}^{t}\left| x_{i}^{*}\left( t-s\right) -\varphi _{i}\left( t-s\right) \right| \nabla s. \end{aligned}$$

Reasoning in a similar way, we can obtain the following estimation

$$\begin{aligned} DV_{4}^{+}\left( t\right)= & {} \sum \limits _{j=1}^{n}\sum \limits _{i=1}^{n}\int _{t-\xi _{ij}(t)}^{t }\int \limits _{s}^{0}L_{j}\widetilde{D}_{ij}^{+}\left| (x_{i}^{*}) ^{\nabla }\left( u\right) -\varphi _{i}^{\nabla }\left( u\right) \right| \nabla u\,\ \nabla s \\\le & {} -\sum \limits _{j=1}^{n}\sum \limits _{i=1}^{n}L_{j}\widetilde{D}_{ij}^{+}\int _{t-\xi _{ij}(t)}^{t}\left| (x_{i}^{*})^{\nabla }\left( s\right) -\varphi _{i}^{\nabla }\left( s\right) \right| \nabla s, \end{aligned}$$

and,

$$\begin{aligned} DV_{5}^{+}\left( t\right)= & {} -c_{i}^{-}\left| S_{i}^{*}\left( t\right) -\phi _{i}\left( t\right) \right| +E_{i}^{+}\left| f_{i}(x_{i}(t))-f_{i}(\varphi _{i}(t))\right| \\\le & {} -c_{i}^{-}\left| S_{i}^{*}\left( t\right) -\phi _{i}\left( t\right) \right| +E_{i}^{+}L_{i}\left| x_{i}^{*}\left( t\right) -\varphi _{i}\left( t\right) \right| . \end{aligned}$$

By using the inequality

$$\begin{aligned} D^{+}\left( F_{1}+F_{2}\right) \le D^{+}\left( F_{1}\right) +D^{+}\left( F_{2}\right) , \end{aligned}$$

we get

$$\begin{aligned} D^{+}\left( V(t)\right)\le & {} DV_{1}^{+}(t)+DV_{2}^{+}(t)+DV_{3}^{+}(t)+DV_{4}^{+}(t) \\\le & {} -\sum \limits _{i=1}^{n} \sum \limits _{j=1}^{n}\max \left\{ \alpha _{i}^{+}-D_{ij}^{+}L_{j}-(D_{ij}^{\tau })^{+}L_{j}-\overline{D}_{ij}^{+}\sigma _{ij}^{+}L_{j}\right. \\&-\left. \widetilde{D}_{ij}^{+}\xi _{ij}^{+}L_{j}-E_{i}^{+}L_{i},c_{i}^{+}-B_{i}^{+}\right\} \Vert y^{*}\left( t\right) -\psi \left( t\right) \Vert \\= & {} -\sum \limits _{i=1}^{n}\beta _{i}\Vert y^{*}\left( t\right) -\psi \left( t\right) \Vert <0. \end{aligned}$$

By integrating the above inequality from $t_{0}$ to t, we get

$$\begin{aligned} V(t)+\sum \limits _{i=1}^{n}\beta _{i}\int \limits _{t_{0}}^{t}\Vert y^{*}\left( t\right) -\psi \left( t\right) \Vert \nabla s<V(t_{0})<+\infty . \end{aligned}$$

Now, we remark that $V(t)>0.$ It follows that

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }\sup \int \limits _{t_{0}}^{t}\beta _{i}\Vert y^{*}\left( s\right) -\psi \left( s\right) \Vert \nabla s<V(t_{0})<+\infty . \end{aligned}$$

Note that $y^{*}\left( \cdot \right)$ is bounded on $\mathbb {R}^{+}$. Therefore

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }\Vert y^{*}\left( t\right) -\psi \left( t\right) \Vert =0. \end{aligned}$$

The proof of this theorem is now completed.

Remark 5

Theorem 1, Theorem 2 and Theorem 3 are new even for the both cases of differential equations ($\mathbb {T}=\mathbb {R}$) and difference equations ($\mathbb {T}=\mathbb {Z}$).

Remark 6

The model studied in [16] is considered without leakage time-varying delays and the system investigated have not contained some information about the derivative of the past state. In addition, the coefficients $a_{i}$ ($i=1,\ldots ,n)$ (playing the role of $\alpha _{i}(\cdot )$ in our work) are constant. Furthermore, using the outcomes in this manuscript we can generalize the sufficient conditions for keeping the original system of the model, with leakage time-varying delays and contained some information about the derivative of the past state, to be stable. Besides, by the technique in the paper [16], we can study the Hopf bifurcation of the novel class of competitive neutral-type neural networks with mixed time-varying delays and leakage delays.

6 Example and Computer Simulations

In this section, we will present an example to illustrate the feasibility of our results that were derived in the previous sections.

In system (3), let $i,j=1,2$, and take coefficients as follows:

$$\begin{aligned}&\displaystyle \alpha _{1}(t)=\alpha _{2}(t)=0.73+0.02\cos (16\pi t), \,\ f_{1}(x)=f_{2}(x)=0.1\arctan x;&\\&\displaystyle \left( \begin{array}{cc} D_{11}(t) &{} D_{12}(t) \\ D_{21}(t) &{} D_{22}(t) \\ \end{array} \right) =\left( \begin{array}{cc} \tilde{D}_{11}(t) &{} \tilde{D}_{12}(t) \\ \tilde{D}_{21}(t) &{} \tilde{D}_{22}(t) \\ \end{array} \right) =\left( \begin{array}{cc} \bar{D}_{11}(t) &{} \bar{D}_{12}(t) \\ \bar{D}_{21}(t) &{} \bar{D}_{22}(t) \\ \end{array} \right) =\left( \begin{array}{cc} \frac{\sin (t)}{15} &{} \frac{\sin (t)}{15} \\ \frac{\cos (t)}{15} &{} \frac{\cos (t)}{15} \\ \end{array} \right) ;&\\&\displaystyle B_{1}(t)=0.15\cos (\sqrt{3}t);\,\ B_{2}(t)=0.13\cos (\sqrt{2}t);\,&\\&\displaystyle c_{1}(t)=0.55+0.02\sin (16\pi t);&\\&\displaystyle c_{2}(t)=0.54\!+\!0.02\sin (16\pi t);\,\ E_{1}(t)\!=\!0.12\sin (t);\,\ E_{2}(t)\!=\!0.12\cos (\sqrt{3}t);&\\&\displaystyle I_{1}(t)=0.02\sin (\sqrt{3}t);\,\ I_{2}(t)=0.04\cos (\sqrt{5}t);\,\ J_{1}(t)=0.04\cos (t);&\\&\displaystyle J_{2}(t)=0.1\sin (\sqrt{5}t);\,\ \eta _{1}(t)=0.07\cos (\sqrt{2}t);\,\ \eta _{2}(t)=0.02\cos (\sqrt{2} t);&\\&\displaystyle \varsigma _{1}(t)=0.02\cos (\sqrt{3}t);\,\ \varsigma _{2}(t)=0.02\cos (\sqrt{3} t);\,\ \tau _{11}(t)=0.02\sin (\sqrt{2}t);&\\&\displaystyle \tau _{12}(t)=0.03\sin (\sqrt{2}t);\,\ \tau _{21}(t)=0.02\cos (\sqrt{2}t); \,\ \tau _{22}(t)=0.03\sin (\sqrt{2}t);&\\&\displaystyle \sigma _{11}(t)=0.04\cos (\sqrt{2}t); \,\ \sigma _{12}(t)=0.02\sin (\sqrt{2}t);\,\ \sigma _{21}(t)=0.03\cos (\sqrt{3}t);&\\&\displaystyle \sigma _{12}(t)=0.02\cos (\sqrt{3}t);\, \xi _{11}(t)=0.03\cos (\sqrt{2}t); \,\ \xi _{12}(t)=0.05\sin (\sqrt{2}t);&\\&\displaystyle \xi _{21}(t)=0.02\sin (\sqrt{2}t); \,\ \xi _{22}(t)=0.04\cos (\sqrt{2}t).&\end{aligned}$$

By a simple calculation, we have

$$\begin{aligned} \alpha _{1}^{+}= & {} 0.75,\,\ \alpha _{1}^{-}=0.71,\,\ \alpha _{2}^{+}=0.75,\,\ \alpha _{2}^{-}=0.71,\\ c_{1}^{+}= & {} 0.57, \,\ c_{1}^{-}=0.53, \,\ c_{2}^{+}=0.56, \,\ c_{2}^{-}=0.52,\\ \left( \begin{array}{cc} D_{11}^{+} &{} D_{12}^{+} \\ D_{21}^{+} &{} D_{22}^{+} \\ \end{array} \right)= & {} \left( \begin{array}{cc} \tilde{D}_{11}^{+} &{} \tilde{D}_{12}^{+}\\ \tilde{D}_{21}^{+} &{} \tilde{D}_{22}^{+} \\ \end{array} \right) =\left( \begin{array}{cc} \bar{D}_{11}^{+} &{} \bar{D}_{12}^{+} \\ \bar{D}_{21}^{+} &{} \bar{D}_{22}^{+} \\ \end{array} \right) =\left( \begin{array}{cc} \frac{1}{20} &{} \frac{1}{20} \\ \frac{1}{20} &{} \frac{1}{20} \\ \end{array} \right) ;\\ I_{1}^{+}= & {} 0.02; \,\ I_{2}^{+}=0.04;\,\ J_{1}^{+}=0.01;\,\ J_{2}^{+}=-0.1;\\ B_{1}^{+}= & {} 0.15; \,\ B_{2}^{+}=0.13; \,\ E_{1}^{+}=0.12; \,\ E_{2}^{+}=0.12;\\ \eta _{1}^{+}= & {} 0.07; \,\ \eta _{2}^{+}=0.02; \,\ \varsigma _{1}^{+}=0.02; \varsigma _{2}^{+}=0.02;\\ (\sigma _{ij}^{+})_{1\le i,j\le 2}= & {} \left( \begin{array}{cc} 0.04 &{} 0.02 \\ 0.03 &{} 0.02 \\ \end{array} \right) ; (\xi _{ij}^{+})_{1\le i,j\le 2}=\left( \begin{array}{cc} 0.03 &{} 0.05 \\ 0.02 &{} 0.04 \\ \end{array} \right) ; \end{aligned}$$

We can take $L_{1}=L_{2}=0.1$, $r=0.5$ and we have

$$\begin{aligned}&M_{1}=\alpha _{1}^{+}\eta _{1}^{+}r+\sum \limits _{j=1}^{2}\left( D_{1j}^{+}+(D_{1j}^{\tau })^{+}+\overline{D}_{1j}^{+}\sigma _{1j}^{+}\right. \\&+\left. \widetilde{D}_{1j}^{+}\xi _{1j}^{+}\right) (L_{j}r+|f_{j}(0)|)+B_{1}^{+}r+I_{1}^{+},\\&= 0.75\times 0.07\times 0.5+\left( \frac{1}{20}+\frac{1}{20}+\frac{1}{20}\times 0.04+\frac{1}{20}\times 0.03\right) \left( 0.1\times 0.5+0.1\right) \\&+ \left( \frac{1}{20}+\frac{1}{20}+\frac{1}{20}\times 0.02+\frac{1}{20}\times 0.05\right) \left( 0.1\times 0.5+0.1\right) \\&+ \,0.15\times 0.5+0.02\\&= 0.0773. \end{aligned}$$

$$\begin{aligned}&\overline{M}_{1}=\alpha _{1}^{+}\eta _{1}^{+}+\sum \limits _{j=1}^{2}\left( D_{1j}^{+}+(D_{1j}^{\tau })^{+}+\overline{D}_{1j}^{+}\sigma _{ij}^{+}+\widetilde{D}_{1j}^{+}\xi _{1j}^{+}\right) L_{j} +B_{1}^{+},\\&= 0.75\times 0.07+\left( \frac{1}{20}+\frac{1}{20}+\frac{1}{20}\times 0.03+\frac{1}{20}\times 0.02\right) \left( 0.1\times 0.5+0.1\right) \\&+\left( \frac{1}{20}+\frac{1}{20}+\frac{1}{20}\times 0.02+\frac{1}{20}\times 0.04\right) \left( 0.1\times 0.5+0.1\right) +0.13\\&= 0.2132. \\&N_{1}= c_{1}^{+}\varsigma _{1}^{+}r+E_{1}^{+}(L_{1}r+|f_{1}(0)|)+J_{1}^{+}\\&= 0.57\times 0.02\times 0.5+0.12(0.1\times 0.5+0.1)+0.01\\&=0.0337, \\&\overline{N}_{1}=c_{1}^{+}\varsigma _{1}^{+}+E_{1}^{+}L_{1}\\&= 0.57\times 0.02+0.12\times 0.1\\&=0.0234.\\&M_{2}=\alpha _{2}^{+}\eta _{2}^{+}r+\sum \limits _{j=1}^{2}\left( D_{2j}^{+}+(D_{2j}^{\tau })^{+}+\overline{D}_{2j}^{+}\sigma _{2j}^{+} +\widetilde{D}_{2j}^{+}\xi _{2j}^{+}\right) (L_{j}r+|f_{j}(0)|)+B_{2}^{+}r+I_{2}^{+}\\&=0.75\times 0.02\times 0.5+\left( \frac{1}{20}+\frac{1}{20}+\frac{1}{20}\times 0.03+\frac{1}{20}\times 0.02\right) \left( 0.1\times 0.5+0.1\right) \\&+ \left( \frac{1}{20}+\frac{1}{20}+\frac{1}{20}\times 0.02+\frac{1}{20}\times 0.04\right) \left( 0.1\times 0.5+0.1\right) +0.13\times 0.5+0.04\\&= 0.143,\\ \end{aligned}$$

$$\begin{aligned}&\displaystyle \overline{M}_{2}=\alpha _{2}^{+}\eta _{2}^{+}+\sum \limits _{j=1}^{2}\left( D_{2j}^{+}+(D_{2j}^{\tau })^{+}+\overline{D}_{2j}^{+}\sigma _{2j}^{+}+\widetilde{D}_{2j}^{+}\xi _{2j}^{+}\right) L_{j} +B_{2}^{+}&\\&\displaystyle = 0.75\times 0.02+\left( \frac{1}{20}+\frac{1}{20}+\frac{1}{20}\times 0.03+\frac{1}{20}\times 0.02\right) \times 0.1&\\&\displaystyle + \left( \frac{1}{20}+\frac{1}{20}+\frac{1}{20}\times 0.02+\frac{1}{20}\times 0.04\right) \times 0.1+0.13&\\&\displaystyle = 0.165,&\end{aligned}$$

$$\begin{aligned} N_{2}= & {} c_{2}^{+}\varsigma _{2}^{+}r+E_{2}^{+}(L_{2}r+|f_{2}(0)|)+J_{2}^{+}\\= & {} 0.56\times 0.02\times 0.5+0.12(0.1\times 0.5+0.1)-0.1\\= & {} -0.0764,\\ \overline{N}_{2}= & {} c_{2}^{+}\varsigma _{2}^{+}+E_{2}^{+}L_{2}\\= & {} 0.56\times 0.02+0.12\times 0.1\\= & {} 0.0232. \end{aligned}$$

The conditions $(H_{1})$ and $(H_{2})$ are satisfied and it is easy to verify

$$\begin{aligned} \max \left\{ \frac{M_{1}}{\alpha _{1}^{-}},\frac{M_{2}}{\alpha _{2}^{-}}, \left( 1+\frac{\alpha _{1}^{+}}{\alpha _{1}^{-}}\right) M_{1}, \left( 1+\frac{\alpha _{2}^{+}}{\alpha _{2}^{-}}\right) M_{2}, \frac{N_{1}}{c_{1}^{-}},\right. \\ \left. \left( 1+\frac{c_{1}^{+}}{c_{1}^{-}}\right) N_{1}, \frac{N_{2}}{c_{2}^{-}},\left( 1+\frac{c_{2}^{+}}{c_{2}^{-}}\right) N_{2}\right\} \le 0.5, \end{aligned}$$

and

$$\begin{aligned} \max \left\{ \frac{\overline{M}_{1}}{\alpha _{1}^{-}},\frac{\overline{M}_{2}}{\alpha _{2}^{-}},\left( 1+\frac{\alpha _{1}^{+}}{\alpha _{1}^{-}}\right) \overline{M}_{1}, \left( 1+\frac{\alpha _{2}^{+}}{\alpha _{2}^{-}}\right) \overline{M}_{2},\right. \\ \left. \frac{\overline{N}_{1}}{c_{1}^{-}},\frac{\overline{N}_{2}}{c_{2}^{-}}, \left( 1+\frac{c_{1}^{+}}{c_{1}^{-}}\right) \overline{N}_{1},\left( 1+\frac{c_{2}^{+}}{c_{2}^{-}}\right) \overline{N}_{2}\right\} \le 1, \end{aligned}$$

so, condition $(H_{3})$ holds. Therefore, using Theorem 1 and Theorem 2, we conclude that system (2) has only one pseudo-almost periodic solution. Besides, this unique solution is globally exponentially stable.

Fig. 1

The trajectories of $x_{1}$, $x_{2}$, $S_{1}$ and $S_{2}$ for $t\in [0,150]$ (continuous case $\mathbb {T}=\mathbb {R}$)

Fig. 2

The trajectories of $x_{1}$, $x_{2}$, $S_{1}$ and $S_{2}$ in the discrete case $\mathbb {T}=\mathbb {Z}$

Fig. 3

In the left figure, the orbits of $x_{1}{-}x_{2}$. In the right figure, the orbits of $S_{1}{-}S_{2}$

Fig. 4

In the left figure, the orbits of $x_{1}{-}S_{1}$. In the right figure, the orbits of $x_{2}{-}S_{2}$

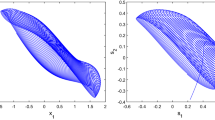
Figures 1, 2, 3 and 4 confirm that the proposed conditions in our theoretical results are effective for this example. Furthermore, it can be easily seen that the solutions of the system in this example for the both continuous time and discrete time are exponentially stable (Figs. 1, 2). Besides, it is clear that from a certain time we have the same distance between the two pseudo-almost periodic trajectories of the orbit (Figs. 3, 4).

Remark 7

In many cases, the delays in leakage terms have a negative effect on ensuring the stability of the system. In this case, people usually take a small value to the delays in leakage terms, such as $\max \limits _{i=1,2}\eta _{i}(t)=\frac{(1+|\sin (t)|)}{2000}\le \frac{1}{1000}$ and $\max \limits _{i=1,2}\eta _{i}(t)=0.1$, respectively in the examples of references ([11, 13]). When $\eta _{1}^{+}=0.07$, $\eta _{2}^{+}=0.02$, $\varsigma _{1}^{+}=0.02$ and $\varsigma _{2}^{+}=0.02$, their condition swill not be satisfied, but ours can. Therefore, our conditions are less conservative than that in ([11, 13]).

7 Conclusion and Open Problem

As it is widely known, the leakage delay has great impact on the dynamical behavior of neutral-type neural networks. Hence, it is necessary and rewarding to investigate the leakage delay effects on the dynamic behaviors of pseudo-almost periodic solution of competitive neutral-type neural networks. It is the first time that a class of neutral-type competitive with mixed delays and leakage delays on time-space scales is presented. In addition, the existence and exponential stability of pseudo almost periodic solutions for the system of equation modeling this system are also considered. The problem is investigated for the differential equations and difference equations. In the best of our knowledge, the model is general in the meaning that is considered with mixed time-varying delays and leakage time-varying delays. Finally, we formulate some open problems. We would like to extend our results to more general competitive neural networks with mixed time-varying delays and leakage delays, such as high-order competitive neural networks models.

$$\begin{aligned} \left\{ \begin{array}{l} STM{:} x^{\nabla }_{i}\left( t\right) = -\alpha _{i}(t)x_{i}\left( t-\eta _{i}(t)\right) +\sum \limits _{j=1}^{n}D_{ij}\left( t\right) f_{j}\left( x_{j}\left( t\right) \right) \\ \quad +\sum \limits _{j=1}^{n}D_{ij}^{\tau }\left( t\right) f_{j}\left( x_{j}\left( t -\tau _{ij}(t)\right) \right) +\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}T_{ijk}f_{k}(x_{k}(t-\chi _{k}(t)))f_{j}(x_{j}(t-\chi _{j}(t)))\\ \quad +\sum \limits _{j=1}^{n}\overline{D}_{ij}\left( t\right) \displaystyle {\int }_{t-\sigma _{ij}(t)} ^{t}f_{j}\left( x_{j}\left( s\right) \right) \nabla s+\sum \limits _{j=1}^{n}\widetilde{D}_{ij}\left( t\right) \int _{t-\xi _{ij}(t)} ^{t}f_{j}\left( x_{j}^{\nabla }\left( s\right) \right) \nabla s\\ B_{i}\sum \limits _{j=1}^{n}m_{ij}(t)y_{j}+I_{i}\left( t\right) ,\\ LTM{:} m_{ij}^{\nabla }(t)=-c_{i}(t)m_{ij}(t-\varsigma _{i}(t))+y_{j}E_{i}(t)f_{i}(x_{i}(t))+J_{i}(t),\,\ t\in \mathbb {T}, \end{array} \right. \end{aligned}$$

(17)

where, for all $i,j,k=1,\ldots n,$ $T_{ijk}$ are the second-order connection weights of delayed feedback.

And stochastic high-order competitive neural networks model on time-space scales with mixed time-varying delays and leakage delays:

$$\begin{aligned} \left\{ \begin{array}{l} STM{:}\nabla x_{i}\left( t\right) =\left[ -\alpha _{i}(t)x_{i}\left( t-\eta _{i}(t)\right) +\sum \limits _{j=1}^{n}D_{ij}\left( t\right) f_{j}\left( x_{j}\left( t\right) \right) \right. \\ \quad +\sum \limits _{j=1}^{n}D_{ij}^{\tau }\left( t\right) f_{j}\left( x_{j}\left( t -\tau _{ij}(t)\right) \right) +\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}T_{ijk}f_{k}(x_{k}(t-\chi _{k}(t)))f_{j}(x_{j}(t-\chi _{j}(t)))\\ \quad +\sum \limits _{j=1}^{n}\overline{D}_{ij}\left( t\right) \displaystyle {\int }_{t-\sigma _{ij}(t)} ^{t}f_{j}\left( x_{j}\left( s\right) \right) \nabla s+\sum \limits _{j=1}^{n}\widetilde{D}_{ij}\left( t\right) \int _{t-\xi _{ij}(t)} ^{t}f_{j}\left( x_{j}^{\nabla }\left( s\right) \right) \nabla s\\ \left. \quad +\,B_{i}\sum \limits _{j=1}^{n}m_{ij}(t)y_{j}+I_{i}\left( t\right) \right] \nabla t+\sum \limits _{j=1}^{n}\kappa _{ij}(x_{j}(t))\nabla \omega _{j}(t),\\ LTM{:}\nabla m_{ij}(t)=\left[ -c_{i}(t)m_{ij}(t-\varsigma _{i}(t))+y_{j}E_{i}(t)f_{i}(x_{i}(t))+J_{i}(t)\right] \nabla t\\ \quad +\,\sum \limits _{j=1}^{n}\delta _{ij}(m_{ij}(t))\nabla \omega _{j}(t),\,\ t\in \mathbb {T}, \end{array} \right. \end{aligned}$$

(18)

where $\omega (t)=(\omega _{1}(t),\ldots ,\omega _{n}(t))^{\mathbb {T}}$, $(t\in \mathbb {T})$ is the n-dimensional Brownian motion defined on complete probability space $({\varOmega },\mathcal {F},\mathbb {P})$; $\delta _{ij}$ are Borel measurable functions; $A=(\delta _{ij})_{n\times n}$ is the diffusion coefficient matrix.

The corresponding results will appear in the near future.