Ensemble Multiple-Kernel Based Manifold Regularization

Abstract

As a class of semi-supervised learning methods, manifold regularization learning has recently attracted a lot of attention, due to their great success in exploiting the underlying geometric structures among data. This paper presents a novel semi-supervised approach by combining manifold regularization learning with the idea of multiple kernels, named after ensemble multiple-kernel manifold regularization learning. In our approach, multiple kernels we introduced are not only used to add the flexibility and diversity of the candidate space for the learning problem, but also act as a similarity measure to search for an optimal graph Laplacian in some sense. In other words, the proposed method allows us to learn an ’ideal’ kernel and an optimal graph Laplacian simultaneously, which is of significant difference from existing methods. The associated optimization problem is solved efficiently by an alternating iteration procedure. We implement experiments over four real world data sets to demonstrate the benefits of the proposed method.

1 Introduction

Learning knowledge from labeled and unlabeled samples plays a key role in semi-supervised learning (SSL). Manifold regularization (MR) learning [1] is one of the representative and successful SSL methods which is achieved by exploiting the intrinsic geometric structure of the probability distribution of the data, and it recently has attracted a lot of attention [3, 8, 12–14, 17]. Until recently, the researchers have extended the MR learning to many areas of machine learning. For example, [17] and [14] relaxed the label function so that it is better to deal with novel samples and classification, and [3] aimed at solving small scale problems appearing in the consequent inverse operation, and [8] transformed the problem of manifold regularization into learning an optimal graph Laplacian.

Under the framework of MR learning, the decision function or a learner, is a linear combination of a single kernel function at the given instances and the performance of MR algorithms strongly depends on the choice of the kernel and the given data. Thus the misspecification of the kernel function may result in the distortion of the manifold structure, meanwhile it often leads to the underfitting for modeling data. Fortunately, multiple kernel learning (MKL) [2, 9–11, 15, 20, 21] has been proven useful and effective in terms of theoretical analysis and practical applications, compared to several single kernel methods. The main idea of MKL is to learn kernels with linear combinations of multiple specified kernels, so that the greater flexibility can be gained for any kernel-based method.

Among kernel-based methods [4, 5, 16, 19], kernel function is either used as the so called kernel trick, i.e. mapping input sample into a high dimensional kernel space for learning nonlinear problem, or used as similar function for measuring the difference between two input samples. Compared to the existing work, one of significant differences is that we here make full use of the two advantages of kernel function. Based on this idea, the proposed method can produce a decision function with greater flexibility, and also find out an ideal graph Laplacian. Furthermore, the intrinsic manifold structure among data can be exploited efficiently. The MR methods utilize a graph Laplacian regularizer to constrain the decision function to be smooth with respect to the data manifold, a low-dimensional subspace on which the high-dimensional data actually resides; in application, the manifold is determined by a graph Laplacian from the given data. The graph Laplacian construction step is critical and important in MR methods but is still an open issue that has not been comprehensively studied [6, 18]. In multiple manifolds or multiple view learning[22–24], the approximation of the optimal graph Laplacian draws on some pre-given manifold candidates according to different manifolds or views. In this paper, we utilize the pregiven multiple basis kernel functions to generate initial graph Laplacian candidates, and then a convex set over the constrained coefficients is constructed to search for the optimal graph Laplacian. At this point, it is a learning problem of the optimal graph Laplacian. Since the optimal coefficients in the learning problem of graph Laplacian are the same as the combination coefficients of kernels used in the decision function, we can solve the graph Laplacian optimization problem together with the learning problem of multiple kernel functions function.

In this paper, we propose a novel semi-supervised approach by combining manifold regularization with the idea of multiple kernels. In our case, a flexible learner within multi-kernel class and the optimal graph Laplacian are selected simultaneously. The advantages of our proposed method mainly consists of the following points: (1) learning both the composite manifold and the multiple kernel functions jointly; (2) the decision function is built by using multiple kernel functions for extracting more data information from data, in other words, the reproducing kernel Hilbert space associated with multiple kernels enables us to enrich and expand the search range of the optimal solution of learning problem; (3) the intrinsic manifold is further approximated by some initial manifold candidates that are induced by the multiple kernel functions. In term of theory, we present the formulations of the proposed algorithm and search for the optimal decision function in the sum space of reproducing kernel Hilbert spaces (RKHS). In term of numerical computation, the associated optimization problem is solved efficiently by an alternating iteration procedure like [15].

The paper is organized as follows. In Sect. 2, we introduce the framework of manifold regularization learning and some related concepts. Section 3 introduces our proposed approach called multiple-kernel manifold regularization (MKMR) and the details of its optimization problem. The experimental results on both synthetic and real-world data sets are presented in Sect. 4. Finally, some conclusive remarks are given in Sect. 5.

2 Manifold Regularization

In the semi-supervised learning, consider an available set $X=\{x_{1},\dots ,x_{l+u}\}\subseteq \varOmega , x_{i}\in R^{n}$, where $\{x_{1},\dots ,x_{l}\}$ are the labeled samples with the corresponding labels $\{y_{1},\dots ,y_{l}\}$ and $\{x_{l+1},\dots ,x_{l+u}\}$ are the unlabeled samples. We suppose that $X_L=\{x_{1},\dots ,x_{l}\}$ is the set of labeled samples drawn according to the joint distribution P defined on $\varOmega \times R$, and $X_U=\{x_{1+u},\dots ,x_{l+u}\}$ is the set of unlabeled samples drawn according to the marginal distribution $P_X$ of P.

Manifold regularization aims at exploiting the geometry of the marginal distribution $P_X$. It assumes that if the two data points $x, x' \in X$ are close in the intrinsic geometry of $P_X$, then the conditional distributions $P(y\vert x)$ and $P(y\vert x')$ are similar accordingly. Then an additional regularization term is introduced to characterize manifold structure for the given learning problem. Consider an reproducing kernel Hilbert space (RKHS) H associated with a symmetric nonnegatively definite kernel $\{k(x,x'): \varOmega \times \varOmega \rightarrow R\}$, and the manifold regularization learning problem can be expressed as the following form:

$$\begin{aligned} \mathop {min}\limits _{f\in H} \Bigg \{ \frac{1}{l}\sum _{i=1}^l V(y_{i},f(x_{i})) +\kappa \Vert f \Vert ^{2}_{H}+\lambda \Vert f \Vert ^{2}_{M}\Bigg \}, \end{aligned}$$

(1)

where $f:\varOmega \rightarrow R$ is the decision function. The first term of the objective function(1) is defined on the loss function V which measures the discrepancy between the predicted value $f(x_i)$ and the actual label $y_i$. $\Vert f \Vert ^{2}_{M}$ is the manifold regularizer and measures the smoothness of the function f on data manifold and $\Vert f \Vert ^{2}_{H}$ is the norm of the function f in the RKHS H. $\kappa$ and $\lambda$ are the regularization parameters, balancing different terms. The aim of the objective function (1) is to find the optimal function f in the RKHS space H.

In most applications, $P_X$ is not known. Therefore, the manifold regularizer is usually approximated by the graph Laplacian matrix associated with X and the function prediction $\mathbf {f}=[ f(x_{1}) \cdots f(x_{l+u})]^{T}$. Hence the optimization problem can be reformulated as:

$$\begin{aligned} \mathop {min}\limits _{f\in H} \Bigg \{ \frac{1}{l}\sum _{i=1}^l V(y_{i},f(x_{i})) +\kappa {\Vert } f {\Vert }^{2}_{H} +\lambda \mathbf {f}^{T}L\mathbf {f}\Bigg \}, \end{aligned}$$

(2)

where L is the graph Laplacian matrix given by $L=D-W$. Here D is the diagonal matrix with $d_{ii}=\sum _{j=1}^{l+u} w_{ij}$ and W is the similar matrix, where the element $w_{ij}$ denotes the similarity between points $x_{i}$ and $x_{j}$. For example, a commonly-used measurement of $w_{ij}$ is the Gaussian kernel function defined on the Euclidean distance [5, 12], i.e., if the data $x_{j}\in N(x_i)$ or $x_{i}\in N(x_j)$, $w_{ij}=exp({-\frac{\Vert x_i-x_j\Vert ^{2}}{t^{2}}})$ and 0 otherwise, where $N(x_i)$ is the neighborhood of $x_i$ and t is the tuning parameter.

Following the Representer Theorem [9], the minimizer of optimization problem (2) admits an expansion

$$\begin{aligned} f(x) = \sum _{i=1}^{l+u}\alpha _{i} k(x,x_{i}) \end{aligned}$$

(3)

in term of the unlabeled and labeled samples [1]. Therefore, the decision of the kernel function k plays a key role for the performance of MR algorithms. When lose function V in Eq.(2) is adopt to be the squared loss function $V(y_{i},f(x_{i}))=(y_{i}-f(x_{i}))^{2}$, the problem of (2) can be reduced to a typical quadratic programme, and its analytic solution can be easily obtained (refer to [1] in details). And the MR algorithm formulates the Laplacian Regualrized Least Squares (LapRLS).

3 Proposed Ensemble Multiple-Kernel Manifold Regularization (MKMR)

In this section, we propose a novel semi-supervised method that combines the two characteristics of multiple kernels and the specific merit of manifold regularization.

3.1 Framework

We denote by $\{k_b(x,x{^\prime }):b=1,\dots ,m\}$ the set of m base kernels to be combined. Each base kernel $k_{b}$ can generate an RKHS $H_{b}$. Under the MKL framework, $f (x)= \sum _b f_b(x)$ where each function $f_b$ belongs to the different RKHS $H_b$ . Therefore with a non-negative coefficient $\beta _{b}$, we can define an equivalent space of $H_b$ by $H^{\prime }_{b}=\{f_b: \frac{ \Vert f_b \Vert ^{2}_{H_{b}} }{ \beta _{b} } < \infty , f_b\in H_{b}\}$. When $\sum _{b=1}^{m}\beta _{b}=1$ is constrainted, a new RKHS $H^{\prime }$ is defined as the direct sum of the spaces $H^{\prime }_{b}$, i.e., $H^{\prime }=H^{\prime }_{1}\oplus \dots \oplus H^{\prime }_{m}$, and its reproducing kernel is the combined kernel function $k^{\prime }(x,x{^\prime })= \sum _{b=1}^{m}\beta _{b} k_{b}(x,x{^\prime })$. $H^{\prime }$ is a multiple-kernel space and can be used to further explore the data and solve the problems involved in multiple data sources. The learning problem of MKMR method is working in the new RKHS $H^{\prime }$, formulated as the following minimization

$$\begin{aligned} \mathop {min}\limits _{f\in H^{\prime }} \Bigg \{ \frac{1}{l}\sum _{i=1}^l V(y_{i},f(x_{i})) +\kappa \Vert f \Vert ^{2}_{H^{'}}+\lambda \Vert f \Vert ^{2}_{M}\Bigg \}, \end{aligned}$$

(4)

where $\Vert f \Vert ^{2}_{H^{\prime }}$ penalizes the classifier complexities measured in the RKHS $H^{\prime }$. Obviously, the solution range of f is expanded from the single kernel space to the multiple-kernel space.

As mentioned before, the kernel function can be used to measure the similar relationship between pair data. Therefore, in order to find an optimal graph Laplacia for manifold regularizer, we employ a series of initial graph Laplacian candidates $\{L_{b}\}^{m}_{1}$ corresponding to the multiple kernels $\{k_{b}\}^{m}_{1}$ to construct a convex set $\{ L\arrowvert L=\beta _{1}L_{1}+\cdots +\beta _{m}L_{m}, \sum _{b=1}^{m}\beta _{b}=1\}$. Such a combination for graph Laplacian naturally allows us to learn a better graph Laplacian. Note that the initial graph candidates may be not limited to those base kernels. By using the above expression, the manifold regularizer becomes

$$\begin{aligned} \Vert f \Vert ^{2}_{M}=\mathbf {f}^{T}\Bigg (\sum _{b=1}^m \beta _{b}L_{b}\Bigg )\mathbf {f}=\sum _{b=1}^m \beta _{b}\Vert f \Vert ^{2}_{M_{b}}. \end{aligned}$$

(5)

Substituting (5) into the framework (4), we have

$$\begin{aligned} \mathop {min}\limits _{\beta _b\in \Delta }\mathop {min}\limits _{f_{b}\in H^{'}_{b}} \Bigg \{ \frac{1}{l}\sum _{i=1}^l V(y_{i},f(x_{i}))+\kappa \sum _{b=1}^m \beta _{b}\Vert f_{b}\Vert ^{2}_{H^{\prime }_{b}}+\lambda \sum _{b=1}^m \beta _{b}\Vert f \Vert ^{2}_{M_{b}}\Bigg \}, \end{aligned}$$

(6)

where $\Delta = \{\beta _b\in R_{+}^{m}: \sum _{b=1}^{m}\beta _{b}=1\}$ is the domain of $\beta _b$ . It can be seen that we actually establish two learning problems: the learning problem of the classifier f and the optimization problem of graph Laplacian. We can also use different parameters in our learning problem, denoted by $\beta _b$ and $\beta _b^{\prime }$. However, by doing this, we need to estimate additional m coefficients, resulting in adding computation cost. In view of computational efficiency, we only use the single tuning parameter $\lambda$ to measure the differences between the two sets of coefficients in Eq. (6), instead of the set of coefficients $\beta _b^{\prime }$.

3.2 Parameters Optimization

In our current work, we adopt the group-Lasso minimization MKL method [15] as a solution to optimize the decision function of MKMR. Following the Representer Theorem [9], the solution of the optimization problem (6) admits

$$\begin{aligned} f(x) =\sum _{i=1}^{l+u}\alpha _{i} \sum _{b=1}^{m}\beta _{b}k_{b}(x,x_{i}). \end{aligned}$$

(7)

Therefore, the MKMR problem only refers to the optimization of coefficients $\{\alpha _{i}\}^{l+u}_{1}$ and $\{\beta _{b}\}^{m}_{1}$. To solve it, we employ the alternating way with two steps: finding the optimal $\{\beta _{b}^{*} \}^{l+u}_{1}$ with fixed $\{\alpha _{i}\}^{l+u}_{1}$, and then finding the best classifier weights $\{\alpha _{i}\}^{l+u}_{1}$ with the fixed $\{\beta _{b}^{*} \}^{l+u}_{1}$. In the first step, inspired by the method [9] we can define a new classification functions set

$$\begin{aligned} \hat{f_{b}}=\beta _{b}f_{b}, \end{aligned}$$

(8)

where $b=1\cdots m$. With it, the formulation in (6) is rewritten as

$$\begin{aligned} \mathop {min}\limits _{\beta \in \Delta }\mathop {min}\limits _{\hat{f_{b}}\in H^{'}_{b}} \Bigg \{\frac{1}{l}\sum _{i=1}^l V(y_{i},\sum _{b=1}^m\hat{f_{b}}(x_{i})) +\kappa \sum _{b=1}^m \frac{1}{\beta _{b}}\Vert \hat{f_{b}}\Vert ^{2}_{H^{'}_{b}}+ \lambda \Bigg (\sum _{b=1}^m\hat{f_{b}}\Bigg )^{T}\Bigg (\sum _{b=1}^m \beta _{b}L_{b}\Bigg )\Bigg (\sum _{b=1}^m\hat{f_{b}}\Bigg )\Bigg \}. \end{aligned}$$

(9)

By taking the minimization over $\beta$, we obtain:

$$\begin{aligned} \beta _{b}^{*}=\frac{\Vert \hat{f_{b}}\Vert ^{2}_{H^{\prime }_{b}}}{\sum _{b=1}^{m}\Vert \hat{f_{b}}\Vert ^{2}_{H^{\prime }_{b}} }. \end{aligned}$$

(10)

When taking derivative of the Lagrangian with respect to $\beta _{b}$, we set

$$\begin{aligned} \sum \beta _{b}L_{b}=\sum _{j\ne b} \beta _{j}L_{j}+L_{b}\Bigg (1-\sum _{j\ne b}\beta _{j}\Bigg ),\quad j=1\cdots m. \end{aligned}$$

Observing from the Eq. (10), we update the parameter $\beta _{b}$ by the norm of the decision function. Second, with the fixed $\mathbf {\beta ^*}$, the object $J(\mathbf {\alpha })$ is given by

(11)

where $\mathbf {y}=[y_{1},\dots ,y_{l},0,\dots ,0]_{1\times (l+u)}$ is the label vector; $K^{\prime }$ is the kernel matrix of the combined kernel function $k^{\prime }$. When the squared loss is used as the loss function V, i.e., $V=(\mathbf {y}-GK^{\prime }\mathbf {\alpha })^{T}(\mathbf { y}-GK^{\prime }\mathbf {\alpha })$, we have

(12)

where G is the diagonal matrix in which the first l diagonal elements are 1 and the rest are 0. The problem above becomes a typical symmetric quadratic form, that is

(13)

where $B=K^{{^\prime }T}G^{T}\mathbf {y}$, $A=K^{{^\prime }T}G^{T}GK^{\prime }+\kappa K^{\prime }+\lambda K^{{^\prime }T}\big (\sum _{b=1}^m \beta _{b}L_{b}\big )K^{\prime }$. Note that the matrix A is a symmetric and positive definite matrix, and then the final analytic solution is

$$\begin{aligned} \mathbf {\alpha }^{*}= \Bigg (K^{{^\prime }T}\Bigg (G^{T}G+\kappa I+\lambda \Bigg (\sum _{b=1}^m \beta _{b}L_{b}\Bigg )\Bigg )K^{\prime } \Bigg )^{-1}K^{\prime }G^{T}\mathbf {y}, \end{aligned}$$

(14)

where I is the unit matrix. Repeat the above two steps until meeting the stopping criteria of the alternating optimization procedure.

4 Experiments

This experimental study aims at verifying the effectiveness and advantages of MKMR. The proposed approach introduces the multiple kernels to the MR approach and jointly learns the optimal graph Laplacian. In order to validate the proposed MKMR, the classical MR [1] and the general multi-kernel based MR approach (be called MMR in short) [7] are considered for comparisons with the proposed MKMR. This study includes the two parts: first, we focus on MR, MMR, and MKMR for classification problem with four real-world datasets; second, we compare MKMR with MMR and an optimized MMR method (be called OMMR in short) to show the effectiveness of learning the optimal graph Laplacian. OMMR method uses a pre-optimized graph Laplacian obtained by the cross-validation method.

4.1 Data Sets

In our experiments, we use one object database(ETH80), one handwritten digits database(USPS), one face database(Yale-B), and the Caltech 101 dataset. These datasets are chosen since they correspond to several types.

The ETH-80¹ dataset has been used in many object recognition studies. It contains eight categories (apples, pears, tomatoes, cows, dogs, horses, cups, and cars) of images. Each class has 10 objects, and each object is represented by 41 views. Thus there are 3,280 images in total in this dataset. The size of image is 16 $\times$ 16.

The USPS² handwritten digits database contains 10 handwritten digits from “0” to “9”, and each digit consists of 1100 grayscale images. The images we loaded have been resized to 16 $\times$ 16 pixels. The size is already small.

The Caltech 101³ dataset contains 9146 images of 101 categories (about 40 to 800 images per category). We resize all the images and the final size is 150 $\times$ 150. This dataset object displays a wide variety of complex geometry and reflectance characteristic.

The Yale-B⁴ face dataset contains 10 individuals, and each is seen under 576 viewing conditions (9 poses and 64 illumination conditions). All images are cropped based on the location of eyes, and resize to 32 $\times$ 32 pixels. We select a subset, including 64 images of 8 individuals (under the front pose) to evaluate the performance of algorithms.

4.2 Parameters Settings

There are three parameters (the number of nearest neighbors, and the two regularization parameters $\kappa$ and $\lambda$) to be tuned for all comparison methods. For all experiments, the number of nearest neighbors is set to 6. and the two regularization parameters are selected from set $\{10^{-4},10^{-2}, 10^{-1},1,10, 100\}$ through a twofold cross-validation of labeled training samples on the training set. We use the Gaussian RBF kernel $k(x,v)=exp({-\frac{\Vert x-v\Vert ^{2}}{t^{2}}})$ with 10 different widths, i.e., $t=\{2^{-4}, 2^{-3}, 2^{-2}, 2^{-1}, 2^{0}, 2^{2} , 2^{3}, 2^{4}, 2^{5}, 2^{7}\}*\theta$, and the Polynomial kernel of degree 1 to 3 to construct base kernels, where $\theta$ is set to the average of squared distances in the training set. During the training procedure of MR, we calculated the kernel matrix with linear one-order polynomial, two-order polynomial and a Gaussian kernel, respectively. For MKMR, MMR, and OMMR, the maximum number of iterations as the stopping criteria is set to 15 for all datasets.

Fig. 1

Binary classification results ($\%$) of five methods on the ETH-80 data set

Fig. 2

Binary classification results ($\%$) of five methods on the USPS data set

Fig. 3

Binary classification results ($\%$) of five methods on the Caltech 101 data set

Fig. 4

Binary classification results ($\%$) of five methods on the Yale-B data set

The entire classification proceeds on the four datasets include a binary classification problem and a multiple-class problem. The multiple-class problem can be converted into a set of binary classification problems via the one-vs-rest strategy. For the binary classification (two-class) experiments, 60 $\%$ of the data per class is used as the training set and the remaining 40 $\%$ as the test set. The number of labeled samples l for ETH-80 and USPS datasets is set to 1, 3, 5, 10, 15, 30, 50, and 100, respectively, and for Yale-B and Caltech 101 datasets it is set to 1, 3, 5, 8, 10, and 15, respectively. It is a critical variable in semisupervised learning algorithms. Each two-class experiment is repeated ten times, and the average classification error rates are reported. For the multiclass experiments, we vary the number of training data. For ETH80 and USPS datasets, we randomly select 20, 30, 40, 50, 80, 100, and 120 data from each class to form the training set, and use the remaining data as the test set. For Caltech 101 and Yale-B datasets, the number of the data in most cases is less than 60, then we randomly choose 20, 30, and, 40 data per class to form the training set, the remaining data serve as the test set. At the same time, l is set to 5. The multiclass process is run on the same set of 10 randomly drawn replication of the training and test set. Then the averaged error rates and the corresponding standard deviation are reported. The running time of MKMR, MMR, and OMMR in multiclass experiments are presented for discussing the effectiveness of MKMR. All the kernel matrices are pre-computed and loaded into the memory. This enables us to avoid re-computing and loading kernel matrices at each iteration of optimization. Our experiments are implemented in a 64 b Windows PC with 2.3 GHz CPU and 4 GB RAM. All the algorithms are implemented with MATLAB.

4.3 Classification Results

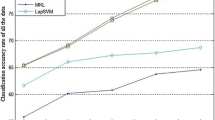
The binary classification results of five methods (MR-L, MR-P, MR-G, MMR, and MKMR) for ETH-80, USPS, Caltech 101, and Yale-B datasets are shown in Figs. 1, 2, 3, and 4, respectively. MR-L, MR-P, and MR-G represent the MR method with a linear kernel, a polynomial kernel, and a Gaussian kernel, respectively. For MR and MMR, the graph Laplacian matrix is estimated by an empirical value. In this experiment, we use the average of squared distances of training data $\theta$ to compute the graph Laplacian for MMR and MR.

From the Fig. 1, we see that our MKMR method has got the smallest classification error rates on both the test and unlabeled training samples. Moreover, MKMR performs much better than MR methods (MR-L, MR-P, and MR-G). For MR, in most case, polynomial kernel gives better performance compared to linear kernel because of its nonlinearity. We also observe that the performance of MKMR is better than MMR, that indicates the effectiveness of MMR for applying the two benefits of kernel function. Fig. 2 shows that the proposed MKMR method provides more stable and effective classification results. From this figure, we see that MKMR performs much better than MR-L, MR-P, and MR-G, particularly for a small amount of labeled samples. The proposed MKMR works better than MMR consistently along with different number of labeled data. In Fig. 3, our proposed MKMR has got the best classification results on both the test and unlabeled training samples. Moreover, the improvement obtained by the proposed MKMR method on unlabeled data is significant compared with the MR methods (MR-L, MR-P, and MR-G) and the MMR approach. For Caltech 101 dataset, MMR performs a little worse than MR-G on the classification of test data when $l=1$. The reason may be that when the number of training examples is small, it may be insufficient to determine the appropriate kernel combination. For face dataset Yale-B, the binary classification results of MKMR are better than the MR methods, particularly for the test data (see Fig. 4). MKMR also performs better than MMR. Moreover, the MKMR becomes more effective as the number of labeled examples increase.

The overall multiclass classification results obtained by the proposed MKMR and the comparison methods are listed in Tables 1, 2, 3 and 4.

Table 1 Multiclass experimental results ($\%$) on the ETH-80 data set using five methods

Table 2 Multiclass experimental results ($\%$) on the USPS data set using five methods

Table 3 Multiclass experimental results ($\%$) on the Caltech 101 data set using five methods

Table 4 Multiclass experimental results ($\%$) on the Yale-B data set using five methods

Table 1 summarizes the multiclass classification results of five methods (MR-L, MR-P, MR-G, MMR, and MKMR) on the ETH-80 dataset. First, we observe that the MKMR algorithm outperforms the MR algorithms on both the training and test data. In particular, the proposed MKMR can obtain about 5–15 $\%$ improvements to the MR algorithms in object recognition of the ETH-80 dataset. We also observe that MKMR performs better than MMR. Moreover, MKMR becomes more effective as the number of training data increases.

The multiple-class experiments results of five comparison methods for the USPS dataset are reported in Table 2. A good improvement can be observed. First, we observe that the MKMR method outperforms the MR methods on both the training and test samples. Particularly, MKMR obtains about 5–10 $\%$ improvements to MR in the handwritten digit classification of the USPS dataset. Compared to the MMR approach, the MKMR algorithm has about 1–4 $\%$ improvements.

Table 3 shows the classification error results of five methods on the Caltech 101 dataset. Again, we see that the MKMR algorithm outperforms the MR algorithms and obtains about 7–30 % improvements to them. Moreover, our proposed algorithm has about 1–5 % improvements to the MMR approach. The competitive results of our method indicate the good generalization to the multiple object dataset.

For the face dataset Yale-B, the multiple-class classification error rates of five methods are listed in Table 4. As can been see, the MKMR method outperforms the MR methods on both the training and test data and obtains about 1–18 % improvements to them. Moreover, the proposed MKMR performs better than MMR.

4.4 Running Time

In the second experiments, we evaluate the training time and the error rates of MMR, OMMR, and MKMR on four datasets. We empirically use $\theta$ to compute the graph Laplacian of MMR. By the cross-validation method, the graph Laplacian of OMMR is selected from the Laplacian candidates set used in MKMR. For ETH-80 and USPS sets, the number of training data per class is set to 120, and for Caltech 101 and Yale-B sets it is set to 40. We only report the multiple-class results and training time of MMR, OMMR, and MMR on the training data. Table 5 summarizes the classification error rates and time of different methods. We observe that compared to the proposed MKMR, OMMR achieves similar classification performance but requires a considerable time cost. This is not surprising because OMMR applies the cross-validation method to decide the optimal graph Laplacian matrix. At the same time, we observe that although the training time of MMR is similar to MKMR, the performance MMR becomes worse.

Table 5 Comparison of classification error rate ($\%$) and training time (s) among MMR, oMMR, and MKMR on the training set

5 Conclusion

Manifold regularization learning is a successful SSL approach in machine learning. From the viewpoint of kernel choice, we introduce multiple kernels to improve the original MR learning. In the proposed MKMR, the reproducing kernel Hilbert space associated with multiple kernels contains multiscale structures, such as functional complexity and the measurement of the graph Laplacian. Therefore, the MKMR learning has comparable performance compared to the classical MR learning, in term of exploiting the intrinsic geometric structure of the data. We also implement several real-data experiments to show this improvement.