Introduction

The self-potential or spontaneous polarization technique is one of the most passive geophysical methods, measuring the natural potential difference (∆V) in the subsurface that results from electrochemical, thermoelectric, and electrokinetic fields within the earth’s interior (Biswas 2017; Essa 2020). There are many geophysical problems that can be solved by using the self-potential method, such as groundwater exploration, mining, geothermal investigation, archeology, paleo-shear zone detection, and cavity detection (Corwin and Hoover 1979; Wynn and Sherwood 1984; Sundararajan et al. 1998; Vichabian and Morgan 2002; Drahor 2004; Minsley et al. 2008; Fernandez-Martinez et al. 2010; Mehanee 2014, 2015; Essa and Elhussein 2017; Essa 2019, 2020). Since non-unique and ill-posed problems are encountered in the interpretation of self-potential anomalies caused by different mineralized sources, different inversion modeling techniques have been developed to handle these problems (Zhdanov 2002; Tarantola 2005; Biswas 2013; Biswas and Sharma 2014b; Mehanee and Essa 2015; Wang 2016; Essa 2020). Inversion modeling techniques have been based upon the approximation of the different geo-electric sources with simple geometric structures (horizontal cylinder, vertical cylinder, sphere, and 2-D inclined sheet) to determine the structure parameters (Stoll et al. 1995; El-Kaliouby and Al-Garni 2009; Essa 2011, 2019; Dmitriev 2012; Sharma and Biswas 2013; Roudsari and Beitollahi 2013; Mehanee 2014; Essa and Elhussein 2017; Kawada and Kasaya 2018). These techniques include the use of nomograms and the characteristic point method (Paul 1965; Bhattacharya and Roy 1981; Murthy and Haricharan 1985; Sundararajan et al. 1990; Fedi and Abbas 2013), window curves method (Abdelrahman et al. 2006b, 2009a; Essa 2007), linear inversion modeling (Asfahani and Tlas 2016), non-linear inversion modeling (Asfahani and Tlas 2005; Abdelrahman et al. 2006a; Essa et al. 2008), horizontal gradient method (Abdelrahman et al. 2009b; Essa and Elhussein 2017), and neural networks (El-Kaliouby and Al-Garni 2009). Many of the previous methods require a priori information about the model’s parameters and a suitable range for searching for the best solution for each parameter. The most recent techniques include simulated annealing (Göktürkler and Balkaya 2012), very fast simulated annealing (Sharma and Biswas 2013; Biswas and Sharma 2015; Biswas 2016), genetic algorithm (Göktürkler and Balkaya 2012), and particle swarm optimization (PSO) (Santos 2010; Göktürkler and Balkaya 2012; Essa 2019, 2020; Essa and Elhussein 2020).

In this study, a new technique based upon global PSO was developed to invert self-potential datasets for different mineralized sources (horizontal cylinder, vertical cylinder, sphere, and 2-D inclined sheet) to calculate the different models parameters, namely, amplitude coefficient (Ac), depth (h), polarization angle (α), inclination angle (β), half-width (d), shape factor (Sf), and source origin (w). The technique used here applies PSO to the first horizontal gradient anomalies of the self-potential data to remove the effect of the regional background. The proposed method was applied to five different synthetic models with and without 15% random noise and to three real cases from Canada and India.

Methodology

The measured self-potential anomaly is composed of the residual anomaly due to different mineralized sources (horizontal cylinder, vertical cylinder, sphere, and 2-D inclined sheet) and the unwanted regional anomaly, which is the measured anomaly (Essa 2020), thus:

$$\Delta V\left({x}_{i}\right)={V}_{\text{res}}\left({x}_{i},h, \alpha \right)+Z\left({x}_{i}\right) ,$$
(1)

where \(\Delta V\left({x}_{i}\right)\) is the total measured self-potential anomaly, \({V}_{\text{res}}\left({x}_{i},h, \alpha \right)\) is the residual anomaly caused by different sources, and \(Z\left({x}_{i}\right)\) is the regional anomaly. In this study, the PSO algorithm was applied to invert the residual anomalies, which were separated from the total anomalies using the first horizontal gradient.

Forward Modeling of Different Structures and the First Horizontal Gradient

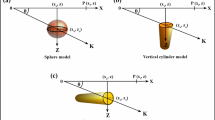
The self-potential anomaly (\({V}_{\text{res}})\) for different simple geometric structures (Figs. 1a, b, c) at any point (\({x}_{i}\)) is given by (Bhattacharya and Roy 1981; Essa 2019):

Fig. 1
figure 1

Geometric structures for different simple bodies: a vertical cylinder, b horizontal cylinder, c sphere, and d 2-D inclined sheet

Full size image
$${V}_{\text{res}}\left({x}_{i},h, \alpha \right)={A}_{c}\frac{\left({x}_{i}-w\right)\cos\alpha -h\sin\alpha }{{\left({\left({x}_{i}-w\right)}^{2}+{h}^{2}\right)}^{{S}_{f}}}, i=0, 1, 2, 3,\ldots , M$$
(2)

where M is number of data points, \({S}_{\text{f}}\) is shape factor (dimensionless), h is depth of structure (m), \({A}_{\text{c}}\) is the amplitude coefficient, \(({\text{mV}}\;{\text{m}}^{{2S}_{\text{f}}-1})\), w is position of source body (m), and \(\alpha\) is polarization angle (degree). The Sf is dependent on the shape of the structure and is equal to 1.5 for a sphere-like structure, 1 for a horizontal cylinder-like structure, and 0.5 for a semi-infinite vertical cylinder.

The self-potential anomaly (\({V}_{\text{res}})\) caused by a 2-D inclined sheet (Fig. 1d) at any location \(({x}_{i})\) on a profile perpendicular to the strike of this sheet is defined as (Murthy and Haricharan 1985; Sundararajan et al. 1998; Sharma and Biswas 2013; Essa 2020):

$${V}_{\text{res}}\left({x}_{i},h, \beta ,d\right)={A}_{c} ln\left[\frac{{\left(\left({x}_{i}-w\right)-d\cos\beta \right)}^{2}+{\left(h-d\sin\beta \right)}^{2}}{{\left(\left({x}_{i}-w\right)+d\cos\beta \right)}^{2}+{\left(h+d\sin\beta \right)}^{2}}\right], i=0, 1, 2, 3,\ldots, M$$
(3)

where \({A}_{\text{c}}\) is the amplitude coefficient, \(({\text{mV}})\), d is half-width, and \(\beta\) is sheet inclination angle.

To remove regional background, the first horizontal gradient was applied to Eq. (1) by using two different observation locations \(({x}_{i}+s\,{\textrm{and}}\,{x}_{i}-s)\) along the anomaly profile. The first horizontal gradient anomaly can be defined as follows:

$${\Delta V}_{x}\left({x}_{i}, s\right)=\frac{\Delta V\left({x}_{i}+s\right)-\Delta V\left({x}_{i}-s\right)}{2s},$$
(4)

where s = 1, 2, 3, …, N spacing units and is called window length or graticule spacing. The inversion algorithm was then applied to Eq. (4) to estimate the different source parameters.

Inversion Algorithm

The inversion algorithm applied in this study is based on the global PSO technique, which was proposed by Eberhart and Kennedy (1995). The method was developed for utilization in the solution of different geophysical problems (Sen and Stoffa 2013; Singh and Biswas 2016; Essa and Elhussein 2018, 2020; Essa 2019). The PSO technique is stochastic and, in this context, it can be used to represent a group of birds or school of fish looking for food. In this study, the models or particles represent the birds. Each model has a position and velocity vector, with the position vector representing the parameter value. A swarm is initiated with random models using the ranges of different variables, followed by updating the location and velocity of the different particles using the following formulas:

$${x}_{i}^{k+1}={x}_{i}^{k}+{V}_{i}^{k+1},$$
(5)

where \({x}_{i}^{k}\) is the ith particle position at the kth iteration, and \({V}_{i}^{k}\) is the ith particle velocity at kth iteration and is obtained as follows:

$${V}_{i}^{k+1}={c}_{3}{V}_{i}^{k}+{c}_{1}{\text{rand}}1\left({T}_{\text{best}}-{x}_{i}^{k+1}\right)+{c}_{2}{\text{rand}}2\left({J}_{\text{best}}-{x}_{i}^{k+1}\right),$$
(6)

where rand1 and rand2 are any two random values in the range [0,1], \({c}_{1}\,\text{and}\,{c}_{2}\) are cognitive and social coefficients, \({c}_{3}\) is the inertial factor that controls the velocity of the model and takes on a value of < 1, \({T}_{\text{best}}\) is the best position reached by an individual model, and \({J}_{\text{best}}\) is the global best position achieved by any model in the swarm. The \({c}_{1}\,\text{and}\,{c}_{2}\) are usually equal to two (Parsopoulos and Vrahatis 2002; Singh and Biswas 2016; Essa 2019; Essa and Elhussein 2020). Then, the best solution reached by each individual model \({(T}_{\text{best}})\) and the global best solution reached \({(J}_{\text{best}})\) are stored in memory, and the location and velocity of the models are updated during the iteration process. The iteration process terminates when convergence is reached (Venter and Sobieski 2002; Essa and Elhussein 2020).

The global best solution \({(J}_{\text{best}})\) is reached when the following objective function \(({\psi }_{\text{obj}})\) is optimized:

$${\psi }_{\text{obj}}=\frac{1}{M}\sum_{i=1}^{M}{[{V}_{{\text{res}} i}^{O}\left({x}_{i}\right)-{V}_{{\text{res}} i}^{c}\left({x}_{i}\right)]}^{2},$$
(7)

where M is number of data points, \({V}_{{\text{res}} i}^{O}\) is the observed self-potential anomaly, and \({V}_{{\text{res}} i}^{c}\) is the calculated self-potential anomaly.

The different source parameters \(\left({A}_{\text{c}}, h, {\alpha, \beta, d, S}_{\text{f}}, {\text{and}}\ w\right)\) were estimated by minimizing Eq. (7) for the different s (window length) values used in Eq. (4). Then, the average value (\({\mathcal{E}}\)) of the estimated parameters for the different s values was calculated. Finally, the root-mean-square (RMS) error was calculated as follows:

$${\text{RM}}{\text{S}}=\sqrt{\frac{1}{M}\sum_{i=1}^{M}{[{V}_{{\text{res}} i}^{O}\left({x}_{i}\right)-{V}_{{\text{res}} i}^{c}\left({x}_{i}\right)]}^{2}} .$$
(8)

Synthetic Models

In these models, the proposed method was applied to five synthetic examples representing different sources (semi-infinite vertical cylinder, horizontal cylinder, sphere, and 2-D inclined sheet) contaminated with and without 15% random noise. One of these examples includes a regional background to determine the effect of the background on the proposed method.

Semi-Infinite Vertical Cylinder Example

A pure self-potential anomaly from a semi-infinite vertical cylinder was calculated using profile length = 120 m, \({A}_{c}\) = 250 mV, h = 10 m, \(\alpha\) = 55°, \({S}_{f}\) = 0.5, and w = 0 m (Fig. 2a). The first horizontal gradient was then applied to the self-potential anomaly profile using different s values (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 2b), and the global PSO technique was applied to these gradient anomalies to estimate the vertical cylinder model parameters using different ranges per parameter (Table 1). Table 1 shows the estimated parameters \(\left({A}_{\text{c}},h, \alpha ,{S}_{\text{f}}, {\text{and}}\ w\right)\), where the errors of \({A}_{\text{c}},h, \alpha , {{\text{and}}\ S}_{\text{f}}\) were 0% and the RMS error was 0 mV. The correlation between the noise-free anomaly and estimated anomaly is shown in Fig. 2a.

Fig. 2
figure 2figure 2figure 2

a Synthetic noise-free self-potential anomaly from the vertical cylinder model with the following parameters: \({A}_{c}\) = 250 mV, h = 10 m, \(\alpha\) = 55°, \({S}_{f}\) = 0.5, w = 0 m, and profile length = 120 m. The estimated anomaly is also presented. b First horizontal gradient anomalies of the self-potential anomaly in a. c Self-potential anomaly in a with 15% random noise and the estimated anomaly. d First horizontal gradient anomalies of the noisy self-potential anomaly in c

Full size image
Table 1 Numerical results of the global PSO inversion algorithm applied to first horizontal gradient anomalies from the vertical cylinder model (Ac = 250 mV, h = 10 m, \(\alpha\) = 55°, Sf = 0.5, w = 0 m, profile length = 120 m), with and without 15% random noise
Full size table

To test the efficiency of the proposed method in the case of noisy data, the previous synthetic model was contaminated with 15% random noise (Fig. 2c). The first horizontal gradient anomalies were calculated using the same previous window lengths (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 2d); then, by applying the PSO method to the gradient anomalies, the different parameters were estimated (Table 1). Table 1 shows the estimated parameters (\({A}_{\text{c}}= 255.68 \pm 4.71\;{\text{mV}}, h=10.13 \pm 0.19\;{\text{m}}, \alpha = 55.75 \pm {1.67}^{\circ}, {S}_{f}= 0.5 \pm 0, {\text{and}}\ w= {-\;0.17} \pm 0.23\;{\text{m}})\), where the errors of \({A}_{\text{c}}, h, \alpha , {\text{and}}\ {S}_{\text{f}}\) were 2.27%, 1.30%, 1.36%, and 0% respectively, and the RMS error was 5.82 mV. Figure 2c compares the noisy and calculated anomalies.

Horizontal Cylinder Example

A noise-free self-potential anomaly from a horizontal cylinder was calculated using: profile length = 120 m, Ac = 1800 mV m, h = 7 m, \(\alpha\) = 45°, Sf = 1, and w = 0 m (Fig. 3a). The first horizontal gradient was then applied to the self-potential anomaly profile using different s values (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 3b); then, the global PSO technique was applied to these gradient anomalies to estimate the horizontal cylinder model parameters using different ranges per parameter (Table 2). Table 2 shows the estimated parameters \(\left({A}_{\text{c}},h, \alpha ,{S}_{\text{f}}, {\text{and}}\ w\right)\), where the errors of \({A}_{\text{c}},h, \alpha , {\text{and}}\ {S}_{\text{f}}\) were 0% and the RMS error was 0 mV.

Fig. 3
figure 3figure 3figure 3

a Synthetic noise-free self-potential anomaly from the horizontal cylinder model with the following parameters: \({A}_{c}\) =1800 mV·m, h = 7 m, \(\alpha\) = 45°, \({S}_{f}\) = 1, w = 0 m, and profile length = 120 m. The estimated anomaly is also presented. b First horizontal gradient anomalies of the self-potential anomaly in a. c Self-potential anomaly in a with 15% random noise and the estimated anomaly. d First horizontal gradient anomalies of the noisy self-potential anomaly in c

Full size image
Table 2 Numerical results of the global PSO inversion algorithm applied to first horizontal gradient anomalies from the horizontal cylinder model (Ac = 1800 mV m, h = 7 m, \(\alpha\) = 45°, Sf = 1, w = 0 m, profile length = 120 m), with and without 15% random noise
Full size table

To apply the proposed method to noisy data, as most real data include noise, the previous synthetic model was contaminated with 15% random noise (Fig. 3c). The first horizontal gradient anomalies were calculated using the same previous window lengths (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 3d); then, by applying the PSO method to the gradient anomalies, the different parameters were estimated (Table 2). Table 2 shows the estimated parameters (\({A}_{\text{c}}= 1759.87 \pm 62.94\;\text{mV\;m}, h=6.97 \pm 0.10 \;{\text{m}}, \alpha = 45.05 \pm {0.56}^{\circ}, {S}_{\text{f}}= 1 \pm 0, {\text{and}}\ w=0.00 \pm 0.06 \;{\text{m}})\), where the errors of \({A}_{c}, h, \alpha , \mathrm{a}\mathrm{n}\mathrm{d}\ {S}_{f}\) were 2.23%, 0.43%, 0.11%, and 0%, respectively, and the RMS error was 2.85 mV. Figure 3c compares the noisy and calculated anomalies.

Sphere Example

A pure self-potential anomaly from a sphere was calculated using: profile length = 120 m, Ac = 2500 mV m2, h = 5 m, \(\alpha\) = 35°, Sf = 1.5, and w = 0 m (Fig. 4a). The first horizontal gradient was then applied to the self-potential anomaly profile using different s values (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 4b); then, the global PSO technique was applied to these gradient anomalies to estimate the sphere model parameters using different ranges per parameter (Table 3). Table 3 shows the estimated parameters \(\left({A}_{\text{c}},h, \alpha ,{S}_{\text{f}}, {\text{and}}\ w\right)\), where the errors of \({A}_{\text{c}},h, \alpha , {and\ S}_{\text{f}}\) were 0% and the RMS error was 0 mV.

Fig. 4
figure 4figure 4figure 4

a Synthetic noise-free self-potential anomaly from the sphere model with the following parameters: \({A}_{\text{c}}\) = 2500 mV·m2, h = 5 m, \(\alpha\) = 35°, \({S}_{\text{f}}\) = 1.5, w = 0 m, and profile length = 120 m. The estimated anomaly is also presented. b First horizontal gradient anomalies of the self-potential anomaly in a. c Self-potential anomaly mentioned in a with 15% random noise and the estimated anomaly. d First horizontal gradient anomalies of the noisy self-potential anomaly in c

Full size image
Table 3 Numerical results of the global PSO inversion algorithm applied to first horizontal gradient anomalies from the sphere model (Ac = 2500 mV m2, h = 5 m, \(\alpha\) = 35°, Sf = 1.5, w = 0 m, profile length = 120 m), with and without 15% random noise
Full size table

To examine the effect of noisy data on the proposed method, the previous synthetic model was contaminated with 15% random noise (Fig. 4c). The first horizontal gradient anomalies were calculated using the same previous window lengths (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 4d); then, by applying the PSO method to the gradient anomalies, the different parameters were estimated (Table 3). Table 3 shows the estimated parameters (\({A}_{\text{c}}= 2528.35 \pm 33.44 \;{\text{mV}}\; {\text{m}}^{2} , h=5.12 \pm 0.23 \; \text{m}, \alpha = 34.62 \pm {0.87}^{o}, {S}_{f}= 1.5 \pm 0.06, \text{and}\ w=-0.03 \pm 0.07 \; \text{m})\), where the errors of \({A}_{\text{c}}, h, \alpha , {\text{and}}\ {S}_{\text{f}}\) were 1.13%, 2.4%, 1.09%, and 0%, respectively, and the RMS error was 2.19 mV. Figure 4c compared the noisy and calculated anomalies.

2-D Inclined Sheet Example with Regional Background

The efficiency of our method in the presence of a regional background was tested. To do so, a noise-free self-potential anomaly from a 2-D inclined sheet (Ac = 200 mV, h = 12 m, \(\beta\) = 50°, d = 6 m, and w = 10 m) was added to a deep-seated first-order regional anomaly \((3{x}_{i}-30)\) (Fig. 5a) with a profile length of 120 m. The composite anomaly was obtained as follows:

Fig. 5
figure 5figure 5figure 5

a Noise-free composite synthetic self-potential anomaly of a 2-D inclined sheet model with the following parameters; Ac = 200 mV, h = 12 m, \(\beta\) = 50°, \(d\) = 6 m, w = 10 m, profile length = 120 m, and deep-seated first-order regional anomaly \((3{x}_{i}-30)\). The estimated anomaly is also presented. b First horizontal gradient anomalies of the composite self-potential anomaly in a. c Composite self-potential anomaly mentioned in a with 15% random noise and the estimated anomaly. d First horizontal gradient anomalies of the noisy composite self-potential anomaly in c

Full size image
$$\Delta V\left({x}_{i},h, \beta ,d\right)=200\ln\left[\frac{{\left(\left({x}_{i}-10\right)-6\cos{50}^{\circ}\right)}^{2}+{\left(12-6\sin{50}^{\circ}\right)}^{2}}{{\left(\left({x}_{i}-10\right)+6\cos\beta \right)}^{2}+{\left(12+6\sin{50}^{\circ}\right)}^{2}}\right]+\left(3{x}_{i}-30\right), i=0, 1, 2, 3,\ldots, M$$
(9)

The first horizontal gradient was then applied to the self-potential composite anomaly profile using different s values (window lengths) (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 5b); then, the global PSO technique was applied to these gradient anomalies to estimate the sheet model parameters using different ranges per parameter (Table 4). Table 4 shows the estimated parameters \(\left({A}_{\text{c}}, h, \beta , d, {\text{and}}\ w\right)\), where the errors of \({A}_{\text{c}}, h, \beta , d, and\ w\) were 0% and the RMS error was 0 mV. Table 4 shows that the proposed technique gives the best results of the model parameters, even if the model was contaminated with regional background.

Table 4 Numerical results of the global PSO inversion algorithm applied to first horizontal gradient anomalies from the composite anomaly of 2-D inclined sheet (Ac = 200 mV, h = 12 m, \(\beta\) = 50°, \(d\) = 6 m, w = 10 m, profile length = 120 m) and deep-seated first-order regional anomaly \((3{x}_{i}-30)\), with and without 15% random noise
Full size table

To apply the proposed method to noisy data, 15% random noise was added to the previous synthetic model (Fig. 5c). The first horizontal gradient anomalies were calculated using the same previous window lengths (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 5d); then, by applying the PSO method to the gradient anomalies, the different parameters were estimated (Table 4). Table 4 shows the estimated parameters (\({A}_{\text{c}}= 202.11 \pm 15.61 \;{\text{mV}}, h=12.03\pm 0.14 \;{\text{m}}, \beta = 49.31 \pm {1.70}^{\circ}, d= 6.03 \pm 0.55\; {\text{m}}, {\text{and}}\ w=9.90 \pm 0.41 \;{\text{m}})\), where the errors of \({A}_{\text{c}}, h, \beta , d, {\text{and}}\ w\) were 1.06%, 0.25%, 1.38%, 0.5% and 1%, respectively, and the RMS error was 6.13 mV. Figure 5c compares the noisy and calculated anomalies.

Multi-model

The applicability and the efficiency of the used technique in estimating the multiple model parameters were tested. To do so, the method was applied to a composite anomaly composed of a sphere model with the following parameters: Sf = 1.5, Ac = 4500 mV m2, h = 3 m, \(\alpha\) = 60°, and w = 0 m—and a horizontal cylinder model with the following parameters: Sf = 1, Ac = 3000 mV m, h = 9 m, \(\alpha\) = 30°, and w = 30 m (Fig. 6a). The profile length was 120 m, and the composite anomaly was obtained as:

Fig. 6
figure 6figure 6figure 6

a Noise-free composite multi-model anomaly of the sphere (Ac = 4500 mV·m2, h = 3 m, \(\alpha\) = 60°, Sf = 1.5 m, and w = 0 m). and horizontal cylinder (Ac = 3000 mV·m, h = 9 m, \(\alpha\) = 30°, Sf = 1 m, and w = 30 m). using a profile length of 120 m. The estimated anomaly is also presented. b First horizontal gradient anomalies of the composite self-potential anomaly in a. c Composite self-potential anomaly mentioned in a with 15% random noise and the estimated anomaly. d First horizontal gradient anomalies of the noisy composite self-potential anomaly in c

Full size image
$${V}_{\text{comp}}\left({x}_{i},h, \alpha \right)=4500\frac{{x}_{i}\cos{60}^{\circ}-3\sin{60}^{\circ}}{{\left({{x}_{i}}^{2}+9\right)}^{1.5}}+3000\frac{\left({x}_{i}-30\right)\cos{30}^{\circ}-9\sin{30}^{\circ}}{\left({\left({x}_{i}-30\right)}^{2}+81\right)}, i=0, 1, 2, 3,\ldots , M$$
(10)

The first horizontal gradient was then applied to the composite anomaly profile using different s values (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 6b); then, the global PSO technique was applied to these gradient anomalies to estimate the multiple model parameters using different ranges for each parameter (Table 5). Table 5 shows the estimated parameters: (\({A}_{\text{c}}= 4523.2 \pm 31.65 \;\text{mV}\;{\text{m}}^{2}, h=3.02 \pm 0.08 \;{\text{m}}, \alpha =59.37 \pm {0.60}^{\circ}, {S}_{\text{f}}=1.53 \pm 0.05, {\text{and}}\ w=0.013 \pm 0.02 \;{\text{m}})\) for the sphere model and \({A}_{\text{c}}= 3012.73 \pm 24.69 \;{\text{mV}} \;{\text{m}}, h=9.08 \pm 0.13 \;{\text{m}}, \alpha =30.19\pm {0.40}^{\circ}, {S}_{\text{f}}=1.02 \pm 0.04, {\text{and}}\ w=30.02 \pm 0.03 \;{\text{m}}\) for the horizontal cylinder model. The errors of \({A}_{\text{c}}, h, \alpha , {\text{and}}\ {S}_{\text{f}}\) were 0.52%, 0.67%, 1.05%, and 2%, respectively, for the sphere model, whereas for the horizontal cylinder model, the errors of \({A}_{\text{c}}, h, \alpha , {S}_{\text{f}}, {\text{and}} w\) were 0.42%, 0.8%, 0.63%, 2%, and 0.07%, respectively, and the RMS error of the multiple model anomaly was 14.43 mV. Figure 6a shows the correlation between the multiple model anomaly and the estimated anomaly.

Table 5 Results of the global PSO inversion algorithm applied to first horizontal gradient anomalies from the composite multi-model anomaly of sphere (Ac = 4500 mV·m2, h = 3 m, \(\alpha\) = 60°, Sf = 1.5 m, w = 0 m, profile length = 120 m) and horizontal cylinder (Ac = 3000 mV m, h = 9 m, \(\alpha\) = 30°, Sf = 1 m, w = 30 m, profile length = 120 m), with and without 15% random noise
Full size table

To apply the proposed method to noisy data, 15% random noise was added to the previous composite model (Fig. 6c). The first horizontal gradient anomalies were calculated using the same previous window lengths (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 6d); then, by applying the PSO method to the gradient anomalies, the different parameters were estimated (Table 5). Table 5 shows the estimated parameters: (\({A}_{\text{c}}=4533.73 \pm 48.39 \;{\text{mV}} \;{\text{m}}^{2}, h=3.02 \pm 0.17 \;{\text{m}}, \alpha =60.73 \pm {2.38}^{\circ}, {S}_{\text{f}}=1.52 \pm 0.08, {\text{and}}\ w=-0.04 \pm 0.21 \;{\text{m}})\) for the sphere model and \({A}_{\text{c}}= 3030.95 \pm 47.09 \;{\text{mV}}\; {\text{m}}, h=8.95 \pm 0.26 \;{\text{m}}, \alpha =29.72 \pm {1.61}^{\circ}, {S}_{\text{f}}=1.03 \pm 0.08, {\text{and}} w=30.14 \pm 0.28 \;{\text{m}})\) for the horizontal cylinder model. The errors of \({A}_{\text{c}}, h, \alpha , {\text{and}}\ {S}_{\text{f}}\) were 0.75%, 0.67%, 1.22%, and 1.33%, respectively, for the sphere model, whereas for the horizontal cylinder model, the errors of \({A}_{\text{c}}, h, \alpha , {S}_{\text{f}}, {\text{and}}\ w\) were 1.03%, 0.56%, 0.93%, 3%, and 0.47%, respectively, and the RMS error of the multiple model anomaly was 17.85 mV. Figure 6c compares the multiple model noisy anomaly and the estimated anomaly.

From the results shown above, the proposed method can be used to determine the multi-source parameters efficiently and accurately.

Field Examples

To examine the applicability and accuracy of the proposed algorithm in mining, the proposed technique was applied to three real field examples: one from Canada, which is the multi-source example, and two examples from India.

Self-potential Anomaly of Sulfide Deposit, Senneterre, Quebec, Canada (Multi-source)

Senneterre in Quebec is rich in minerals, in which pyrite and pyrrhotite account for approximately 30% of the entire zone, and the mineralized rocks that host pyrite and pyrrhotite are meta-sedimentary breccias and tuffs that are interbedded with lava flows (Telford et al. 1990; Biswas 2017). A self-potential anomaly profile was taken above the massive sulfide deposits (Telford et al. 1990; Biswas 2017). The profile length was 209 m, sampled at 1 m intervals (Fig. 7a). Figure 7a reveals that there were three anomalies. The self-potential profile was then filtered by the first horizontal gradient using different s values (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 7b). Then, the global PSO technique was applied to the first horizontal gradient anomalies to estimate the different parameters \(({A}_{\text{c}}, h, \alpha , {S}_{\text{f}}, {\text{and}}\ w)\) of the three anomalies using different ranges (Table 6); the calculated parameters were: \({A}_{\text{c}}=202.32 \pm 5.78 \;{\text{mV}}, h=7.97 \pm 0.38 \;{\text{m}}, \alpha =64.17 \pm {2.56}^{\circ}, {S}_{\text{f}}=0.52 \pm 0.08, {\text{and}}\ w=152.19 \pm 3.15 \;{\text{m}}\) for the first anomaly; \({A}_{\text{c}}=578.63 \pm 3.62 \;{\text{mV}}, h=3.4 \pm 0.32 \;{\text{m}}, \alpha =97.29 \pm {4.79}^{\circ}, {S}_{\text{f}}=0.5 \pm 0.06, {\text{and}}\ w=175.45 \pm 2.76 \; {\text{m}}\) for the second anomaly; and \({A}_{\text{c}}=2314.68 \pm 21.13 \;{\text{mV}}\; {\text{m}}, h=7.8 \pm 0.34 \;{\text{m}}, \alpha =145.11 \pm {5.22}^{\circ}, {S}_{\text{f}}=0.92 \pm 0.15, {\text{and}}\ w=245.39 \pm 2.63 \;{\text{m}}\), for the third anomaly. The RMS error for the calculated self-potential field was 24.01 mV. From the results shown in Table 6, we can conclude that the first and second bodies were vertical cylinders, whereas the third body was a horizontal cylinder. The correlation between the observed and calculated anomalies is shown in Fig. 7a. Table 7 compares the estimated parameters of the present method and those from other methods in the literature.

Fig. 7
figure 7figure 7

Senneterre, Quebec, Canada: a Observed and the estimated self-potential anomaly profile for the multi-source field example of sulfide deposit, and the geometric structure of the three different sources. b First horizontal gradient anomalies of the observed self-potential anomaly in a

Full size image
Table 6 Results of the global PSO inversion algorithm applied to first horizontal gradient anomalies for the multi-
Full size table
Table 7 Comparison of results obtained from different methods for the self-potential anomaly of sulfide deposit, Senneterre, Quebec, Canada
Full size table

Kalava Fault, Cuddapah Zone, India

Cuddapah basin covers an area of approximately 35,000 km2, with a maximum basin thickness at any point of approximately 6 km. It overlies the Archean basement (Plumb 1981). The Cuddapah basin comprises the following units (Plumb 1981; Saha and Tripathy 2012) (Fig. 8a). The Cuddapah Supergroup consists of the Papaghni, Chitravati, and Nallamalai Groups. The Papaghni Group is composed of fluviatile sandstone, conglomerate, flaggy buff dolomite, red to brown sandstone, and red siltstone. The Chitravati Group, which overlies disconformably the Papaghni Group, comprises Pulivendla quartzite, gray to green shale, flaggy sandstone, stromatolitic limestone (including thick dolerite sills), and Gandikota quartzite. The Nallamalai Group, which overlies unconformably the Chitravati Group, is composed of Bairenkonda quartzite, shale, phyllite, dolomite, and quartzite. The Cuddapah Supergroup is overlain unconformably by the Kurnool Group. The latter is composed of Banganapalle quartzite, Narji limestone, Auk shale, Paniam quartzite, Koilkuntla limestone, and Nandyal shale.

Fig. 8
figure 8figure 8figure 8

Cuddapah basin, India: a Geological map (modified after Plumb 1981; Saha and Tripathy 2012). b Observed and estimated self-potential anomaly profile for the Kalava fault. c First horizontal gradient anomalies of the observed self-potential anomaly in b

Full size image

A self-potential anomaly profile was taken across the Kalava fault area, Cuddapah basin, India (Rao et al. 1982; Tlas and Asfahani 2008; El-Kaliouby and Al-Garani 2009) (Fig. 8b). The profile length was 40 m, which was sampled at 0.25 m. The self-potential profile was then filtered by the first horizontal gradient using different s values (s = 0.5, 0.75, 1, 1.25, 1.5, and 1.75 m) (Fig. 8c). Then, the global PSO technique was applied to the horizontal gradient anomalies to estimate the different parameters \({(A}_{\text{c}}, h, \beta , d, {\text{and}}\ w)\) using different ranges (Table 8), with the calculated parameters as follows: \({A}_{\text{c}}=76.83 \pm 4.09 \;{\text{mV}}, h=8.42 \pm 0.31 \;{\text{m}}, \beta =99.55 \pm {3.85}^{\circ}, d=4.45 \pm 0.31 \;{\text{m}}, {\text{and}}\ w=0.67 \pm 0.20 \;{\text{m}}\), and the RMS error was 4.14 mV. The correlation between the observed and calculated anomalies is shown in Fig. 8b. Table 9 compares the estimated parameters of the present method and those from other methods in the literature.

Table 8 Results of the global PSO inversion algorithm applied to first horizontal gradient anomalies for the self-potential anomaly of Kalava fault, Cuddapah zone, India
Full size table
Table 9 Comparison of results obtained from different methods for the self-potential anomaly of Kalava fault, Cuddapah zone, India
Full size table

Self-potential Anomaly of the Copper Sulfide Deposit, Surda Zone, India

The Surda area of the Rakha mines is endowed with copper sulfide deposits. These are located within the Singhbhum shear zone (Singhbhum copper belt), which extends to approximately 200 km from Duarparam in the western part to Baharagora in the southeastern part (Mishra et al. 2003).

A self-potential anomaly profile was taken above the copper sulfide deposits in Surda area, India (Murthy et al. 2005; Santos 2010; Biswas and Sharma 2014a) (Fig. 9a). The profile length was 243 m, and it was digitized at 1 m intervals. The first horizontal gradient filter was then applied to the self-potential anomaly profile using different s values (s = 2, 3, 4, 5, 6, and 7 m) (Fig. 9b). Then, the global PSO technique was applied to the first horizontal gradient anomalies to estimate the different parameters \({(A}_{\text{c}}, h, \beta , d, {\text{and}}\ w)\) of the sheet using different ranges (Table 10). The calculated parameters were as follows: \({A}_{\text{c}}=97.44 \pm 3.15 \;{\text{mV}}, h=32.17 \pm 0.41 \;{\text{m}}, \beta =49.33 \pm {0.38}^{\circ}, d=28.97 \pm 0.23 \;{\text{m}}, {\text{and}}\ w=152.94 \pm 0.42 \;{\text{m}}\); and the RMS error was 5.86 mV. The correlation between the observed and calculated anomalies is shown in Fig. 9a. Table 11 compares the estimated parameters of the present method and those from other methods in the literature.

Fig. 9
figure 9figure 9

Surda zone, India: a Observed and estimated self-potential anomaly profile for the copper sulfide deposit. b First horizontal gradient anomalies of the observed self-potential anomaly in a

Full size image
Table 10 Results of the global PSO inversion algorithm applied to first horizontal gradient anomalies for the self-potential anomaly of copper sulfide deposit, Surda zone, India
Full size table
Table 11 Comparison of results obtained from different methods for the self-potential anomaly of copper sulfide Deposit, Surda Zone, India
Full size table

Conclusions

The applicability and the efficiency of the proposed technique (global PSO method applied to the first horizontal gradient) was explained and demonstrated for synthetic datasets and for real self-potential datasets from Canada and India. The method proposed here can be applied in mineral resource development, as it can be utilized to determine the different parameters (amplitude coefficient (Ac), depth (h), polarization angle (α), inclination angle (β), half-width (d), shape factor (Sf), and source origin (w)) of mineralized sources with different shapes (horizontal cylinder, vertical cylinder, sphere, and 2-D inclined sheet). A major advantage of this method is that it removes regional background from the observed data such that the residual anomaly parameters are determined effectively. The global PSO provides fast convergence and does not require information regarding the source shape. However, the time needed to reach the global best solution increases when the number of models used in inversion increases, which can be considered a minor disadvantage of the method. The results obtained from the synthetic and real datasets show that the method is effective in interpreting self-potential data, even if there are multiple sources, and it can determine the parameters of the multiple sources. Finally, the results of the real field data are strongly comparable with those from other methods in the literature.