1 Introduction

The self potential method is considered one of the oldest geophysical methods in exploration. The self potential anomalies can be induced by different phenomena such as electrokinetic, electrochemical that involving reduction and oxidation of ores or minerals contacted with groundwater or rock fluids, thermoelectric, and redox processes, which can be measured among any two points on Earth’s surface (natural potential) (Sato and Mooney 1960; Corry 1985; Naudet et al. 2004). From the time when the self potential discovered, it has been used for solving many problems such as mineral and ore exploration, underground water investigation, tracing paleo shear zones, and archaeological prospection (Drahor 2004; Naudet et al. 2008; Abdelrahman et al. 2009a; Fernandez-Martinez et al. 2010; Mehanee 2015; Roy 2019).

Estimation of the unknown model parameters of the buried structures, which are very important to recognize the mineralization zones and its economic quantities, from self potential data is a challenge faced by the researchers in this field. Because of the self potential data interpretation is suffering from non-unique in finding a stable solution (global minimum) and sometimes trapped in local minimums (Biswas 2013; Mehanee 2015). So, the use of simple geological models (geologic contacts, thin dike, cylinders, and spheres), which are not wholly geologically accurate, but they are usually employed in self potential elucidation to assess the model parameters and have a vital role in many exploration issues. Also, the user of these models decreases the trapped in local minima solution and helps in getting the accurate solution faster (Abdelrahman et al. 2006a; Mehanee et al. 2011; Hinze et al. 2013).

Several numerical and graphical methods have been established to elucidate the self potential data utilizing the simple-geometric models (Yungul 1950; Fitterman 1979; Bhattacharya and Roy 1981; Tlas and Asfahani 2007; Essa 2011; Mehanee 2014; Abdelrahman et al. 2016; Biswas 2017). Besides, methods that use linear and non-linear least-squares (Abdelrahman et al. 2006b; Essa et al. 2008), fair function algorithm (Tlas and Asfahani 2013), spectral analysis (Asfahani and Tlas 2001; Di Maio et al. 2017), particle swarm optimization (Essa 2019), simulated annealing algorithm (Tlas and Asfahani 2008; Biswas and Sharma 2015), genetic-price algorithm (Di Maio et al. 2019), gradients (Abdelrahman et al. 2004; Essa and Elhussein 2017), black-hole algorithm (Sungkono and Warnana 2018), extreme points (Fedi and Abbas 2013), 2D and 3D normal full gradient and Euler deconvolution (Agarwal and Sirvastava 2009; Sindirgi and Özyalin 2019), moving-average (Abdelrahman et al. 2009b).

The investigation for self potential anomalies of the dike-models like geologic structures that considered to be the main sources of minerals and ores are very important to locate and delineate the economic interest of these sources. Roudsari and Beitollahi (2013) investigated a zinc-copper inclined dike to simulate a dike-like ore body because this simple approximation phenomenon exists in the near subsurface. Biswas (2016) studied and examined the self potential anomaly for the 2D inclined sheets utilizing least-squares and VFSA methods for delineating the buried model parameters. Mehanee (2015) proposed a deterministic elucidation method for self potential anomalies due to sheet-type for tracing a paleo shear zones based on minimizes an objective function in the space of the logarithmic and non-logarithmic model parameters.

Finally, this study is focusing on elucidating the residual self potential anomalies for the 2D finite dike-like a geologic model structure extracted from the measured data using a moving average method. After that, the utilizing of the particle swarm optimization to infer these anomalies to estimate the buried dike parameters (the polarization parameter, the depth, the inclination angle, the width, and the location of the dike center) for all available window lengths. The accuracy and stability of using the combination of these methods have been tested on various synthetic examples including the effect of the regional background and neighboring effects. Besides, using the suggested approach for mineralized zones field data from Germany and India.

1.1 The method

The general self potential anomaly is represented by the following form:

$$T_{otal} \left( {x_{j} } \right) = V\left( {x_{j} , z,\theta ,w} \right) + R_{egional} \left( {x_{j,} z} \right), \quad j = 0, 1, 2, 3, \ldots , N$$
(1)

where \(T_{otal} \left( {x_{j} } \right)\) represented the collected self potential data, \(V\left( {x_{j} , z,\theta ,w} \right)\) represented the residual self potential anomaly for the 2D inclined dike which is mentioned below, and \(R_{egional} \left( {x_{j,} z } \right)\) is the regional back ground field (Obasi et al. 2016).

1.2 The self potential anomaly for the 2D inclined dike

The self potential anomaly for 2D inclined dike at any point xj is (Sundararajan et al. 1998; Sharma and Biswas 2013)

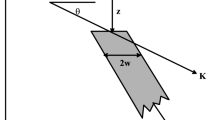
$$V\left( {x_{j} , z,\theta ,w} \right) = K\ln \left\{ {\frac{{\left[ {\left( {x_{j} - d} \right) - w\cos \theta } \right]^{2} + \left[ {z - w\sin \theta } \right]^{2} }}{{\left[ {\left( {x_{j} - d} \right) + w\cos \theta } \right]^{2} + \left[ {z + w\sin \theta } \right]^{2} }}} \right\} ,$$
(2)

where K is the polarization parameter \(\left( { = \frac{I\rho }{2\pi }} \right)\), z is the depth of the structure, d is the coordinate of the center of the source body, θ is the inclination angle, w is the half-width, xj is the coordinate of the measuring point in the X-direction, and N is the number of data collected. The systematic diagram of the 2D inclined dike containing the model parameters are presented in Fig. 1.

Fig. 1
figure 1

A sketch diagram for the 2D finite inclined dike including the model parameters

Full size image

1.3 The moving average method

The moving average method is considered as one of the pioneer methods in eliminating the regional background effect, which is represented by first-order polynomial (Griffin 1949; Essa and Munschy 2019). The moving average regional anomaly along the profile is:

$$R_{egional} \left( {x_{j} , z,s} \right), = \frac{{T_{otal} \left( {x_{j} + s} \right) + T_{otal} \left( {x_{j} - s} \right)}}{2}.$$
(3)

So, the moving average residual anomaly is well-defined as:

$$R\left( {x_{j} , z,\theta ,w} \right) = T_{otal} \left( {x_{j} } \right) - \left[ {\frac{{T_{otal} \left( {x_{j} + s} \right) + T_{otal} \left( {x_{j} - s} \right)}}{2}} \right],$$
(4)

where s = 1, 2, 3,…, units and is so-called the window length.

Hence, using Eq. (2) and relieving in Eq. (4), we get:

$$\begin{aligned} R\left( {x_{j} , z,\theta ,w} \right) &= K\ln \left\{ {\frac{{\left[ {\left( {x_{j} - d} \right) - w\cos \theta } \right]^{2} + \left[ {z - w\sin \theta } \right]^{2} }}{{\left[ {\left( {x_{j} - d} \right) + w\cos \theta } \right]^{2} + \left[ {z + w\sin \theta } \right]^{2} }}} \right\} \\ & \quad - \frac{K}{2}\left\{ {ln\left( {\frac{{\left[ {\left( {x_{j} - d + s} \right) - w\cos \theta } \right]^{2} + \left[ {z - w\sin \theta } \right]^{2} }}{{\left[ {\left( {x_{j} - d + s} \right) + w\cos \theta } \right]^{2} + \left[ {z + w\sin \theta } \right]^{2} }}} \right) + ln\left( {\frac{{\left[ {\left( {x_{j} - d - s} \right) - w\cos \theta } \right]^{2} + \left[ {z - w\sin \theta } \right]^{2} }}{{\left[ {\left( {x_{j} - d - s} \right) + w\cos \theta } \right]^{2} + \left[ {z + w\sin \theta } \right]^{2} }}} \right)} \right\} . \\ \end{aligned}$$
(5)

Now, Eq. (5) is used to determine the 2D inclined dike parameters (K, z, θ, w, and d) for all available s-values using the particle swarm optimization algorithm, which is accomplished in resolving problematic issues consistently and truthfully.

1.4 The global optimization particle swarm algorithm

The global optimization particle swarm was developed and introduced during the last years to solve many geophysical problems (Sen and Stoffa 2013; Singh and Biswas 2016; Essa and Elhussein 2018; Karcıoğlu and Gürer 2019). The particle swarm progression is stochastic and stirred by the communal repetitive in a journey of birds for searching the foods where the birds are the models. The individually model has a position and velocity vectors where the position vectors signify the value of the parameters. The particle swarm is adjusted with random models and looking for sources by apprising generations. In every iteration step, each model modernizes its velocity and place utilizing the next formulas:

$${\text{V}}_{\text{j}}^{{{\text{k}} + 1}} = {\text{c}}_{3} {\text{V}}_{\text{j}}^{\text{k}} + {\text{c}}_{1} {\text{rand}}\left( {{\text{T}}_{\text{best}} - {\text{P}}_{\text{j}}^{{{\text{k}} + 1}} } \right) + {\text{c}}_{2} {\text{rand}}\left[ {\left( {{\text{J}}_{\text{best}} - {\text{P}}_{\text{j}}^{{{\text{k}} + 1}} } \right){\text{P}}_{\text{j}}^{{{\text{k}} + 1}} } \right] = {\text{P}}_{\text{j}}^{\text{k}} + {\text{V}}_{\text{j}}^{{{\text{k}} + 1}} ,$$
(6)
$${\text{x}}_{\text{j}}^{{{\text{k}} + 1}} = {\text{x}}_{\text{j}}^{\text{k}} + {\text{v}}_{\text{j}}^{{{\text{k}} + 1}} .$$
(7)

where \({\text{v}}_{\text{j}}^{\text{k}}\) is the jth particle velocity at the kth iteration, \({\text{P}}_{\text{j}}^{\text{k}}\) is the present jth particle place at the kth iteration, rand is random numbers amongst \(\left[ {0,1} \right]\), \({\text{c}}_{1}\) and \({\text{c}}_{2}\) are cognitive and social parameters and equivalent 2 (Parsopoulos and Vrahatis 2002), c3 is the inertial coefficient that controls the particle velocity and its value < 1 and \({\text{x}}_{\text{j}}^{\text{k}}\) is the particle j-location at kth iteration. The inspiration behind selecting and utilizing the particle swarm technique is to get a global solution of various geometrical bodies from the self potential data quickly and point out the prominence of employing this technique between various conventional, non-conventional and optimization approaches. Furthermore, quick convergence to the optimum solution in real time influence managing and well recital assessment. Then, synthetic and real examples mentioned-below have been examined to confirm the motivation of using the particle swarm method at any time in the future.

1.5 The 2D inclined dike parameters estimation

The started model is gradually refined at every iterative-step to catch the optimum-fit amid the measured and the calculated data. In each step, the body parameters (K, z, θ, w, and d) are improved to catch the best values by minimizing the subsequent objective function. The optimal-solution of the body parameters (K, z, θ, w, and d) attained through applying the following objective function \(\left( {\varphi_{obj} } \right)\):

$$\varphi_{obj} = \frac{1}{N}\mathop \sum \limits_{{{\text{i}} = 1}}^{\text{N}} \left[ {V_{j}^{o} \left( {{\text{x}}_{\text{j}} } \right) - V_{j}^{p} \left( {{\text{x}}_{\text{j}} } \right)} \right]^{2} ,$$
(8)

where N is the observed points, \(V_{j}^{o}\) is the observed self potential anomaly and \(V_{j}^{p}\) is the calculated self potential anomaly at the point xj.

Finally, after estimated the body parameters (K, z, θ, w, and d) of the buried 2D inclined dike structures, the complete error (RMSE) between the observed and calculated fields are assessed by taking the square-root of Eq. (8).

1.6 Synthetic examples

So, the examination of the accuracy and the benefits of the suggested approach were inspected through two synthetic anomalies tests as follow: First test contains the effect of adding the regional background and various level of noise 10% and 20%. The second test contains the effect of multi neighboring structures and also adding a 10% random noise. These self potential data interpreted using the particle swarm algorithm to recover the actual model parameters.

1.7 First model

A residual self potential anomaly for an inclined dike model with K = 100 mV, z = 12 m, θ = 30°, w = 8 m, d = 5 m, and profile length = 200 m was produced. The study of the effect of the regional field, which is representing by a first-order polynomial, has been added to the residual self potential anomaly of the inclined dike to constitute the following composite (observed) self potential anomaly (Fig. 2a, g):

Fig. 2
figure 2

a A composite synthetic self potential anomaly generated using Eq. (9). b The moving average residual self potential anomalies for a composite anomaly in (a). c A noisy composite anomaly (10% noise added). d The moving average residual self potential anomalies for a noisy composite anomaly in (c). e A noisy composite anomaly (20% noise added). f The moving average residual self potential anomalies for a noisy composite anomaly in (e). g A sketch diagram for the buried 2D inclined dike. h The misfit between the observed and calculated anomalies in all cases

Full size image
$$T_{otal} \left( {x_{j} } \right) = 100\ln \left\{ {\frac{{\left[ {\left( {x_{j} - 5} \right) - 8\cos \left( {30^{ \circ } } \right)} \right]^{2} + \left[ {12 - 8\sin \left( {30^{ \circ } } \right)} \right]^{2} }}{{\left[ {\left( {x_{j} - 5} \right) + 8\cos \left( {30^{ \circ } } \right)} \right]^{2} + \left[ {12 + 8\sin \left( {30^{ \circ } } \right)} \right]^{2} }}} \right\} + 2x_{j} + 15 .$$
(9)

This anomaly exposed to the moving average method to exclude the effect of the regional field utilizing several window lengths (s = 2, 3, 4, 5, 6, 7, 8, 9, and 10 m). After that, the particle swarm method is applied to achieve the inclined dike parameters (K, z, θ, w, d) (Table 1). Table 1 shows the ranges of every parameter; the polarization parameter (K) is between 10 and 200 mV, the depth (z) is between 1 and 20 m, the inclination angle (θ) is between 5° and 85°, the half-width (w) is between 1 and 20 m, and the origin location of the buried body is between 1 and 10 m. Besides, Table 1 displays the estimated results for each parameter at every s-value, the average value (μ), uncertainty, percentage error (E), and the RMSE-value, which reveals the misfit amongst the observed and the calculated anomalies.

Table 1 Numerical results for the PSO-method application on the moving average residual self potential data using several s-values for an inclined dike model (K = 100 mV, z = 12 m, θ = 30°, w = 8 m, d = 5, and profile length = 200 m) and added a first-order regional background without, with a 10% and a 20% random noise
Full size table

The analysis of this self potential anomaly example was done in two stages as follow:

  1. 1.

    The first stage is considered the anomaly contains zero noise (free-noise case). In this case, the anomaly (Fig. 2a) is exposed to the moving average method utilizing the s-values mentioned above (Fig. 2b). After that, the residual moving average anomalies interpreted using the particle swarm algorithm to estimate the buried inclined dike parameters as mentioned in Table 1. The estimated results are in an outstanding agreement with the actual ones where the μ-values for each parameter (K, z, θ, w, d) are 100 mV, 12 m, 30°, 8 m, and 5 m, respectively. Besides, the RMSE-value and the misfit between the observed and the calculated anomalies is zero (Fig. 2h).

  2. 2.

    The second stage is considered the anomaly is tainted with various levels of noise (10% and 20%) to test the validity and stability of the suggested approach.

In case of adding a 10% random noise on the composite anomaly in Fig. 2a (Fig. 2c), the moving average method was used to eliminate the regional background in this field (Fig. 2d) using the same s-values mentioned above. In addition, it is interpreted by utilizing the particle swarm algorithm to assess the body parameters (Table 1). In Table 1, the μ-values for K, z, θ, w, and d are 96.2 ± 2.6 mV, 11.7 ± 0.3 m, 28.7 ± 1°, 7.7 ± 0.3, and 4.8 ± 0.2, the E-values are 3.8%, 2.6%, 4.4%, 4.3%, and 4.4%, respectively, and the RMSE-value equals 5.9 mV. Besides, the misfit is figured in Fig. 2h.

Moreover, we increased the level of noise to be 20% adding to the composite anomaly in Fig. 2a (Fig. 2e). Using the same procedures as above, the residual moving averages self potential anomalies are shown in Fig. 2f and the results are tabulated and demonstrated in Table 1. From this table, the estimated μ-values for K, z, θ, w, and d are 94.4 ± 8.3 mV, 11.6 ± 1 m, 28.3 ± 3.2°, 7.5 ± 0.7, and 4.7 ± 0.5, and the E-values are 5.6%, 3.1%, 5.7%, 6.5%, and 6.0%, respectively. The correlation between the observed and the calculated is estimated (the RMSE-value equals 9.4 mV). Also, the difference (residual) between them is drawn in Fig. 2h.

These achieved values for noise-free and noisy test cases for an inclined dike model expresses that the suggested combination methods between using the moving average method that eliminated the regional background and noise and the particle swarm optimization method, which estimate the model parameters are steady and robust.

1.8 Second model

This examination shows the influence of nearby intrusions from different sources. A self potential anomaly for an inclined dike model with K = 50 mV, z = 8 m, θ = 40°, w = 5 m, d = 3 m, and profile length = 200 m and an interfered structures signified by spherical with K = 10000 mV × m2, z = 16 m, θ = 55°, d = -60 m and horizontal cylindrical with K = 1000 mV × m, z = 12 m, θ = 25°, d = 40 m models (Fig. 3a and 3e) have been created using the following form:

Fig. 3
figure 3

a A composite synthetic self potential anomaly generated using Eq. (10). b The moving average residual self potential anomalies for a composite anomaly in (a). c A noisy composite anomaly (10% noise added). d The moving average residual self potential anomalies for a noisy composite anomaly in (c). e A sketch diagram for the buried 2D inclined dike. f The misfit between the observed and calculated anomalies in all cases

Full size image
$$\begin{aligned} T_{otal} \left( {x_{j} } \right) &= 50\ln \left\{ {\frac{{\left[ {\left( {x_{j} - 3} \right) - 5\cos \left( {40^{{^\circ }} } \right)} \right]^{2} + \left[ {8 - 5\sin \left( {40^{{^\circ }} } \right)} \right]^{2} }}{{\left[ {\left( {x_{j} - 3} \right) + 5\cos \left( {40^{{^\circ }} } \right)} \right]^{2} + \left[ {8 + 5\sin \left( {40^{{^\circ }} } \right)} \right]^{2} }}} \right\} \\ & \quad + 10000\frac{{\left( {x_{j} + 60} \right)\cos \left( {55^{{^\circ }} } \right) - 16\sin \left( {55^{{^\circ }} } \right)}}{{\left[ {\left( {x_{j} + 60} \right)^{2} + \left( {16} \right)^{2} } \right]^{1.5} }} \\ & \quad + 1000\frac{{\left( {x_{j} - 40} \right)\cos \left( {25^{{^\circ }} } \right) - 12\sin \left( {25^{{^\circ }} } \right)}}{{\left[ {\left( {x_{j} - 40} \right)^{2} + \left( {12} \right)^{2} } \right]}} . \\ \end{aligned}$$
(10)

The moving average method was adopted for this composite anomaly applying several s-value (s = 2, 3, 4, 5, 6, 7, 8, 9, and 10 m) to revenue the moving average residual self potential anomalies (Fig. 3b). Then, the particle swarm method is utilized to estimate the body parameters (K, z, θ, w, d) (Table 2). Table 2 reveals that the errors (E) in all inverted model parameters are zero and the RMSE-value is also zero. In other words, the misfit between the observed and the calculated is shown in Fig. 3f and is completely identically.

Table 2 Numerical results for the PSO-method application on the moving average residual self potential data using several s-values value for an inclined dike model (K = 50 mV, z = 8 m, θ = 40°, w = 5 m, d = 3, and profile length = 200 m) and effected by neighboring structures without and with a 10% random noise
Full size table

We introduced a random noise of 10% to the composite self potential (Fig. 3c) to test the practicability of this approach. For the similar s-values (s = 2, 3, 4, 5, 6, 7, 8, 9, and 10 m), the moving average residual self potential anomalies are presented in Fig. 3d. By utilizing the particle swarm algorithm for the noisy data, the outcomes of the source parameters (K, z, θ, w, d) are presented (Table 2). According to the inspection of these results, the μ-value for K, z, θ, w, and d are 48.7 ± 3 mV, 7.8 ± 0.4 m, 38.1 ± 2.8°, 4.7 ± 0.3 m, and 2.8 ± 0.3 m, the E-values are 2.7%, 2.8%, 4.7%, 6.2%, and 8.1%, correspondingly, and the RMSE-value is 3.9 mV. The misfit between observed and calculated anomalies is demonstrated in Fig. 3f.

These results express that the suggested approach is capable of catching the accurate parameters with acceptable error for the observed self potential data even it’s affected by neighboring structures.

1.9 Field examples

After successful application of the using of combination between the moving average method and the particle swarm optimization method in retrieving the actual model parameters for the inclined dike, this suggested approach were examined again utilizing two field self potential data for a graphite ore body from the southern Bavarian woods, Germany and a Kalava fault zone, which include a sulfide deposits, India.

1.10 The Bavarian woods self potential anomalous, Germany

Meiser (1962) described the area under investigation (the Bavarian woods). The Bavarian woods graphite ores are found in a Hercynian gneissic complex. This deposit is conformably sandwiched amongst the paragneiss and the crystalline limestone of the identical period. Usually, the deposit forms strata, which are nominated as bituminous sediments of probable Precambrian age. The graphite mineral deposits are not pure carbon and frequently happens in flakes in metamorphosed rocks enriching with carbon, nevertheless, it can also be initiated in veins and pegmatites. Anywhere huge deposits are found, it is excavated and utilized as an industrial lubricant and for ‘lead’ in pencils. The crystallinity relies on the temperature of the formation and the grade of metamorphism.

Overall, the graphite veins are sandwiched amongst the limestone and the gneisses, which form a parallel sequence of lenses and are very inconstant in thickness. The surface topography has a difference in altitude of about 130 m and the measured anomaly was smoothed by 0.5 mV/m. The data were acquired at a 10-m interval between the measuring points. Generally, the individual lenses, in any case, are frequently non-autonomous bodies; they are associated with one another in their strike and plunge. The outcome is the presence of a store with the graphite somewhat cogged and incompletely lump out (thickened) as needs be. As often as possible they may likewise be punctured by the wall-rock.

The self potential anomaly profile with length 525 m was acquired over a graphite ore body from the southern Bavarian woods, Germany (Meiser 1962) and revealed in Fig. 4a. A sample interval of 10.41 m was utilized to this self potential profile. The interpretation procedure revealed above is again applied for this data. For several s-value (s = 20.82, 31.23, 41.64, 52.03, 62.46, 72.87, 83.28, 93.69, 104.1, 114.51, and 124.92 m), the moving average residual self potential anomalies was created (Fig. 4b). The particle swarm method was utilized for these anomalies to assess the target parameters (K, z, θ, w, d) (Table 3). The inferred outcomes in Table 3 represents the fitting among the observed and calculated, i.e., the μ-value for K, z, θ, w, and d are 258.5 ± 1.6 mV, 51.6 ± 0.9 m, 134.3 ± 1°, 27.7 ± 0.9 m, and 260.2 ± 1 m, respectively, and the RMSE-value equals 9.8 mV (Fig. 4a and 4c). The misfit between the observed and calculated anomalies are presented in Fig. 4d.

Fig. 4
figure 4

a A self potential anomaly profile collected for the southern Bavarian woods, Germany (after Meiser 1962). b The moving average residual self potential anomalies of the anomaly in (a). c A sketch diagram for the buried model resulted from the suggested approach. d The misfit between the observed and calculated anomalies

Full size image
Table 3 Numerical results for the PSO-method application on the moving average residual self potential data using several s-values value for the Bavarian wood anomalous, Germany
Full size table

The expected parameters of the body by applying the particle swarm method convolved with the moving average method have a good covenant with the outcomes accomplished from bore-hole information and further inversion methods (Table 4). Table 4 shows the comparison results of the suggested method with other published approaches (Meiser 1962; Abdelrahman et al. 2009b; Sharma and Biswas 2013; Mehanee 2014; Di Maio et al. 2016).

Table 4 The comparative interpreted model parameters for the Bavarian wood anomalous, Germany
Full size table

In more detail, the Bavarian woods self potential anomaly interpreted by Abdelrahman et al. (2009b) by semi-automatic method to decide the depth (z = 51.9 m) and shape (horizontal cylinder), like in Mehanee (2014) applying Tikhonov regularization and the conjugate gradient method to estimate the model parameters, especially the depth (46 m) for a horizontal cylinder shape. In contrast, Sharma and Biswas (2013) applying the very fast simulated-annealing optimization for a 2D inclined sheet to evaluate all the model sheet parameters (for example, z = 50.9 m and d = 20.5 m because they used a profile length from − 300 to 300 m). Also, Di Maio et al. (2016) used a Genetic-Price hybrid algorithm for identifying the source parameters (i.e. z = 49 m and d = 278 m because the profile used is between 0 and 520 m like in the proposed method). Finally, the suggested method gives a more stable and accurate result because it has the minimum RMSE (9.8 mV) comparing to other published literature because of applying the moving average method, which has the ability to remove the effect of regional background and noise.

1.11 Kalava fault self potential anomalous, India

The complex structure of the Cuddapah Basin has been taken into consideration in economic interest to discover. The date of formation is back to the Paleoproterozoic, which contains interaction with sediment formations with mafic magmatism. The Gani-Kalava belt (GKF) involves the Vempalle limestone and the Pulivendla quartzite of the lower Cuddapah super-group has superimposed by Tadapatri shales of the Kurnool-group (Fig. 5a upper panel). There is a noticeable angular unconformity among the sub-Cuddappahs and the Tadapatri shales. The Cuddapahs and the Kurnool in the area are imposed by sills and sheets of the metagabbro and the metadolerite. Mineralization is restricted to WNW-ESE-trending shear faults taking place in the Tadapatri shales (Chetty 2011; Saha and Tripathy, 2012).

Fig. 5
figure 5

a Upper panel: the geologic map of the Cuddapah Basin area including the Kalava fault zone, India (Saha and Tripathy 2012). Lower panel: A self potential anomaly profile collected for the Kalaval fault zone, the Cuddapah Basin, India (after Tlas and Asfahani 2008). b The moving average residual self potential anomalies of the anomaly in (a) lower panel. c A sketch diagram for the buried model resulted from the suggested approach. d The misfit between the observed and calculated anomalies

Full size image

A self potential profile was collected across the Kalava fault area to infer the mineralization zone, Cuddapah Basin, India (Atchuta Rao et al. 1982; Narayan et al. 1982; Tlas and Asfahani 2008) with 255 m length and digitized with an interim of 6.375 m (Fig. 5a lower panel).

This anomaly exposed to the moving average method to eliminate the effect of regional background utilizing several window lengths (s = 12.75, 19.125, 25.5, 31.875, 38.25, 44.625, 51, 57.375, and 63.75 m) (Fig. 5b). After that, the particle swarm optimization method is applied to achieve the inclined dike parameters (K, z, θ, w, d) (Table 5). Table 5 shows the ranges of every parameter and the estimated results for each parameter at every s-value, the average value (μ), uncertainty, and the RMSE-value, which demonstrates the misfit amongst the observed and the calculated anomalies. According to this table, the estimated results are K = 71.1 ± 0.9 mV, z = 34.4 ± 1.2 m, θ = 103.3 ± 1.4°, w = 13.1 ± 0.7 m, d = 128.4 ± 1.6, and the RMSE-value equals 14.3 mV. These results agree very well with those published in literature (Table 6). The forward model due to the estimated parameters is drawn in Fig. 5a (lower panel) and a sketch diagram showing the 2D inclined dike (Fig. 5c) to show the misfit between them (Fig. 5d).

Table 5 Numerical results for the PSO-method application on the moving average residual self potential data using several s-values value for the Kalava fault anomalous, India
Full size table
Table 6 The comparative interpreted model parameters for the Kalava fault anomalous, India
Full size table

Table 6 shows that this anomaly is interpreted for different structures such as a semi-infinite vertical cylinder (Mehanee 2014 that calculated the depth to the top, i.e. z = 5 m) and an inclined sheet-like structure applying the modular neural network (El-Kaliouby and Al-Garni 2009 that used a profile length between − 20 to 20 m), the adaptive simulated annealing (Tlas and Asfahani 2008 that used a profile length between − 20 to 20 m), and the Fourier transform (Atchuta Rao et al. 1982 that also utilized a profile length of − 2 to 20 m). Lastly, the suggested method used the whole profile length from 0 to 255 m as mentioned in all published literatures. So, the results of this method are more consistent and robust because the observed data processed through the moving average method to eliminate the regional background effect while the other methods do not mention to this effect.

Finally, the use of the suggested method has fully successfully interpreted the real data due to an inclined dike for mineral exploration in Germany and India that indicate that this method can be extended to investigate more regions around the world.

2 Conclusions

An accomplished particle swarm optimization method is hired for inferring the moving average residual self potential anomalies utilizing various window lengths. The moving average method has a capability to remove the effect of regional background from the observed data. The present approach reveals that all model parameters of the inclined dike (the polarization parameter, the depth, the inclination angle, the width, and the location of the source) together and revenues respectable results without any ambiguity in the parameters. The ability of this approach has been fruitfully verified, recognized and confirmed utilizing two synthetic examinations and two real cases for mineral investigations. The estimated parameters for the real data are initiated to be in admirable covenant with the other approaches as well as the bore-holes information. From the results of the suggested method, the optimum-fit model parameters for the inclined dike reflects the consistent and robust of this method. So, the suggested method can be further extended to interpret gravity and magnetic data for mining and ore exploration.