GDE4: The Generalized Differential Evolution with Ordered Mutation

Abstract

Differential Evolution (DE) is one the most popular evolutionary algorithm (EA) to handle optimization problems with an efficient performance. Due to its success and popularity, it has been utilized by researchers in multi-objective optimization, so there are various multi-objective versions of DE. Similar to other population-based algorithms, DE uses a mutation operator to produce the new individual for the next generation. Although the original version of DE randomly selects three candidate solutions from the population without considering any ordering in its mutation scheme, this paper proposes ordering strategy of individuals which influences the performance of the algorithm. An enhanced version (GDE4) of Generalized Differential Evolution (GDE) with ordered mutation operator is designed. GDE is a multi-objective evolutionary algorithm based on DE. The proposed approach orders candidate individuals using popular ranking measures of multi-objective optimization problems to utilize the ordered solutions in mutation operator. The best one of three randomly selected solutions is considered as the parent, and two others are applied as second and third candidate solutions in DE mutation, respectively. Unlike most of the multi-objective methods which consider multi-objectiveness during the selection process, the proposed method improves the performance using a modification on the genetic operator. The standard benchmark functions and measures are adopted to evaluate the performance of GDE4. The conducted experiments are on 5, 10, and 15 objectives for the utilized benchmark set. The comparison results reveal that GDE4 algorithm outperforms GDE3, the last version of GDE.

1 Introduction

Since many real-world problems involve more than one objective, solving multi-objective optimization problems is considered as an important subject in many fields of science and engineering. The main issue that makes such problems harder than single objective problems is that how it is possible to compare solutions with two or more conflicting objectives. Evolutionary computation (EC) as a powerful method has been used to solve multi-objective optimization problems. There are a wide variety of single objective evolutionary algorithms (EA’s) which have been adapted for multi-objective schemes [1, 2]. Differential evolution (DE) is one of them which its simplicity offers a great characteristic to apply it in single- and multi-objective optimization. Generalized differential evolution (GDE) [3] is a multi-objective version of DE. There are some research works to improve GDE to be more successful in the optimization. The third version (GDE3) [4] was proposed to handle all types of multi-objective optimization problems including non-constrained and constrained ones.

Creation of a new individual in population-based algorithms, is one of the most important steps to make the generation more progressive. So selecting parents can influence producing better population and increasing elitism in the next generations. DE mutation which uses three randomly selected individuals from the population to create a new offspring. For single objective DE, there are some designed schemes of ordered mutation based on objective function value which have shown significant improvement in obtained results [5,6,7].

GDE3 also uses DE mutation operator, so ordered selection can improve the results of multi-objective optimization. The difficulty of ordered selection in multi-objective optimization case compared to the single objective one is the defining strategy of ranking of three selected individuals. Since there are two or more conflicting objective values, decision making in which candidate solutions are better, is sophisticated. This paper presents a version of GDE3 with ordered mutation (GDE4) for multi-objective optimization problems. Three selected candidate solutions are sorted based on two known measures, non-dominating sorting and crowding distance [8]. The best one is used as a base vector, and two other ranked candidate solutions are considered as the second and third individuals in DE mutation of GDE3. Since optimality doesn’t have a straightforward definition, most of the multi-objective algorithms consider multi-objectiveness during their selection process. They concentrate on the proposing a method to rank candidate solutions while the proposed method improves multi-objectiveness in generative operator. Experiments show an enhancement of results in GDE4 compared to GDE3 in standard benchmarks. The organization of the rest of this paper is as follows. Section 2 gives a brief background review of GDE3 algorithms. Section 3 describes the proposed scheme in detail. Section 4 presents a simple algorithm and the experimental results to support discussion on the proposed scheme. Finally, the paper is concluded in Sect. 5.

2 Background Review

Many real-world optimization problems have more than one conflicting objectives to be optimized. The definition of the optimality is not as simple as the single-objective optimization. Therefore it is necessary to make a tradeoff between objective values. There are some well-known concepts to compare two candidate solutions in the multi-objective problem space. Since this paper utilizes non-dominated sorting and crowding distance to order candidate solutions for DE mutation scheme, in this section, we define these measures in detail. A minimization multi-objective optimization problem is defined as follows:

$$\begin{aligned} Minimize \ F(x)=[f_{1}(x),f_{2}(x),...,f_{M}(x)] \quad L_{i}\le x_{i}\le U_{i}, i=1,2,...,d \end{aligned}$$

(1)

where M is the number of objectives, d is the number of variables (dimension) of solution vector, $x_{i}$ is in interval $[L_{i},U_{i}]$. $f_{i}$ represent the objective function which should be minimized.

If $x=(x_{1},x_{2},...,x_{d})$ and $\acute{x}=(\acute{x}_{1},\acute{x}_{2},...,\acute{x}_{d})$ are two vectors in search space, x dominates $\acute{x}$ ($x\succ \acute{x}$) if and only if:

$$\begin{aligned} \forall i\in {\{1,2,...,d\}}, f(x_{i})\le f(\acute{x_{i}}) \wedge \exists i \in {\{1,2,...,d\}}: f(x_{i})<f(\acute{x_{i}}) \end{aligned}$$

(2)

It defines optimality for solutions in objective space. Candidate solution x is better than $\acute{x}$ if it is not bigger than $\acute{x}$ in any of objectives and at least it has a smaller value in one of the objectives. All solutions that are not dominated using none of other solutions in the population called non-dominated solutions and they create the Pareto front set.

Non-dominated sorting is an algorithm to rank obtained solutions to different levels in the processing of multi-objective optimization. All non-dominated solutions are in the first rank and then the second rank is made of solutions which are non-dominated by removing the first rank from the population. This process is repeated until all solutions are ranked using this concept.

Crowding distance is another measure which usually completes comparison of solutions along with non-dominating sorting. It is a measure to compute the diversity of obtained solutions by calculating the distance between adjacent solutions. In the beginning, the set of solutions in the same rank are sorted according to each objective function value in ascending order. To get crowding distance, the difference between neighbors objective values of each solution is computed. This computation is done for all objectives, then the sum of individual distance values corresponding to each objective is considered as overall crowding distance. The bigger value of crowding distance for a vector in population shows less diversity around that vector.

2.1 Generalized Differential Evolution

The DE is an evolutionary algorithm originally for solving continuous optimization problems which improves initial population using the crossover and mutation operations. Creation of new generation is done by a mutation and a crossover operator. The mutation operator for a gene, j, is defined as follows:

$$\begin{aligned} v_{j,i}=x_{j,i_{1}}+F\,.\,(x_{j,i_{2}}-x_{j,i_{3}}) \end{aligned}$$

(3)

Applying this operator generates a new D dimensional vector, ${v_{i}}$, using three randomly selected individuals, $x_{j,i_{1}}$, $x_{j,i_{2}}$, and $x_{j,i_{2}}$ from the current population. Parameter F, mutation factor, scales difference between two vectors. The crossover operator changes some or all of the genes of parent solution based on Crossover Rate (CR). Similar to other population-based algorithms, the single objective version of DE starts with a uniform randomly generated population. Next generation is created using mentioned mutation and crossover operations; then best individual (between parent and new individual) is selected based on their objective values; which is called a greedy selection. It iterates until meeting stopping criterion such as a predefined number of generations.

There are also several variants of DE algorithms for multi-objective optimization. The first version of Generalized Differential Evolution (GDE) [3] changed the DE selection mechanism for producing the next generation. The idea in the selection was based on constraint-domination. The new vector is selected if it dominates the old vector. GDE2 [9], the next version of multi-objective DE algorithm, added the crowding distance measure to its selection scheme. If both vectors are non-dominating each other, the vector with a higher crowding distance will be selected.

The third version of GDE (GDE3) extends DE algorithm for multi-objective optimization problems with M objectives and K constraints. DE operators are applied using three randomly selected vectors to produce an offspring per parent in each generation. The selection strategy is similar to the GDE2 except in two parts: 1. Applying constraints during selection process. 2. The non-dominating case of two candidate solutions. Selection rules in GDE3 are as follows: when old and new vectors are infeasible solutions, each solution that dominates other in constraint violation space is selected. In the case that one of them is feasible vector, feasible vector is selected. If both vectors are feasible, then one is selected for the next generation that dominates other. In non-dominating case, both vectors are selected. Therefore, the size of the population generated may be larger than the population of the previous generation. If this is the case, it is then decreased back to the original size. Selection strategy for this step is similar to NSGA-II algorithm [10]; it sorts individuals in the population, based on the non-dominated sorting algorithm and crowding distance measure. Similar to other population-based multi-objective algorithms, the selected individuals go to the next generation to continue optimization processing. The common point about all of these versions is the utilizing randomly selected individuals to produce a new vector using the main mutation operator of DE which will be modified in our proposed algorithm in this paper. So, even the mutation scheme would be tailored to support multi-objective optimization strategy.

2.2 Existing Single Objective Differential Evolution with Ordered Mutation

In some versions of DE algorithm, the ordering of the candidate solutions is utilized for the mutation operator to enhance the performance of DE algorithm for solving the single objective optimization problems. A new scheme of mutation operator, DE/2-Opt, was defined in [5] which sorts two first candidate solutions in the mutation operator according (for minimization case) to their objective function value in ascending order to place as $x_{i_1}$ and $x_{i_2}$ in the mutation operator as:

‘DE/2-Opt/1’:

$$\begin{aligned} v_i= {\left\{ \begin{array}{ll} x_{i_1} + F\,.\,(x_{i_2} - x_{i_3}) &{} \text{ if } \quad f(x_{i_1})<=f(x_{i_2})\\ x_{i_2} + F\,.\,(x_{i_1} - x_{i_3}) &{} \text{ if } \quad f(x_{i_2})<f(x_{i_1}) \end{array}\right. } \end{aligned}$$

(4)

‘DE/2-Opt/2’:

$$\begin{aligned} v_i= {\left\{ \begin{array}{ll} x_{i_1} + F\,.\,(x_{i_2} - x_{i_3}+x_{i_4} - x_{i_5}) &{} \text{ if } \quad f(x_{i_1})<=f(x_{i_2})\\ x_{i_2} + F\,.\,(x_{i_1}- x_{i_3}+x_{i_4}-x_{i_5}) &{} \text{ if } \quad f(x_{i_2})<f(x_{i_1}) \end{array}\right. } \end{aligned}$$

(5)

In [6], the winner mutation (DE/win) was proposed which uses the best candidate of three selected random candidate solutions for the base vector as follows:

‘DE/win/1’:

$$\begin{aligned} v_i= {\left\{ \begin{array}{ll} x_{i_1} + F\,.\,(x_{i_2} - x_{i_3}) &{} \text{ if } \quad f(x_{i_1})<={f(x_{i_2}),f(x_{i_3})}\\ x_{i_2} + F\,.\,(x_{i_1} - x_{i_3}) &{} \text{ if } \quad f(x_{i_2})<{f(x_{i_1}),f(x_{i_3})}\\ x_{i_3} + F\,.\,(x_{i_2} - x_{i_1}) &{} \text{ if } \quad f(x_{i_3})<{f(x_{i_2}),f(x_{i_1})} \end{array}\right. } \end{aligned}$$

(6)

In [7], a modified DE algorithm with the order mutation scheme was proposed which three selected random solutions are sorted in ascending order according to their fitness values for placing as vectors ($x_{i_1}$, $x_{i_2}$, and $x_{i_3}$) in the mutation operator.

‘DE/order/1’:

$$\begin{aligned} v_i = x_{i_1} + F\,.\,(x_{i_2} - x_{i_3}) s.t.\,\,\, f(x_{i_1})<=f(x_{i_2})<=f(x_{i_3}) \end{aligned}$$

(7)

Where f(x) indicates the objective function. This method outperforms previous mentioned DE schemes.

3 Proposed Algorithm: The Generalized Differential Evolution with the Ordered Mutation (GDE4)

The proposed enhanced version of GDE3 method has the same components of GDE3 method except for the mutation operator in the DE algorithm. In this paper, a new mutation scheme is proposed according to a defined order for the candidate solutions involved in the mutation of the DE algorithm. GDE3 uses the DE/rand/1/bin method to solve problems with M objectives and K constraints. The basic mutation, in the classical DE (DE/rand/1/bin) generates the mutant vector as a linear combination of three selected individual candidate solutions from the current population as follows:

$$\begin{aligned} v_i = x_{i_1} + F\,.\,(x_{i_2} - x_{i_3}) \end{aligned}$$

(8)

Where $i_1$, $i_2$, $i_3$ are different random integer numbers within [1, NP] and NP is the population size. In [7], an ordered mutation scheme was proposed to improve the performance of DE algorithm and we change this mutation scheme by defining a new order of the randomly selected candidate solutions for the problems with M objectives. In the GDE4, we propose an order mutation scheme which uses non-dominance and crowding distance measures to sort three different random candidate solutions to set as vectors in the mutation scheme. The sorted candidate solutions can be called as the best ($x_b$), the second best ($x_{sb}$), and the worst candidate ($x_w$) solutions.

In the following, we explain how the three randomly selected candidate solutions are sorted. First, all candidate solutions are sorted by non-dominated sorting method [10] and they are associated with their corresponding non-dominated ranks ($Rank_{d}$) obtained from non-dominated sorting. Random candidate solutions can be faced with four possible cases based on their non-dominance ranks:

• 1. In the first case, all three candidate solutions are in different Pareto fronts; therefore, they are set to $x_b$, $x_{sb}$, and $x_w$ to their non-dominated ranks. The ordered mutation scheme (DE / order / 1) is defined as follows: ‘DE/order/1’:

  $$\begin{aligned} \begin{array}{c} v_i= x_{i_b} + F\,.\,(x_{i_{sb}} - x_{i_w}) \\ s.t. \,\, Rank_{d}(x_{i_b})<Rank_{d}(x_{i_{sb}})<Rank_{d}(x_{i_w}) \end{array} \end{aligned}$$

• 2. In this case, two candidate solutions are in the same Pareto front, so we compute crowding distance (CD) measure to sort these solutions. The ordered mutation scheme (DE / order / 1) is defined as two possible cases:

  • (a) ‘DE/order/1’:

    $$\begin{aligned} \begin{array}{c} v_i = x_{i_b} + F\,.\,(x_{i_{sb}} - x_{i_w}) \\ s.t. \,\, Rank_{d}(x_{i_b})=Rank_{d}(x_{i_{sb}}) <Rank_{d}(x_{i_w})\\ \,\, CD(x_{i_b})>CD(x_{i_{sb}}) \end{array} \end{aligned}$$

  • (b) ‘DE/order/1’:

    $$\begin{aligned} \begin{array}{c} v_i = x_{i_b} + F\,.\,(x_{i_{sb}} - x_{i_w}) \\ s.t.\,\, Rank_{d}(x_{i_b})< Rank_{d}(x_{i_w})=Rank_{d}(x_{i_{sb}})\\ \, and \, CD(x_{i_{sb}})>CD(x_{i_w}) \end{array} \end{aligned}$$

• 3. If all three random candidate solutions are in the same Pareto front, they are sorted based on their crowding distance (CD) to place in the mutation scheme. The ordered mutation scheme (DE / order / 1) is defined as follows: ‘DE/order/1’:

  $$\begin{aligned} \begin{array}{c} v_i = x_{i_b} + F\,.\,(x_{i_{sb}} - x_{i_w}) \\ s.t. \,\, CD(x_{i_b})>CD(x_{i_{sb}})>CD(x_{i_w}) \end{array} \end{aligned}$$

The proposed method uses the order mutation scheme for DE algorithm in GDE3, and other components remain untouched. Generalized Differential Evolution with the ordered mutation (GDE4) suggests that placing the best solution of three selected candidate solutions according to two measures, non-dominance and crowding distance, as the base vector causes to generate more promising trial solutions. Also, we use the worst candidate solution of three candidate solutions as the third vector in the mutation which causes the new trial candidate solution to get away from the worst candidate and move toward the second best candidate solution.

Fig. 1.

An example of variable and objective spaces for ordered DE mutation.

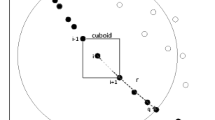
Figure 1 presents variable and objective spaces in a case of ordered mutation and clarifies the benefits of this strategy in creating a promising new solution. As it is shown, for a parent solution, $x_{i}$, three randomly selected candidate solutions are ordered based on the proposed strategy in GDE4 algorithm. In this case, the first candidate solution, $x_{i1}$ is in the first rank of non-dominated sorting, so it is considered as the base vector (best). $x_{i2}$ and $x_{i3}$ are in the same rank therefore they ordered according to crowding distance. $x_{i2}$ has a bigger crowding distance comparing to $x_{i3}$, so they are ordered as second (better) and third vector (worst) in mutation operator. Right sub-figure in Fig. 1 shows the operation of mutation on selected vectors. $F\,.\,(x_{i2}-x_{i3})$ leads new vector moves toward to better solution and gets away from the worst while F is considered 1. In this example, better solution is one with a bigger crowding distance. Moving toward this solution causes the creation of a vector in a less crowded region to have a well-distributed Pareto front. Then summation operation on $x_{i1}$ and $F\,.\,(x_{i2}-x_{i3})$ causes the final resulted vector goes toward the best candidate solution. So it is expected to generate a more promising candidate solution.

Table 1. Main properties of the test functions [11].

4 Experiment

GDE4 is evaluated with a set of test problems and compared to GDE3 regarding multi-objective evaluation measures. The same settings are considered for two algorithms. The mutation amplification factor (F) and crossover rate (CR) are set to 0.5 and 1, respectively. For population size and maximum evaluation number, value 100 and 3000$\,*\,D$ are considered. To evaluate the performance of the proposed algorithm, we use the inverse generational distance (IGD) metric [12,13,14], which measures the convergence and the diversity of the obtained Pareto-optimal solutions at the same time. The IGD metric measures the distances between each solution composing the Pareto-optimal front and the obtained solution. The IGD metric is defined as follow:

$$\begin{aligned} IGD=\frac{\sqrt{\sum }_{i=1}^{n} d_i}{n} \end{aligned}$$

(9)

Where n is the number of solutions in the Pareto-optimal front, and $d_i$ is the Euclidean distance (measured in the objective space) between each point of the Pareto-optimal front (reference Pareto front) and the nearest member of obtained solution. Also, all algorithms were executed 51 times independently, and the best, the worst, the median, and the average results of each algorithm are reported. Additionally, the Wilcoxon’s signed rank statistical test with a confidence interval of 95% is conducted to evaluate the statistical significance of the obtained results. We have utilized GDE3 algorithm in the MATLAB based MOEA platform (PlatEMO) [15] and it was modified by changing its mutation operator to the order mutation as explained for the GDE4.

In the experiments, fifteen test problems are used to evaluate the performance of the proposed algorithm from the MaF test suite which is designed for the assessment of MOEAs in the CEC 2017 competition on evolutionary many-objective optimization [11]. These benchmark functions have many properties to resemble various real-world scenarios such as multi-modal, disconnected, degenerate, and/or nonseparable, and having an irregular Pareto front shape, a complex Pareto set or a large number of decision variables. The main properties of functions are detailed in Table 1. Experiments are performed on 5, 10 and 15 objective functions.

Figure 2 illustrates the distribution of obtained solutions by GDE4 and GDE3 for MFa11 test problem in different number of objectives. The diagrams are resulted based on median value of IGD. As the figure shows both algorithms are able to find distributed solutions with same performance when the number of objectives is 5. However, as the number of objectives of the test problem increases, GDE4 performs significantly better to find well-distributed solutions. The difference between diversity of obtained solutions using GDE3 and GFE4 is more remarkable with 15 objectives.

The results of IGD metric for two comparing methods are summarized in Table 2. Better mean of IGDs are highlighted based on Wilcoxon’s signed rank statistical test. It can be seen from the tables, on functions with five objectives, GDE4 can achieve the better results than GDE3 on seven functions while GDE3 is better than GDE4 on five functions, and they are similar results on three functions. On functions with ten objectives, GDE4 can achieve the better results than GDE3 on ten functions while GDE3 can obtain better results than GDE4 on three functions; and they are similar results on two functions. On functions with fifteen objectives, GDE4 outperforms GDE3 on nine functions while GDE3 can obtain better results than GDE4 on five functions; and they are similar results on one functions. Results show that by increasing the number of objectives in the many-objective functions, GDE4 preforms significantly better than GDE3 regarding statistical test. Furthermore, comparing results according to median and best IGD confirms better performance of GDE4. Median IGDs of GDE4 are better in 9, 11 and 9 out of 15 functions for 5, 10, and 15 objective problems respectively comparing to GDE3.

According to best IGDs, GDE4 achieve better results in 7, 9, and 8 out of 15 functions for 5, 10, and 15 objective problems respectively. So the order of solutions in DE mutation operator improves the search processing in many-objective optimization problems using generating better (non-dominated) solutions. The generated solution is expected to create in place close to the best solution in term of the rank of non-dominated sorting and the less crowded region. As another advantage of the proposed method, it can be clarified that this improvement is achieved without any extra objective function evaluation. The method needs only ordering of three existing solutions, so there isn’t overhead computation for applying mutation comparing to previous version.

Fig. 2.

Comparison of obtained Pareto fronts by GDE3 and GDE4 for MFa11 test problem in different dimensions.

Table 2. Results of GDE3 and GDE4 algorithms for the functions $MaF_{1}$-$MaF_{15}$. The highlighted entries are significantly better.

5 Conclusion Remarks

This paper proposes GDE4, a new version of Generalized Differential Evolution algorithm for multi-objective optimization problems. The ordering of randomly selected candidate solutions for DE mutation operator is investigated. Method sorts three solutions at first, based on non-dominated sorting approach and then crowding distance measure to utilize as first, second and best solutions in DE mutation to generate a new individual exhibiting better fitness. DE summation and subtraction operators cause moving of new solution toward the first and second vectors and getting away from the third vector. So ordered vectors has inherited the quality of best and better candidate solutions. The performance of the method is evaluated using standard benchmark functions of CEC 2017 competition on evolutionary many-objective optimization problems. The results indicate that the proposed algorithm outperforms GDE3 which puts solutions in mutation operator randomly in most test problems. In the future, it is intended to investigate new strategies to order candidate solutions, such as the distance of each vector from an ideal point.