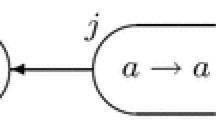Asynchronous Spiking Neural P Systems with Structural Plasticity

Abstract

Spiking neural P (in short, SNP) systems are computing devices inspired by biological spiking neurons. In this work we consider SNP systems with structural plasticity (in short, SNPSP systems) working in the asynchronous (in short, asyn mode). SNPSP systems represent a class of SNP systems that have dynamic synapses, i.e. neurons can use plasticity rules to create or remove synapses. We prove that for asyn mode, bounded SNPSP systems (where any neuron produces at most one spike each step) are not universal, while unbounded SNPSP systems with weighted synapses (a weight associated with each synapse allows a neuron to produce more than one spike each step) are universal. The latter systems are similar to SNP systems with extended rules in asyn mode (known to be universal) while the former are similar to SNP systems with standard rules only in asyn mode (conjectured not to be universal). Our results thus provide support to the conjecture of the still open problem.

1 Introduction

Spiking neural P systems (in short, SNP systems) are parallel, distributed, and nondeterministic devices introduced into the area of membrane computing in [7]. Neurons are often drawn as ovals, and they process only one type of object, the spike signal represented by a. Synapses between neurons are the arcs between ovals: neurons are then placed on the vertices of a directed graph. Since their introduction, several lines of investigations have been produced, e.g. (non)deterministic computing power in [7, 13]; language generation in [4]; function computing devices in [11]; solving computationally hard problems in [9]. Many neuroscience inspirations have also been included for computing use, producing several variants (to which the previous investigation lines are also applied), e.g. use of weighted synapses [15], neuron division and budding [9], the use of astrocytes [10]. Furthermore, many restrictions have been applied to SNP systems (and variants), e.g. asynchronous SNP systems as in [3, 6] and [14], and sequential SNP systems as in [6].

In this work the variant we consider are SNP systems with structural plasticity, in short, SNPSP systems. SNPSP systems were first introduced in [1], then extended and improved in [2]. The biological motivation for SNPSP systems is structural plasticity, one form of neural plasticity, and distinct from the more common functional (Hebbian) plasticity. SNPSP systems represent a class of SNP systems using plasticity rules: synapses can be created or deleted so the synapse graph is dynamic. The restriction we apply to SNPSP systems is asynchronous operation: imposing synchronization on biological functions is sometimes “too much”, i.e. not alway realistic. Hence, the asynchronous mode of operation is interesting to consider. Such restriction is also interesting mathematically, and we refer the readers again to [3, 6] and [14] for further details.

In this work we prove that (i) asynchronous bounded (i.e. there exists a bound on the number of stored spikes in any neuron) SNPSP systems are not universal, (ii) asynchronous weighted (i.e. a positive integer weight is associated with each synapse) SNPSP systems, even under a normal form (provided below), are universal. The open problem in [3] whether asynchronous bounded SNP systems with standard rules are universal is conjectured to be false. Also, asynchronous SNP systems with extended rules are known to be universal [5]. Our results provide some support to the conjecture, since neurons in SNPSP systems produce at most one spike each step (similar to standard rules) while synapses with weights function similar to extended rules (more than one spike can be produced each step). This work is organized as follows: Section 2 provides preliminaries for our results; syntax and semantics of SNPSP systems are given in Sect. 3; our (non)universality results are given in Sect. 4. Lastly, we provide final remarks and further directions in Sect. 5.

2 Preliminaries

It is assumed that the readers are familiar with the basics of membrane computing (a good introduction is [12] with recent results and information in the P systems webpage (http://ppage.psystems.eu/) and a recent handbook [13] ) and formal language theory (available in many monographs). We only briefly mention notions and notations which will be useful throughout the paper.

We denote the set of positive integers as $\mathbb {N} = \{1,2, \ldots \}$. Let V be an alphabet, $V^*$ is the set of all finite strings over V with respect to concatenation and the identity element $\lambda$ (the empty string). The set of all non-empty strings over V is denoted as $V^+$ so $V^+ = V^* - \{\lambda \}$. If $V = \{a\}$, we simply write $a^*$ and $a^+$ instead of $\{a\}^*$ and $\{a\}^+$. If a is a symbol in V, we write $a^0 = \lambda$ and we write the language generated by a regular expression E over V as L(E).

In proving computational universality, we use the notion of register machines. A register machine is a construct $M = (m,I, l_0, l_h, R)$, where m is the number of registers, I is the set of instruction labels, $l_0$ is the start label, $l_h$ is the halt label, and R is the set of instructions. Every label $l_i \in I$ uniquely labels only one instruction in R. Register machine instructions have the following forms:

• $l_i : ( \mathtt {ADD}(r), l_j, l_k)$, increase n by 1, then nondeterministically go to $l_j$ or $l_k$;

• $l_i: ( \mathtt {SUB}(r), l_j, l_k)$, if $n \ge 1,$ then subtract 1 from n and go to $l_j$, otherwise perform no operation on r and go to $l_k$;

• $l_h: \mathtt {HALT}$, the halt instruction.

Given a register machine M, we say M computes or generates a number n as follows: M starts with all its registers empty. The register machine then applies its instructions starting with the instruction labeled $l_0$. Without loss of generality, we assume that $l_0$ labels an $\mathtt {ADD}$ instruction, and that the content of the output register is never decremented, only added to during computation, i.e. no $\mathtt {SUB}$ instruction is applied to it. If M reaches the halt instruction $l_h$, then the number n stored during this time in the first (also the output) register is said to be computed by M. We denote the set of all numbers computed by M as N(M). It was proven that register machines compute all sets of numbers computed by a Turing machine, therefore characterizing NRE [8]. A strongly monotonic register machine is one restricted variant: it has only one register which is also the output register. The register initially stores zero, and can only be incremented by 1 at each step. Once the machine halts, the value stored in the register is said to be computed. It is known that strongly monotonic register machines characterize SLIN, the family of length sets of regular languages.

3 Spiking Neural P Systems with Structural Plasticity

In this section we define SNP systems with structural plasticity. Initial motivations and results for SNP systems are included in the seminal paper in [7]. A spiking neural P system with structural plasticity (SNPSP system) of degree $m \ge 1$ is a construct of the form ${\varPi } = (O, \sigma _1, \ldots , \sigma _m, syn, out )$, where:

• $O = \{a\}$ is the singleton alphabet (a is called spike);

• $\sigma _1, \ldots , \sigma _m$ are neurons of the form $(n_i, R_i), 1 \le i \le m$; $n_i \ge 0$ indicates the initial number of spikes in $\sigma _i$; $R_i$ is a finite rule set of $\sigma _i$ with two forms:

  • 1. Spiking rule: $E/a^c \rightarrow a$, where E is a regular expression over O, $c \ge 1$;

  • 2. Plasticity rule: $E/a^c \rightarrow \alpha k (i, N)$, where E is a regular expression over O, $c \ge 1$, $\alpha \in \{+,-, \pm , \mp \}$, $k \ge 1$, and $N \subseteq \{1, \ldots , m\} - \{i\}$;

• $syn \subseteq \{1, \ldots , m\} \times \{1, \ldots , m\}$, with $(i,i) \notin syn$ for $1 \le i \le m$ (synapses between neurons);

• $out \in \{1, \ldots , m\}$ indicate the output neuron.

Given neuron $\sigma _i$ (we also say neuron i or simply $\sigma _i$) we define the set of presynaptic (postsynaptic, resp.) neurons $pres(i) = \{ j | (i,j) \in syn \}$ (as $pos(i) = \{j | (j,i) \in syn \}$, resp.). Spiking rule semantics in SNPSP systems are similar with SNP systems in [7]. In this work we do not use forgetting rules (rules of the form $a^s \rightarrow \lambda$) or rules with delays of the form $E/a^c \rightarrow a;d$ for some $d \ge 1$. Spiking rules (also known as standard rules) are applied as follows: If neuron $\sigma _i$ contains b spikes and $a^b \in L(E)$, with $b \ge c$, then a rule $E/a^c \rightarrow a \in R_i$ can be applied. Applying such a rule means consuming c spikes from $\sigma _i$, thus only $b - c$ spikes remain in $\sigma _i$. Neuron i sends one spike to every neuron with label in pres(i) at the same step as rule application. A nonzero delay d means that if $\sigma _i$ spikes at step t, then neurons receive the spike at $t+d$. Spikes sent to $\sigma _i$ from t to $t+d-1$ are lost (i.e. $\sigma _i$ is closed), and $\sigma _i$ can receive spikes (i.e. $\sigma _i$ is open) and apply a rule again at $t+d$ and $t+d+1$, respectively. If a rule $E/a^c \rightarrow a$ has $L(E) = \{a^c\}$, we simply write this as $a^c \rightarrow a$. Extended rules are of the form $E/a^c \rightarrow a^p, p \ge 1$, where more than one spike can be produced.

Plasticity rules are applied as follows. If at step t we have that $\sigma _i$ has $b \ge c$ spikes and $a^b \in L(E)$, a rule $E/a^c \rightarrow \alpha k (i, N) \in R_i$ can be applied. The set N is a collection of neurons to which $\sigma _i$ can connect to or disconnect from using the applied plasticity rule. The rule application consumes c spikes and performs one of the following, depending on $\alpha$:

• If $\alpha := +$ and $N - pres(i) = \emptyset$, or if $\alpha := -$ and $pres(i) = \emptyset$, then there is nothing more to do, i.e. c spikes are consumed but no synapses are created or removed. Notice that with these semantics, a plasticity rule functions similar to a forgetting rule, i.e. the former can be used to consume spikes without producing any spike.

• for $\alpha := +,$ if $|N - pres(i)| \le k$, deterministically create a synapse to every $\sigma _l$, $l \in N_j - pres(i)$. If however $|N - pres(i)| >k$, nondeterministically select k neurons in $N - pres(i)$, and create one synapse to each selected neuron.

• for $\alpha := -,$ if $|pres(i)| \le k$, deterministically delete all synapses in pres(i). If however $|pres(i)|>k$, nondeterministically select k neurons in pres(i), and delete each synapse to the selected neurons.

If $\alpha \in \{\pm ,\mp \}:$ create (respectively, delete) synapses at step t and then delete (respectively, create) synapses at step $t+1$. Only the priority of application of synapse creation or deletion is changed, but the application is similar to $\alpha \in \{+,-\}$. Neuron i is always open from t until $t+1$, but $\sigma _i$ can only apply another rule at time $t+2$.

An important note is that for $\sigma _i$ applying a rule with $\alpha \in \{ +, \pm , \mp \}$, creating a synapse always involves an embedded sending of one spike when $\sigma _i$ connects to a neuron. This single spike is sent at the time the synapse creation is applied, i.e. whenever $\sigma _i$ attaches to $\sigma _j$ using a synapse during synapse creation, we have $\sigma _i$ immediately transferring one spike to $\sigma _j$.

Let t be a step during a computation: we say a $\sigma _i$ is activated at step t if there is at least one $r \in R_i$ that can be applied; $\sigma _i$ is simple if $|R_i| = 1$, with a nice biological and computing interpretation, i.e. some neurons do not need to be complex, but merely act as spike repositories or relays. We have the following nondeterminism levels: rule-level, if at least one neuron has at least two rules with regular expressions $E_1$ and $E_2$ such that $E_1 \ne E_2$ and $L(E_1) \cap L(E_2) \ne \emptyset$; synapse-level, if initially $\varPi$ has at least one $\sigma _i$ with a plasticity rule where $k < |N - pres(i)|$; neuron-level, if at least one activated neuron with rule r can choose to apply its rule r or not (i.e. asynchronous).

By default SNP and SNPSP systems are locally sequential (at most one rule is applied per neuron) but globally parallel (all activated neurons must apply a rule). The application of rules in neurons is usually synchronous, i.e. a global clock is assumed. However, in the asynchronous (asyn, in short) mode we release this synchronization so that neuron-level nondeterminism is implied. A configuration of an SNPSP system is based on $(\mathtt {a})$ distribution of spikes in neurons, and $(\mathtt {b})$ neuron connections based on syn. For some step t, we can represent: $(\mathtt {a})$ as $\langle s_1, \ldots , s_m \rangle$ where $s_i, 1 \le i \le m$, is the number of spikes contained in $\sigma _i$; for $(\mathtt {b})$ we can derive pres(i) and pos(i) from syn, for a given $\sigma _i$. The initial configuration therefore is represented as $\langle n_1,$ $\ldots ,$ $n_m \rangle$, with the possibility of a disconnected graph, or $syn = \emptyset$. A computation is defined as a sequence of configuration transitions, from an initial configuration, and following rule application semantics. A computation halts if the system reaches a halting configuration, i.e. no rules can be applied and all neurons are open.

A result of a computation can be defined in several ways in SNP systems literature. For SNP systems in asyn mode however, and as in [3, 5, 14], the output is obtained by counting the total number of spikes sent out by $\sigma _{out}$ to the environment (in short, Env) upon reaching a halting configuration. We refer to $\varPi$ as generator, if $\varPi$ computes in this asynchronous manner. $\varPi$ can also work as an acceptor but this is not given in this work.

For our universality results, the following simplifying features are used in our systems as the normal form: (i) plasticity rules can only be found in purely plastic neurons (i.e. neurons with plasticity rules only), (ii) neurons with standard rules are simple, and (iii) we do not use forgetting rules or rules with delays. We denote the family of sets computed by asynchronous SNPSP systems (under the mentioned normal form) as generators as $N_{tot}SNPSP^{asyn}$: subscript tot indicates the total number of spikes sent to Env as the result; Other parameters are as follows: $+syn_k$ ($-syn_j$, respectively) where at most k (j, resp.) synapses are created (deleted, resp.) each step; $nd_\beta , \beta \in \{ syn, rule, neur \}$ indicate additional levels of nondeterminism source; $rule_m$ indicates at most m rules (either standard or plasticity) per neuron; Since our results for k and j for $+syn_k$ and $-syn_j$ are equal, we write them instead in the compressed form $\pm syn_k$, where $\pm$ in this sense is not the same as when $\alpha := \pm$. A bound p on the number of spikes stored in any neuron of the system is denoted as $bound_p$. We omit $nd_{neur}$ from writing since it is implied in asyn mode.

Fig. 1.

An SNPSP system $\varPi _{ej}$.

To illustrate the notions and semantics in SNPSP systems, we take as an example the SNPSP system $\varPi _{ej}$ of degree 4 in Fig. 1, and describe its computations. The initial configuration is as follows: spike distribution is $\langle 1, 0, 0, 1 \rangle$ for the neuron order $\sigma _i$, $\sigma _j$, $\sigma _k$, $\sigma _l$, respectively; $syn = \{ (j,k), (k,l) \}$; output neuron is $\sigma _l$, indicated by the outgoing synapse to Env.

Given the initial configuration, $\sigma _i$ and $\sigma _l$ can become activated. Due to asyn mode however, they can decide to apply their rules at a later step. If $\sigma _{l}$ applies its rule before it receives a spike from $\sigma _i$, then it will spike to Env twice so that $N_{tot}(\varPi _{ej}) = \{2\}$. Since $k = 1 < |\{j,k\}|$ and $pres(i) = \emptyset$, $\sigma _i$ nondeterministically selects whether to create synapse (i, j) or (i, k); if (i, j) ((i, k), resp.) is created; a spike is sent from $\sigma _i$ to $\sigma _j$ ($\sigma _k$, resp.) due to the embedded sending of a spike during synapse creation. Let this be step t. If (i, j) is created then $syn' := syn \cup \{(i,j)\}$, otherwise $syn'' := syn \cup \{(i,k)\}$. At $t+1$, $\sigma _i$ deletes the created synapse at t (since $\alpha := \pm$), and we have syn again. Note that if $\sigma _l$ does not apply its rule and collects two spikes (one spike from $\sigma _i$), the computation is aborted or blocked, i.e. no output is produced since $a^2 \notin L(a)$.

4 Main Results

In this section we use at most two nondeterminism sources: $nd_{neur}$ (in asyn mode), and $nd_{syn}$. Recall that in asyn mode, if $\sigma _i$ is activated at step t so that an $r \in R_i$ can be applied, $\sigma _i$ can choose to apply r or not. If $\sigma _i$ did not choose to apply r, $\sigma _i$ can continue to receive spikes so that for some $t'>t$, it is possible that: r can never be applied again, or some $r' \in R_i, r' \ne r,$ is applied.

For the next result, each neuron can store only a bounded number of spikes (see for example [3, 6, 7] and references therein). In [6], it is known that bounded SNP systems with extended rules in asyn mode characterize SLIN, but it is open whether such result holds for systems with standard rules only. In [3], a negative answer was conjectured for the following open problem: are asynchronous SNP systems with standard rules universal? First, we prove that bounded SNPSP systems in asyn mode characterize SLIN, hence they are not universal.

Lemma 1

$N_{tot}SNPSP^{asyn}(bound_p, nd_{syn}) \subseteq SLIN, p \ge 1.$

Proof

Taking any asynchronous SNPSP system $\varPi$ with a given bound p on the number of spikes stored in any neuron, we observe that the number of possible configurations is finite: $\varPi$ has a constant number of neurons, and that the number of spikes stored in each neuron are bounded. We then construct a right-linear grammar G, such that $\varPi$ generates the length set of the regular language L(G). Let us denote by $\mathcal {C}$ the set of all possible configurations of $\varPi$, with $C_0$ being the initial configuration. The right-linear grammar $G = ( \mathcal {C}, \{a\}, C_0, P )$, where the production rules in P are as follows:

• (1) $C \rightarrow C',$ for $C,C' \in \mathcal {C}$ if $\varPi$ has a transition $C \Rightarrow C'$ in which the output neuron does not spike;

• (2) $C \rightarrow aC',$ for $C,C' \in \mathcal {C}$ if $\varPi$ has a transition $C \Rightarrow C'$ in which the output neuron spikes;

• (3) $C \rightarrow \lambda$, for any $C \in \mathcal {C}$ in which $\varPi$ halts.

Due to the construction of G, $\varPi$ generates the length set of L(G), hence the set is semilinear. $\square$

Lemma 2

$SLIN \subseteq N_{tot}SNPSP^{asyn}(bound_p,nd_{syn}), p \ge 1.$

The proof is based on the following observation: A set Q is semilinear if and only if Q is generated by a strongly monotonic register machine M. It suffices to construct an SNPSP system $\varPi$ with restrictions given in the theorem statement, such that $\varPi$ simulates M. Recall that M has precisely register 1 only (it is also the output register) and addition instructions of the form $l_i:( \mathtt {ADD}(1), l_j, l_k)$. The ADD module for $\varPi$ is given in Fig. 2. Next, we describe the computations in $\varPi$.

Fig. 2.

Module ADD simulating $l_i: ( \mathtt {ADD}(1): l_j, l_k)$ in the proof of Lemma 2

Once $\mathtt {ADD}$ instruction $l_i$ of M is applied, $\sigma _{l_i}$ is activated and it sends one spike each to $\sigma _1$ and $\sigma _{l_i^1}$. At this point we have two possible cases due to asyn mode, i.e. either $\sigma _1$ spikes to Env before $\sigma _{l_i^1}$ spikes, or after. If $\sigma _1$ spikes before $\sigma _{l_i^1}$, then the number of spikes in Env is immediately incremented by 1. After some time, the computation will proceed if $\sigma _{l_i^1}$ applies its only (plasticity) rule. Once $\sigma _{l_i^1}$ applies its rule, either $\sigma _{l_j}$ or $\sigma _{l_k}$ becomes nondeterministically activated.

However, if $\sigma _1$ spikes after $\sigma _{l_i^1}$ spikes, then the number of spikes in Env is not immediately incremented by 1 since $\sigma _1$ does not consume a spike and fire to Env. The next instruction, either $l_j$ or $l_k$, is then simulated by $\varPi$. Furthermore, due to asyn mode, the following “worst case” computation is possible: $\sigma _{l_h}$ becomes activated (corresponding to $l_h$ in M being applied, thus halting M) before $\sigma _1$ spikes. In this computation, M has halted and has applied an m number of $\mathtt {ADD}$ instructions since the application of $l_i$. Without loss of generality we can have the arbitrary bound $p > m$, for some positive integer p. We then have the output neuron $\sigma _1$ storing m spikes. Since the rules in $\sigma _1$ are of the form $a^q/a \rightarrow a$, $1 \le q \le p$, $\sigma _1$ consumes one spike at each step it decides to apply a rule, starting with rule $a^m/a \rightarrow a,$ until rule $a \rightarrow a$. Thus, $\varPi$ will only halt once $\sigma _1$ has emptied all spikes it stores, sending m spikes to Env in the process.

The FIN module is not necessary, and we add $\sigma _{l_h}$ without any rule (or maintain $pres(l_h) = \emptyset$). Once M halts by reaching instruction $l_h$, a spike in $\varPi$ is sent to neuron $l_h$. $\varPi$ is clearly bounded: every neuron in $\varPi$ can only store at most p spikes, at any step. We then have $\varPi$ correctly simulating the strongly monotonic register machine M. This completes the proof. $\square$

From Lemmas 1 and 2, we can have the next result.

Theorem 1

$SLIN = N_{tot}SNPSP^{asyn}(bound_p,nd_{syn}), p \ge 1.$

Next, in order to achieve universality, we add an additional ingredient to asynchronous SNPSP systems: weighted synapses. The ingredient of weighted synapses has already been introduced in SNP systems literature, and we refer the reader to [15] (and references therein) for computing and biological motivations. In particular, if $\sigma _i$ applies a rule $E/a^c \rightarrow a^p$, and the weighted synapse (i, j, r) exists (i.e. the weight of synapse (i, j) is r) then $\sigma _j$ receives $p \times r$ spikes.

It seems natural to consider weighted synapses for asynchronous SNPSP systems: since asynchronous SNPSP systems are not universal, we look for other ways to improve their power. SNPSP systems with weighted synapses (in short, WSNPSP systems) are defined in a similar way as SNPSP systems, except for the plasticity rules and the synapse set. Plasticity rules in $\sigma _i$ are now of the form

$$ E/a^c \rightarrow \alpha k (i, N,r) ,$$

where $r \ge 1$, and $E,c, \alpha , k, N$ are as previously defined. Every synapse created by $\sigma _i$ using a plasticity rule with weight r receives the weight r. Instead of one spike sent from $\sigma _i$ to a $\sigma _j$ during synapse creation, $j \in N$, r spikes are sent to $\sigma _j$. The synapse set is now of the form

$$syn \subseteq \{1,2, \ldots , m\} \times \{1,2, \ldots , m\} \times \mathbb {N} .$$

We note that SNPSP systems are special cases of SNPSP systems with weighted synapses where $r=1$, and when $r = 1$ we omit it from writing. In weighted SNP systems with standard rules, the weights can allow neurons to produce more than one spike each step, similar to having extended rules. In this way, our next result parallels the result that asynchronous SNP systems with extended rules are universal in [5]. However, our next result uses $nd_{syn}$ with asyn mode, while in [5] their systems use $nd_{rule}$ with asyn mode. We also add the additional parameter l in our universality result, where the synapse weight in the system is at most l. Our universality result also makes use of the normal form given in Sect. 3.

Theorem 2

$N_{tot}WSNPSP^{asyn}(rule_{m}, \pm syn_k, weight_l, nd_{syn}) = NRE, m \ge 9, k \ge 1, l \ge 3.$

Proof

We construct an asynchronous SNPSP system with weighted synapses $\varPi$, with restrictions given in the theorem statement, to simulate a register machine M. The general description of the simulation is as follows: each register r of M corresponds to $\sigma _r$ in $\varPi$. If register r stores the value n, $\sigma _r$ stores 2n spikes. Simulating instruction $l_i: ( \mathtt {OP}(r): l_j, l_k)$ of M in $\varPi$ corresponds to $\sigma _{l_i}$ becoming activated. After $\sigma _{l_i}$ is activated, the operation $\mathtt {OP}$ is performed on $\sigma _r$, and $\sigma _{l_j}$ or $\sigma _{l_k}$ becomes activated. We make use of modules in $\varPi$ to perform addition, subtraction, and halting of the computation.

Module ADD: The module is shown in Fig. 3. At some step t, $\sigma _{l_i}$ sends a spike to $\sigma _{l_i^1}$. At some $t'>t$, $\sigma _{l_i^1}$ sends a spike: the spike sent to $\sigma _r$ is multiplied by two, while 1 spike is received by $\sigma _{l_i^2}$. For now we omit further details for $\sigma _r$, since it is never activated with an even number of spikes.

At some $t''>t'$, $\sigma _{l_i^2}$ nondeterministically creates (then deletes) either $(l_i^2,l_j)$ or $(l_i^2,l_k)$. The chosen synapse then allows either $\sigma _{l_j}$ or $\sigma _{l_k}$ to become activated. The ADD module thus increments the contents of $\sigma _r$ by 2, simulating the increment by 1 of register r. Next, only one among $\sigma _{l_j}$ or $\sigma _{l_k}$ becomes nondeterministically activated. The addition operation is correctly simulated.

Fig. 3.

Module ADD simulating $l_i: ( \mathtt {ADD}(r): l_j, l_k)$ in the proof of Theorem 2.

Module SUB: The module is shown in Fig. 4. Let $|S_r|$ be the number of instructions with form $l_i:( \mathtt {SUB}(r), l_j, l_k )$, and $1 \le s \le |S_r|$. $|S_r|$ is the number of $\mathtt {SUB}$ instructions operating on register r, and we explain in a moment why we use a size of a set for this number. Clearly, when no $\mathtt {SUB}$ operation is performed on r, then $|S_r| = 0$, as in the case of register 1. At some step t, $\sigma _{l_i}$ spikes, sending 1 spike to $\sigma _r$, and $4|S_r|-s$ spikes to $\sigma _{l_i^1}$ (the weight of synapse $(l_i,l_i^1)$).

Fig. 4.

Module SUB simulating $l_i: ( \mathtt {SUB}(r): l_j, l_k)$ in the proof of Theorem 2.

$\sigma _{l_i^1}$ has rules of the form $a^p \rightarrow -1(l_i^1, \{r\},1)$, for $3|S_r| \le p <8|S_r|$. When one of these rules is applied, it performs similar to a forgetting rule: p spikes are consumed and deletes a nonexisting synapse $(l_i^1,r)$. Since $\sigma _{l_i^1}$ received $4|S_r| - s$ spikes from $\sigma _{l_i}$, and $3|S_r| \le 4|S_r| - s < 8|S_r|$, then one of these rules can be applied. If $\sigma _{l_i^1}$ applies one of these rules at $t'>t$, no spike remains. Otherwise, the $4|S_r| - s$ spikes can combine with the spikes from $\sigma _r$ at a later step.

In the case where register r stores $n = 0$ (respectively, $n \ge 1$), then instruction $l_k$ (respectively, $l_j$) is applied next. This case corresponds to $\sigma _r$ applying the rule with $E = a$ (respectively, $E = a(a^2)^+$), which at some later step allows $\sigma _{l_k}$ (respectively, $\sigma _{l_j}$) to be activated.

For the moment let us simply define $S_r = \{l_i^1\}$. For case $n = 0$ (respectively, $n \ge 1$), $\sigma _r$ stores 0 spikes (respectively, at least 2 spikes), so that at some $t'' >t$ the synapse $(r,l_i^1,5|S_r| + s)$ (respectively, $(r,l_i^1,4|S_r| + s)$) is created and then deleted. $\sigma _{l_i^1}$ then receives $5|S_r| + s$ spikes (respectively, $4|S_r| + s$ spikes) from $\sigma _r$. Note that we can have $t'' \ge t'$ or $t''\le t'$, due to asyn mode, where $t'$ is again the step that $\sigma _{l_i^1}$ applies a rule. If $\sigma _{l_i^1}$ previously removed all of its spikes using its rules with $E = a^p$, then it again removes all spikes from $\sigma _r$ because $3|S_r| \le x < 8|S_r|$, where $x \in \{ 4|S_r| + s, 5|S_r| + s \}$. At this point, no further rules can be applied, and the computation aborts, i.e. no output is produced. If however $\sigma _{l_i^1}$ did not remove its spikes previously, then it collects a total of either $8|S_r|$ or $9|S_r|$ spikes. Either $\sigma _{l_j}$ or $\sigma _{l_k}$ is then activated by $\sigma _{l_i^1}$ at a step after $t''$.

To remove the possibility of “wrong” simulations when at least two $\mathtt {SUB}$ instructions operate on register r, we give the general definition of $S_r$: $S_r = \{ l_v^1| l_v$ is a $\mathtt {SUB}$ $\text {instruction on register } r \}.$ In the SUB module, a rule application in $\sigma _r$ creates (and then deletes) an $|S_r|$ number of synapses: one synapse from $\sigma _r$ to all neurons with label $l_v^1 \in S_r$. Again, each neuron with label $l_v^1$ can receive either $4|S_r| + s,$ or $5|S_r|+s$ spikes from $\sigma _r$, and $4|S_r| -s$ spikes from $\sigma _{l_v}$.

Let $l_i$ be the $\mathtt {SUB}$ instruction that is currently being simulated in $\varPi$. In order for the correct computation to continue, only $\sigma _{l_i^1}$ must not apply a rule with $E=a^p$, i.e. it must not remove any spikes from $\sigma _r$ or $\sigma _{l_i}$. The remaining $|S_r| - 1$ neurons of the form $l_v^1$ must apply their rules with $E=a^p$ and remove the spikes from $\sigma _r$. Due to asyn mode, the $|S_r| -1$ neurons can choose not to remove the spikes from $\sigma _r$: these neurons can then receive further spikes from $\sigma _r$ in future steps, in particular they receive either $4|S_r| +s'$ or $5|S_r| +s'$ spikes, for $1 \le s' \le S_r$; these neurons then accumulate a number of spikes greater than $8|S_r|$ (hence, no rule with $E=a^p$ can be applied), but not equal to $8|S_r|$ or $9|S_r|$ (hence, no plasticity rule can be applied). Similarly, if these spikes are not removed, and spikes from $\sigma _{l_{v'}}$ are received, $v \ne v'$ and $l_{v'} \in S_r$, no rule can again be applied: if $l_{v'}$ is the $s'$th $\mathtt {SUB}$ instruction operating on register r, then $s \ne s'$ and $\sigma _{l_{v'}}$ accumulates a number of spikes greater than $8|S_r|$ (the synapse weight of $(l_{v'}, l_{v'}^1)$ is $4|S_r| - s'$), but not equal to $8|S_r|$ or $9|S_r|$. No computation can continue if the $|S_r| - 1$ neurons do not remove their spikes from $\sigma _r$, so computation aborts and no output is produced. This means that only the computations in $\varPi$ that are allowed to continue are the computations that correctly simulate a $\mathtt {SUB}$ instruction in M.

The SUB module correctly simulates a $\mathtt {SUB}$ instruction: instruction $l_j$ is simulated only if r stores a positive value (after decrementing by 1 the value of r), otherwise instruction $l_k$ is simulated (the value of r is not decremented).

Module FIN: The module FIN for halting the computation of $\varPi$ is shown in Fig. 5. The operation of the module is clear: once M reaches instruction $l_h$ and halts, $\sigma _{l_h}$ becomes activated. Neuron $l_h$ sends a spike to $\sigma _1$, the neuron corresponding to register 1 of M. Once the number of spikes in $\sigma _{1}$ become odd (of the form $2n + 1$, where n is the value stored in register 1), $\sigma _1$ keeps applying its only rule: at every step, 2 spikes are consumed, and 1 spike is sent to Env. In this way, the number n is computed since $\sigma _1$ will send precisely n spikes to Env.

The ADD module has $nd_{syn}$: initially it has $pres(l_i^2) = \emptyset ,$ and its $k = 1 < |N|$. We also observe the parameter values: m is at least 9 by setting $|S_r| = 1$, then adding the two additional rules in $\sigma _{l_i^1}$; k is clearly at least 1; lastly, the synapse weight l is at least 3 by again setting $|S_r| = 1$. This completes the proof. $\square$

Fig. 5.

Module FIN in the proof of Theorem 2.

5 Conclusions and Final Remarks

In [5] it is known that asynchronous SNP systems with extended rules are universal, while the conjecture is that asynchronous SNP systems with standard rules are not [3]. In Theorem 1, we showed that asynchronous bounded SNPSP systems are not universal where, similar to standard rules, each neuron can only produce at most one spike each step. In Theorem 2, asynchronous WSNPSP systems are shown to be universal. In WSNPSP systems, the synapse weights perform a function similar to extended rules in the sense that a neuron can produce more than one spike each step. Our results thus provide support to the conjecture about the nonuniversality of asynchronous SNP systems with standard rules. It is also interesting to realize the computing power of asynchronous unbounded (in spikes) SNPSP systems.

It can be argued that when $\alpha \in \{ \pm , \mp \}$, the synapse creation (resp., deletion) immediately followed by a synapse deletion (resp., creation) is another form of synchronization. Can asynchronous WSNPSP systems maintain their computing power, if we further restrict them by removing such semantic? Another interesting question is as follows: in the ADD module in Theorem 2, we have $nd_{syn}$. Can we still maintain universality if we remove this level, so that $nd_{neur}$ in asyn mode is the only source of nondeterminism? In [5] for example, the modules used asyn mode and $nd_{rule}$, while in [14], only asyn mode was used (but with the use of a new ingredient called local synchronization).

In Theorem 2, the construction is based on the value $|S_r|$. Can we have a uniform construction while maintaining universality? i.e. can we construct a $\varPi$ such that $N(\varPi ) = NRE$, but is independent on the number of $\mathtt {SUB}$ instructions of M? Then perhaps parameters m and l in Theorem 2 can be reduced.