Supercritical probabilistic cellular automata: how effective is the synchronous updating?

Abstract

Probabilistic cellular automata generalise CA by implementing in a synchronous way an updating rule defined through a probability. A probabilistic synchronous updating scheme does it mean an efficient parallel evolution mechanism? This article deals with the question of quantifying the effectiveness of the parallel updating. A good indicator of this effectiveness is the fraction of components whose value is updated between two time steps. Two classes of parameterised models are considered. Multiple stationary distributions may occur when an infinite number of interacting components is considered (ergodicity breaks/supercritical regime). As a consequence, these models both exhibit different dynamical regimes in the corresponding case when a finite number of sites are interacting. These two classes’ non trivial steady states are of different nature. One is a family of positive rates reversible PCA dynamics. The other one is the Stavskaja PCA dynamics. It exhibits an absorbing state. Thanks to numerical simulations, both these PCA dynamics are shown to behave nearly asynchronous when these phase transition phenomena occur.

A probabilistic synchronous updating scheme does it mean an efficient parallel evolution mechanism? That is one main general issue this article will consider. Probabilistic cellular automata (PCA) are cellular automata (CA) where the updating rule is defined through a probability. Like their deterministic version (Dennunzio et al. 2014, 2012), PCA are a very useful class of models for simulation and analysis of complex systems (Kari 2005; Cervelle et al. 2013; Mairesse and Marcovici 2014). They constitute a large family of discrete-time Markov stochastic processes where the transition probability has a product form (synchronous updating). Each constituting site or elementary cell may have its state updated between two steps of time. These updating may effectively not happen so often according to the associated probability which strongly depends on the state of the site’s neighbourhood. In particular, when phase transition occurs (supercritical regime), the effective parallelism may be impacted. This general notion will be precised. Is the synchronous updating more effective in the ergodic regime?

Another category of processes is asynschronous (P)CA, as investigated for instance in Dennunzio et al. (2012, 2013), Fatès (2009, 2013), Fatès et al. (2005), Regnault et al. (2009) and Worsch (2013). They are CA/PCA where the parallel updating is relaxed and where only a given proportion of sites are submitted to the updating procedure and whose value is then potentially modified. Does a supercritical PCA behave like asynchronous PCA? To be specific, two parameterised families of PCA dynamics are considered which may be in a phase transition regime. Yet these supercritical phases are of different nature: the first one is constituted with non trivial, non degenerated distributions whereas the second one admits an absorbing state. Another question to deal with, is: do these PCA dynamics have similar behaviour concerning the effective updating?

In this contribution, we aim at quantifying the effectiveness of the parallel updating procedure through numerical simulations. To this aim, we introduce and consider different indicators, like the fraction of sites whose value is modified through the probabilistic updating.

Let us give a brief introduction to the chosen PCA dynamics and emphasise their respective behaviour when a finite or infinite number of interacting components is considered.

The first considered family is a parameterised positive rates PCA family which is the parallel version of the Gibbs sampler associated to the famous Ising interaction potential (with nearest neighbour interaction or finite range). The ${{\mathbb {Z}}}^2$ case is considered for the numerical analysis. Under some light assumptions, this family builds reversible stochastic processes, meaning a kind of “dynamical equilibrium” holds (aka detailed balance condition). More precise theoretical results were proven. In a non exhaustive way, let us briefly mention the following ones. The form of the time-asymptotic distribution is explicitly known (Dai Pra et al. 2002) both for a finite collection of interacting cells and for an infinite collection (countable, ${{\mathbb {Z}}}^d$ lattice case). Ergodicity versus phase transition/loss of ergodicity region were proven in the ${{\mathbb {Z}}}^2$ case (Dai Pra et al. 2002). Metastability results hold, giving insight on escape times (Cirillo et al. 2008; Nardi and Spitoni 2012) in the finitely many interacting sites case. Through a mean field approximation the parameters’ influence is more precisely understood (Cirillo et al. 2014). A very nice generalisation of this family was studied in order to sample from a Gibbs measure by tuning the application of the updating rule in a similar way as in the $\alpha$-asynchronous case (Dai Pra et al. 2012) and a very interesting non reversible variation was considered in Lancia and Scoppola (2013). Due to the detailed balance, an “energy” potential is naturally associated to this PCA family. This potential is much more complicated than the nearest-neighbour Ising case (Cirillo et al. 2014). This family may be considered as a gradient dynamics aiming at minimising this potential. From the perspective of understanding relationships between synchronous/asynchronous updating scheme, a natural question to address on this PCA family is the behaviour of the effective flipping rate (case of a finite number of interacting cells) when the parameters are in a region where, in the infinite ${{\mathbb {Z}}}^d$ case, loss of ergodicity holds. In this region, the transition probability becomes very small and the effective change of a cell’s state becomes rare. The PCA dynamics becomes de facto quasi a sequential one or an $\alpha$-synchronous one.

We then examine the Stavskaja PCA on ${{\mathbb {Z}}}$ (or a finite subset) which admits an absorbing state. Thus it is not a positive rates dynamics and not building reversible stochastic processes. The second family is thus of different nature. Nevertheless it share with the first one the existence of a non equilibrium phase transition regime. When considering finitely many interacting sites, the almost sure time-asymptotics behaviour is indeed the absorption in the configuration 1. This is a particular case of ergodicity. On ${{\mathbb {Z}}}$, in some parameter region, phase transition is observed in the sense of loss of ergodicity: there exists an infinity of stationary distributions. We address the same questions as for the first family about the effective flipping rate and simultaneous effective bond flipping rate when loss of ergodicity occurs.

This article is organised as follows: the general framework is first introduced from a probabilistic point of view (Sect. 1). The analogies and differences with another category of stochastic processes, interacting particle systems, is emphasised. The interest come from the fact that these dynamics are mainly driven by a sequential updating scheme. We then study in Sect. 2 the first family of parameterised reversible positive rates PCA dynamics. The introduced indicators to quantify the effectiveness are introduced in Sect. 2.3. Numerical results concerning the effective updating rate are then summarised. The second family, Stavskaja PCA dynamics, is then studied in Sect. 3. The last section is dedicated to conclusive remarks.

1 General framework from a probabilistic perspective

Consider a collection of sites indexed by a network G. Each site $k\in G$ has an associated value $\sigma _k$ in a finite space S. Typically, $S=\{0,1\}$ or $S=\{-1,+1\}$. The association of a value in S to each site is called a configuration and is denoted by $\sigma =(\sigma _k)_{k \in G}$. A probabilistic CA dynamics is defined through the synchronous use of an updating rule $p_k(\cdot |\eta )$ where, given the configuration $\eta$ at the previous time step, $p_k(\cdot |\eta )$ is a probability on S. The global probability to jump towards a configuration $\sigma$, starting from a configuration $\eta$, is defined as

$$P(\sigma | \eta )=\prod _{k \in G} p_k(\sigma _k|\eta ).$$

Given an initial condition, possibly sampled from a starting distribution, the PCA dynamics becomes a discrete-time Markov stochastic process on the state space $S^G$ whose transition matrix is P. It means, knowing what happened up to time $(n-1)$—more precisely the last state $\eta$ (markovianity)—, each site is updated independently. In general, the updating rule is assumed to be translation invariant, meaning $p_k(\cdot |\eta )=p_0(\cdot |\theta _k\eta )$ where $\theta _k\eta$ denotes the configuration $(\theta _k\ \eta )_j:=\eta _{j+k}$. Just as for CA, the local rule is assumed to be finite range: there exists a finite neighbourhood $V_k$ on the graph G such that $p_k(\cdot |\eta )=p_k(\cdot |\eta _{V_k})$ where $\eta _{V_k}$ denotes $(\eta _j)_{j \in V_k}$. In particular, when G is infinite, this condition ensures the existence of such a stochastic process. It is unique (in distribution) as soon as a starting distribution is fixed. When $p_k(\cdot |\eta )$ is positive, the PCA dynamics is called positive rates.

A different family of stochastic processes is more amenable to a theoretical analysis in the framework of probability theory. These are called interacting particle systems (IPS) (see Chap. I in Liggett 1985). As well as PCA, they are Markov stochastic processes on a state space which has a product form. They are in general continuous-time Markov processes defined through an updating rate. There are few general results and detailed analysis is developed for more particular categories of models. Most of the IPS for which detailed theoretical results are available have a kind of sequential updating procedure: at most one site may be updated when an exponentially distributed clock rings. An analogous discrete time version of this mechanism is possible. Briefly, these continuous-time stochastic processes allow a small updating infinitely often contrary to the PCA where all sites may be updated at discrete time step. An interacting particle system is a continuous-time Markov stochastic process $(\eta _t)_{t \in {{\mathbb {R}}}^+}$ defined on $S^G$. The infinitesimal local updating rate $c_k(\cdot |\eta )$ is the analogous of $p_k$, requiring only to be positive. For any event A, let $P_t(\eta ,A)$ denotes the probability that the process is in A at time t knowing the process started in the configuration $\eta$ at time 0. The global updating procedure is defined through an infinitesimal generator L defined for continuous functions on $S^G$.

Let us first precise what continuous functions are. The set $S^G$ is a metric space for instance using the distance $d(\sigma ,\eta )= \sum _{k \in G} \tfrac{1}{2^{v(k)}} {1}_{\sigma _k \ne \eta _k}{}$ for any bijection $v \ : \ G \rightarrow {{\mathbb {N}}}$. The symbol ${1}_{}{}$ stands for the indicator function. Continuous functions on $S^G$ are uniform limits of local functions, which means functions depending on a finite number of sites.

For a general Markov stochastic process, the infinitesimal generator L is then defined through

$$\int _{S^G} g (y) P_t(\eta ,dy) := {{\mathrm{{{\mathbb {E}}}}}}(g(\eta _t) | \eta _0=\eta ) = g(\eta ) + Lg(\eta ) \cdot t + o(t)$$

for any continuous function $g : S^G \rightarrow {{\mathbb {R}}}$. For an interacting particle system, the infinitesimal generator is related to local updating rates $c_k(\cdot |\eta )$ through the following relation. For any g continuous function on $S^G$, it holds

$$Lg(\eta ) = \sum _{k \in G} \left[ g\left( \eta ^{k,s}\right) - g(\eta ) \right] \ c_k(\eta ^{k,s} |\eta )$$

where $\eta ^{k,s}$ is the configuration equal to $\eta$ on $\{k\}^c$ and taking the value s at site k. Similarly to the PCA, the rates $c_k(\cdot |\eta )$ are local, meaning they only depend on $\eta _{V_k}$ where $V_k$ is a finite neighbourhood of k. Such processes may be constructed through a sequential updating procedure. It is the graphical construction due to Harris (1972). Independent Poissonian clocks (defined through independent identically exponentially distributed waiting times) are associated to each sites k. When a clock rings at any site, the process jumps: the value $\eta _t(k)$ at site k is modified to the value s. It means, the process jumps from a configuration $\eta$ to the configuration $\eta ^{k,s}$. At most one site is updated during an infinitesimally small amount of time. The probability that clocks at, at least two, different sites ring at the same time is negligible with respect to the infinitesimal time o(t). Remark, the general definition allows to update when a jump occurs, a finite collection of sites. See in particular Sect. 3 Chap. I in Liggett (1985) for more details.

In the comparison between continuous-time IPS and discrete-time PCA stochastic dynamics, the specificity of PCA dynamics as kernel for Markov stochastic processes is more blatant when G is infinite. It allows indeed infinitely many local configuration’s modifications. When G is finite, PCA processes have the particularity to allow more possible jumps on $S^G$, especially when it has positive rates. In that case, the transition matrix is a matrix whose entries are all positive. For these reasons, PCA dynamics could be a priori considered as more effective since the synchronous updating procedure is allowing more jumps.

2 A family of reversible positive rates PCA dynamics

2.1 Reversible PCA dynamics

In this section we study a generic family of positive rates reversible PCA dynamics. Pay attention, the reversibility for a deterministic CA dynamics is a different notion as the one presented hereafter. A CA dynamics is said reversible if the global deterministic transformation $F: S^G\, \mapsto\, S^G,\ \sigma (n) \,\mapsto\, \sigma (n+1)$ is injective. See for instance Kari and Taati (2015) for an up-to-date reference.

In this subsection, we recall some basic facts and well-known comments. Briefly: reversibility for Markov processes is a property of the transition kernel and being reversible for a PCA dynamics is a specific requirement.

A Markov process is said to be reversible if it admits at least one reversible distribution. It means, there exists a probability measure $\mu$ on $S^G$ such that

$$\forall \sigma , \ \eta , \quad \mu (\eta ) P(\sigma |\eta )= \mu (\sigma ) P(\eta |\sigma ).$$

For a continuous-time process, the similar relation is

$$\forall f\ {{\text {continuous on }}} \;S^G,\quad \int f \ Lg \ d\mu = \int g \ Lf \ d\mu .$$

Both mean the stochastic process’s distribution, with starting distribution $\mu$, is invariant by time inversion $t \,\mapsto \,-t$. So called equilibrium statistical mechanics is mainly concerned about Gibbs measure and phase diagram and study associated reversible stochastic dynamics. The time symmetry invariance in distribution means indeed what is called an “equilibrium dynamics”.

Despite the definition of reversibility through the existence of a reversible distribution, this property is related only to the dynamics’ kernel. The explanation comes from the following statement proved by Kolmogorov: consider an irreducible Markov chain on a finite state space with transition probability P, the (unique) stationary probability measure is reversible (w.r.t P) if and only if

$$P(\sigma _2|\sigma _1) P(\sigma _3|\sigma _2) \cdots P (\sigma _1|\sigma _k) = P (\sigma _k|\sigma _1)\cdots P(\sigma _2|\sigma _3) P(\sigma _1|\sigma _2)$$

for any finite sequence of states $\sigma _1,\ldots ,\sigma _k$. It means the probability of any loop does not depend on the travel’s orientation.

To be reversible for a PCA dynamics means the kernel of the time-reversed chain has to be the same, which means to have the same product form. This is a strong requirement. It was stated as consequence in Kozlov and Vasilyev (1980), Künsch (1984) (see section 4.1.1 in Louis 2002 too) that reversible PCA dynamics need to be of a special form. Thus, the particular form of $p_{k}$ introduced herafter is, up to the coefficients’ parametrisation, the most general one for a shift invariant, positive rate, reversible PCA on $\{-1,1\}^{{{\mathbb {Z}}}^{d}}$.

2.2 Theoretical results

We choose $S = \{-1,1\}$ and $G={{\mathbb {Z}}}^d$ or $G= \varLambda _L := [0,L]^d \cap {{\mathbb {Z}}}^d$ for any $L>0$. Consider a function ${{\mathrm{{{\mathcal {K}}}}}}:{{\mathbb {Z}}}^{d} \rightarrow {{\mathbb {R}}}$ of finite range: there exists $R>0$ such that ${{\mathrm{{{\mathcal {K}}}}}}(i) = 0$ for $|i|>R$, and symmetric ${{\mathrm{{{\mathcal {K}}}}}}(i) = {{\mathrm{{{\mathcal {K}}}}}}(-i)$ for every $i \in {{\mathbb {Z}}}^{d}$. This last assumption is necessary and sufficient to ensure the reversibility of the PCA dynamics. Moreover, let $\tau \in \{-1,1\}^{{{\mathbb {Z}}}^{d}}$ be a fixed configuration. It plays the role of boundary condition. For $\varLambda \subset {{\mathbb {Z}}}^{d}$, we define the transition probability $P_{\varLambda }^{\tau }(\sigma |\eta ) = \otimes _{k \in \varLambda } P_{k}^{\tau }( \sigma _{k}|\eta )$ by

$$P^{\tau }_{k}(\sigma _{k} = s|\eta ) = p_{k}(s|\tilde{\eta }) = \frac{1}{2} \left[ 1+s \tanh \left( \beta \sum _{k \in {{\mathbb {Z}}}^{d}} {{\mathrm{{{\mathcal {K}}}}}}(k-j)\tilde{\eta }_{j} + \beta h \right) \right] ,$$

(1)

where $\tilde{\eta } = \eta _{\varLambda } \tau _{\varLambda ^c}$ ; $h \in {{\mathbb {R}}}$, $\beta >0$ are given parameters. The usual notation $\eta _{\varLambda } \tau _{\varLambda ^c}$ denotes the configuration equal to $\eta$ (resp. $\tau$) for sites in $\varLambda$ (resp. $\varLambda ^c$).

This family of PCA dynamics was studied in Grinstein et al. (1985), Derrida (1990). It is important because of the main following two reasons. First, as emphasised in the previous subsection, reversibility is a strong assumption for a PCA dynamics and this particular form of the updating rule $p_k$ is a generic one. Second, when ${{\mathrm{{{\mathcal {K}}}}}}(\pm e_i)=J>0$ and 0 otherwise ($i \in \{1,\ldots ,d\}$ with $(e_i)_{1 \le i \le d}$ canonical basis), this updating rule is the parallel version of the Gibbs sampler associated to the famous ferromagnetic Ising interaction potential with nearest neighbour interaction. Thus, this family was used in several applications in connection with the Ising model.

Precise theoretical results were proven for this family of positive rates PCA, parameterised by $\beta$ and h. The form of the time-asymptotic distribution is explicitly known (Prop. 3.1 in Dai Pra et al. 2002) both when G is finite and when $G={{\mathbb {Z}}}^d$ (in that case, as limiting object). In the ${{\mathbb {Z}}}^2$ case, ergodicity versus phase transition/loss of ergodicity region were proven (Dai Pra et al. 2002; Louis 2004) using probabilistic and statistical mechanics techniques.

Central mathematical objects used are Gibbs measures. They are used to analyse the asymptotics, when an infinite number of sites are interacting. A potential is a family of functions $(\varphi _A)_{A \Subset G}$ encoding the interaction. The symbol ${A \Subset G}$ stands for A finite subset of G. It is required that for any $A \Subset G$, $\forall \sigma \in S^G,\; \varphi _A(\sigma )=\varphi _A(\sigma _A)$ where $\sigma _A=(\sigma _k)_{k \in A}$. It means the function $\varphi _A$ depends on the configuration $\sigma$ only through sites in $\varLambda$. Let $\varLambda \Subset G$ and $\tau \in S^G$ be a boundary condition. A Gibbs distribution is the probability measure defined on $S^\varLambda$ such that

$$\begin{aligned} \mu _\varLambda ^\tau (\sigma _\varLambda ) &:= \frac{1}{{{\mathcal {Z}}}_\varLambda ^\tau } e^{-\sum _{A : A \cap \varLambda \ne 0} \varphi _A (\sigma _\varLambda \tau _{\varLambda ^c})}\\&= \frac{1}{{{\mathcal {Z}}}_\varLambda ^\tau } \prod _{A : A \cap \varLambda \ne 0} e^{-\varphi _A (\sigma _\varLambda \tau _{\varLambda ^c})} \end{aligned}$$

(2)

where ${{{\mathcal {Z}}}_\varLambda ^\tau }$ is the normalisation constant defined with

$${{{\mathcal {Z}}}_\varLambda ^\tau } := \sum _{\sigma _\varLambda \in S^\varLambda } e^{- \sum _{A : A \cap \varLambda \ne 0} \varphi _A (\sigma _\varLambda \tau _{\varLambda ^c})}$$

and where $\sigma _{\varLambda } \tau _{\varLambda ^c}$ stands for the configuration equal to $\sigma$ (resp. $\tau$) for sites in $\varLambda$ (resp. $\varLambda ^c$). Due to this form, the following relationship holds, for any subsets $\varLambda _2 \subset \varLambda _1$,

$$\mu _{{\varLambda }_1}^{\tau _{{\varLambda 1}^c}} (\sigma _{\varLambda _2} | \sigma _{\varLambda _1 \setminus \varLambda _2}) = \mu _{\varLambda _2}^{\tau _{\varLambda _1^c}\sigma _{\varLambda _1 \setminus \varLambda _2}} (\sigma _{\varLambda _2}).$$

(3)

When G’s cardinality is infinite, a Gibbs distribution is a probability measure on $S^G$ (with the Borel $\sigma$-field), such that the distribution $\mu$, conditioned on a finite subset $\varLambda \subset G$ to have the values $\tau$ outside $\varLambda$, is the distribution $\mu _\varLambda ^\tau$. Formally, this means the following relationship

$$\forall \varLambda \Subset {G},\quad \ \forall \tau \in S^G,\quad \mu (\ (\cdot )_\varLambda \ | \ \tau _{\varLambda ^c} \ )=\mu _\varLambda ^\tau ( \ \cdot \ ).$$

(4)

The finite cardinality of S ensures $S^G$ is a compact set. This implies the existence of at least such a measure. These probability measures are the distribution of random fields $(\sigma _k)_{k \in G}$ of, through the potential $\varphi$, interacting sites $k \in G$. Pay attention, this definition does not imply the uniqueness of $\mu$. By definition, phase transition is said to hold when several Gibbs measures exist for the same potential. Gibbs measures $\mu$ are proven to be found too as asymptotics for suitable limits in the subset of interacting sites in G. These distributions give maximal probability to configurations minimising the potential $\varphi$. The following basic examples aim to precise this notion. When $\varphi \equiv 0$, the Gibbs measure associated to $\varphi$ is the uniform distribution on $S^G$. Let $\sharp$ denotes the cardinality. When $\forall A\subset G, \ \sharp A >1, \varphi _A=0$, the Gibbs measure is a product of independent distributions on S. When $\varphi _A(\sigma ):=\prod _{k \in A} \sigma _k$ for $A=\{i,j\}$ where $i\sim j$ (meaning i and j are connected through a bond of the graph G), the interaction hold between nearest neighbours. The well known Ising potential (without magnetic field) corresponds to the choice $\varphi _{\{i,j\}}(\sigma )=J \sigma _i \sigma _j$ when $i \sim j$. The uniform parameter J is tuning the interaction’s intensity.

Back to the analysis of the PCA dynamics defined through (1). Thanks to the reversibility, there is an interaction potential $\varphi$ associated to this PCA dynamics on ${{\mathbb {Z}}}^d$:

$$\begin{aligned} &\varphi _{\{k\}}(\sigma _{k})= - \beta h \sigma _{k} \\ &\varphi _{V_{k}}(\sigma _{V_k})= - \log \cosh \left[ \beta \sum _{j} {{\mathrm{{{\mathcal {K}}}}}}(k-j) \sigma _{j} + \beta h \right] \\ &\varphi _{\varLambda }(\sigma _{\varLambda })= 0 \quad {{\text {otherwise}}}, \end{aligned}$$

(5)

This potential is much more complicated than the nearest neighbour Ising model. In particular, it is a genuinely multi-body interaction and is not reducible to a two sites/bond interaction. The aim of the Gibbs sampler procedure is to write down a stochastic dynamics admitting as time-asymptotic an a priori prescribed distribution. Starting from the Ising Gibbs measure and implementing the Gibbs sampler updating rule in a fully parallel way leads to a different time-asymptotic, now characterised as Gibbs measures w.r.t. this new potential $\varphi$.

When $d=1$, $G={{\mathbb {Z}}}$, since reversible probability measures are Gibbs measures w.r.t $\varphi$, the dynamics admits a unique reversible measure. On ${{\mathbb {Z}}}$, for finite range potentials, there is no phase transition, meaning there exists a unique Gibbs measure (Georgii 1988).

Let us consider from now on the cases $d=2$, ${{\mathrm{{{\mathcal {K}}}}}}(0) \ge 0$, ${{\mathrm{{{\mathcal {K}}}}}}(\pm e_i)=1$ ($i \in \{1,2\}$ with $(e_1,e_2)$ canonical basis), $h=0$. The set $V_k$ is the Von Neumann neighbourhood with the site k itself when ${{\mathrm{{{\mathcal {K}}}}}}(0)\ne 0$. In the infinite case $G={{\mathbb {Z}}}^2$, there exists a critical value $\beta _c$ such that for $\beta <\beta _c$, the PCA dynamics is ergodic, converging in distribution towards the unique Gibbs measure associated to the potential $\varphi$. For $\beta >\beta _c$, the PCA dynamics is not ergodic anymore, there exist many reversible distributions, characterised as Gibbs measures w.r.t $\varphi$. When ${{\mathrm{{{\mathcal {K}}}}}}(0)=0$, $\beta _c$ is exactly the Ising critical value $\log (1+\sqrt{2})/2 \sim 0.44$. In the corresponding $G=\varLambda _L$ cases, two analogous regimes are observed numerically and characterised by a drastic change in the speed of convergence towards the unique stationary distribution. Theoretically it was stated in Louis (2004) that the convergence holds exponentially fast when $\beta <\beta _c$. When ${{\mathrm{{{\mathcal {K}}}}}}(0)=1$, $\beta _c \in [0.3;0.35]$ was numerically estimated (Louis 2002). Finally, remark when ${{\mathrm{{{\mathcal {K}}}}}}(0)=1$, for $\beta$ large, the PCA dynamics becomes a CA with majority-voting updating rule over the four nearest neighbours and the site itself.

2.3 Effective flipping rate

For the sake of simplicity we consider from now on periodic boundary conditions. These are convenient to insure a shift-invariant situation for a finite number of interacting sites. We use numerical simulation through programs written in R and make use of the “vectorisation” possibilities in order to improve the running time. We consider the case where $V_k$ is the Von Neumann neighbourhood, including possibly the site k itself. Since the probabilistic updating rule depends on the state of the neighbourhood $\eta _{V_k}$, the global jump probability, given the past, has a product form of elements like $p_0(\cdot |\xi )$ where $\xi \in S_{V_0}$. When the system evolves towards an ordered configuration, the modification of the sites’ states may become very unlikely. We want to quantify this loss of effectiveness in the parallel updating.

On $S=\{-1,+1\}$, we call a flip, the change of a site’s state. Rewrite the updating rule $p_k(\cdot |\eta )$ as a flipping probability $\tilde{p}_k(\eta )$ which is the probability, conditionally to the past, that $\eta _k$ jumps to $-\eta _k$

$${{\tilde{p}}}_k(\eta ) = p_k(+1 |\eta ){1}_{\eta _k=-1} + p_k(-1 |\eta ){1}_{\eta _k=+1}$$

where ${1}_{\eta _k=-1}$ is short notation for ${1}_{\{ \eta : \eta _k=-1\}}$ with, for any subset A, ${1}_{A}(x)=1$ if $x \in A$, and 0 otherwise. We define an effective flipping rate ($d=2$ case)

$$\lambda _{n+1} = \frac{\sum _{k\in \varLambda _L} {1}_{\sigma _k(n+1) \ne \sigma _k(n)}}{L^2}.$$

(6)

The quantity $\lambda _{n+1}$ denotes the density of sites in $\varLambda _L$ changing values between time steps n and $n+1$. It depends on the configurations $(\sigma (n),\sigma (n+1))$.

Denoting by ${{\mathcal {F}}}_n$ the filtration generated by the process up to time n, ${{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n}(\cdot )$ denotes the conditional expected value operator, knowing all the sampled events up to time n. Mathematically, for any random variable W, ${{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n}(W)$ is a ${{\mathcal {F}}}_n$-measurable random variable and the expectation of this random variable over sets of ${{\mathcal {F}}}_n$ is the same as the expectation of W:

$$\forall A \in {{\mathcal {F}}}_n, \ {{\mathrm{{{\mathbb {E}}}}}}({{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n}(W) {1}_{A})={{\mathrm{{{\mathbb {E}}}}}}(W {1}_{A}).$$

Since a Markovian framework is considered here, the result of such an average given ${{\mathcal {F}}}_n$ depends on the process’ value $\sigma (n)$ at time n. The quantity ${{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n} (\lambda _{n+1})$ is, given $\sigma (n)$, the average value of the effective flipping rate $\lambda _{n+1}$. It depends on the configuration $\sigma (n)$. Since, given ${{\mathcal {F}}}_n$, the random variables $(\sigma _k(n+1))_{k \in G}$ are independent, it holds:

$${{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n} (\lambda _{n+1}) = \sum _{\xi \in S^{V_0}} \frac{\sharp \{ k \in \varLambda _L : \sigma _{V_k}(n)=\xi \}}{L^2} \ \tilde{p}_0(\xi ),$$

where both quantities depend on $\sigma (n)$. $({{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n} (\lambda _{n+1}))_n$ build a kind of instantaneous averaged flipping rate.

It is another natural, worth mentioning, alternative indicator to be considered for quantifying the effectiveness of the synchronous updating rule. It is using the simultaneous conditionally independent updating characteristic of the PCAs. In the phase transition regime, since there are less random fluctuations, this indicator is of the same order as the effectiveness of a sequential updating scheme. For this indicator, we then need to compute the different probabilities $\tilde{p}_0(\xi )$ and the proportion of different local configurations.

Another quantity’s trajectory to be considered as a measure of the effective parallelism of the dynamics is the following one. Let us consider the density of nearest neighbours’ bonds really flipped at the same time

$$q_{n+1}= \frac{\sum _{j \sim k} {1}_{\sigma _k(n+1) \ne \sigma _k(n)} {1}_{\sigma _j(n+1) \ne \sigma _j(n)}}{2L^2},$$

where $j\sim k$ denotes neighbouring sites. It is indeed interesting to notice, when the nearest-neighbour Ising associated Gibbs sampler is only partly synchronised, alternatively on even/odd sites, meaning no pair of neighbouring sites is updated at the same time, then the stationary measure remains the Gibbs measure w.r.t. Ising potential. The potential’s modification is then induced by the possible updating of two even/odd neighbouring sites simultaneously. In an analogous way, the associated instantaneous averaged quantity ${{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n}(q_{n+1})$ was recorded. These averaged quantities leads to no further informative result. The results concerning ${{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n}(q_{n+1})$ are thus not presented hereafter.

2.4 Numerical results, case d = 2

2.4.1 Typical parameters’ values chosen

We choose to consider here the results when ${{\mathrm{{{\mathcal {K}}}}}}(\pm e_i)=1$ ($i \in \{1,2\}$), ${{\mathrm{{{\mathcal {K}}}}}}(0)=1$ and with $h=0$. Similar results hold modifying the ${{\mathrm{{{\mathcal {K}}}}}}(\cdot )$ function. ${{\mathrm{{{\mathcal {K}}}}}}(\cdot )$ not positive should not modify the main question we address here. When $h\ne 0$, there is a drift toward one value of S. It is more interesting to consider a symmetrical situation. Periodic boundary conditions are chosen for the same reason. We consider $G=\varLambda _L$ with $L=60$ (3600 sites). Since G is finite in these simulations, the PCA dynamics is always ergodic and as explained, there is, for any parameters value of $\beta ,h$, convergence in distribution towards a unique stationary probability measure $\mu _\beta$. As stated by theoretical results, and confirmed by these simulations, for $\beta$ close to 0, $\mu _\beta$ looks like the uniform measure (independent product of 0.5-Bernoulli distributions). For large $\beta$, $\mu _\beta$ is concentrated on configurations close to ${+1}$ and ${-1}$ where $\sigma = {+1}$ means $\forall k\in G$, $\sigma _k=+1$. On Fig. 1 results from two typical samples in the cases $\beta =0.1$ and $\beta =0.5$ are presented.

Fig. 1

Reversible PCA: one sample simulation’s results, case $\beta = 0.1$ left, case $\beta =0.5$ right

Fig. 2

Reversible PCA, simulation’s results: average on an i.i.d. sample, case $\beta =0.1$ left, case $\beta =0.5$ right

Fig. 3

Reversible PCA, simulation’s results: average on an i.i.d. sample

2.4.2 Non phase transition regime

When $\beta \,< \,\beta _c$ the PCA dynamics on $G={{\mathbb {Z}}}^2$ is ergodic with exponential speed of convergence. This corresponds to the non phase transition regime for the associated potential $\varphi$. Consider $\beta =0.1$ for illustration. Running the algorithm up to final time $T=200$ shows the stationary states is reached. We check for instance the stabilisation of the magnetisation $\sum _{k \in G} \sigma _k / \sharp G$. Notice, one step time is one step of the PCA dynamics, which means $\sharp G$ potential flips. Since ergodicity holds, the starting distribution does not matter. Nevertheless, the phenomenon is more interesting starting with a random configuration distributed according to independent distributions giving weight 0.9 to +1 (see left bar-chart, Fig. 1g). One sample of the evolution of $\lambda _n$ (red curve) and ${{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n} (\lambda _{n+1})$ (in green) is shown in Fig. 1a. This sample, in the stationary regime, gives a constant effective updating rate around 0.44 for both the indicators $\lambda _n$ and ${{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n} (\lambda _{n+1})$. On Fig. 3a, at $\beta =0.1$ a mean value on independent trials is coherent with this one sample value of $\lambda _n$. Figure 1c illustrates the time evolution of the different possible flipping probabilities. The symmetries imply that different values of $\sigma _{V_k}$ give rise to the same flipping probability $\tilde{p}_k(\sigma _{V_k})$. In this example, only five different flipping probabilities are associated to the $2^5$ values of $\sigma _{V_k}$. The associated colour goes from blue to red, blue denotes the configurations less favourable to flip and red the more likely to flip. Figure 1e is the plot of the time evolution of the bond updating rate $q_n$. Figure 1g represents the bar-chart of the flipping probability. At $T=100$, this sampled configuration shows a large proportion of local configurations $\sigma _{V_k}$ with a moderate flipping probability. This matches with previous knowledge about the equilibrium distribution $\mu$ this configuration is sampled from (up to the finite simulation time bias). Figure 2a shows the bar-plot of the flipping probabilities on a sample from size 100 both at the starting time and at $T=500$ confirming the previous one sample observations.

2.4.3 Phase transition regime

When $\beta >\beta _c$, the PCA dynamics on $G={{\mathbb {Z}}}^2$ is non ergodic (phase transition regime for the associated potential $\varphi$). Consider $\beta =0.5$. Running the algorithm up to final time $T=1300$, stationarity is reached for this sample at $T=1000$. This is slightly observable on Fig. 1d, b. For this sample, the configuration reached is close to ${-1}$. In order to emphasise the polarisation phenomenon occurring, the starting condition was chosen w.r.t the uniform probability on $S^{\varLambda _L}$. The effective flipping rate is, in this regime, very quickly lower than 0.1, non increasing, stabilising around $1.6\times 10^{-2}$. Figure 1d shows the tiny proportion of local configurations very likely to flip and the large proportion of sites whose neighbourhood make them very unlikely to flip. The bar-plot associated to this sample’s flipping distribution illustrates it on Fig. 1h, and on Fig. 2b for an i.i.d. sample with size 100.

On Fig. 3a the effective flipping rate is observed for a sample at a large enough time in order to be close to equilibrium. This average is plotted against $\beta$. As expected from the theoretical results, there is a drastic change when approaching $\beta _c$ and for $\beta > \beta _c$ it is small. Since there are less fluctuations of $\sigma (n)$ in this regime, ${{\mathrm{{{\mathbb {E}}}}}}_{{\mathcal {F}}_n} (\lambda _{n+1})$ is of the same order as the effective flipping rate of a sequential procedure. The simulations shows then that the effectiveness of the parallel scheme is of the same order as the one of a sequential procedure. The same phenomenon occurs for the effective bond updating rate $q_n$. It is evident to expect a value close (but not equal) to the square of the single site updating rate. This is plotted on Fig. 3b as dashed green line. Indeed, for small and large value of $\beta$, neighbouring local configurations $\sigma _{V_k}$ and $\sigma _{V_j}$ (with $j\sim k$) tends to be the same or similar.

3 Stavskaja PCA dynamics

3.1 Theoretical results

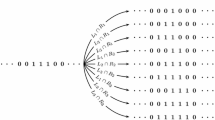
The Stavskaja Model is defined on ${{\mathbb {Z}}}$ or on a interval. We refer to Taggi (2015) for up-to-date references and more detailed results. The spin space is $S=\{0,1\}$ and the neighbourhood is $V_k=\{k-1,k\}$. The local updating rule is defined as

$$\begin{aligned} p_k(1 | \sigma ) = \left\{ \begin{array}{ll} 1&{{\text { if }}} \;\,\sigma _k=\sigma _{k-1}=1, \\ \varepsilon \in [0,1]& {{\text { otherwise.}}} \\ \end{array} \right. \end{aligned}$$

The Dirac distribution $\delta _{{1}}$, concentrated on 1 is a trivial stationary distribution. When finitely-many interacting sites are considered, the a.s. long-time behaviour is absorption in the configuration 1. In the infinitely-many interacting sites case $\varLambda ={{\mathbb {Z}}}$, the following behaviour was proven by the Russian school of Markov processes at the end of the 1960s (Shnirman 1968; Vaserstein and Leontovich 1970; Toom et al. 1978): there exists a critical parameter’s value $\varepsilon ^*>0$ such that

• for any $\varepsilon$ such that $\varepsilon > \varepsilon ^*$, the dynamics is ergodic which means $\forall \mu {{\;\text { starting\;distribution}}}, \ \lim _{n \rightarrow \infty } {{\mathbb {P}}}_{\mu } (\sigma (n)= \cdot )= \delta _{{1}};$

• when $\varepsilon < \varepsilon ^*$, the dynamics is non-ergodic, in particular $\lim _{n \rightarrow \infty } {{\mathbb {P}}}_{\delta _{{0}}}( \sigma (n)= \cdot ) = \mu _{\varepsilon } (\cdot ) \ne \delta _{{1}},$ more precisely, $0< \mu _\varepsilon ({1}) < 1$ and every stationary distribution translation-invariant on ${{\mathbb {Z}}}$ is of the form $\alpha \mu _\varepsilon + (1-\alpha ) \delta _{{1}},{{\text { where }}} \alpha \in [0,1].$

The notation ${{\mathbb {P}}}_{\delta _{{0}}}( \sigma (n)= \cdot )$ denotes the marginal distribution at time n of the stochastic process with the Stavskaja PCA dynamics as kernel and starting in 0. A sharp numerical estimation based on a Monte Carlo simulation provided by Mendonça (2011) gives $\varepsilon _c = 0.29450$. In this reference, the critical exponents of the model are numerically studied and indicate that this phase transition belongs to the directed percolation universality class of critical behaviour.

3.2 Numerical results

3.2.1 Typical parameters’ values chosen

For comparison purposes with the previous systems, the situation with $\sharp G = 3600$ sites is considered. Periodic boundary conditions are chosen and time runs up to 2500 steps. Using the mean number of 1 values along the trajectory $\sum _{k \in G} \sigma _k / \sharp G$, it is checked that the transitory part is over and that some kind of quasi-stationary situation holds. One trajectory is represented in Fig. 4a, resp. b, when $\varepsilon =0.26$, resp. $\varepsilon =0.2950$. Considered the size of the system, this amount of steps is not enough, for the $\varepsilon$ values considered, to see the final absorption happening. The trajectories considered start with the configuration 0.

Fig. 4

Stavskaja PCA: one sample simulation’s results, case $\varepsilon = 0.26$ left, case $\varepsilon =0.2950$ right

Fig. 5

Stavskaja PCA dynamics, simulation’s results: average flipping rates

3.2.2 Effective flipping rates

When $\varepsilon =0.26$, resp. $\varepsilon =0.2950$, one sample of the evolution of $\lambda _n$ (red curve) and ${{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n} (\lambda _{n+1})$ (in green) is shown in Fig. 4c, resp. d. This sample, in the quasi-stationary regime, gives a constant effective updating rate around 0.288, resp. 0.138, for both the indicators $\lambda _n$ and ${{\mathrm{{{\mathbb {E}}}}}}_{{{\mathcal {F}}}_n} (\lambda _{n+1})$. Figure 4e, resp. f, illustrates the time evolution of the different possible flipping probabilities $\tilde{p}_k(\sigma _{V_k})$. The symmetries imply that different values of $\sigma _{V_k}$ give rise to the same flipping probability $\tilde{p}_k(\sigma _{V_k})$. The associated colour goes from blue to red, blue denotes the configurations less favourable to flip and red the more likely to flip. The Fig. 4g, resp. h, show the time evolution of the bond flipping rate.

When $\varepsilon <\varepsilon _c$, the PCA dynamics on $G={{\mathbb {Z}}}$ is non ergodic. Again it is worth noticing, as expected from the theoretical results, that for simulations with finitely many interacting sites, an abrupt change of behaviour happens.

On Fig. 5a the mean effective flipping rate is measured on a sample. This average is plotted against $\varepsilon$. When $\varepsilon <\varepsilon _c$, since trajectories starting from 0 are considered, the flipping rate is with respect to $\mu _\varepsilon$. When $\varepsilon >\varepsilon _c$, the dynamics is ergodic and there is a quick absorption in 1 explaining that $\lambda _n$ is 0. Clearly, the same phenomenon of abrupt change occurs for the effective bond flipping rate $q_n$ represented on Fig. 5b.

For the Stavskaja PCA dynamics, the non ergodicity regime is then more effective in comparison with the ergodicity regime.

4 Conclusive remarks

This paper presents from a probabilistic point of view two families of PCA dynamics which exhibit a phase transition phenomenon when the infinitely-many interacting sites case is considered and when some parameters are tuned below or above a critical value. The first family is representative of the reversible positive rates PCA dynamics. When the parameter $\beta$ varies, the system goes from an ergodic situation around a disordered “fluctuating” state to a non ergodic/phase transition situation with two fluctuating phases (meaning extremal stationary distributions not concentrated in a few configurations). The second family of Stavskaja PCA is representative of PCA dynamics with one absorbing state and exhibiting a critical phenomenon. When the parameter $\varepsilon$ varies, the system goes from an degenerate ergodic situation around an absorbing state to a non ergodic/phase transition situation with one fluctuating phase $\mu _\varepsilon$ and an absorbing one $\delta _{1}$. For both kind of systems, when finitely-many sites interacts, the phase transition phenomenon is not sharp anymore. The stochastic processes are indeed always ergodic and typical times are exponentially large, in the parameters’ region where phase transition occurs for the associated infinitely many interacting cases. Nevertheless, an abrupt change of behaviour happens for typical quantities, related to the dynamical evolution on finitely-many interacting sites, like the single-site and bond flipping rate we considered. Change of behaviour observed in the numerical simulations are in agreement with theoretical results and estimations concerning the parameters’ critical values. The main motivation of this paper was to quantify the evolution of the single-site and bond flipping rates when the parameter varies. Figures 3a, b and 5a, b put in perspective these curves for two main families of PCA dynamics for which phase transition occurs. Moreover, it highlights that effective synchronicity rate is not so high as could have been expected considering the parallel nature of the kernel. This is clearly due to the local constraints. Finally, we conclude that the two family of models behave differently from the effectiveness perspective. The synchronicity rate goes close to 0 in the phase transition regime for reversible positive rates PCA dynamics whereas it goes to 0 in the ergodic regime for the Stavskaja absorbing dynamics. The reversible positive rates PCA dynamics are more effective in the ergodic regime. The Stavskaja dynamics are more effective in the non ergodic regime. We conclude the effectiveness of the synchronous updating strongly depend on the nature of the running regime. The two families of PCA dynamics share some similar behaviours: two regimes separated by a critical parameter value, one ergodic, the other regime related to a non ergodic one when infinitely many components interact. Despite this fact, these two models behave differently concerning the effectiveness. This is mainly due to the nature of the phases. For the reversible PCA dynamics, in the non ergodic regime, strong correlations forbid an effective synchronous updating scheme. For the Stavskaja PCA dynamics, strong correlations are observed in the ergodic regime, where configurations are attracted towards the absorbing state. The non ergodic regime corresponds in that case to the regime where fluctuations are strong enough to make a non trivial stationary distribution survive. These random fluctuations implies an effective synchronous updating in the non ergodic regime.