A new direction-of-arrival estimation method exploiting signal structure information

Abstract

A new method is proposed to estimate the direction-of-arrival (DOA) based on uniform linear array sampling and named as sparsity and temporal correlation exploiting (SaTC-E). By exploiting the structure information of source signals, including spatial sparsity and temporal correlation of sources, SaTC-E accomplishes DOA estimation with superior performance via block sparse bayesian learning methodology and grid refined strategy. SaTC-E is applicable into time-varying manifold scenario, such as wideband sources, time-varying array, provided that the array manifold matrix is determinable. It has improved performance with some other merits, including superior resolution, requirement for a few snapshots, no knowledge of source number, and applicability to spatially and temporally corrected sources. Real data tests and numerical simulations are carried out to demonstrate the advantages of SaTC-E.

1 Introduction

Direction-of-arrival (DOA) estimation based on antenna array is an attractive issue in array signal processing and plays an important role in the application of radar, sonar, wireless communication, radio-astronomy. A number of high resolution methods have sprung up during the past years. As a representative of the classical super-resolution algorithms, the multiple signal classification (MUSIC; Schmidt 1986) has been used very widely. However, the performance of MUSIC deteriorates significantly with only a few snapshots or in the presence of correlated sources. In addition, it always requires the prior information about the number of sources, which is rarely practicable in the application.

Recently, thanks to the development of sparse signal recovery (Candes et al. 2006; Donoho 2006; Baraniuk 2007), many sparsity-based methods have been proposed to estimate the DOA (Malioutov et al. 2005; Hyder and Mahata 2010; Guo et al. 2010; Kim et al. 2012; Zhu and Chen 2015; Northardt et al. 2013; Du and Cheng 2014; Liu et al. 2012; Carlin et al. 2013), including ${{\ell }_{1}}$ mixed-norm minimization approach (Malioutov et al. 2005; Hyder and Mahata 2010; Guo et al. 2010; Kim et al. 2012; Zhu and Chen 2015; Northardt et al. 2013; Du and Cheng 2014), and sparse bayesian learning (SBL) (Tipping (2001); Wipf et al. 2011)) technique. It has been demonstrated that most of the sparsity-based methods are adaptive to many scenarios, including closely spatial sources, a few snapshots, spatially correlated sources, and no requirement of source number (Malioutov et al. 2005). However, these methods mainly focus on the spatial sparsity but rarely take the temporal information of sources into account, whereas the temporal correlation exists universally in the practical applications. In this paper, we propose a new method called sparsity and temporal correlation exploiting (SaTC-E) based on the block sparse bayesian learning (BSBL) framework (Zhang and Rao 2011, 2013), which can exploit and self-adaptively learn the temporal correlation among the snapshots of each source to improve the performance of DOA estimation.

The original BSBL algorithm (Zhang and Rao 2011) has been successfully applied for multi-task learning (Wan et al. 2012) and wireless telemonitoring of fetal ECG (Zhang et al. 2013a, b). However, the performance of BSBL is very poor for DOA estimation, because the sensing matrix is determined by the specific array system and the discretization of bearing-space. BSBL has to discretize the bearing-space and assumes the sources lie on the bearing-grid, and yet the true sources are usually not located in this discretized grid. In particular, a large grid-interval leads to serious error of DOA estimation because of off-grid effect, while a small grid-interval results in strong column-coherence of the sensing matrix. To deal with this issue, we introduce a grid refined strategy in this paper. This strategy is made up of coarse and refined estimation stages. At the coarse stage, the grid-interval is relatively large and a local scope covering the DOA of sources is estimated by using a modified BSBL algorithm. Then at the refined stage, 1-D (one-dimensional) searching with fine grid-interval is implemented in the scope estimated previously to find the exact DOA. The processing technique at the refined stage keeps away from sparse signal recovery, so that the strong coherence of the refined sensing matrix does not destroy the performance of DOA estimation. Our criterion of grid refined strategy is to minimize the identical cost function derived from the BSBL methodology both at the coarse and refine stages (by using different mathematical tools), which is quite different from Malioutov et al. (2005), Northardt et al. (2013). In Liu et al. (2012), independent relevance vector machine-DOA (iRVM-DOA) algorithm employs SBL perspective and grid refined strategy as well, but it neglects the temporal information of sources.

The proposed method has many advantages, such as improved resolution, requirement of only a few snapshots, and no requirement of source number. Furthermore, it is adaptive to temporally and spatially correlated sources, as well as being applicable to any time-varying manifold scenario, provided that the manifold matrix is determinable, such as wideband sources and time-varying array.

The rest of this paper is organized as follows. In Sect. 2, we formulate the problem of DOA estimation and describe the main contributions of this paper briefly. In Sect. 3, we propose a new method called SaTC-E for narrowband DOA estimation, which can exploit the spatial sparsity and temporal correlation of sources. In Sect. 4, we generalize SaTC-E for time-varying manifold scenario as long as the manifold matrix is determinable. In Sect. 5, real data tests and numerical simulations are presented to verify the performance of SaTC-E.

The notations in this paper are introduced as follows: $\mathbf{I }_{L}$ denotes the identity matrix with size $L\times L$, and $\mathbf{I }$ stands for the identity matrix, of which the dimension can be determined from the context. $\mathbf{A }_{i\cdot }$ and $\mathbf{A }_{\cdot j}$ are the ith row and the jth column of the matrix $\mathbf{A }$, respectively. $\mathbf{A }_{ij}$ is the element of $\mathbf{A }$ in the ith row and jth column. $\mathbf{A }\otimes \mathbf{B }$ reprensents the Kronecker product of matrices $\mathbf{A }$ and $\mathbf{B }$. ${\text {vec}}\left( \mathbf{A }\right)$ denotes the vectorization of $\mathbf{A }$ by stacking its columns one by one into a column-vector. $\mathbf{A }^{T}$ and $\mathbf{A }^{H}$ are the transpose and the conjugate transpose of $\mathbf{A }$, respectively. $\bar{\mathbf{a }}$ means the conjugate of the complex vector $\mathbf{a }$. ${\text {Toep}}(\mathbf{a })$ denotes the $M \times M$ Hermitian Toeplitz matrix determined by its first column $\mathbf{a }$.

2 Problem formulation

In this section, we formulate the problem of DOA estimation and present the main contributions of our work. The narrowband and stationary sources are taken into account.

Assume that K far-field narrowband sources impinge on an M-sensor array from directions $\varvec{\theta }={{\left[ {{\theta }_{1}}, \ldots , {{\theta }_{K}}\right] }^{T}}$, and the inter-sensor spacing is half the wavelength of the incident signals. The array output at snapshot t is represented as

$$\begin{aligned} {\mathbf {y}}\left( {t} \right) ={\mathbf {A}}\left( \varvec{\theta } \right) {\mathbf {s}}\left( {t} \right) +{\mathbf {n}}\left( {t} \right) ,\quad t=1,2,\ldots ,L, \end{aligned}$$

(1)

where L denotes the number of snapshots, ${\mathbf {s}}\left( {t}\right) ={{\left[ {{s}_{1}}\left( {t}\right) , \ldots ,{{s}_{K}}\left( {t} \right) \right] }^{T}}$ is the signal vector of sources, and ${\mathbf {n}}\left( {t} \right)$ is the zero-mean additive complex white Gaussian noise with covariance matrix ${{\mathbf {R}}_{\mathbf {n}}}={{\sigma }^{2}}{\mathbf {I}}$ and ${{\sigma }^{2}}$ unknown. The noise is uncorrelated with sources. The array manifold matrix ${\mathbf {A}}\left( \varvec{\theta } \right)$ is represented as,

$$\begin{aligned} {\mathbf {A}}\left( \varvec{\theta } \right) =\left[ {{\mathbf {a}}}\left( {{\theta }_{1}} \right) , \ldots ,{\mathbf {a}}\left( {{\theta }_{K}} \right) \right] , \end{aligned}$$

(2)

where ${{\mathbf {a}}}\left( {{\theta }_{k}} \right) ={{\left[ {{e}^{-j2\pi {{f}_{0}}{{\tau }_{1,k}}}}, \ldots ,{{e}^{-j2\pi {{f}_{0}}{{\tau }_{M,k}}}} \right] }^{T}}$ is the kth steering vector, and ${{f}_{0}}$ denotes the carrier frequency. ${{\tau }_{m,k}}$ related to ${{\theta }_{k}}$ is the propagational time-delay of the kth source between the reference and the mth sensor.

The purpose of DOA estimation is to estimate the directions $\varvec{\theta }$ using the given observation $\big \{ {\mathbf {y}}\left( {t} \right) \big \}_{t=1}^{L}$ and the formulation of matrix ${\mathbf {A}}\left( \varvec{\theta } \right)$. The main contributions of this paper are listed as follows:

• We exploit the spatial joint sparsity of all sources and the temporal correlation in each source simultaneously to estimate DOA without any parameter tuning and knowledge of source number.

• After coarse estimation, we implement a local 1-D searching at the refined stage to minimize the cost function derived consistently from BSBL methodology. This procedure reduces the error of DOA estimation caused by off-grid effect and strong coherence of the manifold matrix.

• We generalize the proposed method for any time-varying manifold scenario, provided that the array manifold matrix has a determinable formulation.

3 Narrowband DOA estimation based on spatial sparsity and temporal correlation

To cast the addressed DOA estimation as a problem of sparse signal recovery, we present the sparse representation of (1) firstly, and then propose an efficient method for DOA estimation. This method can capture the structure information of source signals and improve the accuracy of DOA estimation using a grid refined strategy.

3.1 Sparse representation and temporal correlation

Since the sources are spatially sparse, the potential bearing-space can be discretized to form a bearing-grid $\varvec{\varTheta }={{\left[ {{\vartheta }_{1}}, \ldots ,{{\vartheta }_{N}} \right] }^{T}} (N \gg K)$, which covers the true directions $\varvec{\theta }$. The array output (1) can be rewritten as a sparse linear combination of the steering vectors,

$$\begin{aligned} {\mathbf {y}}\left( {t} \right) ={{\varvec{\Phi }}}\left( \varvec{\varTheta } \right) {\mathbf {x}}\left( {t} \right) +{\mathbf {n}}\left( {t} \right) ,\quad t=1,2,\ldots ,L, \end{aligned}$$

(3)

where ${\mathbf {x}}\left( {t} \right) \in {{\mathbb {C}}^{N\times 1}}$ is a zero-padded version of ${\mathbf {s}}\left( {t} \right)$ from $\varvec{\theta }$ to $\varvec{\varTheta }$, that is, if ${\vartheta }_{i} = \theta _{k}\in \varvec{\theta }$, then ${x}_{i}\left( {t} \right) = s_{k}\left( {t} \right) \ne 0$; otherwise, ${x}_{i}\left( {t} \right) = 0$. Therefore, ${\mathbf {x}}\left( {t} \right)$ has only $K\left( \ll N \right)$ nonzero elements. ${{\varvec{\Phi }}}\left( \varvec{\varTheta } \right) \in {{{\mathbb {C}}}^{M\times N}}$ is a corresponding extension of the manifold matrix ${\mathbf {A}}\left( \varvec{\theta } \right)$, that is

$$\begin{aligned} {{\varvec{\Phi }}}\left( \varvec{\varTheta } \right) =\left[ {\mathbf {a}}\left( {{\vartheta }_{1}} \right) , \ldots ,{\mathbf {a}}\left( {{\vartheta }_{N}} \right) \right] , \end{aligned}$$

(4)

where ${\mathbf {a}}\left( {{\vartheta }_{k}} \right) = \left[ e^{-j 2\pi {f}_{0} \tilde{\tau }_{1,k} }, \ldots , e^{-j 2\pi {f}_{0} \tilde{\tau }_{M,k} } \right] ^{T}$ with $\tilde{\tau }_{1,k}$ related to ${\vartheta }_{k}$. Since the cardinality of $\varvec{\varTheta }$ is usually much larger than the number of sensors, i.e., $N\gg M$, ${{\varvec{\Phi }}}\left( \varvec{\varTheta } \right)$ is an overcomplete dictionary.

Since the true directions are rarely located in the spatial grid $\varvec{\varTheta }$ exactly, (3) is not an accurate extension of (1). However, the processing of sparse signal recovery based on (3) will be always feasible with some recovery error, while how to reduce the error of DOA estimation caused by off-grid effect is another assignment we will study in the following section. Therefore, the model error in (3) is skipped over.

In the following we present the BSBL model (Zhang and Rao 2011) for DOA estimation. The array output (3) with L snapshots is represented as a multiple measurement vectors (MMV) model (Eldar and Mishali 2009)

$$\begin{aligned} {\mathbf {Y}}=\varvec{{\Phi }} {\mathbf {X}}+{\mathbf {N}}, \end{aligned}$$

(5)

where ${\mathbf {Y}}=\left[ {\mathbf {y}}\left( {{t}_{1}} \right) , \ldots ,{\mathbf {y}}\left( {{t}_{L}} \right) \right] \in {{{\mathbb {C}}}^{M\times L}}$, ${\mathbf {X}}=\left[ {\mathbf {x}}\left( {{t}_{1}} \right) , \ldots ,{\mathbf {x}}\left( {{t}_{L}} \right) \right] \in {{{\mathbb {C}}}^{N\times L}}$, ${{\varvec{\Phi }}}={{\varvec{\Phi }} }\left( \varvec{\varTheta } \right)$, and ${\mathbf {N}}=\left[ {\mathbf {n}}\left( {{t}_{1}} \right) , \ldots ,{\mathbf {n}}\left( {{t}_{L}} \right) \right] \in {{{\mathbb {C}}}^{M\times L}}$. For stationary sources, the supports of all columns in ${\mathbf {X}}$ are identical, so that ${\mathbf {X}}$ has only K nonzero rows and each row ${{{\mathbf {X}}}_{i\cdot }}$ denotes a potential source from direction ${\vartheta }_{i}$. As the sources are stochastic and temporally correlated, that is, the source signal at the time t is related to the signal at the last time $t-1$, we assume that each row ${{{\mathbf {X}}}_{i\cdot }}$ has a parameterized Gaussian distribution

$$\begin{aligned} p\left( {{{\mathbf {X}}}_{i\cdot }};{{\gamma }_{i}},{{\mathbf {B}}_{i}} \right) \sim {\mathcal {CN}}\left( {\mathbf {0}},{{\gamma }_{i}}{{\mathbf {B}}_{i}} \right) ,\qquad i=1,2,\ldots ,N \end{aligned}$$

(6)

with parameters ${{\gamma }_{i}}$ and ${{\mathbf {B}}_{i}}$ to be estimated. Obviously, ${{\gamma }_{i}}$ is a parameter controlling the row-support of ${\mathbf {X}}$, that is, if ${{\gamma }_{i}}=0$, then ${{{\mathbf {X}}}_{i\cdot }}$ is a zero vector and there is no source from direction ${{\vartheta }_{i}}$; otherwise, ${{{\mathbf {X}}}_{i\cdot }}\ne {\mathbf {0}}$ and there is a source from ${{\vartheta }_{i}}$. ${{\mathbf {B}}_{i}}\in {{\mathbb {R}}^{L\times L}}$ is a Hermitian matrix that captures the correlation among the elements in ${{{\mathbf {X}}}_{i\cdot }}$, and can be interpreted as a covariance matrix of ${{{\mathbf {X}}}_{i\cdot }}$ up to a constant factor ${{\gamma }_{i}}$. Obviously, the temporal correlation of source signals is characterized by matrix ${{\mathbf {B}}_{i}}$. The estimate of $\{{\gamma }_{i}\}$ is what we need for DOA estimation, that is, by finding the peaks of $\big \{ {\gamma }_{i}\big \}$ we can get the DOA estimation according to the indices of those peaks.

For convenience of computing the temporal correlation of sources, (5) is transformed to a single measurement vector (SMV) model as follows,

$$\begin{aligned} \mathbf {z}={\varvec{\Psi }} {\mathbf {w}}+\varvec{\varepsilon }, \end{aligned}$$

(7)

where $\mathbf {z}={\text {vec}} \left( {{{\mathbf {Y}}}^{T}} \right) \in {{{\mathbb {C}}}^{ML\times 1}}$, $\varvec{{\Psi }}=\varvec{{\Phi }}\otimes {{\mathbf {I}}_{L}}\in {{{\mathbb {C}}}^{ML\times NL}}$, ${\mathbf {w}}={\text {vec}}\left( {{{\mathbf {X}}}^{T}} \right) \in {{{\mathbb {C}}}^{NL\times 1}}$, and $\varvec{\varepsilon }={\text {vec}}\left( {{{\mathbf {N}}}^{T}} \right) \in {{{\mathbb {C}}}^{ML\times 1}}$. Consequently, ${\mathbf {w}}={{\left[ {{\mathbf {w}}}_{1}^{T}, \ldots ,{{\mathbf {w}}}_{N}^{T} \right] }^{T}}$ is a block-sparse vector with ${{{\mathbf {w}}}_{i}}={{\mathbf {X}}}_{i\cdot }^{T}$.

Under the assumption that the sources are spatially uncorrelated, the prior distribution of ${\mathbf {w}}$ in (7) is also a Gaussian distribution,

$$\begin{aligned} p\left( {\mathbf {w}};{{\left\{ {{\gamma }_{i}},{{\mathbf {B}}_{i}} \right\} }} \right) \sim {\mathcal {CN}}\left( 0,{{{{\varvec{\Sigma }} }}_{0}} \right) \end{aligned}$$

(8)

with the covariance matrix ${{{{\varvec{\Sigma }} }}_{0}}={\text {diag}}\left[ {{\gamma }_{1}}{{\mathbf {B}}_{1}}, \ldots ,{{\gamma }_{N}}{{\mathbf {B}}_{N}} \right]$.

Assume that the noises are mutually independent and ${{{\mathbf {N}}}_{ij}}\sim {\mathcal {CN}}\left( 0,{{\sigma }^{2}} \right)$, then the conditional distribution of $\mathbf {z}$ in (7) is

$$\begin{aligned} p\left( \left. \mathbf {z} \right| {\mathbf {w}};{{\sigma }^{2}} \right) \sim {\mathcal {CN}}\left( {\varvec{\Psi }} {\mathbf {w}},{{\sigma }^{2}}\mathbf {I} \right) . \end{aligned}$$

(9)

According to the Bayes rule, the posterior PDF of ${\mathbf {w}}$ is expressed as

$$\begin{aligned}&p\left( \left. {\mathbf {w}} \right| \mathbf {z};{{\left\{ {{\gamma }_{i}},{{\mathbf {B}}_{i}} \right\} }},{{\sigma }^{2}} \right) \ \nonumber \\&\quad = {{\left( 2\pi \right) }^{-\frac{NL}{2}}}{{\left| {{{{\varvec{\Sigma }} }}_{{\mathbf {w}}}} \right| }^{-\frac{1}{2}}}{e}^{ \left\{ -\frac{1}{2}{{\left( {\mathbf {w}}-{{{{{\mu }} }}_{{\mathbf {w}}}} \right) }^{H}}{{{{\varvec{\Sigma }} }}_{{\mathbf {w}}}}^{-1}\left( {\mathbf {w}}-{{{{{\mu }} }}_{{\mathbf {w}}}} \right) \right\} }, \end{aligned}$$

(10)

then obviously, $p\left( \left. {\mathbf {w}} \right| \mathbf {z};{{\left\{ {{\gamma }_{i}},{{\mathbf {B}}_{i}} \right\} }},{{\sigma }^{2}} \right) \sim {\mathcal {CN}}\left( {{{{{\mu }} }}_{{\mathbf {w}}}},{{{{\varvec{\Sigma }} }}_{{\mathbf {w}}}} \right)$ with

$$\begin{aligned} {{\varvec{\varSigma }}_{{\mathbf {w}}}}= & {} {{\left( {{\sigma }^{-2}}{{{{\varvec{\Psi }} }}^{H}}{{\varvec{\Psi }} }+{{{{\varvec{\Sigma }} }}_{0}}^{-1} \right) }^{-1}}, \nonumber \\ {{\varvec{\mu }}_{{\mathbf {w}}}}= & {} {{{{\varvec{\Sigma }} }}_{0}}{{{{\varvec{\Psi }} }}^{H}}{{\left( {{\sigma }^{2}}{\mathbf {I}}+{{\varvec{\Psi }} }{{{{\varvec{\Sigma }} }}_{0}}{{{{\varvec{\Psi }} }}^{H}} \right) }^{-1}}{{\mathbf {z}}}. \end{aligned}$$

(11)

As we mentioned above, the final task remains on the estimate of parameters ${{\left\{ {{\gamma }_{i}} \right\} }}$. We achieve the estimate of ${{\left\{ {{\gamma }_{i}} \right\} }}$ by maximizing $p\left( {\mathbf {z}};{{\left\{ {{\gamma }_{i}},{{\mathbf {B}}_{i}} \right\} }},{{\sigma }^{2}} \right)$, and find the remarkable peaks in the estimate $\varvec{\hat{\gamma }}$ of $\varvec{\gamma }={{\left[ {{\gamma }_{1}}, \ldots ,{{\gamma }_{N}} \right] }^{T}}$ which indicates the DOA of the incident sources. In Zhang and Rao (2011), the authors employed expectation–maximization (EM) technique (Dempster et al. 1977) to learn ${{\left\{ {{\gamma }_{i}},{{\mathbf {B}}_{i}} \right\} }}$ and ${{\sigma }^{2}}$. Before estimating these parameters, they supposed ${\mathbf {B}}_{i} = \mathbf {B} (i=1,2,\ldots ,N)$ to avoid the overfitting problem. The learning rules for ${{\gamma }_{i}},\mathbf {B}$ and ${{\sigma }^{2}}$ are presented as (Zhang and Rao 2011)

$$\begin{aligned} {{{{\varvec{\Omega }} }}^{\left( k+1 \right) }}= & {} {{\left( {{\left( {{{{\varvec{\Gamma }} }}^{\left( k \right) }} \right) }^{-1}}+{{\left[ {{\left( {{\sigma }^{2}} \right) }^{\left( k \right) }} \right] }^{-1}}{{{{\varvec{\Phi }} }}^{H}}{{\varvec{\Phi }} }\right) }^{-1}},\nonumber \\ {{{\mathbf {X}}}^{\left( k+1 \right) }}= & {} {{{{\varvec{\Gamma }} }}^{\left( k \right) }}{{{{\varvec{\Phi }} }}^{H}}{{\left( {{\left( {{\sigma }^{2}} \right) }^{\left( k \right) }}{\mathbf {I}}+\varvec{{\Phi }}{{\varvec{{\Gamma }}}^{\left( k \right) }}{{\varvec{{\Phi }}}^{H}}\right) }^{-1}}{\mathbf {Y}},\nonumber \\ {{\gamma }_{i}}^{\left( k+1 \right) }= & {} \frac{1}{L}{{\left( {{{\mathbf {X}}}^{\left( k+1 \right) }} \right) }_{i\cdot }}{{\left( {{\mathbf {B}}^{\left( k \right) }} \right) }^{-1}}{\left( {{{\mathbf {X}}}^{\left( k+1 \right) }} \right) }_{i\cdot }^{H}+{{\left( {{\varvec{{\Omega }}}^{\left( k+1 \right) }} \right) }_{ii}},\nonumber \\ {{\mathbf {B}}^{\left( k+1 \right) }}= & {} \frac{1}{N}\sum \limits _{i=1}^{N}{\frac{{{\left( {{{\varvec{\Sigma }} }}_{{\mathbf {w}}}^{\left( k \right) } \right) }^{ii}}+{{\left( {{{{\mu }} }}_{{\mathbf {w}}}^{\left( k \right) } \right) }^{i}}{{\left( {{\left( {{{{\mu }} }}_{{\mathbf {w}}}^{\left( k \right) } \right) }^{i}} \right) }^{H}}}{{{\gamma }_{i}}^{\left( k+1 \right) }}},\nonumber \\ {{\left( {{\sigma }^{2}} \right) }^{\left( k+1 \right) }}= & {} \frac{\left\| {\mathbf {z}}-{{\varvec{\Psi }} }{{{{\mu }} }}_{{\mathbf {w}}}^{\left( k \right) } \right\| _{2}^{2}+{{\left( {{\sigma }^{2}} \right) }^{\left( k \right) }}\left[ NL-{\text {tr}}\left( {{{\varvec{\Sigma }} }}_{{\mathbf {w}}}^{\left( k \right) }{{{\varvec{\Sigma }} }}_{0}^{-1} \right) \right] }{ML}, \end{aligned}$$

(12)

where $\varvec{{\Gamma }}={\text {diag}}\left( {{\gamma }_{1}}, \ldots ,{{\gamma }_{N}}\right)$, ${{\left( {\varvec{\Sigma } }_{{\mathbf {w}}}^{\left( k \right) } \right) }^{ii}}$ denotes the ith principal diagonal block with size $L\times L$ in the previous estimate of ${{\varvec{\Sigma }}}_{{\mathbf {w}}}$, and ${{\left( {\varvec{\mu }}_{{\mathbf {w}}}^{\left( k \right) } \right) }^{i}}$ is the ith block-subvector with size $L\times 1$ in the previous estimate of ${{\varvec{\mu }}_{{\mathbf {w}}}}$. The iteration procedure for updating ${{\gamma }_{i}},\mathbf {B}$ and ${{\sigma }^{2}}$ will continue until a predefined criterion is satisfied. For example, if the $k+1$th iteration satisfies ${{{\left\| {{\varvec{\gamma }}^{\left( k+1 \right) }}-{{\varvec{\gamma }}^{\left( k \right) }} \right\| }_{2}}}/{{{\left\| {{\varvec{\gamma }}^{\left( k \right) }} \right\| }_{2}}}\;\le \delta$ where $\delta$ is a small enough positive threshold, the iteration is over. The details of the derivation for the above learning rules refer to Zhang and Rao (2011).

We observe that the quadratic Mahalanobis distance (MD) measure of ${{{\mathbf {X}}}_{i\cdot }}$, ${{{\mathbf {X}}}_{i\cdot }}{{\mathbf {B}}^{-1}}{{{\mathbf {X}}}_{i\cdot }}^{H}$, is applied for the learning rule of ${{\gamma }_{i}}$, while the Euler distance (ED) measure is used for parameter estimation in iRVM-DOA algorithm (Liu et al. 2012). The MD measure can capture the correlations among the elements of ${{{\mathbf {X}}}_{i\cdot }}$, while the ED measure cannot. Theorem 1 in Zhang and Rao (2011) has verified that regardless of the choice of ${{\mathbf {B}}_{i}}$, the global minimum of the cost function $L\left( \left\{ {{\gamma }_{i}} \right\} ,{{\mathbf {B}}_{i}},\sigma \right)$ (see (15)) always leads to the true sparse solution in noiseless case. Supported by this fact, assuming ${{\mathbf {B}}_{i}} = \mathbf {B},i=1,2,\ldots ,N$ is reasonable. In the rest of this paper, $\mathbf {B}$ is parameterized as (Zhang and Rao 2013)

$$\begin{aligned} \mathbf {B}={\text {Toep}}\left( \left[ 1,b,{{b}^{2}},\ldots ,{{b}^{L-1}} \right] \right) . \end{aligned}$$

(13)

As we know, the accuracy of $\varvec{\hat{\gamma }}$ is the core of DOA estimation. However, the accuracy of noise variance estimation ${{\hat{\sigma }}^{2}}$ will affect the accuracy of $\varvec{\hat{\gamma }}$ significantly. Unfortunately, the estimate method of ${{\sigma }^{2}}$ based on learning rule (12) is not effective enough. Instead of (12), we use the specific maximum likelihood estimator (MLE) of ${{\sigma }^{2}}$ given as (Stoica and Nehorai 1989)

$$\begin{aligned} {{\hat{\sigma }}^{2}}=\frac{1}{ML}tr\left[ {{{\mathbf {Y}}}^{H}}\left( I-\hat{\mathbf {A}}{{\left( {{{\hat{\mathbf {A}}}}^{H}}\hat{\mathbf {A}} \right) }^{-1}}\hat{\mathbf {A}} \right) {\mathbf {Y}} \right] , \end{aligned}$$

(14)

where $\hat{\mathbf {A}}=\left[ {\mathbf {a}}\left( {{{\hat{\vartheta }}}_{{{k}_{1}}}} \right) {\mathbf {a}}\left( {{{\hat{\vartheta }}}_{{{k}_{2}}}} \right) \ldots {\mathbf {a}}\left( {{{\hat{\vartheta }}}_{{{k}_{h}}}} \right) \right]$, and ${{\hat{\vartheta }}_{{{k}_{i}}}}$ is the estimate of DOA corresponding to the ith peak of $\varvec{\hat{\gamma }}$.

3.2 Grid refined strategy associated with cost function

In this subsection, a grid refined strategy is presented to mitigate the error of DOA estimation caused by off-grid effect. This strategy includes the coarse and refined estimation stages. At the coarse stage with relatively large grid-interval, we learn $\varvec{\hat{\gamma }}$ by EM iteration (12), followed by finding the peaks of $\varvec{\hat{\gamma }}$. Then at the refined stage with fine grid-interval, the DOA is estimated via local 1-D searching around the bearing-scopes corresponding to the peak-indices of $\varvec{\hat{\gamma }}$ obtained at the coarse stage.

The EM technique at the coarse stage is essentially equivalent to minimizing the cost function (Zhang and Rao 2011)

$$\begin{aligned} L\left( {{\left\{ {{\gamma }_{i}} \right\} }},\mathbf {B},\sigma \right) = \log \left| \varvec{\Sigma } \right| +{{{\mathbf {z}}}^{H}}{{ \varvec{\Sigma }}}^{-1}{\mathbf {z}} \end{aligned}$$

(15)

with $\varvec{\Sigma }= {{\sigma }^{2}}{\mathbf {I}}+\varvec{\Psi }{{\varvec{\Sigma }}_{0}}{{\varvec{\Psi }}^{H}}$. At the refined stage, we aim to minimize the cost function (15) consistently with a fine grid-interval as well. The procedure of the refined stage is derived as follows.

Let $\varvec{\Psi }=\varvec{{\Phi }}\otimes {{{\mathbf {I}}}_{L}}$, $\varvec{{\Phi }}=\left[ {\mathbf {a}}\left( {{\vartheta }_{1}} \right) , \ldots ,{\mathbf {a}}\left( {{\vartheta }_{N}} \right) \right]$, and ${{\varvec{\Sigma }}_{0}}=\varvec{{\Gamma }}\otimes {\mathbf {B}}$. The matrix $\varvec{\Sigma }$ can be represented as

$$\begin{aligned} \varvec{\Sigma }={{\sigma }^{2}}{\mathbf {I}}+\sum \limits _{i=1}^{N}{{{\gamma }_{i}}{\mathbf {a}}\left( {{\vartheta }_{i}} \right) {{{\mathbf {a}}}^{H}}\left( {{\vartheta }_{i}} \right) }\otimes {\mathbf {B}}. \end{aligned}$$

(16)

In order to facilitate the DOA of the kth source, $\varvec{\Sigma }$ is approximated by

$$\begin{aligned} \varvec{\Sigma }\approx {{\varvec{\Sigma }}_{-k}}+{{\tilde{\gamma }}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes {\mathbf {B}}, \end{aligned}$$

(17)

where ${{\varvec{\Sigma }}_{-k}}={{\sigma }^{2}}{\mathbf {I}}+\sum \limits _{i=1,i\ne k,{k}'}^{N}{{{\gamma }_{i}}{\mathbf {a}}\left( {{\vartheta }_{i}} \right) {{{\mathbf {a}}}^{H}}\left( {{\vartheta }_{i}} \right) }\otimes {\mathbf {B}}$. ${{\gamma }_{i}} ( i\ne k,{k}', {k}'=k-1$ or ${k}'=k+1)$, ${\mathbf {B}}$ and ${\sigma }^{2}$ have been learned previously at the coarse stage. ${{\tilde{\gamma }}_{k}}$ and ${{\tilde{\vartheta }}_{k}}$ are the parameters to be estimated.

As we mentioned, we calculate ${{\tilde{\gamma }}_{k}}$ and ${{\tilde{\vartheta }}_{k}}$ by minimizing the cost function $L\left( {{\left\{ {{\gamma }_{i}} \right\} }},{\mathbf {B}},\sigma \right)$ approximately, that is,

$$\begin{aligned} \left\{ {{{\hat{\tilde{\gamma }}}}_{k}},{{{\hat{\tilde{\vartheta }}}}_{k}} \right\} =\mathop {\arg \min }\limits _{{{\tilde{\gamma }_{k}}, {\tilde{\vartheta }}_{k}}\in {{\varTheta }_{k}}}\,\left\{ L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right) \right\} , \end{aligned}$$

(18)

where

$$\begin{aligned} L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right)= & {} \log \left| {{\varvec{\Sigma }}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes {\mathbf {B}} \right| \nonumber \\&+\,{{{\mathbf {z}}}^{H}}{{\left( {{\varvec{\Sigma }}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes {\mathbf {B}} \right) }^{-1}}{\mathbf {z}}, \end{aligned}$$

(19)

and ${{\varTheta }_{k}}$ denotes the searching scope for the kth source. In this paper, we set ${{\varTheta }_{k}}=\left[ {\underline{\vartheta }_{k}}, {\hat{\vartheta }_{k}} \right]$ or ${{\varTheta }_{k}}=\left[ {\hat{\vartheta }_{k}},{{{\bar{\vartheta }}}_{k}} \right]$, where ${\underline{\vartheta }_{k}}$ and ${{\bar{\vartheta }}_{k}}$ are the adjacent directions of DOA estimation ${\hat{\vartheta }_{k}}$ obtained previously according to the peaks of $\varvec{\hat{\gamma }}$ learned at the coarse stage. We repeat (18) for all ${\hat{\vartheta }_{k}}, k=1, 2, \ldots , K$.

To solve (18), the alternating minimization strategy (AMS) on ${{\tilde{\gamma }}_{k}},{{\tilde{\vartheta }}_{k}}$ is utilized. Firstly, the partial derivatives of $L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right)$ with respect to (w.r.t.) ${{\tilde{\gamma }}_{k}}$ and ${{\tilde{\vartheta }}_{k}}$ are calculated as

$$\begin{aligned} \frac{\partial L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right) }{\partial {{{\tilde{\gamma }}}_{k}}}= & {} \sum \limits _{i=1}^{{{r}_{\mathbf {B}}}}{{{\left[ {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {u}_{i}^{\mathbf {B}} \right] }^{H}}\mathbf {V}\left[ {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {u}_{i}^{\mathbf {B}} \right] }, \nonumber \\ \frac{\partial L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right) }{\partial {{{\tilde{\vartheta }}}_{k}}}= & {} {{\tilde{\gamma }}_{k}}{\text {tr}}\left\{ \mathbf {V}\left[ {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{\mathbf {d}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {B} \right] \right\} \nonumber \\&+{{\tilde{\gamma }}_{k}}{\text {tr}}\left\{ \mathbf {V}\left[ \mathbf {d}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {B} \right] \right\} , \end{aligned}$$

(20)

where $\mathbf {V}={{\mathbf {W}}^{-1}}-{{\mathbf {W}}^{-1}} {\mathbf {z}}{{{\mathbf {z}}}^{H}}{{\mathbf {W}}^{-1}}$, $\mathbf {W}= {{\varvec{\Sigma }}_{-k}}+{{\tilde{\gamma }}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {B}$, $\mathbf {B}=\sum \limits _{i=1}^{{{r}_{\mathbf {B}}}} {\mathbf {u}_{i}^{\mathbf {B}}{{\left( \mathbf {u}_{i}^{\mathbf {B}} \right) }^{H}}}$, and $\mathbf {u}_{i}^{\mathbf {B}}$ is the product of the ith singular value and the corresponding eigenvector of $\mathbf {B}$. ${{r}_{\mathbf {B}}}={\text {rank}}\left( \mathbf {B} \right)$, and ${\mathbf {d}}\left( {{{\tilde{\vartheta }}}_{k}} \right) ={\partial {\mathbf {a}} \left( {{{\tilde{\vartheta }}}_{k}} \right) }/{\partial {{{\tilde{\vartheta }}}_{k}}}$. The detail for these derivations is presented in the Appendix 1. Based on (20), the procedure for the refined DOAs estimation is shown as in Algorithm 1.

It is obvious that if the spatial grid-interval $\varDelta \vartheta _{c}$ at the coarse stage is small enough, e.g., $\varDelta \vartheta _{c} ={1}^{\circ }$, then the scope we search is only $K \varDelta \vartheta _{c}$ and much smaller than the whole space $\left[ -{{90}^{\circ }},{{90}^{\circ }} \right]$. Therefore, when the proposed method can mitigate the error of DOA estimation resulted by off-grid effect, it reduces the computational cost of the original BSBL algorithm as well. Meanwhile, since the refined estimation keeps away from the processing of sparse signal recovery, its performance has not been destroyed by the strong coherence among the refined steering vectors.

Remark 1

The iRVM-DOA algorithm in Liu et al. (2012) also employs the ideal of SBL (but not BSBL) and grid-refinement to estimate DOA and has an excellent performance. However, there exists a fact that if we set $\mathbf {B}={{{\mathbf {I}}}_{L}}$, the derived algorithm in this work is exactly equivalent to the iRVM-DOA.

Proposition 1

With ${{\sigma }^{2}}$ fixed and $\mathbf {B}={{{\mathbf {I}}}_{L}}$, the updating formula of ${{\gamma }_{i}}$ at the coarse stage is simplified into

$$\begin{aligned} {{\gamma }_{i}}^{\left( k+1 \right) }=\frac{1}{L}{{\left( {{{\mathbf {X}}}^{\left( k+1 \right) }} \right) }_{i\cdot }}{{\left( {{{\mathbf {X}}}^{\left( k+1 \right) }} \right) }_{i\cdot }}^{H}+{{\left( {{\varvec{{\Omega }}}^{\left( k+1 \right) }} \right) }_{ii}}, \end{aligned}$$

(21)

which is exactly identical to the one used in the iRVM-DOA.

Besides the equivalence at the coarse stage, the equivalence at the refined stage should also be proved. In fact, we have

Proposition 2

When $\mathbf {B}={{{\mathbf {I}}}_{L}}$, the objective function at the refined stage (19) is equal to

$$\begin{aligned} \breve{L}\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right)= & {} L \log \left| {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right| \nonumber \\&+\,tr\left[ {{{\mathbf {Y}}}^{H}}{{\left( {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) }^{-1}}{\mathbf {Y}} \right] , \end{aligned}$$

(22)

with ${{{\breve{{\varvec{\Sigma }} }}}_{-k}}={{\sigma }^{2}}{{{\mathbf {I}}}_{M}}+\sum \limits _{i=1, i\ne k,{k}'}^{N}{{{\gamma }_{i}}{\mathbf {a}}\left( {{\vartheta }_{i}} \right) {{{\mathbf {a}}}^{H}}\left( {{\vartheta }_{i}} \right) }$, which is the objective function at the refined stage in the iRVM-DOA.

The proof of Proposition 2 is given in the Appendix 2.

These results demonstrate that the proposed method generalizes the iRVM-DOA algorithm, and the latter cannot exploit the temporal correlation in each source while the former can.

4 Extension to time-varying manifold

In this section, we extend the proposed method to time-varying manifold scenario, such as wideband sources and time-varying array. In time-varying manifold scenario, the array manifold matrix is associated with time-variable so that the existing sparsity-based methods are no longer in force for DOA estimation. Fortunately, the array output can be represented as a block-sparsity model like (7), provided that the manifold matrix at each snapshot is determinable. Therefore, the proposed method is applicable to time-varying manifold scenario. In this section, wideband sources are considered.

Consider the sources are linear modulated frequency (LFM) signals,

$$\begin{aligned} {{s}_{k}}\left( t \right) ={{u}_{k}}\left( t \right) {{e}^{j2\pi \left( {{f}_{0}}t+\frac{1}{2}{{K}_{c}}{{t}^{2}} \right) }},\quad k=1,2,\ldots ,K, \end{aligned}$$

(23)

where ${{u}_{k}}\left( t \right)$ is the complex amplitude, ${f}_{0}$ is the initial frequency, and ${K}_{c}$ is the chip rate. Then the output of the mth sensor is represented as

$$\begin{aligned} {{y}_{m}}\left( t \right) =\sum \limits _{k=1}^{K}{{{s}_{k}}\left( t \right) {{e}^{j2\pi \left( \frac{1}{2}{{K}_{c}}\tau _{mk}^{2}-t{{K}_{c}}{{\tau }_{mk}}-{{f}_{0}}{{\tau }_{mk}} \right) }}+{{n}_{m}}\left( t \right) },\quad t=1,2,\ldots , L, \end{aligned}$$

(24)

with noise ${{n}_{m}}\left( t \right)$.

Based on the spatial discretization described in Sect. 3.1, the array output takes a matrix-vector form as

$$\begin{aligned} {\mathbf {y}}(t)={\mathbf {A}}({{{\varvec{\Theta }}} },t){\mathbf {s}}(t)+{\mathbf {n}}(t),\quad t=1,2,\ldots ,L, \end{aligned}$$

(25)

where ${\mathbf {y}}(t)={{\left[ {{y}_{1}}(t), \ldots ,{{y}_{M}}(t) \right] }^{T}}$ is the array observation at snapshot t, ${\mathbf {s}}(t)={{\left[ {{s}_{1}}(t), \ldots ,{{s}_{N}}(t) \right] }^{T}}$ is the source signal-vector, and ${\mathbf {n}}(t)={{\left[ {{n}_{1}}(t) ,\ldots ,{{n}_{M}}(t) \right] }^{T}}$ denotes the receiving noise. ${\mathbf {A}}(\varvec{\varTheta },t)$ is the array manifold matrix at snapshot t, which is denoted as

$$\begin{aligned} {\mathbf {A}}(\varvec{\varTheta },t) = \left[ {\mathbf {a}}\left( {{\vartheta }_{1}},t \right) , \ldots ,{\mathbf {a}}\left( {{\vartheta }_{N}},t \right) \right] , \end{aligned}$$

(26)

with bearing-grid $\varvec{\varTheta }={{\left[ {{\vartheta }_{1}}, \ldots ,{{\vartheta }_{N}} \right] }^{T}}$ and steering vector

$$\begin{aligned} {\mathbf {a}}\left( {{\vartheta }_{n}},t \right) ={{\left[ 1,\ldots ,{{e}^{-j2\pi \left( {{f}_{0}}+{{K}_{c}}t \right) {{\tau }_{Mn}}+j\pi {{K}_{c}}\tau _{Mn}^{2}}} \right] }^{T}}. \end{aligned}$$

(27)

Note that ${\mathbf {A}}(\varvec{\varTheta },t)$ changes as snapshot t, so (25) is a time-varying manifold model.

In order to exploit the advantages of the spatial joint sparsity and the temporal correlation, we reformulate (25) as a block-sparsity model in the following.

Let ${\mathbf {w}}$ denote a stack of vector-blocks ${{\mathbf {s}}_{n}}\left( \mathbf {t} \right) ={{\left[ {{s}_{n}}\left( 1 \right) , \ldots ,{{s}_{n}}\left( L \right) \right] }^{T}}$ $(n=1, 2, \ldots , N)$ as

$$\begin{aligned} {\mathbf {w}}={{\left[ \underbrace{{{s}_{1}}\left( 1 \right) ,\ldots ,{{s}_{1}}\left( L \right) }_{{\mathbf {s}}_{1}^{T}\left( \mathbf {t} \right) },\ldots ,\underbrace{{{s}_{N}}\left( 1 \right) ,\ldots ,{{s}_{N}}\left( L \right) }_{{\mathbf {s}}_{N}^{T}\left( \mathbf {t} \right) } \right] }^{T}}, \end{aligned}$$

(28)

Let ${{\mathbf {D}}_{\left[ ij\right] }}={\text {diag}}\left[ {{a}_{ij}}\left( 1 \right) , \ldots ,{{a}_{ij}}\left( L \right) \right] , \, i=1,2,\ldots M, j=1, 2,\ldots ,N$, where ${{a}_{ij}}\left( t \right)$ stands for the element lying at the ith row and the jth column of ${\mathbf {A}}\left( {{\varvec{\Theta }} },t \right)$, then an overcomplete dictionary is constructed as

$$\begin{aligned} \mathbf {D}=\left[ \begin{array}{lccr} {\mathbf {D}}_{\left[ 11\right] } &{} {\mathbf {D}}_{\left[ 12\right] } &{} \cdots &{} {\mathbf {D}}_{\left[ 1N\right] } \\ {\mathbf {D}}_{\left[ 21\right] } &{} {\mathbf {D}}_{\left[ 22\right] } &{} \cdots &{} {\mathbf {D}}_{\left[ 2N\right] } \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {\mathbf {D}}_{\left[ M1\right] } &{} {\mathbf {D}}_{\left[ M2\right] } &{} \cdots &{} {\mathbf {D}}_{\left[ MN\right] } \\ \end{array} \right] \in {{{\mathbb {C}}}^{ML\times NL}} \end{aligned}$$

(29)

Now the array output (25) with multiple snapshots can be reformulated as a block-sparsity model

$$\begin{aligned} {\mathbf {z}}=\mathbf {Dw}+\varvec{\varepsilon }, \end{aligned}$$

(30)

where ${\mathbf {z}}= {\text {vec}}\left( {{{\mathbf {Y}}}^{T}} \right)$ with ${\mathbf {Y}}=\left[ {\mathbf {y}}({{t}_{1}}) \quad \ldots \quad {\mathbf {y}}({{t}_{L}}) \right]$, and $\varvec{\varepsilon }= {\text {vec}}\left( {{{\mathbf {N}}}^{T}} \right)$ with ${\mathbf {N}}=\left[ {\mathbf {n}}({{t}_{1}}) \quad \ldots \quad {\mathbf {n}}({{t}_{L}}) \right]$.

Under the assumption that each source ${{{\mathbf {s}}}_{n}}\left( \mathbf {t} \right)$ is Gaussian distributed, i.e., $p\left( {{{\mathbf {s}}}_{n}}\left( \mathbf {t} \right) ;{{\gamma }_{i}},\mathbf {B} \right) \sim {\mathcal {CN}}\left( {\mathbf {0}},{{\gamma }_{i}}\mathbf {B} \right) ,i=1,2,\ldots ,N$, we have the learning rules (Zhang and Rao 2011) by EM technique

$$\begin{aligned} {{\gamma }_{i}}^{\left( k+1 \right) }= & {} \frac{{\text {tr}}\left[ {{\left( {{\mathbf {B}}^{\left( k \right) }} \right) }^{-1}}\left( {{\left( {{{{\widetilde{{\varvec{\Sigma }} }}}}_{{\mathbf {w}}}}^{\left( k \right) } \right) }^{ii}}+{{\left( {{{{\widetilde{{{\mu }} }}}}_{{\mathbf {w}}}}^{\left( k \right) } \right) }^{i}}{{\left( {{{{\widetilde{{{\mu }} }}}}_{{\mathbf {w}}}}^{\left( k \right) } \right) }^{H}} \right) \right] }{L}, \nonumber \\ {{\mathbf {B}}^{\left( k+1 \right) }}= & {} \frac{1}{N}\sum \limits _{i=1}^{N}{\frac{{{\left( {{{{\widetilde{{\varvec{\Sigma }} }}}}_{{\mathbf {w}}}}^{\left( k \right) } \right) }^{ii}}+{{\left( {{{{\widetilde{{{\mu }} }}}}_{{\mathbf {w}}}}^{\left( k \right) } \right) }^{i}}{{\left( {{{{\widetilde{{{\mu }} }}}}_{{\mathbf {w}}}}^{\left( k \right) }\right) }^{H}}}{{{\gamma }_{i}}^{\left( k+1 \right) }}},\nonumber \\ {{\left( {{\sigma }^{2}} \right) }^{\left( k+1 \right) }}= & {} \frac{\left\| {\mathbf {z}}-\mathbf {D}{{{{\widetilde{{{\mu }} }}}}_{{\mathbf {w}}}}^{\left( k \right) } \right\| _{2}^{2}+{{\left( {{\sigma }^{2}} \right) }^{\left( k \right) }}\left[ NL-{\text {tr}}\left( {{{{\widetilde{{\varvec{\Sigma }} }}}}_{{\mathbf {w}}}}^{\left( k \right) }{{\varvec{\Sigma }}_{0}}^{-1} \right) \right] }{ML}, \end{aligned}$$

(31)

with all the notations similar to the mentioned in Sect. 3. Matrix $\varvec{\Psi }$ in Sect. 3 is replaced by $\mathbf {D}$ here, so that the covariance and mean in (11) become

$$\begin{aligned} {{{{\widetilde{{\varvec{\Sigma }} }}}}_{{\mathbf {w}}}}= & {} {{\left( {{\sigma }^{-2}}{{\mathbf {D}}^{H}}\mathbf {D}+{{\varvec{\Sigma }}_{0}}^{-1} \right) }^{-1}}, \nonumber \\ {{{{\widetilde{{{\mu }} }}}}_{{\mathbf {w}}}}= & {} {{\varvec{\Sigma }}_{0}}{{\mathbf {D}}^{H}}{{\left( {{\sigma }^{2}}{\mathbf {I}}+\mathbf {D}{{\varvec{\Sigma }}_{0}}{{\mathbf {D}}^{H}} \right) }^{-1}}{\mathbf {z}}. \end{aligned}$$

(32)

Remark 2

By setting ${\mathbf {A}}({{\varvec{\Theta }} },t)=\varvec{{\Phi }}({{\varvec{\Theta }} })$, $t=1,2,\ldots ,L$, it is easy to verify that the learning rules in time-varying manifold scenario are the generalization of the counterpart for narrowband scenario, while the latter ones are only used for the fixed manifold model.

Similarly to narrowband scenario, by following the coarse estimation via EM iteration (31), we turn into the refined estimation stage. Based on the cost function

$$\begin{aligned} \widetilde{L}\left( {{\left\{ {{\gamma }_{i}} \right\} }},\mathbf {B},\sigma \right)= & {} \log \left| {{\sigma }^{2}}{\mathbf {I}}+\mathbf {D}{{\varvec{\Sigma }}_{0}}{{\mathbf {D}}^{H}} \right| \nonumber \\&+\,{{{\mathbf {z}}}^{H}}{{\left( {{\sigma }^{2}}{\mathbf {I}}+\mathbf {D}{{\varvec{\Sigma }}_{0}}{{\mathbf {D}}^{H}} \right) }^{-1}}{\mathbf {z}} \end{aligned}$$

(33)

and the approximation

$$\begin{aligned} {\widetilde{{\varvec{\Sigma }} }}= {{\sigma }^{2}}{\mathbf {I}}+\mathbf {D}{{\varvec{\Sigma }}_{0}}{{\mathbf {D}}^{H}}\approx {{{\widetilde{{\varvec{\Sigma }} }}}_{-k}}+{{\tilde{\gamma }}_{k}}\mathbf {D}\left[ {{{\tilde{\vartheta }}}_{k}} \right] {\mathbf {BD}}{{\left[ {{{\tilde{\vartheta }}}_{k}} \right] }^{H}} \end{aligned}$$

(34)

we have the cost function reformulated as

$$\begin{aligned} \widetilde{L}\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right)= & {} \log \left| {{{{\widetilde{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}\mathbf {D}\left[ {{{\tilde{\vartheta }}}_{k}} \right] {\mathbf {BD}}{{\left[ {{{\tilde{\vartheta }}}_{k}} \right] }^{H}} \right| \nonumber \\&+\,{{{\mathbf {z}}}^{H}}{{\left( {{{{\widetilde{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}\mathbf {D}\left[ {{{\tilde{\vartheta }}}_{k}} \right] {\mathbf {BD}}{{\left[ {{{\tilde{\vartheta }}}_{k}} \right] }^{H}} \right) }^{-1}}{\mathbf {z}}. \end{aligned}$$

(35)

where ${{{\widetilde{{\varvec{\Sigma }} }}}_{-k}}={{\sigma }^{2}}{\mathbf {I}}+\sum \limits _{ n=1, n\ne k,{k}'}^{N}{{{\gamma }_{n}}}\mathbf {D}\left[ {{\vartheta }_{n}} \right] {\mathbf {BD}}{{\left[ {{\vartheta }_{n}} \right] }^{H}}$ and

$$\begin{aligned} \mathbf {D}\left[ {{\vartheta }_{n}} \right] =\left[ \begin{array}{c@{~}l} {{\mathbf {D}}_{\left[ 1n\right] }} \\ {{\mathbf {D}}_{\left[ 2n\right] }} \\ \vdots \\ {{\mathbf {D}}_{\left[ Mn\right] }} \end{array} \right] ,n=1,2,\ldots ,N. \end{aligned}$$

(36)

The partial derivatives of $\widetilde{L}\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right)$ w.r.t. ${{\tilde{\gamma }}_{k}}$ and ${{\tilde{\vartheta }}_{k}}$ are calculated as

$$\begin{aligned} \frac{\partial \widetilde{L}\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right) }{\partial {{{\tilde{\gamma }}}_{k}}}= & {} \sum \limits _{i=1}^{{{r}_{\mathbf {B}}}}{{{\left( \mathbf {D}\left[ {{{\tilde{\vartheta }}}_{k}} \right] \mathbf {u}_{i}^{\mathbf {B}} \right) }^{H}}\widetilde{\mathbf {V}}\left( \mathbf {D}\left[ {{{\tilde{\vartheta }}}_{k}} \right] \mathbf {u}_{i}^{\mathbf {B}} \right) }, \nonumber \\ \frac{\partial \widetilde{L}\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right) }{\partial {{{\tilde{\vartheta }}}_{k}}}= & {} {{\tilde{\gamma }}_{k}}{\text {tr}}\left\{ \widetilde{\mathbf {V}}\mathbf {D}\left[ {{{\tilde{\vartheta }}}_{k}} \right] \mathbf {B}{{\left( \mathbf {F}\left[ {{{\tilde{\vartheta }}}_{k}} \right] \right) }^{H}} \right\} \nonumber \\&+\,{{\tilde{\gamma }}_{k}}{\text {tr}}\left\{ \widetilde{\mathbf {V}}{\mathbf {F}}\left[ {{{\tilde{\vartheta }}}_{k}} \right] \mathbf {B}{{\left( \mathbf {D}\left[ {{{\tilde{\vartheta }}}_{k}} \right] \right) }^{H}} \right\} , \end{aligned}$$

(37)

where $\mathbf {\widetilde{V}}={{\widetilde{\mathbf {W}}}^{-1}} -{{\widetilde{\mathbf {W}}}^{-1}} {\mathbf {z}}{{{\mathbf {z}}}^{H}}{{\widetilde{\mathbf {W}}}^{-1}}$, $\widetilde{\mathbf {W}}= {{\widetilde{{{\varvec{\Sigma }} }}}_{-k}}+{{\tilde{\gamma }}_{k}}\mathbf {D}\left[ {{{\tilde{\vartheta }}}_{k}} \right] {\mathbf {BD}}{{\left[ {{{\tilde{\vartheta }}}_{k}} \right] }^{H}}$ and $\mathbf {F}\left[ {{{\tilde{\vartheta }}}_{k}} \right] ={\partial \mathbf {D}\left[ {{{\tilde{\vartheta }}}_{k}} \right] }/{\partial {{{\tilde{\vartheta }}}_{k}}}\;$. The procedure for the refined estimation in time-varying manifold scenario is similar to Algorithm 1 for narrowband scenario, so we do not show it again.

Remark 3

Similarly as the discussion in Sect. 3, in time-varying manifold scenario we replace the learning rule of noise variance ${{\sigma }^{2}}$ with the MLE

$$\begin{aligned} {{\hat{\sigma }}^{2}}=\frac{1}{M}\left[ {{{\mathbf {z}}}^{H}}\left( I-\hat{\mathbf {D}}{{\left( {{{\hat{\mathbf {D}}}}^{H}}\hat{\mathbf {D}} \right) }^{-1}}\hat{\mathbf {D}} \right) {\mathbf {z}} \right] , \end{aligned}$$

(38)

where $\hat{\mathbf {D}}=\left[ \mathbf {D}\left[ {{{\hat{\vartheta }}}_{{{k}_{1}}}} \right] \mathbf {D}\left[ {{{\hat{\vartheta }}}_{{{k}_{2}}}} \right] \ldots \mathbf {D}\left[ {{{\hat{\vartheta }}}_{{{k}_{h}}}} \right] \right]$, ${{\hat{\vartheta }}_{{{k}_{i}}}}$ is the DOA estimation corresponding to the ith peak of $\hat{{{\varvec{\gamma }}}}$, and $\mathbf {D}\left[ {{{\hat{\vartheta }}}_{{{k}_{1}}}} \right]$ has an identical form as $\mathbf {D}\left[ {{\vartheta }_{n}} \right]$.

Remark 4

While the learning rules (31) at the coarse stage are proved to be the extension of that in narrowband scenario, the generalization at the refined stage is obvious in terms of Proposition 3.

Proposition 3

Let ${\mathbf {A}}({{\varvec{\Theta }} },t)=\varvec{{\Phi }}({{\varvec{\Theta }} })$, we have that the cost function (35) in time-varying scenario equals to the cost function (19) in narrowband scenario.

In summary, we propose a unified method, which utilizes the spatial sparsity and exploits the temporal correlation of sources simultaneously, to accomplish the DOA estimation for any time-varying manifold scenario in this section. This method is called as SaTC-E, which means exploiting the sparsity and temporal correlation simultaneously.

5 Experiment results

In this section, several experiments are carried out to compare SaTC-E with some classical algorithms, including MUSIC Schmidt (1986), L1-SVD (Malioutov et al. 2005), iRVM-DOA (Liu et al. 2012) for narrowband scenario, and two-side correlation transformation (TCT; Valaee and Kabal 1995), coherent signal-subspace method (CSSM; Wang and Kaveh 1985), wideband iRVM-DOA (WiRVM-DOA; Liu et al. 2012) for wideband scenario. L1-SVD algorithm is taken as one of the representatives of the sparsity-based methods.

The setups are as follows. For narrowband scenario, the incident sources are two complex sinusoid signals with carrier frequency ${{f}_{0}}=2.143$ GHz, while for wideband scenario the sources are two LFM signals. The center frequency, the bandwidth, and the chip rate of LFMs are ${{f}_{c}}=2.118$ GHz, $B=50$ MHz, and ${{K}_{c}}={{10}^{3}}$ , respectively. The directions of the incident sources are ${-6.54}^{\circ }$ and ${6.54}^{\circ }$. The uniform linear array (ULA) is considered. The number of sensors is $M=8$, and the inter-sensor spacing is half the wavelength. The number of snapshots is L. The number of sources is assumed to be known for MUSIC, TCT, and CSSM. The uniform spatial grids are equipped, and the grid-intervals are set to $\varDelta {{\vartheta }_{c}}$ for SaTC-E, iRVM-DOA and WiRVM-DOA at the coarse stage and $\varDelta {{\vartheta }_{r}}$ for MUSIC, TCT and CSSM, respectively. The searching precision at the refined stage is also set to $\varDelta {{\vartheta }_{r}}$ for iRVM-DOA, WiRVM-DOA and SaTC-E. The stopping criterion of EM iteration for SaTC-E is ${{{\left\| {{\varvec{\gamma }}^{\left( k+1 \right) }}-{{\varvec{\gamma }}^{\left( k \right) }} \right\| }_{2}}}/{{{\left\| {{\varvec{\gamma }}^{\left( k \right) }} \right\| }_{2}}}\;\le \delta$ with $\delta ={{10}^{-4}}$, or that EM iteration achieves 3000 times. If no special mention, the covariance matrix for SaTC-E is calculated as $\mathbf {B}={\text {Toep}}\left( \left[ 1,b,{{b}^{2}},\ldots ,{{b}^{L-1}} \right] \right)$ with $b=-0.99$. L1-SVD is implemented as in Malioutov et al. (2005).

5.1 Real data tests

In this subsection, we utilize the real data to present the spectra of SaTC-E and the compared methods and illustrate the performance of SaTC-E. The real data was collected by the antenna ULA in a microwave black-room. The sampling frequency was 500 Msps. Before DOA estimation, the array output has already been pre-treated with phase correction and amplitude correction.

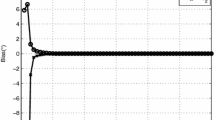
Firstly, we compare the performance of SaTC-E using the learning rule of ${{\sigma }^{2}}$ with that using the MLE of ${{\sigma }^{2}}$. The sources are wideband LFM signals. Ten snapshots are used. The spectra are shown in Fig. 1. The spectrum-peaks using the MLE of ${{\sigma }^{2}}$ are much sharper than those using the learning rule of ${{\sigma }^{2}}$. The reason is that ${{\hat{\sigma }}^{2}}$ learned from the cost function (33) is not accurate enough for the specific application of DOA estimation, while the MLE (38) is derived from the spectral analysis of DOA estimation. According to this result, we employ MLE to estimate ${{\sigma }^{2}}$ for SaTC-E in the following experiments.

Fig. 1

Spatial spectra of SaTC-E using the learning rule and the MLE of ${{\sigma }^{2}}$, respectively. The sources are two LFM signals. The number of snapshots is $L=10$

For narrowband scenario, Fig. 2a plots the spatial spectrum of MUSIC and spectra of L1-SVD, iRVM-DOA and SaTC-E at the coarse stage. The spectra at the refined stage of SaTC-E and iRVM-DOA within the local scope are displayed in Fig. 2b, c. The number of snapshots is $L=20$, the grid-intervals are $\varDelta {{\vartheta }_{c}}={{1}^{\circ }}$ and $\varDelta {{\vartheta }_{r}}={0.01}^{\circ }$. The peaks of SaTC-E are much shaper than those of MUSIC and L1-SVD, and thus SaTC-E surpasses MUSIC and L1-SVD. Meanwhile, SaTC-E has similar performance to iRVM-DOA. The counterparts for wideband scenario are shown in Fig. 3. The grid-intervals are set to $\varDelta {{\vartheta }_{c}}={{2}^{\circ }}$ and $\varDelta {{\vartheta }_{r}}={0.01}^{\circ }$. Although the number of snapshots used by TCT and CSSM ($L=320$) is much larger than that used by SaTC-E ($L=10$), the spectrum of SaTC-E is more remarkable than those of TCT and CSSM. On the other hand, the spectrum of WiRVM-DOA surfers several false peaks. The comparison results illustrate that SaTC-E is applicable to DOA estimation both for narrowband and wideband, even it uses only a few snapshots.

Fig. 2

a Spatial spectrum of MUSIC and spatial spectra of L1-SVD, iRVM-DOA and SaTC-E at the coarse stage, and b, c spatial spectra of SaTC-E and iRVM-DOA at the refined stage. The two sources are narrowband. The number of snapshots is $L=20$

Fig. 3

a Spatial spectra of TCT and CSSM, and spatial spectra of WiRVM-DOA and SaTC-E at the coarse stage, and b, c spatial spectra of SaTC-E and WiRVM-DOA at the refined stage. The sources are two LFM signals. The number of snapshots for TCT and CSSM is $L=320$, while the number of snapshots for WiRVM-DOA and SaTC-E is $L=10$

5.2 Numerical simulations

In this subsection, we analyze the statistical performance of SaTC-E. Monte Carlo trials are carried out to evaluate the statistical performance of the various methods. The statistical performance is measured by root mean square error (RMSE) of DOA estimation, which is calculated as

$$\begin{aligned} \mathrm {RMSE}=\sqrt{\frac{1}{K\cdot MC}{\sum \limits _{mc=1}^{MC}{\sum \limits _{k=1}^{K} {{{\left( {{{\hat{\theta }}}_{k}}^{\left( mc \right) }-{{\theta }_{k}}^{\left( mc \right) } \right) }^{2}}}}}}, \end{aligned}$$

(39)

where MC is the total number of Monte Carlo trials, and ${{\hat{\theta }}_{k}}^{\left( mc \right) }$ is the estimate of the true direction ${{\theta }_{k}}^{\left( mc \right) }$of the kth source in the mcth trial. 200 independent trials are carried out to calculate the RMSE.

Before comparing the RMSE, we show the iteration convergence property of $\varvec{\gamma }$ updated as (12). Two narrowband sources are considered. The SNR is set to 20 dB, and the number of snapshots is $L=20$. We repeat 30 trials with 1000 iterations in each trial. The relative update ratio of $\varvec{\gamma }$, ${{{\left\| {{\varvec{\gamma }}^{\left( k+1 \right) }}-{{\varvec{\gamma }}^{\left( k \right) }} \right\| }_{2}}}/{{{\left\| {{\varvec{\gamma }}^{\left( k \right) }} \right\| }_{2}}}\;$, is presented in Fig. 4. The curves indicate that in each trial, the estimate of $\varvec{\gamma }$ is approximately convergent with some small perturbations.

Fig. 4

The relative update ratio of $\varvec{\gamma }$ in narrowband scenario. SNR=20 dB and $L=20$

Assume that two temporally correlated sources imping on the 8-sensor ULA from directions $-{{5}^{\circ }}+\varDelta \theta$ and ${{5}^{\circ }}+\varDelta \theta$, respectively, with $\varDelta \theta$ produced uniformly and randomly within the spatial scope $\left[ -{{1}^{\circ }},{1}^{\circ } \right]$. The grid-intervals are $\varDelta {{\vartheta }_{c}}={1}^{\circ }$ and $\varDelta {{\vartheta }_{r}}={0.01}^{\circ }$, and thus the source directions are off-grid usually. Each source is generated as AR(1) process, and thus the AR coefficient indicates the temporal correlation of this source. In this simulation, the AR coefficients of two sources in each trial are randomly chosen from [0.8, 1). The RMSEs of DOA estimation with respect to SNR are presented in Fig. 5. The number of snapshots is $L=20$. The SNR varies from $-6$ to 20 dB with step 2 dB. The result shows that the RMSE of SaTC-E is very close to Cramer–Rao lower bound (CRLB) and performs as well as iRVM-DOA algorithm when SNR is larger than 0 dB. It significantly outperforms L1-SVD and MUSIC. Both for Fig. 5 and Fig. 6, when SNR is low, e.g., SNR ${<}0$ dB, the RMSE of SaTC-E is larger than iRVM-DOA. This is because when the noise dominates the model error, the temporal correlation modeled by $\mathbf {B}$ maybe not accurate enough.

Fig. 5

The RMSEs versus the SNR for two temporally correlated sources produced by AR(1) process. The number of snapshots is $L=20$

Fig. 6

The RMSEs versus the SNR for two complex sinusoid sources. The number of snapshots is $L=20$

In the following simulations, we consider a common scenario in array signal processing that two complex sinusoids sources imping on the 8-sensor ULA. Other parameters are set as the simulation in Fig. 5. The complex sinusoid signal at time t is represented as

$$\begin{aligned} {{s}_{k}}\left( t \right) ={{u}_{k}}\left( t \right) \exp \left( 2\pi {{f}_{0}}t \right) ,\qquad k=1,2, \end{aligned}$$

(40)

where the amplitude ${{u}_{k}}\left( t \right)$ obeys a Gaussian distribution with mean 100 and variance 5.

The RMSEs of DOA estimation versus the SNR are shown in Fig. 6. The SNR varies from $-6$ to 20 dB with step 2 dB. The number of snapshots is $L=20$. In this simulation, when SNR is high enough (e.g., SNR exceeds 0 dB), the RMSE of SaTC-E is very close to CRLB, while MUSIC fails in each SNR. In particular, the result in Fig. 6 indicates that SaTC-E surpasses the other methods including L1-SVD, MUSIC, and iRVM-DOA in middle SNR. When SNR is high, e.g., SNR $\ge$ 10 dB in this simulation, SaTC-E significantly outperforms L1-SVD and MUSIC, and meanwhile it has quite similar performance to iRVM-DOA.

Figure 7 exhibits the curves of RMSE versus the number of snapshots. The number of snapshots L varies from 5 to 40. SNR is set to 0 dB. When L is large, e.g., $L > 10$ in this simulation, the RMSE of SaTC-E is smaller than that of iRMV-DOA. Furthermore, the RMSE of SaTC-E is much smaller than those of L1-SVD and MUSIC all along. The bad performances at SNR = 9 and 12 dB are caused by few outliers among the 200 Monte Carlo trials. This result demonstrates that SaTC-E has a superior performance of DOA estimation even uses a few snapshots.

Fig. 7

The RMSEs versus the number of snapshots. SNR$=0$ dB

Finally, we illustrate numerically that our method SaTC-E can reduce the computational complexity of BSBL proposed in Zhang and Rao (2011) for the problem of DOA estimation. TMSBL (Zhang and Rao 2011) is utilized as the original BSBL algorithm. The sources are produced as (40), the number of snapshots are $L=20$, and the SNR varies from $-4$ to 20 dB with step 4 dB. The coarse grid-interval for SaTC-E is $\varDelta {{\vartheta }_{c}}={2}^{\circ }$ and the refined one is $\varDelta {{\vartheta }_{r}}={0.1}^{\circ }$. The grid-interval for TMSBL is $\varDelta {\vartheta }={0.1}^{\circ }$, too. This experiment is implemented in Matlab v.7.8.0 on a PC with a Window XP system and a 4 GHz CPU. The average running times of SaTC-E and TMSBL over 200 trials are presented in Table 1. The data in Table 1 indicates that SaTC-E is much faster than TMSBL as our expectation. In addition, we find that TMSBL almost can not recover the power $\varvec{\gamma }$, especially in low SNR, because of the serious correlation between the adjacent steering vectors. Consequently, TMSBL does no longer work for DOA estimation, while SaTC-E has improved performance with much higher efficiency.

Table 1 The average running time for DOA estimation (in seconds)

6 Conclusion

A new method called SaTC-E has been proposed to estimate DOA for time-varying manifold scenario, which treats the scenario of narrowband stationary sources as a special case. SaTC-E exploits the spatial joint sparsity and temporal correlation of sources simultaneously via the BSBL methodology. In order to enhance the adaptation of BSBL algorithm to DOA estimation, SaTC-E utilizes the MLE of noise variance to take the place of the learning rule used in original BSBL algorithm. Meanwhile, it establishes a grid refined strategy to mitigate the estimate error caused by off-grid effect and reduce the computational complex of BSBL with improved performance. SaTC-E has some merits, including improved resolution, requirement of a few snapshots, no prior knowledge of source number, and applicability to spatially and temporally correlated sources. Real data tests and numerical simulations have been implemented to demonstrate the superiority of SaTC-E.

Appendices

Appendix 1

The detail for the derivatives (20) is presented as follows.

Let $\mathbf {W}= {{\varvec{\Sigma }}_{-k}}+{{\tilde{\gamma }}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {B},$ and the derivatives are expressed as

$$\begin{aligned} \frac{\partial L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right) }{\partial {{{\tilde{\gamma }}}_{k}}}= & {} \frac{\partial \ln \left| \mathbf {W} \right| }{\partial {{{\tilde{\gamma }}}_{k}}}+\frac{\partial {{{\mathbf {z}}}^{H}}{{\mathbf {W}}^{-1}}{\mathbf {z}}}{\partial {{{\tilde{\gamma }}}_{k}}}\\= & {} \left\langle \frac{\partial \ln \left| \mathbf {W} \right| }{\partial \mathbf {W}},\frac{\partial \mathbf {W}}{\partial {{{\tilde{\gamma }}}_{k}}} \right\rangle +\left\langle \frac{\partial {{{\mathbf {z}}}^{H}}{{\mathbf {W}}^{-1}}{\mathbf {z}}}{\partial \mathbf {W}},\frac{\partial \mathbf {W}}{\partial {{{\tilde{\gamma }}}_{k}}} \right\rangle ,\\ \frac{\partial L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right) }{\partial {{{\tilde{\vartheta }}}_{k}}}= & {} \frac{\partial \ln \left| \mathbf {W} \right| }{\partial {{{\tilde{\vartheta }}}_{k}}}+\frac{\partial {{{\mathbf {z}}}^{H}}{{\mathbf {W}}^{-1}}{\mathbf {z}}}{\partial {{{\tilde{\vartheta }}}_{k}}} \\= & {} \left\langle \frac{\partial \ln \left| \mathbf {W} \right| }{\partial \mathbf {W}},\frac{\partial \mathbf {W}}{\partial {{{\tilde{\vartheta }}}_{k}}} \right\rangle +\left\langle \frac{\partial {{{\mathbf {z}}}^{H}}{{\mathbf {W}}^{-1}}{\mathbf {z}}}{\partial \mathbf {W}},\frac{\partial \mathbf {W}}{\partial {{{\tilde{\vartheta }}}_{k}}} \right\rangle . \end{aligned}$$

Employing the matrix differential formulas that

$$\begin{aligned} \frac{\partial \ln \left| \mathbf {W} \right| }{\partial \mathbf {W}}= & {} {{\mathbf {W}}^{-1}}, \\ \frac{\partial \mathbf {W}}{\partial {{{\tilde{\gamma }}}_{k}}}= & {} {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {B}, \\ \frac{\partial \mathbf {W}}{\partial {{{\tilde{\vartheta }}}_{k}}}= & {} {{\tilde{\gamma }}_{k}}\left( {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{\mathbf {d}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) +\mathbf {d}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) \otimes \mathbf {B}, \\ \frac{\partial {{{\mathbf {z}}}^{H}}{{\mathbf {W}}^{-1}}{\mathbf {z}}}{\partial \mathbf {W}}= & {} -{{\mathbf {W}}^{-1}}{\mathbf {z}}{{{\mathbf {z}}}^{H}} {{\mathbf {W}}^{-1}}, \end{aligned}$$

where $\mathbf {W}$ is a conjugated symmetrical matrix, and $\mathbf {d}\left( {{{\tilde{\vartheta }}}_{k}}\right) ={\partial {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}}\right) }/{\partial {{{\tilde{\vartheta }}}_{k}}}\;$, and let $\mathbf {V}={{\mathbf {W}}^{-1}}-{{\mathbf {W}}^{-1}}{\mathbf {z}} {{{\mathbf {z}}}^{H}}{{\mathbf {W}}^{-1}}$, we have

$$\begin{aligned} \frac{\partial L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right) }{\partial {{{\tilde{\gamma }}}_{k}}}= & {} \left\langle \mathbf {V},{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {B} \right\rangle \\= & {} {\text {tr}}\left\{ \left( \mathbf {V} \right) \left[ {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {B} \right] \right\} , \\ \frac{\partial L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right) }{\partial {{{\tilde{\vartheta }}}_{k}}}= & {} {{{\tilde{\gamma }}}_{k}}\left\langle \mathbf {V},\left( {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{\mathbf {d}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) +\mathbf {d}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) \otimes \mathbf {B} \right\rangle \\= & {} {{{\tilde{\gamma }}}_{k}}{\text {tr}}\left\{ \mathbf {V}\left[ \left( {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{\mathbf {d}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) \otimes \mathbf {B} \right] \right\} \\&+ \, {{{\tilde{\gamma }}}_{k}}{\text {tr}}\left\{ \mathbf {V}\left[ \left( \mathbf {d}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) \otimes \mathbf {B} \right] \right\} . \end{aligned}$$

In terms of the singular value decomposition (SVD), $\mathbf {B}$ can be rewritten as

$$\begin{aligned} \mathbf {B}=\sum \limits _{i=1}^{{{r}_{\mathbf {B}}}} {\mathbf {u}_{i}^{\mathbf {B}}{{\left( \mathbf {u}_{i}^{\mathbf {B}} \right) }^{H}}} \end{aligned}$$

with ${r}_{\mathbf {B}}={\text {rank}}\left( \mathbf {B} \right)$ and $\mathbf {u}_{i}^\mathbf {B}$ being the product of the ith singular value and the associated eigenvector of $\mathbf {B}$, So that

$$\begin{aligned} \quad \frac{\partial L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right) }{\partial {{{\tilde{\gamma }}}_{k}}}= & {} {\text {tr}}\left\{ \mathbf {V}\left[ {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \sum \limits _{i=1}^{{{r}_{\mathbf {B}}}} {\mathbf {u}_{i}^{\mathbf {B}}{{\left( \mathbf {u}_{i}^{\mathbf {B}} \right) }^{H}}} \right] \right\} \\= & {} \sum \limits _{i=1}^{{{r}_{\mathbf {B}}}}{{\text {tr}}\left\{ \mathbf {V}\left[ \left( {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {u}_{i}^{\mathbf {B}} \right) \left( {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes {{\left( \mathbf {u}_{i}^{\mathbf {B}} \right) }^{H}} \right) \right] \right\} }\\= & {} \sum \limits _{i=1}^{{{r}_{\mathbf {B}}}}{{{\left[ {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {u}_{i}^{\mathbf {B}} \right] }^{H}}\mathbf {V}\left[ {\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \otimes \mathbf {u}_{i}^{\mathbf {B}} \right] }. \end{aligned}$$

The derivation is accomplished.

Appendix 2

Proof of Proposition 2

when $\mathbf {B}={{{\mathbf {I}}}_{L}}$, we get ${{\varvec{\Sigma }}_{-k}}={{{\breve{{\varvec{\Sigma }} }}}_{-k}}\otimes {{{\mathbf {I}}}_{L}}$, and then $L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right)$ can be rewritten as

$$\begin{aligned} L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right)= & {} \log \left| \left( {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) \otimes {{{\mathbf {I}}}_{L}} \right| \\&+\,{{{\mathbf {z}}}^{H}}{{\left( \left( {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) \otimes {{{\mathbf {I}}}_{L}} \right) }^{-1}}{\mathbf {z}}, \end{aligned}$$

and the first term of $L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right)$ equals to the first term of $\breve{L}\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right)$, because

$$\begin{aligned}&\log \left| \left( {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) \otimes {{{\mathbf {I}}}_{L}} \right| \\&\quad = \log \left( {{\left| {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right| }^{L}}{{\left| {{{\mathbf {I}}}_{L}} \right| }^{M}} \right) \\&\quad =\log {{\left| {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right| }^{L}} \\&\quad = L\log \left| {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right| . \end{aligned}$$

Let $\mathbf {Q}= {{\left( {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) }^{-1}}$, and write the array output matrix ${\mathbf {Y}}$ as the form of

$$\begin{aligned} {\mathbf {Y}}=\left[ \begin{array}{c@{~}l} {{{\mathbf {y}}}_{1}} \\ {{{\mathbf {y}}}_{2}} \\ \vdots \\ {{{\mathbf {y}}}_{M}} \\ \end{array} \right] \in {{{\mathbb {C}}}^{M\times L}},\, {{{\mathbf {y}}}_{i}}=\left[ {{y}_{i1}} \, {{y}_{i2}} \, \ldots \, {{y}_{iL}} \right] \in {{{\mathbb {C}}}^{1\times L}}, \end{aligned}$$

so that ${{{\mathbf {z}}}^{T}}=\left[ {{{\mathbf {y}}}_{1}} \, {{{\mathbf {y}}}_{2}} \, \ldots \, {{{\mathbf {y}}}_{M}} \right] \in {{{\mathbb {C}}}^{1\times ML}}$. The second terms of $L\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right)$ and $\breve{L}\left( {{{\tilde{\gamma }}}_{k}},{{{\tilde{\vartheta }}}_{k}} \right)$ can be calculated, respectively, as

$$\begin{aligned}&{{{\mathbf {z}}}^{H}}{{\left( \left( {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) \otimes {{{\mathbf {I}}}_{L}} \right) }^{-1}}{\mathbf {z}}\\&\quad ={{{\mathbf {z}}}^{H}}\left( \mathbf {Q}\otimes {{{\mathbf {I}}}_{L}} \right) {\mathbf {z}}\\&\quad =\sum \limits _{i=1}^{M}{\sum \limits _{j=1}^{M}{{{q}_{ij}} {{{\bar{\mathbf{y}}}}_{i}}{\mathbf {y}}_{j}^{T}}},\\&{\text {tr}}\left( {{{\mathbf {Y}}}^{H}}{{\left( {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) }^{-1}}{\mathbf {Y}} \right) \\&\quad ={\text {tr}}\left( \mathbf {QY}{{{\mathbf {Y}}}^{H}} \right) \\&\quad =\sum \limits _{i=1}^{M}{\sum \limits _{j=1}^{M}{{{q}_{ij}} {{{\mathbf {y}}}_{j}}{\mathbf {y}}_{i}^{H}}}. \end{aligned}$$

Because of ${{{\mathbf {y}}}_{j}}{\mathbf {y}}_{i}^{H}= \sum \limits _{k=1}^{L}{{{y}_{jk}}{{{\bar{y}}}_{ik}}} ={{\bar{\mathbf {y}}}_{i}}{\mathbf {y}}_{j}^{T}$, we have

$$\begin{aligned}&{{{\mathbf {z}}}^{H}}{{\left( \left( {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) \otimes {{{\mathbf {I}}}_{L}} \right) }^{-1}}{\mathbf {z}}\\&\quad = {\text {tr}}\left( {{{\mathbf {Y}}}^{H}}{{\left( {{{{\breve{{\varvec{\Sigma }} }}}}_{-k}}+{{{\tilde{\gamma }}}_{k}}{\mathbf {a}}\left( {{{\tilde{\vartheta }}}_{k}} \right) {{{\mathbf {a}}}^{H}}\left( {{{\tilde{\vartheta }}}_{k}} \right) \right) }^{-1}}{\mathbf {Y}} \right) , \end{aligned}$$

and thus Proposition 2 is proved. $\square$