1 Introduction

DOA estimation is an important research topic in array signal processing, and it is widely applied in radar, sonar and other fields. The subspace-based direction-of-arrival (DOA) estimation methods such as MUSIC [8, 14] and ESPRIT [13] have high resolution. However, they need the accurate information of the number of sources to separate the signal and noise subspace. In recent decades, the sparse representation (SR) DOA estimation methods have been widely studied because they do not require the accurate knowledge of the number of sources and gain higher DOA resolution than the subspace-based methods. The \(l_1\)-SVD method [9] estimates the DOA by sparsely representing the signal subspace obtained from singular value decomposition (SVD) of the data received by an array. Due to the SVD involved, the \(l_1\)-SVD method requires the assumed number of sources. However, it is more robust to the mistakes in estimating the number of sources, compared to the subspace-based methods. Based on the acoustic intensity principle and sparse representation technique, the \(l_1\)-SRLSV method obtains high-resolution DOA estimation without knowing the number of sources [17]. The \(l_1\)-SRACV method [19] uses the sparse representation of the array covariance matrix for DOA estimation, which does not require the information of the number of sources and improves the robustness in a low signal-to-noise ratio (SNR). However, it leads to high computational complexity due to sparse representation of the array covariance matrix. SPICE [15] uses a robust covariance-fitting criterion and iterative method to estimate the sparse parameters in linear models to obtain DOA estimation, while LIKES [16] estimates the sparse parameters according to the maximum-likelihood principle. LIKES obtains more accurate parameter estimation performance than SPICE at the cost of increasing computational burden. In [4], the Khatri–Rao product was explored to cast the array covariance matrix SR DOA estimation as the SR problem of only a single measurement vector, which significantly reduces the computational load. Based on the vectorization of the array covariance matrix, a DOA estimation method is obtained by employing the sparse recovery concept and maximum likelihood estimation criteria, which gains high computational efficiency [6]. Based on the matrix completion theory, the MC-SRSSVWL1 method proposes a SR method to combine the second-order statistical vector and weighted \(l_1\)-norm for DOA estimation, which has high angle estimation accuracy and resolution in low SNRs [2].

In order to eliminate the influence of noise on DOA estimation, Tian Ye proposed a SR-based covariance differencing method (SR-CD) [20],which applied the SR on the difference of the array covariance matrix and its transpose. The SR-CD method has high resolution and DOA estimation accuracy. In addition, it overcomes the drawbacks that the conventional covariance differencing methods require multiple estimates of the array covariance matrix [11, 18] or has the angle ambiguity issue [12]. Moreover, its computational complexity is clearly lower than the \(l_1\)-SVD and \(l_1\)-SRACV methods. It was demonstrated by simulation that the spatial spectrum of SR-CD method has false peaks, which can be recognized by the sign of the spatial spectrum. In this paper, the reason why the SR-CD method produces false peaks is analyzed. It is also proved that the SR-CD method fails when the sources are with the DOAs of 0 degree and/or the symmetric DOAs. In order to overcome the shortcomings of the SR-CD method, this paper proposes a SR-based DOA estimation method by applying SR on the beamspace and element-space covariance differencing, named as SR-BECD. Similar to the SR-CD method, the SR-BECD method eliminates noise by using the covariance differencing and it has a low computational complexity. Different from the SR-CD method, it employs the covariance differencing in the beamspace and element-space instead of the covariance differencing between the array covariance matrix and its transpose, avoiding the false peaks encountered in the SR-CD method. Simulation results demonstrate its superior performance in angle resolution and estimation accuracy in low SNRs. In addition, it is not limited to specific arrays such as a uniform linear array.

2 Data Model

We assume that K far-field narrow-band stationary source signals impinging on an array with M elements. By taking the first element as the reference, the data received by the array at time t can be expressed as:

$$\begin{aligned} {\varvec{x}}(t) = {{\varvec{A}}}{\varvec{s}}(t) + {{\varvec{n}}}(t) \end{aligned}$$
(1)

where \({\varvec{x}(t)} =[x_1(t), \cdots , x_M(t)]^{T}\) is the M-dimensional data received by the array, \(x_m(t)\)(m=1,...,M) is the data of the m-th array element at time t. \({{\varvec{A}}} = [{{\varvec{a}}}(\theta _1),{\varvec{a}}(\theta _2),\cdots ,{{\varvec{a}}}(\theta _K)]\) is the matrix of steering vectors, \({\varvec{a}}(\theta _k)\) is the M-dimensional steering vector, \(\theta _k\) is the DOA of the k-th source. \( {\varvec{s}(t)} =[s_1(t), \cdots , s_K(t)]^{T}\) is the K-dimensional source signal vector, \(s_k(t)\) is the k-th source signal. \({\varvec{n}(t)} =[n_1(t), \cdots , n_M(t)]^{T}\) is the M-dimensional noise vector, and \(n_m(t)\) is the noise of the m-th array element at time t. We give the following assumptions of source signals and noises:

  1. (1)

    The source signals are uncorrelated.

  2. (2)

    The noises at different elements are uncorrelated with each other and have zero mean and same covariance.

  3. (3)

    The source signals and noises are uncorrelated.

Under the aforementioned assumptions, the array covariance matrix \(\varvec{R}\) is expressed as:

$$\begin{aligned} {\varvec{R}}= & {} {\mathrm{E}} \left[ {\varvec{x}}(t) {\varvec{x}^{H}} (t) \right] \nonumber \\= & {} {\varvec{A}}{\varvec{R}_s} {\varvec{A}^{H}} + {\sigma ^{2}\varvec{I}_{M}}\nonumber \\= & {} \sum _{k=1}^{K} {p_k} {\varvec{a}}\left( \theta _k\right) {\varvec{a}}^{H}\left( \theta _k\right) + {\sigma ^{2}\varvec{I}_{M}} \end{aligned}$$
(2)

where \(\mathrm{E}[\cdot ]\) is the expectation, \((\cdot )^{H}\) is the conjugate transpose, \({\varvec{R}_s}={\mathrm{E}} \{ {\varvec{s}}(t) {\varvec{s}^{H}} (t) \}\) is the covariance matrix of source signals, \(p_k\) is the power of the k-th source signal, \(\sigma ^{2}\) is the noise variance, and \(\varvec{I}_{M}\) is the identity matrix.

3 Analysis on SR-CD Method

The methodology of the SR-CD method is to first obtain the difference matrix \(\varDelta {\varvec{R}}_t\) based on the array covariance matrix \(\varvec{R}\) and its transpose \({\varvec{R}}^{T}\), and then vectorize \(\varDelta {\varvec{R}}_t\) to establish a sparse representation model for DOA estimation. In this section, we use the uniform linear array for analysis. The SR-CD method first obtains \(\varDelta {\varvec{R}}_t\) as follows

$$\begin{aligned} {\varDelta {\varvec{R}}_t}= & {} {\varvec{R}}-{{\varvec{R}}^{T}}\nonumber \\= & {} {\varvec{A}}{\varvec{R}_s} {\varvec{A}^{H}} - {\varvec{A}}^{*}{\varvec{R}_s} {\varvec{A}^{T}} \end{aligned}$$
(3)

where \((\cdot )^{*}\) is the conjugate operation and \((\cdot )^{T}\) is the transpose. For the uniform linear array, we have

$$\begin{aligned} {{\varvec{a}}\left( \theta _k\right) }=\left[ 1,{\exp }\left( -j2{\pi }d_2{\sin }\left( \theta _k\right) /{\lambda }\right) ,\cdots ,{\exp }\left( -j2{\pi }d_M{\sin }\left( \theta _k\right) /{\lambda }\right) \right] ^{T} \end{aligned}$$
(4)

where \(d_m\) represents the distance from the m-th element to the first element, \(\lambda \) is the wavelength of the source signals. The SR-CD method then vectorizes the difference matrix by columns to obtain

$$\begin{aligned} {{\varvec{r}}_{t}}=vec\left( \varDelta {\varvec{R}}_t\right) \end{aligned}$$
(5)

where \(vec(\cdot )\) means stack operation, which returns the vector obtained by stacking the columns of the matrix one above the other. Afterward, based on \({\varvec{r}}(t)\), the SR-CD method builds the sparse representation model to implement the DOA estimation.

This section analyzes the reason that the SR-CD method products the false peaks and it fails when the sources are with the DOA of \(0^{\circ }\) and/or from symmetric angles, that is, \({\pm }{\theta }\).

According to Eq.(2), we obtain

$$\begin{aligned} {{\varvec{R}}^{T}}=\sum _{k=1}^{K} {p_k} {\varvec{a}}^{*}\left( \theta _k\right) {\left( {\varvec{a}}^{*}\left( \theta _k\right) \right) }^{H} + {\sigma ^{2}\varvec{I}_{M}} \end{aligned}$$
(6)

Based on Eqs. (2) and (6), we get the vectorization of the difference matrix as

$$\begin{aligned} {{\varvec{r}}_t}= & {} vec\left( \varDelta {\varvec{R}}_t\right) \nonumber \\= & {} vec\left( \sum _{k=1}^{K} {p_k} {\varvec{a}}\left( \theta _k\right) {\varvec{a}}^{H}\left( \theta _k\right) -\sum _{k=1}^{K} {p_k} {\varvec{a}}^{*}\left( \theta _k\right) {\left( {\varvec{a}}^{*}\left( \theta _k\right) \right) }^{H}\right) \nonumber \\= & {} {\varvec{V}}{\varvec{p}} \end{aligned}$$
(7)

where \({\varvec{V}}=[\varvec{v}(\theta _1),\cdots ,\varvec{v}(\theta _K)]\) is an \(M^{2}\times K\) matrix, \(\varvec{v}(\theta _k)={\varvec{a}}^{*}(\theta _k){\bigotimes }{\varvec{a}}(\theta _k)-{\varvec{a}}(\theta _k){\bigotimes }{{\varvec{a}}^{*}(\theta _k)}\) is an \(M^{2}\times 1\) vector, \(\bigotimes \) is the Kronecker product operation and \({\varvec{p}}=[p_1,\cdots ,p_K]^{T}\) is the K-dimensional signal power vector.

Because \({\varvec{a}}^{*}(-\theta )={\varvec{a}}(\theta )\) and \({\varvec{a}}^{*}(\theta )={\varvec{a}}(-\theta )\), we have

$$\begin{aligned} {{\varvec{v}}(-\theta )}= & {} {\varvec{a}}^{*}(-\theta ){\bigotimes }{\varvec{a}}(-\theta )-{\varvec{a}}(-\theta ){\bigotimes }{\varvec{a}}^{*}(-\theta )\nonumber \\= & {} {\varvec{a}}(\theta ){\bigotimes }{\varvec{a}}^{*}(\theta )-{\varvec{a}}^{*}(\theta ){\bigotimes }{\varvec{a}}(\theta )\nonumber \\= & {} {-{\varvec{v}}(\theta )} \end{aligned}$$
(8)

According to Eq. (8), when \({{\theta }_1=-{\theta }}\), \(p_{s1}=-p_s\), we obtain

$$\begin{aligned} {{\varvec{v}}(\theta )}p_s={{\varvec{v}}\left( \theta _1\right) }p_{s1} \end{aligned}$$
(9)

From Eqs. (8) and (9), we conclude that the SR-CD method produces the false peaks at \(-\theta _k\), \(k=1,\cdots ,K\). Moreover, the amplitudes of the false peaks are negative, which can be used for recognizing the false peaks. However, due to the false peaks, the SR-CD method fails when the sources are with symmetric DOAs such as \(\pm \theta _k\). In addition, when \({\theta }=0^{\circ }\), \({{\varvec{v}}(\theta )}=\varvec{0}\). Therefore, the SR-CD method fails as well, when the source is with a DOA of \(0^{\circ }\).

4 Proposed Method

In contrast to the SR-CD method, we propose the SR-BECD method which implements the covariance differencing by using the matrix in the beamspace and that in the element space. For that purpose, the dimensions of the covariance matrix in the element space (denoted by \({\varvec{R}}\)) and that in the beamspace (denoted by \({\varvec{R}}_b\)) are required to be the same. Therefore, \({\varvec{R}}_b\) must be an \(M\times M\)-dimensional matrix since the dimension of \({\varvec{R}}\) is \(M\times M\). As a result, we first construct an \(M\times M\)-dimensional beamforming matrix \({\varvec{B}}\) that satisfies \({\varvec{B}}^{H}{\varvec{B}}={\varvec{B}}{\varvec{B}}^{H}={\varvec{I}}_M\), which has the following formulation [7]

$$\begin{aligned} {\varvec{B}}=\left[ \varvec{b}\left( {\widetilde{\theta }}_1\right) ,\varvec{b}\left( {\widetilde{\theta }}_2\right) ,,\cdots ,\varvec{b}({\widetilde{\theta }}_M)\right] \end{aligned}$$
(10)

where \(\varvec{b}({\widetilde{\theta }}_m)\) is the m-th column of the beamforming matrix \(\varvec{B}\). In addition, \({\widetilde{\theta }}_m\) is the m-th beam direction in the beamforming matrix B.

$$\begin{aligned} {\varvec{b}\left( {\widetilde{\theta }}_m\right) } ={\frac{1}{\sqrt{M}}}\left[ 1,{\exp }\left( -j{\pi }{\sin }\left( {\widetilde{\theta }}_m\right) \right) , \cdots ,{\exp }\left( -j(M-1){\pi }{\sin }\left( {\widetilde{\theta }}_m\right) \right) \right] ^{T} \end{aligned}$$
(11)

where \(\sin ({\widetilde{\theta }}_m)=(M-2m+1)/M\), \(m=1,\cdots ,M\).

According to Eqs. (1) and (10), the linear transformation of the beamforming matrix \(\varvec{B}\) is applied on the M-dimensional data \(\varvec{x}(t)\)to obtain the M-dimensional beamspace data vector \({\varvec{x}}_b(t)\) as follows

$$\begin{aligned} {{\varvec{x}}_b}(t)={\varvec{B}}^{H}{\varvec{x}}(t) \end{aligned}$$
(12)

where \({\varvec{C}}={\varvec{B}}^{H}{\varvec{A}}=[{\varvec{c}}(\theta _1),{\varvec{c}}(\theta _2),\cdots ,{\varvec{c}}(\theta _K)]\) is composed of the steering vectors in the beamspace, that is, \({\varvec{c}}(\theta _k)={\varvec{B}}^{H}{\varvec{a}}(\theta _k)\).

The covariance matrix in the beamspace is then obtained below

$$\begin{aligned} {{\varvec{R}}_b}= & {} {\mathrm{E}} \left[ {\varvec{x}}_{b}(t) {\varvec{x}_{b}^{H}} (t) \right] \nonumber \\= & {} \sum _{k=1}^{K} {p_k} {\varvec{c}}\left( \theta _k\right) {\varvec{c}}^{H}\left( \theta _k\right) + {\sigma ^{2}\varvec{I}_{M}} \end{aligned}$$
(13)

Afterward, the matrix differencing \(\varDelta {\varvec{R}}\) between the beamspace covariance matrix \(\varvec{R}_b\) and the element-space covariance matrix \(\varvec{R}\) is constructed as

$$\begin{aligned} {\varDelta {\varvec{R}}}={\varvec{R}}-{{\varvec{R}}_{b}} \end{aligned}$$
(14)

According to Eqs. (2) and (13), the noise covariance matrices in the covariance matrices \(\varvec{R}\) and \(\varvec{R}_b\) are the same. Therefore, the noise is eliminated in the difference matrix between \(\varvec{R}\) and \(\varvec{R}_b\), as shown in Eq.(15).

$$\begin{aligned} {\varDelta {\varvec{R}}}=\sum _{k=1}^{K} {p_k} {\varvec{a}}\left( \theta _k\right) {\varvec{a}}^{H}\left( \theta _k\right) -\sum _{k=1}^{K} {p_k} {\varvec{c}}\left( \theta _k\right) {\varvec{c}}^{H}\left( \theta _k\right) \end{aligned}$$
(15)

Afterward, the vectorization of \(\varDelta {\varvec{R}}\) leads to

$$\begin{aligned} {\varvec{r}}= & {} vec(\varDelta {\varvec{R}}) \nonumber \\= & {} \left( {\varvec{A}}^{*}{\odot }{\varvec{A}}-{\varvec{C}}^{*}{\odot }{\varvec{C}}\right) \varvec{p}\nonumber \\= & {} {\varvec{A}}_{c}{\varvec{p}} \end{aligned}$$
(16)

where \(\varvec{r}\) is an \(M^{2}\times 1\)-dimensional vector, \(\bigodot \) represents the Khatri–Rao product, \({\varvec{A}}_{c}=[{\varvec{a}}_c{(\theta _1)},{\varvec{a}}_c{(\theta _2)},\cdots ,{\varvec{a}}_c{(\theta _K)}]\) is an \(M^{2}\times K\) matrix, \({\varvec{a}}_c{(\theta _k)}={\varvec{a}}^{*}{(\theta _k)}{\otimes }{\varvec{a}}{(\theta _k)}-{\varvec{c}}^{*}{(\theta _k)}{\otimes }{\varvec{c}}{(\theta _k)}\). Based on simulations, for an amount of signal cases with difference directions and different number, we confirm that the matrix \({\varvec{A}}_{c}\) is full column rank when \(K<M\). Therefore, \({\varvec{A}}_{c}\) can yield correct DOA estimation.

The potential space of the source signals is sampled discretely to form a grid set \({\overline{\varvec{\theta }}}=[{\overline{\theta }}_1,\cdots ,{\overline{\theta }}_N]\). Here, we assume that the real DOAs is on this grid set \(\overline{\varvec{\theta }}\) and \(N\gg M^{2}\). Therefore, \(\varvec{r}\) can be expressed as the following sparse representation

$$\begin{aligned} {\varvec{r}}={\varvec{\overline{A}}}{\overline{\varvec{p}}} \end{aligned}$$
(17)

where \({\varvec{\overline{A}}}_c=[\varvec{a}_c({\overline{\theta }}_1),\varvec{a}_c({\overline{\theta }}_2),\cdots ,\varvec{a}_c({\overline{\theta }}_N)]\) is the \(M^{2}\times N\) over-complete basis matrix, \(\overline{\varvec{p}}=[{\overline{p}}_1,{\overline{p}}_2,\cdots ,{\overline{p}}_N]^{T}\) is the \(N\times 1\) vector. When \({\theta }_k(k=1,...,K)\) is equal to \({\overline{\theta }}_i(i=1,...,N)\), \({\overline{p}}_i\) equals \(p_k\). On the contrary, \({\overline{p}}_i\) is equal to zero when \({\theta }_k\) does not equal to \({\overline{\theta }}_i\). That is, \(\overline{\varvec{p}}\) has K nonzero element which correspond to the DOAs of the sources. As a result, the DOA estimation problem can be solved by recovering the sparse vector \(\overline{\varvec{p}}\).

Similar to the methodology used in [5], recovery of sparse vector \(\overline{\varvec{p}}\) in Eq.(17) can be obtained by solving the following minimization problem

$$\begin{aligned} \mathop {{\text {min}}}\limits _{\overline{\varvec{p}}}~\parallel {\varvec{r}} -{\varvec{\overline{A}}}_c\overline{\varvec{p}} \parallel _2 + \mu \parallel \overline{\varvec{p}} \parallel _1 \end{aligned}$$
(18)

where \(\parallel {\cdot } \parallel _2\) denotes the \(l_2\)-norm, \(\parallel {\cdot } \parallel _1\) denotes the \(l_1\)-norm, regularization parameter \(\mu \) balances the sparsity of \(\overline{\varvec{p}}\) and \(\parallel {\cdot } \parallel _2\)-norm term.

In practice, finite sampling is required to estimate the covariance matrix. In this paper, \(\hat{\cdot }\) is used to represent the estimated value. The covariance matrixes in the beamspace and the element-space are, respectively, obtained as follow

$$\begin{aligned} {\hat{\varvec{R}}}= & {} {\frac{1}{T_1}}\sum _{t=1}^{T_1}{\varvec{x}}(t){\varvec{x}}^{H}(t) \end{aligned}$$
(19)
$$\begin{aligned} {\hat{\varvec{R}}}_b= & {} {\frac{1}{T_1}}\sum _{t=1}^{T_1}{\varvec{x}}_b(t){\varvec{x}}_b^{H}(t) \end{aligned}$$
(20)

As a summary, the steps of the proposed SR-BECD method are given in Algorithm 1 as follows.

\(\varvec{Algorithm \quad 1}\): DOA Estimation Using Sparse Representation of Beamspace

and Element-space Covariance Differencing (SR-BECD)

  1. 1:

    Difference \({\hat{\varvec{R}}}\) and \({\hat{\varvec{R}}}_b\) according to Eq. (14) to get \({\varDelta {\hat{\varvec{R}}}}\);

  2. 2:

    The vector \(\hat{\varvec{r}}\) is obtained by vectorizing \({\varDelta {\hat{\varvec{R}}}}\);

  3. 3:

    Sparse representation of \(\hat{\varvec{r}}\) according to Eq. (17), i.e.,

    $$\begin{aligned} \hat{\varvec{r}}={\overline{\varvec{A}}}_c{\hat{\overline{\varvec{p}}}} \end{aligned}$$
    (21)
  4. 4:

    Solving the following minimization problem obtain the sparse vector \(\overline{\varvec{p}}\)

    $$\begin{aligned} \mathop {{\mathrm{min}}}\limits _{\hat{\overline{\varvec{p}}}}~\parallel {\hat{\varvec{r}}} -{\varvec{\overline{A}}}_c\hat{\overline{\varvec{p}}} \parallel _2 + \mu \parallel \hat{\overline{\varvec{p}}} \parallel _1 \end{aligned}$$
    (22)
  5. 5:

    The locations of the spectral peaks of \(\hat{\overline{\varvec{p}}}\) give the estimated value of the source DOAs.

The problem of DOA estimation in (22) can be efficiency solved in the second-order cone (SOC) programming framework[1, 10].

5 Computational Complexity

Note that the sparse vector \(\hat{\overline{\varvec{p}}}\) in Eq. (22) can be obtained through the optimization software CVX. Regarding computational complexity, only the main part of each algorithm, that is, the computational complexity of the sparse recovery, is considered here. The computational complexity of the proposed algorithm and the existing algorithms is shown in Table 1.

Table 1 Computational Complexity of each algorithm
Full size table

It can be seen from Table 1 that in the case of multiple sources, the computational complexity of the SR-CD and SR-BECD methods based on matrix differencing is significantly reduced compared to other methods. This is because in the sparse recovery process, the SR-CD and SR-BECD methods are independent of the number of sources and the number of array elements. In contrast, the computational complexity of the \(l_1\)-SVD method is related to the number of sources, while the computational complexity of the \(l_1\)-SRACV method is related to the number of elements. In addition, in Table 1, for a fair comparison, we assume that the SR-CD method uses Eq. (18) in the sparse recovery process for DOA estimation, which does not involve the weighted \(l_1\)-norm. In this case, the SR-CD and SR-BECD methods have the same computational complexity. This is because each of them requires only one time sparse recovery process for recovering the sparse vector of the source powers, which has a computational complexity of \(O(N^{3})\).

6 Simulation

A uniform linear array with an element spacing of half a wavelength (\(\lambda /2\)) is used. The number of array elements is 8, the number of snapshots is 500, and the signal powers for different sources are equal. The space area \(\varOmega =[-90^{\circ },90^{\circ }]\) is divided into equal angle intervals, and the angle interval is \(1^{\circ }\). In the following simulations, an empirical parameter value (\(\mu =3\)) is selected for the proposed SR-BECD method. In addition, we compare the proposed SR-BECD method with the \(l_1\)-SVD, \(l_1\)-SRACV, SR-CD, MUSIC and the method in [9]. In the following simulation, the simulation conditions are as described above if not stated otherwise.

6.1 Spatial Spectrum

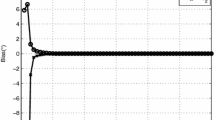
Assuming that two far-field narrowband source signals are incident on the array with a SNR of 0 dB. First, the DOAs of the source signal are set as \(\theta _1=10^{\circ }\) and \(\theta _2=16^{\circ }\), respectively. The spatial spectra are provided in Fig. 1a. Then, the DOAs of the source signals are changed as \(\theta _1=0^{\circ }\) and \(\theta _2=6^{\circ }\), respectively. In this case, the spatial spectra are given in Fig. 1b. At the end, the DOAs of the source signal are set as \(\theta _1=-3^{\circ }\) and \(\theta _2=3^{\circ }\), respectively, which leads to the spatial spectra in Fig. 1c. Since the SR-CD method uses the positive and negative signs of the recovered sparse vector to identify locations of the sources, the spatial spectra are given as the recovered sparse vector instead of the form of dB.

Fig. 1
figure 1

Spatial spectrums. a \(\theta _1=10^{\circ }\) and \(\theta _2=16^{\circ }\); b \(\theta _1=0^{\circ }\) and \(\theta _2=6^{\circ }\); c \(\theta _1=-3^{\circ }\) and \(\theta _2=3^{\circ }\)

Full size image

It can be seen from Fig.1a that for the SR-CD method, when the DOAs of the two source signals are \(\theta _1=10^{\circ }\) and \(\theta _2=16^{\circ }\), the false peak appears at \(\theta _1=-10^{\circ }\) and \(\theta _2=-16^{\circ }\), and the false peak sign is opposite to the sign of the peak value at the location of the source. In Fig.1b, when the DOA of the source is \(\theta =0^{\circ }\), the SR-CD method does not show a peak at \(\theta =0^{\circ }\). As shown in Fig.1c, the SR-CD method does not provide spectral peaks at the DOAs of the symmetric sources; therefore, it cannot estimate the DOAs of the symmetric sources. On the other hand, as shown in Fig. 1a-Fig. 1c, the proposed SR-BECD method has no false peaks and can accurately estimate the DOA of the source with an angle of \(\theta =0^{\circ }\) and the DOAs of the symmetric sources.

In addition, it is illustrated in Fig. 1a–c that when the DOA interval is small, the \(l_1\)-SVD, \(l_1\)-SRACV and the method in [9] cannot accurately estimate the DOA. The spectral peak of MUSIC method is not sharp enough. However, the proposed SR-BECD method has sharp spectral peaks at the locations of sources and thus can accurately estimate the DOAs of sources.

Consider two source signals impinging on the array from \(10^{\circ }\) and \(30^{\circ }\), respectively. The SNR is -10 dB, and the other simulation conditions are the same as the above simulation. In Fig. 2, we compare the spatial spectra of SR-BECD to those of \(l_1\)-SVD, \(l_1\)-SRACV, MUSIC and the method in [9]. It can be seen from Fig. 2 that the spectral peak of MUSIC method is not sharp enough. In the case of a low SNR such as -10 dB, the peaks of the \(l_1\)-SVD and \(l_1\)-SRACV obviously deviate from the true target direction. The peak of the method in [9] has a deviation of \(1^{\circ }\) at \(\theta =30^{\circ }\). In contrast, the SR-BECD method remains sharp peaks at the true source direction.

Fig. 2
figure 2

Spatial spectra. SNR=-10 dB

Full size image

6.2 Probability of DOA Resolution

Suppose that two far-field narrow-band source signals impinging on the array, each of them has a SNR equal to -5 dB, and the DOAs of the sources are \(\theta _1=20^{\circ }\) and \(\theta _2=20^{\circ }+\varDelta \), respectively. The DOA of the second source increases with \(\varDelta =1^{\circ }\) per time until \(\theta _2=30^{\circ }\). 100 independent repeated experiments are conducted at each angle separation. If the estimated DOA \(\hat{\theta }_1\) and \(\hat{\theta }_2\) of a certain experiment satisfy the following equation[3]

$$\begin{aligned} |{\hat{\theta }_1-\theta _1}|+|{\hat{\theta }_2-\theta _2}|<|{\theta }_1-\theta _2| \end{aligned}$$
(23)

then it is said that the two sources in the experiment are correctly resolved. The probability of DOA resolution refers to the percentage of correct resolution times included in the total number of experiments. The probability of DOA resolution against the angle separation (i.e.,\({\theta }_2-\theta _1\)) is shown in Fig. 3.

Fig. 3
figure 3

Probability of DOA resolution

Full size image

In Fig. 3, as the angle interval of the source signal increases, the probability of DOA resolution is gradually increased. When the angle interval is less than \(8^{\circ }\), the probabilities of DOA resolution by the SR-BECD and SR-CD methods are significantly higher than those of other methods. On the other hand, when the angle interval is larger than \(9^{\circ }\), the probabilities of DOA resolution by the aforementioned methods are all approaching to 1.

6.3 RMSE

We assume that two far-field narrowband signals impinging on the array, the DOAs of the sources are \(\theta _1=0^{\circ }\) and \(\theta _2=8^{\circ }\), respectively, and the SNR varies from -12 dB to 8 dB, the angle interval is \(0.25^{\circ }\). The root mean square error (RMSE) of DOA estimation is defined as follows

$$\begin{aligned} {\mathrm{RMSE}}= \sqrt{\frac{1}{{M_l}K} \sum _{l=1}^{{M_l}} \left\{ \sum _{k=1}^{K} \left( \hat{\theta }_{k,l}-\theta _k\right) ^2 \right\} } \end{aligned}$$
(24)

where \(M_l=100\) is the number of Monte Carlo simulation experiments, \(\hat{\theta }_{k,l}\) is the estimated DOA of the k-th source in the l-th experiment, and \({\theta }_k\) is the DOA of the k-th source. The RMSE of all the aforementioned methods against SNRs is given in Fig. 4.

Fig. 4
figure 4

RMSE against SNR

Full size image

As shown in Fig. 4, the RMSE of all the methods decreases with the increment of the SNR. In addition, from Fig. 4, we observe that the SR-CD method fails. This is because that the SR-CD method cannot handle the case of the sources with DOAs of \(0^{\circ }\). In addition, we can see that the RMSE of the proposed SR-BECD method is obviously lower than that of the \(l_1\)-SRACV, \(l_1\)-SVD and the method in [9]. Moreover, when the SNR is lower than -6 dB, the SR-BECD method behaves better than the MUSIC method.

Consider three signals that arrive from \([-20^{\circ },10^{\circ },35^{\circ }]\). The SNR of all three signals is set to 0 dB. Figure 5 depicts the RMSE versus the number of snapshots. From Fig. 5, we observe that the performances of \(l_1\)-SRACV and the method in [9] are sharply degrading when the number of snapshots is less than about 200. This is because the error-suppression criterion of \(l_1\)-SRACV and the method in [9] are derived under the large snapshots. Similarly, the performance of the MUSIC method also declines under low snapshots condition. However, \(l_1\)-SVD method has better performance in low snapshots. Under the condition of low snapshots, the estimation error of SR-BECD method is smaller than that of \(l_1\)-SRACV, the method in [9] and MUSIC. When the number of snapshots is higher than 400, the RMSE of each method is less than \(1^{\circ }\).

Fig. 5
figure 5

RMSE against the number of the snapshots

Full size image

7 Conclusion

In this paper, the SR-BECD method is developed to estimate the DOAs of sources. The SR-BECD method eliminates the noises by using the covariance differencing between the covariance matrixes in the beamspace and element space. The existing SR-CD method also uses the difference covariance matrix to eliminate the noises. However, it is based on the difference between the covariance matrix and its transpose. In this paper, it is proved that the false peaks occur in the SR-CD method when the array is a linear array. Moreover, when the DOAs of the sources are equal to \(0^{\circ }\) and/or symmetric, the SR-CD algorithm fails. In contrast, the proposed SR-BECD method avoids the aforementioned problems encountered in the SR-CD method and it is not limited to specific arrays such as a uniform linear array. In addition, the sparse recovery process of the proposed SR-BECD method is regardless of the number of sources and the number of array elements and it has low computational complexity. Simulation results demonstrate that the SR-BECD method has high DOA resolution and estimation accuracy even in low SNRs.