Dynamics of a multi-beam structure connected with nonlinear joints: modelling and simulation

Abstract

A dynamic modelling approach for a multi-beam structure connected with nonlinear joints is presented and subsequently used to obtain its reduced-order analytical model. Firstly, by applying the matching and boundary conditions, the natural frequencies and global mode shapes of the system are derived. According to the nonlinear transmitted torque formulations of the joints, the joints nonlinearities are introduced into the system by using the equilibrium conditions between the beams and the joints. Then, the global mode shapes and their orthogonality relations are used to obtain an explicit set of reduced-order nonlinear ordinary differential equations(ODEs) of motion for the flexible structure with nonlinear joints. A flexible structure composed of 4 beams and nonlinear joints is given as an example to illustrate the application of the modelling approach proposed. And a comparison between the natural frequencies obtained by the proposed approach and those from the finite element method is given to verify the validity of the derived model. Through the nonlinear ODEs obtained by the Galerkin truncation of the original dynamic model, a study on the variation in dynamic responses of the system with different numbers of modes is performed. The results are used to determine the number of modes taken in nonlinear vibration analysis for certain range of the vibration amplitude of the external excitation. The dynamic responses of the system with various joint parameters are worked out, which show that the transmission characteristics of the joints can strongly affect the dynamic behavior of the whole structure.

1 Introduction

A specific structure composed of multiple flexible beams and flexible joints is widely used in the fields of aerospace and civil engineering, such as the solar array and large truss structure. Due to the strong nonlinearities of the joints, complex micromechanical phenomena under the effect of applied loadings may be produced. This makes the dynamic behavior of the whole structure become more complicated. Therefore, an understanding of the dynamic characteristics of such systems is essential for their design and control of vibration.

A first step toward investigating the dynamic behavior of these structural systems must be intended to understand how to describe the relationship between load and deformation in a dynamic model of the joint. Based on the Hertz contact theory [1,2,3,4,5,6], the joint can be described as a spring damping system in terms of the contact force and deformation. According to the relative velocity of the contact, the geometry of the contact surface and the properties of the material and the contact duration, many scholars have proposed a variety of contact force models which have been used to investigate the dynamic behavior of contact and collision in a mechanical system with joint clearance. On the other hand, an alternative approach for establishing a theoretical model of the joint is to extract the model parameters from experimental data using joint identification techniques [7,8,9,10,11,12]. Crawley [8, 9] developed a force-state mapping technique to measure the parameters of the joint, where the force transmitted by the joint is represented as the function of the full mechanical state of the joint.

For these structures with numerous joints, there have been some research on the overall dynamics of the structure considering the effects of the joints characteristics [13,14,15,16,17,18,19,20,21]. Bowden [19] formulated the equations of motion for the three-joint beam model and investigated the effect of three cubic nonlinear stiffness and linear damping of the joint on the global dynamics of the jointed structures in Ref [14], which shows the interesting relationship between linear properties of the system, such as resonant-free frequencies and joint participation, and nonlinear system properties, such as the shape of the backbone curves. The dynamic behavior of multi-degree-of-freedom flexible jointed structures is then analyzed in Sarkar [18] using a Fourier–Galerkin algorithm. Further studies on the dynamic formulation of jointed space structures have been presented in Tomihiko [17] and Zhang et al [21]. For the practical engineering problems, the dynamic analysis of the structure is usually carried out by the finite element model of the spacecraft structure. Wei and Zheng [20] investigated the nonlinear vibration of satellites with joint nonlinearities by using an improved frequency domain method, which is applicable to large-scale and complicated finite element models.

In the case of modelling of complex flexible multi-body structures, the structural complexity and full coupling result in a model with a great many DOFs and strong nonlinearity, which also bring a challenge for the design of control laws. In order to derive a low-dimensional model for the flexible structure, an effective technique for converting the continuous system into an equivalent discrete system is to use the mode functions [22]. Compared to FEM, the method of using the mode functions to discrete continuous system can greatly reduce the DOFs of the system, which is very suitable for the controller design. However, the accuracy of the dynamic model is highly dependent on how truthful the adopted mode functions can represent the real deformations of the system. For the multi-beam structure connected with flexible joints, due to the interactions of the beams and flexible joints, it is difficult to select the appropriate mode functions to discretize the system when using the assumed mode method. Recently, Wei et al [23] proposed an analytical method to obtain the global mode shapes, which are used to truncate the PDEs of the system to the ODE with a few DOFs. Through the simulation examples for the manipulator system, it shows that the model derived by this method has a relatively high accuracy in comparison with those using the assumed mode method. Therefore, for the multi-beam structure, it is very suitable to use the global modes to obtain the dynamic model of the system, because the global modes obtained by this method are accurate and can represent the real deformations of the system.

For the multi-body structure of spacecraft in orbit, the damping and nonlinearity in the joints are much higher than those produced by other factors such as structural material and geometric large deformations, which makes that the joints become the dominant sources of damping and nonlinearities of the whole structure [24]. Meanwhile, the damping and nonlinearity in the joints are not continuously distributed throughout the whole structure but occur at discrete locations. This brings difficulties to the establishment of the accurate model of the system. In this paper, according to the nonlinear transmitted torque formulations of the joints, the joints nonlinearities are introduced into the system by using the equilibrium conditions between the beams and the joints. Thus, an explicit set of reduced-order nonlinear ODEs are obtained for the multi-beam structure considering the joints nonlinearities by using the global modes discretization technique. Furthermore, the reduced-order nonlinear ODEs are put into a form which is convenient for an analytical investigation to predict nonlinear phenomena exhibited by this structure.

In this article, the natural frequencies and the corresponding global mode shapes of the whole system are obtained by the method proposed in Refs [23, 25,26,27]. Through the nonlinear transmitted torque formulations of the joints, the joint nonlinearities are introduced into the system by using the equilibrium conditions between the beams and the joints. In this way, the global mode shapes and their orthogonality relations are used to obtain an explicit set of reduced-order nonlinear ODEs of motion for the structure with nonlinear joints. Then, an application example of such structure is presented to illustrate the use of the presented approach. Based on the application example, a comparison of the natural frequencies is given to verify the validity of the derived model. Through the dynamic equations presented in the example, the dynamic responses of the system with different numbers of modes are studied, and the dynamic responses of the system with various joint parameters are performed to investigate the effect of the nonlinear joints.

2 Dynamic modelling for a flexible structure with nonlinear joints

2.1 Governing equations of motion

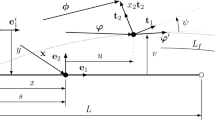
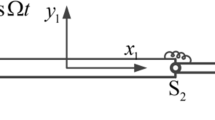
Consider the planar motion of a flexible structure that consists of a number of beams and torsional joints, as shown in Fig. 1. The beams are connected by the torsional joints. The length, mass per unit length, elastic modulus and area moment of inertia of the $i\hbox {th}$ beam $b_i$ are denoted by $2l_i ,\rho _i ,E_i$ and $I_i$, respectively. $\theta _i$ is used to describe the torsional deformation of the $i\hbox {th}$ joint $S_i$. Let $(x_i ,y_i )$ be the local coordinates of the beam $b_i$ in the vertical plane, with the origin located in the middle of the beam $b_i$.

Fig. 1

Schematic of the flexible structure connected with nonlinear joints

The Euler–Bernoulli beam theory is used to derive the equation [28] of motion for the $i\hbox {th}$ beam

$$\begin{aligned} \rho _i {\ddot{w}}_i +\xi _i {\dot{w}}_{i} +E_i I_i {w}^{'''\,'}_i +\eta _i I_i {\dot{w}}_{i}^{'''\,'} =0,\quad i=1,2,\ldots ,N, \end{aligned}$$

(1)

where an overdot denotes partial differentiation with respect to time t, a prime denotes partial differentiation with respect to $x_i$, $w_i$ is the vertical displacement of the $i\hbox {th}$ beam, $\xi _i$ and $\eta _i$ are the external and internal damping coefficient of the $i\hbox {th}$ beam, respectively.

Fig. 2

Schematic of the joint model

As shown in Fig. 2, the torsional joint is described as a single-degree-of-freedom massless system with a nonlinear spring and a linear damper. Based on the parameter identification method, the torque transmitted by the joint can be represented as the function of the instantaneous state of the joint. Then, the nonlinear transmitted torque formulation [9] of the $i\hbox {th}$ joint can be expressed as

$$\begin{aligned} M_i^T =c_i \dot{\theta }_i +k_i^L \theta _i +k_i^N \theta _i ^{3}+\mu _i \hbox {sign}(\dot{\theta }_i ), \end{aligned}$$

(2)

where the first three terms of Eq. (2) represent a linear damping, a linear spring and a third-order nonlinear spring, respectively, and the last term represents Coulomb friction. $c_i ,k_i^L ,k_i^N$ and $\mu _i$ are linear damping coefficient, linear spring stiffness coefficient, third-order spring stiffness coefficient and Coulomb friction torque of the $i\hbox {th}$ joint $S_i$, respectively.

Fig. 3

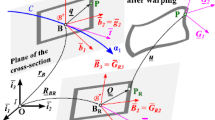
Schematic of the a geometric and b force matching conditions at the torsional joint; $\tilde{w}_j =w_j (l_j ,t), \quad \tilde{w}_{j+1} =w_{j+1} (-l_{j+1} ,t),{\tilde{w}}'_j ={w}'_j (l_j ,t),{\tilde{w}}'_{j+1} ={w}'_{j+1} (-l_{j+1} ,t)$, $\theta _j$ describes the torsional deformation of the $j\hbox {-th}$ torsional joint, $Q_j$ and $Q_{j+1}$ are the shear forces acting on the left and right sides of the $j\hbox {-th}$ torsional joint, $Q_j =E_j I_j {w}'''_j (l_j ,t),Q_{j+1} =E_{j+1} I_{j+1} {w}'''_{j+1} (-l_{j+1} ,t),M_j$ and $M_{j+1}$ are the bending moments acting on the left and right sides of the $j\hbox {-th}$ torsional joint, $M_j^T \hbox {=}M_j =E_j I_j {w}''_j (l_j ,t),M_j^T =M_{j+1} =E_{j+1} I_{j+1} {w}''_{j+1} (-l_{j+1} ,t)$

To complete the formulation for the boundary value problem of the system, one must specify the matching conditions at the joints $S_1 ,S_2 ,\ldots ,S_{N-1}$ and the boundary conditions at the free ends A and B. As shown in Fig. 3a, the geometric matching conditions at the joint $S_j (j=1,2,\ldots ,N-1)$ can be written as

$$\begin{aligned} w_j (l_j ,t)= & {} w_{j+1} (-l_{j+1} ,t), \end{aligned}$$

(3)

$$\begin{aligned} {w}'_j (l_j ,t)+\theta _j= & {} {w}'_{j+1} (-l_{j+1} ,t). \end{aligned}$$

(4)

As shown in Fig. 3b, the torsional joint $S_j$ is subjected to the shear forces and bending moments of the beams $b_j$ and $b_{j+1}$, respectively. The force and moment matching conditions at the joint $S_j$ are

$$\begin{aligned} E_j I_j {w}'''_j (l_j ,t)= & {} E_{j+1} I_{j+1} {w}'''_{j+1} (-l_{j+1} ,t), \end{aligned}$$

(5)

$$\begin{aligned} E_j I_j {w}''_j (l_j ,t)= & {} M_j^T =E_{j+1} I_{j+1} {w}''_{j+1} (-l_{j+1} ,t). \end{aligned}$$

(6)

The boundary conditions at A and B are

$$\begin{aligned} A:E_1 I_1 {w}'''_1 (-l_1 ,t)= & {} 0,E_1 I_1 {w}''_1 (-l_1 ,t)=0, \end{aligned}$$

(7)

$$\begin{aligned} B:E_N I_N {w}'''_N (l_N ,t)= & {} 0,E_N I_N {w}''_N (l_N ,t)=0. \end{aligned}$$

(8)

2.2 Determination of natural frequencies and global mode shapes

In order to obtain a low-dimensional dynamic model, it is necessary to study the eigenvalue problem of the system to obtain the global mode shapes. Therefore, it is assumed that the displacements of the flexible structure are separable in space and time to solve the eigenvalue problem of the system. Let

$$\begin{aligned} w_i (x_i ,t)=\varphi _i (x_i )e^{{{\mathrm{j}}\omega t}},\theta _i =\Theta _i e^{{\mathrm{j}}\omega t}, \end{aligned}$$

(9)

where $\omega$ is an unknown constant corresponding to the natural frequency of the system. Substituting the separable solutions given in Eq. (9) into Eq. (1) without damping yields

$$\begin{aligned} E_i I_i {{\varphi }'''\,'}_i (x_i )-\omega ^{2}\rho _i \varphi _i (x_i )=0,\quad i=1,2,\ldots ,N. \end{aligned}$$

(10)

The solutions of Eq. (10) can be written as

$$\begin{aligned} \varphi _i (x_i )=A_i \cos (\beta _i x_i )+B_i \sin (\beta _i x_i )+C_i \cosh (\beta _i x_i )+D_i \sinh (\beta _i x_i ),\quad x_i \in [-l_i ,l_i ], \end{aligned}$$

(11)

where $\beta _i =\left( {\frac{\rho _i \omega ^{2}}{E_i I_i }} \right) ^{1/4}$. Let

$$\begin{aligned} {{\varvec{\Psi }}}_i =\left[ {{\begin{array}{lllll} {A_i }&{} {B_i }&{} {C_i }&{} {D_i }&{} {\Theta _i } \\ \end{array} }} \right] ,{\varvec{\Psi }}=\left[ {{\begin{array}{llll} {{\varvec{\Psi }}_1 }&{} {{\varvec{\Psi }}_2 }&{} \cdots &{} {{\varvec{\Psi }}_N } \\ \end{array} }} \right] ^{\mathrm{T}}. \end{aligned}$$

(12)

Substituting Eq. (11) into the linearized matching conditions (3)–(6) and boundary conditions in (7) and (8) yields

$$\begin{aligned} \mathbf{H}(\omega ){\varvec{\Psi }}=0, \end{aligned}$$

(13)

where the matrix $\mathbf{H}(\omega )\in R^{(5N-1)\times (5N-1)}$.

The positive roots of the frequency equation $\det (\mathrm{H}(\omega ))=0$, denoted in ascending order by $\omega _{\;1} ,\omega _{\;2} ,\cdots$, are the natural frequencies of the linearized dynamic model of the structure. The eigenvector ${\varvec{\Psi }} ^{(s)}$, where $s=1,2,\ldots$, corresponding to the natural frequency $\omega _{s}$ can be obtained by Eq. (13). Once the natural frequency $\omega _{s}$ and the corresponding vector ${\varvec{\Psi }} ^{(s)}$ are obtained, the $s\hbox {th}$ mode shapes for the flexible structure can be determined by Eq. (11).

2.3 Orthogonality of the global mode shapes

The global mode shapes associated with the two distinct eigenvalues $\omega _r$ and $\omega _s$ are denoted by ${\varvec{\upphi }} _{r} (x)$ and ${\varvec{\upphi }}_{s} (x)$, respectively, where

$$\begin{aligned} {\varvec{\upphi }} _{r} (x)=\left[ {{\begin{array}{llll} {\varphi _1^{r} }&{} {\varphi _2^r }&{} \cdots &{} {\varphi _N^r } \\ \end{array} }} \right] ^{\mathrm{T}}, r=1,2,\ldots . \end{aligned}$$

(14)

By Eq. (10), one has

$$\begin{aligned} E_i I_i \varphi _{i}^{{r}^{{\prime \prime \prime \, \prime }}}(x_i )=\omega _r^{2} \rho _i \varphi _i^r (x_i ). \end{aligned}$$

(15)

Then, multiply Eq. (15) by $\varphi _{i}^{s}$ and integrate the resulting equations over the domain $-l_i \le x_i \le l_i$ for the $i\hbox {th}$ beam, and add the resulting equations to get

$$\begin{aligned} \sum _{i=1}^N {\int _{-l_i }^{l_i } {E_i I_i \varphi _{i}^{{r}^{{\prime \prime \prime \, \prime }}}(x_i )\varphi _i^s } (x_i )\hbox {d}x_i } =\omega _r ^{2}\sum _{i=1}^N {\int _{-l_i }^{l_i } {\rho _i \varphi _i^r (x_i )\varphi _i^s } (x_i )\hbox {d}x_i } . \end{aligned}$$

(16)

Integrating Eq. (16) by parts, using the matching and boundary conditions in Eqs. (3)$\sim$(8), yields

$$\begin{aligned} \sum _{i=1}^N {\int _{-l_i }^{l_i } {E_i I_i \varphi _i^{{r}^{{\prime \prime \prime \,\prime }}}(x_i )\varphi _i^s } (x_i )\hbox {d}x_i } =\sum _{i=1}^N {\int _{-l_i }^{l_i } {E_i I_i \varphi _i^{{r}^{{\prime \prime }}}(x_i )\varphi _i^{{s}^{{\prime \prime }}}} (x_i )\hbox {d}x_i +\sum _{i=1}^{N-1} {k_i^L \Theta _i^r \Theta _i^s } } . \end{aligned}$$

(17)

Substituting Eq. (17) into the left-hand side of Eq. (16) yields

$$\begin{aligned} \omega _r ^{2}\sum _{i=1}^N {\int _{-l_i }^{l_i } {\rho _i \varphi _i^r (x_i )\varphi _i^s } (x_i )\hbox {d}x_i } =\sum _{i=1}^N {\int _{-l_i }^{l_i } {E_i I_i \varphi _i^{{r}^{{\prime \prime }}}(x_i ) \varphi _i^{{s}^{{\prime \prime }}}} (x_i )\hbox {d}x_i +\sum _{i=1}^{N-1} {k_i^L \Theta _i^r \Theta _i^s } } . \end{aligned}$$

(18)

Exchanging the superscripts s and r in Eq. (18) yields

$$\begin{aligned} \omega _s ^{2}\sum _{i=1}^N {\int _{-l_i }^{l_i } {\rho _i \varphi _{i}^{r} (x_i )\varphi _i^s } (x_i )\hbox {d}x_i } =\sum _{i=1}^N {\int _{-l_i }^{l_i } {E_i I_i \varphi _i^{{r}^{{\prime \prime }}}(x_i ) \varphi _i^{{s}^{{\prime \prime } }}} (x_i )\hbox {d}x_i +\sum _{i=1}^{N-1} {k_i^L \Theta _i^r \Theta _i^s } } . \end{aligned}$$

(19)

Subtracting Eq. (19) from Eq. (18) yields

$$\begin{aligned} (\omega _r ^{2}-\omega _s ^{2})\sum _{i=1}^N {\int _{-l_i }^{l_i } {\rho _i \varphi _i^r (x_i )\varphi _i^s } (x_i )\hbox {d}x_i } =0. \end{aligned}$$

(20)

From Eq. (20), the first orthogonality relation can be obtained

$$\begin{aligned} \sum _{i=1}^N {\int _{-l_i }^{l_i } {\rho _i \varphi _i^r (x_i )\varphi _i^s} (x_i )\hbox {d}x_i } =M_s \delta _{rs} , \end{aligned}$$

(21)

where $M_s$ is a positive constant and $\delta _{rs}$ is the Kronecker delta. Using Eqs. (18) and (21), the second orthogonality relation can be obtained

$$\begin{aligned} \sum _{i=1}^N {\int _{-l_i }^{l_i } {E_i I_i \varphi _i^{{r}^{{\prime \prime }}}(x_i )\varphi _i^{{s}^{{\prime \prime }}}} (x_i )\hbox {d}x_i +\sum _{i=1}^{N-1} {k_i^L \Theta _i^r \Theta _i^s } } =K_s \delta _{rs}, \end{aligned}$$

(22)

where $K_s$ is a positive constant.

2.4 Dynamic model with multi-DOF

Applying the Galerkin procedure to Eqs. (1) and (2), the reduced-order nonlinear ODEs are obtained for the system. By using the first n global mode shapes, the displacements of the system can be written as

$$\begin{aligned} w_i (x_i ,t)=\sum _{j=1}^n {\varphi _i^j (x_i )q_j (t)} ,\theta _i =\sum _{j=1}^n {\Theta _i^j q_j (t)}, \end{aligned}$$

(23)

where $q_j (t)$ is a modal coordinate.

Substituting Eq. (23) into Eqs. (1) and (2) yields

$$\begin{aligned}&\sum _{j=1}^n {\rho _i \varphi _i^j (x_i )\ddot{q}_j } +\sum _{j=1}^n {\xi _i \varphi _i^j (x_i )\dot{q}_j } \hbox {+}\sum _{j=1}^n {E_i I_i \varphi _i^{{j}^{{\prime \prime \prime \,\prime }}}(x_i )q_j } \hbox {+}\sum _{j=1}^n {\eta _i I_i \varphi _i^{{j}^{{\prime \prime \prime \,\prime }}}(x_i )\dot{q}_j } =0, \end{aligned}$$

(24)

$$\begin{aligned}&M_i^T =\sum _{j=1}^n {c_i \Theta _i^j \dot{q}_j } +\sum _{j=1}^n {k_i^L \Theta _i^j q_j } +\sum _{j=1}^n {\sum _{k=1}^n {\sum _{r=1}^n {k_i^N \Theta _i^j \Theta _i^k \Theta _i^r q_j } } q_k q_r } +\sum _{j=1}^n {\mu _i \hbox {sign}(\Theta _i^j \dot{q}_j )} . \end{aligned}$$

(25)

Multiplying Eq. (24) by $\varphi _{i}^{s}$, integrating the resulting equations over the domain $-l_i \le x_i \le l_i$ for the $i\hbox {th}$ beam, adding all of the resulting equations and using the matching and boundary conditions in Eqs. (3)$\sim$(8) and the orthogonality relations in Eqs. (21) and (22), we have

$$\begin{aligned} M_s \ddot{q}_s +\left[ {\sum _{i=1}^N {\sum _{j=1}^n {\int _{-l_i }^{l_i } {\xi _i \varphi _i^j (x_i )\varphi _i^s (x_i )\hbox {d}x_i } +\sum _{i=1}^N {\sum _{j=1}^n {\int _{-l_i }^{l_i } {\eta _i I_i \varphi _i^{{j}^{{\prime \prime \prime \,\prime } }}(x_i )\varphi _i^s (x_i ) \hbox {d}x_i } } } +\sum _{i=1}^{N-1} {\sum _{j=1}^n {c_i \Theta _i^j \Theta _i^s } } } } } \right] \dot{q}_j \nonumber \\ +K_s q_s +\sum _{i=1}^{N-1} {\sum _{j=1}^n {\mu _i \Theta _i^s } } \hbox {sign}(\Theta _i^j \dot{q}_j )+\sum _{i=1}^{N-1} {\sum _{j=1}^n {\sum _{k=1}^n {\sum _{r=1}^n {k_i^N \Theta _i^j \Theta _i^k \Theta _i^r \Theta _i^s } } } } q_j q_k q_r =0,\quad s=1,2,\ldots ,n.\nonumber \\ \end{aligned}$$

(26)

3 Example of application

Fig. 4

Schematic of the solar array

Now, let us consider the solar array as an example of the multi-beam structure connected with nonlinear joints, as shown in Fig. 4. The solar array is composed of four solar panels connected by the torsional joints. Furthermore, the solar array is subjected to the external excitation due to the moving support. For a long solar array, it is appropriate to model the solar array as an assembly of the beams connected by the torsional joints [29]. In this example, the system is subjected to an excitation due to the moving support, as shown in Fig. 4b. Assume that the solar panels have the same dimensions of the cross section and material property. Similarly, the joints have the same geometric parameter and material property. For the sake of convenience, the subscripts of the corresponding symbols are removed, for example, $\rho _i =\rho ,k_i^L =k_L$. The physical parameters of the array are listed in Table 1.

Table 1 Values of the parameters of the solar array

As shown in Fig. 4, the governing equation of motion for the $i\hbox {th}$ beams is

$$\begin{aligned} \rho \ddot{w}_i +\xi \dot{w}_i +EI{{w}'''\,'}_i +\eta I\dot{{{w}'''\,'}}_i =\rho \ddot{w}_s (t),i=1,2,3,4, \end{aligned}$$

(27)

where $w_s (t)$ is the displacement of the support.

Based on the dynamic modelling approach developed here, the nonlinear ODEs of motion for the system are obtained as follows:

$$\begin{aligned} \ddot{q}_s +\omega _s^{2} q_s +2\alpha _s \omega _s \dot{q}_s +\gamma _s \dot{q}_j +b_s^j \hbox {sign}(\Theta _i^j \dot{q}_j )+d_s^{jkr} q_j q_k q_r =f_s (t),s=1,2,\ldots ,n, \end{aligned}$$

(28)

where $\alpha _s$ is the modal damping ratio of the solar panels, $\gamma _s$ is the damping of the joints, and $b_s^j$ is the Coulomb friction torque of the joints. The relevant terms in Eq. (28) are given in “Appendix A”.

4 Results and discussion

In this section, a comparison of the natural frequencies of the application example, which are obtained from the presented approach and the commercial software ANSYS, is performed. Then, the dynamic responses of the system with different numbers of modes are discussed, and the dynamic responses of the system with various joint parameters are given to investigate the effect of the nonlinear joints.

4.1 Model validation

In order to verify the validity of the model as shown in Fig. 4, the first eight natural frequencies of the solar array with different joint linear stiffness are calculated by the proposed approach and compared with those obtained from the ANSYS, as shown in Table 2. Denote the dimensionless stiffness parameter of the joint by $K_L$, which defines the ratio between the linear torsional stiffness and the flexural rigidity of the solar panel, as

$$\begin{aligned} K_L =\frac{k_L l}{EI}. \end{aligned}$$

(29)

The first eight natural frequencies obtained from the proposed approach and ANSYS for different $K_L$ are listed in Table 2. It can be seen from Table 2 that the results from the proposed approach are in good agreement with those from the ANSYS. The maximum relative error between the natural frequencies from the current and finite element methods, defined by ${\left( {\left\| {\omega _s -\omega _s^{\mathrm{ANSYS}} } \right\| } \right) }/{\omega _s^{\mathrm{ANSYS}} }$, is $3.85\%$. This shows the correctness of the model obtained by this paper. Furthermore, Table 2 reveals that by increasing $K_L$, the natural frequencies increase, as expected.

Table 2 First eight natural frequencies of the solar array $\omega \, (\hbox {H}z)$

4.2 Dynamic responses

To determine the number of modes taken for nonlinear vibration analysis, the forced harmonic responses of the system with different numbers of modes are worked out numerically, as shown in Figs. 5, 6, 7 and  8. The vertical displacement of the support is assumed as $w_s (t)=w_0 \cos \Omega t$. The first four natural frequencies of the system are $\omega _1 =0.398\,\hbox { Hz, }\omega _2 =2.475\,\hbox { Hz, }\omega _3 =6.873\,\hbox { Hz }$ and $\omega _4 =13.10\,\hbox { Hz}$. The results are obtained from the cases with increasing $\Omega$ and $w_0$. In these figures, the initial conditions for the first point are assumed to be zero, and some steady-state response data at the current $\Omega$ and $w_0$ are used as the initial conditions for the next $\Omega$ and $w_0$, respectively.

Fig. 5

Frequency-response curves of the solar array tip with different numbers of modes, $w_0 =0.004\,\hbox {m}$

When the external excitation frequency $\Omega$ varies from 0.3 to 0.55 Hz, the frequency response curves of the solar array tip with different numbers of modes for $w_0 =0.004, 0.01 \hbox { and } 0.012\,\hbox {m}$ are shown in Figs. 5, 6 and 7, respectively. From these figures, it can be seen clearly that as $w_0$ is increased, the jump phenomenon is more obvious. Although the external excitation frequency is much smaller than the higher-order natural frequency of the system, the higher-order modes are needed to ensure the accuracy of the response of the system in the case of large vibration amplitude. This can be observed from the Figs. 6 and 7. For instance, the first two and three modes should be taken in dynamic models for $w_0 =0.01 \hbox { and } 0.012\,\hbox {m}$, respectively, so that the accuracy of nonlinear vibration analysis can be satisfied. It can be concluded that with the increase in the amplitude of the excitation, due to the effects of the joints nonlinearities, the contribution of the higher-order modes in the response of the system is increased. However, in the case of small vibration amplitude, the contribution of the higher-order modes in the response of the system can be ignored when the external excitation frequency is near the first linear natural frequency of the system. This can be observed from Fig. 5. At this time, the first mode is enough for the dynamic model, which makes that the dynamic equation presented in this paper is more convenient for solving the system with the analytic method, such as perturbation techniques. From Figs. 5, 6 and 7, it is concluded that how many modes should be taken for nonlinear vibration analysis depends on the amplitude of the excitation.

Fig. 6

Frequency-response curves of the solar array tip with different numbers of modes, $w_0 =0.01\,\hbox {m}$

Fig. 7

Frequency-response curves of the solar array tip with different numbers of modes, $w_0 =0.012\,\hbox {m}$

When the amplitude of the excitation $w_0$ is varied from 0.001 to $0.02\,\hbox {m}$, the force-response curves of the solar array tip with different numbers of modes for $\Omega =0.42\,\hbox {Hz}$ are shown in Fig. 8. From Fig. 8, a similar jump phenomenon can be observed. With the increase in the amplitude of the excitation, the difference of the response curves with different numbers of modes becomes larger. All these clearly show that the contribution of the higher-order modes in the response of the system is closely related to the vibration amplitude of the system. This can also be observed from Figs. 5, 6 and 7.

Fig. 8

Force-response curves of the solar array tip with different numbers of modes, $\Omega =0.42\,\hbox {Hz}$

From Figs. 5, 6, 7 and 8, it is found that when the vibration amplitude of the system is relatively large, more modes need to be taken to meet the requirements of accuracy. Therefore, in the next study on the effect of the joints nonlinearities on the system, the first three modes are selected to calculate the dynamic responses of the system. The forced harmonic responses of the system with various joint parameters are worked out numerically, as shown in Figs. 9, 10, 11, 12, 13 and 14. In these figures, the initial conditions for the first point are assumed to be zero, and some steady-state response data at the current $\Omega$ and $w_0$ are used as the initial conditions for the next $\Omega$ and $w_0$, respectively.

Fig. 9

Frequency-response curves of the solar array tip for various values of $k_N$, $w_0 =0.01\,\hbox {m}$

Fig. 10

Force-response curves of the solar array tip for various values of $k_N$, $\Omega =0.42\,\hbox {Hz}$

Fig. 11

Frequency-response curves of the solar array tip for various values of c, $w_0 =0.01\,\hbox {m}$

Fig. 12

Force-response curves of the solar array tip for various values of c, $\Omega =0.42\,\hbox {Hz}$

When $\Omega$ varies from 0.3 to $0.55\,\hbox {Hz}$, the response curves of the solar array tip for various values of $k_N$ are shown in Fig. 9. From Fig. 9, it can be observed that with the increase in the nonlinear stiffness of the joints, the jump occurs at a higher frequency. In addition, the jump phenomenon is more apparent for a larger $k_N$.

The response curves for various values of $k_N$ are presented with the frequency of the excitation held fixed $\Omega =0.42\,\hbox {Hz}$ when the amplitude of the excitation $w_0$ is varied from 0.001 to $0.02\,\hbox {m}$ as shown in Fig. 10. It is found that with the increase in the nonlinear stiffness of the joints, the jump occurs at a lower $w_0$, and the vibration amplitude of the system decreases.

The frequency-response and force-response curves of the solar array tip for various values of c are shown in Figs. 11 and 12, respectively. From Figs. 11 and 12, it can be observed that in the case of small damping of the joints, obvious jump phenomenon takes place. With the increase in the damping of the joints, this phenomenon gradually diminished until disappeared. Meanwhile, it is clear that the damping of the joints can reduce the vibration amplitude of the system.

Fig. 13

Frequency-response curves of the solar array tip for various values of $\mu$, $w_0 =0.01\,\hbox {m}$

Fig. 14

Force-response curves of the solar array tip for various values of $\mu$, $\Omega =0.42\,\hbox {Hz}$

The frequency-response and force-response curves of the solar array tip for various values of $\mu$ are shown in Figs. 13 and 14, respectively. From Figs. 13 and 14, it is also found that the friction of the joints can reduce the vibration amplitude of the system. With the increase in the friction of the joints, the jump phenomenon becomes less obvious, and the hysteresis loop becomes smaller as the frequency is increased and decreased. From Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14, it is concluded that the transmission characteristics of the joints have a great influence on the dynamic behavior of the whole structure.

It is well known that the spacecraft with the solar array is usually extremely flexible and has low-frequency fundamental vibration modes. These modes might be excited in a variety of tasks such as slewing and pointing maneuvers. Thus, damping and friction are simple but effective ways to suppress the induced vibrations. However, in the space environment, solar panels do not provide enough damping to quickly suppress the vibration caused by the maneuvers. Therefore, the overall damping and friction contribution from the joints are very important for suppressing the vibration of the system. In order to investigate the role of the joints in suppressing vibration of the system, the vibration responses of the solar array are carried out. Assume that the external excitation acceleration is

$$\begin{aligned} \ddot{w}_s (t)=\left\{ {\begin{array}{ll} a,&{}\quad 0\le t\le T, \\ 0,&{}\quad t>T. \\ \end{array}} \right. \end{aligned}$$

(30)

The time history of the external excitation acceleration with $T=200\,\hbox {s},a=0.2\,\hbox {m}/{\hbox {s}^{2}}$ is considered as shown in Fig. 15. When the external and internal damping of the solar panel are selected as $\xi =0.03\,{\hbox {N}\, \hbox {s}}/\hbox {m}$ and $\eta =1.9\times 10^{5}{\hbox {N}\, \hbox {s}}/\hbox {m}^{2}$ as shown in Table 1, the first four modal damping ratios of the solar panel are $\alpha _1 =0.005,\alpha _2 =0.0059,\alpha _3 =0.0146$ and $\alpha _4 =0.0279$, respectively. The vibration responses of the solar array tip with different numbers of modes are shown in Fig. 16. From Fig. 16, it can be seen that the model for the first one mode has been unable to calculate the system response accurately, and at least the first two modes should be taken to ensure the accuracy of the system response.

Fig. 15

Time history of external excitation acceleration

Fig. 16

Responses of the solar array tip with different numbers of modes

The vibration responses of the solar array tip with the first three modes for various values of c and $\mu$ are shown in Figs. 17 and 18, respectively. In Fig. 17, the Coulomb friction torque of the joint is selected as $\mu =0\,\hbox {N}\, \hbox {m}$. In Fig. 18, the damping of the joint is selected as $c=0\,{\hbox {N}\, \hbox {m}\, \hbox {s}}/{\hbox {rad}}$. From Figs. 17 and 18, it is clear that with the increase in the damping and friction of the joint, the time of vibration suppression is reduced. In Fig. 17, even if the damping of the joint is selected as $c=100\,{\hbox {N}\, \hbox {m}\, \hbox {s}}/{\hbox {rad}}$, it also requires 100s to suppress the vibration of the system without the friction of the joint. However, it only needs 14s to suppress the vibration of the system when the friction of the joint is selected as $\mu =0.3\,\hbox {N}\, \hbox {m}$ as shown in Fig. 18. This shows that the friction of the joint is very effective to suppress the vibration of the system.

Fig. 17

Responses of the solar array tip for various values of c

Fig. 18

Responses of the solar array tip for various values of $\mu$

5 Conclusions

A dynamic modelling approach has been proposed to obtain a reduced-order analytical model for a multi-beam structure considering the nonlinearities in the joints by using the global modes discretization technique. The model formulation presented in this paper is a general one, which can be exploited to obtain an explicit set of nonlinear ODEs for such structures with any number of beams and nonlinear joints. Moreover, the nonlinear dynamic model derived here is not only convenient for solving the system with the analytic method, such as perturbation techniques, but also is preferred to be used for real-time control because fewer DOFs mean less computation time.

Based on the dynamic modelling approach, the flexible structure with 4 beams and nonlinear joints has been presented as an example. Then, a comparison of the natural frequencies has been given to verify the validity of the derived model. Through the nonlinear ODEs of the model, the dynamic responses of the system with different numbers of modes have been obtained, and the dynamic responses of the system with various joint parameters have been discussed. Two main conclusions are summarized as follows:

• (1) With the increase in the amplitude of the external excitation, due to the effects of the joints nonlinearities, the contribution of the higher-order modes in the response of the system is increased. In the case of large vibration amplitude, the higher-order modes are needed to ensure the accuracy of the response of the system although the external excitation frequency is much smaller than the higher-order natural frequency of the system. In the case of small vibration amplitude, the dynamic equation for the first mode is enough for nonlinear vibration analysis of the system when the external excitation frequency is near the first natural frequency of the system.

• (2) The damping and friction of the joints can increase the stability of the space structure and restrain the vibration of the structure, which are very helpful for the design of vibration sensitive structure.

Appendix A

The relevant terms in Eq. (28)

$$\begin{aligned} M_s= & {} \sum _{i=1}^4 {\int _{-l}^l {\rho \left[ {\varphi _i^s (x)} \right] } ^{2}\hbox {d}x} ,K_s =\sum _{i=1}^4 {\int _{-l}^l {EI \left[ {\varphi _i^{{s}^{{\prime \prime }}}(x)} \right] ^{2}} \hbox {d}x +\sum _{i=1}^4 {2k_L } } \left[ {\Theta _i^s } \right] ^{2}, \omega _s^{2} =\frac{K_s }{M_s }, \\ \alpha _s= & {} \frac{1}{2}\left( {\frac{\xi }{\rho \omega _s } +\frac{\eta \omega _s }{E}} \right) ,\gamma _s =\frac{1}{M_s } \sum _{i=1}^4 {\sum _{j=1}^n {2c\Theta _i^j \Theta _i^s } } ,b_s^j =\frac{1}{M_s }\sum _{i=1}^4 {\sum _{j=1}^n {2\mu \Theta _i^s } } , \\ d_s^{jkr}= & {} \frac{1}{M_s }\sum _{i=1}^4 {\sum _{j=1}^n {\sum _{k=1}^n {\sum _{r=1}^n {2k_N \Theta _i^j \Theta _i^k \Theta _i^r \Theta _i^s } } } } , f_s (t)=\frac{1}{M_s }\sum _{i=1}^4 {\int _{-l}^l {\rho \varphi _i^s (x)\ddot{w}_s (t)\hbox {d}x}}. \end{aligned}$$