Real-time trajectory control of an overhead crane using servo-constraints

Abstract

In this paper, the system dynamics of an overhead crane are inverted by servo-constraints. The inversion provides a feedforward control for trajectory tracking of the system output. The overhead crane is inherently underactuated and modeled as a two-dimensional mechanical system with nonlinear system dynamics. Actuators are modeled as first-order systems to simplify implementation and account for velocity-controlled drives. The control based on servo-constraints is shown to be an effective method of trajectory control for overhead cranes. It will be demonstrated that the formulation is solvable in real-time using linear implicit Euler integration. The feedforward solution is made robust by an augmentation with LQR as well as a sliding mode controller. Experiments are conducted on a laboratory crane of 13 m motion range.

1 Introduction

Overhead cranes are typical underactuated multibody systems since they possess less control inputs than degrees of freedom. Specifically, they pose demanding control problems since the load swinging cannot be controlled directly. However, undesirable load swinging is easily excited during motion. Many control strategies have been investigated to maneuver the crane without inducing load swinging [1]. Due to the underactuated and nonlinear dynamics of the crane system, feedforward control for load trajectory tracking based on system inversion is not straightforward. The crane system analyzed in this paper is differentially flat [10]. Hence, an analytical feedforward control can be derived, which depends on the desired output and a finite number of its derivatives. This property can also be used as a basis for feedback linearization, where for the crane system dynamic extension needs to be utilized and robustness issues need to be addressed [6]. However, the analytic derivation of the flatness based inversion or feedback linearization is not straightforward and might not be possible for more complex systems. An alternative and more general method of system inversion is the concept of servo-constraints. The servo-constraints append the system dynamics to form a set of differential algebraic equations (DAEs). A general framework considering servo-constraints is presented in [4]. The method has been applied to underactuated systems including cranes. Thereby it occurs that in crane problems often higher index DAEs appear [8]. An alternative servo-constraints formulation based on the system dynamics written in redundant coordinates is presented in [5]. Different methods for solving the resulting higher index DAEs have been presented recently. Most of them include an index reduction in the first step. Index reduction based on a coordinate projection and a coordinate transformation are introduced in [4] and [14], respectively. Index reduction based on minimal extension is proposed in [3]. For solving the reduced index problem, an implicit Euler scheme is proposed in [4] and [3].

The numerical solution of the servo-constraints formulation yields the feedforward control inputs for the system output to follow a prescribed trajectory. If the system model is accurate, the system output will move along the prescribed trajectory. In order to reject disturbances and account for modeling errors, additional feedback control is necessary. Therefore, a stabilized servo-constraints formulation is proposed in [4]. Alternatively, a two-degree of freedom controller design can be applied. For example, a simple feedback LQR controller could be added to the feedforward controller to stabilize the system around the prescribed trajectory [7]. Moreover, the servo-constraints solution could be used in combination with traditional sliding mode control [15], or other approaches such as [9]. The sliding mode control law requires information of the desired trajectory in state space. For underactuated systems, it is normally not straightforward to obtain the desired state trajectory based on the prescribed output trajectory. This normally makes the sliding mode controller difficult to apply. However, servo-constraints yield a simple and fast calculation of the desired trajectory in state space and enable a straightforward application of sliding mode control.

So far, the servo-constraints control approach has been investigated theoretically and verified by simulation. In this paper, it will be shown that the servo-constraints formulation can be solved by a linear implicit Euler method in real-time. Thus, the scheme can be used as an online feedforward controller which could allow online adaption of the desired load trajectory. The effective combination of the servo-constraints controller with an LQR as well as a sliding mode controller is also shown. All results are verified on an experimental test bench of an overhead crane with 13 m motion range.

The remainder of the paper is organized as follows. In Sect. 2, the crane model is derived in generalized and redundant coordinates. The servo-constraints problem is formulated in Sect. 3 for both coordinate formulations. A solution code for the formulated problem is proposed in Sect. 4. An LQR and a sliding mode controller that can be combined with the servo-constraints inversion are presented in Sect. 5. Section 6 presents experimental results including analysis of the real-time capability of the various numerical formulations and the accuracy of the different control strategies. Section 7 summarizes the paper.

2 Modeling of the crane test bench

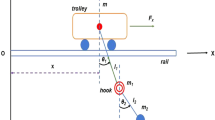
The crane test bench is an overhead gantry crane with variable rope length, shown in Fig. 1(a). Since the trolley moves along a linear axis, planar motion is assumed. Each of the four ropes connecting the load to the trolley is assumed to be massless and rigid. The rope lengths are adjustable by synchronized winches on the trolley, which prevents the load from rotating around itself. Thus, the model can be reduced to a point mass which is attached to the trolley by a single rope, shown in Fig. 1(b). The model has $n=3$ degrees of freedom, namely the trolley position $s$, the rope length $\ell$ and the swing angle $\varphi$. They are collected in the vector of generalized coordinates $\boldsymbol {y}$ and velocities $\boldsymbol {v}$

$$\mathit{y}=\left[\begin{array}{c}{\mathit{y}}_{\mathrm{a}}\\ {\mathit{y}}_{\mathrm{u}}\end{array}\right]=\left[\begin{array}{c}s\\ \ell \\ \phi \end{array}\right],\mathit{v}=\dot{\mathit{y}}=\left[\begin{array}{c}{\dot{\mathit{y}}}_{\mathrm{a}}\\ {\dot{\mathit{y}}}_{\mathrm{u}}\end{array}\right]=\left[\begin{array}{c}\dot{s}\\ \dot{\ell }\\ \dot{\phi }\end{array}\right],$$

(1)

where the dashed lines denote the separation into actuated and unactuated coordinates $\boldsymbol {y}_{\mathrm{a}}$, $\boldsymbol {v}_{\mathrm{a}}$ and $\boldsymbol {y}_{\mathrm{u}}$, $\boldsymbol {v}_{\mathrm{u}}$, respectively. The $m=2$ system inputs are realized by trolley and winch actuators. Due to ${m< n}$, the system is underactuated. In theory, the control inputs are the actuator force on the trolley and actuator torque on the winch. However, force and torque controlled actuators are difficult to realize and often pose robustness issues due to drive train friction. Therefore, the test bench actuators are velocity-controlled. Hence, the system control inputs $u_{\text{s}}$ and $u_{\ell }$ are modeled as reference velocities of trolley and rope length, respectively. The rope velocity $\dot{\ell}$ and trolley velocity $\dot {s}$ are then rheonomic constraints on the system. This accelerates implementation and yields a more robust control design. The inputs are collected in the vector

$$\begin{aligned} \boldsymbol {u}= \left[\textstyle\begin{array}{c} u_{\text{s}}\\ u_{\ell } \end{array}\displaystyle \right] . \end{aligned}$$

(2)

The actuator dynamics are modeled as first-order dynamics

$$\begin{aligned} \tau_{\text{s}} \ddot{s} + \dot{s} &= u_{\text{s}} , \end{aligned}$$

(3)

$$\begin{aligned} \tau_{\ell } \ddot{\ell} + \dot{\ell} &= u_{\ell}, \end{aligned}$$

(4)

with the time constants $\tau_{\text{s}}$ and $\tau_{\ell }$ of trolley and winch actuator, respectively. The time constants can be identified experimentally on the test bench.

Fig. 1

Laboratory crane setup and its model. (a) Test bench. (b) Two-dimensional crane model

The equations of motion of a multibody system arise in the form

$$\begin{aligned} \boldsymbol{M}(\boldsymbol{y},t) \dot{\boldsymbol{v}} + \boldsymbol{k}( \boldsymbol{y},\boldsymbol{v},t) &= \boldsymbol{q}(\boldsymbol{y}, \boldsymbol{v},t) + \boldsymbol{B} \boldsymbol{u}, \end{aligned}$$

(5)

with the generalized mass matrix $\boldsymbol {M}$, the vector of Coriolis, centrifugal and gyroscopic forces $\boldsymbol{k}$, the vector of applied forces $\boldsymbol{q}$ and the distribution matrix of the system inputs $\boldsymbol {B}$. For underactuated multibody systems, Eq. (5) can be split into an actuated and unactuated parts

$$\begin{aligned} \left[\textstyle\begin{array}{c@{\quad}c} \boldsymbol {M}_{\mathrm{aa}} & \boldsymbol {M}_{\mathrm{au}} \\ \boldsymbol {M}_{\mathrm{ua}} & \boldsymbol {M}_{\mathrm{uu}} \end{array}\displaystyle \right] \left[\textstyle\begin{array}{c} \dot{\boldsymbol{v}}_{\mathrm{a}}\\ \dot{\boldsymbol{v}}_{\mathrm{u}} \end{array}\displaystyle \right] + \left[\textstyle\begin{array}{c} \boldsymbol{k}_{\mathrm{a}} \\ \boldsymbol{k}_{\mathrm{u}} \end{array}\displaystyle \right] &= \left[\textstyle\begin{array}{c}\boldsymbol{q}_{\mathrm{a}} \\ \boldsymbol{q}_{\mathrm{u}} \end{array}\displaystyle \right] + \left[\textstyle\begin{array}{c} \boldsymbol {B}_{\mathrm{a}} \\ \boldsymbol{0} \end{array}\displaystyle \right] \boldsymbol {u}. \end{aligned}$$

(6)

For the considered crane, the equation of motion (5) is derived with the Newton–Euler formalism for the swing angle $\varphi$, under rheonomic constraints of rope and trolley velocities. Adding the actuator models of Eq. (3) and Eq. (4) yields the equations

where the dashed lines denote the separation into actuated and unactuated parts. Due to the inclusion of the actuator dynamics as first-order systems, the matrix $\boldsymbol {M}$ is not symmetric anymore but is still non-singular. Note that the equations of motion only depend on the time constants $\tau_{\text{s}}$ and $\tau_{\ell }$ and the gravitational constant $g$. They depend on neither trolley mass nor load mass. The output $\boldsymbol{z}$ of the crane model is defined as the load position

$$\begin{aligned} \boldsymbol{z} = \boldsymbol{h}(\boldsymbol{y}) = \left[\textstyle\begin{array}{c} s + \ell\sin( \varphi) \\ \ell\cos ( \varphi) \end{array}\displaystyle \right] . \end{aligned}$$

(8)

Alternatively to using minimal coordinates, a set of redundant coordinates ${\boldsymbol{y}_{\mathrm{r}}}$ in combination with constraint equations can be used to describe the crane motion. This yields a system of differential-algebraic equations

$$\begin{aligned} \boldsymbol{M}_{\mathrm{r}}(\boldsymbol{y}_{\mathrm{r}},t) \dot{ \boldsymbol{v}}_{\mathrm{r}} + \boldsymbol{k}_{\mathrm{r}}( \boldsymbol{y}_{\mathrm{r}},\boldsymbol{v}_{\mathrm{r}},t) &= \boldsymbol{q}_{\mathrm{r}}(\boldsymbol{y}_{\mathrm{r}},\boldsymbol {v}_{\mathrm{r}},t) + \boldsymbol {Q}^{\mathrm{T}} \boldsymbol{\lambda}+ \boldsymbol {B}_{\mathrm{r}} \boldsymbol{u} , \end{aligned}$$

(9)

$$\begin{aligned} \boldsymbol{c}(\boldsymbol {y}_{\mathrm{r}}) &= \boldsymbol{0}, \end{aligned}$$

(10)

where the vector $\boldsymbol{\lambda}$ contains the Lagrangian multipliers which arise to fulfill the geometric constraints $\boldsymbol{c} (\boldsymbol {y}_{\mathrm{r}})$ [13]. The Jacobian of the constraints is

$$\begin{aligned} \boldsymbol {Q}&= \frac{\partial\boldsymbol{c}(\boldsymbol {y}_{\mathrm{r}})}{\partial \boldsymbol {y}_{\mathrm{r}}}. \end{aligned}$$

(11)

For the presented system, it is convenient to describe the load dynamics in redundant coordinates. Then, the complete vector of redundant coordinates is

$${\mathit{y}}_{\mathrm{r}}=\left[\begin{array}{c}{\mathit{y}}_{\mathrm{r},\mathrm{a}}\\ {\mathit{y}}_{\mathrm{r},\mathrm{u}}\end{array}\right]=\left[\begin{array}{c}s\\ \ell \\ x_2\\ z_2\end{array}\right],{\dot{\mathit{y}}}_{\mathrm{r}}={\mathit{v}}_{\mathrm{r}}=\left[\begin{array}{c}{\dot{\mathit{y}}}_{\mathrm{r},\mathrm{a}}\\ {\dot{\mathit{y}}}_{\mathrm{r},\mathrm{u}}\end{array}\right]=\left[\begin{array}{c}\dot{s}\\ \dot{\ell }\\ {\dot{x}}_2\\ {\dot{z}}_2\end{array}\right],$$

(12)

where $x_{2}$ and $z_{2}$ describe the load position in the coordinate system depicted in Fig. 1(b). Once again replacing the trolley dynamics by the actuator dynamics of Eq. (3) and Eq. (4) yields the crane dynamics in DAE form

where the only Lagrangian multiplier represents the rope force $F_{\mathrm{S}}$ to fulfill the rigid rope constraint (14). The system output in redundant coordinates simply is

$$\begin{aligned} \boldsymbol{z} = \boldsymbol{h}_{\mathrm{r}}(\boldsymbol{y}_{\mathrm{r}}) = \boldsymbol {y}_{\mathrm{r},\mathrm{u}}= \left[\textstyle\begin{array}{c} x_{2} \\ z_{2} \end{array}\displaystyle \right] . \end{aligned}$$

(15)

The control objective is to move the load along a trajectory prescribed in time and space. An inverse model is derived in the following section to accomplish trajectory tracking.

3 Servo-constraints problem formulation

Servo-constraints impose additional constraints on the system formulations of either Eq. (7) or Eqs. (13) and (14) by enforcing the desired output trajectory $\boldsymbol {z}_{\text{d}}(t)$. The servo-constraints therefore are

$$\begin{aligned} \mathbf{0}=\boldsymbol{h}(\boldsymbol{y})- \boldsymbol{z}_{\text{d}}(t), \end{aligned}$$

(16)

where both coordinate definitions can be used. The servo-constraints Eq. (16) extend the equations of motion to form a system of DAEs

$$\begin{aligned} \dot{\boldsymbol{y}} &= \boldsymbol{v} , \end{aligned}$$

(17)

$$\begin{aligned} \boldsymbol{M}(\boldsymbol{y},t) \dot{\boldsymbol{v}} + \boldsymbol{k}( \boldsymbol{y},\boldsymbol{v},t) &= \boldsymbol{q}(\boldsymbol{y}, \boldsymbol{v},t) + \boldsymbol {Q}^{\mathrm{T}}(\boldsymbol {y}) \boldsymbol{\lambda} +\boldsymbol{B} \boldsymbol{u} , \end{aligned}$$

(18)

$$\begin{aligned} \mathbf{0} &= \boldsymbol{h}(\boldsymbol{y}) - \boldsymbol{z}_{\text{d}}(t) , \end{aligned}$$

(19)

$$\begin{aligned} \boldsymbol{0} &= \boldsymbol{c}(\boldsymbol {y}), \end{aligned}$$

(20)

for both formulations in generalized coordinates (1) and redundant coordinates (12). The DAE setup in generalized coordinates will be abbreviated GC, while the formulation using redundant coordinates will be abbreviated RC in the following. In case of GC, the geometric constraints $\boldsymbol{c}(\boldsymbol {y})$ vanish. Note that the dependencies of the matrices on the state vectors are omitted due to readability reasons in the following.

3.1 Formulation in generalized coordinates

For the crane system in generalized coordinates, the DAE system of Eqs. (17)–(20) is of index 5 and will be referred to as GC5 formulation. It is analyzed in detail in [4], where the formulation includes torque and force inputs in contrast to the reference velocity inputs used here. The inclusion of actuator dynamics does not change the index of the DAE. A projection approach is proposed in [4] to reduce the formulation to an index 3 formulation. Equations (17)–(19) are projected into a constrained and unconstrained subspace. The constrained subspace is spanned by the Jacobian of the output

$$\begin{aligned} \boldsymbol{C} = \frac{\partial\boldsymbol{h}}{\partial\boldsymbol{y}}, \end{aligned}$$

(21)

while the unconstrained subspace is constructed as a complementary subspace. The unconstrained subspace is spanned by the matrix $\boldsymbol {D}$, which is constructed by demanding

$$\begin{aligned} \boldsymbol{C}\boldsymbol{D} = \boldsymbol{0}. \end{aligned}$$

(22)

Following [4], a premultiplication of the DAE system in Eqs. (17)–(19) by the matrix ${ [\boldsymbol {D}^{\mathrm{T}} \ \ \boldsymbol {C}\boldsymbol {M}^{-1} ] ^{\mathrm{T}}}$ yields a new set of index 3 DAEs

$$\begin{aligned} \dot{\boldsymbol{y}} &= \boldsymbol{v} , \end{aligned}$$

(23)

$$\begin{aligned} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{v}} &= \boldsymbol{D}^{\mathrm{T}} ( \boldsymbol{q}- \boldsymbol{k} ) + \boldsymbol {D}^{\mathrm{T}}\boldsymbol {B}\boldsymbol {u} , \end{aligned}$$

(24)

$$\begin{aligned} \mathbf{0} &= \boldsymbol {C}\boldsymbol {M}^{-1} ( \boldsymbol{q}- \boldsymbol{k} ) + \boldsymbol {C}\boldsymbol {M}^{-1} \boldsymbol {B}\boldsymbol {u}- \ddot {\boldsymbol {z}}_{\text{d}} + \dot {\boldsymbol {C}}\boldsymbol {v} , \end{aligned}$$

(25)

$$\begin{aligned} \mathbf{0} &= \boldsymbol {h}- \boldsymbol {z}_{\text{d}}. \end{aligned}$$

(26)

This formulation will be referred to as GC3 formulation. Note that here, Eq. (23) is of dimension ${n=3}$, Eq. (24) of dimension ${n-m=1,}$ and Eqs. (25) and (26) are of dimension ${m=2}$. The total number of equations, ${2n+m=8,}$ matches the number of unknowns, which are the desired state states $\boldsymbol {y}_{\text{d}}$, its derivatives $\boldsymbol {v}_{\text{d}}$, and the corresponding inputs $\boldsymbol {u}_{\text{d}}$. The desired input trajectory $\boldsymbol {u}_{\text{d}}$ poses the feedforward control input.

3.2 Formulation in redundant coordinates

In redundant coordinate formulation, the DAE system of Eqs. (17)–(20) is also of index 5 and will be referred to as RC5 formulation. It is even more straightforward to set up the servo-constraints

$$\begin{aligned} \boldsymbol{0} =\boldsymbol {y}_{\mathrm{r},\mathrm{u}}- \boldsymbol {z}_{\text{d}}, \end{aligned}$$

(27)

because the load position is directly part of the coordinate vector. It was proposed in [5] to substitute Eq. (27) into the original crane dynamics of Eqs. (13)–(14), yielding

The last two equations of Eq. (29) are now algebraic instead of differential equations, and the original servo-constraints are removed from the set of equations. This reduces the number of equations and unknowns by $m=2$ equations. Note that the substitution of the servo-constraints already yields an index 3 DAE which will be referred as RC3. Another projection is not necessary.

The approach of using redundant coordinates has some advantages since the derivation of the equations of motion is easier and a projection to obtain an index 3 DAE is not necessary in this case. Moreover, the rope force $F_{\mathrm{S}}$ is contained in Eq. (29) in terms of $\boldsymbol{\lambda}$ and is therefore one of the unknowns of the system. This is convenient for checking feasible trajectories by demanding $F_{\mathrm{S}}(t)>0$ $\forall t$. On the other hand, the servo-constraints solution does not contain the desired generalized coordinates $\boldsymbol {y}_{\text{d}}$ anymore. If necessary for feedback control, it has to be generated from the desired output $\boldsymbol {z}_{\text{d}}$ and desired redundant coordinates $\boldsymbol {y}_{\mathrm{r},\mathrm{d}}$ during post-processing.

4 Solution code

In Sect. 3, four servo-constraints formulations were introduced, namely index 5 formulations in generalized (GC5) and redundant coordinates (RC5) and index 3 formulations in generalized (GC3) and redundant coordinates (RC3). All formulations can be solved by numerical schemes. For notational simplicity, the DAE system is collected in the vector

$$\begin{aligned} \boldsymbol {F}( \boldsymbol {v}, \boldsymbol {y}, \boldsymbol {u}, \dot {\boldsymbol {v}}, \dot {\boldsymbol {y}}, \boldsymbol{\lambda}) = \mathbf{0} \end{aligned}$$

(31)

for all formulations. Different numerical schemes can be applied to solve Eq. (31) [11]. An implicit Euler scheme is applied here as also proposed in [4] for such servo-constraints problem. All derivatives at time $t_{k+1}$ are approximated by finite differences

$$\begin{aligned} \dot {\boldsymbol {y}}_{k+1}\approx\frac{\boldsymbol {y}_{k+1}-\boldsymbol {y}_{k}}{\Delta t}, \end{aligned}$$

(32)

where the indices $k+1$ and $k$ denote the corresponding values at time $t_{k+1}$ and time $t_{k}$, respectively. In total, a set of nonlinear equations arises as follows:

$$\begin{aligned} \boldsymbol {F}\biggl( \boldsymbol {v}_{k+1}, \boldsymbol {y}_{k+1}, \boldsymbol {u}_{k+1}, \frac{\boldsymbol {v}_{k+1}-\boldsymbol {v}_{k}}{\Delta t},\frac{\boldsymbol {y}_{k+1}-\boldsymbol {y}_{k}}{\Delta t},\boldsymbol{\lambda }_{k+1} \biggr) = \mathbf{0}, \end{aligned}$$

(33)

which is solved for the solution vector

$$\begin{aligned} \boldsymbol {x}_{k+1} = \left[\textstyle\begin{array}{c} \boldsymbol {v}_{k+1} \\ \boldsymbol {y}_{k+1} \\ \boldsymbol {u}_{k+1} \\ \boldsymbol {\lambda}_{k+1} \end{array}\displaystyle \right] \end{aligned}$$

(34)

at each time step $t_{k+1}$. Note that for GC, the vector $\boldsymbol {\lambda}_{k+1}$ vanishes. Newton’s method is applied to solve the nonlinear equations in Eq. (33). The solution of the previous time step ${\boldsymbol {x}_{k}}$ is chosen as an initial guess $\boldsymbol {x}_{k+1}^{0}$ for the next iteration. Theoretically, convergence of Newton’s method within the available control loop step time cannot be assured. Therefore, only one Newton iteration is proposed to solve Eq. (33). This is equivalent to the linear implicit Euler scheme [11]. In Sect. 6, the accuracy of the linear implicit Euler scheme is compared to the implicit Euler scheme. For the implicit Euler scheme, the convergence criterion of Newton’s method is chosen as the absolute criterion

$$\begin{aligned} \| \boldsymbol {F}\|_{\text{max}} < 1.0 \cdot10^{-9}. \end{aligned}$$

(35)

However, to ensure fast computation, Newton’s method is stopped after a maximum of $i_{\mathrm{max}}$ iterations. Computational speed is further increased by symbolically precalculating the Jacobian

$$\begin{aligned} \boldsymbol {J}_{\mathrm{F}} &= \frac{\partial \boldsymbol {F}}{\partial \boldsymbol {x}_{k+1}} = \left[\textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \frac{\partial \boldsymbol {F}}{\partial \boldsymbol {v}_{k+1}} & \frac {\partial \boldsymbol {F}}{\partial \boldsymbol {y}_{k+1}} & \frac{\partial \boldsymbol {F}}{\partial \boldsymbol {u}_{k+1}}& \frac{\partial \boldsymbol {F}}{\partial\boldsymbol{f}^{\mathrm{r}}_{\mathrm{r},k+1} } \end{array}\displaystyle \right] . \end{aligned}$$

(36)

Real-time applicability of the proposed scheme will be investigated in detail in Sect. 6.

5 Stabilizing control

If the system model represented the overhead crane perfectly and no disturbances occurred, the feedforward input $\boldsymbol {u}_{\text{d}}$ would be sufficient for trajectory tracking. However, due to model errors and disturbances, feedback control is necessary to stabilize the system around the prescribed trajectory. The feedback channel makes use of the desired state trajectories $\boldsymbol {y}_{\text{d}}$ and $\boldsymbol {v}_{\text{d}}$ which result from the servo-constraints solution. A linear quadratic regulator (LQR) and a sliding mode controller are designed for stabilizing.

In order to apply the LQR optimization problem, the cost function $J$ is defined as

$$\begin{aligned} J = \frac{1}{2} \int_{t_{0}}^{\infty} \boldsymbol {x}(t)^{\mathrm{T}} \boldsymbol {Q}\boldsymbol {x}(t) + \boldsymbol {u}(t)^{\mathrm{T}} \boldsymbol {R}\boldsymbol {u}(t) \,\text{d} t, \end{aligned}$$

(37)

where $\boldsymbol {Q}\in\mathbb{R}^{6\times6}$ and $\boldsymbol {R}\in\mathbb {R}^{2\times 2}$ are weighting matrices used for tuning [7]. The system dynamics are linearized around the final state of the trajectory to apply the LQR. The obtained gains are then used for the entire trajectory. Solving the LQR problem yields a linear time invariant gain matrix ${\boldsymbol {K}\in\mathbb{R}^{m\times2n}}$. It is used in the feedback law

$$\begin{aligned} \boldsymbol {u}_{\mathrm{LQR}} = \boldsymbol {K}\left[\textstyle\begin{array}{c} \widetilde {\boldsymbol {y}}\\ \widetilde {\boldsymbol {v}}\end{array}\displaystyle \right], \end{aligned}$$

(38)

where the tilde denotes the error between desired and measured trajectory of the generalized coordinates

$$\begin{aligned} \widetilde {\boldsymbol {y}}&= \left[\textstyle\begin{array}{c} \widetilde {\boldsymbol {y}}_{\mathrm{a}} \\ \widetilde {\boldsymbol {y}}_{\mathrm{u}} \end{array}\displaystyle \right] =\boldsymbol {y}-\boldsymbol {y}_{\text{d}}, \qquad \widetilde {\boldsymbol {v}}= \boldsymbol {v}- \boldsymbol {v}_{\text{d}}. \end{aligned}$$

(39)

The feedback control $\boldsymbol {u}_{\mathrm{LQR}}$ accounts for small variations around the prescribed trajectory. The main control action for following the trajectory is provided by the feedforward control $\boldsymbol {u}_{\text{d}}$. This results in less noise amplification in the feedback loop. Alternatively to the constant gain matrix, one might use a linearization around the prescribed trajectory $\boldsymbol {y}_{\text{d}}$. This yields a linear time variant system for each trajectory. Solving the corresponding Riccati differential equation yields a time variant gain matrix $\boldsymbol {K}(t)$. A comparison with the simple time-invariant approach shows no advantage for the presented system [12].

Additionally, a sliding mode controller is compared to the LQR controller. The sliding mode controller is set up for the underactuated multibody system as proposed in [2]. A sliding surface $\boldsymbol{s}$ of dimension $n=2$ is defined as

$$\begin{aligned} \boldsymbol{s} &= \boldsymbol {\varTheta }_{\mathrm{a}} {\widetilde {\boldsymbol {v}}}_{\mathrm{a}} + \boldsymbol {\varLambda }_{\mathrm{a}} \widetilde {\boldsymbol {y}}_{\mathrm{a}} +\boldsymbol {\varTheta }_{\mathrm{u}} { \widetilde {\boldsymbol {v}}}_{\mathrm{u}} +\boldsymbol {\varLambda }_{\mathrm{u}} \widetilde {\boldsymbol {y}}_{\mathrm{u}} \end{aligned}$$

(40)

$$\begin{aligned} &= \boldsymbol {\varTheta }_{\mathrm{a}} {\boldsymbol {v}}_{\mathrm{a}}+\boldsymbol {\varTheta }_{\mathrm{u}} { \boldsymbol {v}}_{\mathrm{u}} \underbrace{ -\boldsymbol {\varTheta }_{\mathrm{a}} {\boldsymbol {v}}_{\mathrm{d},\mathrm{a}}- \boldsymbol {\varTheta }_{\mathrm{u}} {\boldsymbol {v}}_{\mathrm{d},\mathrm{u}}+\boldsymbol {\varLambda }_{\mathrm{a}} \widetilde {\boldsymbol {y}}_{\mathrm{a}}+\boldsymbol {\varLambda }_{\mathrm{u}} \widetilde {\boldsymbol {y}}_{\mathrm{u}}}_{\boldsymbol{s}_{\mathrm{p}}}. \end{aligned}$$

(41)

The surface parameters ${\boldsymbol {\varTheta }_{\mathrm{a}}, \boldsymbol {\varLambda }_{\mathrm{a}} \in\mathbb {R}^{2\times2}}$, and ${\boldsymbol {\varTheta }_{\mathrm{u}}, \boldsymbol {\varLambda }_{\mathrm{u}} \in\mathbb {R}^{2\times1}}$ are chosen to yield stable sliding mode surfaces [2]. Stable sliding mode surfaces can, for example, also be obtained by singular LQ surface design; see [9]. The control law for the sliding mode input $\boldsymbol {u}_{\mathrm{SMC}}$ is obtained from $\dot{\boldsymbol{s}}=\mathbf{0}$, so that

$$\begin{aligned} \boldsymbol {u}_{\mathrm{SMC}} &= -\boldsymbol {M}_{\mathrm{s}}^{-1} \bigl( \boldsymbol{f} _{\mathrm{s}} +\dot{\boldsymbol{s}}_{\mathrm{p}} + \boldsymbol {\kappa }\text{sat} \bigl( \boldsymbol{s}\boldsymbol {\varPhi }^{-1} \bigr) \bigr), \end{aligned}$$

(42)

where the matrices $\boldsymbol {M}_{\mathrm{s}}$ and $\boldsymbol{f}_{\mathrm{s}}$ are defined as

$$\begin{aligned} \boldsymbol {M}_{\mathrm{s}} &= \boldsymbol {\varTheta }_{\mathrm{a}} \boldsymbol {M}_{\mathrm{aa}}^{\prime-1} - \boldsymbol {\varTheta }_{\mathrm{u}} \boldsymbol {M}_{\mathrm{uu}}^{\prime-1} \boldsymbol {M}_{\mathrm{ua}} \boldsymbol {M}_{\mathrm{aa}}^{\prime-1}, \end{aligned}$$

(43)

$$\begin{aligned} \boldsymbol{f}_{\mathrm{s}} &= \boldsymbol {\varTheta }_{\mathrm{a}} \boldsymbol {M}_{\mathrm{aa}}^{\prime-1} \boldsymbol{f}^{\prime}_{\mathrm{a}} + \boldsymbol {\varTheta }_{\mathrm{u}} \boldsymbol {M}_{\mathrm{uu}}^{\prime-1} \boldsymbol{f} ^{\prime\mathrm{T}}_{\mathrm{u}}, \end{aligned}$$

(44)

and

$$\begin{aligned} \boldsymbol {M}^{\prime}_{\mathrm{aa}} &= \boldsymbol {M}_{\mathrm{aa}}-\boldsymbol {M}_{\mathrm{au}} \boldsymbol {M}_{\mathrm{uu}}^{\mathrm{T}}\boldsymbol {M}_{\mathrm{ua}}, \end{aligned}$$

(45)

$$\begin{aligned} \boldsymbol{f}^{\prime}_{\mathrm{a}} &= ( \boldsymbol {q}_{\mathrm{a}}-\boldsymbol{k}_{\mathrm{a}} ) - \boldsymbol {M}_{\mathrm{au}} \boldsymbol {M}_{\mathrm{uu}}^{\mathrm{T}} ( \boldsymbol{q} _{\mathrm{u}}- \boldsymbol{k}_{\mathrm{u}} ), \end{aligned}$$

(46)

$$\begin{aligned} \boldsymbol {M}^{\prime}_{\mathrm{uu}} &= \boldsymbol {M}_{\mathrm{uu}}-\boldsymbol {M}_{\mathrm{ua}} \boldsymbol {M}_{\mathrm{aa}}^{\mathrm{T}}\boldsymbol {M}_{\mathrm{au}}, \end{aligned}$$

(47)

$$\begin{aligned} \boldsymbol{f}^{\prime}_{\mathrm{u}} &= ( \boldsymbol {q}_{\mathrm{u}}-\boldsymbol{k}_{\mathrm{u}} ) - \boldsymbol {M}_{\mathrm{ua}} \boldsymbol {M}_{\mathrm{aa}}^{\mathrm{T}} ( \boldsymbol{q} _{\mathrm{a}}- \boldsymbol{k}_{\mathrm{a}} ). \end{aligned}$$

(48)

Hereby the partition of the equations of motion (6) is used. For the detailed derivation, see [2]. The gains $\boldsymbol {\kappa }$ in Eq. (42) are chosen to ensure that the sliding surface is reached in finite time [2, 15]. The width $\boldsymbol {\varPhi }$ of the saturation function is tuned to minimize the error while avoiding chattering. The desired states $\boldsymbol {y}_{\mathrm{d}}$, $\dot {\boldsymbol {y}}_{\mathrm{d}}$, and $\ddot {\boldsymbol {y}}_{\mathrm{d}}$ are necessary to calculate Eq. (42). They are obtained from solving the servo-constraints formulation. The second derivatives of the state trajectory $\ddot {\boldsymbol {y}}_{\mathrm{d}}$ are obtained by finite differences

$$\begin{aligned} \ddot {\boldsymbol {y}}_{\text{d},k+1}\approx\frac{\boldsymbol {v}_{{\mathrm{d},}k+1}-\boldsymbol {v}_{{ \mathrm{d},}k}}{\Delta t}. \end{aligned}$$

(49)

Both the LQR feedback control $\boldsymbol {u}_{\mathrm{LQR}}$ in combination with the feedforward law $\boldsymbol {u}_{\text{d}}$ and the sliding mode control $\boldsymbol {u}_{\mathrm{SMC}}$ are tested in experiments.

6 Experimental results

The crane test bench is set up at the Institute of Mechanics and Ocean Engineering at Hamburg University of Technology and is depicted in Fig. 1(a). The nominal physical parameters are listed in Table 1. Trolley and winches are actuated by synchronous servo-motors. The motion range lies within 13 m and 9 m for trolley and ropes, respectively. Additional kinematic constraints are shown in Table 2.

Table 1 Physical parameters of the container crane test bench

Table 2 Kinematic parameters of the container crane test bench

A Labview program running on a real-time computer controls the test bench. The real-time computer runs a 32 bit version of the National Instruments real-time operating system Phar lab 13.1. The Labview control loop is running with a time step size of ${\Delta t=10~\mbox{ms}}$. Absolute angle encoders measure the current trolley position $s$ and the rope length $\ell$. The swing angle is estimated by an unscented Kalman filter based on measurements of rope length and rope force. The estimated angle $\hat{\varphi}$, the measured trolley position $\hat{s}$ and measured rope length $\hat{\ell}$ determine the estimated load position $\hat{\boldsymbol {z}}$ by

$$\begin{aligned} \hat{\boldsymbol {z}} = \left[\textstyle\begin{array}{c} \hat{s} + \hat{\ell} \sin( \hat{\varphi} ) \\ \hat{\ell} \cos( \hat{\varphi} ) \end{array}\displaystyle \right]. \end{aligned}$$

(50)

For control performance evaluation, the estimated load trajectory $\hat{\boldsymbol {z}}(t)$ is compared to the desired trajectory $\boldsymbol {z}_{\text{d}}(t)$. In the experiments, the desired trajectory is a straight path or semicircle defined by an initial and final load position ${\boldsymbol{p}_{0}= [x_{20} \ \ y_{20} \ \ z_{20}] ^{\mathrm{T}}}$ and ${\boldsymbol{p}_{\text{f}}= [x_{2\text{f}} \ \ y_{2\text{f}} \ \ z_{2\text{f}}]^{\mathrm{T}}}$, respectively, defined in the coordinate system depicted in Fig. 1(b). Every point $\boldsymbol{p}(s)$ on the straight path is parameterized by the scalar $\sigma$ so that

$$\begin{aligned} \boldsymbol{p}(\sigma) &= \boldsymbol{p}_{0} + \frac{\sigma }{\sigma _{\text{t}}} ( \boldsymbol{p}_{\text{f}}-\boldsymbol{p}_{0} ), \qquad \sigma \in \left[\textstyle\begin{array}{c@{\quad}c}0,& \sigma_{\text{t}} \end{array}\displaystyle \right] , \end{aligned}$$

(51)

where the parameter $\sigma_{\text{t}}$ is the total arc length $\sigma_{\text{t}} = \lVert\boldsymbol{p}_{\text{f}}-\boldsymbol {p}_{0} \rVert_{2}$. The temporal sequence is defined by a timing law ${\sigma= \sigma (t)}$. The parameter $\sigma(t)$ must be four times continuously differentiable and is given by

$$\begin{aligned} \sigma(t) &= \biggl( 126 \biggl( \frac{t}{t_{\text{f}}} \biggr) ^{5} -420 \biggl( \frac{t}{t_{\text{f}}} \biggr) ^{6} +540 \biggl( \frac {t}{t_{\text{f}}} \biggr) ^{7} -315 \biggl( \frac{t}{t_{\text{f}}} \biggr) ^{8} + 70 \biggl( \frac{t}{t_{\text{f}}} \biggr) ^{9} \biggr) \sigma_{\text{t}}, \end{aligned}$$

(52)

where the initial time is $t_{0}=0~\mbox{s}$ and the transition time is $t_{\mathrm{f}}$; see, e.g., [4].

6.1 Analysis of servo-constraints solution

Firstly, the solution code proposed in Sect. 4 is analyzed with respect to its accuracy. For this purpose, the servo-constraints solution is compared to the analytical feedforward solution $\boldsymbol {u}_{\mathrm{ flat}}$ based on differential flatness [10]. The trajectory error $e(t)$ is defined as the largest difference of the feedforward control inputs at each time instant

$$\begin{aligned} e(t) = \max_{i}\bigl\Vert u_{\mathrm{d},i}(t)-u_{\mathrm{flat} ,i}(t) \bigr\Vert . \end{aligned}$$

(53)

The maximum error $e_{\mathrm{max}}$ is the maximum of the error $e(t)$ over time

$$\begin{aligned} e_{\mathrm{max}} = \max _{t} \Bigl( \max _{i}\bigl\Vert u_{{ \mathrm{d}},i}(t)-u_{\mathrm{flat},i}(t) \bigr\Vert \Bigr) = \max_{t} \bigl( e(t) \bigr). \end{aligned}$$

(54)

Both formulations in generalized and redundant coordinates are solved in index 3 and index 5 configuration. All four formulations are solved with the linear implicit Euler (${i_{\max}=1}$) and the implicit Euler with at most ${i_{\max}=10}$ Newton iterations. The simulations are performed for a linear trajectory with initial position ${\boldsymbol{p}_{0} = [15\ \ 0\ \ 4]^{\mathrm{T}}~\mbox{m}}$, final position ${\boldsymbol{p}_{\text{f}} = [11\ \ 0\ \ 7] ^{\mathrm{T}}~\mbox{m}}$ and transition time ${t_{\text{f}} = 10~\mbox{s}}$.

First-order convergence of the implicit Euler method is demonstrated in Fig. 2, where the maximum error $e_{\mathrm{max}}$ is plotted over the step size $\Delta t$. For all formulations except RC5, the maximum error $e_{\mathrm{max}}$ of the linear implicit Euler scheme is comparable to the error of the implicit Euler scheme with possibly more than one iteration. Therefore, the linear implicit Euler scheme is applicable on the test bench. This ensures real-time applicability. Moreover, all index 3 formulations and all index 5 formulations, except for RC5 with ${i_{\max}=1}$, yield comparable errors $e_{\mathrm{max}}$, respectively. The index 5 formulations run into numerical rounding errors for time step smaller than ${\Delta t=10~\mbox{ms}}$. Both formulations RC3 and GC3 are stable for time steps larger than ${\Delta t=0.5~\mbox{ms}}$ for the simulated scenario. The results show that a time step ${\Delta t=10~\mbox{ms}}$, which is available on the test bench, is sufficient for the accuracy of the numerical solution in both index 3 formulations. The maximum error $e_{\mathrm{max}}\approx 1\cdot10^{-3}~\mbox{m/s}$ is small compared to inaccuracies, e.g., due to actuator friction. This justifies the usage of the Euler scheme. Note that since the system is differentially flat, numerical effects such as numerical damping do not significantly influence the solution. Therefore, both index 3 formulations GC3 and RC3 are used for experiments.

Fig. 2

Maximum error $e_{\mathrm{max}}$ between numerical and analytical solution for different time step sizes $\Delta t$

Note that the maximum error $e_{\mathrm{max}}$ does not grow over integration time. There is no drift-off effect of the algebraic variables, since the servo-constraints are fulfilled exactly at position level in each integration step. This is demonstrated in Fig. 3. This is an important property concerning long-term applicability.

Fig. 3

Error $e(t)$ over time for both index 3 formulations with time step ${\Delta t=10~\mbox{ms}}$

6.2 Experiments

In experiments, the pure servo-constraints feedforward controller (SC), the feedforward controller stabilized by LQR (SC+LQR), and the sliding mode controller (SMC) proposed in Sect. 5 are compared. Note that for the servo-constraints feedforward controller, both formulations in GC3 and RC3 are implemented and compared. It is also noted that the SMC uses the desired state trajectories $\boldsymbol {y}_{\text{d}}$, $\boldsymbol {v}_{\text{d}}$ from the servo-constraints inverse model which is also solved for the SMC online. The tuning parameters of LQR and SMC are shown in Table 3. The stability properties of both LQR and SMC are demonstrated independently from the feedforward loop in the first experiment. For this purpose, the trolley is disturbed with a constant step velocity $u_{\text{s}}= -0.5~\mbox{m/s}$ for $3~\mbox{s}$. This induces load swinging. After a waiting time of another $3~\mbox{s}$, the feedback controllers are turned on to dampen the induced load swinging of $\varphi_{0}\approx 5.2^{\circ}$ and bring the system to rest. The input $\boldsymbol {u}$ and estimated angle $\hat{\varphi}$ are shown in Fig. 4. The corresponding load swinging of the free system is also shown. Both feedback controllers are able to dampen the load swinging efficiently compared to the free system. The sliding mode controller shows superior performance compared to the LQR controller. It reduces load swinging much faster.

Fig. 4

Experimental results for the load swing reduction experiment

Table 3 Control parameters of the feedback and sliding mode control, where $\boldsymbol {I}_{i}$ denotes the identity matrix of size $i$

After verification of the stabilizing properties of the feedback controller, trajectory tracking is analyzed. For the straight trajectory defined in Sect. 6.1, called trajectory 1, the estimated load position $\hat{\boldsymbol {z}}$ and the input and state trajectories are shown in Fig. 5. All proposed controllers are able to follow the prescribed trajectory. Note that only the angle $\hat{\varphi}$ is shown for all three experiments because the other trajectories are not distinguishable in the plots.

Fig. 5

Experimental results for the straight trajectory 1

In terms of numerical accuracy, it is shown in Fig. 2 that both formulations GC3 and RC3 yield similar numerical errors. This results in similar performance in terms of tracking accuracy. Regarding real-time capability, the calculation time ${t}_{\mathrm{calc},k}$ which is necessary to solve the servo-constraints formulation in each time step $k$ is measured on the real-time target with a resolution of $1~\upmu \mbox{s}$ for both Gc3 and RC3. The mean calculation time for each trajectory is calculated by

$$\begin{aligned} \bar{t}_{\mathrm{calc}}=\frac{1}{N}\sum_{k=1}^{N}{t}_{\mathrm{ calc},k}, \end{aligned}$$

(55)

where $N$ is the maximum amount of steps $N=100t_{\mathrm{f}}$ due to a time step size $\Delta t=10~\mbox{ms}$. To estimate measurement errors, the mean calculation time $\bar{t}_{\mathrm{calc}}$ is measured 10 times for each formulation. Its mean and twice the standard deviation is shown in Fig. 6 for the linear implicit Euler and the implicit Euler with at most ${i_{\mathrm{max}}=10}$ iterations for both RC3 and GC3. For comparison, the time necessary to evaluate the analytical solution $\boldsymbol {u}_{\mathrm{flat}}$ is shown as well. Due to possibly more Newton iterations, the implicit Euler schemes are at most 22% slower than the linear implicit Euler schemes. This difference is rather small because Newton’s method converges within 2 to 3 iterations for this experiment. The mean calculation time $\bar{t}_{\mathrm{calc}}$ of the servo-constraints formulation GC3 and RC3 is approximately 74% and 113% larger compared to the analytical solution, respectively. However, all mean calculation times are orders of magnitude smaller than the available control loop step time ${\Delta t=10~\mbox{ms}}$, proofing again the real-time capability. Therefore, online generation of feedforward inputs is possible. Moreover, there is enough time for far more complex systems to be solved in real-time.

Fig. 6

Mean and twice the standard deviation of 10 measurements each of the mean calculation time $\bar{t}_{\mathrm{calc}}$ for each time step for trajectory 1 with transition time ${t_{\mathrm{f}}=10~\mbox{s}}$

Controller robustness is analyzed by introducing an initial trolley position error $s_{\Delta}=0.5~\mbox{m}$ to trajectory 1. For this experiment, the actual initial position is chosen as ${\boldsymbol{p}_{0}= [11\ \ 0\ \ 4.5]~\mbox{m}}$ and the final position is ${\boldsymbol{p}_{\text{f}}= [15\ \ 0\ \ 6]~\mbox{m}}$, while the transition time is ${t_{\mathrm{f}}=15~\mbox{s}}$. This is called trajectory 2. The measured load position $\hat{\boldsymbol {z}}$ and the input and state trajectories are shown in Fig. 7. The pure feedforward control SC cannot detect the initial error and finishes the trajectory with the same error $s_{\Delta}$. The controllers which include a feedback loop detect the initial position error. The LQR controller provides a large initial input $u_{\text{s}}$ to reduce the initial error quickly. This results in load swinging, which is reduced during the course of the trajectory. On the other hand, the SMC has a slower reaction to the initial error. Less load swinging is introduced. However, convergence to the desired trajectory is slower and the trajectory error $e(t)$ is larger compared to the LQR controller.

Fig. 7

Experimental results for the straight trajectory 2 with initial error $s_{\Delta}=0.5~\mbox{m}$

With the presented problem formulation, trajectory control is not only possible for straight but also for various other trajectories. For example, a semicircular trajectory can be used for collision avoidance. Experimental results are shown for a semicircle with radius $r=0.95~\mbox{m}$ in Fig. 8, where the initial position is ${\boldsymbol{p}_{0}= [9.65\ \ 0\ \ 4.5] }~\mbox{m}$ and the transition time ${t_{\mathrm{f}}=9~\mbox{s}}$. This is called trajectory 3. Figure 8(a) shows that all controllers are able to follow this trajectory. The sliding mode controller shows some performance drawbacks for this trajectory. The feedforward controller augmented by LQR yields the best tracking results here. It reduces the small tracking errors initiated by the feedforward controller. An overlay of videos frames of the experiment is shown in Fig. 8(b).

Fig. 8

Experimental results for tracking a semicircle with radius $r=0.95~\mbox{m}$ applicable for collision avoidance, trajectory 3. (a) Measured position $\hat{\boldsymbol{z}}$. (b) Overlayed video frames of the experiment

In total, the sliding mode controller shows superior performance in load swing damping, but the combination of servo-constraints feedforward and LQR control yields better results in trajectory tracking.

7 Conclusion

Servo-constraints are applicable to underactuated multibody systems described in either generalized or redundant coordinates. For the presented system, the formulation in generalized coordinates yields an index 5 DAE which has to be reduced to index 3. By formulating the system dynamics in redundant coordinates, a more simple representation of the servo-constraints is possible. By directly applying these constraints to the equations of motion, an index 3 DAE system arises. No further projection is necessary. Servo-constraints pose a simple method to design a feedforward tracking controller. Experiments with an overhead crane test bench show that the servo-constraints formulation can be solved in real-time using a linear implicit Euler scheme. The servo-constraints solution can be augmented with an LQR feedback controller for a robust controller performance. Moreover, it can also be used as a basis for sliding mode control.