1 Introduction

Compared to manual cranes, automated crane systems provide various control features to facilitate safe transportation of massive or hazardous payloads. Overhead crane systems are specifically designed to operate in locations where space is limited. Therefore, it is critical to design a robust, stable, and user-friendly control scheme capable of minimizing payload swing in point-to-point maneuvers under different payload conditions [1, 2].

Feedback control strategies have been historically used for payload oscillation suppression of flexible systems [3, 4]. So far, various closed-loop techniques have been developed and evaluated for the control overhead cranes. Sliding mode control [5], adaptive sliding mode control [6], fuzzy logic [7], and adaptive tracking [8] are among the adopted feedback strategies for sway suppression. As a powerful and robust alternative to conventional closed-loop techniques, Model Prediction Control (MPC) has been also implemented by several researchers for overhead crane applications. MPC enables imposing soft or hard constraints on the states of the system, and therefore it is ideal for safety-critical control missions. Smoczek et al. [9] constructed a soft-constrained MPC to minimize the oscillation angle for a laboratory-scaled overhead crane. In another work [10], a Nonlinear Model Predictive Control (NMPC) was proposed to minimize the tracking error at the end of the preceding prediction horizon. MPC has been also used to optimize the velocity of the crane cart over the prediction horizon with the objective of minimizing the payload oscillation [11].

Despite their ability to compute errors and apply corrective actions, the performance of feedback controllers heavily relies on the availability and accuracy of payload mass and states measurements. Cranes are designed to carry payloads with a wide range of characteristics, leading to significantly different dynamic behaviors. The stability of feedback controllers, however, is strongly compromised by this dynamic uncertainty. Also, it is usually infeasible and/or very costly to continuously sense the states of the payload. Due to these limitations, feedback controllers are not applicable in many overhead crane setups.

Input shaping has been traditionally employed as an alternative control strategy for overhead crane applications [12,13,14,15]. Due to their open-loop nature, input shapers do not rely on the continuous sensing of the system states. This independence makes them simpler and less expensive to implement. However, the lack of feedback can make the system more sensitive to initial turbulences. On the other hand, with input shaping, the human operator has more control over the system behavior because the shapers are driven by the operators commands [16, 17]. Some early implementations of command shaping, called Zero Vibration (ZV) shapers, were merely designed to reduce the residual oscillations of the payloads. Although these shapers were proven to be highly robust [18], they suffer from slow time responses. Another category of input shaping techniques was developed based on linear approximation of the system to generate double-step acceleration profiles needed to suspend an overhead payload [19]. Other researchers [20, 21] explored a single variable acceleration profile to remove residual vibrations of an overhead crane. Compared to simple ZV shapers, more intricate input shaping strategies, including Zero Vibration and Minimum Integral (ZVI) and Minimum Vibration and Integral (MVI), were proven to offer flexibility in maneuver time, crane cable length, and jib input settings [22]. Zero Vibration and Derivative Shaper (ZVD) were introduced to address the sensitivity of ZV shapers to the variations of the cable length. Although compared to a ZV shaper, ZVD provides a more robust response, it requires more input steps to meet the final system and boundary conditions. ZVDs are formulated with a standard maneuver time that minimizes the required number of steps in order to achieve the system requirements [18]. In a recent work [23], genetic algorithms were used to optimize the input acceleration profiles of a non-linear input shaper developed for an overhead crane with motion and safety constraints. By optimizing the job input in the form of a continuous acceleration profile, this GA-optimized input shaper provided faster system response, while adhering to the system constraints. By simplifying the initial conditions, most of the existing literature has focused on rest-to-rest maneuvers. However, this assumption limits the applicability of the controller to rest-to-rest maneuvers [24]. However, in practice, an overhead crane must still be able to carry loads when the motion begins with an acceptable amount of initial disturbance. While several research efforts have been conducted to mitigate the adverse effects of modeling errors, parameter and process uncertainty on the performance of the shapers [25,26,27], there have been limited efforts on directly improving the sensitivity of the shapers to initial conditions. Closed-loop signal shapers were used to add disturbance-rejecting features to input shaping controllers [28, 29]. Although these modified shapers provide stable performance, their implementation is limited by the availability of the feedback signals. Modified versions of input shaping were studied for cases when the initial disturbances were caused by an emergency command or a fully known disturbance source [30,31,32]. However, these techniques do not provide a general input shaping scheme insensitive to initial conditions.

It is desired to implement a control technique that benefits from the robustness and user-friendly advantages of input shaping while it also remains insensitive to initial disturbances. Therefore, this article expands the previous work on input shaping and presents new techniques to improve the performance of an overhead crane controller in the presence of initial disturbances. A new Zero Vibration with non-zero Initial Conditions (ZVIC) shaper is introduced, and its performance is compared against other input shaping methods for different crane configurations and initial disturbances. A comprehensive sensitivity analysis is also conducted to discover the advantages and shortcomings of the new approach.

2 Details of method

2.1 Model overview

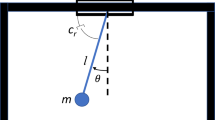
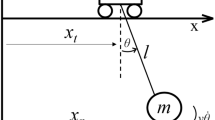
An overhead crane can be classically modeled as a lumped mass (m) attached to a massless slider (jib) by a cable with the constant length of l, as shown in Fig 1. The lumped mass represents the payload, which is assumed to swing in the x-y plane with angle \(\theta \). The slider receives a piecewise input acceleration function (\(\ddot{u}\)), and moves in the x-direction.

Fig. 1
figure 1

Overhead crane model with a massless slider

Full size image

Based on the kinetic and potential energies of the system and following the Lagranges equations, the equation of angular motion of the system is found as:

$$\begin{aligned} \ddot{\theta } + \omega _{n}^2 sin(\theta ) = \ddot{u} /l \end{aligned}$$
(1)

where \(\omega _n = \sqrt{g/l}\) is the natural frequency of the system. Assuming a small swing angle \(\theta \), Eq. 1 is linearized and reduced to:

$$\begin{aligned} \ddot{\theta } + \omega _n^2 \theta = \ddot{u}/l \end{aligned}$$
(2)

where \(\ddot{u}\) is a constant acceleration input. The system initial conditions are:

$$\begin{aligned} \theta (0) = \theta _i, \dot{\theta }(0) = \dot{\theta _i} \end{aligned}$$
(3)

Considering the initial states, the general solution of Eq. 1 is given by:

$$\begin{aligned} \theta (t)= & {} \theta _i cos(\omega _n t) + {\dot{\theta _i} \over {\omega _n}} sin(\omega _n t) + {\ddot{u} \over {g}} (1 - cos(\omega _n t)) \end{aligned}$$
(4)
$$\begin{aligned} \dot{\theta (t)}= & {} - \omega _n \theta _i sin(\omega _n t) + \dot{\theta _i} cos(\omega _n t) + { \omega _n \ddot{u} \over {g}} sin(\omega _n t) \end{aligned}$$
(5)

The equation of the motion can then be written in the matrix form as follows:

$$\begin{aligned} \begin{array}{l} \begin{bmatrix} \theta (t)\\ \dot{\theta (t)} \end{bmatrix} = \begin{bmatrix} cos(\omega _n t) &{} sin(\omega _n t)/\omega _n\\ -\omega _n sin(\omega _n t) &{} cos(\omega _n t) \end{bmatrix} \begin{bmatrix} \theta _i \\ \dot{\theta _i} \end{bmatrix} \\ + \begin{bmatrix} (1-cos(\omega _n t) )/g \\ \omega _n sin(\omega _n t) /g \end{bmatrix} \ddot{u} \end{array} \end{aligned}$$
(6)

2.2 ZVIC shaper

ZVIC shaper is introduced to address the shortcoming of open-loop input shaping methods in the event of non-zero initial states. Assuming the input function u for N steps, applied in time increments of \(\Delta t=\tau /N\), and substituting Eq. 6 at the end of the first step, gives:

$$\begin{aligned} \begin{array}{l} \begin{bmatrix} \theta (\Delta t)\\ \dot{\theta (\Delta t)} \end{bmatrix} = \begin{bmatrix} cos(\omega _n \Delta t) &{} sin(\omega _n \Delta t)/\omega _n\\ -\omega _n sin(\omega _n \Delta t) &{} cos(\omega _n \Delta t) \end{bmatrix} \begin{bmatrix} \theta _i \\ \dot{\theta _i} \end{bmatrix} \\ + \begin{bmatrix} (1-cos(\omega _n \Delta t) )/g \\ \omega _n sin(\omega _n \Delta t) /g \end{bmatrix} \ddot{u}_1 \end{array} \end{aligned}$$
(7)

The solution given by Eq. 7 depends on the initial conditions of the current time step, which is the final condition of the previous step. Therefore, a recurrence solution for all time steps needs to be implemented. The extended solution of Eq. 7 for all time steps, which is the response at the end of each step is given by:

$$\begin{aligned} \Theta = A I_C + B \ddot{u}, \dot{\Theta } = \dot{A}I_C + \dot{B}\ddot{u} \end{aligned}$$
(8)

where the matrix coefficients and acceleration functions are defined as:

$$\begin{aligned}&\begin{array}{l} I_C =\begin{bmatrix} \theta _i \\ \dot{\theta _i} \end{bmatrix}\\ \ddot{u} = {\begin{bmatrix} \ddot{u_1} &{} \ddot{u_2} &{} \dots &{} \ddot{u_N} \end{bmatrix}}^T \\ \end{array} \end{aligned}$$
(9)
$$\begin{aligned}&\begin{array}{l} A = \begin{bmatrix} cos(\omega _n \Delta t) &{} sin(\omega _n \Delta t)/\omega _n \\ \vdots &{} \vdots \\ A_{N,1} &{} A_{N,2} \end{bmatrix} \\ \dot{A} = \begin{bmatrix} -\omega _n sin(\omega _n \Delta t) &{} cos(\omega _n \Delta t) \\ \vdots &{} \vdots \\ \dot{A}_{N,1} &{} \dot{A}_{N,2} \end{bmatrix} \\ B = \begin{bmatrix} (1 - cos(\omega _n \Delta t))/g &{} 0 &{} 0 &{} 0 \\ \vdots &{} \ddots &{} &{} \vdots \\ B_{N,1} &{} B_{N,2} &{} \dots &{} B_{N,N} \end{bmatrix} \\ \dot{B} = \begin{bmatrix} \omega _n sin(\omega _n \Delta t)/g &{} 0 &{} 0 &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ \dot{B}_{N,1} &{} \dot{B}_{N,2} &{} \dots \dot{B}_{N,N} \end{bmatrix} \\ \end{array} \end{aligned}$$
(10)
$$\begin{aligned}&\begin{array}{l} A_{i,j} = A_{i-1,j} cos(\omega _n \Delta t) + \dot{A}_{i-1,j}sin(\omega _n \Delta t)/\omega _n \\ \dot{A}_{i,j} = -A_{i-1,j} \omega _n sin(\omega _n \Delta t) + \dot{A}_{i-1,j} cos(\omega _n \Delta t) \\ \end{array} \end{aligned}$$
(11)
$$\begin{aligned}&\begin{array}{l} B_{i,j} = {\left\{ \begin{array}{ll} B_{i-1,j} cos(\omega _n \Delta t) + \dot{B}_{i-1,j} sin (\omega _n \Delta t)/\omega _n &{} j< i\\ (1-cos(\omega _n \Delta t))/g, &{} j = i\\ 0, &{} j> i \end{array}\right. } \\ \dot{B}_{i,j} = {\left\{ \begin{array}{ll} -B_{i-1,j} \omega _n sin(\omega _n \Delta t) + \dot{B}_{i-1,j} cos (\omega _n \Delta t) &{} j < i\\ \omega _n sin(\omega _n \Delta t) /g &{} j = i\\ 0 &{} j > i\\ \end{array}\right. } \end{array} \end{aligned}$$
(12)
$$\begin{aligned}&\begin{array}{l} \Theta = {\begin{bmatrix} \theta (\Delta t) &{} \theta (2\Delta t) &{} \dots &{} \theta (\tau ) \end{bmatrix}}^T \\ \dot{\Theta } = {\begin{bmatrix} \dot{\theta }(\Delta t) &{} \dot{\theta }(2\Delta t) &{} \dots &{} \dot{\theta }(\tau ) \end{bmatrix}}^T \end{array} \end{aligned}$$
(13)

System final conditions at the end of maneuver (\(\tau \)) are given by:

$$\begin{aligned} \begin{array}{l} \theta (\tau ) = \dot{\theta }(\tau ) = 0 \\ \dot{u}(\tau ) = v_f \end{array} \end{aligned}$$
(14)

where \(v_f\) is the desired final constant speed of the slider at the end of the maneuver. The satisfaction of all three final conditions of the system given by Eq. 14 implies three piecewise input steps to the system, each with a duration of \(\Delta t= \tau /3\). Therefore, setting \(N=3\) in Eqs. 9–12, is enough to meet the three conditions given in Eq. 14. Considering the final state of the system (\(t= \tau \)) from Eqs. 9–12, and substituting Eq. 14 yield:

$$\begin{aligned} \begin{array}{ll} F_C = M_1 I_C + M_2 \ddot{u} \\ F_C = {\begin{bmatrix} 0 &{} 0 &{} 3v_f/\tau \end{bmatrix}}^T \\ M_1 = \begin{bmatrix} A_{N,1} &{} A_{N,2} \\ \dot{A}_{N,1} &{} \dot{A}_{N,2} \\ 0 &{} 0 \end{bmatrix} \\ M_2 = \begin{bmatrix} B_{N,1} &{} B_{N,2} &{} B_{N,3} \\ \dot{B}_{N,1} &{} \dot{B}_{N,2} &{} \dot{B}_{N,3} \\ 1 &{} 1 &{}1 \end{bmatrix} \end{array} \end{aligned}$$
(15)

Thus, the input acceleration piecewise function \(\ddot{u}\) to the slider can be found as:

$$\begin{aligned} \ddot{u} = M_3 = M_4 I_C \end{aligned}$$
(16)

where:

$$\begin{aligned} \begin{array}{ll} M_3 = M_2^{-1} F_C \\ M_4 = M_2^{-1} M_1 \end{array} \end{aligned}$$
(17)

Differentiating Eq. 16 with respect to \(I_C\) gives:

$$\begin{aligned} {d\ddot{u} \over {d I_C}} = -M_4 \end{aligned}$$
(18)

Equation 16 is a linear function of the initial conditions. Thus, its constant matrix derivative (Eq. 18) cannot be solved in terms of inputs. This implies that the system has no optimal input that can eliminate the vibration amplitude at the end of the maneuver. Therefore, the system with non-zero initial conditions is sensitive to disturbances in the initial states of the system. However, increasing the number of input steps provide additional flexibility for the controller to minimize system sensitivity to the initial conditions [22]. By adding more inputs, \(M_2\) (originally defined in Eq. 17) needs to be reformatted as:

$$\begin{aligned} \begin{array}{ll} M_2^{\prime } = \begin{bmatrix} M_2 &{} M_{2i} \end{bmatrix} \\ M_{2i} = \begin{bmatrix} B_{N,4} &{} B_{N,5} &{} \dots &{} B_{N,3+k} \\ \dot{B}_{N,4} &{} \dot{B}_{N,5} &{} \dots &{} \dot{B}_{N, 3+k} \\ 1 &{} 1 &{} \dots &{} 1 \end{bmatrix} \end{array} \end{aligned}$$
(19)

where k is the total number of additional inputs. These extra inputs are independent and can be optimized to decrease the system sensitivity, while the first fundamental three inputs remain dependent in order to satisfy the final conditions. Thus, we can rewrite the inputs as:

$$\begin{aligned} \begin{array}{ll} F_C = M_1 I_C + M_2 \ddot{u}_d + M_{2i}\ddot{u}_i \\ \ddot{u}_d = {\begin{bmatrix} \ddot{u}_1 &{} \ddot{u}_2 &{} \ddot{u}_3 \end{bmatrix}}^T \\ \ddot{u}_i = {\begin{bmatrix} \ddot{u}_4 &{} \ddot{u}_5 &{} \dots &{} \ddot{u}_{3+k} \end{bmatrix}}^T \end{array} \end{aligned}$$
(20)

where \(\ddot{u}_d\) and \(\ddot{u}_i\) are the vectors of the dependent and independent inputs, respectively. Hence,

$$\begin{aligned} \begin{array}{ll} \ddot{u}_d = M_5 - M_6 I_C - M_6 \ddot{u}_i \\ M_5 = {M_2}^{-1} F_C \\ M_6 = {M_2}^{-1} M_1 \\ M_7 = {M_2}^{-1} M_{2i} \end{array} \end{aligned}$$
(21)

Finally, the complete input vector \(\ddot{u}\) can be written as:

$$\begin{aligned} \ddot{u} = \begin{bmatrix} \ddot{u}_d \\ \ddot{u}_i \end{bmatrix} \end{aligned}$$
(22)

Substituting Eq. 21 into Eq. 22 gives:

$$\begin{aligned} \begin{array}{ll} \ddot{u} = M_8 - M_9 I_C - M_10\ddot{u}_i \\ M_8 = \begin{bmatrix} M_5 \\ Z_1 \end{bmatrix}, M_9 = \begin{bmatrix} M_6 \\ Z_2 \end{bmatrix}, M_10 = \begin{bmatrix} M_6 \\ I_1 \end{bmatrix} \end{array} \end{aligned}$$
(23)

where \(Z_1\),\(Z_2\), and \(I_1\) are zero matrices and identity matrix, respectively. Differentiating Eq. 23 with respect to \(I_C\) yields:

$$\begin{aligned} {{d \ddot{u}} \over {dI_C}} = -M_9 \end{aligned}$$
(24)

Similar to Eq. 18, Eq. 24 indicates that adding extra independent inputs does not alter the system sensitivity, i.e., it does not result in optimality.

2.3 MVIC shaper

The Minimum Vibration with non-zero Initial Conditions (MVIC) shaper is introduced to minimize the vibrations at the end of the maneuver. Applying this shaper does not eliminate the residual sway at the end of the maneuver, but instead, it reduces the amplitude of the vibrations. MVIC shaper is formulated to address the case when the system experiences a deviation from its designated initial condition. In this case and if the deviations remain in a limited range, although system conditions in Eq. 14 are violated, the input condition can be satisfied by introducing one dependent input and N independent inputs. These extra terms optimize the input function intending to minimize the final vibration amplitudes over a discrete range of permissible initial conditions. The input condition in can be satisfied by setting the dependent input \(\ddot{u}_d\) as:

$$\begin{aligned} \ddot{u}_d = Nv_f \ \tau - \Sigma _{i=1}^{N} u_i \end{aligned}$$
(25)

where \(u_i\) for \(i=1\) to N are the independent inputs. For every different set of initial conditions, the final angular position and angular velocity are given by:

$$\begin{aligned} \begin{array}{ll} \theta _f = \begin{bmatrix} A_{N,1}&A_{N,2} \end{bmatrix} I_C + \begin{bmatrix} B_{N,1} &{} B_{N,2} &{} \ldots B_{N,1+N} \end{bmatrix} \begin{bmatrix} \ddot{u}_d \\ \ddot{u}_i \end{bmatrix}\\ \dot{\theta }_f = \begin{bmatrix} \dot{A}_{N,1} &{} \dot{A}_{N,2} \end{bmatrix} I_C + \begin{bmatrix} \dot{B}_{N,1} &{} \dot{B}_{N,2} &{} \ldots &{} \dot{B}_{N,1+N} \end{bmatrix} \begin{bmatrix} \ddot{u}_d \\ \ddot{u}_i \end{bmatrix} \end{array} \end{aligned}$$
(26)

Substituting Eq. 25 into Eq. 26 and considering a discrete deviation range containing m number of different initial condition sets give:

$$\begin{aligned} \begin{array}{ll} \Theta _f = Q_1 + Q_2 \ddot{u}_i \\ \dot{\theta }_f = \dot{Q}_1 + \dot{Q}_2 \ddot{u}_i \end{array} \end{aligned}$$
(27)

where:

$$\begin{aligned}&\begin{array}{ll} Q_1 = \alpha I_C + \alpha ^{\prime } \\ \dot{Q}_1 = \dot{\alpha }I_C + \dot{\alpha }^{\prime }_{i,j} \end{array} \end{aligned}$$
(28)
$$\begin{aligned}&\begin{array}{ll} {Q}_{2}{i,j} = B_{N,j}^{(i)} - B_{N,1}^{(i)}, \dot{Q}_{2}{i,j} = \dot{B}_{N,j}^{(i)} - \dot{B}_{N,1}^{(i)} \\ i = 1,2,\ldots ,m , \quad j = 2,3,\ldots , 1+N \end{array} \end{aligned}$$
(29)
$$\begin{aligned}&\begin{array}{ll} \alpha _{i,j} = A_{N,j}^{(i)}, \alpha _{i,j}^{\prime } = N v_f B_{N,1}^{(i)} / \tau \\ \dot{\alpha _{i,j}} = \dot{A}_{N,j}^{(i)}, \dot{\alpha }^{\prime }_{i,j} = Nv_f \dot{B}_{N,1}^{(i)}/\tau \\ i = 1,2,\dots , m ,\quad j = 1,2 \end{array} \end{aligned}$$
(30)

At this point, a set of final angular positions and angular velocities are determined to correspond to the given set of initial conditions. The cost function J that needs to be minimized includes all final amplitudes from a designated range of initial conditions. This cost function is given by:

$$\begin{aligned} J = \Sigma _{k=1}^m (\theta ^2_f + \dot{\theta }^2_f / \omega _n^2)_k = \Theta _f^T \Theta _f + \dot{\Theta }_f^T \dot{\Theta }_f / \omega _n^2 \end{aligned}$$
(31)

Substituting Eq. 30 into Eq. 31 gives:

$$\begin{aligned} \begin{array}{ll} J= (Q_1^T Q_1 + \dot{Q}_1^{\prime T} \dot{Q}_1^{\prime }) + 2(Q_2^T Q_1 + \dot{Q}_2^{\prime T}\dot{Q}_1^{\prime })\ddot{u}_i \\ \qquad + \ddot{u}_i^T(Q_2^T Q_2 + \dot{Q}_2^T \dot{Q}_2^{\prime })\ddot{u}_i \end{array} \end{aligned}$$
(32)

where

$$\begin{aligned} \begin{array}{ll} \dot{Q}_i^{\prime } = \dot{Q}_i / \omega _n , i = 1,2 \\ {dJ \over {d\ddot{u}_i}} = 2(Q_2^T Q_1 + \dot{Q}_2^{\prime }\dot{Q}_1^\prime ) + 2(Q_2^TQ_2 +\dot{Q}_2^{\prime T} \dot{Q}_2^{\prime })\ddot{u}_i \end{array} \end{aligned}$$
(33)

Now, setting \({dJ \over {d\ddot{u}_i}} = 0\) gives:

$$\begin{aligned} \ddot{u}_i = - (Q_2^TQ_2 + \dot{Q}_2^{\prime T} \dot{Q}_2^{\prime })^{-1}(Q_2^TQ_1 + \dot{Q}_2^{\prime T} \dot{Q}_1^{\prime }) \end{aligned}$$
(34)

where \(\ddot{u}_i\) is the optimal independent system input vector. Substituting Eq. 34 into Eq. 25 results in the dependent input \(\ddot{u}_d\). Subsequently, substituting \(\ddot{u}_i\) and \(\ddot{u}_d\)d into Eq. 22 gives the optimal input acceleration piecewise function to the slider such that it satisfies the system final conditions, while at the same time it minimizes the final vibration amplitudes.

2.4 Shaper simulations and discussions

Numerical simulations are conducted to assess the performance, sensitivity, and responsivity of the proposed control scheme for different crane system configurations under various initial disturbance conditions. The controller properties are compared against other common input shaping methods to determine the functional domain, stability, and shortcomings of the implemented ZVIC shapers.

Figure 2 compares the overhead crane model predictions for different cable length and initial condition settings. The system requirements are met by applying the ZVIC step inputs. As the plots suggest, changing the initial conditions affects the total time that the system needs to reach its final states. The reason behind this behavior is that the initial conditions of the system determine the total energy that the system needs to dissipate throughout the maneuver. Also, for a fixed cable length, the amplitude of the first phase of the motion (acceleration) is a function of the initial conditions. However, the third phase (deceleration) is independent of the initial condition settings because the motions start from the same conditions at the end of the cruising phase.

Fig. 2
figure 2

Payload angle versus time for different initial conditions and cable lengths

Full size image

Figure 3 shows how the minimum maneuver time is affected by the initial conditions. For a constant vibration amplitude, different initial conditions result in the different minimum required time to finish the maneuver depending on the correlation between the direction of the payload motion during the maneuver and the direction of the initial conditions. The minimum maneuver time is decreased when the initial conditions take the same direction as the motion. So, for a positive motion and with similar vibration amplitude, \(+\theta _0\) and \(+\dot{\theta }_0\) conditions will decrease the time because they are applied in the same direction as the motion, but when the initial conditions are reversed, i.e.\(-\theta _0\) and \(-\dot{\theta }_0\)0 , the system will need more time to suppress the sway. Therefore, it is possible for a case with higher maximum vibration amplitudes to yield shorter maneuver time. This implies that if it is not possible to adequately suppress the initial vibrations at the beginning of a maneuver, it may be more effective to delay the suppression to a later time in the maneuver when the direction of motion is aligned with the direction of the initial conditions.

Fig. 3
figure 3

Maneuver time versus initial conditions

Full size image

Figure 4 compares ZV, ZVD, and ZVIC shapers generated for systems with identical non-zero initial conditions and different cable length settings. Regardless of the cable length and initial states, the ZVIC can finally bring the system to rest, while the systems controlled by ZV and ZVD shapers suffer from residual vibrations when the maneuvers end. However, ZVIC can result in slightly higher vibration peaks throughout the maneuver. Thus, ZV or ZVD may perform better than ZVIC when the initial conditions are close to zero.

Fig. 4
figure 4

Maneuver time versus initial conditions

Full size image

ZVIC shapers are designed for a known range of initial conditions. Therefore, if the system takes initial conditions that are outside its pre-set domain, the generated shaping commands cannot completely cancel the oscillations and non-zero final states will not be achieved. Figure 5 shows how the final vibration amplitude of the system changes by changing the initial vibration amplitude. Amplitude ratio is defined as the ratio between the initial vibration amplitude of the system and the pre-set initial amplitude defined for the ZVIC shaper. Changing the initial conditions from the pre-set conditions increases the final vibration amplitude. Changing the initial conditions while maintaining the same initial vibration amplitude increases the final amplitude as well. The plot is generated using 2000 random initial conditions. The black line depicts the average final vibration amplitude for all initial condition settings with a similar amplitude, and the green line represents the zero initial angular velocity cases. Comparing these results to the ZV shaper (red line), it is evident that the red line is in the middle of the blue area, which means that ZV shaper has a smaller final amplitude than half of the cases. This suggests that if the initial conditions are explicitly known or can be measured before the maneuver, then it is recommended to implement a ZVIC shaper as it can effectively cancel the sway. Otherwise, if only the initial amplitude is known, a ZV shaper should be used.

Fig. 5
figure 5

Final oscillation amplitude of the system versus the amplitude ratio of one independent input (IC = [\(5\pi /180\) 0])

Full size image

Figure 6 compares MVIC shapers with one (MVIC1), two (MVIC2), and three (MVIC3) independents to ZVIC shaper. The initial condition settings and the maneuver times achieved by these four shapers for the three studied cases are listed in Table 1 for comparison purposes. MVIC shaper minimizes the final vibration amplitude over a range of initial conditions. MVIC1 that has one independent is not enough to yield zero final states at any initial condition within the pre-set range. However, adding one or more independent inputs decreases the final vibration amplitude to zero for the initial condition in the middle of the pre-set range. MVIC2 and MVIC3 are identical, which means adding more independent inputs (steps) does not affect the sensitivity of the system to the initial conditions. Also, MVIC2 and MVIC3 are identical to ZVIC. This means that minimizing the final vibration amplitude over a range of initial conditions is equivalent to applying a ZVIC shaper, which minimizes the final amplitude of the system at an initial condition in the middle of that range.

Fig. 6
figure 6

Final amplitude of vibration versus a range of initial angles of different shapers

Full size image
Table 1 Initial conditions and maneuver times of shapers compare in Fig. 6
Full size table

Figure 7 shows the effect of maneuver time on the sensitivity of the system to the initial conditions for different cable lengths. For a fixed set of cable length and initial conditions, the system final amplitude does not change by increasing the maneuver time. Increasing the maneuver time generally decreases the amplitude of the step inputs, but it does not make the system less sensitive to the initial conditions.

Fig. 7
figure 7

Final amplitude of vibration achieved by ZVIC over a range of initial angles for different cable lengths and maneuver times

Full size image

Different initial conditions may be considered to minimize the required maneuver time. Figure 8a shows how the minimum maneuver time changes by changing the initial swing angle while maintaining zero initial angular velocity. Starting with a small positive initial swing angle decreases the minimum maneuver time, while on the other hand, a small negative initial swing angle increases the maneuver time.

Figure 8b shows how the system maneuver time changes by changing the initial conditions while maintaining a constant initial vibration amplitude. This case is practically identical to a swinging pendulum that has a constant vibration amplitude. As illustrated in this figure, starting the ZVIC shaper with a small positive swing angle (aligned with the motion) can decrease the total maneuver time. On the other hand, starting from a negative initial swing angle increases the maneuver time. Generally, systems with smaller cables tend to need shorter maneuver times. This is because the systems with short cables have higher natural frequencies, which leads to shorter periodic times. However, for systems with long cable, it is still possible to decrease the maneuver time by introducing a positive swing angle increase.

Fig. 8
figure 8

Minimum maneuver time versus a range of initial angles for systems with different lengths with different settings: a \(\dot{\theta }_i = 0\), and b Constant vibration amplitude

Full size image

3 Conclusions

This article presented a new input shaping approach to address the control of overhead cranes with non-zero initial states. Insensitivity to initial conditions is achieved through the introduction of new sets of shaping inputs. This technique allows for the initial disturbance cancelation of a human-operated crane system without the need for a feedback control setup. The proposed command shaping method is numerically compared against other methods, and its behavior is extensively studied for a different system and initial condition settings.