Separable finite viscoelasticity: integral-based models vs. experiments

Abstract

In the present paper, the predictive capabilities of some integral-based finite strain viscoelastic models under the time–strain separability assumption have been investigated through experimental data for monotonic, relaxation and dynamic shear loads, in time and frequency domains. This analysis is instigated by experimental investigation results on two vulcanized carbon black filled rubbers. A unified identification procedure has been deployed to all models to determine the constitutive parameters. The monotonic tests were performed to capture the rate dependent and the long-term response of the materials. For the purely hyperelastic response, we considered the proposed hyperelastic potential proposed in Abaqus for incompressible materials. Relaxation tests were intended to identify the time-dependent material properties, and completed with a dynamic mechanical analysis. Models under consideration are Christensen, Fosdick & Yu, a variant of BKZ model, and the Simo model implemented in Abaqus. In the time domain, for each test case and for each model, the nominal stress is hence compared to experimental data, and the predictive capabilities are then examined with respect to three polynomial hyperelastic potentials forms. The dynamic properties had been investigated in the frequency domain with respect to the frequency and predeformation dependencies, and then comparison conclusions have been drawn.

1 Introduction

Elastomeric compounds are widely used in the industry for their high deformability and damping capabilities (Treloar 1975). Subjected to complex combinations of manufacturing and service loadings, elastomers undergo severe loading conditions, and the load case of large static predeformation superimposed by small amplitude dynamic excitation is commonly encountered in industrial applications, e.g., tires, shock-absorbing bushes, construction industry, aerospace applications, etc. To design such industrial compounds efficiently, it is of major importance to predict the response of the products through simple modeling processes. Nevertheless, it has been pointed out through experimental observations that the constitutive behavior of rubber materials is highly nonlinear in static and dynamic regimes, which have multiple analysis methods: experimental (Treloar 1975; Lockett 1972; Tschoegl 1997), theoretical (Valanis 1972; Holzapfel 2002; Drozdov 1996) and numerical (Le Tallec 1990) among others.

Thus the objective of the present paper is to propose an analysis of the predictive capabilities of some models for engineering applications. The choice is made herein on some hereditary integral-based constitutive models in time and frequency domains, under the separability assumption (Hong et al. 1981; Sullivan 1983). This work is instigated by an experimental investigation on two vulcanized rubber materials intended for a damping application. Moreover, the choice of the considered models is motivated by the fact that these models do not require a special identification procedure, and all parameters have been identified using Abaqus Evaluate module.

A literature overview provides several modeling approaches for the evaluation and prediction of the response of rubber materials. While many contributions to the kinetic theory of elasticity (Treloar 1943; Ogden 1997) represent the foundation for rubbers showing rate-independent behavior, Green and Tobolsky (1946) extended this theory to include relaxation effects, and based on this, many contributions including viscoelastic phenomena have been developed (Lockett 1972; Schapery 1966; Valanis 1966). Modeled strain-rate dependent response of rubber materials is derived following different frameworks which can be classified according to different criteria. In this work, we made use of the following criteria: The first is related to the formulation of the model which can be integral based or differential/internal-variables based, while the second is the time–strain separability or factorability (Hong et al. 1981; Sullivan 1983), which is frequently introduced in the formulation of finite strain viscoelastic constitutive models and provides extensive theoretical simplicity.

Firstly, the integral-based framework is founded on an extension of the Boltzmann superposition principle to finite strain. From an historically point of view, multiple-integral representation of the finite strain viscoelastic behavior has been originally proposed by Green and Rivlin (1997). This work has been followed by other contributions (Pipkin 2012; Lockett 1972), and more recently (Ravasoo 2013), among others. Multiple-integral models are known to be generally nonseparable (Sullivan and Mazich 1989) and mainly hardly identifiable. Meanwhile, the constitutive theory of finite linear viscoelasticity (Coleman and Noll 1961) has been of a major contribution within this framework, and small deviations away from the thermodynamic equilibrium are assumed. The proposed models with respect to this theory are generally of single integral representation and have been widely investigated, e.g. in Batra and Yu (1999), Haupt and Lion (2002) and Ciambella et al. (2010), for their simplicity they are common in engineering applications. Some of most used models of this construction type, which are separable and do not require hard identification procedure, could be found in Christensen (1980), Fosdick and Yu (1998), De Pascalis et al. (2014) and Bernstein et al. (1963). We note that a new class of quasi-linear models, consisting on a generalization of Fung’s models describing nonlinear viscoelastic response of materials, has been recently proposed in Muliana et al. (2013, 2015) where the strain is expressed in terms of a nonlinear measure of the stress. Within this framework, other models are found to be nonseparable, as those in Sullivan (1987), Höfer and Lion (2009), Lion and Kardelky (2004) and Khajehsaeid et al. (2014) among others. The recently proposed model of Pucci and Saccomandi (2015) offers the possibility to make it separable or nonseparable according to the choice of some functions.

The second framework, differential/internal-variables, consists of a 3D generalization of the 1D rheological models with large deformations. Within this framework, two different approaches could be considered: differential models without thermodynamics considerations (Drozdov 1996), and the thermodynamically consistent internal-variables approach (Sidoroff 1975a, 1975b). The focus herein is on the second approach, based on internal-variables, which was originally proposed by Schapery (1966) and Valanis (1966). This approach has found more interest in mid-1970s (Sidoroff 1975a, 1975b). The key point to develop models of this form is the choice of the evolution equation for the internal variables which is neither evident nor unique. The particularity of these models is that in some cases they can lead to an integral equation, and in particular, some contributors introduced linear evolution equations for the internal variables: separable models are investigated in Simo (1987), Holzapfel and Simo (1996), Valanis (1972) and nonseparable models in Schapery (1966). Even though some models could take the integral form and are separable, they are found to be hardly identifiable and require a large number of material parameters, except for the Simo model. Examples of nonseparable internal-variables models that don’t lead to an integral equation include (Lubliner 1985; Lion 1996; Reese and Govindjee 1998; Reese 2003; Amin et al. 2006; Spathis and Kontou 2008) among others.

After this short review, we recall our objective, which is analysis of the predictive capabilities of some integral-based finite strain viscoelastic models under separability assumption, in the time and frequency domains. It is to note that recently Ciambella et al. (2010) have proposed a comparison of some integral-based viscoelastic models only in the time domain for compression tests, while some other contributors investigated the purely hyperelastic behavior of elastomers (Marckmann and Verron 2006).

This paper is organized as follows. In Sect. 2 we discuss experimental investigation conducted to identify the material parameters, the experimental setup, as well as the used procedures for an efficient specimen testing (Charlton et al. 1994; Tschoegl 1997). Multi-step tests were performed to capture the long-term hyperlastic response of the materials, for uniaxial tension and simple shear motions (Hooper et al. 2012). Since for the intended industrial application a preconditioning procedure is applied to eliminate the Mullins effect (Bueche 1961; Govindjee and Simo 1992), this effect is neglected herein. Relaxation tests are intended to identify the kernel function modeling material memory effects. This experimental investigation was completed by a dynamic mechanical analysis, aiming to be compared to model responses with respect to frequency and predeformation dependence effects (Lee and Kim 2001). We intentionally avoid the Payne effect (Payne and Whittaker 1970), which consists of a dynamic amplitude dependent softening effect (Lion and Kardelky 2004). In the same section, conclusions are drawn concerning a comparison of the material properties, with consideration to industrial applications. The following Sect. 3 is dedicated to the constitutive relations, which are single integral hereditary models under the incompressibility constraint and separability assumption: Christensen (1980), Fosdick and Yu (1998), a variant of BKZ (Petiteau et al. 2013), and Simo models (Simo 1987). In this section, a unified identification procedure for constitutive parameters is presented. Section 4 is dedicated to the identification of the purely hyperelastic response. General hyperelastic constitutive equations have been presented and potential forms proposed in Abaqus for incompressible materials have been examined. Section 5 concerns the identification of the time-dependent material parameters through relaxation tests. The three-dimensional constitutive equations are reduced to a one-dimensional stress–strain relation for shear relaxation loading path, and the model responses are compared to experimental data. Conclusions for the time domain comparison are drawn in the following Sect. 6, with the investigation of monotonic predictive capabilities. The frequency domain analysis as described in Christensen (1980) and Bechir and Kaci (2004), and is made in Sect. 7, with the focus on the capability of the considered models to predict dynamic properties in terms of storage modulus and loss factor with respect to the predeformation levels. A more generalized procedure can be found in Lion et al. (2009), where the authors propose a methodology of geometric linearization around a predeformed state, applicable to arbitrary constitutive models. The last section reports the obtained comparison results on constitutive equations and experimental observations, and conclusions are drawn about the predictive capabilities of the considered models.

2 Experimental setup

2.1 Materials

The vulcanized rubber materials investigated throughout this work are:

• a filled natural rubber NR vulcanizate

• a filled bromo butyl BIIR vulcanizate

The considered rubbers are especially relevant to damping applications, and were provided by “EMAC Technical Rubber Compounds.” The mechanical behavior of both materials is known to be hyperviscoelastic (Treloar 1975). Table 1 summarizes the measured hardness and vulcanization parameters.

Table 1 Hardness and vulcanization parameters

2.2 Experimental procedure

Taking different loading paths into account, sets of experiments, including uniaxial tension and simple shear tests, were carried out on an Instron 3345 Table machine. The tension tests were performed using standardized Haltere type 2 specimens. Shear tests were achieved with the use of quad-shear specimens holders (Charlton et al. 1994; Combette and Ernoult 2005), as shown in Fig. 1, with four elastomeric inserts of 25 mm height, 15 mm width, and 2.3 mm thickness, cut out from plates. An industrial cyanoacrylate fast-acting adhesive was used to hold the assembly. Note that preliminary tests showed that the shear occurs on inserts not on glue. The monotonic experiments were performed at room temperature under displacement-control, and the engineering strain was calculated assuming a homogeneous deformation on the whole specimen. At least three tests were carried out for each loading path.

Fig. 1

Quad-shear sample

For the uniaxial tension, the specimens were loaded till 500% of deformation under strain-rates of 10, 100 and 200%/min. To avoid the shear occurring on glue, the shear tests were loaded till 100% of deformation at 5, 10 and 20%/min.

Focusing on the equilibrium stress response, we made use of multistep experiments at different strains with holding periods of 10 minutes (Shim and Mohr 2011; Fernandes and De Focatiis 2014) during which the applied strain was held constant (Lion 1996; Bergström and Boyce 1998), as shown in Fig. 2. We note that the chosen holding period of 10 minutes is used in an industrial context.

Fig. 2

Strain history for monotonic testing

It is important to underline that a preconditioning procedure allows us not to consider the Mullins effect, which is known to be a stress softening of virgin specimens in the first loading cycles (Bueche 1961; Cantournet et al. 2009). The elastomeric samples were subjected to 5 loading–unloading cycles, under a constant strain-rate of 100%/min for uniaxial tension and 10%/min for shear loadings. To identify the time-dependent viscoelastic behavior, stress relaxation experiments were conducted on a Metravib DMA machine having load capacity of 50 N by means of the double shear specimens holder as shown in Fig. 3a. It consists of an assembly of metallic cylinders with elastomer sheet cut out of plates of 10 mm diameter and 2.3 mm thickness, as shown in Fig. 3b. The experimental procedure consists of deforming the specimen with a traverse rate of 100%/min at different strain levels, ranging from 10% to 50%, and holding the assembly for four hours. A hysteresis is seen to quickly vanish and the steady relaxation response is measured.

Fig. 3

DMA shear specimen preparation and holding system

Investigating the dynamic properties of the considered elastomers, the experimental procedure consists of superimposing a simple shear predeformation and a sinusoidal strain after sufficient relaxation time of about 10 mn as

$$ \epsilon (t) = \epsilon_{0} + \triangle \epsilon \sin \bigl( \omega ( t ) \bigr), $$

(1)

where $\epsilon_{0}$ denotes the predeformation and $\triangle\epsilon$ the strain amplitude.

To consider the frequency-dependence of the material’s behavior, frequency sweep tests with stepwise changing frequency from 0.1 up to 40 Hz at constant predeformation were used (Lee and Kim 2001). Furthermore, the predeformation-dependence was investigated through imposing different levels of prestrain levels from 10% up to 30% (Jalocha et al. 2015; Suphadon and Busfield 2011). The dynamic deformation amplitude was set as a maximum dynamic strain which was less than 1%, in order to avoid another softening effect, the so-called Payne effect (Payne and Whittaker 1970; Klüppel 2009). The Payne effect is an amplitude dependent stress softening that leads to a decrease of the storage modulus for increasing dynamic strain amplitude and a maximum of the loss modulus at middle strains.

2.3 Experimental results

2.3.1 Strain-rate dependence

Both elastomers exhibit strain-rate dependence in the studied range of deformation. Increasing deformation rate leads to a higher stress, till a glassy hyperelastic response is obtained (Yi et al. 2006; Hooper et al. 2012). Figure 4a shows that NR is dependent for all the applied strain-rates, while BIIR exhibits the glassy behavior for strain-rates higher than 100%/min. Moreover, for BIIR, this dependence is seen to be pronounced for strains higher than 200% of deformation.

Fig. 4

Monotonic response of the two materials

Focusing on the hyperelastic equilibrium stress–strain curve, the constant strain-rate was interrupted by several holding times, with a duration of 10 minutes. Many authors (Lion 1996; Bergström and Boyce 1998) suggest that there exists a unique equilibrium response, approached in an asymptotic sense, as the strain rate goes to zero. In our experiments, we have seen that the value of stress reached at the end of each relaxation period is approximately constant at the lower strain-rate. The set of these points is defined as the time-independent equilibrium hyper-elastic stress–strain curve. Figure 4b graphically shows the equilibrium response of the tested elastomers. The NR is seen to be stiffer than BIIR.

2.3.2 Stress relaxation

When vulcanized rubbers are deformed, the stress gradually decreases with time (Ferry 1980; Findley and Davis 2013). In other circumstances, when viscoelastic materials are subjected to a constant stress, the resulting deformation is seen to increase continuously, which is the creep phenomenon (Ferry 1980). Stress relaxation experiments were conducted on simple shear specimens, measuring the stress over four hours of relaxation for different constant strains. Figures 5a and 5c show that both materials relax and the shift from the levels of maintained strain is quasi-linear. Direct comparison of the material responses shows that the relaxation of the natural rubber NR is less obvious than for the bromobutyl filled material (BIIR).

Fig. 5

Relaxation test curves

The separable viscoelastic behavior is determined by normalized relaxation stress curves (Findley and Davis 2013; Tschoegl 2012), graphically shown in Figs. 5b and 5d. The normalized stress response is seen to be independent of the deformation. For each material, the different curves form an “envelope” with a maximum deviation of 5%. This observation confirms the separability assumption (Sullivan and Demery 1982; Bloch et al. 1978). The stress quantity can hence be written as a product of two separate functions of time and deformation: $\sigma(t,\epsilon)=f(t)\cdot g(\epsilon)$.

2.3.3 Dynamic properties

To investigate the frequency-dependent material behavior, frequency sweep tests from 0.1 up to 40 Hz were performed at room temperature of about 23°C. Shear storage modulus and loss factor show the same behavior for the tested materials, as illustrated in Figs. 6a, 6c, 6b, and 6d. In the investigated frequency range, increasing this parameter leads to greater modulus and damping factors. As mentioned above, the materials are relevant to a damping application. Comparing the behavior of both materials to a dynamic excitation, loss factor curves show that BIIR possesses higher damping ability.

Fig. 6

Frequency and predeformation dependence

Depending on the application, rubber compounds are generally used at a predeformed configuration (Combette and Ernoult 2005). Several authors (Mullins 1969; Sullivan 1983; Thorin et al. 2012) have investigated this phenomena, and defined three zones: a linear domain, transition zone and nonlinear domain of dependency, depending on the amount of installed predeformation. The tested materials exhibit predeformation-dependence. In terms of shear storage modulus, the experimental curves in Figs. 6a and 6c show that increasing the static predeformation leads to a lower storage modulus. Greater predeformation leads to a softening phenomenon. The decrease between 0% and 10% of predeformation is greater than that between 20% and 30% of predeformation for the tested materials. As for the loss factor, increasing installed predeformation for both NR and BIIR decreases the loss factor, as graphically shown in Figs. 6b and 6d.

In relation with the authors’ observations mentioned above, we can define the deformation zones (Thorin et al. 2012) as:

• Deformation less than 10%, corresponding to the linear domain, where the curves are qualitatively the same with a slight transition

• From 10% to 20% of deformation, corresponding to the transition domain, where the transition is greater

• Deformation greater than 20%, corresponding to the nonlinear domain

3 Separable finite strain viscoelastic models under consideration

3.1 Models under consideration

In the present work, some of major contributions to finite strain viscoelastic models involving hereditary integral have been considered under the separability assumption. This choice is motivated by the experimental observation confirming the separability assumption, as mentioned above. Models were chosen so as to not require a special identification procedure. All parameters have been identified using Abaqus Evaluate module. The models under consideration are:

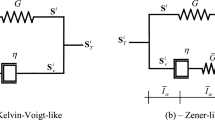
• Christensen model (2a), applicable for moderate and large strain ranges, consisting of a viscoelastic generalization of the kinetic theory of rubber elasticity with specific attention to stress-imposed problems (Christensen 1980)

• Fosdick & Yu model (Fosdick and Yu 1998) (2b), based on the QLV model, consisting of a simple convolution between the Cauchy stress tensor $\boldsymbol{\sigma(t)}$ and the relative Green–Saint-Venant deformation gradient $\mathbf{E_{t}(s)}$

• A variant of the BKZ model (2c), based on a hyperelastic part and a K-BKZ fluid (Bernstein et al. 1963) for the viscous part. This variant has been proposed in a recent work (Petiteau et al. 2013)

• Simo model (2d), proposed in 1987 (Simo 1987), based on an uncoupled volumetric and deviatoric response over any range of deformation, with decomposition of the stress tensor into initial and nonequilibrium parts. We note that the Simo model is used in finite element software Abaqus (Abaqus 2015b)

We have considered two other models for the analysis:

• Fung’s model, commonly referred to as Quasi-Linear Viscoelastic QLV model (Fung et al. 1972), which is one of the most used models and a simple way to incorporate nonlinearity and time dependence in a simplified integral model. This model is intended especially for biological tissues, and can find application for elastomers. Analysis of this model has shown that, for an incompressible material, we obtain the same expression as that of the Simo model.

• Yang et al.’s model (Yang et al. 2000) was proposed in 2000, and is an extension of the BKZ model. This model is mainly used for very high strain-rates. Considering the $A_{5}$ term as zero in the originally proposed model, we note that the expression is the same as in Fosdick and Yu model.

We consider a homogeneous, isotropic and incompressible material. Intending to have the same parameter number for the hyperelastic part, we make use of a generalization of some models originally introduced with respect to a neo-Hookean material. Moreover, we introduced an extension of the original version of single relaxation time in some models to a Prony’s series of at least 3 characteristic times. The constitutive relations for respectively Christensen, Fosdick & Yu, the BKZ variant, and Simo models are:

$$\begin{aligned} \boldsymbol{\sigma}^{\mathit{Ch}} =&-p\mathbf{I}+2\mathbf{B}\frac{\partial W}{\partial \mathbf{B}}+ \mathbf{F} G_{0} \int_{0}^{t} g_{1}(t-s)\frac{\mathbf{\partial E(s)}}{\partial s} \,ds \mathbf{F}^{T} , \end{aligned}$$

(2a)

$$\begin{aligned} \boldsymbol{\sigma}^{\mathit{FY}} =&-p\mathbf{I}+2\mathbf{B}\frac{\partial W}{\partial \mathbf{B}}+ G_{0} \int_{0}^{t} g_{1}(t-s)\frac{\mathbf{\partial E}_{t}(s)}{\partial s} \,ds , \end{aligned}$$

(2b)

$$\begin{aligned} \boldsymbol{\sigma}^{\mathit{BKZ}} =&-p\mathbf{I}+2\mathbf{B}\frac{\partial W}{\partial \mathbf{B}}- 2 \mathbf{F} G_{0} \int_{0}^{t} g_{1}(t-s) \frac{\partial \mathbf{C}^{-1}}{\partial s} \,ds \mathbf{F}^{T} , \end{aligned}$$

(2c)

$$\begin{aligned} \boldsymbol{\sigma}^{\mathit{Si}} =&-p\mathbf{I}+2\mathbf{B}\frac{\partial W}{\partial \mathbf{B}} \frac{1}{g_{\infty}} \\ &{}+ \mathrm{dev} \biggl[ \int_{0}^{t} \frac{\partial g_{1}(s)}{\partial s} \mathbf{F}^{-1}_{t}(t-s) \frac{2}{g_{\infty}}\mathbf{B}(t-s) \frac{\partial W}{\partial \mathbf{B}} \mathbf{F}^{-T}_{t}(t-s) \, ds \biggr] , \end{aligned}$$

(2d)

where $\mathbf{F}= \frac{\partial \mathbf {x}}{\partial \mathbf {X}}$ is the deformation gradient, while $\mathbf{x}$ is the position vector in the current configuration of a material particle, which was located at position $\mathbf {X}$ in the reference configuration. The right and left Cauchy–Green strain tensors are respectively $\mathbf {C}= \mathbf {F}^{T} \mathbf {F}$ and $\mathbf {B}= \mathbf {F} \mathbf {F}^{T}$. The Green–Saint-Venant strain tensor is $\mathbf {E}= \frac{1}{2} ( \mathbf {C} - \mathbf{I} )$. The compressibility constraint, $\det \mathbf {F}=1$, is taken into account by adding a pressure field $p\mathbf{I}$ depending on the initial and boundary conditions (Ogden 1997); $W=W(I_{1},I_{2})$ is the hyperelastic free energy potential and $I_{1}$ and $I_{2}$ stand for the isotropic scalar-valued invariants of $\mathbf{C}$:

$$\begin{aligned} I_{1}&= \mathrm{trace}(\mathbf{C}) , \end{aligned}$$

(3a)

$$\begin{aligned} I_{2}&= \frac{1}{2} \bigl(\mathrm{trace}(\mathbf{C})^{2}- \mathrm{trace}\bigl(\mathbf{C^{2}}\bigr) \bigr), \end{aligned}$$

(3b)

$$\begin{aligned} I_{3}&= \det(\mathbf{C})=1 \quad \text{for an incompressible material,} \end{aligned}$$

(3c)

$g_{1}(t)$ is the dimensionless relaxation kernel defined as a Prony series and commonly taken as

$$ g_{1}(t)=\sum_{i=1}^{N} g_{i} \bigl(e^{\frac{-t}{\tau_{i}}}\bigr) $$

(4)

with $g_{i}$ and $\tau_{i}$ being material parameters. Also $g_{i}>0$ , $g_{\infty}=1-\sum_{i=1}^{N} g_{i}$; $G_{0}$ is the instantaneous linear shear modulus.

The convolution integral-based approach is based on the relative deformation gradient $\mathbf {F}_{t}(s)=\mathbf{F}(s)\mathbf{F}^{-1}(t)$, which is the deformation gradient at the current time $s$ at the current configuration. For the Simo model, the “dev” operator is defined as $\mathrm{dev}(\cdot)=(\cdot)- (\frac{1}{3}(\cdot):\mathbf{I} ) \mathbf{I}$.

The first Piola–Kirchoff stress $\boldsymbol{\Pi}$ is called nominal stress and will be used for experimental considerations. This tensor expresses the actual stress in the reference configuration, and is related to the Cauchy stress tensor by

$$ \boldsymbol{\Pi}= \boldsymbol{\sigma}\mathbf{F}^{-T}. $$

(5)

3.2 Motions under consideration

The available experimental data are for a uniaxial tension test and a simple shear test, with different strain-rates. Considering purely hyperelastic response, we make use of the equilibrium strain–stress curves for the identification of the hyperelastic potential. Considering viscoelastic phenomena, we identified the Prony series through normalized shear relaxation data.

The Evaluate module of the finite element software Abaqus has been used for this purpose, and the identification of material parameters, summarized in Tables 2 to 5, consisted of fitting theoretical solution with experimental data through a least-squares procedure, while minimizing the relative error in stress (Abaqus 2015c).

Table 2 Identified parameters of NR

Table 3 Identified parameters of BIIR

Table 4 Prony series parameters, NR

Table 5 Prony series parameters, BIIR

We have considered the following motions:

3.2.1 Uniaxial tension

We consider a uniaxial tension test. The transformation has the form:

$$ x_{1}=\lambda(t) X_{1}, \qquad x_{2}= \frac{1}{\sqrt{\lambda_{t}}} X_{2}, \qquad x_{3}=\frac{1}{\sqrt{\lambda_{t}}} X_{3}. $$

(6)

The deformation gradient and the right Cauchy–Green strain tensor have components:

$$ \mathbf{F}(t)= \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \lambda(t)&0 &0\\ 0&\frac{1}{\sqrt{\lambda(t)}}& 0 \\ 0&0&\frac{1}{\sqrt{\lambda(t)}} \end{array}\displaystyle \right ], \qquad \mathbf{C}(t)=\mathbf{B}(t)= \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \lambda^{2}(t)&0 &0\\ 0&\frac{1}{\lambda(t)}& 0 \\ 0&0&\frac{1}{\lambda(t)} \end{array}\displaystyle \right ] . $$

(7)

The hydrostatic pressure is eliminated through the relation $\Pi_{22}=0$.

The obtained constitutive equations for uniaxial tension motion are then

$$\begin{aligned} \Pi^{\mathit{Ch}}_{\mathit{tension}}(t) = & 2 \biggl( \lambda(t)- \frac{1}{\lambda^{2}(t)} \biggr) \biggl( \frac{\partial W}{\partial I_{1}}+ \frac{1}{\lambda(t)} \frac{\partial W}{\partial I_{2}} \biggr) \\ &{} +\frac{G_{0}}{2}\lambda(t) \int_{0}^{t} g_{1}(t-s) \frac{\partial \lambda^{2}(s)}{\partial s} \,ds \\ &{} - \frac{G_{0}}{2\lambda^{2}(t)} \int_{0}^{t} g_{1}(t-s) \frac{\partial \frac{1}{\lambda(s)}}{\partial s} \,ds, \end{aligned}$$

(8a)

$$\begin{aligned} \Pi^{\mathit{FY}}_{\mathit{tension}}(t) = &2 \biggl( \lambda(t)- \frac{1}{\lambda^{2}(t)} \biggr) \biggl( \frac{\partial W}{\partial I_{1}}+ \frac{1}{\lambda(t)} \frac{\partial W}{\partial I_{2}} \biggr) \\ &{} +\frac{G_{0}}{2\lambda(t)^{3}} \int_{0}^{t} g_{1}(t-s) \frac{\partial \lambda^{2}(s)}{\partial s} \,ds \\ &{}- \frac{G_{0}}{2} \int_{0}^{t} g_{1}(t-s) \frac{\partial \frac{1}{\lambda(s)}}{\partial s}\,ds, \end{aligned}$$

(8b)

$$\begin{aligned} \Pi^{\mathit{BKZ}}_{\mathit{tension}}(t) = &2 \biggl( \lambda(t)- \frac{1}{\lambda^{2}(t)} \biggr) \biggl( \frac{\partial W}{\partial I_{1}}+ \frac{1}{\lambda(t)}\frac{\partial W}{\partial I_{2}} \biggr) \\ &{} +\frac{2G_{0}}{\lambda^{2}(t)} \int_{0}^{t} g_{1}(t-s) \frac{\partial \lambda(s)}{\partial s} \,ds \\ &{}- 2G_{0} \lambda(t) \int_{0}^{t} g_{1}(t-s) \frac{\partial \frac{1}{\lambda(s)^{2}}}{\partial s}\,ds, \end{aligned}$$

(8c)

$$\begin{aligned} \Pi^{\mathit{Si}}_{\mathit{tension}}(t) = &\frac{2}{g_{\infty}} \biggl( \lambda(t)- \frac{1}{\lambda^{2}(t)} \biggr) \biggl( \frac{\partial W}{\partial I_{1}}+ \frac{1}{\lambda(t)}\frac{\partial W}{\partial I_{2}} \biggr) \\ &{} + \frac{2}{g_{\infty}} \biggl( \lambda(t)- \frac{1}{\lambda^{2}(t)} \biggr) \int_{0}^{t} \frac{\partial {g_{1}}(s)}{\partial s} \biggl( \frac{\partial W}{\partial I_{1}}+ \frac{1}{\lambda(t-s)}\frac{\partial W}{\partial I_{2}} \biggr) \, ds \\ &{}- \frac{2}{\lambda^{2}(t) g_{\infty}} \int_{0}^{t} \frac{\partial {g_{1}}(s)}{\partial s} \frac{\partial W}{\partial I_{2}} \lambda^{2}(t-s) \,ds. \end{aligned}$$

(8d)

3.2.2 Simple shear motion

Considering a simple shear motion, the asymmetric deformation gradient has components

$$ \mathbf{F}(t)= \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} 1&\gamma(t)&0\\ 0&1& 0 \\ 0&0&1 \end{array}\displaystyle \right ] . $$

(9)

The right and left Cauchy–Green strain tensors are

$$ \mathbf{C}(t)= \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} 1&\gamma(t)&0\\ \gamma(t)&1+\gamma^{2}(t)& 0 \\ 0&0&1 \end{array}\displaystyle \right ], \qquad \mathbf{B}(t)= \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} 1+\gamma^{2}(t)&\gamma(t)&0\\ \gamma(t)&1& 0 \\ 0&0&1 \end{array}\displaystyle \right ] . $$

(10)

The obtained constitutive equations for a simple shear motion are then

$$\begin{aligned} \Pi^{\mathit{Ch}}_{12}(t) =&2\gamma(t) \biggl( \frac{\partial W}{\partial I_{1}}+\frac{\partial W}{\partial I_{2}} \biggr)+\frac{G_{0}}{2} \int_{0}^{t}g_{1}(t-s)\frac{\partial\gamma(s)}{\partial s}\, ds \\ &{}+\frac{G_{0}}{2}\gamma(t) \int_{0}^{t}g_{1}(t-s) \frac{\partial\gamma^{2}(s)}{\partial s}\,ds, \end{aligned}$$

(11a)

$$\begin{aligned} \Pi^{\mathit{FY}}_{12}(t) =&2\gamma(t) \biggl( \frac{\partial W}{\partial I_{1}}+\frac{\partial W}{\partial I_{2}} \biggr)+\frac{G_{0}}{2} \int_{0}^{t}g_{1}(t-s)\frac{\partial\gamma(s)}{\partial s} \,ds, \end{aligned}$$

(11b)

$$\begin{aligned} \Pi^{\mathit{BKZ}}_{12}(t) =&2\gamma(t) \biggl( \frac{\partial W}{\partial I_{1}}+\frac{\partial W}{\partial I_{2}} \biggr)+2 G_{0} \int_{0}^{t}g_{1}(t-s)\frac{\partial\gamma(s)}{\partial s} \,ds, \end{aligned}$$

(11c)

$$\begin{aligned} \Pi^{\mathit{Si}}_{12}(t) = &\frac{2}{g_{\infty}} \gamma(t) \biggl( \frac{\partial W}{\partial I_{1}}+\frac{\partial W}{\partial I_{2}} \biggr) - \frac{2}{g_{\infty}} \int_{0}^{t} \frac{\partial g_{1}(s)}{\partial s} \frac{\partial W}{\partial I_{2}} \gamma(t-s) \, ds \\ &{}+ \frac{2}{g_{\infty}}\gamma(t) \int_{0}^{t} \frac{\partial g_{1}(s)}{\partial s} \biggl( \frac{\partial W}{\partial I_{1}}+2\frac{\partial W}{\partial I_{2}} \biggr) \, ds. \end{aligned}$$

(11d)

4 Hyperelastic potential choice

4.1 Hyperelasticity constitutive equations

Hyperelastic behavior is a special case of the Cauchy elasticity concept (Ogden 1997; Beatty 1987) and the strain-energy function $W$ from which stress quantities are derived satisfies objectivity and material symmetry principles. The purely hyperelastic component is expressed as follows:

$$\begin{aligned} \boldsymbol {\sigma}&= 2 \mathbf{B} \frac{\partial W}{\partial \mathbf{B}} -p \mathbf{I}, \end{aligned}$$

(12a)

$$\begin{aligned} \boldsymbol {\Pi}&= \frac{\partial W}{\partial \mathbf{F}} -p \mathbf{F}^{-T}. \end{aligned}$$

(12b)

Stress–stretch relationships corresponding to homogeneous tests can be derived as follows:

• Uniaxial Tension

  $$ \Pi= 2 \biggl( \lambda - \frac{1}{\lambda^{2}} \biggr) \biggl( \frac{\partial W}{\partial I_{1}} + \frac{\partial W}{\partial I_{2}} \frac{1}{\lambda} \biggr) ; $$

  (13)

• Simple Shear

  $$ \Pi = 2 \biggl( \frac{\partial W}{\partial I_{1}} + \frac{\partial W}{\partial I_{2}} \biggr) \gamma . $$

  (14)

4.2 Incompressible hyperelastic models in Abaqus 6.14

There are several forms of strain energy potentials available in Abaqus to model incompressible or quasi-incompressible isotropic elastomers (Abaqus 2015a):

• The polynomial form (Rivlin and Saunders 1951) and its particular cases: reduced polynomial, neo-Hookean (Treloar 1943), Mooney–Rivlin (Mooney 1940) and Yeoh form (Yeoh 1993)

  $$ W= \sum_{i=0,j=0}^{\infty}C_{ij}(I_{1}-3)^{i}(I_{2}-3)^{j} , $$

  (15)

  where $C_{ij}$ are material parameters;

• Ogden real exponents form (Ogden 1972)

  $$ W= \sum_{i=1}^{N} \frac{\mu_{i}}{\alpha_{i}} \bigl( \lambda_{1}^{\alpha_{i}} +\lambda_{2}^{\alpha_{i}} +\lambda_{3}^{\alpha_{i}} -3 \bigr) , $$

  (16)

  where $\mu_{i}$ and $\alpha_{i}$ are material parameters;

• Arruda–Boyce form, commonly referred to as “8 chain model” (Arruda and Boyce 1993)

  $$\begin{aligned} W =& \mu \biggl[ \frac{1}{2} (I_{1}-3) + \frac{1}{20\lambda_{m}^{2}}\bigl(I_{1}^{2}-9\bigr) + \frac{11}{1050\lambda_{m}^{4}}\bigl(I_{1}^{3}-27\bigr) \\ &{} + \frac{19}{7000\lambda_{m}^{6}}\bigl(I_{1}^{4}-81\bigr) + \frac{519}{67375\lambda_{m}^{8}}\bigl(I_{1}^{5}-243\bigr) \biggr] , \end{aligned}$$

  (17)

  where $\mu$ and $\lambda_{m}$ are temperature-dependent material parameters;

• van der Waals form (Enderle and Kilian 1987)

  $$ W =\mu \biggl[ -\bigl(\lambda_{m}^{2}-3 \bigr) \bigl[ ln(1-\eta)+\eta \bigr] -\frac{2}{3}a { \biggl( \frac{\tilde{I}-3}{2} \biggr)}^{\frac{3}{2}} \biggr] , $$

  (18)

  where $\tilde{I}=(1-\beta) I_{1} +\beta I_{2}$ is a generalized strain invariant and $\beta$ and $a$ are material parameters.

4.3 Prediction of purely hyperelastic response

Comparison results are graphically shown in Fig. 7. For a given model, a unique set of material parameters must be able to reproduce set of experimental data with good approximation (Liu et al. 2015). In the considered deformation range, we observed that:

• Arruda–Boyce, van der Walls and Yeoh models have shown slightly the same response in uniaxial or shear modes. These models are seen to underestimate the uniaxial tension nominal stress and overestimate that of shear. Nevertheless, the response has the same curvature as experimental data and the maximum measured error for highest strains is about 18%.

• Mooney–Rivlin and neo-Hookean potentials are seen incapable of predicting experimental data. The response is quasi-linear for both models. An acceptable range of deformation for both models can be less than 150% of deformation.

• The reduced polynomial model with $N=6$ is seen to have a response similar to that of Arruda–Boyce model. It underestimates tension stress and overestimates shear stress. Nevertheless, at moderate or large strains, the models is seen to have some instabilities, and the origin of some curvatures (as shown in Fig. 7) is not clear.

  Fig. 7

  

  Comparison of experimental data and different hyperelastic strain energy potential responses

• Both Ogden ($N=3$) and Polynomial ($N=2$) strain energy potentials are seen to give a well approximated response of the experimental data for a large strain loading. For moderate strains (approximately 300% in shear), the Polynomial model is seen unable to fit the curvature. Ogden model exhibits a slight underestimation of the tension stress and an overestimation of the shear stress. Nevertheless, the measured error is acceptable.

5 On the capability to predict relaxation experiments

The evaluation of the Prony series is available in the Abaqus Evaluate module (Abaqus 2015c) for normalized shear stress relaxation experiments, with a specification on the maximum relative error, which we have chosen to be $10^{-2}$. We make use of the normalized stress relaxation curves for the tested materials at mean deformation level (30%).

The deformation taken into account for relaxation tests is less than 50% of deformation. For simplification reasons, and since experimental data are well approximated in this range, we consider in this section neo-Hookean, Mooney–Rivlin and 2nd order Polynomial hyperelastic potentials.

For a stress relaxation test,

$$ \gamma(t)=\gamma_{0} H(t), $$

(19)

where $H(t)$ is the Heaviside function. This equation is to be introduced in the governing shear equations (11a), (11b), (11c), and (11d).

Relaxation equilibrium response

For a very long relaxation time, i.e., when $t\rightarrow \infty$, the relaxation equations for the considered hyperelastic potentials give the following equilibrium expressions:

$$\begin{aligned} \sigma^{\text{Neo-Hook Equil}}_{12}&=2 C_{10}\gamma_{0}, \end{aligned}$$

(20a)

$$\begin{aligned} \sigma^{\text{MR Equil}}_{12}&=2 ( C_{10}+C_{01} ) \gamma_{0}, \end{aligned}$$

(20b)

$$\begin{aligned} \sigma^{\text{Poly Equil}}_{12}&=2 \bigl( C_{10}+2C_{20} \gamma_{0}^{2}+C_{11}\gamma_{0}^{2}+C_{01}+2C_{02} \gamma_{0}^{2}+C_{11}\gamma_{0}^{2} \bigr)\gamma_{0}. \end{aligned}$$

(20c)

Comparison results are reported in Figs. 8 and 9 and can be summarized as follows:

• Considering the neo-Hookean hyperelastic potential, the models are seen to well reproduce the relaxation test data for a low deformation level. For higher deformation levels, the predicted response is seen to be overestimated. This can be dedicated to the few hyperelastic model parameters, which are clearly not able to predict the long-term viscoelastic response with good accuracy.

• Considering the Mooney–Rivlin hyperelastic potential, the response of the models improves. With material BIIR as shown in Fig. 9b, the response is well approximated at 10% and 30% of deformation. This hyperelastic model still can’t predict the long-term stress for the NR material since the response between the two deformation levels is not really linear.

• The 2nd order Polynomial hyperelastic model offers the best prediction for the long-term relaxation stress response. The measured error between experimental test data and predicted data is of an acceptable level.

• The major difference of the considered hyperviscoelastic models is seen for the hysteretic part. Focusing on Figs. 8c and 9c, the Simo model is seen to offer a good fidelity to approximate low stress. Christensen and Fosdick & Yu models underestimate the hysteretic stress level while the BKZ model is observed to highly overestimate the instantaneous relaxation stress.

  Fig. 8

  

  Comparison of the relaxation response for different hyperelastic models; the case of NR

  Fig. 9

  

  Comparison of the relaxation response for different hyperelastic models; the case of BIIR

6 On the capability to predict monotonic experiments

6.1 Monotonic uniaxial tension

In this section we keep the polynomial hyperelasic form and its particular cases, neo-Hookean and Mooney–Rivlin. Since the available experimental data for uniaxial tension are only for monotonic testing, we consider the elongation function as

$$ \lambda(t)=1+\dot{\lambda} t $$

(21)

with $\dot{\lambda}=\mathit{const}$. The integration of the equations has been done using numerical approximation methods (Simo and Hughes 2006).

The monotonic tension responses in terms of nominal stresses ($\boldsymbol{\Pi}$) are reported in Figs. 10 and 11. The considered models present the capability to take into account the strain-rate effect, with higher stain rates leading to a higher stress at same deformation level. Considering a neo-Hookean or Mooney–Rivlin hyperelastic potential, the predicted data are seen to be inaccurate, and all the models could not predict the second inflection point. Considering the 2nd order polynomial hyperelastic potential, we made the following observations:

• All the considered models are able to predict the strain-rate effect.

• Christensen model is seen to highly overestimate the nominal stress level for high strains, not exceedinf 100% of deformation for the BIIR material as Figs. 11e and 11f show. For the NR material, this model was able to predict the stress level with accepted overestimation, and the error increased as the strain rate increased.

• Fosdick & Yu model is seen to underestimate the stress level for both materials, and has the lowest stress level among all models. Nevertheless, the predicted level is seen to be acceptable.

• Both BKZ and Simo models were able to give a better approximation of the stress level. The prediction is quite good and the predicted stress is in a good range.

Fig. 10

NR monotonic tension model response for neo-Hookean, Mooney–Rivlin and polynomial hyperelastic potentials

Fig. 11

BIIR monotonic tension model response for neo-Hookean, Mooney–Rivlin and polynomial hyperelastic potentials

6.2 Monotonic simple shear

For a monotonic simple shear motion, we consider

$$ \gamma(t)=\gamma_{0} t. $$

(22)

We introduce this equation into Eqs. (11a), (11b), (11c), and (11d) to obtain the constitutive equations for a monotonic simple shear motion. Model response results at different strain rates has been compared to the experimental data. Results for each material are reported in Figs. 12 and 13. For all models, the shear response is quasi-linear as observed by Rivlin and Saunders (1951). Considering the NR material, and for both presented strain rates of 5 and 20%/min, the experimental data are well approximated only for low strain levels, not exceeding 50% of deformation by neo-Hookean and Mooney–Rivlin potentials. Above this range, the response of the different models overestimates the experimental data. The 2nd order polynomial hyperelastic potential is seen to underestimate the stress level along loading, and reaches the stress level at the end of loading. Considering the BIIR material, the prediction quality is worse than for the NR material. Increasing the hyperelastic potential order leads to a softening of the material response. Fosdick & Yu model shows a good estimation of the material data with a neo-Hookean potential for deformation level less than 50%. The response is overestimated over this limit. Christensen model has the ability to stiffen and approximate the stress level at 100% of deformation, but the error is large. BKZ and Simo models show close responses, at each strain rate. The stress level is underestimated, and the maximum error is of about 0.4 MPa.

Fig. 12

NR monotonic shear model response for neo-Hookean, Mooney–Rivlin and polynomial hyperelastic potentials

Fig. 13

BIIR monotonic shear model response for neo-Hookean, Mooney–Rivlin and polynomial hyperelastic potentials

7 On the capability to predict dynamic properties

7.1 Determination of the complex shear modulus

The determination of the complex shear modulus was introduced in Christensen (1980) and is a Fourier transform of the governing equations. The frequency domain viscoelasticity is defined for a kinematically small perturbation about a predeformed state. The procedure consists of a linearized vibration solution associated with a long-term hyperelastic material behavior. This assumes that the linear expression for the shear stress still governs the system. Since the available experimental data in the frequency domain are limited to moderate strains, not exceeding 30%, and the procedure is linearized for high order strains, a simple Mooney–Rivlin hyperelastic potential leads to sufficiently good results. Therefore, we used the following state of loading:

$$ \textstyle\begin{array}{l@{\quad }l} \gamma(s)=0, & s < 0, \\ \gamma(s)=\gamma_{0}, & 0 \leqslant s \leqslant t_{0}, \\ \gamma(s)=\gamma_{0}+\gamma_{a} e^{(i\omega s)}, & t_{0} \leqslant s \leqslant t. \end{array} $$

(23)

We assume that $\vert \gamma_{a} \vert \ll1$ and that the specimen has been oscillating for a very long time so that a steady-state solution is obtained and the dynamic stress has the form

$$\begin{aligned} \sigma^{*}(\omega)&=G^{*}(\omega,\gamma_{0})\gamma(\omega), \end{aligned}$$

(24a)

$$\begin{aligned} G^{*}(\omega,\gamma_{0})&=G_{s}(\omega, \gamma_{0})+iG_{l}(\omega,\gamma_{0}), \end{aligned}$$

(24b)

where $G_{s}=\Re [ G^{*}(\omega,\gamma_{0}) ]$ and $G_{l}=\Im [ G^{*}(\omega,\gamma_{0}) ]$ are respectively the shear storage and loss modulus expressed in terms of the Fourier transform of the time-dependent shear relaxation modulus.

Taking into account only the first order terms of $\gamma(\omega)$, calculations lead to

$$\begin{aligned} \sigma^{*,\mathit{Ch}}_{12}(\omega,\gamma_{0}) =& 2(C_{10}+C_{01})\gamma^{*}(\omega) \\ &{}+ G_{0} \biggl( \frac{1}{2}+\gamma^{2}_{0} \biggr) \biggl[i\omega \int_{0}^{\infty}g_{1}(s)e^{(-i\omega s)}\,ds \biggr]\gamma^{*}(\omega), \end{aligned}$$

(25a)

$$\begin{aligned} \sigma^{*,\mathit{FY}}_{12}(\omega,\gamma_{0}) =& 2(C_{10}+C_{01})\gamma^{*}(\omega) \\ &{}+ \frac{G_{0}}{2} \biggl[i\omega \int_{0}^{\infty}g_{1}(s)e^{(-i\omega s)}\,ds \biggr]\gamma^{*}(\omega), \end{aligned}$$

(25b)

$$\begin{aligned} \sigma^{*,\mathit{BKZ}}_{12}(\omega,\gamma_{0}) =& 2(C_{10}+C_{01})\gamma^{*}(\omega) \\ &{}+ 2G_{0} \biggl[i\omega \int_{0}^{\infty}g_{1}(s)e^{(-i\omega s)}\,ds \biggr]\gamma^{*}(\omega), \end{aligned}$$

(25c)

$$\begin{aligned} \sigma^{*,\mathit{Si}}_{12}(\omega,\gamma_{0}) =& \biggl( \frac{2}{g_{\infty}}(C_{10}+C_{01})- 2 C_{01} \frac{(1-g_{\infty})}{g_{\infty}} \biggr) \gamma^{*}(\omega) \\ &{} -\frac{2C_{01}}{g_{\infty}} \biggl[i\omega \int_{0}^{\infty}g_{1}(s)e^{(-i\omega s)}\,ds \biggr]\gamma^{*}(\omega), \end{aligned}$$

(25d)

where $\sigma^{*}_{12}(\omega,\gamma_{0})$ is the dynamic stress component that should be added to the equilibrium static stress $\sigma^{Equilibrium}_{12}=2(C_{10}+C_{01})\gamma_{0}$ component to obtain the total stress.

The determined complex shear modulus for the considered models is then

$$\begin{aligned} G^{*,\mathit{Ch}}(\omega,\gamma_{0}) =& 2(C_{10}+C_{01}) \\ &{}+ G_{0} \biggl( \frac{1}{2}+\gamma^{2}_{0} \biggr) \biggl[i\omega \int_{0}^{\infty}g_{1}(s)e^{(-i\omega s)}\,ds \biggr], \end{aligned}$$

(26a)

$$\begin{aligned} G^{*,\mathit{FY}}(\omega,\gamma_{0}) =& 2(C_{10}+C_{01}) \\ &{}+ \frac{G_{0}}{2} \biggl[i\omega \int_{0}^{\infty}g_{1}(s)e^{(-i\omega s)}\,ds \biggr], \end{aligned}$$

(26b)

$$\begin{aligned} G^{*,\mathit{BKZ}}(\omega,\gamma_{0}) =& 2(C_{10}+C_{01}) \\ &{}+ 2G_{0} \biggl[i\omega \int_{0}^{\infty}g_{1}(s)e^{(-i\omega s)}\,ds \biggr], \end{aligned}$$

(26c)

$$\begin{aligned} G^{*,\mathit{Si}}(\omega,\gamma_{0}) =& \biggl( \frac{2}{g_{\infty}}(C_{10}+C_{01})- 2 C_{01} \frac{(1-g_{\infty})}{g_{\infty}} \biggr) \\ &{} -\frac{2C_{01}}{g_{\infty}} \biggl[i\omega \int_{0}^{\infty}g_{1}(s)e^{(-i\omega s)}\,ds \biggr]. \end{aligned}$$

(26d)

7.2 Complex modulus comparison results

We first report on the results concerning the shear storage modulus, which are shown in Figs. 14 and 15. The considered materials have shown a frequency-dependent dynamic behavior. Increasing frequency leads to increasing shear storage modulus in the frequency range. At each considered predeformation level, the following observations have been made:

• Simo model have shown an excellent approximation of the dynamic shear storage modulus with respect to frequency and predeformation, with a relative error not exceeding 4%. At lowest frequencies, the experimental data are seen to be slightly overestimated.

• Christensen model underestimates the shear modulus at 10% of deformation and overestimates the properties at higher predeformation; this model was not able to predict the softening of the material occurring with increasing predeformation level.

• Fosdick and Yu model’s response underestimates the materials response, diverging by more than 20%. Even though increasing predeformation leads to a stiffening of the model response, the predicted data are slightly lower than the experimental data.

• The BKZ model’s response is not in an acceptable range, with an error exceeding 160%. The predicted shear storage modulus shows the ability to take into account the frequency effect and the predeformation level but not the moduli level.

Fig. 14

NR dynamic properties and model response for Mooney–Rivlin hyperelastic potential

Fig. 15

BIIR dynamic properties and model response for Mooney–Rivlin hyperelastic potential

For the shear loss factor, the frequency dependence of the compared models is pronounced, and all models are seen to offer a good approximation of this factor as Figs. 14 and 15 show. The Simo model slightly underestimates the response, and the maximum deviation is about 10%. One can observe that although the BKZ model could not predict the storage modulus, it has shown the ability to well approximate the damping of the materials.

8 Conclusion

Within this work, we propose an analysis of the predictive capabilities of some finite strain viscoelastic models under time–strain separability assumption, based on experimental observations in a recent work. We determined the response of four models, well adapted for engineering applications, for monotonic uniaxial tension/simple shear motions, shear relaxation and shear dynamic response. We have found that the choice of the hyperelastic potential is of major importance, since this choice defines the equilibrium point commonly called the service point for dynamic problems in the industrial context. We determined the strain-rate dependent response of the considered models; and the major difference has been found on the transient response. For Christensen model, we have seen that it is more suitable to be used for mid-range deformations, while with a good choice of a hyperelastic potential all other models could predict the response over a wider range of deformations. In the frequency domain, models have shown the capability to take into account frequency and predeformation effects. For shear storage modulus, except for BKZ model, all predicted data were in an acceptable range. For the damping capability governed by the estimation of the loss factor, all models could estimate it in an acceptable range. In the future, this analysis can be conducted with consideration of the temperature effect, which highly influences the phenomenological behavior of elastomerers in the frequency domain in particular and could lead to brittle damage of the materials.

Appendix

This appendix lists material parameters identified with the Abaqus 6.14 “Evaluate” module.