Complex order fractional derivatives in viscoelasticity

Abstract

We introduce complex order fractional derivatives in models that describe viscoelastic materials. This cannot be carried out unrestrictedly, and therefore we derive, for the first time, real valued compatibility constraints, as well as physical constraints that lead to acceptable models. As a result, we introduce a new form of complex order fractional derivative. Also, we consider a fractional differential equation with complex derivatives, and study its solvability. Results obtained for stress relaxation and creep are illustrated by several numerical examples.

1 Introduction

Fractional calculus is a powerful tool for modeling various phenomena in mechanics, physics, biology, chemistry, medicine, economy, etc. Last few decades have brought a rapid expansion of the non-integer order differential and integral calculus, from which both the theory and its applications benefit significantly. However, most of the work done in this field so far has been based on the use of real order fractional derivatives and integrals. It is worth to mention that there are several authors who also applied complex order fractional derivatives to model various phenomena, see the work of Machado or Makris, (Machado 2013; Makris 1994; Makris and Constantinou 1993). In all of these papers, restrictions on constitutive parameters that follow from the Second Law of Thermodynamics were not examined. In the analysis that follows, this issue will be addressed.

The main goal of this paper is to motivate and explain basic concepts of fractional calculus with complex order fractional derivatives. Throughout the paper, we will investigate constitutive equations in the dimensionless form, for all independent ($t$ and $x$) and dependent ($\sigma$ and $\varepsilon$) variables. Thus, consider a constitutive equation given by (1), connecting the stress $\sigma(t,x)$ at the point $x\in \mathbb {R}$ and time $t\in \mathbb {R}_{+}$ with the strain $\varepsilon (t,x)$:

$$ \sum_{n=0}^{N}a_{n} \, {}_{0}D_{t}^{\alpha_{n}}\sigma(t,x) =\sum _{m=0}^{M}b_{m}\,{}_{0}D_{t}^{\beta_{m}} \varepsilon (t,x) $$

(1)

that contains fractional derivatives of complex order $\alpha_{1},\ldots,\alpha_{N},\beta_{1},\ldots,\beta_{M}$. The precise definition of the operator ${}_{0}D_{t}^{\eta}$ of fractional differentiation with respect to $t$ is given below. In order to make a useful framework for the study of (1), we involve two types of conditions: (i) real valued compatibility constraints, and (ii) thermodynamical constraints. Since this paper deals only with the well-posedness of constitutive equations of type (1) and their solvability for strain if stress is prescribed, we may, without loss of generality, assume that both $\sigma$ and $\varepsilon$ are functions only of $t$. Also, equation (1) can be seen as a generalization of different models considered in the literature so far (see, e.g., Atanacković et al. 2014; Caputo and Mainardi 1971a, 1971b; Gonsovski and Rossikhin 1973; Hanyga 2002a, 2002b; Mainardi et al. 2007; Rossikhin and Shitikova 2001a), since by taking all $\alpha_{n}$ and $\beta_{m}$ to be real numbers, the problem is reduced to the real case studied in the mentioned papers.

Our results will show that constitutive equations of the form (1) may lead to creep and stress relaxation curves that are not monotonic. We note that the conditions of complete monotonicity required in, e.g., Amendola et al. (2012), Fabrizio and Morro (1992), Mainardi (2010) turn out not to be necessary but rather sufficient to meet the thermodynamic restrictions. It seems that conditions of monotonicity are stronger than the conditions following from the Second Law of Thermodynamics in the form of Bagley and Torvik (1986) analogously as in Fabrizio and Lazzari (2014) where it is shown that the asymptotic stability, for a certain class of constitutive equations, requires more extensive conditions on the coefficients compared with the restrictions that the classical formulation of the Second Law of Thermodynamics imposes. Non-monotonic creep curves were observed experimentally, however, such a behavior was attributed to inertia either of the rod itself or of the rheometer.

The paper is organized as follows. In Sect. 2, we investigate conditions leading to constitutive equations containing complex derivatives of stress and strain that can be used in viscoelastic models of the wave equation. More precisely, we derive restrictions on parameters in constitutive equation of the form (1) under which the Laplace and Fourier transforms, as well as their inverses, of real-valued functions will remain real-valued. Also, in order to impose the validity of the Second Law of Thermodynamics, we follow the procedure presented in Bagley and Torvik (1986), and obtain additional restrictions on model parameters in constitutive equations. As a result, we shall introduce a new form of the fractional derivative of complex order. Then, in Sect. 3, we treat the fractional Kelvin–Voigt complex order constitutive equation for viscoelastic body, find thermodynamical restrictions, and prove sufficient conditions for its invertibility. Several numerical examples are presented in Sect. 4, as an illustration of creep and stress relaxation in viscoelastic materials.

To the end of this section, we recall basic definitions and results that will be used in our work. Fractional operators of complex order are introduced as follows (see Love 1971; Samko et al. 1993): For $\eta\in \mathbb {C}$ with $0<\operatorname {Re}\eta<1$, definition of the left Riemann–Liouville fractional integral of an absolutely continuous function on $[0,T]$, $T>0$ ($y\in \mathit{AC}([0,T])$) coincides with the case of real $\eta$, i.e., ${}_{0}I_{t}^{\eta}y(t) :=\frac{1}{\varGamma(\eta)} \int_{0}^{t} \frac{y(\tau)}{(t-\tau)^{1-\eta}} \,d\tau$, $t\in[0,T]$, where $\varGamma$ is the Euler gamma function. If $\eta=i\theta$, $\theta\in \mathbb {R}$, then the latter integral diverges, and hence one introduces the fractional integration of imaginary order as

$${}_{0}I_{t}^{i\theta}y(t) := \frac{d}{dt} {}_{0}I_{t}^{1+i\theta}y(t) = \frac{1}{\varGamma(1+i\theta)} \frac{d}{dt} \int_{0}^{t} (t-\tau)^{i\theta} y(\tau)\,d \tau, \quad t\in[0,T]. $$

However, in both cases the left Riemann–Liouville fractional derivative of order $\eta\in \mathbb {C}$ with $0\leq \operatorname {Re}\eta<1$ is given by

$${}_{0}D_{t}^{\eta} y(t) : = \frac{d}{dt} {}_{0}I_{t}^{1-\eta}y(t) = \frac{1}{\varGamma(1-\eta)} \frac{d}{dt} \int_{0}^{t} \frac{y(\tau)}{(t-\tau)^{\eta}}\,d\tau, \quad t \in[0,T]. $$

The basic tool for our study will be the Laplace and Fourier transforms. In order to have a good framework, we will perform these transforms in $\mathcal {S} '(\mathbb {R})$, the space of tempered distributions. It is the dual space for the Schwartz space of rapidly decreasing functions $\mathcal {S} (\mathbb {R})$. In particular, we are interested in the space $\mathcal {S} '_{+}(\mathbb {R})$ whose elements are of the form $y=P(D)Y_{0}$, where $Y_{0}$ is a locally integrable polynomial bounded function on ℝ that vanishes on $(-\infty,0)$, and $P(D)$ denotes a partial differential operator.

The Fourier transform of $y\in L^{1}(\mathbb {R})$ (or $y\in L^{2}(\mathbb {R})$) is defined as

$$ \mathcal {F} y (\omega)=\hat{y}(\omega)= \int_{-\infty}^{\infty} e^{-i\omega x}y(x)\,dx, \quad\omega \in \mathbb {R}. $$

(2)

In the distributional setting, one has $\langle \mathcal {F} y, \varphi \rangle =\langle y, \mathcal {F} \varphi \rangle$, $y\in \mathcal {S} '(\mathbb {R})$, $\varphi \in \mathcal {S} (\mathbb {R})$, where $\mathcal {F} \varphi$ is defined by (2). For $y\in L^{1}(\mathbb {R})$ with $y(t)=0$, $t<0$, and $|y(t)| \leq Ae^{at}$, $a,A>0$, the Laplace transform is given by

$$\mathcal {L} y(s)= \tilde{y}(s) = \int_{0}^{\infty} e^{-st} y(t)\, dt, \quad \operatorname {Re}s>a. $$

If $y\in \mathcal {S} '_{+}(\mathbb {R})$ then $a=0$ (since $y$ is bounded by a polynomial). Then $\mathcal {L} y$ is a holomorphic function in the half plane $\operatorname {Re}s>0$ (see, e.g., Vladimirov 1984).

Let $Y(s)$, $\operatorname {Re}s>0$, be a holomorphic function bounded by a polynomial in that domain. Then, for a suitable polynomial $P$, $Y(s)/P(s)$ is integrable along the line $\varGamma=(a-i\infty, a+i\infty)$, and the inverse Laplace transform of $Y$ is a tempered distribution $y(t)=P(\frac{d}{dt})Y_{0}(t)$, where $Y_{0}(t) = \mathcal {L} ^{-1}[Y](t)=\frac{1}{2\pi i} \int_{\varGamma}\frac {Y(s)}{P(s)} e^{st}\, ds$.

Let $y\in \mathcal {S} '_{+}$. Recall:

$$\begin{aligned} \mathcal {F} \biggl[\frac{d^{n}}{dx^{n}}y \biggr] (\omega) =& (i\omega)^{n} \mathcal {F} y(\omega) \quad (\omega\in \mathbb {R}), \qquad \mathcal {L} \biggl[\frac{d^{n}}{dt^{n}}y \biggr] (s) = s^{n} \mathcal {L} y(s) \quad (\operatorname {Re}s>0), \ n\in \mathbb {N}, \\ \mathcal {F} \bigl[{}_{0}D_{x}^{\alpha}y\bigr](\omega) =& (i\omega)^{\alpha} \mathcal {F} y(\omega) \quad (\omega\in \mathbb {R}), \qquad \mathcal {L} \bigl[{}_{0}D_{t}^{\alpha}y\bigr](s) = s^{\alpha} \mathcal {L} y(s) \quad (\operatorname {Re}s>0), \ \alpha\in \mathbb {C}. \end{aligned}$$

2 Linear fractional constitutive equations with complex derivatives

In what follows, we shall denote by $\alpha$ and $\beta$ the orders of fractional derivatives. $\alpha$ will be assumed to be a real number, while $\beta$ will be an element of ℂ which is not real, i.e., $\beta=A+iB$, with $B\neq0$. Also, we shall assume that $0<\alpha$, $A<1$.

2.1 Real valued compatibility constraints

Similarly as in the real case (see Atanacković et al. 2011), it is quite difficult to begin with a study of the most general case of (1). Therefore, in order to try to recognize the essence of the problem and find possibilities for overcoming it, we shall first concentrate to simpler forms of constitutive equations that contain complex derivatives. Consider the following generalization of the Hooke law in the complex setting:

$$ \sigma(t) = b\, {}_{0}D_{t}^{\beta} \varepsilon (t), $$

(3)

where $\beta\in \mathbb {C}$ and $b\in \mathbb {R}$. In order to find restrictions on parameters $b$ and $\beta$ in (3) which yield a physically acceptable constitutive equation, we shall verify the next two conditions: For real strain $\varepsilon$, the stress $\sigma$ has to be real valued function of $t$. We call this a real-valued compatibility requirement. Thermodynamical restrictions will result from the Second Law of Thermodynamics, and will be studied in the next section. Note that in the case of constitutive equations with only real-valued fractional derivatives, the real-valued compatibility requirement always holds true, while the thermodynamical restrictions had to be investigated (cf. Atanacković et al. 2011).

Theorem 2.1

Let $\varepsilon \in \mathit{AC}([0,T])$ be real-valued, for all $T>0$, $0< A<1$ and $b\neq0$. Then function $\sigma$ defined by (3) is real valued if and only if $\beta\in \mathbb {R}$.

Proof

It follows from (3), with $\beta=A+iB$, and $1/\varGamma(1-\beta)=h+ir$, that

$$\operatorname {Im}\sigma(t) = b\,\frac{d}{dt} \int_{0}^{t} \varepsilon (t-\tau) \tau^{-A} \bigl(r\cos(B\ln\tau) - h\sin(B\ln\tau) \bigr) \,d\tau, \quad t\geq0. $$

Denoting by $\frac{r}{h}:=\operatorname {tg}\phi$, for $h\neq0$, we obtain

$$\operatorname {Im}\sigma(t) = \frac{bh}{\cos\phi} \frac{d}{dt} \int_{0}^{t} \varepsilon (t-\tau) \tau^{-A} \sin(\phi-B\ln\tau)\,d\tau, \quad t\geq0. $$

In the case $h=0$, the imaginary part of $\sigma$ reduces to $br\frac{d}{dt} \int_{0}^{t} \varepsilon (t-\tau) \tau^{-A} \cos(B\ln\tau)\, d\tau$.

If $B=0$ then $r=0$ and $\phi=0$, hence $\operatorname {Im}\sigma=0$ and $\sigma$ is a real-valued function.

Next, suppose that $B\neq0$. But then one can find a subinterval $(t_{1},t_{2})$ of $(0,T)$ where $\sin(\phi-B\ln\tau)$ (resp., $\cos(B\ln\tau)$) is positive (resp., negative), and choose $\varepsilon \in \mathit{AC}([0,T])$ which is compactly supported in $(t_{1},t_{2})$ and strictly positive. This leads to a contradiction of the assumption $\operatorname {Im}\sigma=0$. □

The previous theorem implies that equations of form (3) with $\beta\in \mathbb {C}\backslash \mathbb {R}$ cannot be constitutive equations for a viscoelastic body.

Next, consider the equation

$$ \sigma(t) = b_{1}\, {}_{0}D_{t}^{\beta_{1}} \varepsilon (t)+ b_{2} \,{}_{0}D_{t}^{\beta _{2}}\varepsilon (t), \quad t\geq0, $$

(4)

where $b_{1},b_{2}\in \mathbb {R}$, and $\beta_{1},\beta_{2}\in \mathbb {C}\backslash \mathbb {R}$, i.e., $\beta_{k}=A_{k}+iB_{k}$ and $B_{k}\neq0$ ($k=1,2$). Suppose again that $\varepsilon \in \mathit{AC}([0,T])$ is a real-valued function, for every $T>0$.

Remark 2.2

Note that dimension $[{}_{0}D_{t}^{\beta_{1}} \varepsilon ]$ is $T^{-\beta_{1}}$, where $T$ is the time unit. Therefore, (4) makes sense if $[b_{1}]=T^{\beta_{1}}$ and $[b_{2}]=T^{\beta_{2}}$.

Theorem 2.3

Function $\sigma$ given by (4) is real-valued for all real-valued positive $\varepsilon \in \mathit{AC}([0,T])$ if and only if $b_{1}=b_{2}$ and $\beta_{2}=\bar{\beta_{1}}$.

Proof

We continue with the notation of Theorem 2.1. Let $t\geq0$. Then

$$\sigma(t) = \frac{b_{1}}{\varGamma(1-\beta_{1})} \frac{d}{dt} \int_{0}^{t} \varepsilon (t-\tau) \tau^{-\beta_{1}}\, d \tau + \frac{b_{2}}{\varGamma(1-\beta_{2})} \frac{d}{dt} \int_{0}^{t} \varepsilon (t-\tau) \tau^{-\beta_{2}}\, d \tau. $$

Denote by $h_{k}+ir_{k}:=1/\varGamma(1-\beta_{k})$, $k=1,2$. Then the imaginary part of the right-hand side reads

$$\begin{aligned} \operatorname {Im}\sigma(t) =& \frac{d}{dt} \int_{0}^{t} \varepsilon (t-\tau) \tau^{-A_{1}} \bigl(b_{1} r_{1}\cos(B_{1}\ln\tau) - b_{1} h_{1}\sin(B_{1}\ln \tau) \bigr)\,d\tau \\ & {} + \frac{d}{dt} \int_{0}^{t} \varepsilon (t-\tau) \tau^{-A_{2}} \bigl(b_{2} r_{2}\cos(B_{2}\ln\tau) - b_{2} h_{2}\sin(B_{2}\ln \tau) \bigr)\,d\tau. \end{aligned}$$

(5)

Using the identity $\varGamma(\bar{z})=\overline{\varGamma(z)}$, it is straightforward to check that $b_{1}=b_{2}$ and $\beta_{2}=\bar{\beta_{1}}$ imply that $\operatorname {Im}\sigma=0$, and hence $\sigma$ is a real-valued function on $[0,T]$, for every $T>0$.

Conversely, we want to find conditions on parameters which yield a real-valued function $\sigma$. Thus, we look at (5), with the change of variables $p=\ln\tau$, $\tau\in(0,t)$, $t\leq T$, and solutions of the equation

$$\begin{aligned} & \frac{d}{dt} \int_{-\infty}^{\ln t} e^{p} \varepsilon \bigl(t-e^{p}\bigr) \bigl(b_{1}r_{1} e^{-A_{1} p} \cos(B_{1}p) - b_{1}h_{1} e^{-A_{1} p} \sin(B_{1}p) \\ & \quad {} + b_{2}r_{2} e^{-A_{2} p} \cos(B_{2} p) - b_{2}h_{2} e^{-A_{2} p} \sin(B_{2} p) \bigr)\,dp =0, \quad t\in[0,T]. \end{aligned}$$

(6)

Set $\frac{r_{k}}{h_{k}}:=\operatorname {tg}\phi_{k}$, $k=1,2$, for $h_{1},h_{2}\neq0$. (For $h_{k}=0$ set $\phi_{k}:=\frac{\pi}{2}$, $k=1,2$.) Then (6) gives

$$\frac{d}{dt} \int_{-\infty}^{\ln t} e^{p} \varepsilon \bigl(t-e^{p}\bigr) \biggl( \frac{b_{1}h_{1}}{\cos\phi_{1}} e^{-A_{1} p} \sin( \phi_{1}-B_{1}p) + \frac{b_{2}h_{2}}{\cos\phi_{2}} e^{-A_{2} p} \sin( \phi_{2}-B_{2}p) \biggr)\,dp = 0. $$

Assume first that $|B_{1}|\neq|B_{2}|$, say $|B_{1}|>|B_{2}|$. Since the basic period of $\sin(\phi_{1}-B_{1} p)$ ($T_{0}=2\pi/|B_{1}|$) is smaller than for $\sin(\phi_{2}-B_{2} p)$, it follows that for every $k\in \mathbb {N}$, $k>k_{0}$, where $k_{0}$ depends on $\ln t$, the function $\sin(\phi_{1}-B_{1}p)$ changes its sign at least three times in the interval $(k\pi,k\pi +2\pi/|B_{2}|)$. Thus, on that interval, there exist at least two intervals where $\sin(\phi_{1}-B_{1}p)$ and $\sin(\phi_{2}-B_{2} p)$ have the same sign, and two intervals where they have opposite signs. We conclude that there exists an interval $[a,b]\subseteq(k\pi,k\pi+2\pi/|B_{2}|)\subset(-\infty, \ln t)$, so that

$$ \frac{b_{1}h_{1}}{\cos\phi_{1}} e^{-A_{1} p} \sin(\phi_{1}-B_{1}p) + \frac{b_{2}h_{2}}{\cos\phi_{2}} e^{-A_{2} p} \sin(\phi_{2}-B_{2}p) >0, \quad p\in[a,b]. $$

(7)

Choose $\delta>0$ and $k\in \mathbb {N}$ so that

$$\bigl\{ t-e^{p};\ t\in(T/2-\delta,T/2+\delta),\ p\in[a,b] \bigr\} = \bigl(T/2-\delta -e^{b},T/2+\delta-e^{a}\bigr)=I\subset(0,T). $$

Now, we choose a non-negative function $\varepsilon \in \mathit{AC}([0,T])$ with the following properties: $\operatorname {supp}\varepsilon \subseteq I$, so that the function $p\mapsto \varepsilon (t-e^{p})$, $p\in[a,b]$, is strictly positive on some $[a_{1},b_{1}]\subseteq(a,b)$. This implies that for $t\in(T/2-\delta ,T/2+\delta)$,

$$\int_{a}^{b} e^{p} \varepsilon \bigl(t-e^{p}\bigr) \biggl( \frac{b_{1}h_{1}}{\cos\phi_{1}} e^{-A_{1} p} \sin( \phi_{1}-B_{1}p) + \frac{b_{2}h_{2}}{\cos\phi_{2}} e^{-A_{2} p} \sin( \phi_{2}-B_{2}p) \biggr)\,dp $$

is not a constant function. This is in contradiction with (6).

Therefore, in order to have (6), one must have $|B_{1}|=|B_{2}|$. Moreover, arguing as above, one concludes that $|\phi_{1}-B_{1}p|=|\phi_{2}-B_{2}p|$ must hold, for all $p\in(-\infty,\ln t)$, $t\geq0$. Then we examine the equation

$$b_{1}h_{1} e^{-A_{1} p} - b_{2}h_{2} e^{-A_{2} p}= 0, \quad\mbox{or} \quad b_{1}h_{1} e^{-A_{1} p} + b_{2}h_{2} e^{-A_{2} p}= 0, \quad p \in[k\pi,k\pi+2\pi/|B_{1}|]. $$

Now in both cases, $b_{1}b_{2}>0$ or $b_{1}b_{2}<0$, it is easy to conclude that $A_{1}=A_{2}$, $b_{1}=b_{2}$ and $B_{1}=-B_{2}$ have to be satisfied. This proves the theorem. □

Remark 2.4

(i) Theorem 2.3 states that a real-valued compatibility constraint for constitutive equations of form (4) holds if they contain complex fractional derivatives of strain, whose orders have to be complex conjugated numbers. Therefore, we may assume in the sequel, without loss of generality, that $B>0$.

(ii) According to the above analysis, one can take arbitrary linear combination of pairs of complex conjugated fractional derivatives of strain. Moreover, one can also allow the same type of fractional derivatives of stress. Thus, one can consider the most general stress–strain constitutive equation with fractional derivatives of complex order:

$$\sigma(t) + \sum_{i=1}^{N} c_{i} \bigl({}_{0}D_{t}^{\gamma_{i}} + {}_{0}D_{t}^{\bar{\gamma}_{i}} \bigr) \sigma(t) = \varepsilon (t) + \sum_{j=1}^{M} b_{j} \bigl({}_{0}D_{t}^{\beta_{j}} + {}_{0}D_{t}^{\bar {\beta}_{j}} \bigr) \varepsilon (t), $$

where $c_{i},b_{j}\in \mathbb {R}$ and $\gamma_{i},\beta_{j}\in \mathbb {C}$, $i=1,\ldots ,N$, $j=1,\ldots,M$.

(iii) As a consequence, one has that stress–strain relations can also contain arbitrary real order fractional derivatives, without any additional restrictions. This fact has already been known from previous work.

(iv) The same conclusions can also be obtained using a different approach. One can apply the result from (Doetsch 1950, p. 293, Satz 2), which tells that a function $F$ is real-valued (almost everywhere), if its Laplace transform is real-valued, for all real $s$ in the half-plane of convergence right from some real $x_{0}$, in order to show that an admissible fractional constitutive equation (1) may be of complex order only if it contains pairs of complex conjugated fractional derivatives of stress and strain.

2.2 Thermodynamical restrictions

In the analysis that follows, we shall consider the isothermal processes only. For such processes the Second Law of Thermodynamics, i.e., the entropy of the system increases, is equivalent to the dissipativity condition

$$ \int_{0}^{T} \sigma(t) \dot{\varepsilon }(t)\, dt \geq0. $$

(8)

Equation (8) is a one-dimensional version of the Second Principle of Thermodynamics for simple materials under isothermal conditions (see Amendola et al. 2012, p. 83). Also, in writing (8) we observe the fact that for $t\in(-\infty,0)$ the system is in virginal state. Note that $T=\infty$ in Day (1972, p. 113). Since we consider arbitrary $T$, condition (8) is stronger than the condition in Day (1972).

In Amendola et al. (2012) stress is assumed as

$$ \sigma(t)=G_{0} \varepsilon (t) + \int_{0}^{\infty}G'(u)\varepsilon (t-u)\,du, $$

(9)

where $G_{0}$ is instantaneous elastic modulus, and $G$ is relaxation function, while the stain is taken in the form

$$\varepsilon (s) = \varepsilon _{0}\cos(\omega s) + \varepsilon _{0} \sin(\omega s), \quad s\leq t,\ \omega>0, $$

where $\varepsilon _{0}$ is the amplitude of strain. These assumptions, along with (8) and $T=\frac{2n\pi}{\omega}$, lead to

$$ \int_{0}^{\infty}G'(u) \sin(\omega u) \, du < 0. $$

(10)

Note that (10) is equivalent to

$$\mathcal {F} _{s}\bigl[G'(t)\bigr](\omega) = \operatorname {Im}\bigl( \mathcal {F} \bigl[G'(t)\bigr](\omega) \bigr) > 0, $$

where $\mathcal {F} _{s}[f(t)](\omega)=\int_{0}^{\infty}f(t)\sin(\omega t)\, dt$.

Since constitutive equations containing fractional derivatives that we shall treat in this work do not obey (9), we follow the approach of Bagley and Torvik (1986). Namely, in Bagley and Torvik (1986) it was assumed that periodic strain $\varepsilon$ results in periodic stress $\sigma$ at the end of a transient regime. Positivity of dissipation work (8) for a cycle and each time instant within the cycle leads to

$$\operatorname {Re}\hat{E}(\omega) \geq0 \quad\mbox{and} \quad \operatorname {Im}\hat{E}(\omega) \geq0, \quad\forall \omega>0, $$

where $\hat{E}=\frac{\hat{\sigma}}{\hat{\varepsilon }}$ is the complex modulus obtained from the constitutive equation by applying the Fourier transform (cf. Bagley and Torvik 1986, Eq. (20), (21)). Note that $\operatorname {Re}\hat{E}$ and $\operatorname {Im}\hat{E}$ are referred to as storage and loss modulus, respectively.

We start with the constitutive equation

$$ \sigma(t) = 2b\, {}_{0}\bar{D}_{t}^{\beta} \varepsilon (t), \qquad {}_{0}\bar{D}_{t}^{\beta}:= \frac{1}{2} \bigl({}_{0}D_{t}^{\beta} + {}_{0}D_{t}^{\bar {\beta}} \bigr), \quad t\geq0, $$

(11)

where we assume that $b>0$ and $\beta=A+iB$, $0< A<1$, $B>0$. Note that (11) generalizes the Hooke law in the complex fractional framework. In the case $\beta\in \mathbb {R}$, this new complex fractional operator ${}_{0}\bar{D}_{t}^{\beta}$ coincides with the usual left Riemann–Liouville fractional derivative.

We apply the Fourier transform to (11): $\hat{\sigma}(\omega) = b ((i\omega)^{\beta} + (i\omega)^{\bar{\beta}}) \hat{\varepsilon }(\omega)$, $\omega\in \mathbb {R}$. Then, define the complex modulus $\hat{E}$ such that $\hat{\sigma}(\omega) = \hat{E}(\omega) \cdot\hat{\varepsilon }(\omega)$, $\omega\in \mathbb {R}$, i.e.,

$$\hat{E}(\omega) : = b \bigl((i\omega)^{\beta} + (i\omega)^{\bar {\beta}} \bigr) = b \omega^{A} \bigl(e^{-\frac{B\pi}{2}} e^{i(\frac{A\pi}{2} + B\ln\omega)} +e^{\frac{B\pi}{2}} e^{i(\frac{A\pi}{2} - B\ln\omega)} \bigr), \quad\omega\in\mathbb {R}. $$

Thermodynamical restrictions involve, for $\omega\in \mathbb {R}_{+}$,

$$\begin{aligned} \operatorname {Re}\hat{E}(\omega) =& b \omega^{A} \biggl( e^{-\frac{B\pi}{2}} \cos \biggl(\frac{A\pi}{2} + B\ln\omega \biggr) + e^{\frac{B\pi}{2}} \cos \biggl( \frac{A\pi}{2} - B\ln\omega \biggr) \biggr) \geq0, \end{aligned}$$

(12)

$$\begin{aligned} \operatorname {Im}\hat{E}(\omega) =& b \omega^{A} \biggl( e^{-\frac{B\pi}{2}} \sin \biggl(\frac{A\pi}{2} + B\ln\omega \biggr) + e^{\frac{B\pi}{2}} \sin \biggl( \frac{A\pi}{2} - B\ln\omega \biggr) \biggr) \geq0. \end{aligned}$$

(13)

But this is in contradiction with $B>0$, since for $\omega>0$, (12) and (13) imply $B=0$.

In order not to confront the real-valued compatibility requirement and the Second Law of Thermodynamics for (11), one may require that (12) and (13) hold for $\omega$ in some bounded interval instead of in all of ℝ. Alternatively, as we shall do in the sequel, one can modify (11) by adding additional terms, in order to preserve the Second Law of Thermodynamics.

Thus, we proceed by proposing the following constitutive equation

$$ \sigma(t) = a\, {}_{0}D_{t}^{\alpha} \varepsilon (t) + 2b\, {}_{0}\bar{D}_{t}^{\beta} \varepsilon (t), \quad t\geq0, $$

(14)

where we assume that $a,b>0$, $\alpha\in \mathbb {R}$, $0<\alpha<1$, and $\beta=A+iB$, $0< A<1$, $B>0$. Again we follow the procedure described above for deriving thermodynamical restrictions: $\hat{\sigma}(\omega) = [a(i\omega)^{\alpha}+ b ((i\omega)^{\beta} + (i\omega)^{\bar{\beta}})] \hat{\varepsilon }(\omega)$, $\omega\in \mathbb {R}$. Consider the complex module ($\omega\in \mathbb {R}$)

$$\begin{aligned} \hat{E}(\omega) =& a\omega^{\alpha}e^{i\frac{\alpha\pi}{2}} + b \omega^{A} \bigl(e^{-\frac{B\pi}{2}} e^{i(\frac{A\pi}{2} + B\ln \omega)} +e^{\frac{B\pi}{2}} e^{i(\frac{A\pi}{2} - B\ln\omega)} \bigr); \end{aligned}$$

(15)

$$\begin{aligned} \operatorname {Re}\hat{E}(\omega) =& a \omega^{\alpha}\cos\frac{\alpha\pi}{2} + b \omega^{A} \biggl( e^{-\frac{B\pi}{2}} \cos \biggl(\frac{A\pi}{2} + B \ln\omega \biggr) \\ &{}+ e^{\frac{B\pi}{2}} \cos \biggl(\frac{A\pi}{2} - B\ln\omega \biggr) \biggr), \end{aligned}$$

(16)

$$\begin{aligned} \operatorname {Im}\hat{E}(\omega) =& a\omega^{\alpha}\sin\frac{\alpha\pi}{2} + b \omega^{A} \biggl( e^{-\frac{B\pi}{2}} \sin \biggl(\frac{A\pi}{2} + B \ln\omega \biggr) \\ &{} + e^{\frac{B\pi}{2}} \sin \biggl(\frac{A\pi}{2} - B\ln\omega \biggr) \biggr). \end{aligned}$$

(17)

We will investigate conditions $\operatorname {Re}\hat{E}\geq0$ and $\operatorname {Im}\hat {E}\geq0$ on $\mathbb {R}_{+}$. The assumption $\alpha>A$ leads to a contradiction since for $\omega\searrow0$ the sign of the second term in (16) determines the sign of $\operatorname {Re}\hat{E}$, and it can be negative. Thus, we must have $\alpha\leq A$. If $\alpha< A$. then for $\omega\to\infty$, the second term in (16) could be negative. This together yields that the only possibility is $A=\alpha$. (The same conclusion is obtained if one considers $\operatorname {Im}\hat{E}\geq 0$, $\omega>0$.)

Therefore, with $A=\alpha$, (16) and (17) become:

$$\begin{aligned} \operatorname {Re}\hat{E}(\omega) =& a \omega^{\alpha}\cos\frac{\alpha\pi}{2} + 2b \omega^{\alpha}f(\omega), \quad\omega>0, \end{aligned}$$

(18)

$$\begin{aligned} \operatorname {Im}\hat{E}(\omega) =& a \omega^{\alpha}\sin\frac{\alpha\pi}{2} + 2b \omega^{\alpha}g(\omega), \quad\omega>0, \end{aligned}$$

(19)

with

$$\begin{aligned} f(\omega) := & \cos\frac{\alpha\pi}{2}\cos\bigl(\ln\omega^{B}\bigr) \cosh \frac{B\pi}{2} + \sin\frac{\alpha\pi}{2}\sin\bigl(\ln\omega^{B} \bigr)\sinh\frac{B\pi}{2}, \quad\omega>0, \end{aligned}$$

(20)

$$\begin{aligned} g(\omega) := & \sin\frac{\alpha\pi}{2}\cos\bigl(\ln\omega^{B}\bigr) \cosh \frac{B\pi}{2} - \cos\frac{\alpha\pi}{2}\sin\bigl(\ln\omega^{B} \bigr)\sinh\frac{B\pi}{2}, \quad\omega>0. \end{aligned}$$

(21)

We further have that $\operatorname {Re}\hat{E}(\omega)\geq a\omega^{\alpha}\cos \frac{\alpha\pi}{2} +2b\omega^{\alpha}\min_{\omega\in \mathbb {R}_{+}} f(\omega)$, $\omega>0$, and the similar estimate for $\operatorname {Im}\hat{E}$, hence we now look for the minimums of functions $f$ and $g$ on $\mathbb {R}_{+}$. Using the substitution $x=\ln\omega^{B}$ we find that $f'(x)=0$ and $g'(x)=0$ at $x_{f}$ and $x_{g}$ so that

$$\operatorname {tg}x_{f} = \operatorname {tg}\frac{\alpha\pi}{2} \operatorname {tgh}\frac{B\pi}{2} \quad \mbox{and} \quad \operatorname {tg}x_{g} = - \operatorname {ctg}\frac{\alpha\pi}{2} \operatorname {tgh}\frac{B\pi}{2}. $$

Solutions $x_{f1}$, $x_{f2}$, $x_{g1}$ and $x_{g2}$ satisfy: $x_{f1}\in(0,\frac{\pi}{2})$, $x_{f2}\in(\pi,\frac{3\pi}{2})$, and $x_{g1}\in(\frac{\pi}{2},\pi)$, $x_{g2}\in(\frac{3\pi }{2},2\pi)$, since $\operatorname {tg}\frac{\alpha\pi}{2}, \operatorname {ctg}\frac{\alpha\pi}{2}, \operatorname {tgh}\frac{B\pi}{2}>0$, and

$$\begin{aligned} f(x_{f}) =& \pm\cos\frac{\alpha\pi}{2} \cosh\frac{B\pi}{2} \sqrt{1+ \biggl(\operatorname {tg}\frac{\alpha\pi}{2} \operatorname {tgh}\frac{B\pi}{2} \biggr)^{2}}, \\ g(x_{g}) =& \pm\sin\frac{\alpha\pi}{2} \cosh\frac{B\pi}{2} \sqrt{1+ \biggl(\operatorname {ctg}\frac{\alpha\pi}{2} \operatorname {tgh}\frac{B\pi}{2} \biggr)^{2}}. \end{aligned}$$

Therefore, we have $\min_{x\in \mathbb {R}} f(x) = f(x_{f2})$ and $\min_{x\in \mathbb {R}}g(x) = g(x_{g1})$, so that (18) and (19) can be estimated as

$$\begin{aligned} \operatorname {Re}\hat{E}(\omega) \geq& \omega^{\alpha}\cos\frac{\alpha\pi }{2} \biggl( a-2b \cosh\frac{B\pi}{2}\sqrt{1+ \biggl(\operatorname {tg}\frac{\alpha\pi}{2} \operatorname {tgh}\frac{B\pi}{2} \biggr)^{2}} \biggr), \quad\omega>0, \\ \operatorname {Im}\hat{E}(\omega) \geq& \omega^{\alpha}\sin\frac{\alpha\pi }{2} \biggl( a-2b\cosh\frac{B\pi}{2}\sqrt{1+ \biggl(\operatorname {ctg}\frac{\alpha\pi}{2} \operatorname {tgh}\frac{B\pi}{2} \biggr)^{2}} \biggr), \quad\omega>0. \end{aligned}$$

We obtain the thermodynamical restrictions for (14) by requiring $\operatorname {Re}\hat{E}(\omega) \geq0$ and $\operatorname {Im}\hat{E}(\omega) \geq0$, for $\omega\in \mathbb {R}_{+}$:

$$ a \geq2b \cosh\frac{B\pi}{2}\sqrt{1+ \biggl(\operatorname {ctg}\frac{\alpha\pi }{2} \operatorname {tgh}\frac{B\pi}{2} \biggr)^{2}}, \quad\mbox{if} \ \alpha\in \biggl(0,\frac{1}{2} \biggr], $$

(22)

and

$$ a \geq2b \cosh\frac{B\pi}{2}\sqrt{1+ \biggl(\operatorname {tg}\frac{\alpha\pi }{2}\operatorname {tgh}\frac{B\pi}{2} \biggr)^{2}}, \quad\mbox{if}\ \alpha\in \biggl[\frac{1}{2},1 \biggr). $$

(23)

Notice that both restrictions further imply $a\geq2b$.

Remark 2.5

(i) Fix $a$ and $\alpha$. Inequalities (22) and (23) imply that as $B$ increases, the constant $b$ has to decrease, i.e., the contribution of complex fractional derivative of strain in the constitutive equation (14) is smaller if its imaginary part is larger.

(ii) Also, inequalities (22) and (23) lead to the same restrictions on parameters $a, b, \alpha$ and $B$, since for $\alpha \in(0,\frac{1}{2}]$ one has $1-\alpha\in[\frac{1}{2},1)$, and the values of (22) and (23) coincide.

(iii) Under the same conditions, constitutive equation (14) can be extended to $\sigma(t) = \varepsilon (t) + a\, {}_{0}D_{t}^{\alpha} \varepsilon (t) + 2b\, {}_{0}\bar {D}_{t}^{\beta} \varepsilon (t)$, $t\geq0$, which will be investigated in the next section.

3 Complex order fractional Kelvin–Voigt model

Consider the constitutive equation involving the complex order fractional derivative

$$ \sigma(t) = \varepsilon (t) + a\, {}_{0}D_{t}^{\alpha} \varepsilon (t) + 2b\, {}_{0}\bar {D}_{t}^{\beta} \varepsilon (t), \quad t\geq0. $$

(24)

We assume $a,b, E>0$, $0<\alpha<1$, $B>0$, $\beta=\alpha+iB$, and $\sigma$ and $\varepsilon$ are real-valued functions. Note that (24) is a generalization of the model proposed in Rossikhin and Shitikova (2001b). Namely, (24) agrees with the latter when $\beta$ is real and positive. The inverse relation, i.e., $\varepsilon$ as a function of $\sigma$ is given in Theorem 3.2.

The Laplace transform of (24) is $\tilde{\sigma}(s) = E (1+a s^{\alpha}+b (s^{\beta}+s^{\bar {\beta}}) ) \tilde{\varepsilon }(s)$, $\operatorname {Re}s>0$, and hence

$$ \tilde{\varepsilon }(s) = \frac{1}{1+a s^{\alpha}+b (s^{\beta}+s^{\bar {\beta}})} \tilde{\sigma}(s), \quad \operatorname {Re}s>0. $$

(25)

In order to determine $\varepsilon$ from (25) we need to analyze zeros of

$$ \psi(s) = 1+ a s^{\alpha}+b \bigl(s^{\beta}+s^{\bar{\beta}} \bigr), \quad s\in \mathbb {C}. $$

(26)

Note that if we put $s=i\omega$, $\omega\in \mathbb {R}_{+}$, in (26), it becomes the complex modulus:

$$ \psi(i\omega) = 1+ \hat{E}(\omega) = 1+a\,(i\omega)^{\alpha}+b \bigl((i\omega)^{\beta}+(i\omega)^{\bar {\beta}} \bigr), \quad\omega>0, $$

(27)

where $\hat{E}$ is given in (15).

Let $s=re^{i\varphi }$, $r>0$, $\varphi \in[0,2\pi]$. Then (with $\beta =\alpha+iB$)

$$\psi(s) = 1+ar^{\alpha}e^{i\alpha \varphi }+br^{\alpha}\bigl( e^{-B\varphi } e^{i(\ln r^{B}+\alpha \varphi )}+ e^{B\varphi } e^{-i(\ln r^{B}-\alpha \varphi )} \bigr), $$

and

$$\begin{aligned} \operatorname {Re}\psi(s) =&1+ar^{\alpha}\cos(\alpha \varphi ) + 2br^{\alpha}\bigl( \cos\bigl(\ln r^{B}\bigr) \cos(\alpha \varphi ) \cosh(B\varphi ) \\ &{} + \sin\bigl(\ln r^{B}\bigr) \sin(\alpha \varphi ) \sinh(B \varphi ) \bigr), \end{aligned}$$

(28)

$$\begin{aligned} \operatorname {Im}\psi(s) =& ar^{\alpha}\sin(\alpha \varphi ) + 2br^{\alpha}\bigl( \cos\bigl(\ln r^{B}\bigr) \sin(\alpha \varphi ) \cosh(B\varphi ) \\ &{}- \sin\bigl(\ln r^{B}\bigr) \cos(\alpha \varphi ) \sinh(B \varphi ) \bigr). \end{aligned}$$

(29)

3.1 Thermodynamical restrictions

In the case of (27), using (28) and (29) we obtain:

$$\begin{aligned} \operatorname {Re}\psi(i\omega) =& 1+\operatorname {Re}\hat{E}(\omega) \geq1+a\omega^{\alpha}\cos \frac{\alpha\pi}{2} + 2b\omega^{\alpha}\min_{x\in \mathbb {R}} f(x), \quad x=\ln\omega^{B}, \ \omega>0, \\ \operatorname {Im}\psi(i\omega) =& \operatorname {Im}\hat{E}(\omega) \geq a\omega^{\alpha}\sin \frac{\alpha\pi}{2} +2b\omega^{\alpha}\min_{x\in \mathbb {R}} g(x), \quad x=\ln\omega^{B}, \ \omega>0, \end{aligned}$$

where $f$ and $g$ are as in (20) and (21). This leads to the same thermodynamical restrictions (22) and (23), as in Sect. 2.2.

Therefore, from now on, we shall assume (22) and (23) to hold true. Now we shall examine the zeros of $\psi$.

3.2 Zeros of $\psi$ and solutions of (24)

Theorem 3.1

Let $\psi$ be the function given by (26). Then

• (i) $\psi$ has no zeros in the right complex half-plane $\operatorname {Re}s\geq0$.

• (ii) $\psi$ has no zeros in ℂ if the coefficients $a, b, \alpha$ and $B$ satisfy

  $$ \begin{aligned} a & \geq2b \cosh(B\pi) \sqrt{1+ \bigl( \operatorname {tg}(\alpha\pi) \operatorname {tgh}(B\pi ) \bigr)^{2}}, \quad \mathit{for} \ \alpha \in \biggl[\frac{1}{4},\frac{3}{4} \biggr]\backslash \biggl\{ \frac{1}{2} \biggr\} , \\ a & \geq2b \cosh(B\pi) \sqrt{1+ \bigl(\operatorname {ctg}(\alpha\pi) \operatorname {tgh}(B\pi ) \bigr)^{2}}, \quad\mathit{for} \ \alpha\in \biggl(0, \frac{1}{4} \biggr) \cup \biggl\{ \frac{1}{2} \biggr\} \cup \biggl( \frac{3}{4}, 1 \biggr). \end{aligned} $$

  (30)

Proof

First, we notice that if $s_{0}$ is a solution to $\psi(s) = 0$, then $\bar{s}_{0}$ (the complex conjugate of $s_{0}$) is also a solution, since $\psi(\bar{s}) = 1+a\bar{s}^{\alpha}+b(\bar{s}^{\beta}+ \bar{s}^{\bar{\beta}}) = \overline{\psi(s)}$. Thus, we restrict our attention to the upper complex half-plane $\operatorname {Im}s\geq0$, i.e., $\varphi \in[0,\pi]$.

Using (28) and (29) we have, with $s=re^{i\varphi }$, $r>0$, $\varphi \in[0,\pi]$, and $x=\ln r^{B}$,

$$\begin{aligned} \operatorname {Re}\psi(s) \geq&1+ar^{\alpha}\cos(\alpha \varphi ) +2br^{\alpha} \min _{x\in \mathbb {R}} f(x), \end{aligned}$$

(31)

$$\begin{aligned} \operatorname {Im}\psi(s) \geq& ar^{\alpha}\sin(\alpha \varphi ) +2br^{\alpha} \min _{x\in \mathbb {R}}g(x), \end{aligned}$$

(32)

where

$$\begin{aligned} f(x) =&\cos(x) \cos(\alpha \varphi ) \cosh(B \varphi ) + \sin(x) \sin(\alpha \varphi ) \sinh(B \varphi ), \quad x\in \mathbb {R}, \end{aligned}$$

(33)

$$\begin{aligned} g(x) =& \cos(x) \sin(\alpha \varphi ) \cosh(B \varphi ) - \sin(x) \cos(\alpha \varphi ) \sinh(B \varphi ), \quad x\in \mathbb {R}. \end{aligned}$$

(34)

The critical points $x_{f}$ and $x_{g}$ of $f$ and $g$, respectively, satisfy

$$ \operatorname {tg}x_{f} = \operatorname {tg}(\alpha \varphi ) \operatorname {tgh}(B \varphi ) \geq0 \quad \mbox{and} \quad \operatorname {tg}x_{g}=-\operatorname {ctg}(\alpha \varphi ) \operatorname {tgh}(B \varphi ) \leq0, $$

(35)

The proof of (i) and (ii) will be given by the argument principle.

(i) Consider $\psi$ in the case $\operatorname {Re}s, \operatorname {Im}s >0$. Choose a contour $\varGamma= \gamma_{R1}\cup\gamma_{R2}\cup\gamma_{R3}\cup\gamma_{R4}$, as it is shown in Fig. 1.

Fig. 1

Contour $\varGamma$

$\gamma_{R1}$ is parametrized by $s=x$, $x\in(\varepsilon ,R)$ with $\varepsilon \to0$ and $R\to\infty$, so that (28) and (29) yield

$$\begin{aligned} \operatorname {Re}\psi(x) =&1+x^{\alpha} \bigl(a+2b\cos\bigl(\ln x^{\beta}\bigr) \bigr) \geq 1+x^{\alpha} (a-2b) \geq0, \\ \operatorname {Im}\psi(x) =& 0, \end{aligned}$$

since both (22) and (23) imply $a\geq2b$. Moreover, we have $\lim_{x\to0} \psi(x)=1$ and $\lim_{x\to\infty} \psi(x)=\infty$.

Along $\gamma_{R2}$ one has $s=Re^{i\varphi }$, $\varphi \in[ 0,\frac {\pi}{2}]$, with $R\rightarrow\infty$. By (35) we have $\operatorname {tg}x_{f} \geq0$, so that

$$\min_{x\in \mathbb {R}}f(x) = -\cos(\alpha \varphi ) \cosh(B \varphi ) \sqrt {1+ \bigl( \operatorname {tg}(\alpha \varphi ) \operatorname {tgh}(B \varphi ) \bigr)^{2}}, $$

and therefore (31) becomes

$$\operatorname {Re}\psi(s) \geq1+R^{\alpha}\cos(\alpha \varphi ) \bigl(a-2b\cosh(B\varphi ) \sqrt{1+\bigl( \operatorname {tg}(\alpha \varphi ) \operatorname {tgh}(B \varphi ) \bigr)^{2}}\bigr) \geq0. $$

The previous inequality holds true, since for $\varphi \in[ 0,\frac{\pi }{2}]$ we have that

$$p(\varphi ) = \cosh(B \varphi ) \sqrt{1+\bigl(\operatorname {tg}(\alpha \varphi ) \operatorname {tgh}(B \varphi ) \bigr)^{2}} \leq\cosh\frac{B \pi}{2}\sqrt{1+ \biggl(\operatorname {tg}\frac{\alpha\pi }{2}\operatorname {tgh}\frac{B \pi}{2} \biggr)^{2}}, $$

because of the fact that the function $p$ monotonically increases on $[0,\frac{\pi}{2}]$. Moreover, by (28) and (29), we have

$$\begin{aligned} \operatorname {Re}\psi(s) \rightarrow& \infty \quad\mbox{and} \quad \operatorname {Im}\psi(s) = 0, \quad \mbox{for} \ \varphi =0, \ R\rightarrow\infty, \\ \operatorname {Re}\psi(s) \rightarrow& \infty, \quad\mbox{for} \ \varphi = \frac{\pi}{2}, \ R\rightarrow\infty. \end{aligned}$$

The next segment is $\gamma_{R3}$, which is parametrized by $s=i\omega$, $\omega\in[R,\varepsilon ]$, with $\varepsilon \rightarrow0$ and $R\rightarrow\infty$. Then (28) and (29) yield

$$\operatorname {Re}\psi(i\omega) = 1 + \operatorname {Re}\hat{E} (\omega) \geq0 \quad\mbox{and} \quad \operatorname {Im}\psi(i\omega) = \operatorname {Im}\hat{E} (\omega) \geq0, \quad \omega\in(\varepsilon ,R), $$

due to the thermodynamical requirements. Moreover, by (28) and (29), we have

$$\begin{aligned} \operatorname {Re}\psi(\omega) \rightarrow&1 \quad\mbox{and} \quad \operatorname {Im}\psi(\omega) \rightarrow0, \quad\mbox{as}\ \omega\rightarrow0, \\ \operatorname {Re}\psi(\omega) \rightarrow&\infty \quad\mbox{and} \quad \operatorname {Im}\psi(\omega) \rightarrow\infty, \quad\mbox{as}\ \omega\rightarrow\infty. \end{aligned}$$

The last part of the contour $\varGamma$ is the arc $\gamma_{R4}$, with $s=\varepsilon e^{i\varphi }$, $\varphi \in[0,\frac{\pi}{2}]$, with $\varepsilon \rightarrow0$. Using the same arguments as for the contour $\gamma_{R2}$, we have

$$ \operatorname {Re}\psi(s) \geq1+\varepsilon ^{\alpha}\cos(\alpha \varphi ) \bigl(a-2b \cosh(B\varphi ) \sqrt{1+\bigl(\operatorname {tg}(\alpha \varphi ) \operatorname {tgh}(B\varphi )\bigr)^{2}} \bigr) \geq1. $$

(36)

Also, by (29) and (36), we have

$$\operatorname {Re}\psi(s) \rightarrow1 \quad\mbox{and} \quad \operatorname {Im}\psi(s) \rightarrow0, \quad \mbox{as}\ \varepsilon \rightarrow0. $$

We conclude that $\Delta\arg\psi(s)=0$ so that, by the argument principle, there are no zeroes of $\psi$ in the right complex half-plane $\operatorname {Re}s\geq0$.

(ii) In order to discuss the zeros of $\psi$ in the left complex half-plane, we use the contour $\varGamma_{L}=\gamma_{L1}\cup\gamma_{L2}\cup \gamma_{L3}\cup\gamma_{L4}$, shown in Fig. 1. The contour $\gamma_{L1}$ has the same parametrization as the contour $\gamma_{R3}$, so the same conclusions as for $\gamma_{R3}$ hold true.

The parametrization of the contour $\gamma_{L2}$ is $s=Re^{i\varphi }$, $\varphi \in[\frac{\pi}{2},\pi]$, with $R\rightarrow\infty$. Let us distinguish two cases.

• Case a1. $\alpha \varphi \in(0,\frac{\pi}{2})$

  Then $\sin(\alpha \varphi ) >0$, $\cos(\alpha \varphi ) > 0$, so the critical points of $f$ and $g$, see (33) and (34), given by (35), satisfy $\operatorname {tg}x_{f}>0$ and $\operatorname {tg}x_{g}< 0$. For the minimums of $f$ and $g$ in (31) and (32) we have

  $$\begin{aligned} \min_{x\in \mathbb {R}} f(x) =& -\cos(\alpha \varphi ) \cosh(B\varphi ) \sqrt{1+ \bigl(\operatorname {tg}(\alpha \varphi ) \operatorname {tgh}(B\varphi )\bigr)^{2}}, \\ \min_{x\in \mathbb {R}} g(x) =& -\sin(\alpha \varphi ) \cosh(B\varphi ) \sqrt{1+ \bigl(\operatorname {ctg}(\alpha \varphi ) \operatorname {tgh}(B\varphi )\bigr)^{2}}, \end{aligned}$$

  respectively, so that (31) and (32) become

  $$\begin{aligned} \operatorname {Re}\psi(s) \geq&1+R^{\alpha}\cos(\alpha \varphi ) \bigl(a-2b\cosh(B\varphi ) \sqrt{1+ \bigl(\operatorname {tg}(\alpha \varphi ) \operatorname {tgh}(B\varphi ) \bigr)^{2}} \bigr), \end{aligned}$$

  (37)
  $$\begin{aligned} \operatorname {Im}\psi(s) \geq& R^{\alpha}\sin(\alpha \varphi ) \bigl(a-2b\cosh(B\varphi ) \sqrt{1+ \bigl( \operatorname {ctg}(\alpha \varphi ) \operatorname {tgh}(B\varphi ) \bigr)^{2}} \bigr). \end{aligned}$$

  (38)

  Function $H_{f}(\varphi ) = \cosh(B\varphi ) \sqrt{1+(\operatorname {tg}(\alpha \varphi ) \operatorname {tgh}(B\varphi ))^{2}}$ is monotonically increasing for $\varphi \in[\frac{\pi}{2},\pi]$, since $\alpha \varphi \in (0,\frac{\pi}{2})$, thus

  $$\operatorname {Re}\psi(s) \geq1+R^{\alpha}\cos(\alpha \varphi ) \bigl( a-2b \cosh (B\pi) \sqrt{1+ \bigl( \operatorname {tg}(\alpha\pi) \operatorname {tgh}(B\pi)\bigr)^{2}} \bigr) \geq0, $$

  if (30) is satisfied. Note that $\operatorname {Re}\psi(s) \rightarrow \infty$ and $\operatorname {Im}\psi(s) \rightarrow\infty$, for $\varphi = \pi$, $R\rightarrow\infty$.

• Case b1. $\alpha \varphi \in[\frac{\pi}{2},\pi)$

  Then $\sin(\alpha \varphi ) >0$, $\cos(\alpha \varphi )\leq0$, so the critical points of $g$, see (34), given by (35), satisfy $\operatorname {tg}x_{g}\geq0$. For the minimum of $g$ in (34) we have

  $$\min_{x\in \mathbb {R}} g(x) = -\sin(\alpha \varphi ) \cosh(B\varphi ) \sqrt{1+ \bigl( \operatorname {ctg}(\alpha \varphi ) \operatorname {tgh}(B\varphi ) \bigr)^{2}}, $$

  so that (32) becomes

  $$\operatorname {Im}\psi(s) \geq R^{\alpha}\sin(\alpha \varphi ) \bigl( a-2b \cosh(B\varphi ) \sqrt{1+ \bigl(\operatorname {ctg}(\alpha \varphi ) \operatorname {tgh}(B\varphi ) \bigr)^{2}} \bigr). $$

  Function $H_{g}(\varphi ) =\cosh(B\varphi ) \sqrt{1+(\operatorname {ctg}(\alpha \varphi ) \operatorname {tgh}(B\varphi ))^{2}}$ is monotonically increasing for $\varphi \in[\frac{\pi}{2},\pi]$, since $\alpha \varphi \in[\frac{\pi}{2},\pi)$, and (30) implies

  $$\operatorname {Im}\psi(s) \geq R^{\alpha}\sin(\alpha \varphi ) \bigl( a-2b \cosh (B\pi) \sqrt{1+ \bigl( \operatorname {ctg}(\alpha\pi) \operatorname {tgh}(B\pi) \bigr)^{2}} \bigr) \geq0. $$

  Note that $\operatorname {Im}\psi(s) \rightarrow\infty$, for $\varphi =\pi$, $R\rightarrow\infty$.

Now we discuss possible situations for $\alpha\in(0,1)$ and $\varphi \in[\frac{\pi}{2},\pi]$.

If $\alpha\in(0,\frac{1}{2})$ then Case a1 holds so that $\operatorname {Re}\psi (s)\geq0$.

If $\alpha\in[\frac{1}{2},1)$ then we distinguish two cases. For $\varphi \in[\frac{\pi}{2}, \frac{\pi}{2\alpha})$ Case a1 holds, so $\operatorname {Re}\psi(s)\geq0$. For $\varphi \in[\frac{\pi}{2\alpha}, \pi)$ Case b1 holds, and $\operatorname {Im}\psi(s)\geq0$.

Parametrization of the contour $\gamma_{L3}$ is $s=xe^{i\pi}$, $x\in(\varepsilon ,R)$, with $\varepsilon \rightarrow0$ and $R\rightarrow\infty$. Again, we have two cases.

• Case a2. $\alpha\in(0,\frac{1}{2})$

  Then, for $x\in(\varepsilon ,R)$, using the same argumentation as in Case a1, we have, by (37) and (38) (with $R=x$), $\operatorname {Re}\psi(s)\geq1$ and $\operatorname {Im}\psi(s)\geq0$, due to (30). Thus, looking at (37) and (38) (with $R=x$), we conclude

  $$\begin{aligned} \operatorname {Re}\psi(s) \rightarrow&\infty \quad\mbox{and} \quad \operatorname {Im}\psi(s) \rightarrow \infty, \quad\mbox{for} \ x \rightarrow\infty, \\ \operatorname {Re}\psi(s) \rightarrow&1 \quad\mbox{and} \quad \operatorname {Im}\psi(s) \rightarrow0, \quad\mbox{for}\ x\rightarrow0. \end{aligned}$$

• Case b2. $\alpha\in[\frac{1}{2},1)$

  Then, for $x\in(\varepsilon ,R)$, using the same argumentation as in Case b1, we have (by (38)) that $\operatorname {Im}\psi(s)\geq0$, and

  $$\operatorname {Im}\psi(s) \rightarrow\infty, \quad\mbox{for}\ x\rightarrow\infty \quad \mbox{and} \quad \operatorname {Im}\psi(s) \rightarrow0, \quad\mbox{for}\ x \rightarrow0. $$

The parametrization of the contour $\gamma_{L4}$ is $s=\varepsilon e^{i\varphi }$, $\varphi \in[ \frac{\pi}{2},\pi]$, with $\varepsilon \rightarrow0$. From (28) and (29), for sufficiently small $\varepsilon$, we have

$$\operatorname {Re}\psi(s) \rightarrow1 \quad\mbox{and} \quad \operatorname {Im}\psi(s) \rightarrow0, \quad \mbox{for} \ \varepsilon \rightarrow0,\ \varphi \in \biggl[ \frac{\pi}{2},\pi \biggr]. $$

Summing up all results from Cases a1, a2, b1, and b2, we obtain the following:

• For $\alpha\in(0,\frac{1}{2})$, $\operatorname {Re}\psi(s) \geq0$, for $s\in\varGamma_{L}$, which implies that $\Delta\arg\psi(s) =0$. Therefore, using the argument principle, we conclude that in this case $\psi$ has no zeros in the left complex half-plane.

• If $\alpha\in[\frac{1}{2},1)$, then for $s\in\gamma_{L1}$ and $s\in\{z\in\gamma_{L2} \,|\, \arg z\leq\frac{\pi}{2\alpha}\}$, we have $\operatorname {Re}\psi(s) \geq0$, while for $s\in\{z\in\gamma_{L2} \,|\, \arg z>\frac{\pi}{2\alpha}\}$ and $s\in\gamma_{L3}$, we have $\operatorname {Im}\psi(s) \geq0$. For $s\in\gamma_{L4}$ we again have $\operatorname {Re}\psi(s) \geq0$. Hence, we conclude that $\Delta\arg\psi(s) =0$, and therefore, using the argument principle, neither in case $\alpha\in[\frac{1}{2},1)$ function $\psi$ has zeros in the left complex half-plane.

This completes the proof. □

Rewrite (25) as

$$ \tilde{\varepsilon }(s) = \tilde{K}(s) \tilde{\sigma}(s), \quad \tilde{K}(s) = \frac{1}{1+as^{\alpha}+b(s^{\beta}+s^{\bar{\beta}})}, \ \operatorname {Re}s>0. $$

(39)

Theorem 3.2

Let $\tilde{\varepsilon }$ be given by (39). Then

$$ \varepsilon (t) = K(t) \ast\sigma(t), \quad t\geq0. $$

(40)

Moreover, if (30) holds, then

$$\begin{aligned} K(t) = K_{I}(t) = & \frac{1}{2\pi i} \int_{0}^{\infty} \biggl( \frac{e^{-qt}}{1+q^{\alpha} e^{i\alpha\pi} [ a + b(e^{i\ln q^{B}} e^{-B \pi}+ e^{- i\ln q^{B}} e^{B \pi}) ]} \\ & {}- \frac{e^{-qt}}{1+q^{\alpha} e^{-i\alpha\pi} [ a + b(e^{i\ln q^{B}} e^{B \pi}+ e^{- i\ln q^{B}} e^{-B \pi}) ]} \biggr)\,dq. \end{aligned}$$

(41)

If condition (30) is violated, then $\psi$ has at most a finite number of zeros in the left complex half-plane, and

$$K=K_{I} \quad \mathit{or} \quad K=K_{I}+K_{R}, $$

where

$$ K_{R}(t) = \sum_{\psi(s_{i})=0 \atop i=1,2,\ldots, n} \bigl( \operatorname {Res}\bigl(\tilde{K}(s) e^{st},s_{i}\bigr) +\operatorname {Res}\bigl( \tilde{K}(s) e^{st},\bar{s}_{i}\bigr) \bigr), $$

(42)

with $\tilde{K}$ given by (39).

Proof

The first part is clear. We invert now $\tilde{K}$, given in (39), by the use of the Cauchy residues theorem

$$ \oint_{\tilde{\varGamma}}\tilde{K}(s) e^{st}\,ds=2\pi i\sum_{\psi (\tilde{s})=0}\operatorname {Res}\bigl(\tilde{K}(s) e^{st}, \tilde{s}\bigr) $$

(43)

and the contour $\tilde{\varGamma} =\varGamma_{1}\cup\varGamma_{2}\cup\varGamma_{r}\cup \varGamma_{3}\cup\varGamma_{4}\cup\gamma_{0}$ shown in Fig. 2.

Fig. 2

Contour $\tilde{\varGamma}$

If condition (30) is satisfied, then, by Theorem 3.1, the residues equal zero. One can show that the integrals over the contours $\varGamma_{1}$, $\varGamma_{r}$ and $\varGamma_{4}$ tend to zero when $R\rightarrow\infty$ and $r\rightarrow0$. The remaining integrals give:

$$\begin{aligned} \lim_{\substack{ R\rightarrow\infty, \\ r\rightarrow0}} \int _{\varGamma_{2}} \tilde{K}(s) e^{st}\,ds =& - \int_{0}^{\infty} \frac{e^{-qt}}{1+q^{\alpha} e^{i\alpha\pi } [ a + b(e^{i\ln q^{B}} e^{-B \pi}+ e^{- i\ln q^{B}} e^{B \pi}) ]} \,dq, \\ \lim_{\substack{ R\rightarrow\infty, \\ r\rightarrow0}} \int _{\varGamma_{3}} \tilde{K}(s) e^{st}\,ds =& \int_{0}^{\infty} \frac{e^{-qt}}{1+q^{\alpha} e^{-i\alpha\pi} [ a + b(e^{i\ln q^{B}} e^{B \pi}+ e^{- i\ln q^{B}} e^{-B \pi}) ]} \,dq, \\ \lim_{\substack{ R\rightarrow\infty, \\ r\rightarrow0}} \int _{\gamma_{0}} \tilde{K}(s) e^{st}\,ds =&2\pi i K_{I}(t), \end{aligned}$$

which, by the Cauchy residues theorem (43), leads to (41).

If condition (30) is violated, then, by Theorem 3.1, the denominator of $\tilde{K}$ either has no zeros in the complex plane, and so $K=K_{I}$, or it has zeros in the left complex half-plane, which comes in pairs with complex conjugates. We show now that $\psi$ (which is the dominator of $\tilde{K}$) can have at most a finite number of zeros for $\operatorname {Im}s\leq0$. Rewrite $\psi(s)=0$ as $a+b (s^{iB} + s^{-iB}) = s^{-\alpha}$. If $s=re^{i\varphi }$, $\varphi \in[\frac{\pi}{2}, \pi]$, then we have

$$a+b \bigl(r^{iB}e^{-\varphi B} + r^{-iB} e^{\varphi B} \bigr) = r^{-\alpha} e^{-\alpha \varphi i}. $$

When $r\to\infty$ the right-hand side tends to zero, while the left-hand side tends to $a$. As $r\to0$ we see that the left-hand side is bounded, while the right-hand side is not bounded. Thus, the zeros in the left half-plane of function $\psi$, if exist, have to be bounded both from above and below. In that case we have $K=K_{I}+K_{R}$, where $K_{R}$ is given by (42). □

Remark 3.3

In the cases of standard and fractional linear solid model creep compliance and relaxation modulus are exponential functions and derivative of a one-parameter Mittag–Leffler function. Also, these models have different relaxation and retardation times as well as the limiting values of the material functions. For more complicated models, as our is, functions representing creep compliance and relaxation modulus are possibly not so well known special functions. We note that other generalizations of standard linear viscoelastic solids, e.g., the one presented in Rossikhin and Shitikova (2001b), also do not tackle this question.

4 Numerical verifications

Here we present several examples of the proposed constitutive equation. We shall treat stress relaxation, creep and periodic loading cases.

4.1 Stress relaxation experiment

We take (24) with $\varepsilon (t) = H(t)$, $H$ is the Heaviside function, and regularize it as $H_{\varepsilon }(t) =1-\exp(-t/k)$, $k\rightarrow0$. In order to determine $\sigma$, we calculate

$$ \sigma(t) = H_{\varepsilon }(t) +a\,{}_{0} D_{t}^{\alpha} H_{\varepsilon }(t) +b\,{}_{0} \bar{D}_{t}^{\beta} H_{\varepsilon }(t), \quad t\geq0, $$

(44)

with $\sigma(0) =0$, using the expansion formula (see Atanacković and Stanković 2004, 2008),

$$ {}_{0}D_{t}^{\gamma} y(t) \approx \frac{y(t)}{t^{\gamma}} A(N,\gamma) - \sum_{p=1}^{N} C_{p-1}(\gamma) \frac{V_{p-1}(y)(t)}{t^{p+\gamma}}, $$

(45)

where

$$A(N,\gamma) = \frac{\varGamma(N+1+\gamma)}{\gamma\varGamma(1-\gamma) \varGamma (\gamma) N!}, \qquad C_{p-1}(\gamma) = \frac{\varGamma(p+\gamma)}{\varGamma(1-\gamma) \varGamma(\gamma)(p-1)!}, $$

and

$$ V_{p-1}^{(1)}(y) (t) = t^{p-1}y(t), \qquad V_{p-1}(y) (0) =0, \quad p=1,2,3,\ldots $$

(46)

Inserting (45) into (44), we obtain

$$\begin{aligned} \sigma(t) \approx& \biggl\{ 1+ \biggl[ \frac{a\,A(N,\alpha)}{t^{\alpha}} +b \biggl( \frac{A(N,\alpha+iB)}{t^{\alpha+iB}}+ \frac{A(N,\alpha-iB)}{t^{\alpha-iB}} \biggr) \biggr] \biggr\} H_{\varepsilon }(t) \\ &{} - \sum_{p=1}^{N} \biggl\{ \frac{C_{p-1}(\alpha)}{t^{p+\alpha}}+ \biggl[ \frac{C_{p-1}(\alpha+iB)}{t^{p+\alpha+iB}} +\frac{C_{p-1}(\alpha- iB)}{t^{p+\alpha-iB}} \biggr] \biggr\} V_{p-1}(H_{\varepsilon }) (t), \end{aligned}$$

(47)

where

$$ V_{p-1}^{(1)}(H_{\varepsilon }) (t)=t^{p-1}H_{\varepsilon }(t) , \quad p=1,2,3,\ldots $$

(48)

We will compare (47) with the stress $\sigma$ obtained by (44) and by the definition of fractional derivative (11):

$$\begin{aligned} \sigma(t) =& H_{\varepsilon }(t)+a\frac{d}{dt}\frac{1}{\varGamma(1-\alpha)} \int_{0}^{t} \frac{H_{\varepsilon }(\tau) \,d\tau}{(t-\tau)^{\alpha}} \\ &{} + b\frac{d}{dt} \biggl[\frac{1}{\varGamma(1-\alpha-iB)} \int_{0}^{t} \frac{H_{\varepsilon }(\tau)\,d\tau}{(t-\tau)^{\alpha+iB}} \\ &{} + \frac{1}{\varGamma(1-\alpha+iB)} \int_{0}^{t}\frac{H_{\varepsilon }(\tau)\,d\tau}{(t-\tau)^{\alpha -iB}} \biggr]. \end{aligned}$$

(49)

In Fig. 3, we show results obtained by determining $\sigma$ from (49) for small times and different values of $B$. In the same figure, we show, by dots, the values of $\sigma$, at several points, obtained by using (47), (48) for $k=0.01$, $N=100$. As could be seen from Fig. 3, the results obtained from (49) and (47), (48) agree well. The stress relaxation curves are shown in Fig. 4, for the same set of parameters and for larger times. As could be seen, regardless of the values of $B$, we have $\lim_{t\to\infty} \sigma(t) =1$. Note that in all cases of $B$, the restriction which follows from the dissipation inequality is satisfied.

Fig. 3

Stress relaxation curves for $\alpha=0.4$ and $B\in\{0.4,0.6,0.8,0.99\}$, $a=0.8$, $b=0.1$, $t\in[0,0.25]$

Fig. 4

Stress relaxation curves for $\alpha=0.4$ and $B\in\{0.4,0.6,0.8,0.99\}$, $a=0.8$, $b=0.1$, $t\in[ 0,10]$

4.2 Creep experiment

Suppose that $\sigma(t) =H(t)$, i.e.,

$$ H(t) = \bigl(1+a\,{}_{0}D_{t}^{\alpha} + 2b\,{}_{0}\bar{D}_{t}^{\beta}\bigr) \varepsilon (t), \quad t\geq0. $$

(50)

By (45), we obtain

$$\varepsilon (t) \approx\frac{H(t) +\sum_{p=1}^{N} \{ \frac{C_{p-1}(\alpha)}{t^{p+\alpha}} + \frac{C_{p-1}(\alpha+iB)}{t^{p+\alpha+ iB}} +\frac{C_{p-1}(\alpha-iB)}{t^{p+\alpha-iB}} \} V_{p-1}(\varepsilon )(t)}{1+ \frac{a A(N,\alpha)}{t^{\alpha}}+2b ( \frac{A(N,\alpha+iB)}{t^{\alpha+iB}}+\frac{A(N,\alpha -iB)}{t^{\alpha-iB}} )}, $$

or

$$ \varepsilon (t) \approx\frac{H(t) t^{\alpha} + \sum_{p=1}^{N} \{ \frac{C_{p-1} (\alpha)}{t^{p}} + \frac{C_{p-1}(\alpha+iB)}{t^{p+iB}} +\frac{C_{p-1}(\alpha-iB)}{t^{p-iB}} \} V_{p-1}(\varepsilon )(t)}{t^{\alpha}+ a A(N,\alpha)+2b ( \frac{A(N,\alpha+iB)}{t^{iB}}+\frac{A(N,\alpha-iB)}{t^{-iB}} )}. $$

(51)

By using (51) in (46), we obtain

$$\begin{aligned} V_{p-1}^{(1)}(\varepsilon ) (t) \approx& t^{p-1} \frac{H(t) t^{\alpha} +\sum_{p=1}^{N} \{ \frac{C_{p-1}(\alpha)}{t^{p}}+ \frac{C_{p-1}(\alpha+iB)}{t^{p+ iB}}+\frac{C_{p-1}(\alpha-iB)}{t^{p-iB}} \} V_{p-1}(\varepsilon )(t)}{t^{\alpha} + a A(N,\alpha)+2b ( \frac{A(N,\alpha+iB)}{t^{iB}} + \frac{A(N,\alpha-iB)}{t^{-iB }} )}, \\ V_{p-1}(\varepsilon ) (0) =& 0, \quad p=1,2,3,\ldots. \end{aligned}$$

Equation (50) may also be solved by contour integration

$$ \varepsilon (t) = K(t)\ast H(t), \quad t\geq0, $$

(52)

where $K$ is given by (41), see (40). Finally, the values of $\varepsilon$, at discrete points, could be determined directly from $\tilde{\varepsilon }(s) = \frac{1}{s} \tilde{K}(s)$, $\operatorname {Re}s>0$, see (39), by the use of Post inversion formula, see Cohen (2010). Thus,

$$ \varepsilon (t) = \lim_{n\to\infty} \frac{(-1)^{n}}{n!} \biggl[s^{n+1} \frac{d^{n}}{ds^{n}} \frac{1}{s(1+as^{\alpha }+b(s^{\beta}+s^{\bar{\beta}}))} \biggr]_{s=\frac{n}{t}}, \quad t\geq0. $$

(53)

In Figs. 5, 6 and 7, we show $\varepsilon$ for several values of parameters determined from (52). In Fig. 5, for specified values of $t$ we present values of $\varepsilon$ determined from (51), with $N=7$, denoted by dots, as well as the values of $\varepsilon$ determined by (53), with $n=25$, denoted by squares. As could be seen, the agreement of results determined by different methods is significant.

Fig. 5

Creep curve for $\alpha=0.4$ and $B=0.4$, $a=0.8$, $b=0.1$, $t\in[0,100]$

Fig. 6

Creep curves for $\alpha=0.4$ and $B\in\{ 0.2,0.4,0.6\}$, $a=0.8$, $b=0.1$, $t\in[0,200]$

Fig. 7

Creep curves for $\alpha=0.4$ and $B\in\{ 0.7,0.8,0.9,0.99\}$, $a=0.8$, $b=0.1$, $t\in[0,200]$

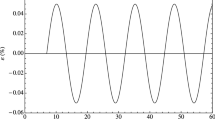
From Figs. 6 and 7 one sees that, regardless of the value of $B$, creep curves tend to $\varepsilon =1$. In Fig. 6, the creep curves are monotonically increasing, while in Fig. 7 the creep curves have oscillatory character, characteristic for the case when the mass of the rod is not neglected. Note that in all cases of $B$, the restriction determined by the dissipation inequality is satisfied.

5 Conclusion

In this work, we proposed a new constitutive equation with fractional derivatives of complex order for viscoelastic body of the Kelvin–Voigt type. The use of fractional derivatives of complex order, together with restrictions following from the Second Law of Thermodynamics, represent the main novelty of our work. Our results can be summarized as follows.

• 1. In order to obtain real stress for given real strain, we used two fractional derivatives of complex order that are complex conjugated numbers, see Theorem 2.3.

• 2. The restrictions that follow from the Second Law of Thermodynamics for isothermal process implied that the constitutive equation must additionally contain a fractional derivative of real order. Thus, the simplest constitutive equation that gives real stress for real strain and satisfies the dissipativity condition is given by (24).

• 3. We provided a complete analysis of solvability of the complex order fractional Kelvin–Voigt model given by (24) (see Theorems 3.1 and 3.2).

• 4. We studied stress relaxation and creep problems through equation (24). An increase of $B$ implied that the stress relaxation decreases more rapidly to the limiting value of stress, i.e., $\lim_{t\to\infty} \sigma(t) =1$.

• 5. We presented numerical experiments when the dissipation inequality is satisfied. The creep experiment showed that the increase in the imaginary part of the complex derivative $B$ changes the character of creep curve from monotonic to oscillatory form, see Figs. 6 and 7. However, the creep curves never cross the value equal to 1. The creep curve resembles the form of a creep curve when either the mass of the rod, see Atanacković et al. (2014, p. 124), or inertia of the rheometer, see Jaishankar and McKinley (2012), is taken into account. Recently, Zingales (2015) presented experimental results of creep curves for some biological materials that exhibit non-monotonic creep curve. Thus, our model (24) is applicable to such a case.

• 6. The parameters in the proposed model (24) could be determined from experimental data using, for instance, the least squares method.

• 7. Our further study will be directed to the problems of vibration and wave propagation of a rod with finite mass and constitutive equation (24), along the lines presented in Atanacković et al. (2014), see also Hanyga (2007).