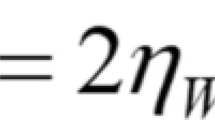Shear-thinning and constant viscosity predictions for rotating sphere flows

Abstract

The steady motion of a rotating sphere is analysed through two contrasting viscoelastic models, a constant viscosity (FENE-CR) model and a shear-thinning (LPTT) model. Giesekus (Rheol. Acta 9:30–38, 1970) presented an intriguing rotating viscoelastic flow, which to date has not been completely explained. In order to investigate this flow, sets of parameters have been explored to analyse the significant differences introduced with the proposed models, while the momentum-continuity-stress equations are solved through a hybrid finite-element/finite volume numerical scheme. Solutions are discussed for first, sphere angular velocity increase ($\varOmega$), and second, through material velocity-scale increase ($\alpha$). Numerical predictions for different solvent-ratios ($\beta$) show significant differences as the sphere angular velocity increases. It is demonstrated that an emerging equatorial anticlockwise vortex emerges in a specific range of $\varOmega$. As such, this solution matches closely with the Giesekus experimental findings. Additionally, inside the emerging inertial vortex, a contrasting positive second normal stress-difference ($N_{2} ( \dot{\gamma} ) = \tau_{rr} - \tau_{\theta\theta}$) region is found compared against the negative $N_{2}$-enveloping layer.

1 Introduction

Thomas and Walters (1964) theoretically studied the flow patterns produced by a rotating sphere immerse in a viscoelastic Boger fluid. Similarly, Walters and Savins (1965) studied this same flow problem experimentally, as did Giesekus (1970) subsequently. Giesekus exposed some intriguing results, based on those for two different types of fluids, a Boger fluid (silicone oil) and a shear-thinning fluid (polyisobutylene/decalin solution). Giesekus reported that the Boger fluid also captured the secondary flow cell, typically shown previously in the second-order flow regime (Thomas and Walters 1964; Walters and Savins 1965). In order to investigate the effect of shear-thinning, Giesekus selected a solution of 1.3 % polyisobutylene in decalin. At low rotational speeds, the shear-thinning fluid created the same flow patterns as exhibited by a Boger fluid (second-order regime). Notwithstanding this, at rotational speed of 150 min⁻¹, a flow pattern is observed that cannot be characterized by the second-order regime. A detailed analysis of Fig. 1 shows clearly the coexistence of three different flow zones, as described by Boger and Walters (1993) and Giesekus (1994): an outer inertial zone (not highlighted by the dye-injection technique); a dominant viscoelastic zone (restricted to the central region as a polar vortex); and an elusive inner inertial zone (an equator vortex). This scenario is presented in the cover of the book: Fluid Mechanics of Viscoelasticity by Huilgol and Phan-Thien (1997) as an illustration for the dye-injection technique.

Fig. 1

Giesekus (1970) experimental evidence for 1.3 % polyisobutylene-decalin solution, $\varOmega=150~\mbox{min}^{-1}$; secondary flow regions: right-hand image—three different zones

In the past it has been suggested that some rheological properties of viscoelastic fluids may be assessed using the rotating sphere flow, such as the zero-shear viscosity (Hermes 1966). For example, Walters and Savins (1965) showed that observations of the secondary flow pattern around the rotating sphere could be related to measurement of the second normal stress-differences at very low shear rates. Using this method, Manero and Mena (1978) acquired values of the second normal stress-difference; such findings lay in good agreement with the values obtained through other methods. In addition, some authors, such as Mashelkar et al. (1972), Kelkar et al. (1973), Acharya and Maaskant (1978), have used the torque as a function of rotation-speed, to assess the elastic-viscous parameters of some fluids. One of the most common difficulties in the effective use of torque measurements lies in the elimination of wall-effects, which may also affect the development of diverse flow patterns. According to Walters and Waters (1963), torque measurements should be limited to a lower ratio between the sphere-radius to the vessel-radius (1:12) to effectively avoid wall-effects. However, Mena et al. (1972) later proved that the influence of the retaining vessel-wall could be overcome, by incorporating a wall-correction to the computation for the resultant torque.

Theoretically, Thomas and Walters (1964) explored the problem of a rotating sphere in an elastic medium through a second-order perturbation analysis. They characterized the range for each flow-type encountered through a material parameter $m$ (defined below) that accounted for the effects of the first and second normal-stress coefficients. Subsequently, Fosdick and Kao (1980) performed a perturbation analysis up to fourth-order expansions in the angular velocity for a simple fluid; their findings could be qualitative compared with the results obtained by Giesekus (1970). Fosdick and Kao (1980) illustrated polar cap regions of secondary flow, but they could not detect any trace of an equatorial vortex. These authors concluded that the inertial vortex could not be developed due to the restrictive choice on the value of the parameters used. For an Oldroyd-B fluid, Garduño et al. (2015) explored additional flow regimes, beyond that of second-order. These numerical solutions exhibited an emerging polar vortex within the range of $0.08 < m < 0.16$ for more general flow solutions, in transitional and general flow settings. Indeed, these findings have provided the insight and guidance in the present study to adjust velocity-scaling parameters, in order to more closely capture the experimental observations of Giesekus.

In the present study, a hybrid finite element/finite volume discretisation ($\mathit{fe}/\mathit{fv}$) (Belblidia et al. 2007, 2008) has been used to compare and contrast numerical predictions for this rotating sphere problem. In this direction, the constant-viscosity FENE-CR and shear-thinning LPTT fluid models have been employed, under low Reynolds number settings. The main objective of this work has been to orchestrate matching of these solutions against the Giesekus (1970) experimental findings, whilst also exploring the influence of alternative and wider parameter ranges.

The present paper is structured in the following manner. Firstly, the governing equations are presented; next the specification of the numerical problem and the particular boundary conditions are outlined. Followed by, the respective constitutive relationships for FENE-CR and LPTT. This is pursued by the appropriated choice of materials functions for Oldroyd-B, contrasted against FENE-CR and LPTT models. A brief summary of the in-house finite element/finite volume algorithm employed is offered. In Sect. 4, the parametric analysis is presented: firstly, for the flow-type descriptor $m$; then, using the LPTT model as a base-case with $m=0.14$, findings for the respective solvent fraction ratio ($\beta$) and second normal stress-difference ($N_{2} ( \dot{\gamma} ) = \tau_{rr} - \tau_{\theta\theta}$) patterns are exposed. The parameters for the angular velocity (out-of-plane, $\varOmega$) and material velocity scaling (in-plane, $\alpha$) are shown over both FENE-CR and LPTT model solutions.

Subsequently, this article proceeds to draw out diverse classes of vortex-solutions, discovered through the various combinations of available parameters. Solutions for large-$\alpha$ are explored for both FENE-CR and LPTT solutions, revealing some remarkable differences over a limited range of $\varOmega$. Then, $N_{2}$-values are exposed at two different sample-point locations over the sphere-surface, alongside the theoretical and computational torque estimation. Finally, best matching is considered between present numerical predictions and the experimental findings of Giesekus.

2 Governing equations

Appealing to incompressible viscoelastic flow and isothermal conditions, the governing equations are those for mass balance (continuity),

$$ \nabla\cdot u = 0, $$

(1)

and linear momentum transfer:

$$ \rho \biggl( \frac{\partial u}{\partial t} + u \cdot\nabla u \biggr) = - \nabla p + \nabla \cdot T, $$

(2)

coupled with an equation of state for stress ($T$). Here, the notation implies that $u$ denotes the fluid velocity (vector field), $\rho$ is the fluid density, $p$ the isotropic fluid pressure, $\nabla$ is a spatial differential operator (over spatial variable $\mathbf{x}$) and $t$ represents the independent variable time.

The extra-stress $T$ variable may be decomposed into two parts, viscous and polymeric parts viz.

$$ T = \tau+ 2\eta_{0}\beta\mathbf{d}, $$

(3)

where $\eta_{0}\beta$ is a solvent viscosity (based on zero-shear rate viscosity $\eta_{0}$ and solvent fraction $\beta$, see below) and the rate of deformation tensor is represented by $\mathbf{d} = (\nabla u + \nabla u^{\dagger} )/2$.

2.1 Viscoelastic constitutive models: LPTT and FENE-CR

2.1.1 Finite extendible nonlinear elasticity—Chilcott and Rallison

In addition to the use of the Oldroyd-B model (as in our prior study Garduño et al. 2015), here and by way of contrast, PTT and so-called FENE-CR (Chilcott and Rallison 1988) models have been introduced. Beneficially beyond Oldroyd-B approximation, both additional models manifest finite extensibility. The PTT model offers numerical solutions with shear-thinning properties. In contrast, the FENE-CR model has been chosen for its constant shear viscosity response. Hence, this FENE-CR form is an appropriate constitutive model to use in representation of Boger fluids properties, additionally with a weaker first normal stress-difference than the strong quadratic form displayed by the base-reference Oldroyd-B model. The main point of disparity, between the Oldroyd-B and FENE-CR models, is such that the FENE-CR model does not encounter a singularity in extensional viscosity (exhibiting instead a finite extensional response). The maximum level of FENE-CR extensional viscosity corresponds to the elevation of the Hookean-dumbbell chain-length extensibility parameter ($L_{\mathrm{FENE}}$). This $L_{\mathrm{FENE}}$ model-parameter measures the size of the polymer molecule in relation to its equilibrium size.

This particular model has the following constitutive form, based on a stress conformation tensor ($A$):

$$\begin{aligned} &T = 2\eta_{0}\beta\mathbf{d} + \frac{ ( 1 - \beta )\eta_{0}f ( \operatorname {Tr}( A ) ( A - I ) )}{\lambda_{1}},\qquad \lambda_{1} \mathop{\mathit{A}}\limits^{\nabla} - f \bigl( \operatorname {Tr}( A ) ( A - I ) \bigr) = 0, \\ &\quad f \bigl( \operatorname {Tr}( A ) \bigr) = \frac{1}{1 - \operatorname {Tr}( A )/L_{\mathrm{FENE}}^{2}}. \end{aligned}$$

(4)

The corresponding rheometrical functions, of shear viscosity ($\eta$) extensional viscosity ($\eta_{e}$), and first normal stress-difference ($N_{1}$) and second normal stress-difference ($N_{2}$), for this particular model are then

$$ \begin{aligned}[c] &\eta_{s} = \eta_{0},\qquad N_{1} = \frac{2\eta_{0} ( 1 - \beta )\lambda_{1}\dot{\gamma}^{2}}{f^{2}},\qquad N_{2} = 0, \\ &\eta_{e} = 3\beta\eta_{0} + 3\eta_{0} ( 1 - \beta ) \biggl[ \frac{f^{2}}{f^{2} - f\lambda_{1}\dot{\varepsilon} - 2\lambda_{1}^{2}\dot{\varepsilon}^{2}} \biggr]. \end{aligned} $$

(5)

Here $\dot{\gamma}$ is representing shear rate, $\dot{\varepsilon}$ strain rate and $\lambda_{1}$ as a relaxation time.

2.1.2 Linear Phan-Thien–Tanner model

Phan-Thien and Tanner (1977) introduced a generalized (PTT) model version, based on ideas from rubber network theory, to investigate the effect of shear-thinning. From this work, a restricted Linearized PTT version is often used (LPTT), where the exponential function is truncated in its Taylor series expansion. Such an LPTT form used here presents response of a weakening in $N_{1}$ and a finite extensional viscosity, which is controlled by the material function ($\varepsilon_{\mathrm{LPTT}}$). A second material parameter ($\xi_{\mathrm{LPTT}}$) modifies the shear-viscosity and the second normal stress-difference coefficient; note, often this parameter is taken as zero. As such, these two model parameters, $\varepsilon_{\mathrm{LPTT}}$ and $\xi_{\mathrm{LPTT}}$, may be deployed to control the prescribed extensional and shear response of the model. The LPTT model recovers the original Oldroyd-B form when $\varepsilon_{\mathrm{LPTT}} = 0$ and $\xi_{\mathrm{LPTT}} = 0$. In general, as $\varepsilon_{\mathrm{LPTT}} \to0$, the limiting maximum plateau value of extensional viscosity grows larger (that of Oldroyd-B being infinite). The LPTT constitutive form and rheometrical functions are given by

$$\begin{aligned} &\begin{aligned}[c] &T^{ ( 1 )} = 2\eta_{0}\beta\mathbf{d},\\ &fT^{ ( 2 )} + \lambda_{1} \mathop{T^{(2)}}\limits^{\nabla} = 2\eta_{0} ( 1 - \beta )\mathbf{d}, \end{aligned} \end{aligned}$$

(6)

$$\begin{aligned} &\begin{aligned}[c] &\eta_{s} = \beta\eta_{0} + \frac{\eta_{0} ( 1 - \beta )}{f},\qquad N_{1} = \frac{2\eta_{0} ( 1 - \beta )\lambda_{1}\dot{\gamma}^{2}}{f^{2}},\qquad N_{2} = - \frac{\eta _{0} ( 1 - \beta )\lambda_{1}\dot{\gamma}^{2}\xi_{\mathrm{LPTT}}}{f^{2}}, \\ &\eta_{e} = 3\beta\eta_{0} + 3\eta_{0} ( 1 - \beta ) \biggl[ \frac{f}{f^{2} - f\lambda_{1}\dot{\varepsilon} - 2\lambda_{1}^{2}\dot{\varepsilon}^{2}} \biggr]. \end{aligned} \end{aligned}$$

(7)

For this LPTT model, the $f$ function is represented through the linear function of the trace ($T^{ ( 2 )}$),

$$ f = 1 + \frac{\varepsilon_{\mathrm{LPTT}}\lambda_{1}}{1 - \beta} \operatorname {Tr}\bigl( T^{ ( 2 )} \bigr). $$

(8)

In steady shear flow, the ratio between the normal stress-differences is $N_{2} / N_{1} = - \xi_{\mathrm{LPTT}} / 2$. Hence, the non-zero material parameter $\xi_{\mathrm{LPTT}}$ may be associated with stronger second normal stress-difference affects (non-zero in shear). Typically, Phan-Thien and Tanner (1977) suggested using $\xi_{\mathrm{LPTT}} = 0.2$ for LDPE; nonetheless, the material parameter is mathematically defined and valid for $0 \le \xi_{\mathrm{LPTT}} \le2$.

The difference between LPTT and FENE-CR forms is, basically, the addition of shear-thinning through the LPTT option. One may note, however, these two constitutive models are somewhat different in their background derivations. Both model forms can be associated with the same extensional response by adjusting their material functions, which can be organised by fitting and matching with the appropriate selection of $\varepsilon_{\mathrm{LPTT}}$ and $L$-values, accordingly.

In Figs. 2 and 3, material functions for Oldroyd-B, FENE-CR and LPTT are presented. In this form, the comparative model response, in steady shear and extension, can be gathered on shear viscosity, extensional viscosity, $N_{1}$ and $N_{2}$ (latter, only for LPTT $(\xi_{\mathrm{LPTT}} \ne0)$). Note, from this information and parameter fitting, suitable parameters of solvent fraction $\beta=\{0.9, 1/9\}$, FENE-CR ($L_{\mathrm{FENE}}=5$) and LPTT ($\varepsilon_{\mathrm{LPTT}} = 0.042$) are selected for use in solution extraction for this rotating sphere flow. The $L_{\mathrm{FENE}}=5$ and $\varepsilon_{\mathrm{LPTT}} = 0.042$ parameter choices provide the desired matching on extensional viscosity behaviour.

Fig. 2

Material functions for Oldroyd-B, FENE-CR ($L_{\mathrm{FENE}}=3, 5, 100$), LPTT ($\varepsilon_{\mathrm{LPTT}} = 0.042$, $4\times10^{-4}$, $\xi_{\mathrm{LPTT}} = 0.0$), $\beta=0.9$. (a) shear viscosity, (b) extensional viscosity, (c) first normal stress-difference

Fig. 3

Material functions for Oldroyd-B, LPTT ($\varepsilon_{\mathrm{LPTT}} = 0.042$, $\xi_{\mathrm{LPTT}} = 0.0, 0.2$), $\beta= 0.9,0.1$. (a) shear viscosity, (b) extensional viscosity, (c) first normal stress-difference, (d) second normal stress-difference

2.1.3 Material functions: Oldroyd-B, FENE-CR and LPTT models

The associated rheometrical functions for the Oldroyd-B, FENE-CR and LPTT models are displayed in Figs. 2 and 3. Then, Oldroyd-B predicts a constant shear viscosity $\eta_{0}$, a quadratic first normal stress-difference $N_{1}$, vanishing second normal stress-difference $N_{2}$, and an unbounded extensional viscosity $\eta_{e}$ at finite rates in steady uniaxial extension (see Fig. 2(a)). In contrast, the FENE-CR model captures finite extensibility, predicts a constant shear viscosity, whilst expressing a first normal stress-difference ($N_{1}$) that is weaker than the strong quadratic form of Oldroyd-B. As illustrated in Fig. 2(b), the extensional viscosity for the FENE-CR model is capped, at a limiting level of extensional viscosity plateau, which itself depends on the elevation of the FENE-CR extensibility parameter $L_{\mathrm{FENE}} \geq3$. One notes, however, predictions for large values of extensibility parameter ($L_{\mathrm{FENE}}>100$) asymptote towards Oldroyd-B behaviour in $N_{1}$ and $\eta_{e}$. For small choices of $L_{\mathrm{FENE}}$ ($L_{\mathrm{FENE}}=3$), significant departure in $N_{1}$ is observed from Oldroyd-B response. Moreover, monotonic decline in $N_{1}$ is apparent with falling $L_{\mathrm{FENE}}$.

Finally, and specifically to explore the effects of shear-thinning on the size and position of vortices in the rotating-sphere flows of present interest, a Linear Phan-Thien/Tanner (LPTT) model has been introduced. Then LPTT, as with FENE-CR, also possesses a finite extensional viscosity and a weakening of $N_{1}$. Here, the choice and selection of $\varepsilon_{\mathrm{LPTT}}$ may be made to effectively match LPTT and FENE-CR extensional viscosity response ($\eta_{e}$), eliminating this aspect from the comparison (see Figs. 2 and 3). The FENE-CR ($L_{\mathrm{FENE}}=5$) and LPTT ($\varepsilon_{\mathrm{LPTT}} = 0.042$) parameter choices provide this desired matching on extensional viscosity behaviour. In addition, suitable parameter selection on solvent fraction is $\beta=\{0.9, 1/9\}=\{ \mbox{\textit{high-solvent}}, \mbox{\textit{high-solute}}\}$. Note, that such a network-based LPTT representation is purely strain-hardening, to a limiting finite plateau (unlike Oldroyd), and hence, does not support strain-softening (Fig. 3). In Fig. 3 and with the LPTT approximation, the viscosity solvent-fraction ratio $\beta$-parameter is used to control the degree of departure from the Newtonian zero-rate base-reference to its second-plateau viscosity value. As such, the approximation to constant shear-viscosity for these shear-thinning fluids, is within 10 % for $\beta =0.9$ (close), and for $\beta=0.1$, represents 90 % departure (more distant). In addition, the LPTT ($\xi_{\mathrm{LPTT}} \ne0$) model introduces some non-zero second normal stress-difference ($N_{2}$) in shear, since $N_{2} / N_{1} = - \xi/ 2$. Increasing the parameter $\xi_{\mathrm{LPTT}}$, for constant values of $\varepsilon_{\mathrm{LPTT}}$ and $\beta$, provides a decrease in shear viscosity (Fig. 3(a)). The elongational viscosity is barely affected by such $\xi_{\mathrm{LPTT}}$-adjustment (Fig. 3(b)). Furthermore, note that both $N_{1}$ and $N_{2}$ for LPTT ($\xi_{\mathrm{LPTT}} = 0.2$) adopt a monotonically declining trend in contrast to the LPTT ($\xi_{\mathrm{LPTT}} = 0$) option, with $N_{2}$ showing universally reduced values in comparison to $N_{1}$ (see Fig. 3(d)). Therefore and with a view to $N_{2}$-stimulation in more complex flow, one may anticipate that such adjustment in $\xi_{\mathrm{LPTT}}$-parameter may have some influence on the size, structure and positioning of vortices in the current rotating sphere problem. To verify this hypothesis, two different levels of $\xi_{\mathrm{LPTT}}$-values ($\xi _{\mathrm{LPTT}} = \{ 0.1, 0.2\}$) have been considered and corresponding complex flow solution patterns have been generated.

3 Flow problem specification and numerical algorithm

Let us consider a rotating sphere of radius ($a$) immersed in a bath of viscoelastic fluid of zero shear-rate viscosity $\eta_{0}$ and density $\rho$, defining the kinematic viscosity $\nu= \eta_{0} / \rho$. The rotation is achieved through a constant angular velocity $\varOmega_{\mathrm{sphere}}$, about an axis of rotation into the vertical plane. The coordinate system is chosen in such a way that its origin is located at the centre of the sphere. In this analysis, as also considered elsewhere theoretically (Thomas and Walters 1964), the motion of the fluid is due solely to the rotational movement of the sphere, and is sufficiently small in order to neglect inertia. Hence, any suspending upper-rod intrusion of the experiments (Giesekus 1970) is ignored, to focus on the lower half-sphere flow patterns.

The symmetric nature of the problem allows representation in a single lower quadrant of the ($r, \theta$)-polar plane. The boundary conditions are established over the four different boundaries. Firstly, no-slip is established over the sphere surface; here, only rotational velocity ($\varOmega_{\mathrm{sphere}}a\sin\theta$) is non-zero, imposed as anti-clockwise into the plane (viewed from above); whilst symmetry conditions are applied on the polar-equatorial axes (vanishing shear stress). Additionally, it is assumed that the vessel is of relatively infinite outer dimensions, implying that at larger distance away from the sphere, the fluid is to all intent and purposes relatively at rest.

The quadrant boundary conditions for this problem are defined through the velocities on the sphere itself, the two axes, polar and equatorial, and the far-field boundary. These are given as standard (see Thomas and Walters 1964), in the lower spherical quadrant of interest that satisfy the boundary conditions at the sphere ($r = a$) and in the field. Corresponding velocity components in the spherical quadrant of interest ($U^{\rho},V^{\theta},W^{\phi}$), must satisfy the stream function of equation (Eq. (35) of Thomas and Walters 1964) and the boundary conditions at the sphere surface, so that with $r_{1} = r / a$:

$$ \begin{aligned}[c] &U^{\rho} = \frac{\nu}{a}u_{1}^{\rho} = \frac{\nu}{a}\frac{ ( r_{1} - 1 )^{2}}{8r_{1}^{5}} \bigl[ ( 1 - 4m )r_{1} - 8m \bigr] \bigl( 3\sin^{2}\theta- 2 \bigr), \\ &V^{\theta} = \frac{\nu}{a}u_{2}^{\theta} = \frac{\nu}{a}\frac{ ( r_{1} - 1 )}{4r_{1}^{5}} ( r_{1} - 12m )\sin\theta\cos \theta, \end{aligned} $$

(9)

and on the sphere,

$$ W^{\phi} = \varOmega_{\mathrm{sphere}}au_{3}^{\phi} = \varOmega_{\mathrm{sphere}}a\sin \theta, $$

(10)

from which appropriate non-dimensional velocity components ($u_{1}^{\rho},u_{2}^{\theta},u_{3}^{\phi}$) may be extracted. These expressions are linked to a specific value of the parameter $m$ (see on to Sect. 4), which implies that the initial conditions proceed from these computations. Then, $\varOmega_{\mathrm{sphere}}$ is defined as a base-reference angular velocity of the sphere, $\alpha_{\mathrm{base}\text{-}\mathrm{ref}} = \nu/ a$ as a base-reference viscous material velocity scale, and $\theta$ is the angle measured from the vertical axis of rotation, with orientation taken on the vertical polar-axis as ($\theta= 0^{\circ}$) and on the equatorial-axis ($\theta= 90^{\circ}$). Note in particular, the use of the dual scales on velocity components of Thomas and Walters (1964), who used ($U_{\mathrm{sphere}} = \varOmega_{\mathrm{sphere}}a$) for ($u^{\phi}$) as a sphere rotational velocity scale, and $U_{\mathrm{material}} = (\nu/ a)_{\mathrm{base}\text{-}\mathrm{ref}}$ for ($u^{\rho},u^{\theta}$) as a viscous material velocity scale. These scales imply that two different controlling influences apply in this problem, where the $(\nu/ a)_{\mathrm{base}\text{-}\mathrm{ref}}$-scale has bearing over the in-plane velocity (viscoelastic), and the other ($\varOmega_{\mathrm{sphere}}a$)-scale exerts control over the out-of-plane velocity (inertial).

Hybrid finite element/finite volume scheme

Here, the numerical method used solves for stress, velocity and pressure variables in the plane of interest, and is an extension of that previously cited in Belblidia et al. (2007, 2008), Wapperom and Webster (1998, 1999), Webster et al. (2005). In essence, the numerical solution procedure adopts a time-stepping fractional-staged approach to steady-state, specifically developed and advanced for viscoelastic flow problems. It assumes a Taylor series time expansion and a time-incremental pressure-correction method, to derive a semi-implicit scheme implemented over three sub-staged equations per time-step. Spatial discretisation is accomplished via: first, velocity-pressure finite element approximation, on the parent-level quadratic-linear interpolation over the meshed-domain triangulation. This is followed by a cell-vertex stress finite volume approximation on each triangular sub-cell of an individual parent-triangular cell. Thus, the momentum-continuity equations are discretized and solved through this hybrid combination of: semi-implicit Taylor–Galerkin/incremental pressure-correction algorithm (see, for example, Donea 1984; Zienkiewicz et al. 1985; Matallah et al. 1998), together with that of a cell-vertex finite volume sub-cell technique for stress (see, for example, Wapperom and Webster 1998, 1999). Over the sub-staged equations per time-step, the first and third stages are solved through Jacobi iteration, whilst the second stage invokes a direct Choleski decomposition method. Time-stepping convergence to a steady-state is ensured, from appropriate initial and boundary conditions, through selection of a suitable time-step (here chosen as $10^{-4}$) and time-stepping termination criteria. The former must satisfy standard semi-implicit stability criteria, whilst the latter is taken with respect to a relative temporal increment norm over the evolving solution (with a threshold value of $10^{-6}$). Fuller details on these procedures are provided in the references cited above, so that only a brief outline on the stress discretisation is included below, together with Aboubacar and Webster (2001) and Garduño et al. (2015).

Sub-cell finite volume stress discretisation

The stress discretisation comprises a novel implementation of a finite volume scheme over triangles, of cell-vertex variable location. This scheme has emerged from and lies as an extension to the homogeneous zero-source context for first-order hyperbolic conservation law equations. In the present context, the constitutive laws are inhomogeneous and multidimensional, hence calling upon counterpart flux and source term temporal resolution, to maintain consistency, accuracy (linearity preserving) and stability (positivity preserving) properties. The triangular subcell cell-vertex technique derived for the extra-stress temporal-increment calculation is centred upon a single parent-triangular finite element cell that is sub-divided into four finite volume child-triangular subcells. In order to calculate the individual components of the stress tensor, a series of equivalent linear shape functions is applied over each subcell area of the triangular finite volume ($\mathit{fv}$), thus constituting the integral flux and source term evaluation.

The integrated flux evaluation is extracted through a fluctuation distribution scheme (LDB-method upwinding), which allocates such contributions over each triangular $\mathit{fv}$-subcell to its three vertices. Hence, this procedure distributes the flux control-volume residuals to their respective nodes of the subcell, to provide the associated nodal solution updates. Similarly, concerning inhomogeneous source term evaluation, computations are performed over the so-called Median-Dual-Cell (MDC) zone of each $\mathit{fv}$-subcell. There are three such unique non-overlapping MDC-zones per $\mathit{fv}$-subcell-triangle, each providing its contribution to its nearest nodal MDC-neighbour. A complete solution nodal update is then obtained by summing all such flux and source term contributions, from each (and all) $\mathit{fv}$-subcell-triangle control-volume surrounding a typical node (Aboubacar and Webster 2001).

4 Results and discussion

4.1 $m$-parameter variation {flow type descriptor}

The regions for the different flow patterns are specified through the $m$-parameter, as reported by Walters and Waters (1964) analysis, which takes the form

$$ m = ( \alpha_{T} - 2\beta_{T} )/2\rho a^{2}, $$

(11)

where $\alpha_{T} = N_{1} / \dot{\gamma}^{2}$ and $\beta_{T} = N_{2} / \dot{\gamma}^{2}$ are the respective first and second normal stress-difference coefficients.

The standard and base flow problem is one assumed to be specified in boundary conditions by the second-order theory, but solved over the flow-field domain in a general manner; hence, the adoption of a constant base-form definition for $m$-parameter, as one possible choice. This option permits the comparison with second-order regime solutions (universal to all constitutive models), flow regime solutions beyond second-order, and across constitutive models more generally (as necessary here). An alternative variable classification of $m$-parameter, over the field and constitutive model, would invalidate any such comparison.

Accordingly, the $m$-parameter can be reinterpreted through non-dimensional numbers, viz.

$$ m = \frac{\mathit{Wi}}{\mathit{Re}} ( 1 - \beta ), $$

(12)

where the two non-dimensional group numbers are defined as

$$ \begin{aligned}[c] &\mathit{Re} = \rho aU / \eta_{0} = \varOmega a^{2} / \nu= ( \varOmega a ) ( a / \nu ) = U_{\mathrm{sphere}} / U_{\mathrm{material}}, \\ &\mathit{Wi} = \lambda_{1}U/L_{\mathrm{sphere}} = \lambda_{1} \varOmega_{\mathrm{sphere}}. \end{aligned} $$

(13)

Taking the characteristic length scale ($L_{\mathrm{sphere}}$) in terms of the sphere radius ($a$), and the characteristic velocity scale ($U$), based on the sphere angular velocity ($\varOmega_{\mathrm{sphere}}$), thus in Fig. 4 the different flow types are depicted, highlighting the respective directions of the flow. Type 1 (inertial), $0 \le m \le1 / 12$ represents a classical Stokes flow, where the flow moves from the poles to the equator. Type 3 (viscoelastic), $m \ge1 / 4$ flow is mainly directed from the equator towards the poles; in this pattern the flow field is dominated by fluid elasticity. This study is focused around the dynamically active $m$-range covering flow type 2, classified as intermediate, which manifests many interesting flow phenomena through the interaction of both inertial and elastic effects.

Fig. 4

Second-order regime: types of flow patterns and ranges of $m$-parameter

Within the parametric variation of flow type 2 (intermediate), the numerical solution may display rich and varying forms of flow patterns, according to precise parameter selection. For instance in the second-order regime, a secondary flow region bounding the rotating sphere, as demonstrated by Thomas and Walters (1964), is produced when $m$ lies inside the interval $1 / 12 < m < 1 / 4$. In Garduño et al. (2015) for Oldroyd-B solutions, the concept of shifting, outside the second-order regime flow was addressed. Such a study demonstrated more general flow solutions in transitional and general flow settings beyond those of perturbation-analysis. In accordance with the solutions provided, for relatively low values of $m$ ($0.08 < m < 0.16$), the scenario arises where two vortices (polar and equatorial) co-exist in the flow field, close to the sphere. Here and below, we focus entirely on the general flow scenario for further exploration.

As such and to this point, a number of independent parameters are known to influence vortex structure and arrangement. Hence, it is necessary to adopt a suitable reference state against which to take comparisons. For example, in order to test the independent influences of $\alpha$-increase and $\varOmega$-increase on flow structure and patterns, and to observe the respective changes thus initiated, a specific $m$-setting must be chosen that manifests well-defined vortices. Essentially, this provides a cross-check on the influence over the in-plane and out-of-plane velocity scaling used. For this purpose, $m=0.14$ is selected as the base reference, since it represents the double vortex-pattern ($P$, $E1$), from which the birth, growth and influence of vortex ($E2$) may be traced. In Fig. 5, the respective vortex identification scheme is represented: with the dominant upper polar vortex ($P$, in green), the emerging lower equatorial vortex ($E1$, in yellow), and lastly, the twin equatorial vortex ($E2$, in blue).

Fig. 5

Flow field position and classification of vortex patterns

4.2 Solvent fraction ($\beta$) effects and $N_{2}$ patterns: base-case $\{m=0.14, \alpha_{\mathrm{base}\text{-}\mathrm{ref}}, \varOmega_{\mathrm{sphere}}\}$

At the outset and across each model solution, one finds that Oldroyd-B, FENE-CR and LPTT produce visually identical results at each solvent fraction level (high or low), for the base-case $\{m=0.14, \alpha _{\mathrm{base}\text{-}\mathrm{ref}}, \varOmega_{\mathrm{sphere}}\}$. Hence, and unambiguously below, only flow patterns for the LPTT instance are provided.

As such in streamlines of Fig. 6, the LPTT high-solvent solution (rhs) is compared against its high-solute counterpart (lhs). For the high-solute case, the polar vortex suffers considerable constriction towards the polar axis (horizontally, by about one half times), in contrast to its high-solvent counterpart. Similarly and in the equatorial zone, the high-solute equatorial vortex is distorted away from that of the high-solvent vortex (more circular): this high-solute equatorial vortex shows a tendency to be both elongated vertically (widening), whilst being dragged further around the sphere surface in a clockwise direction (lhs-upper quartile), acquiring a slightly more elliptical shape.

Fig. 6

Second normal stress-difference, LPTT solutions; high-solute ($\beta=1/9$) and high-solvent ($\beta=0.9$); base case $\{m=0.14, \alpha_{\mathrm{base}\text{-}\mathrm{ref}}, \varOmega_{\mathrm{sphere}}\}$

Larger values of second normal stress-difference (colour background contours) are attendant for the high-solute case ($\beta=1/9$, Fig. 6, left), conspicuous in the region close to the equator and travelling away from the sphere. Negative values are predominately found around the line through the centre of the equatorial vortex linking up with the sphere-equator intersection. Regarding the high-solvent case ($\beta=0.9$, Fig. 6, right), the larger field $N_{2}$ values are found around the equatorial axis, close to the sphere; and also, over the small polar region over the sphere. These $N_{2}$ ($\beta=0.9$) values are an order of magnitude smaller than under $N_{2}$ ($\beta=1/9$). In Fig. 6, a common contour scale for comparison is employed, based on the range of values for the high-solute case.

4.3 Sphere speed effects {$\varOmega$-increase}

For this comparison, out-of-plane velocity scaling was assessed, through angular velocity increase in the range of $\varOmega_{\mathrm{sphere}} \le\varOmega \le 5\varOmega_{\mathrm{sphere}}$ (implemented through the boundary conditions Eq. (10)), as can be gathered from Fig. 7. Noticeably, a suppressive effect is observed over both polar and equatorial vortices as rotational speed increases, regardless of solvent ratio.

Fig. 7

Flow patterns: out-of-plane velocity ($\varOmega_{\mathrm{sphere}}$) scaling, LPTT $\{m=0.14, \beta=0.9, \mathit{Wi} = 0.021\}$; two different solvent ratio fractions

On close inspection and first for the particular case of high-solvent, though the increments in angular velocity ($\varOmega$) affect the development of both vortices, a diminishing effect is mainly evident over the polar vortex, being less prominent over the equatorial vortex. Ultimately, the polar vortex is constricted so much, that finally it practically disappears.

In the highly-polymeric case, the polar vortex is initially smaller (more compressed towards the polar axis) than in the high-solvent case. So then, the polar vortex completely disappears, at even earlier stages of $\varOmega$-development than apparent with high-solvent solutions. Likewise with $\varOmega$-rise, the highly-polymeric equatorial vortex decreases in overall size, and its shape becomes more deformed close to the sphere-equator intersection.

4.4 Material velocity scaling: {$\alpha$-increase}

Trends over the scaling of the in-plane viscous material velocity scale ($\alpha$) are presented in Fig. 8 with the following considerations. In general terms, in-plane velocity ($\alpha$) scaling is implemented through the boundary conditions Eq. (9) and has impact over the entire flow field. This has a major enhancing influence on the polar vortex, in particular. As a consequence and for the high-solvent case, the polar-vortex becomes much broader as $\alpha$ is elevated from unity through to three, then ten. The polar-vortex practically doubles its width from the polar axis with each such $\alpha$-increment. This widening effect, over the main polar-viscoelastic vortex, also provokes the equatorial vortex. The equatorial vortex becomes more elliptical, grows and shifts closer towards the polar vortex. Finally, these two vortices collide and begin to merge together, with two central vortex-eyes being apparent at $10\alpha_{\mathrm{base}\text{-}\mathrm{ref}}$. Here, with further $\alpha$ increment, the trend is for the polar vortex to gradually grow and dominate, whilst the equatorial vortex gradually declines ($10\alpha_{\mathrm{base}\text{-}\mathrm{ref}} \le\alpha\le50\alpha _{\mathrm{base}\text{-}\mathrm{ref}}$). This intermediate development state occurs prior to the formation of a single solitary secondary flow region (observed at or around, $100\alpha_{\mathrm{base}\text{-}\mathrm{ref}}$). Such a single zone then encloses the rotating sphere quartile-surface in its entirety.

Fig. 8

Flow patterns: in-plane velocity $\alpha_{\mathrm{base}\text{-}\mathrm{ref}}$-scaling, LPTT $\{m=0.14, \beta=0.9, \mathit{Wi} = 0.021\}$; two different solvent ratio fractions: (a) $\alpha_{\mathrm{base}\text{-}\mathrm{ref}} \le\alpha\le 10\alpha_{\mathrm{base}\text{-}\mathrm{ref}}$, (b) $50\alpha_{\mathrm{base}\text{-}\mathrm{ref}} \le\alpha\le 100\alpha_{\mathrm{base}\text{-}\mathrm{ref}}$

For the high-solute counterpart and for the same levels of $\alpha$-scaling and increments, the polar-vortex is observed again to widen with $\alpha$-elevation, but now with less than half the width increases observed for the high-solvent case, discussed above. For $\alpha\le10\alpha_{\mathrm{base}\text{-}\mathrm{ref}}$, these width increases prove insufficient away from the polar axis, to cause disturbance to the counterpart evolving equatorial-vortex structure. Thus, for this $\alpha$-parameter range, there is no polar-equatorial vortex interaction to report (no early vortex merging, as with high-solvent); this is observed to be delayed to around $100\alpha_{\mathrm{base}\text{-}\mathrm{ref}}$. Pursuing this line of attack with further increment in $\alpha$-value, the equatorial vortex is seen to recede by $200\alpha_{\mathrm{base}\text{-}\mathrm{ref}}$; eventually forming the single vortex structure at ${\sim}500\alpha_{\mathrm{base}\text{-}\mathrm{ref}}$, somewhat later than for the high-solvent instance above.

4.5 Various classes of solution structure—alternative vortex patterns

At this stage, it is useful to summarise findings thus far on vortex structure and patterns. Through the analysis of different stimuli applied over the base-case, it is possible to identify various flow classes; each of which is stimulated by the blend of different factors. A more detailed description of the different solution sets is exposed in Table 1, alongside a representative image for each particular flow class $A$ and $B$ in Fig. 9 (see Appendix also for classes $C$ and $D$).

Fig. 9

Vortex-class obtained through the combination of different stimulus, $\mathit{Wi} = 0.021$, $1000 \alpha_{\mathrm{base}\text{-}\mathrm{ref}}$

Table 1 Flow class and respective stimuli

Class $A$ corresponds to the situation when a secondary flow cell completely encloses the sphere, as in our previous paper in the subject, Garduño et al. (2015). Here, the secondary flow cell Oldroyd-B solutions within the second-order regime are symmetrical; in further alternative regimes, the extracted solutions provide an asymmetrical cell shape. In this work, for this class of flow solutions, the generated cell is asymmetric due to external flow influence. These kinds of solutions can be reached via two parametric directions: one with $m \geq0.16$; or another, as demonstrated above by promoting the $\alpha$-parameter. With the quest to match the Giesekus experiments (Fig. 1) in mind, now the particular case of $1000\alpha_{\mathrm{base}\text{-}\mathrm{ref}}$ becomes the newly refreshed base-case for subsequent comparison.

Class $B$ of flow pattern is promoted via the angular velocity ($\varOmega$) and in-plane velocity-scaling factor ($\alpha$), and is represented by two vortices over the field. One vortex emerges in the equatorial region ($E1$) of the sphere, whilst a major vortex is over the polar region ($P$). It is important to highlight here that the equatorial vortex indicates an anticlockwise rotation, while the main polar vortex rotates in a clockwise direction (front-view perspective, rhs upper quartile of sphere). Around 60° from vertical, it is noticeable that a constriction exists over the secondary flow cell, which promotes the evolution of the anticlockwise vortex and the subsequent appearance of a third vortex over the equator ($E2$).

As has been demonstrated, the role of the variation for the parameters (particularly $\alpha$ and $\varOmega$) expose different solutions. With this in mind, it is necessary to opt for a single base-case in order to capture the significant and elusive vortex structure described in the Giesekus (1970) experimental results. From this stage onwards, the $\alpha$-parameter level of interest switches to $O(10^{3})$. Therefore, the parameter of interest becomes the angular velocity $\varOmega$.

4.6 Flow patterns and vortices: large-$\alpha$, FENE-CR and LPTT, shear-thinning

High-solvent

In both models, FENE-CR (Fig. 10(a)) and LPTT (Fig. 10(b)) high-solvent ($\beta=0.9$) solutions; the first equatorial-zone vortex ($E1$) has anticlockwise rotational orientation, and appears over the sphere surface (lower portion of the quartile). Then, as the rotational speed increases, a pinching effect arises in the lower extremities of the main polar-vortex ($P$). This pinching effect gradually becomes so significant that it is responsible for the birth of a further unique second equatorial-zone vortex ($E2$), now of clockwise rotation, opposite to that of vortex ($E1$). This vortex ($E2$) is located further away from the sphere than vortex ($E1$), lying above the equator, yet still within the equatorial region.

Fig. 10

(a) Development of equatorial vortices, ($\beta=0.9$) solutions, FENE-CR $\{m=0.14, \mathit{Wi} = 0.021, 1000 \alpha_{\mathrm{base}\text{-}\mathrm{ref}}\}$. (b) Development of equatorial vortices, ($\beta=0.9$) solutions, LPTT $\{m=0.14, \mathit{Wi} = 0.021, 1000 \alpha_{\mathrm{base}\text{-}\mathrm{ref}}\}$

Across model comparison and as $\varOmega$ increases, the vortex ($E1$) is more developed for FENE-CR than for LPTT solutions. The stronger flow produced by the polar-vortex (clockwise direction) is itself responsible for driving the first equatorial-zone vortex ($E1$) in an anticlockwise direction. Within FENE-CR solutions and between sphere speeds of $8.2\varOmega_{\mathrm{sphere}}$ and $8.3\varOmega_{\mathrm{sphere}}$, the pinching effect from the polar-vortex is now sufficiently large to stimulate the appearance of the second equatorial-vortex (third vortex, $E2$).

In contrast to FENE-CR findings, the LPTT solution is more sensitive to the rotational speed increase. The shear-thinning influences that are introduced in this phase of $\varOmega$-increase are apparently through the lack of significant size change (delay in development) of the first equatorial-vortex ($E1$), as well as the earlier development of the additional second equatorial-vortex ($E2$) (third vortex, around $7.8\varOmega_{\mathrm{sphere}}$) and the association of this third vortex appearance with the polar-vortex pinching. Hence, this scenario of third vortex appearance occurs at earlier stages in $\varOmega$-increase with shear-thinning LPTT solutions, when compared against constant-viscosity FENE-CR solutions.

Looking at both FENE-CR and LPTT model solutions in greater detail, and to their respective final stages for sphere-speed $8.5\varOmega_{\mathrm{sphere}}$, it is noted that the third vortex ($E2$) has comparable size in both predictions. Conspicuously, the third vortex ($E2$) under LPTT solution has a more rounded-shape than that for FENE-CR, which appears more triangular. Regarding the characteristics of vortex ($E1$) for FENE-CR, it is about one-third larger than that for LPTT, both in size and intensity. The LPTT vortex ($E1$) at $8.5\varOmega_{\mathrm{sphere}}$, would appear to be more comparable to that of FENE-CR at $8.2\varOmega_{\mathrm{sphere}}$. Evidently, this is a localised shear-thinning effect (and would require still further speed stimulus in the LPTT instance to match the $E1$-vortex size of the FENE-CR ($8.5\varOmega_{\mathrm{sphere}}$) with better matching to Giesekus results).

As a counterpart to these high-solvent vortex solutions, for both models, second normal stress-difference fields ($N_{2}$) (Fig. 11) also reflect some interesting findings. Here, there are practically no substantial differences noted about the polar vortex and zone in $N_{2}$; whilst there are substantial differences in the equatorial zone. The region occupied by the first equatorial-vortex ($E1$) shows also a growing spatial occupation of larger $N_{2}$-values as rotational speed increases. Significantly, such $E1$-vortex trends are more exaggerated in the FENE-CR case above the shear-thinning LPTT case. Comparably, the second equatorial-vortex ($E2$) region is rather insensitive to such changes, and with respect to quantification of $N_{2}$-influence. Interestingly, when non-zero $\xi_{\mathrm{LPTT}}$-parameter values are attempted with LPTT ($0 \le \xi_{\mathrm{LPTT}} \le0.2$), this has inconsequential impact on these $N_{2}$-fields.

Fig. 11

Contours of $N_{2}$, FENE-CR and LPTT; high-solvent ($\beta=0.9$); $\{m=0.14, \mathit{Wi} = 0.021, 1000 \alpha_{\mathrm{base}\text{-}\mathrm{ref}}, \varOmega\mbox{ variable}\}$

High-solute

Figure 12 includes the corresponding vortex flow patterns for LPTT ($\beta=1/9$), with high-solute fraction. Here, the more dominant polymeric content completely dictates a common flow structure at this level of rotational speed. So, the rich equatorial vortex evolution of the high-solvent instance is now completely suppressed, leaving only a vestige equatorial-axis thin vortex. The polar vortex remains substantial and undisturbed, so that this does not show any indications of widening away from the polar axis either. For this particular instance, $N_{2}$ fields are invariant and are therefore not shown.

Fig. 12

Development of equatorial vortices, ($\beta=1/9$) solutions, LPTT $\{m=0.14, \mathit{Wi} = 0.021, 1000 \alpha_{\mathrm{base}\text{-}\mathrm{ref}}\}$

4.7 Second normal stress-difference

Thomas and Walters (1964) proposed the material parameter $m$ (Eq. (11)), which can be used to estimate $N_{2}$ theoretical values using the corresponding $N_{1}$ values (experimentally, Manero and Mena (1978), or theoretically, assuming steady simple shear flow). In this manner, $N_{1}$ theoretical values with Oldroyd-B, FENE-CR and LPTT solutions may be used to estimate corresponding $N_{2}$ theoretical values. These values are displayed in Fig. 13, where $N_{1}$ is depicted with solid-lines and $N_{2}$ by dashed-lines. As discussed above, introducing $\xi_{\mathrm{LPTT}} \ne0$ within the LPTT formulation is plausible to stimulate enhanced $N_{2}$-production.

Fig. 13

Second normal stress-difference ($N_{2}$) values for LPTT ($\xi_{\mathrm{LPTT}} = 0.2$) and from Eq. (11), Thomas and Walters (1964)

Theoretical predictions for $N_{1}$ and $N_{2}$ Oldroyd-B adopt the same quadratic trend, as anticipated. FENE-CR and LPTT at low-$\mathit{Wi}$ both shows good agreement with these Oldroyd-B predictions, but as $\mathit{Wi} \sim1$ is approached there is departure from quadratic response, with the predicted $N_{2}$ values now being greater than those for Oldroyd-B. With LPTT ($\xi_{\mathrm{LPTT}} = 0.2$) solutions, a quadratic trend is realised prior to assuming a capped value around $\mathit{Wi} \sim3$.

Here, one may propose a generalisation to the rotating sphere flow $m$-equation of Thomas and Walters (11). This is achieved in the following fashion. From the $J$-model (see Walters et al. 2009, for the $J$-Model as a generalisation of Oldroyd-B),

$$ N_{1} = \frac{2\eta_{0} ( 1 - \beta )\lambda_{1}\dot{\gamma}^{2}}{1 + J\dot{\gamma}^{2}}. $$

(14)

Then, comparing Eq. (14) with that for the LPTT (or FENE-CR) model, one may recognize the duality of the approximation, $1 + J\dot{\gamma}^{2} \approx f^{2}$.

Taking this into account, it is possible to establish wider applicability than for the Oldroyd-B model alone, to include also LPTT ($\xi_{\mathrm{LPTT}} \ne 0$), FENE-CR and $J$-Models. So then, one may define a generalised $N_{2}$ equation, which essentially involves rescaling $N_{2}$, viz.,

$$ N_{2}^{*} = N_{2}\frac{\alpha_{G}}{1 + J\dot{\gamma}^{n}}. $$

(15)

This form appeals to three fitting parameters of $J$, $n$ and $\alpha_{G}$, variables in choice across flow deformation type (rotating sphere flow and steady simple shear flow) and model selection (LPTT($\xi_{\mathrm{LPTT}} \ne0$), FENE-CR, Oldroyd-B and J-Models).

Accordingly, a generalised $m$-equation can be expressed in the form

$$ m = \frac{\alpha_{G}N_{1} - N_{2}^{*} ( 1 + J\dot{\gamma}^{n} )}{2\rho a^{2}\dot{\gamma}^{2}\alpha_{G}}, $$

(16)

from which a corresponding generalised form for $N_{2}$ may also be extracted:

$$ N_{2}^{*} = \bigl( N_{1} - 2m\rho a^{2}\dot{\gamma}^{2} \bigr) \biggl( \frac{\alpha_{G}}{1 + J\dot{\gamma}^{n}} \biggr). $$

(17)

Hence, and for the present purpose of comparison against Eq. (11) evaluation (as of Thomas and Walters), it is necessary to use parameter sets as listed in Table 2. Firstly (see Fig. 14(a)), the new formulated Eq. (17) for the studied models is compared against Oldroyd-B $N_{2}$-theoretical values. Following Fig. 14(b), this new $N_{2}^{*}$-equation is fitted to the LPTT ($\xi_{\mathrm{LPTT}} = 0.2$) theory.

Fig. 14

Second normal stress-difference ($N_{2}$) values with generalised $N_{2}$-equation

Table 2 Model parameter values

Concerning the comparison between these numerical predictions against theory, two alternative sample-point positions over the surface of the sphere have been selected. One sample-point is located at the equatorial axis, $\pi/2$ from the vertical polar axis, and other is taken at $\pi /4$.

With $\{J = 1, n = 1, \alpha_{G} = \xi\}$ $N_{2}$-theoretic data gathered in this manner, whilst using this newly-formulated $m$-equation for LPTT ($\xi_{\mathrm{LPTT}} = 0.2$), agree more closely with the $\pi/4$ sample-point simulated predictions for LPTT ($\xi_{\mathrm{LPTT}} = 0.2$) than with the original $m$-equation theory. This realises a slight shift in fitting predictions against $m$-equation theory, from a match to Oldroyd-B theory to that of the more generalised LPTT ($\xi_{\mathrm{LPTT}} = 0.2$) theory.

Now, considering the usual scaling ($- N_{2} / \eta_{0}\varOmega$), this may be adjusted by the same factor introduced in the generalized $m$-equation

$$ - \frac{N_{2}}{\eta_{0}\varOmega} \biggl( \frac{\alpha_{G}}{1 + J\dot{\gamma}^{n}} \biggr), $$

(18)

where, for the sake of simplicity, one defines $\kappa= \alpha_{G} / ( \eta_{0}\varOmega ( 1 + J\dot{\gamma}^{n} ) )$.

In Fig. 15, the numerical solutions extracted at $\pi/4$ sample-point for FENE-CR reveal quadratic form, which closely follows the theoretical computation. It should be noted here that only LPTT ($\xi_{\mathrm{LPTT}} = 0.2$) solutions are presented amongst those available for LPTT. The data extracted at $\pi/2$ sample-point (not shown) is rather less reliable than that sampled at $\pi/4$. This data is strongly influenced by axial effects and shows significant departure from the theory, whilst at the same time, not showing major differences in $N_{2}$-values for the alternative fluid models.

Fig. 15

Second normal stress-difference against $\mathit{Wi}$, theoretical (dashed) vs numerical (symbols) values, $\beta=0.9$

4.8 Torque calculation

The torque is defined as the force to maintain the steady rotation of a sphere of radius ($a$), with an angular velocity ($\varOmega$), a fluid of viscosity $\eta_{0}$ and density $\rho$. This force can be expressed around the base Stokesian approximation that leads towards other expansions, defined as follows:

$$ \textstyle\begin{array}{l@{\quad }l@{\quad }l} \mbox{Stokes} & \mbox{(a)} & T_{s} = 8\pi a^{3}\varOmega\eta_{0}, \\ \mbox{Mena et~al. (1972)} & \mbox{(b)} & T_{m} = 8\pi a^{3}\varOmega \eta_{0} \biggl[ 1 + \frac{\frac{\mathit{Re}^{2}}{1200}}{1 + \frac {\mathit{Re}^{2}}{1200} ( 1.086 ) + O ( \mathit{Re} )^{6}} \biggr], \\ \mbox{Thomas and Walters (1964)} & \mbox{(c)} & T_{tw} = 8\pi a^{3}\varOmega \eta_{0} \biggl[ 1 + \mathit{Re}^{2} \biggl( \frac{1}{1200} + \frac{m}{140} - \frac{2m^{2}}{15} \biggr) \biggr]. \end{array} $$

(19)

Appealing to the expression for the force over the surface of the sphere $F_{w}$ as (see Tamaddon-Jahromi et al. 2011),

$$ F_{w} = 2\pi a^{2}\int_{0}^{\pi} \bigl\{ T_{rz}\sin\theta+ ( T_{zz} - p )\cos\theta \bigr\} \sin\theta \,d\theta, $$

(20)

then, the torque for an Oldroyd-B fluid may be represented as a function of the $m$-parameter (see Garduño et al. 2015), using the respective equation for the force over the surface of the sphere expressed in (20). This realises the following expression for the torque:

$$T_{\mathrm{OB}} = 8\pi a^{3}\varOmega\eta_{0} [ 1 + F_{w} ], $$

with its relative non-dimensional form represented by

$$ T_{\mathrm{OB}}\lambda_{1} ( 1 - \beta )/ \bigl[ 8\pi a^{5}\eta _{0}\varOmega \bigr] = m [ 1 + F_{w} ]. $$

(21)

The respective torque calculation can be performed through the angular velocity ($\varOmega$), material velocity scale ($\alpha= \nu/ a$), which produces an expression defined in terms of Reynolds number (see Eq. (13) above).

Additionally, the in-plane velocity-scaling factor may be introduced to obtain the unscaled-value of the drag-force over the surface of the sphere, as follows:

$$T_{w} = 8\pi a^{3}\varOmega\eta_{0} \biggl[ 1 + \frac{F_{w}}{\alpha} \biggr], $$

which under scaling and non-dimensionalization yields:

$$ \frac{T_{w}\rho}{8\pi a\eta_{0}^{2}} = \mathit{Re} \biggl[ 1 + \frac{F_{w}}{\alpha} \biggr]. $$

(22)

Accordingly, the non-dimensional torque computations are presented in Fig. 16, at low Reynolds number. Here, the theoretical equations are scaled by $\rho/ ( 8\pi a\eta_{0}^{2} )$, as established over the rhs-axis. The theoretical expressions of Stokes, Thomas and Walters (1964) and Mena et al. (1972) show a consistent linearly increasing trend as they are plotted against $\mathit{Re}$. In our previous paper (Garduño et al. 2015), whilst following the same scaling procedure as in the theoretical expressions, the Oldroyd-B numerical torque solutions were shown plotted as a function of $m$-parameter, with the lhs-axis torque scaled by $\lambda_{1} ( 1 - \beta ) / ( 8\pi\rho a^{5}\varOmega )$. Concerning those solutions, it was appreciable that, at the upper limits of $m$-parameter, there was a slight tendency towards upward departure, whilst at lower values, preserving the linear trend.

Fig. 16

Torque for different theoretical equations (Stokes, Mena et al. 1972; Thomas and Walters 1964) and FENE-CR, LPTT solutions against $\mathit{Re}$, and Oldroyd-B solutions (Garduño et al. 2015) compared against $m$-parameter

In order to detect possible departure from the Stokes torque-value, the respective numerical torque solutions for FENE-CR and LPTT are scaled in the same fashion as theoretical expressions, i.e. using $\rho/ ( 8\pi a\eta_{0}^{2} )$. Adopting such practice, the torque numerical solutions are obtained within the angular velocity range of $\{7.5\varOmega_{\mathrm{sphere}}, 8.5\varOmega_{\mathrm{sphere}}\}$, reflecting a linear trend as $\mathit{Re}$ increases for both model solutions, with little to no departure noted from the Stokes value.

5 Best matching: numerical predictions versus Giesekus experimental findings

First, within Fig. 17, in the rhs image with respect to the polar axis, the FENE-CR $\{m=0.14, 8.2\varOmega_{\mathrm{sphere}}\}$ solution is overlaid on the background Giesekus field pattern. For clarity, the lhs image with respect to the polar axis, displays only the Giesekus field pattern. This match well captures the strong clockwise polar-viscoelastic vortex ($P$) in the rhs image. The prediction vortex centre is shifted slightly to the left of experimental vortex centre, and therefore slightly squeezed up from the full Giesekus (darker) zone occupied in the background. The counterpart equatorial vortex ($E1$) practically fills the Giesekus inner-inertial zone, now assuming anticlockwise rotation. This region is representative of positive values of $N_{2}$, opposed to the zone outside. This equatorial vortex ($E1$) feature emerges because of constriction from the bottom-tail-end of the polar vortex.

Fig. 17

Giesekus experimental evidence versus FENE-CR $\{m=0.14, \mathit{Wi} = 0.021, 8.2 \varOmega_{\mathrm{sphere}}\}$ solution; includes three different Giesekus (1970) zones

In contrast to the foregoing FENE-CR $\{m=0.14, 8.2\varOmega_{\mathrm{sphere}}\}$ solution, the corresponding LPTT $\{m=0.14, 7.6\varOmega_{\mathrm{sphere}}\}$ solution is quite similar in overall flow pattern and structure, but noting that both polar and equatorial vortices are now slightly more reduced against the background Giesekus flow patterns. So, they are less space occupying, due in part to the additional shear-thinning response of the LPTT prediction, as shown in Fig. 18.

Fig. 18

Giesekus experimental evidence versus LPTT $\{m=0.14, \mathit{Wi} = 0.021, 7.6 \varOmega_{\mathrm{sphere}}\}$ solution; includes three different Giesekus (1970) zones

6 Conclusions

This study has addressed viscoelastic numerical predictions for the rotating sphere problem, comparing and contrasting FENE-CR and LPTT model solutions. For the base-case setting $\{m=0.14, \alpha_{\mathrm{base}\text{-}\mathrm{ref}}, \varOmega_{\mathrm{sphere}}\}$ there are no significant differences observed between FENE-CR and LPTT solutions. Beyond this base-case, further parameter variations, that expose significant differences in model predictions, have been investigated. This has aided in recognition of rheological impact, as through shear-thinning effects, and via inertial effects (sphere speed). For $\alpha$-increments (in-plane velocity scaling), a widening effect over the polar-vortex is observed for the high-solvent case. For the high-solute case, the polar-vortex is observed to widen with $\alpha$-elevation, but by less than half the width observed for the high-solvent case.

Solutions for large-$\alpha$ agree well with the Giesekus experimental main flow field. For these kinds of solution, an emerging equatorial vortex is found in the specific range of $\{7.5\varOmega_{\mathrm{sphere}}, 8.5\varOmega_{\mathrm{sphere}}\}$, where this vortex has an anticlockwise flow-direction. Finally, the key objective of the research has been reached; in that best-case matching scenarios are gathered between experimental Giesekus vortex patterns and current numerical predictions. With respect to the FENE-CR $\{m=0.14, 8.2\varOmega_{\mathrm{sphere}}\}$ solution, this has captured the strong clockwise polar-viscoelastic vortex ($P$). Then, the equatorial vortex ($E1$) almost fills the Giesekus inner-inertial zone, assuming anticlockwise rotation. Inside the emerging equatorial vortex is found a highly rich positive $N_{2}$-region compared against the negative $N_{2}$-enveloping layer that surrounds the rotating sphere. This also indicates the significance of second normal stress-difference effects over the development of these various flow structures. With the corresponding shear-thinning LPTT $\{m=0.14, 7.6\varOmega_{\mathrm{sphere}}\}$ solution, both polar and equatorial vortices are now slightly more reduced, compared against the counterpart FENE-CR solutions. They are less space occupying, as a consequence of the additional shear-thinning response in the LPTT solutions.

Appendix: Radius of secondary flow cell {polar-L \(k_{\mathit{pl}}\), equator-L \(k_{\mathit{eq}}\) scaling}

The theory for the second-order regime predicts the emergence of a secondary flow cell covering the entire rotating sphere (Thomas and Walters 1964) over the range of $1 / 12 < m < 1 / 4$. The radius of such cell (also, flow-axis anchor-point) is estimated as:

$$ r_{1}^{*} = \frac{8m}{1 - 4m}. $$

(A.1)

In order to explore variation in the flow patterns, a length-scale ($k$) can be introduced over the axes (adjustment of the sphere from spherical to elliptical form), so that the vortex anchor points on the individual equator and polar axes can be adjusted, affecting the radius of the secondary flow cell. The introduction of a denominator scaling $k$-parameter (identified on each axis separately, ‘$\mathit{eq}$’ for equator and ‘$\mathit{pl}$’ for polar) modifies Eq. (A.1) as:

$$ r_{\mathit{eq}}^{*} = \frac{8m}{ ( 1 - 4m )k_{\mathit{eq}}},\qquad r_{\mathit{pl}}^{*} = \frac{8m}{ ( 1 - 4m )k_{\mathit{pl}}}. $$

(A.2)

This consideration also amends the form for the first velocity component ($U^{\rho}$) in Eq. (9) above as

$$ U^{\rho} = \frac{\nu}{a}u_{1}^{\rho} = \frac{\nu}{a}\frac{ ( r_{1} - 1 )^{2}}{8r_{1}^{5}} \bigl[ ( 1 - 4m )kr_{1} - 8m \bigr] \bigl( 3\sin^{2}\theta- 2 \bigr). $$

(A.3)

Figure 19 shows the variation of this sphere-geometric parameter $k$ over the respective axis (equatorial or polar). The case when $k = 1$ is the base and standard case (perfect sphere). Then, for any particular axis, if $k < 1$, the vortex anchor point is located further away from the sphere centre; whilst, if $k > 1$, the anchor point is located closer to the sphere, producing a diminishing effect over the general vortex structure.

Fig. 19

Flow patterns: equatorial and polar vortices; variation in elliptical $k$-parameter, LPTT $m=0.14$, $\mathit{Wi} = 0.021$

In addition to information exposed in Sect. 4.5 above, two further classes of flows may be identified in Fig. 20, class $C$ and $D$, under $k$-parameter adjustment, which demonstrate equatorial vortex pinching with shift towards the sphere. A diminishing ($k_{\mathit{eq}} > 1$), or amplifying effect ($k_{\mathit{eq}} < 1$), over the vortex structure can be obtained according to the specific value of the sphere-geometric scaling factor ($k$) chosen.

Fig. 20

Vortex-classes $C\{1000 \alpha_{\mathrm{base}\text{-}\mathrm{ref}}, k_{\mathit{eq}} = 1.6, \mathit{Wi} = 0.021\}$ and $D\{400 \alpha_{\mathrm{base}\text{-}\mathrm{ref}}, k_{\mathit{eq}} = 1.7, \mathit{Wi} = 0.021\}$, obtained through the combination of different stimuli

Class C flow pattern presents three vortices in the flow field, with a major vortex over the polar region ($P$), an equatorial vortex ($E1$), itself lying over a third vortex that emerges from the equatorial axis ($E2$). This particular solution pattern is obtained through the manipulation of the $k_{\mathit{eq}}$-factor that is positioned close to the sphere in order to obtain a more constricted secondary flow cell. Accordingly, the main polar vortex ($P$) and $E2$ are rotating in a clockwise direction, whilst driving $E1$ towards its anticlockwise rotation.

Class D flow pattern is characterized through the presence of two vortices in the flow field, a main polar vortex ($P$) and an emerging equatorial vortex ($E2$), now both moving in a clockwise direction. Again, this instance is obtained through the manipulation of the $k_{\mathit{eq}}$-factor that is positioned close to the sphere in order to obtain a more constricted secondary flow cell. In Fig. 20 and for this particular instance, it is appreciable how the secondary flow cell outer perimeter moves below the polar vortex, pinching inwards towards the sphere surface, to finally curtail interaction between both vortices. The secondary flow cell constriction is located around ∼70° and produces a more spherical polar vortex.