1 Introduction

Polymers are often described as viscoelastic bodies, which are shown by stress relaxation and creep deformation at the macroscopic scale when they are subjected to mechanical stimuli. Based on their macroscopic response, viscoelastic materials can be classified as solid-like and fluid-like (see Wineman and Rajagopal 2001; Christensen 2002). In a viscoelastic solid-like behavior, the bodies should exhibit instantaneous (elastic) response and some delayed (time-dependent) response, and upon removal of the mechanical stimuli the materials are expected to recover their original shapes. The creep deformation and stress relaxation in viscoelastic solid-like bodies will reach asymptotic nonzero values.

Several experimental studies on creep–recovery behaviors of polymers (Findley and co-authors 1954, 1962, 1970; Lai and Bakker 1995; Chailleux and Davis 2003, 2005) have shown that under relatively low stress levels and short duration of loading (several hours to thousands of hours), polymers creep and reach steady values, and experience fully recovery; while higher stress levels lead to permanent deformations. Loading–unloading under strain control tests on polymers also showed that higher strain amplitude results in pronounced permanent deformations (Drozdov 2011; Tscharnuter et al. 2012). Another experimental observation showed failure in polymeric specimens under creep testing (Raghavan and Meshii 1997; Regrain et al. 2009; Drozdov 2010; Tajima and Itoh 2010; Melo and de Medeiros 2014). Up to failure, the polymers typically experience primary, secondary, and tertiary stages of creep deformations. The rate of creep deformation in the primary stage decreases with time, followed by a nearly constant rate in the secondary stage, and the creep rate increases with time in the tertiary stage until failure occurs. Higher stresses cause the specimens to fail at shorter time. It is then reasonable to think that before experiencing complete failure, the specimens might undergo several stages of degradation.

In describing the time-dependent behaviors of polymers based on experimental observations of their macroscopic responses, several phenomenological constitutive models have been formulated. Viscoelastic constitutive models are often considered in the literature when the materials experience full recovery upon removal of the mechanical stimuli provided that a sufficient resting time is given, while viscoplastic (or viscoelastic–plastic, elastic–viscoplastic, viscoelastic–viscoplastic) models are typically used for materials that show permanent (residual) deformations upon complete removal of the stimuli. Lai and Bakker (1995), Chailleux and Davis (2003, 2005), Kim and Muliana (2009), Miled et al. (2011), and Tscharnuter et al. (2012) are among the authors who considered viscoelastic–viscoplasticFootnote 1 response of polymers when the polymers exhibit permanent deformations. It is noted that some viscoelastic models, e.g., Maxwell and Burger models, result in permanent deformations upon removal of the prescribed mechanical stimuli, which are used to model viscoelastic fluid or fluid like behaviors (e.g., Pipkin 1986; Christensen 2002, Wineman and Rajagopal 2001). Permanent deformations are also seen after removal of the mechanical stimuli, when the materials experience some degradation during loadings. Several studies have addressed creep failure in polymers, such as Hin and Cherry (1984), Vujosevic and Krajcinovic (1997), Christensen (2004), Regrain et al. (2009), Muliana et al. (2013), etc. Christensen (2004) has associated the creep failure to time-dependent kinetic crack growth in polymers. Vujosevic and Krajcinovic (1997) have considered changes in the microstructural morphologies of the polymers in explaining the macroscopic creep rupture of polymers. Hin and Cherry (1984) and Regrain et al. (2009) used an empirical approach in order to describe creep failure in polymers. Empirical models typically require different material parameters to fit the experimental data for different loading conditions, while the microstructural models often contain a large number of parameters. It might be necessary to conduct a series of experimental tests under various loading histories in order to better understand the performance of the polymers and classify them into certain categories before developing constitutive models that describe the responses of the polymers.

Macroscopic response of polymers depends strongly on their microstructural morphologies and movement of the macromolecular structures. Ferry (1961) has discussed that the shapes of the macroscopic viscoelastic response of polymers are correlated to certain types of molecular motions, such as rearrangements of the chain backbone, entanglement, bending and stretching of the chemical bonds, breaking and reforming of the bonds (scissions), etc. The molecular motions depend also on the rate and duration of loadings, which affect the macroscopic response of polymers. Ferry also mentioned that the time-dependent properties of polymers can be directly associated to their chemical properties, such as molecular weight, cross-linking, and branching. The relationships between viscosity, molecular weight, and temperature have also been addressed by Fox and Flory (1948). The deformation of semi-crystalline polymers is governed by the interaction of the amorphous regions and the crystalline structures. Above the glass transition temperature, the initial deformation occurs on the amorphous regions. As the strain increases, crystalline deformation mechanisms are activated that eventually lead to crystallographic slips and the fragmentation of lamellae. For a comprehensive overview of the research on deformation mechanisms the reader is referred to the review by Pawlak et al. (2014).

It is no doubt that integrating the macromolecular changes to the macroscopic response of polymers will give us a comprehensive understanding on the performance of polymers and help in formulating rigorous constitutive models. Despite some limitations in the phenomenological models in capturing detailed physical mechanisms that describe the viscoelastic response of polymers, properly developed phenomenological models can give sensible prediction of the response of polymers, which are useful for designing devices or structures made of polymers.

In this study, our aim is to formulate a phenomenological constitutive model for viscoelastic solid-like materials undergoing degradation with regards to their mechanical properties. In this study, degradation in the materials is associated to secondary and tertiary stages of creep during loading. When the degradation occurs during loading, upon unloading we often observe some permanent deformation. The motivation of this study is based on experimental observations of the macroscopic response of polymers due to quasi-static loading at different constant rates, creep at different stresses and durations, and relaxation under different strains. It is assumed that the polymers are isotropic and remain isotropic during the deformations. The model is derived for linearized strain measures that incorporates different time-dependent and nonlinear responses for the two independent components in isotropic bodies. An additive decomposition between the recoverable and irrecoverable strains is considered. The model can be easily reduced to one-dimensional viscoelastic-degradation behaviors. In absence of degradation and time-dependent effect, the model reduces to nonlinear elastic behavior, and eventually can be reduced to linearized elastic response. Experimental tests on polypropylene reported by Drozdov (2010) are used to study the one-dimensional behavior. Uniaxial tensile tests on polyoxymethylene (POM) under various loading histories are conducted, and the corresponding axial and transverse responses are recorded and used to examine the three-dimensional response of the model. A discussion on material parameter characterizations for multi-axial deformations of isotropic bodies are also presented, which indicates the need of two time-dependent material parameters in capturing responses of POM. The manuscript is organized as follows. Section 2 presents general formulations of the constitutive model. Section 3 discusses one-dimensional response of the model and material characterization, followed by the multi-axial response in Sect. 4. Section 5 is dedicated to concluding remarks.

2 Constitutive model

This section starts with a brief discussion of linearized strains, followed by formulation of the constitutive relations. Let us consider a solid body with a stress-free reference configuration.Footnote 2 The position of a particle in the reference configuration is denoted by \(\mathbf{X}\), and the motion of a particle in the body is given by \(\mathbf{x} = \boldsymbol{\chi} ( \mathbf{X},t )\). The displacement \(\mathbf{u}\) is then defined by

$$ \mathbf{u} = \mathbf{x} - \mathbf{X}. $$
(2.1)

In the deformable body, we quantify the change in shape of the body from its reference configuration to the current (deformed) configuration by a strain measure. The strain is measured at the localized region in the body. Different strain measures have been considered (see Freed 2014 for discussion on various strain measures) depending on the practical applications. One of the commonly used strain measures is the Green–St. Venant strain \(\mathbf{E}\),Footnote 3

$$ \mathbf{E} = \frac{1}{2} \biggl( \frac{\partial \mathbf{u}}{\partial \mathbf{X}} + \biggl( \frac{\partial \mathbf{u}}{\partial \mathbf{X}} \biggr)^{T} + \biggl( \frac{\partial \mathbf{u}}{\partial \mathbf{X}} \biggr)^{T}\frac{\partial \mathbf{u}}{\partial \mathbf{X}} \biggr) $$
(2.2)

where \(\frac{\partial \mathbf{u}}{\partial \mathbf{X}}\) is the displacement gradient. When the displacement gradient is small, i.e., \(\max \Vert \frac{\partial \mathbf{u}}{\partial \mathbf{X}} \Vert = 0 ( \delta ), \delta \ll 1\), where \(\Vert . \Vert \) is the trace norm, then the Green–St. Venant strain \(\mathbf{E}\) reduces to the linearized strain \(\boldsymbol{\varepsilon}\),

$$ \boldsymbol{\varepsilon} = \frac{1}{2} \biggl( \frac{\partial \mathbf{u}}{\partial \mathbf{X}} + \biggl( \frac{\partial \mathbf{u}}{\partial \mathbf{X}} \biggr)^{T} \biggr). $$
(2.3)

While it is clearly seen from Eqs. (2.2) and (2.3) that the Green–St. Venant is a more general strain measure that is applicable for any range of strains and displacement gradients, the linearized strain measure that is only applicable for problems involving small deformation gradients is often considered. Figure 1 illustrates an example of creep–recovery deformations, measured by the Green–St. Venant and linearized strains, of POM under a uniaxial tensile stress. Deviations in the two strain measures are easily observed when the strain is larger than 10 %. The percent difference between the two strain measures at the peak value (around 4000 minutes and ∼20 % strain) is less than 10 %. In this study, we consider linearized strain measures due to its simplicity in obtaining the solutions to the viscoelastic-degradation model and, except some of the experimental data, most of the strain data considered in this study are less than 10 %; thus the error in neglecting the higher order term of the displacement gradient is relatively small.

Fig. 1
figure 1

Comparisons between linearized and Green–St. Venant strain measures

Full size image

We formulate a constitutive model for viscoelastic solids undergoing degradation due to mechanical stimuli. Based on the time-dependent macroscopic response of polymers, the polymers can experience primary, secondary, and tertiary stages of deformations prior to failure. We assume that the degradation in polymers occurs when they experience secondary and tertiary stages of deformations, while the primary stage is mainly governed by the viscoelastic response. We also neglect a possible healing in the degrading polymers, so that the deformations associated with the degradation are irrecoverable. The time-dependent strain is additively decomposed into the recoverable \(\boldsymbol{\varepsilon}_{R}(t)\) and irrecoverable \(\boldsymbol{\varepsilon}_{D}(t)\) components:

$$ \boldsymbol{\varepsilon} (t) = \boldsymbol{\varepsilon}_{R}(t) + \boldsymbol{\varepsilon}_{D}(t). $$
(2.4)

In Eq. (2.4) the linearized strain is expressed in terms of stresses and time. The recoverable strain component is associated with the viscoelastic response of the body. We adopt the quasi-linear viscoelastic (QLV) model, proposed by Fung (1981),Footnote 4 for the defining the recoverable linearized strain component as a function of the Cauchy stress \(\boldsymbol{\sigma}\):

$$\begin{aligned} \boldsymbol{\varepsilon}_{R}(t) &= \int_{0^{ -}}^{t} \mathbf{D}(t - s)\,d\mathbf{F}^{\mathrm{el}}\bigl(\boldsymbol{\sigma} (s)\bigr) = \int_{0^{ -}}^{t} \mathbf{D}(t - s)\frac{\partial \mathbf{F}^{\mathrm{el}}(\boldsymbol{\sigma} (s))}{\partial \boldsymbol{\sigma}} \frac{d\boldsymbol{\sigma}}{ds}\,ds \\ &= \mathbf{F}^{\mathrm{el}}\bigl(\boldsymbol{\sigma} (0)\bigr)\mathbf{D}(t) + \int_{0^{ +}}^{t} \mathbf{D}(t - s)\frac{\partial \mathbf{F}^{\mathrm{el}}(\boldsymbol{\sigma} (s))}{\partial \boldsymbol{\sigma}} \frac{d\boldsymbol{\sigma}}{ds}\,ds \end{aligned}$$
(2.5)

where \(\mathbf{D}(t)\) is the normalized creep function, which is a general fourth order tensor, \(\mathbf{F}^{\mathrm{el}}\) is the nonlinear elastic strain measure that depends on the stress, \(t\) is the present time, and \(s\) is the history of time, where \(s \in [ 0,t ]\). The term \(\mathbf{F}^{\mathrm{el}} ( \boldsymbol{\sigma} (0) )\mathbf{D}(t)\) in Eq. (2.5) is incorporated when there is a jump discontinuity at \(t=0\). For an isotropic material, the nonlinear elastic strain measure can be written as

$$ \mathbf{F}^{\mathrm{el}}\bigl(\boldsymbol{\sigma} (s)\bigr) = - f_{1} ( I_{1},I_{2},I_{3} )I_{1}\mathbf{I} + f_{2} ( I_{1},I_{2},I_{3} )\boldsymbol{ \sigma} (s) $$
(2.6)

where the stress invariants are defined as \(I_{1} = \mathrm{trace} ( \boldsymbol{\sigma} ),I_{2} = \frac{1}{2}\mathrm{trace} ( \boldsymbol{\sigma}^{2} ),I_{3} = \frac{1}{3}\mathrm{trace} ( \boldsymbol{\sigma}^{3} )\), and \(\mathbf{I}\) is the identity matrix. The choice of the nonlinear functions \(f_{1} ( I_{1},I_{2},I_{3} )\) and \(f_{2} ( I_{1},I_{2},I_{3} )\) should be determined from available experimental data (see Muliana et al. 2015), which will be discussed in Sects. 3 and 4. It is noted that the nonlinear elastic strain measure should reduce to zero in absence of stresses \(\mathbf{F}^{\mathrm{el}}(0) = 0\). In this study we assume \(f_{1} ( I_{2} )\) and \(f_{2} ( I_{2} )\) since the second invariant includes both normal and shear components of the stress tensor, which gives more general nonlinear functions in case shear loadings are considered. For isotropic materials, we further consider two normalized time-dependent functions \(B(t)\) and \(J(t)\), and the viscoelastic strain from Eq. (2.5) reduces to

$$\begin{aligned} \boldsymbol{\varepsilon}_{R}(t) &= - f_{1} \bigl(I_{2}\bigl(\boldsymbol{\sigma} (0)\bigr)\bigr)I_{1} \bigl(\boldsymbol{\sigma} (0)\bigr)B(t)\mathbf{I} - \int_{0^{ +}}^{t} B(t - s)\frac{d [ f_{1}(I_{2}(\boldsymbol{\sigma} (s)))I_{1}(\boldsymbol{\sigma} (s)) ]}{ds}\,ds\mathbf{I} \\ &\quad + f_{2}\bigl(I_{2}\bigl(\boldsymbol{\sigma} (0)\bigr) \bigr)\boldsymbol{\sigma} (0)J(t) + \int_{0^{ +}}^{t} J(t - s)\frac{d [ f_{2}(I_{2}(\boldsymbol{\sigma} (s)))\boldsymbol{\sigma} (s) ]}{ds}\,ds \end{aligned}$$
(2.7a)

or

$$\begin{aligned} \boldsymbol{\varepsilon}_{R}(t) &= - B(0)f_{1} \bigl(I_{2}\bigl(\boldsymbol{\sigma} (t)\bigr)\bigr)I_{1} \bigl(\boldsymbol{\sigma} (t)\bigr)\mathbf{I} - \int_{0}^{t} \frac{dB(t - s)}{d(t - s)}f_{1}\bigl(I_{2}\bigl(\boldsymbol{\sigma} (s)\bigr)\bigr)I_{1}(\boldsymbol{\sigma} (s)\,ds \mathbf{I} \\ &\quad + J(0)f_{2}\bigl(I_{2}\bigl(\boldsymbol{\sigma} (t) \bigr)\bigr)\boldsymbol{\sigma} (t) + \int_{0}^{t} \frac{dJ(t - s)}{d(t - s)}f_{2}\bigl(I_{2}\bigl(\boldsymbol{\sigma} (s)\bigr)\bigr)\boldsymbol{\sigma} (s)\,ds . \end{aligned}$$
(2.7b)

When the stress components at \(t=0\) are smooth and continuous with time and \(\boldsymbol{\sigma} (t) = \boldsymbol{\varepsilon} (t) = \mathbf{0},\forall t < 0\), the first and third terms on the right-hand side of Eq. (2.7a) can be dropped, and the lower limit of the integral shall be written as 0 instead of \(0^{+}\). It is noted that for the normalized time-dependent functions \(B(0)= J(0)=1\). The time-dependent functions are not unique, any function that is positive, continuous, and monotonically increasing with time can be used for \(B(t)\) and \(J(t)\). In this study, we consider the following discrete time functions

$$\begin{aligned} B(t) = B(0) + \sum_{n = 1}^{N} B_{n} \bigl( 1 - e^{ - t/\tau_{n}} \bigr)\quad \mbox{and}\quad J(t) = J(0) + \sum_{n = 1}^{M} J_{n} \bigl( 1 - e^{ - t/\lambda_{n}} \bigr) \end{aligned}$$

that describe the primary creep deformation with a decreasing rate, and at relaxed time the deformation reaches an asymptotic value. Several experimental evidences have also shown that the rate of creep or the rate of relaxation in viscoelastic materials increase with increasing the external mechanical stimuli. Several studies have considered a time-shifting method in order to incorporate the accelerated creep and relaxation due to mechanical stimuli, e.g., Schapery (1969), Wineman (2002), Tscharnuter and Muliana (2013). Equations (2.7a), (2.7b) can be modified to incorporate the accelerated creep/relaxation by incorporating the time-shifting method, which is

$$\begin{aligned} \boldsymbol{\varepsilon}_{R}(t) &= - \int_{0}^{t} B\bigl(\varphi (t) - \varphi (s)\bigr)\frac{d [ f_{1}(I_{2}(\boldsymbol{\sigma} (s)))I_{1}(\boldsymbol{\sigma} (s)) ]}{ds}\,ds\mathbf{I} \\ &\quad + \int_{0}^{t} J\bigl(\varphi (t) - \varphi (s)\bigr)\frac{d [ f_{2}(I_{2}(\boldsymbol{\sigma} (s)))\boldsymbol{\sigma} (s) ]}{ds}\,ds \end{aligned}$$
(2.8)

where the reduced time is given as \(\varphi (t) = \int_{0}^{t} \frac{1}{a(\boldsymbol{\sigma} (x))}\,dx\), and \(a(\boldsymbol{\sigma} )\) is the time-shift factor that depends on the stresses.

Similar to the integral form for viscoelastic response in Eq. (2.5), the degradation strain is described by the following single integral form:

$$ \boldsymbol{\varepsilon}_{D}(t) = \int_{t_{\mathrm{cr}}}^{t} \mathbf{R}(t - s)\,d\bigl(\boldsymbol{\sigma} (s)\bigr) = \boldsymbol{\sigma} (t_{\mathrm{cr}})\mathbf{R}(t - t_{\mathrm{cr}}) + \int_{t_{\mathrm{cr}}}^{t} \mathbf{R}(t - s)\frac{d\boldsymbol{\sigma}}{ ds}\,ds. $$
(2.9)

The irrecoverable part is associated with the secondary and tertiary stages of deformations, and \(\mathbf{R}(t)\) is the time kernel fourth order tensor associated to the degradation strain. Here \(t_{\mathrm{cr}}\) is the critical time at which the degradation starts, according to a strain-based initiation criterion that will be introduced below, and \(s \in [ t_{\mathrm{cr}},t ]\). For isotropic materials we consider two scalar time-dependent functions \(K(t)\) and \(D(t)\) that are chosen to describe deformations with an increasing rate, which in this study we consider the following functions \(K(t) = K_{1} ( e^{t/\omega_{1}} - 1 )\) and \(D(t) = D_{1} ( e^{t/\eta_{1}} - 1 )\). The degradation strain in Eq. (2.9) now reduces to

$$\begin{aligned} \boldsymbol{\varepsilon}_{D}(t) &= - K(t - t_{\mathrm{cr}})I_{1} \bigl(\boldsymbol{\sigma} (t_{\mathrm{cr}})\bigr)\mathbf{I} - \int _{t_{\mathrm{cr}}}^{t} K(t - s)\frac{dI_{1}(\boldsymbol{\sigma} (s))}{ds}\,ds\mathbf{I} \\ &\quad + D(t - t_{\mathrm{cr}})\boldsymbol{\sigma} (t_{\mathrm{cr}}) + \int _{t_{\mathrm{cr}}}^{t} D(t - s)\frac{d\boldsymbol{\sigma} (s)}{ds} \,ds \end{aligned}$$
(2.10a)

or

$$\begin{aligned} \boldsymbol{\varepsilon}_{D}(t) &= - K(0)I_{1}\bigl( \boldsymbol{\sigma} (t)\bigr)\mathbf{I} - \int_{t_{\mathrm{cr}}}^{t} \frac{dK(t - s)}{d(t - s)}I_{1}\bigl(\boldsymbol{\sigma} (s)\bigr)\,ds \mathbf{I} + D(0)\boldsymbol{\sigma} (t) \\ &\quad + \int_{t_{\mathrm{cr}}}^{t} \frac{dD(t - s)}{d(t - s)} \boldsymbol{\sigma} (s)\,ds \end{aligned}$$
(2.10b)

where the first and second terms are expressed in terms of the first stress invariant \(I_{1}\). When \(K(0)\) and \(D(0)\) are equal to zero, then the first and third terms of Eq. (2.10b) can be dropped. Like in the viscoelastic strain component, the rate of the irrecoverable creep in the polymers can also change with stresses. Thus, the irrecoverable strain in Eqs. (2.10a), (2.10b) can be modified to include the time-stress shifting effect:

$$\begin{aligned} \boldsymbol{\varepsilon}_{D}(t) &= - K\bigl(\varphi (t) - \varphi (t_{\mathrm{cr}})\bigr)I_{1}\bigl(\boldsymbol{\sigma} (t_{\mathrm{cr}})\bigr)\mathbf{I} - \int_{t_{\mathrm{cr}}}^{t} K\bigl(\varphi (t) - \varphi (s)\bigr)\frac{dI_{1}(\boldsymbol{\sigma} (s))}{ds}\,ds\mathbf{I} \\ &\quad + D\bigl(\varphi (t) - \varphi (t_{\mathrm{cr}})\bigr)\boldsymbol{ \sigma} (t_{\mathrm{cr}}) + \int_{t_{\mathrm{cr}}}^{t} D\bigl( \varphi (t) - \varphi (s)\bigr)\frac{d\boldsymbol{\sigma} (s)}{ds}\,ds \end{aligned}$$
(2.11)

where the reduced time is given as \(\varphi (t) = \int_{0}^{t} \frac{1}{a_{D}(\boldsymbol{\sigma} (x))}\,dx\), and \(a_{D}(\boldsymbol{\sigma} )\) is the time-degradation shift factor for the irrecoverable strain that depends on the stresses.

Since the irrecoverable part is associated with the degradation, we define a threshold at which degradation starts. When considering phenomenological models in describing responses of materials with permanent deformations (plastic or damage/degradation), the magnitude of stress and/or strain is typically used in the criteria for determining further generation of plastic deformation or degradation. For example, an overstress function has been widely used in determining a yield surface for describing plastic deformations. Perzyna (1971) defined a yield function in terms of the current stress and accumulated plastic strain. As we are dealing with viscoelastic polymers, in which strains continuously increase and stresses relax with time, it is practical to consider a degradation threshold in terms of strains. We consider the following degradation criterion:

$$ f(\boldsymbol{\varepsilon},\varepsilon_{\mathrm{cr}}) = \sqrt{2J_{2}(t)} - \varepsilon_{\mathrm{cr}}(t) $$
(2.12)

where \(J_{2} = \frac{1}{2}\mathrm{trace} ( \boldsymbol{\varepsilon}^{2} )\) is the second invariant of the strain tensor and \(\varepsilon_{\mathrm{cr}}\) is the magnitude of the critical strain analogous to the yield stress in the overstress plasticity. The initial value of the critical strain is \(\varepsilon_{\mathrm{cr}}(0) = \varepsilon_{\mathrm{cr}}^{o}\), which is the strain threshold for the degradation to initiate. We introduce a parameter \(\kappa (t)\), which denotes the current stage of degradation, and in absence of degradation \(\kappa (t) = 0\). The irrecoverable strain is formed when \(f(\boldsymbol{\varepsilon},\varepsilon_{\mathrm{cr}}) \ge 0\). As the degradation progresses, the critical strain is updated as \(\varepsilon_{\mathrm{cr}}(t) = \sqrt{2J_{2}(t)}\) and a new stage of degradation is defined as \(\kappa (t) = \sqrt{2J_{2}(t)} - \varepsilon_{\mathrm{cr}}^{o}\). When \(f(\boldsymbol{\varepsilon},\varepsilon_{\mathrm{cr}}) < 0\), there are no updates for the critical strain and stage of degradation.

It is expected that degradation in polymers would influence the mechanical behaviors of the polymers, in which the material parameters in the viscoelastic and irrecoverable strains change with degradation. It is possible that the polymers would creep or relax faster as they degrade, or the polymers become softer with degradation. Thus, the recoverable and irrecoverable strains can be modified to incorporate such effects:

$$\begin{aligned} \boldsymbol{\varepsilon}_{R}(t) &= - \int_{0}^{t} B\bigl(\varphi (t) - \varphi (s)\bigr)\frac{d [ f_{1}(\kappa (s),\boldsymbol{\sigma} (s))I_{1}(\boldsymbol{\sigma} (s)) ]}{ds}\,ds\mathbf{I} \\ &\quad + \int_{0}^{t} J\bigl(\varphi (t) - \varphi (s)\bigr)\frac{d [ f_{2}(\kappa (s),\boldsymbol{\sigma} (s))\boldsymbol{\sigma} (s) ]}{ds}\,ds , \end{aligned}$$
(2.13)
$$\begin{aligned} \boldsymbol{\varepsilon}_{D}(t) &= - K\bigl( \kappa,\varphi (t) - \varphi (t_{\mathrm{cr}})\bigr)I_{1}\bigl( \boldsymbol{\sigma} (t_{\mathrm{cr}})\bigr)\mathbf{I} - \int_{t_{\mathrm{cr}}}^{t} K\bigl(\kappa,\varphi (t) - \varphi (s)\bigr)\frac{dI_{1}(\boldsymbol{\sigma} (s))}{ds}\,ds\mathbf{I} \\ &\quad + D\bigl(\kappa,\varphi (t) - \varphi (t_{\mathrm{cr}})\bigr) \boldsymbol{\sigma} (t_{\mathrm{cr}}) + \int_{t_{\mathrm{cr}}}^{t} D\bigl(\kappa,\varphi (t) - \varphi (s)\bigr)\frac{d\boldsymbol{\sigma} (s)}{ds}\,ds . \end{aligned}$$
(2.14)

The shift factors inside the reduced times are \(a(\kappa,\boldsymbol{\sigma} )\) and \(a_{D}(\kappa,\boldsymbol{\sigma} )\). The critical time \(t_{\mathrm{cr}}\) is determined when \(\sqrt{2J_{2}(t_{\mathrm{cr}})} = \varepsilon_{\mathrm{cr}}^{o}\).

When the loading history and nonlinear elastic and time-dependent functions are of simple forms, we might be able to solve the above integral and obtain exact solutions. If exact solutions are not possible, then numerical methods are often considered to obtain approximate solutions.

3 One-dimensional responses

Drozdov (2010) has conducted uniaxial tensile tests on polyethylene under various loading histories, which are quasi-static ramp tests under several constant strain rates, relaxation tests under several strains, and creep tests under various stresses. The loading duration was limited to 1200 seconds. The corresponding responses are recorded in the direction of loading, and the engineering stress–strain measure was used in presenting the responses. The presented experimental data from the uniaxial loading would limit the analyses to one-dimensional response. The creep responses showed that failure occurred under high stresses. At low stresses the primary creep behavior was observed for the 1200 seconds of creep tests. The stress relaxation behaviors suggested that polyethylene experienced a viscoelastic solid-like behavior. The quasi-static ramp tests under lower strain rates resulted in smaller magnitude of stresses, indicating significant stress relaxation processes.

We consider the phenomenological model discussed in Sect. 2 in order to describe the response of the studied polyethylene. For one-dimensional case, Eq. (2.4) reduces to a scalar component of strain \(\varepsilon (t) = \varepsilon_{R}(t) + \varepsilon_{D}(t)\) and the invariants \(I_{1} =2I_{2} = \sigma\). The stress, strain, and time relations in the recoverable and irrecoverable parts are:

$$\begin{aligned} \varepsilon_{R}(t) &= - \int_{0}^{t} B \bigl(\varphi (t) - \varphi (s)\bigr)\frac{d [ f_{1}(\sigma (s))\sigma (s) ]}{ds}\,ds \\ &\quad + \int_{0}^{t} J\bigl(\varphi (t) - \varphi (s)\bigr)\frac{d [ f_{2}(\sigma (s))\sigma (s) ]}{ds}\,ds \\ &= \int_{0}^{t} G\bigl(\varphi (t) - \varphi (s) \bigr)\frac{dr(\sigma (s))}{ds}\,ds \\ & = G\bigl(\varphi (t)\bigr)\sigma (0) + \int_{0^{ +}}^{t} G\bigl(\varphi (t) - \varphi (s)\bigr)\frac{dr(\sigma (s))}{ds}\,ds , \end{aligned}$$
(3.1)
$$\begin{aligned} \varepsilon_{D}(t) &= - K\bigl(\varphi (t) - \varphi (t_{\mathrm{cr}})\bigr)\sigma (t_{\mathrm{cr}}) - \int _{t_{\mathrm{cr}}}^{t} K\bigl(\varphi (t) - \varphi (s)\bigr) \frac{d\sigma (s)}{ds}\,ds \\ &\quad + D\bigl(\varphi (t) - \varphi (t_{\mathrm{cr}})\bigr)\sigma (t_{\mathrm{cr}}) + \int_{t_{\mathrm{cr}}}^{t} D\bigl(\varphi (t) - \varphi (s)\bigr)\frac{d\sigma (s)}{ds}\,ds \\ &= H\bigl(\varphi (t) - \varphi (t_{\mathrm{cr}})\bigr)\sigma (t_{\mathrm{cr}}) + \int_{t_{\mathrm{cr}}}^{t} H\bigl(\varphi (t) - \varphi (s)\bigr)\frac{d\sigma (s)}{ds}\,ds . \end{aligned}$$
(3.2)

In the above equations, \(G(t)\) and \(H(t)\) are the time-dependent functions corresponding to the viscoelastic (recoverable) and degradation (irrecoverable) parts, respectively, and \(r(\sigma )\) is the nonlinear elastic strain measure. In order to determine the material parameters in the above model, we start with calibrating the nonlinear viscoelastic response, in absence of degradation \(\varepsilon_{D}(t) = 0\), in which we consider responses under relatively low stresses and strains. All experimental data discussed in this section are digitized from Drozdov (2010). Figure 2 shows the stress–strain responses under the highest constant rate (0.08/s) up to strain around 0.04. It is noted that the degradation is associated with the secondary and tertiary creep deformations. By observing experimental data from the creep tests, it seems that the secondary creep starts when the strain is greater than 0.04. Thus, we consider the initial value of the critical strain is \(\varepsilon_{\mathrm{cr}}^{o} = 0.045\), which is a rough estimate. This is the strain limit at which we calibrate the nonlinear elastic material parameters. It is noted that loading rate 0.08/s is relatively fast, and under this rate the effect of stress relaxation process on the overall responses of the polyethylene is considered negligible. We also plot the isochronous data from the stress relaxation tests at time \(t^{*}\), at which the stress relaxation starts. It is seen that the responses at \(t^{*}\) indicate the instantaneous elastic behavior. We then use the stress–strain response in Fig. 2 to calibrate the nonlinear elastic function \(r(\sigma )\), which is a strain measure, and we assume the following function:

$$ r(\sigma ) = A \bigl( e^{B\sqrt{2I_{2}}} - 1 \bigr) = A \bigl( e^{B\sqrt{ ( \sigma (t) )^{2}}} - 1 \bigr). $$
(3.3)

The linearization of the nonlinear function in Eq. (3.3) reduced to a linear elastic response

$$ \varepsilon = r(\sigma ) = \frac{dr}{d\sigma} \bigg| _{\sigma = 0} \sigma = AB\sigma = D_{o}\sigma $$
(3.4)

where \(D_{{o}}\) is the linear elastic compliance. The calibrated material parameters are given in Table 1. After calibrating the parameters in the nonlinear elastic response, Eq. (3.3), we then calibrate the time-dependent function and consider the following normalized time-function \(G(t) = G(0) + \sum_{n = 1}^{N} G_{n} ( 1 - e^{ - t/\tau_{n}} )\) and the time shift factor \(a(\sigma )\) inside the reduced time is taken as 1. The stress relaxation response under a constant strain 0.044 is used to calibrate the parameters in the above normalized time function (see Fig. 3) and the calibrated parameters are given in Table 2.

Fig. 2
figure 2

Nonlinear elastic response of polyethylene from quasi-static ramp with strain rate \(0.08/s\) and isochronous plot from relaxation tests at time \(t^{*}\), at which the stress relaxation starts

Full size image
Fig. 3
figure 3

Stress relaxation response of polyethylene under strain 0.044

Full size image
Table 1 Material parameters of polyethylene
Full size table
Table 2 Calibrated parameters in the normalized time function of polyethylene
Full size table

We now use the creep responses (Fig. 4) in order to determine the time-dependent degradation behavior. The following function is considered for the degradation part:

$$ H\bigl(\varphi (t)\bigr) = \frac{1}{\eta} \bigl( e^{\varphi (t)/\varsigma} - 1 \bigr). $$
(3.5)

The creep response under stress 28 MPa is used to determine the parameters \(\eta\) and \(\zeta\), and at this stress, the degradation time shift factor \(a_{D}\) is taken as 1. The recoverable and irrecoverable strains are considered in this creep response. The calibrated degradation parameters are given in Table 1. Next, the degradation time-shift factors \(a_{D}\) are determined for the creep responses under stresses 19.7, 21.5, 23.4, and 24.7 MPa. Figure 5 shows the degradation shift-factors calibrated from the secondary and tertiary stages of creep deformations. A polynomial fit is used for the degradation shift factor: \(a_{D} = 0.6674\sigma^{2} - 36.951\sigma + 512.27\). At a relatively small stress, the value of the degradation shift factor reaches a very large number, indicating that the degradation predicted by the model would occur at much longer time, and at a relatively small stress the contribution of the degradation strain at short-term period is negligible since \(\varphi (t) \approx 0\) and \(H(\varphi (t)) \approx 0\). The calibration is done by varying the material parameters to fit the experimental data.

Fig. 4
figure 4

Creep degradation behaviors of polyethylene (stress is in MPa)

Full size image
Fig. 5
figure 5

Degradation shift factor of polyethylene

Full size image

The time-dependent viscoelastic and degradation model with material parameters given in Tables 1 and 2 is now used to predict the response of polyethylene under stress relaxation and quasi-static tensile tests with constant strain rates. Figure 6 illustrates the stress relaxation responses under several constant strains, and Fig. 7 depicts the responses under constant strain rates. The model can reasonably capture the response of polyethylene under various histories of loading. It is noted that the quasi-static responses of the polymers under relatively slow rates are captured well by the model since these responses occurred at relatively long period of time. For example, to reach strain 0.2 with a rate of \(2\times10^{-4}\mbox{/s}\), it takes 1000 seconds, and the viscoelastic and degradation strains have been calibrated for period 1200 second and up to strain level 0.2 and stress level 28 MPa. It is noted that for the quasi-static response under fast loading (\(10^{-2}\mbox{/s}\)) it takes 20 seconds to reach strain 0.2. The response can be considered mainly due to the instantaneous elastic behavior. We assumed that the time-dependent degradation occurs due to an increase in the strain response with time and neglect the possible degradation at the instantaneous elastic response since we do not have enough data to calibrate the material parameters associated to the elastic degradation. This might explain the mismatches between the response obtained from the model and experimental data at strain rate \(10^{-2}\mbox{/s}\).

Fig. 6
figure 6

Stress relaxation response of polyethylene

Full size image
Fig. 7
figure 7

Responses of ramp loading of polyethylene at different constant strain rates (unit /s)

Full size image

4 Three-dimensional responses

We study three-dimensional responses of viscoelastic solid polymers undergoing mechanical degradation. For this purpose, experimental tests were conducted on POM under several histories. The POM specimens (Tenac 3010, Asahi Kasei, Japan) were subjected to uniaxial tensile tests at 23 °C and the responses along the loading (axial) and perpendicular to the loading (transverse) directions were recorded using Digital Image Correlation (DIC). For the monotonic tensile tests, a 3D-DIC system was used (ARAMIS 4M; GOM mbH, Germany). The creep tests were conducted on a custom-built creep testing machine equipped with telecentric lenses for 2D-DIC. To monitor the recovery following the creep tests, the specimens were unloaded and transferred to a dedicated recovery measurement device, where the strain measurement using 2D-DIC was continued. On this test stand, specimens are subjected to variations in the ambient temperature of up to ±2 K, which introduces inaccuracies in the range of ±0.03 % due to thermal strains. As discussed in Sect. 3, we start with calibrating material parameters in the nonlinear elastic function, followed by calibrating normalized time-dependent parameters for the viscoelastic strain. Once the material parameters in the viscoelastic strain have been determined, the parameters in the degradation strains are calibrated. Observing the nonlinear elastic response of POM from the quasi-static test under displacement rate 10 mm/s (Fig. 8), we consider the following nonlinear elastic function for isotropic materials:

$$ \mathbf{F}^{\mathrm{el}}\bigl(\boldsymbol{\sigma} (t)\bigr) = - \alpha \biggl[ \frac{\exp ( \beta \sqrt{2I_{2}} ) - 1}{1 + \sqrt{2I_{2}}} \biggr]I_{1}\bigl(\boldsymbol{\sigma} (t)\bigr) \mathbf{I} + \gamma \biggl[ \frac{\exp ( \delta \sqrt{2I_{2}} ) - 1}{1 + \sqrt{2I_{2}}} \biggr]\boldsymbol{\sigma} (t). $$
(4.1)

We assume that the response of materials under tension and compression is the same. The linearization of Eq. (4.1) reduces to a linear elastic material response:

$$ \boldsymbol{\varepsilon}^{\mathrm{el}} = - \alpha \beta I_{1} \mathbf{I} + \gamma \delta \boldsymbol{\sigma} $$
(4.2)

where \(- \alpha \beta = - \frac{\nu}{E}; \gamma \delta = \frac{1 + \nu}{E} \) and \(E\) and \(\nu\) are the elastic modulus and Poisson’s ratio, respectively. There are four material parameters in Eq. (4.1), i.e., \(\alpha, \beta, \gamma\), and \(\delta\), that need to be calibrated. Following Muliana et al. (2015), we first use the transverse response, where Eq. (4.1) reduces to \(\varepsilon_{22} = F_{22}(\sigma_{11}) = - \alpha ( \frac{\exp (\beta \sigma_{11}) - 1}{1 + \sigma_{11}} )\), in order to determine the parameters \(\alpha, \beta\). Once these parameters have been determined, we use the axial response, \(\varepsilon_{11} = F_{11}(\sigma_{11}) = - \alpha ( \frac{\exp (\beta \sigma_{11}) - 1}{1 + \sigma_{11}} ) + \gamma ( \frac{\exp (\delta \sigma_{11}) - 1}{1 + \sigma_{11}} )\), to calibrate the parameters \(\gamma, \delta\). Table 3 presents the calibrated material parameters corresponding to the nonlinear elastic responses.

Fig. 8
figure 8

Nonlinear elastic response of POM from the quasi-static loading under rate 10 mm/s

Full size image
Table 3 Nonlinear elastic material parameters of POM
Full size table

We then determine the parameters in the normalized time-dependent functions \(B(t)\) and \(J(t)\) from the 1500 minute creep response under 20 MPa (see Fig. 9). With the nonlinear elastic function given in Eq. (4.1) and two time-dependent functions \(B(t)\) and \(J(t)\) the viscoelastic constitutive model is

$$\begin{aligned} \boldsymbol{\varepsilon}_{R}(t) &= - B(0)\alpha \biggl[ \frac{\exp ( \beta \sqrt{2I_{2}(t)} ) - 1}{1 + \sqrt{2I_{2}(t)}} \biggr]I_{1}(t)\mathbf{I} \\ &\quad - \int_{0}^{t} \dot{B}(t - s)\alpha \biggl[ \frac{\exp ( \beta \sqrt{2I_{2}(s)} ) - 1}{1 + \sqrt{2I_{2}(s)}} \biggr]I_{1}(s)\mathbf{I}\,ds \\ &\quad + J(0)\gamma \biggl[ \frac{\exp ( \delta \sqrt{2I_{2}(t)} ) - 1}{1 + \sqrt{2I_{2}(t)}} \biggr]\boldsymbol{\sigma} (t) \\ &\quad + \int_{0}^{t} \dot{J}(t - s)\gamma \biggl[ \frac{\exp ( \delta \sqrt{2I_{2}(s)} ) - 1}{1 + \sqrt{2I_{2}(s)}} \biggr]\boldsymbol{\sigma} (s)\,ds. \end{aligned}$$
(4.3)

Under a uniaxial stress \(\sigma_{11}(t)\), the nonzero components of strains are:

$$\begin{aligned} &\begin{aligned}[b] \varepsilon_{R11}(t) &= - B(0)\alpha \biggl[ \frac{\exp ( \beta \sigma_{11}(t) ) - 1}{1 + \sigma_{11}(t)} \biggr]\sigma_{11}(t) \\ &\quad - \int_{0}^{t} \dot{B}(t - s)\alpha \biggl[ \frac{\exp ( \beta \sigma_{11}(s) ) - 1}{1 + \sigma_{11}(s)} \biggr]\sigma_{11}(s)\,ds \\ &\quad + J(0)\gamma \biggl[ \frac{\exp ( \delta \sigma_{11}(t) ) - 1}{1 + \sigma_{11}(t)} \biggr]\sigma_{11}(t) \\ &\quad + \int_{0}^{t} \dot{J}(t - s)\gamma \biggl[ \frac{\exp ( \delta \sigma_{11}(s) ) - 1}{1 + \sigma_{11}(s)} \biggr]\sigma_{11}(s)\,ds , \end{aligned} \end{aligned}$$
(4.4a)
$$\begin{aligned} &\begin{aligned} \varepsilon_{R22}(t) &= - B(0) \alpha \biggl[ \frac{\exp ( \beta \sigma_{11}(t) ) - 1}{1 + \sigma_{11}(t)} \biggr]\sigma_{11}(t) \\ &\quad - \int_{0}^{t} \dot{B}(t - s)\alpha \biggl[ \exp \frac{ ( \beta \sigma_{11}(s) ) - 1}{1 + \sigma_{11}(s)} \biggr]\sigma_{11}(s)\,ds, \\ \varepsilon_{R33}(t) &= \varepsilon_{R22}(t) . \end{aligned} \end{aligned}$$
(4.4b)
Fig. 9
figure 9

Creep–recovery response of POM under stress 20 MPa

Full size image

We first use the transverse strain response during the 1500 minute creep for determining the parameters in \(B(t)\). Once these parameters have been calibrated, we use the axial creep response to determine the parameters that appear in the expression for \(J(t)\). Table 4 lists the calibrated parameters from the 1500 minute creep responses. We also use the model to capture the recovery stage after 1500 minutes of creep test.

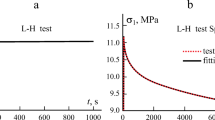
Table 4 Calibrated parameters in the normalized time functions
Full size table

Next, we use the creep–recovery responses under higher stresses (40 and 50 MPa) to study the time-dependent degradation of POM. Figure 10 shows the axial and transverse strain responses of POM under 4000 minute, at 50 MPa, creep followed by recovery. The responses show primary, secondary and tertiary creep stages and residual strains are observed after removal of the stress, indicating some degradation has occurred in the sample. The ramp loading to 50 MPa was done under a relatively short duration (<10 seconds) and the unloading from 50 MPa to zero stress at around 4000 minutes was done also under a short duration (<30 seconds). Thus, it is expected that the responses during ramp loading and unloading are mainly due to elastic (instantaneous) responses. It is also seen that the magnitude of the elastic (instantaneous) strain during ramp loading is smaller than the one during unloading, which suggests that degradation might alter the nonlinear elastic response of POM, i.e., the material is getting softer as it degrades. Figure 11 shows the creep–recovery response of POM under 50 MPa for shorter creep duration (1500 minutes). Residual strains are observed for the transverse and axial strain responses with smaller magnitude compared to the ones presented in Fig. 10. It is seen that longer duration of creep induces more severe degradation due to increases in the strain magnitude, resulting in larger residual strains. Figure 12 illustrates the creep–recovery response of POM under 40 MPa for 1500 minutes of creep. Smaller residual strains are observed in both axial and transverse strains, when compared to the residual strains under 50 MPa after 1500 minutes of creep. It is also noticed from Figs. 11 and 12 that the magnitude of the unloading strains is larger than the ones of the loading, indicating softening in the elastic (instantaneous) response due to degradation.

Fig. 10
figure 10

Creep–recovery responses of POM under stress 50 MPa (data used for calibration)

Full size image
Fig. 11
figure 11

Creep response under 1500 minutes, at 50 MPa stress, followed by recovery

Full size image
Fig. 12
figure 12

Creep–recovery response under 40 MPa

Full size image

In order to describe the creep responses under stresses 40 and 50 MPa, in which degradation occurs, we consider additive decompositions of the recoverable (viscoelastic) and irrecoverable (degraded) strains, as shown in Eq. (2.4). The irrecoverable strain is

$$\begin{aligned} \boldsymbol{\varepsilon}_{D}(t) &= - K_{1} \bigl( e^{(t - t_{\mathrm{cr}})/\omega_{1}} - 1 \bigr)\mathrm{I}_{1}\bigl(\boldsymbol{\sigma} (t_{\mathrm{cr}})\bigr)\mathbf{I} - \int_{t_{\mathrm{cr}}}^{t} K_{1} \bigl( e^{(t - s)/\omega_{1}} - 1 \bigr)\frac{dI_{1}(\boldsymbol{\sigma} (s))}{ds}\,ds \mathbf{I} \\ &\quad + D_{1} \bigl( e^{(t - t_{\mathrm{cr}})/\eta_{1}} - 1 \bigr)\boldsymbol{\sigma} (t_{\mathrm{cr}}) + \int_{t_{\mathrm{cr}}}^{t} D_{1} \bigl( e^{(t - s)/\eta_{1}} - 1 \bigr)\frac{d\boldsymbol{\sigma} (s)}{ds}\,ds . \end{aligned}$$
(4.5)

Under a uniaxial stress \(\sigma_{11}(t)\), the nonzero components of the irrecoverable strain are

$$\begin{aligned} &\begin{aligned}[b] \varepsilon_{D11}(t) &= - K_{1} \bigl( e^{(t - t_{\mathrm{cr}})/\omega_{1}} - 1 \bigr)\sigma_{11}(t_{\mathrm{cr}}) - \int _{t_{\mathrm{cr}}}^{t} K_{1} \bigl( e^{(t - s)/\omega_{1}} - 1 \bigr)\frac{d\sigma_{11}(s)}{ds}\,ds \\ &\quad + D_{1} \bigl( e^{(t - t_{\mathrm{cr}})/\eta_{1}} - 1 \bigr) \sigma_{11}(t_{\mathrm{cr}}) + \int_{t_{\mathrm{cr}}}^{t} D_{1} \bigl( e^{(t - s)/\eta_{1}} - 1 \bigr)\frac{d\sigma_{11}(s)}{ds}\,ds , \end{aligned} \end{aligned}$$
(4.6a)
$$\begin{aligned} &\begin{aligned} \varepsilon_{D22}(t) &= - K_{1} \bigl( e^{(t - t_{\mathrm{cr}})/\omega_{1}} - 1 \bigr)\sigma_{11}(t_{\mathrm{cr}}) - \int_{t_{\mathrm{cr}}}^{t} K_{1} \bigl( e^{(t - s)/\omega_{1}} - 1 \bigr)\frac{d\sigma_{11}(s)}{ds}\,ds, \\ \varepsilon_{D33}(t) &= \varepsilon_{D22}(t) . \end{aligned} \end{aligned}$$
(4.6b)

As discussed above, the degradation in POM affects the elastic (instantaneous) response. In order to incorporate such an effect, the material parameters in Eq. (4.1) can change with the degrading stage. Since the experimental data suggested that the elastic (instantaneous) response becomes softer as POM degrades, we consider the elastic material parameters change with the degradation stage \(\alpha ( \kappa)\) and \(\gamma ( \kappa)\). In this study, we assume that when \(\kappa = 0\) then \(\alpha\) and \(\gamma\) are given in Table 3, otherwise when \(\kappa \ne 0\) then \(\alpha\) and \(\gamma\) change with \(\kappa\). In order to determine the initial critical strain at which degradation starts, a ramp loading to several amplitude of strains is conducted followed by removal of the load and the recovery strains were monitored in order to investigate the residual strains, both along the axial and transverse directions. Table 5 presents the magnitude of the residual axial and transverse strains from the ramp loading with several maximum axial strains. Observing the residual strains in Table 5, we take the initial critical strain to be \(\varepsilon_{\mathrm{cr}}^{o} = 0.03\). We use the creep responses under 50 MPa, depicted in Fig. 10, in order to calibrate the material parameters in Eqs. (4.6a) and (4.6b) and determine \(\alpha ( \kappa)\) and \(\gamma ( \kappa)\). It is noted that \(\kappa = \kappa (t) = \sqrt{2J_{2}(t)} - \varepsilon_{\mathrm{cr}}^{o}\), which depends on both axial and transverse strain components and at the same time the elastic material parameters vary with \(\kappa\); thus we cannot calibrate the material parameters by separately considering the transverse and axial strain responses, as previously done for the elastic and viscoelastic properties. We simultaneously use the axial and transverse strain responses in order to determine \(K_{1},\omega_{1},D_{1},\eta_{1}\) and \(\alpha ( \kappa)\) and \(\gamma ( \kappa)\). The calibrated material parameters are given in Table 3, and the degradation dependent elastic material properties are \(\alpha (\kappa (t)) = 10^{ - 2} ( 0.2589\kappa (t) + 0.21 )\) and \(\gamma (\kappa (t)) = 10^{ - 2} ( 4.222\kappa (t) + 0.74 )\).

Table 5 Axial and transverse residual strains from ramp loading with several maximum strains
Full size table

From Fig. 10, it is seen that the model can capture the overall creep–recovery behaviors, including the residual strains and elastic (instantaneous) responses during the loading and unloading stages. It is also seen that the model shows continuous recovery, while the experiment shows relatively fast recovery before reaching residual strains. This suggests that degradation might affect the creep/relaxation behavior of POM. Unlike the degradation dependent elastic (instantaneous) response that can be determined from the unloading period, the degradation dependent creep/relaxation response cannot be easily captured from the creep–recovery responses in Fig. 10. In order to investigate how the degradation influences the creep and relaxation processes of POM, it might be necessary to perform creep/relaxation tests on the degraded samples, which is beyond the scope of this study. Finally, we also show the prediction of the creep–recovery responses under 50 and 40 MPa stresses for 1500 minute creep tests is Figs. 11 and 12, respectively, using the calibrated material parameters in Tables 3 and 4. The model shows relatively good prediction, and capable in capturing the residual strains. The mismatches are seen due to the continuous recovery after unloading, which has been explained above. Responses from the nonlinear viscoelastic model, in absence of degradation, are also plotted for comparison.

5 Conclusions

We have formulated a constitutive model for nonlinear isotropic viscoelastic solids undergoing degradation due to mechanical stimuli. A linearized strain measure is considered and the strain is additively decomposed into viscoelastic (recoverable) and degradation (irrecoverable) strains. A single integral model with nonlinear integrands is used for the recoverable part. The degradation strains are also expressed in integral forms where the kernel time monotonically increases with time, and the rate of deformation also increases with time. We have defined a threshold for degradation in terms of a critical strain and also determined the stage of degradation in terms of the second invariant of the current strain tensor. Furthermore, we also assume that the degradation affects the elastic response of the polymers.

We have used the presented viscoelastic-degradation model for describing time-dependent behaviors of two polymers, namely polyethylene and polyoxymethylene (POM) under uniaxial tensile tests. Detailed material parameter characterizations from experimental data are presented. The model has been shown capable in capturing time-dependent responses of polymers undergoing various loading histories, i.e., ramp loading under various rates, creep under different stresses, and relaxation at several strain levels. It is concluded that longer duration of loading can lead to increase in the degradation of materials due to the substantial increase in the deformations. The model is also capable in predicting the recovery and residual strains at different stages of degradations.