1 Introduction

Image denoising is a fundamental problem in image processing that occurs in the acquisition, transmission, storage, and processing of images. Image denoising is about removing noise from a noisy image and restoring the true image. In denoising, it is not easy to detect edges and textures that have high-frequency components due to noise, so some details may be lost. Therefore, it is important to develop new algorithms that can recover meaningful information from noisy images and produce high-quality images. The development of two-phase algorithms whose first phase is denoising may be more effective than denoising methods, e.g., see [6,7,8,9, 21, 22]. The second phases of these algorithms can be any optimization methods with small memory requirements, such as conjugate gradient methods and limited memory quasi-Newton methods. These optimization methods can recover the images found by denoising. Therefore, two-phase methods are developed as a version of denoising. There are different types of noise such as Gaussian, Poisson, Rician, and salt and pepper impulse noise in medical images [1, 6, 7]. In medicine, many methods are used to remove impulse noise, such as X-ray, computed tomography, magnetic resonance imaging, ultrasound, and dermoscopy.

2 Related work

There are many methods for removing salt and pepper impulse noise, such as the descent spectral conjugate gradient method of Yu et al. [34], nonmonotone adaptive gradient method of Yu et al. [35] with a low-complexity, generalized trimmed mean filter by Rytsar & Ivasenko [28], wavelet filter of Karthikeyan et al. [20] and Wang et al. [31], fuzzy algorithms of Anisha et al. [1] and Russo et al. [27], trust region method of Kimiaei & Rahpeymaii [21], conjugate gradient method of Kimiaei & Rostami [22] and Zhou et al. [37], and gradient method of Liu et al. [23]. For impulse noise removal methods, other recent references are Chen et al. [11], Halder & Choudhuri [17], Nadeem et al. [24], Shah et al. [29], and Wang et al. [32].

Among all methods, conjugate gradient methods (CG) are popular because they require little memory. CG methods try line search methods along CG directions to speed up reaching an optimal point. Line search methods find step sizes that force a reduction in objective function values. Directions of CG methods are a kind of subspace spanned by two terms (the steepest descent gradient at the current point and the previous direction) or three terms (the steepest descent gradient at the current point and the previous direction, the gradient differences at the old and current points). These terms are scaled by step sizes called CG parameters. These parameters play a key role in the efficiency of CG methods. To ensure that CG methods find an optimal point, CG directions should satisfy the descent condition, i.e., the product of the gradient at the current point and the CG direction should be negative. If CG parameters become too large, the descent condition may be violated and a saddle point or a maximum point will be found instead of a minimum point. On the other hand, if these parameters become small, the corresponding term will be dominated by the other terms and the subspace will become smaller. Therefore, it is very important to generate and control CG parameters so that they do not become too large or too small, unless CG iterations are near an optimal point. In this case, the first term (the steepest descent direction) should dominate the other two terms. When CG iterations are near a minimum point, the gradient is small and the CG direction (which in this case is the steepest descent direction) has a small magnitude. In other words, the risk of skipping the minimum point due to large steps is reduced and CG methods have a high chance of finding the minimum point when noise is present. To achieve this, CG parameters should be slowly reduced by a decreasing factor. So far, there are no known studies on these points. Therefore, if it is possible to improve CG methods, this would be interesting and could significantly improve the efficiency and robustness of CG methods. Then such CG methods can be used in the second phase of two-phase methods (e.g., [6,7,8,9, 21, 22]).

2.1 Variant Median filter methods

Shukla et al. [30] proposed the median filter (MF) method to remove salt and pepper noise by using the median of the window to replace the central pixels with the window. If the central pixels are salt and pepper, they are replaced by the median of the window. MF cannot distinguish true pixels from noise.

The adaptive median filter (AMF) method is a widely used adaptation of MF (cf. [19]). AMF performs spatial processing to determine whether or not pixels in an image are affected by impulse noise. In addition, this method classifies pixels as noise by comparing each pixel in the image with the surrounding neighboring pixels. With AMF, the size of the neighborhood and the threshold for the comparison are adjustable. Impulse noise is a pixel that is different from most of its neighbors but is not matched with similar pixels. In this case, this noisy pixel is replaced by the neighboring pixels.

Notation

Let \(x \in \mathbb {R}^{M\times N}\) be the original image with \(M \times N\) pixels. Then we consider the set

$$\mathcal {A}=\Big \{1,2,...,M\Big \}\times \Big \{1,2,...,N\Big \}$$

of indices. We denote by \(x_{i,j}\) the component of the original image at position (i, j). We form the four neighborhoods

$$\mathcal {V}_{i,j}=\Big \{x_{i-1,j},x_{i,j-1},x_{i,j+1},x_{i+1,j}\Big \}$$

of \(x_{i,j}\). Let \([d_{\min },d_{\max }]\) be the dynamic range of the original image x, i.e., for all \(i=1,2,\cdots ,M\) and \(j=1,2,\cdots ,N\), \(x_{i,j}\in [d_{\min },d_{\max }]\). Then we define

$$y_{i,j}={\left\{ \begin{array}{ll} x_{i,j}&{}\text {with probability}\,\, 1-p-q,\\ d_{\min }&{}\text {with probability}\,\, p,\\ d_{\max }&{}\text {with probability}\,\, q, \end{array}\right. }$$

since the noisy image contains salt and pepper noise. Applying AMF to the noisy image y, we obtain the repaired image \(\tilde{y}\) and the candidate set

$$\mathcal {N}=\Big \{(i,j)\in \mathcal {A} \mid \,\, \tilde{y}_{i,j}\ne y_{i,j},\,\, y_{i,j}=d_{\min } \,\, \text {or}\,\, d_{\max }\Big \}$$

of noise.

2.2 Two-phase methods

In this section, two-phase methods are described. In the first phase, damaged noises are identified. Then, in the second phase, damage noises are recovered by solving an unconstrained optimization problem with a continuously differentiable objective function (e.g., see [6,7,8,9, 21, 22]).

Let us consider now how to work two-phase methods. In first phase, noisy image pixels are identified. If \((i,j)\not \in \mathcal {N}\), then the pixel \(x_{i,j}\) is not damaged and is kept without any change. But for \((i,j) \in \mathcal {N}\) the pixel \(y_{i,j}\) should be denoise. For this, let \(u^*\) be a denoised image. As in [6, 8, 9], in the second phase, if \((m,n)\in \mathcal {V}_{i,j}\setminus \mathcal {N}\), we  set \(u^*_{m,n}=y_{m,n}\) and for \((m,n) \in \mathcal {V}_{i,j} \cap \mathcal {N}\) we obtain \(y_{m,n}\) by solving the following problem with the smooth objective function

$$\begin{aligned} \min _{u \in \mathbb {R}^{|\mathcal {N}|}} \,\,{\textbf {F}}(u):=\sum _{(i,j)\in \mathcal {N}}\Big \{|u_{i,j}-y_{i,j}|&+\eta \Big [\sum _{(m,n)\in \mathcal {V}_{i,j}\setminus \mathcal {N}}\phi _\alpha (u_{i,j}-y_{m,n})\\&+\frac{1}{2}\sum _{(m,n)\in \mathcal {V}_{i,j}\cap \mathcal {N}}\phi _\alpha (u_{i,j}-u_{m,n})\Big ]\Big \}. \end{aligned}$$
(1)

Here \(\eta \) is a regularization parameter and \(\phi _\alpha \) is an even edge-preserving potential function. Some of the most popular edge-preserving potential functions [4, 5, 7, 10, 15] are

$$\begin{aligned} \phi _\alpha (t)&=\sqrt{t^2+\alpha },\quad \alpha >0,\end{aligned}$$
(2)
$$\begin{aligned} \phi _\alpha (t)&=|t|^\alpha ,\quad 1<\alpha \le 2, \end{aligned}$$
(3)
$$\begin{aligned} \phi _\alpha (t)&=\log \Big (\cosh (\alpha t)\Big ),\quad \alpha >0, \end{aligned}$$
(4)
$$\begin{aligned} \phi _\alpha (t)&=\frac{|t|}{\alpha }-\log \Big (1+\frac{|t|}{\alpha }\Big ),\quad \alpha >0, \end{aligned}$$
(5)
$$\begin{aligned} \phi _\alpha (t)&={\left\{ \begin{array}{ll} \frac{t^2}{2\alpha },&{}|t|\le \alpha ,\\ |t|-\frac{\alpha }{2}&{}|t|>\alpha , \end{array}\right. }\qquad \alpha >0. \end{aligned}$$
(6)

There are many ways to solve the problem (1), such as Newton method, quasi-Newton methods, trust region methods, etc. Since this problem is a large problem, only low-memory methods such as CG methods (e.g., see [6,7,8,9, 22]) and limited memory quasi-Newton methods (cf. [21]) can be used to solve these problems.

2.3 Known CG methods

To solve the problem (1), starting from an initial guess \(u_0\in \mathbb {R}^{|\mathcal {N}|}\), CG methods generate a sequence \(\{u_k\}_{k \ge 0}\) by

$$\begin{aligned} u_{k+1}:=u_k+\alpha _k d_k. \end{aligned}$$
(7)

Here \(\alpha _k\) is a step size, obtained by inexact line search methods, and \(d_k\) is a descent search direction satisfying the descent condition

$$\begin{aligned} \nabla {\textbf {F}}_k^Td_k<0, \end{aligned}$$
(8)

computed by

$$\begin{aligned} d_k:={\left\{ \begin{array}{ll} -\nabla {\textbf {F}}_k,&{}k=0,\\ -\nabla {\textbf {F}}_k+\beta _k d_{k-1},&{} k\ge 1. \end{array}\right. } \end{aligned}$$
(9)

Here \(\nabla {\textbf {F}}_k:=\nabla {\textbf {F}}(u_k)\) is the gradient of \({\textbf {F}}\) at \(u_k\) and \(\beta _k \in \mathbb {R}\) is the CG parameter with known choices

$$ \begin{aligned} \beta _k^{HS}:=\frac{\nabla {\textbf {F}}_k^Ty_{k-1}}{d_{k-1}^Ty_{k-1}},\qquad \text {Hestenes } \& \text{ Stiefel}\,\, [18] \end{aligned}$$
(10)
$$ \begin{aligned} \beta _k^{FR}:=\frac{\Vert \nabla {\textbf {F}}_k\Vert ^2}{\Vert \nabla {\textbf {F}}_{k-1}\Vert ^2},\qquad \text {Fletcher } \& \text{ Reeves}\,\, [14] \end{aligned}$$
(11)
$$ \begin{aligned} \beta _k^{DY}:=\frac{\Vert \nabla {\textbf {F}}_k\Vert ^2}{d_{k-1}^Ty_{k-1}},\qquad \text {Dai } \& \text{ Yuan}\,\, [12] \end{aligned}$$
(12)
$$ \begin{aligned} \beta _k^{HZ}:=\beta _k^{HS}-2\Vert y_{k-1}\Vert ^2\frac{\nabla {\textbf {F}}_k^Td_{k-1}}{(d_{k-1}^Ty_{k-1})^2}, \qquad \text {Hager } \& \text{ Zhang} \,\,[16] \end{aligned}$$
(13)
$$ \begin{aligned} \beta _k^{PR}:=\frac{\nabla {\textbf {F}}_k^Ty_{k-1}}{\Vert \nabla {\textbf {F}}_{k-1}\Vert ^2},\qquad {\textsc {Polak } \& \textsc { Ribiere}} \,\,[26] \end{aligned}$$
(14)

where \(y_{k-1}:=\nabla {\textbf {F}}_k-\nabla {\textbf {F}}_{k-1}\) and \(\Vert \cdot \Vert \) denotes the Euclidean norm.

A generic version of three-term CG (TTCG) methods was proposed by Beale [3] to solve unconstrained optimization problems whose search direction

$$\begin{aligned} d_k:=-\nabla {\textbf {F}}_k+\beta _k d_{k-1}+\gamma _k d_t \end{aligned}$$
(15)

is calculated. Here \(\beta _k=\beta _k^{FR}, \beta _k^{HS}, \beta _k^{DY}\), \(d_t\) is a restarted direction, a direction with a restart procedure, and

$$\gamma _k:={\left\{ \begin{array}{ll} 0,&{} k=t+1,\\ \frac{\nabla {\textbf {F}}_k^Ty_t}{d_t^Ty_t}, &{} k>t+1. \end{array}\right. }$$

In fact, the goal of TTCG methods is to improve two-term CG methods. As in [2], a comparison among TTCG methods is made for solving unconstrained optimization problems, showing that TTCG methods are numerically efficient and robust. To obtain the step size \(\alpha _k\), we use the strong Wolfe line search [33]

$$\begin{aligned} &{\textbf {F}}(u_k+\alpha _k d_k)-{\textbf {F}}(u_k) \le c_1 \alpha _k \nabla {\textbf {F}}_k^Td_k, \end{aligned}$$
(16)
$$\begin{aligned}& \Big|\nabla {\textbf {F}}_{k+1}^Td_k\Big| \le -c_2 \nabla {\textbf {F}}_k^T d_k, \end{aligned}$$
(17)

where \(0<c_1<c_2<1\). The inequality (16) is called Armijo which tries to get a decrease in the function value. The inequality (17) is called curvature which lies a step size in the broad neighborhood of a local minimum point of \({\textbf {F}}\) with respect to \(\alpha \).

As discussed in Section 2, CG methods have no plan to control CG parameters. For example, if \(\beta _k\) in (15) is close to zero before CG iterations are near a minimum point, then \(d_k\) will be the steepest descent \(-\nabla {\textbf {F}}_k\), which has a zigzagging behavior, one of the sources of inefficiency of optimization algorithms. However, if CG iterations are close to a minimum point, the steepest descent direction \(-\nabla {\textbf {F}}_k\) can be used effectively. In (17), if one of \(\beta _k\) or \(\gamma _k\) or both are near zero before CG iterations are near an optimal point, the subspace is reduced and \(d_k\) cannot take advantage of \(d_{k-1}\) and \(d_t\). On the other hand, if at least one \(\beta _k\) or \(\gamma _k\) is large, then the descent direction (8) can be violated. In this case, the Wolfe line search method cannot be used the descent condition (8) does not hold.

3 Our contribution and organization

In this work, we develop a two-phase methods to remove noise. First, AMF is used to detect damaged pixels. Second, two efficient TTCG methods are proposed based on the steepest descent direction, the old direction, and the gradient differences at the old and current points.

The new phase of our algorithm is indeed the second phase. The first phase is not new and not very important for us, since it deals only with the detection of the damaged pixels. In practice, the second phase will be very efficient and will be able to recover the noisy pixels with high quality, regardless of how efficient the first phase is or how it can be updated by new techniques.

The parameters of our CG directions are generated and controlled in a new way:

  • None of the terms of the subspace form is large, which does not violate the descent condition (8), which is a prerequisite for using the Wolfe line search method to speed up our CG methods.

  • None of the terms of the subspace form dominates the other in general. In fact, our CG directions use their three terms when CG iterations are not near the optimal point.

  • When CG iterations are near a minimum point, the first term (steepest descent direction) dominates the other two terms because CG iterations should have small gradients in this case and accordingly CG directions has a small size and the risk of significantly skipping the minimum point is reduced.

If the second and third terms dominate the first term in cases where CG iterations are near a minimum point, CG directions may be large, violating the descent condition (8) and causing saddle points or maximum points to be found.

The descent property and global convergence of the proposed algorithms are proved. Numerical results show that our method is competitive compared to the state-of-the-art CG methods. In fact, in our comparison, the first phases of all CG methods are the same; only the second phases use different CG directions along which the Wolfe line search method is tried.

Section 2 describes two efficient CG methods to remove salt and pepper noise. Section 3 gives numerical results to illustrate the efficiency and robustness of the new algorithms. Some conclusions are given in Section 4. Finally, an additional material is reported in Section 5.

4 New efficient CG directions

In this section, we construct two new efficient TTCG methods for impulse noise removal from medical images. Our new directions are spanned by the steepest descent direction \(-\nabla {\textbf {F}}_k\), the previous direction \(d_{k-1}\), and the difference of the gradients \(y_{k-1}\) at the old point \(u_{k-1}\) and at the current point \(u_k\). Moreover, CG parameters are used to improve the numerical results of the noise removal. In practice, each component of \(d_{k-1}\) and \(y_{k-1}\) is adjusted based on the corresponding component of \(g_k\) such that each component of the new direction is no larger than that of \(\nabla {\textbf {F}}_k\). Since in finite precision arithmetic the descent condition cannot be guaranteed numerically without such an adjustment, although this condition holds theoretically, the search direction is almost always orthogonal to the gradient. Hence this adjustment is essential to generate an efficient direction in finite precision arithmetic.

  • The first efficient CG method (ECG1). We first define CG parameters based on our discussed adjustment as follows:

    $$\begin{aligned} \beta _k^1&:=\frac{\eta _1}{(1+k)^{\eta _2}}\max _{i=1,2,...,|\mathcal {N}|}\left\{ ~\Big|\frac{(\nabla {\textbf {F}}_k)_i}{(d_{k-1})_i}\Big| \,\,~| ~ \,\, (d_{k-1})_i\ne 0 \right\} ,\end{aligned}$$
    (18)
    $$\begin{aligned} \beta _k^2&:=\frac{\eta _1}{(1+k)^{\eta _2}}\max _{i=1,2,...,|\mathcal {N}|}\left\{ ~\Big |\frac{(\nabla {\textbf {F}}_k)_i}{(y_{k-1})_i}\Big | \,\,~\Big |~ \,\, (y_{k-1})_i\ne 0\right\} , \end{aligned}$$
    (19)

    in which \(\eta _1,\eta _2 \in (0,1)\) and k counts the number of iterations. Hence, the new iterate is updated by (7) whose direction \(d_k\) is computed by

    $$\begin{aligned} d_k:={\left\{ \begin{array}{ll} -\nabla {\textbf {F}}_k+\beta _k^1d_{k-1}+\beta _k^2 y_{k-1},&{} \text {if}\quad \nabla {\textbf {F}}_k^Td_{k-1}\ge 0,\\ -\nabla {\textbf {F}}_k,&{}\text {otherwise}. \end{array}\right. } \end{aligned}$$
    (20)

    Here the step size \(\alpha _k\) satisfies (16)-(17). Whenever the directions generated by (20) are not descent, they are replaced by \(d_k=-\nabla {\textbf {F}}_k\).

  • The second efficient CG method (ECG2). Before our new direction is introduced, four Boolean variables are defined as follows:

    $$\begin{aligned} \texttt{Dec1}:=\Big (\nabla {\textbf {F}}_k^Td_{k-1}>0\,\,\text {and}\,\, \nabla {\textbf {F}}_k^Ty_{k-1}<0\Big ),\\ \texttt{Dec2}:=\Big (\nabla {\textbf {F}}_k^Td_{k-1}<0\,\,\text {and}\,\, \nabla {\textbf {F}}_k^Ty_{k-1}>0\Big ),\\ \texttt{Dec3}:=\Big (\nabla {\textbf {F}}_k^Td_{k-1}<0\,\,\text {and}\,\, \nabla {\textbf {F}}_k^Ty_{k-1}<0\Big ),\\ \texttt{Dec4}:=\Big (\nabla {\textbf {F}}_k^Td_{k-1}>0\,\,\text {and}\,\, \nabla {\textbf {F}}_k^Ty_{k-1}>0\Big ). \end{aligned}$$

    Therefore the new direction

    $$\begin{aligned} d_k:={\left\{ \begin{array}{ll} -\nabla {\textbf {F}}_k-\beta _k^1d_{k-1}+\beta _k^2 y_{k-1},&{}\text {if } \texttt{Dec1} \text{ is true},\\ -\nabla {\textbf {F}}_k+\beta _k^1d_{k-1}-\beta _k^2 y_{k-1},&{}\text {if }\texttt{Dec2} \text{ is true},\\ -\nabla {\textbf {F}}_k+\beta _k^1d_{k-1}+\beta _k^2 y_{k-1},&{}\text {if }\texttt{Dec3} \text{ is true},\\ -\nabla {\textbf {F}}_k-\beta _k^1d_{k-1}-\beta _k^2 y_{k-1},&{}\text {if }\texttt{Dec4} \text{ is true}, \end{array}\right. } \end{aligned}$$
    (21)

    of ECG2 is computed while satisfying the descent condition (8). The new iterate of ECG2 is updated by (7) while computing the search direction by (21).

Our CG parameters (18) are slowly reduced by a factor \(\frac{\eta _1}{(1+k)^{\eta _2}}\), so that when CG iterations are near an optimal point (k becomes large), the steepest descent direction \(-\nabla {\textbf {F}}_k\) is used, whose size is small in such a case. On the other hand, two terms

$$\begin{aligned} \max _{i=1,2,...,|\mathcal {N}|}\left\{ ~\Big |\frac{(\nabla {\textbf {F}}_k)_i}{(d_{k-1})_i}\Big | \,\,~ |~ \,\, (d_{k-1})_i\ne 0 \right\} \end{aligned}$$

of (18) and

$$ \max _{i=1,2,...,|\mathcal {N}|}\left\{ ~\Big |\frac{(\nabla {\textbf {F}}_k)_i}{(y_{k-1})_i}\Big | \,\,~\Big |~ \,\, (y_{k-1})_i\ne 0\right\} $$

of (19) do not allow \(\beta _k^1\) and \(\beta _k^2\) to quickly become too small. Indeed, these two terms allow none of \(-\nabla {\textbf {F}}_k\), \(d_{k-1}\), and \(y_{k-1}\) to dominate until CG iterations are not near an optimal point.

5 Global convergence

To investigate the descent property and the global convergence of ECG1 and ECG2, we assume the following standard assumptions:

Assumption 3.1

The level set \(L(u_0):=\Big \{u \in \mathbb {R}^\mathcal {N} ~ |~ {\textbf {F}} (u)\le {\textbf {F}}(u_0)\Big \}\) is bounded, i.e., there exists a constant \(M>0\) such that

$$\begin{aligned} \Vert u\Vert \le M, \qquad \text {for all}\,\, u \in L(u_0). \end{aligned}$$
(22)

Assumption 3.2

In some neighbourhood \(\Omega \subseteq L(u_0)\), the gradient of the objective function \({\textbf {F}}\) has Lipschitz continuous gradient, i.e., there exists a constant \(L>0\) such that

$$\begin{aligned} \Vert \nabla {\textbf {F}}(u)-\nabla {\textbf {F}}(v) \Vert \le L \Vert u-v \Vert , \qquad \text {for all}\,\, u,v \in \Omega . \end{aligned}$$
(23)

Assumptions 3.1 and 3.2 imply that there exists a constant \(\epsilon >0\) such that

$$\Vert \nabla {\textbf {F}}_k\Vert \le \epsilon ,\qquad \text {for all}\,\, k\ge 0.$$

The following lemma ensures that the descent property of our algorithms is satisfied, resulting in the angle between the gradient and the search direction is far from \(90^\circ \).

Lemma 1

Let \(d_k\) be the direction generated by ECG1 or ECG2. Then, \(d_k\) is a descent direction, i.e., the condition (8) holds.

The following lemma is called Zoutendijk condition which is used to prove the global convergence of CG methods.

Lemma 2

Let \(d_k\) be a descent direction and the step size \(\alpha _k\) satisfies the strong Wolfe line search (16)-(17). Then, under Assumptions 3.1 and 3.2, the condition

$$\begin{aligned} \sum _{k=0}^{+\infty } \frac{(\nabla {\textbf {F}}_k^Td_k)^2}{\Vert d_k\Vert ^2}< +\infty \end{aligned}$$
(24)

holds.

Proof

See [38].

The following lemma [36] has a key role in the proof of the next theorem below.

Lemma 3

Let \(d_k\) be the direction generated by ECG1 or ECG2 and Assumptions 3.1 and 3.2 hold. If

$$\begin{aligned} \sum _{k=1}^\infty \frac{1}{\Vert d_k\Vert ^2}=+\infty , \end{aligned}$$
(25)

then

$$\liminf _{k \rightarrow \infty } \Vert \nabla {\textbf {F}}_k\Vert =0.$$

The following theorem is the main global convergence of our new algorithms whose proof is discussed in Section 8.2.

Theorem 1

Let \(d_k\) be the descent direction and \(\{u_k\}_{k \ge 0}\) be the sequence generated by ECG1 or ECG2. Then

$$\begin{aligned} \liminf _{k\rightarrow \infty } \Vert \nabla {\textbf {F}}_k\Vert =0. \end{aligned}$$
(26)

6 Numerical results

We compare two versions of our methods ECG1 and ECG2 with two-phase methods, whose first phases are AMF and whose second phases are known CG methods, on several standard images. AMF detects damaged pixels and restores them to some extent and then CG methods (CG directions along which Wolfe line search method is used) uniquely restores the image restored by AMF. As mentioned earlier, any denoising method can be used in the first phase. In fact, these two-phase methods are an evolution of denoising and their efficiency comes from the second phase.

Code compared. The following known CG algorithms are used in our comparison:

CGFR: This algorithm uses \(d_k:=-\nabla {\textbf {F}}_k+\beta _k^{FR}d_{k-1}\).

CGHS: This algorithm uses \(d_k:=-\nabla {\textbf {F}}_k+\beta _k^{HS}d_{k-1}\).

CGPR: This algorithm uses \(d_k:=-\nabla {\textbf {F}}_k+\beta _k^{PR}d_{k-1}\).

CGDY: This algorithm uses \(d_k:=-\nabla {\textbf {F}}_k+\beta _k^{DY}d_{k-1}\).

CGHZ: This algorithm uses \(d_k:=-\nabla {\textbf {F}}_k+\beta _k^{HZ}d_{k-1}\).

NPR1: This algorithm uses \(d_k\!:=-\nabla {\textbf {F}}_k+\beta _k^{NPR1}d_{k-1}\), \(\beta _k^{NPR1}\!=\!\frac{\beta _k^{PR}}{y_{k-1}^Td_{k-1}\!+\!\Vert y_{k-1}\Vert \Vert d_{k-1}\Vert }\).

NPR2: This algorithm uses \(d_k\!:=-\nabla {\textbf {F}}_k+\beta _k^{NPR2}d_{k-1}\), \(\beta _k^{NPR2}\!=\!\frac{\beta _k^{PR}}{\nabla {\textbf {F}}_k^Td_{k-1}\!+\!\Vert \nabla {\textbf {F}}_k\Vert \Vert d_{k-1}\Vert }\).

NPR3: This algorithm uses \(d_k\!:=-\nabla {\textbf {F}}_k+\beta _k^{NPR3}d_{k-1}\), \(\beta _k^{NPR3}\!=\!\frac{\beta _k^{PR}}{\nabla {\textbf {F}}_k^T\nabla {\textbf {F}}_{k-1}\!+\!\Vert \nabla {\textbf {F}}_k\Vert \Vert \nabla {\textbf {F}}_{k-1}\Vert }\).

NPR4: This algorithm uses \(d_k\!:=-\frac{\Vert y_{k-1}\Vert ^2}{\Vert s_{k-1}\Vert ^2}\nabla {\textbf {F}}_k+\beta _k^{NPR4}d_{k-1},\) and

$$\beta _k^{NPR4}:={\left\{ \begin{array}{ll} \frac{\nabla {\textbf {F}}_k^Ty_{k-1}}{\Vert \nabla {\textbf {F}}_{k-1}\Vert ^2},&{} \text{ if } \nabla {\textbf {F}}_k^Ty_{k-1}<0,\\ -\frac{\Vert \nabla {\textbf {F}}_k\Vert ^2}{\Vert \nabla {\textbf {F}}_{k-1}\Vert ^2},&{}\text{ if } \nabla {\textbf {F}}_k^Td_{k-1}>0,\\ 0,&{}\text {otherwise}. \end{array}\right. }$$

Test images. Five standard images are used:

  • Lena has been widely used in image processing since 1973. It is an image of Swedish model Lena Forsé cropped from the centerfold of the November 1972 issue of Playboy magazine. This image has a fixed resolution of 100 lines per inch and \(256 \times 256\) pixels.

  • House’s test image is in many versions due to cropping, scanning, resizing, compression, or conversion from color to grayscale. Here we use the version with \(256 \times 256\) pixels.

  • Cameraman image is one of the most popular standard grayscale test images of size \(256 \times 256\) belonging to MIT. By using standard test images, it is possible to test different image processing and compression algorithms and compare the results both visually and quantitatively. This image presents a number of challenges to image algorithms, such as image enhancements, image compression, etc. The image has a dynamic range of pixels between 0 and 255 (8- bits). The minimum value is 7 and the maximum value is 253. Here we use both versions of \(256 \times 256\) and \(512 \times 512\) pixels.

  • Computed tomography of the head (CT) uses X-rays to produce cross-sectional images of the body. This is possible because different tissues interact with X-rays in different ways. Some tissues allow X-rays to pass through without affecting them much, while other tissues exert a stronger effect. This image has \(512 \times 512\) pixels.

  • The brain sagittal (CerebSagE) MRI study looks at the brain with 24 sagittal (vertical - front to back) slices starting on the right side of the brain and moving to the left. This image consists of \(512 \times 512\) pixels.

Tuning parameters. ECG1 and ECG2 use the tuning parameters \(\eta _1=0.1\) and \(\eta _2=0.85\) while all algorithms in the Wolfe line search use the tuning parameters \(c_1=10^{-4}\) and \(c_2=0.5\).

Stopping tests. All algorithms are stopped whenever \(\Vert \nabla {\textbf {F}}_k\Vert \le 10^{-4}\).

Performance profile. A popular tool for identifying the efficiency of algorithms is the performance profile of Dolan & Moré [13]. This profile uses two cost measures: time in seconds and the peak signal noise ratio

$$ PSNR=10\log _{10}\frac{255^2}{\frac{1}{M\times N}\sum _{i,j}(u_{i,j}^r-u_{i,j}^*)^2}. $$

Here \(M\times N\) is the size of the image, \(u_{i,j}^r\) is the noisy image, \(u_{i,j}^*\) is restored the image and

$$\overline{u}=\frac{1}{M\times N}\sum _{i,j} (u_{i,j}^*)^2,$$

is the mean of the corrupted image. Denote by \(\mathcal S\) the list of compared solvers, by \(\mathcal P\) the list of problems, and by \(c_{p,s}\) the cost measure of the solver s to solve the problem p. The performance profile of the solver \(s\in S\)

$$ \rho _{s}(\tau ):=\frac{1}{|\mathcal P|}\Big |\Big \{p\in \mathcal P ~\Big |~ pr_{p,s}:=\frac{c_{p,s}}{\min (c_{p,s_0}\mid s_0\in S)}\le \tau \Big \}\Big |. $$

is the fraction of problems that the performance ratio \(pr_{p,s}\) is at most \(\tau \). In particular, the fraction of problems that the solver s wins compared to the other solvers is \(\rho _{s}(1)\) and the fraction of problems for sufficiently large \(\tau \) that the solver s can solve is \(\rho _{s}(\tau )\).

Our finding. We say that a method is competitive with others if it is significantly more efficient and robust than others in terms of cost measures: PNSR, time in seconds, relative cost of function and gradient evaluations, and the number of iterations. This can be done by plotting performance profiles of all methods with respect to these cost measures:

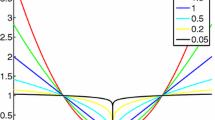
  • First, we compare all known CG with respect to PNSR, as shown in Fig. 1. The result is that NPR4 and NPR1 are the first and second best methods.

  • Then, we compare only NPR1 and NPR4 to find out which of the two methods has the lowest relative cost of function and gradient evaluations, the lowest iterations, and the lowest time in seconds (see Fig. 2), which confirms that NPR4 is competitive compared to NPR1.

  • Next, two versions of our methods ECG1 and ECG2 were compared (see Fig. 3). The result is that ECG2 is competitive compared to ECG1.

  • Finally, we compare our best method ECG2 with the best method NPR4 of the known CG methods shown in Fig. 4, with the result that ECG2 is so competitive compared to NPR4. Figures 5, 6, 7, 8 and 9 show that, after AMF identifies damaged pixels, ECG2 can significantly recover noisy images, even in the presence of high noise. After applying our CG methods, PSNR is significantly increased. Numerical results show that ECG2 is competitive with other known methods in terms of time in seconds and PSNR.

Fig. 1
figure 1

Performance profiles of known CG methods in terms of PSNR

Full size image
Fig. 2
figure 2

Performance profiles of NPR1 and NPR4 in terms of: (a) the total number of iterations; (b) the total number of function evaluations; (c) the total number of gradient evaluations; (d) time in seconds

Full size image
Fig. 3
figure 3

(a) Performance profiles of ECG1 and ECG2 in terms of PSNR; (b) Performance profiles of ECG1 and ECG2 in terms of time in seconds

Full size image
Fig. 4
figure 4

(a) Performance profiles of NPR4 and ECG2 in terms of PSNR; (b) Performance profiles of NPR4 and ECG2 in terms of time in seconds

Full size image
Fig. 5
figure 5

Recovering the \(256\times 256\) noisy Lena image via ECG2. (a)-(c) are the noisy images with \(50\%\), \(70\%\) and \(90\%\) of noises, (d)-(f) are the restored images via adaptive median filter (AMF), (g)-(i) are the restored images via ECG2

Full size image
Fig. 6
figure 6

Recovering the \(512\times 512\) noisy HeadCT image via ECG2. (a)-(c) are the noisy images with \(50\%\), \(70\%\) and \(90\%\) of noises, (d)-(f) are the restored images via adaptive median filter (AMF), (g)-(i) are the restored images via ECG2

Full size image
Fig. 7
figure 7

Recovering the \(512\times 512\) noisy CerebSagE image via ECG2. (a)-(c) are the noisy images with \(50\%\), \(70\%\) and \(90\%\) of noises, (d)-(f) are the restored images via adaptive median filter (AMF), (g)-(i) are the restored images via ECG2

Full size image
Fig. 8
figure 8

Recovering the \(256\times 256\) noisy Cameraman image via ECG2. (a)-(c) are the noisy images with \(50\%\), \(70\%\) and \(90\%\) of noises, (d)-(f) are the restored images via adaptive median filter (AMF), (g)-(i) are the restored images via ECG2

Full size image
Fig. 9
figure 9

Recovering the \(512\times 512\) noisy Cameraman image via ECG2. (a)-(c) are the noisy images with \(50\%\), \(70\%\) and \(90\%\) of noises, (d)-(f) are the restored images via adaptive median filter (AMF), (g)-(i) are the restored images via ECG2

Full size image

7 Conclusion

In this work, a two stages method for removing impulse noise, especially from medical images, was presented. The first stage used AMF to detect damaged pixels. Every new technique welcomes the use of the first stage, but this is not our case because this stage does not affect our method. The second stage included two new three-term CG directions, a kind of subspace spanned by the direction of steepest descent, the old direction and the gradient differences at the old and current points. The second and third terms of this subspace were scaled by two new CG parameters whose goal was to obtain three terms (no dominance among the three terms), guarantee the descent condition, and use the steepest descent directions when CG iterations were near an optimal point.

Our CG methods are independent of the type of line search method and useful in finite precision arithmetic. The global convergence of CG methods are proved. Several standard images were used to show that the new method is robust and efficient compared to other known CG methods for removing impulse noise.

Future work may involve constructing larger subspace techniques that can use other types of directions as a new component of the subspace. For example, the conjugate gradient direction can be enriched and combined with other directions such as the limited memory quasi-Newton method or other low-memory techniques.

8 Tools for ECG

8.1 The proof of Lemma 1

Let \(d_k\) be the direction by ECG1, computed by (20). If \(d_k\) does not satisfy the descent condition, then we have

$$\nabla {\textbf {F}}_k^Td_k=-\Vert \nabla {\textbf {F}}_k\Vert ^2<0.$$

Suppose that \(d_k\) is generated by ECG2. We consider the following four cases.

case 1. Dec1 results in that \(d_k\) is descent, i.e.,

$$\nabla {\textbf {F}}_k^Td_k=-\Vert \nabla {\textbf {F}}_k\Vert ^2-\beta _k^1\nabla {\textbf {F}}_k^Td_{k-1}+\beta _k^2 \nabla {\textbf {F}}_k^Ty_{k-1}<0.$$

case 2. Dec2 results in that \(d_k\) is descent, i.e.,

$$\nabla {\textbf {F}}_k^Td_k=-\Vert \nabla {\textbf {F}}_k\Vert ^2+\beta _k^1\nabla {\textbf {F}}_k^Td_{k-1}-\beta _k^2 \nabla {\textbf {F}}_k^Ty_{k-1}<0.$$

case 3. Dec3 results in that \(d_k\) is descent, i.e.,

$$\nabla {\textbf {F}}_k^Td_k=-\Vert \nabla {\textbf {F}}_k\Vert ^2+\beta _k^1\nabla {\textbf {F}}_k^Td_{k-1}+\beta _k^2 \nabla {\textbf {F}}_k^Ty_{k-1}<0.$$

case 4. Dec4 results in that \(d_k\) is descent, i.e.,

$$\nabla {\textbf {F}}_k^Td_k=-\Vert \nabla {\textbf {F}}_k\Vert ^2-\beta _k^1\nabla {\textbf {F}}_k^Td_{k-1}-\beta _k^2 \nabla {\textbf {F}}_k^Ty_{k-1}<0.$$

As a result, the direction by ECG2 is descent. \(\square \)

8.2 The proof of Theorem 1

Let

$$\begin{aligned} \gamma _k=\max \Big \{ |\beta _k^1|,|\beta _k^2|\Big \}\le M^*. \end{aligned}$$
(27)

Then either (20) or (21) results in

$$\begin{aligned} \Vert d_k\Vert \le \Vert \nabla {\textbf {F}}_k\Vert +|\beta _k^1| \Vert d_{k-1}\Vert +|\beta _k^2| \Vert y_{k-1}\Vert . \end{aligned}$$
(28)

Assumption 3.2 implies

$$\begin{aligned} \Vert y_{k-1}\Vert \le \alpha _k \Vert d_{k-1}\Vert . \end{aligned}$$
(29)

Therefore, (27)-(29) lead to

$$\begin{aligned} \Vert d_k\Vert&\le \epsilon +M^*\Vert d_{k-1}\Vert +M^*L\alpha _k \Vert d_{k-1}\Vert \\&=\epsilon +M^*\Big (1+\alpha _k L)\Vert d_{k-1}\Vert . \end{aligned}$$

In the same way as the proof of Lemma 3.1 in [36], there exists a positive constant M such that

$$\Vert d_k\Vert \le M, \qquad \text{ for all } k \ge 0,$$

so that

$$\sum _{k=1}^\infty \frac{1}{\Vert d_k\Vert ^2} \ge \sum _{k=1}^\infty \frac{1}{M^2}=+\infty .$$

Finally, Lemma 3 implies that

$$\liminf _{k \rightarrow \infty } \Vert \nabla {\textbf {F}}_k\Vert =0.$$

\(\square \)