1 Introduction

It is well known that blurred images are generated due to either motion of the object or due to the motion of the camera while capturing the image. Therefore two types of blurred images exist, i.e., 1) partial blur and 2) global blur. In both cases, researchers have developed numerous techniques for their detection and restoration. Many researchers have discussed the restoration of global blur images, which are presented in [4, 5, 7, 15, 16, 24, 26, 29, 31, 34, 35, 39]. Most of these techniques have followed the well-known blur model for linear motion, which is defined as follows:

$$\begin{aligned} g({\textbf {z}})=h({\textbf {z}})\otimes f({\textbf {z}})+n({\textbf {z}}), \end{aligned}$$
(1)

where \( g({\textbf {z}})\) is an observed image, \(h({\textbf {z}})\) is a degraded function, \( f({\textbf {z}})\) is an original image, and \( n({\textbf {z}})\) is a noise function. And \(''\otimes ''\) is two dimensional convolution operator. Here, we denote \({\textbf {z}}=(x,y)\) as 2 dimensional domain of an image and \({\textbf {dz}}=dxdy\) as suitable integral. This notation will be followed throughout this paper. In this model, the degraded function produces cumulative effects of distortions in the full image after convolution with the original image.

Fig. 1
figure 1

Different kind of Point Spread Functions (PSF): (a) Linear motion PSF (b) Two linear motions in different directions

Full size image

In the case of a partial blur, one or more objects are blurred during photography. Two types of blur models are shown in Fig. 1(a) & (b). Here, we focus on one or more linear motions of an object in the image. To restore this type of blurred object, one needs to detect the blurred object and subsequently apply blur restoration techniques. Many of these techniques are studied in [8, 9, 11, 19, 22, 27, 28, 36, 40]. But the challenge lies in detecting exact blurred regions of the degraded image. Hence, we have focused on detecting precise blurring regions of an image. Several techniques have been proposed in the literature to detect & segment partial blur in the image. Here, we have briefly reviewed a few of them. Pan et al. [14] have used maximum a posteriori framework to segment and deblur various blurred regions in an image. In [1], Chakrabarti et al. have introduced a likelihood measure using local Fourier Transform to determine whether a specific kernel blurs a particular image patch or not. Liu et al. [23] have proposed region-based features, namely, local power spectrum slope, gradient histogram span, and maximum saturation for identifying blur regions. In addition, they have discussed local autocorrelation congruency features for classifying detected blur either in motion or defocus blur. Similarly, Kalalembang et al. [17] have used block-based discrete cosine transform for blur detection, and Tang et al. [37] used log averaged spectrum residual to estimate blur map. In [32], Shi et al. have modified the set of blur features which are derived from multiple domains such as gradient histogram, kurtosis, and local filters, for blur detection. In [2], Bahrami et al. have estimated local blur kernels from gradient images, using an image patch, which generates a relative blur degree for each patch to classify it as blur or non blur patch. Similarly, in [30], Paramanand et al. have used a local image patch to estimate the transformation spread function around each pixel to classify it as blurred or non-blurred pixels by manually selecting the patches. In [3], Bini et al. have proposed PDE based image deblurring method wherein they used diffusive image smoothing term and a reactive image enhancement term to construct the nonlinear level set model. Devy et al. [8] proposed a local blur kernel estimator based on two filters, i.e., Gabor and dictionary, to study the pattern around each pixel. However, the number of filters is decided manually, which limits the scope of this method. In [33], Su et al. have detected blur by examining the singular value information for each image pixel, and subsequently, alpha channel is used to classify the type of the blur. In [10], Golestaneh et al. have proposed a method to estimate spatially varying blur from a single image by using a multi-scale transform decomposition followed by fusion and sorting of high-frequency coefficients of gradient magnitudes. This method detects both defocus and motion blur without prior knowledge of blur type. Similarly, one of the effective technique described by Javaran et al. in [13] also detect and segment blur and nonblur region for both types of a blur - defocus blur and motion blur. In the case of real images, the techniques discussed so far may not produce connected blur/non blur regions. Recently, few deep learning-based methods have been explored. Kim et al. [20] used a deep convolutional neural network for the detection of defocus and motion blur technique. Subsequently, Ma et al. [25] have used a support vector machine (SVM) to classify image patches in a blur and non-blur regions after training Deep Neural Network (DNN). Other DNN based research works can be found in [12, 38]. These techniques are capable of detecting motion blur regions up to a certain accuracy. There is still a need for further improvement in detecting the exact portion of blurred regions.blur In this paper, we propose a novel approach to detect local blur in an image where blurred and non-blurred regions have similar colors. In the existing literature, this issue has been addressed partially. In our approach, we applied Radon transform and Laplacian of Gaussian on a local neighborhood around each pixel in the image and observed that the values of these Radon transform give significant differences for blurred and non-blurred pixels. We utilized this phenomenon along with the work proposed in [18] to classify each pixel either in blurred or non-blurred pixels. The main contributions of this paper are listed below:

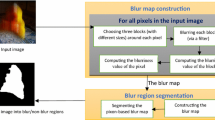
  • A novel local blur estimator is proposed based on the value of Radon transform (RT) of LoG and local blur angle estimator (LBAE). Here, it is emphasized that a local blur estimator is used for calculating blur information, while a local blur angle estimator is used for finding a blur angle at each pixel in an image. The main framework of the proposed method is shown in Fig. 2.

  • Two new weight functions \(k_{1}(z)\) and \(k_{2}(z)\) have been suggested, which play a significant role in deciding pixel-wise weightage of blur information derived from LBAE and the value of RT of LoG, respectively.

  • Few variants of the second weight function \(k_{2}(z)\) are proposed, and their performance analyzed.

The outline of this paper is as follows. In Section 1, we briefly discussed previous works related to the detection and segmentation of partial blur. In Section 2, we have reviewed the concepts of blur model, Radon transform, Laplacian of Gaussian, and local blur angle estimator, which are used extensively in the proposed method. A novel local blur estimator along with two weight functions are proposed in Section 3. Section 4 describes the experimental results of the proposed model and evaluation of the quantitative performance of the proposed method with other existing methods. Conclusions are discussed in Section 5.

Fig. 2
figure 2

Framework of the proposed technique

Full size image

2 Background

In this section, we present the concepts of the blur model, Radon transform, Laplacian of Gaussian, directional derivative and earlier works of local blur angle estimation technique. In this section, we present the concepts of the blur model, Radon transform, Laplacian of Gaussian, directional derivative, and earlier works of local blur angle estimation technique.

2.1 Blur model

Blur kernel of one directional motion blur model [6] is described as:

$$\begin{aligned} K^L = {\left\{ \begin{array}{ll} \frac{1}{L};\text {if } \root 2 \of {x^2+y^2}\le \frac{L}{2} \text { and } \frac{y}{x}=tan\theta , \\ 0; ~\text { otherwise,} \end{array}\right. } \end{aligned}$$
(2)

where, L is a blur length, \(\theta \) is a blur angle, and (x, y) is pixel position. Many techniques are used for estimating blur parameters. Primarily used estimation is mentioned in [21]. The argument related to the maximum value of Radon transform (RT) gives blur angle, and the motion blur length is estimated using the cepstrum of a blurred image which is the distance between two significant negative peaks from the origin [21].

The original image can be restored using a convolution theorem, provided the blur kernel is known. The linear motion blur model described in (2), will work in the case of a partial blur, only if the object is uniformly moving in a linear direction. But, this model fails to deblur an object without finding a proper blur region. Therefore, it is essential to detect the blurred region for applying further post-processing techniques.

2.2 Operators: RT, loG, directional derivative

The Radon transform (RT) is used to measure the strength of a line in an image, the details of RT are well discussed in [29] and is defined as:

$$\begin{aligned} R(I,\rho ,\theta ) =\int _{-\infty }^{\infty }I(\rho cos\theta -y sin\theta ,\rho sin\theta +y cos\theta )dy, \end{aligned}$$
(3)

where \(R(I,\rho ,\theta )\) denotes Radon transform and it is an integral in an image I along the line at an angle \(\theta \) and at distance \(\rho \) from origin. Laplacian of Gaussian (LoG) is used for sharpening the edges after suppressing the noise and it is defined as:

$$\begin{aligned} LoG=\frac{x^{2}+y^{2}-2\sigma ^{2}}{\sigma ^{4}}e^{\frac{-(x^{2}+y^{2})}{2\sigma ^{2}}}, \end{aligned}$$
(4)

where \(\sigma \) is a standard deviation, x and y are pixel locations. Directional derivative of an image I at pixel location \((a,b)\) in the direction of vector \(\nu =(\nu _{1},\nu _{2})\) is defined as

$$\begin{aligned} \nabla _{\nu }{I}=\nabla _{x}{I}.{\nu _{1}}+\nabla _{y}{I}.{\nu _{2}}, \end{aligned}$$
(5)

where \(\nabla _{x} \text { and } \nabla _{y}\) are derivative operators.

2.3 Local blur angle estimation

In this subsection, we have discussed the local blur angle estimation method in detail, which is mentioned in [18]. Here, the authors have introduced a local blur angle estimator (LBAE) to find pixel-wise blur angle throughout an image using LoG and RT, and it is defined as

$$\begin{aligned} \tilde{\theta }^{l}=Arg \max _{\mathbf {\theta }}Var\Big \{\nabla _{y}\Big [ {R}\Big (LoG(\nabla _{u}I)\Big )\Big ]\Big \}, \end{aligned}$$
(6)

where \(\tilde{\theta }^{l}\) denotes estimated blur angle for each pixel, l indicates local blur angle and \(R(LoG(\nabla _{u}))\) is the composition of operators where R, LoG and \(\nabla _{u}\) are denoted as Radon transform, Laplacian of Gaussian and directional derivative, respectively. All these operators are applied sequentially on a small window that is selected around each pixel in an image. Here, a directional derivative operator is used for sharpening the edges. To use a directional derivative, the availability of prior information about the likely blur direction is essential. The prior information of likely blur direction is helpful in increasing the accuracy of blur angle estimation. Blur angle estimators have been proposed for finding likely blur directions, in [18], which are defined as follows:

$$\begin{aligned} \hat{\theta }_{k}^{g}=Arg\max _{\theta \ne \hat{\theta }_{\textbf{1}}^{g},\hat{\theta }_{\textbf{2}}^{g},...,{\hat{\theta }}_{\textbf{k}-1}^{g}}Var\Big \{ \nabla _{y}\Big [ {R}(\nabla I)\Big ]\Big \}, \end{aligned}$$
(7)

where \(\hat{\theta }_{k}^{g}\), \(k=1,2,\cdots ,n\)’s are likely blur angle existing in an image related to n different objects and g indicates for global blur angle. In the case of the non-availability of likely blur directions, one can use a normal gradient operator.

Subsequently, the LoG is applied after applying directional derivative followed by RT. The index of the maximum value of RT gives a blur angle. This estimator determines the blur angle effectively from objects blurred by different blur parameters. However, it fails in segregating blurred and non-blurred regions accurately, which can be seen from Fig. 9(b) for the erroneous outcomes in the non-blurred region. In this paper, we have proposed a new technique to overcome this problem.

3 Proposed technique

In this section, we have described a novel local blur estimator along with two weight functions. The goal of this method is to detect blurred and non-blurred regions accurately and efficiently. The proposed method primarily uses LoG and RT on a small window in two different estimators. The proposed local blur estimator is defined as

$$\begin{aligned} \tilde{B}({\textbf {z}})= k_{1}({\textbf {z}})\tilde{\theta }^{l}({\textbf {z}})+k_{2}({\textbf {z}}) \tilde{R}^{max}({\textbf {z}}), \end{aligned}$$
(8)

where \(\tilde{\theta }^{l}({\textbf {z}})\) is

$$\begin{aligned} \tilde{\theta }^{l}({\textbf {z}})=Arg\max _{\mathbf {\theta }}Var\Big \{ \nabla _{y}\Big [ {R}\big (LoG(\nabla I({\textbf {z}})\big )\Big ]\Big \}. \end{aligned}$$
(9)

Here, \(\tilde{\theta }^{l}\) is locally estimated for each pixel and other parameters in (9) are the same as in (6). Note that the (9) and (6) are the same if likely blur directions in (6) are not considered, and it is used for emphasizing blur region detection. In the second term, \(\tilde{R}^{max}({\textbf {z}})\) is used to emphasize non-blur region and is defined as

$$\begin{aligned} \tilde{R}^{max}({\textbf {z}})=\max _{\mathbf {\theta }}Var\Big \{ \nabla _{y}\Big [ {R}\big (LoG(\nabla I({\textbf {z}})\big )\Big ]\Big \}. \end{aligned}$$
(10)

Here, \(\tilde{R}^{max}({\textbf {z}})\) is the maximum value of \(R(LoG(\nabla ))\) in the neighbourhood of each pixel in \(I({\textbf {z}})\), where R and LoG are defined in (3) & (4), respectively. In each window of an image, RT calculates the strength of the lines at a particular angle. Therefore, the value of \(\tilde{R}^{max}({\textbf {z}})\) is higher at the blurred region points as compared to non-blurred region points. Experimentally, it is observed that in the non-blurred region, the \(\tilde{R}^{max}({\textbf {z}})\) is consistently lower, as also seen from Fig. 3(b).

The weight functions are defined as

$$\begin{aligned} k_{1}({\textbf {z}})=\frac{1}{1+\beta (\tilde{\theta }^{l}({\textbf {z}})-M_{\tilde{\theta }})^{2}} ~~\textrm{and}~~ k_{2}({\textbf {z}})=\frac{1}{1+\alpha d_{l}^{ge}({\textbf {z}})}. \end{aligned}$$
(11)

Here, \(M_{ \tilde{\theta }}\) is mode of \(\tilde{\theta }^{l} (z)\) and \(d_{l}^{ge}(z)\) is a maximum value of edge weighted geodesic distance which is calculated locally from \(\tilde{R}^{max}({\textbf {z}})\) & (12).

The constants \(\alpha \) and \(\beta \) are used for generating weight of the function \(k_{2}({\textbf {z}})\) and \(k_{1}({\textbf {z}})\), respectively. In particular, the smaller value of these constants implies giving more weightage to the corresponding function. The values of these constants taken for various test images are recorded in Table 3.

The first term in (8) provides more weightage to the blurred region of an image. The weight function \(k_{1}({\textbf {z}})\) is selected in such a way that it vanishes at the non-blurred region and approaches to 1 at the blurred region as depicted in Fig. 4(b). Whereas the second term of (8) provides more weightage to the non-blurred region of an image. The weight function \(k_{2}({\textbf {z}})\) is selected in such a way that it vanishes in blurred region and approaches to 1 in non-blurred region, which is opposite of \(k_{1}({\textbf {z}})\) and, can be seen in Fig. 4(c).

Fig. 3
figure 3

a) Test image: Horse b) Corresponding \(\tilde{R}^{max}({\textbf {z}})\) calculated by taking 12\(\times \)12 window size

Full size image
Fig. 4
figure 4

(a) Test image: Horse-500\(\times \)332 (b) The values of the function \(k_{1}(z)\) along the green line inside the rectangle (superimposed as yellow color) (c) The value of the function \(k_{2}(z)\) along the green line inside the rectangle (superimposed as yellow color)

Full size image

In each local window \(I_{B}({\textbf {z}})\), geodesic distance is calculated for each pixel from a central candidate pixel \((x_{0},y_{0})\) by \(d_{l}^{ge}({\textbf {z}})=0 \) for \({\textbf {z}} =(x_{0},y_{0})\) and \( d_{l}^{ge}({\textbf {z}})=\frac{d_{B}({\textbf {z}})}{\parallel d_{B}({\textbf {z}})\parallel _{L^{\infty }}}\) for other pixels \( {\textbf {z}} \) in B, where \(d_{B}({\textbf {z}})\) is determined by solving the following PDE:

$$\begin{aligned} \mid \triangledown d_{B}({\textbf {z}}) \mid= & {} f({\textbf {z}}),\\ \nonumber d_{B}({\textbf {z}})= & {} 0, {\textbf {z}} \in B. \end{aligned}$$
(12)
Fig. 5
figure 5

(a) The average value of \(k_{2}^{'}({\textbf {z}})\) derived using local variance (b) Average value of \(k_{2}({\textbf {z}})\) derived based on geodesic distance function (c) Absolute difference between blurred and non-blurred region. Number of samples: 1000 random pixels from each region. Test image shown in Fig. 4(a) has used for computation

Full size image

Here, \(f({\textbf {z}})=\epsilon _{g}+\beta _{g} \mid \triangledown G_{\sigma } \otimes I_{B}({\textbf {z}}) \mid \), where \( \epsilon _{g}\) and \(\beta _{g} \) are constant parameters and \(G_{\sigma }\) is a Gaussian function with standard deviation \(\sigma \) to make the \(I_{B}({\textbf {z}})\) free from noise and \(\otimes \) is a convolution operator. Here, f(z) is a distance function which calculate distance between central pixel (i.e., \({\textbf {z}} =(x_{0},y_{0})\)) and other pixels in the small window. This distance function \(f({\textbf {z}})=\epsilon _{g}+\beta _{g} \mid \triangledown G_{\sigma } \otimes I_{B}({\textbf {z}}) \mid \) is fulfilling the properties, where if f(z) is small then we have flat region and if f(z) is large then we have edgy region. And keeping the values of the constants \(\epsilon _{g}=10^{-3}\) and \(\beta _{g}=1000\), we get small distance in the flat region because \( \mid \triangledown G_{\sigma } \otimes I_{B}({\textbf {z}}) \mid =0\) in the flat region, whereas \( \mid \triangledown G_{\sigma } \otimes I_{B}({\textbf {z}}) \mid \) will be large in edgy region. Other choices of \(k_{2}({\textbf {z}}) \) are

$$\begin{aligned} k_{2}^{'}({\textbf {z}})=\frac{1}{1+\alpha _{1} Var^{l}({\textbf {z}})} ~~~\textrm{and}~~~ k_{2}^{''}({\textbf {z}})=\frac{1}{1+\alpha _{2} H({\textbf {z}})}, \end{aligned}$$
(13)

where \( Var^{l}({\textbf {z}})\) is local variance in \(\tilde{R}^{max}\) for each pixel and H is the Heaviside function which is defined as

$$\begin{aligned} H({\textbf {z}})= {\left\{ \begin{array}{ll}0 \hspace{1mm}; \tilde{R}^{max}({\textbf {z}}) <\epsilon ~~ \text {for non-blurred region}\\ 1 \hspace{1mm} ; \tilde{R}^{max}({\textbf {z}}) >\epsilon ~~ \text {for blurred region}. \end{array}\right. } \end{aligned}$$

Here, \( \epsilon >0\) needs to be chosen manually dependent on \(\tilde{R}^{max}({\textbf {z}})\) value, which varies from image to image. For instance, if the object is motion blurred with a small blur length, \(\tilde{R}^{max}({\textbf {z}})\) values of blur and non-blur region has narrow difference. In this way, choice of manual \(\epsilon >0\) became significant and picked so that a large portion of the pixels from non-blur region have \(\tilde{R}^{max}({\textbf {z}})<\epsilon \). In view of investigations, we observed that the \(k_{2}({\textbf {z}})\) is more reliable, however \(k_{2}^{'}({\textbf {z}})\) has a superior computational proficiency. While \(k_{2}^{''}({\textbf {z}}) \) is more reliable and efficient if the value of \(\epsilon \) is picked appropriately. For automatic computation, one has to choose either \(k_{2}({\textbf {z}})\) or \(k_{2}^{'}({\textbf {z}})\). By comparing the mean values of \(k_{2}({\textbf {z}})\) for blurred and non-blurred region as shown in Fig. 5 (b), it is seen that the difference is more for \(k_{2}({\textbf {z}})\) in blurred and non-blurred region. By similar comparison for \(k_{2}^{'}({\textbf {z}})\), it is seen that \(k_{2}^{'}({\textbf {z}})\) produces a narrow gap for blurred and non-blurred region which is shown in Fig. 5 (a). This is depicted in Fig. 5(c) in terms of absolute differences in blurred and non-blurred region of \(k_{2}({\textbf {z}})\) and \(k_{2}^{'}({\textbf {z}})\). Therefore, we conclude that geodesic distance based function matches better to the desired function as compared to local variance based function as seen in Fig. 5(c). Pseudo code of the proposed method is presented in algorithm 1.

Fig. 6
figure 6

(a) Test image: Lena-512\(\times \)512. (b), (d) & (f) Blur images with 10 \(^\circ \), 30 \(^\circ \) and 60 \(^\circ \) blur angle and 50 pixels blur length, respectively. (c),(e) & (g) Comparison of the average value of \(\tilde{R}^{max}\) for various blur lengths- 10, 20, 30, 40, and 50 pixels. Here note that BL means blur length

Full size image
Fig. 7
figure 7

(a) Test image: Mandrill-512\(\times \)512. (b), (d) & (f) Blur images with 10\(^\circ \), 30\(^\circ \) and 60\(^\circ \) blur angle and 50 pixels blur length, respectively. (c), (e) & (g) Comparison of the average value of \(\tilde{R}^{max}\) for various blur lengths- 10, 20, 30, 40, and 50 pixels. Here note that BL means blur length

Full size image
Algorithm 1
figure a

Pseudo code of the proposed technique.

Full size image
Fig. 8
figure 8

: Jaccard Similarity (JS) index for \(k_{2}(z)\) for various window size

Full size image
Fig. 9
figure 9

(a) Input image: Horse-533\(\times \)355; (b) Ground truth, (c) Blur information from [18], (d) Segmented object [18], (e-f) Blur information and segmented object using method from [10], (g-h) Blur information and segmented object using method from[32], (i-j) Blur information and segmented object using proposed method

Full size image
Fig. 10
figure 10

(a) Input image: Bike-533\(\times \)355; (b) Ground truth, (c) Blur information and using method from [18] , (d) Segmented object from [18], (e-f) Blur information and segmented object using method in [10], (g-h) Blur information and segmented object using method in [32], (i-j) Blur information and segmented object using proposed method

Full size image
Fig. 11
figure 11

(a) Input image: Rickshaw-640\(\times \)450; (b) Ground truth, (c) Blur information and using method from [18], (d) Segmented object [18], (e-f) Blur information and segmented object using method in [10], resp. (g-h) Blur information and segmented object using [32] method, resp. (i-j) Blur information and segmented object using proposed method, resp

Full size image

4 Experimental results and discussion

In this section, we present the experimental results and evaluation of the performance of the proposed method.

4.1 Estimators, dataset and parameter setting

This subsection describes implementation of the proposed estimators on test images. First, we discuss the significance of the estimator \(\tilde{R}^{max}({\textbf {z}})\) given in (10). To validate the effectiveness of (10), we consider a test image of size 512\(\times \)512 pixels; Lena and Mandrill which are displayed in Figs. 6(a) and 7(a), respectively. To test \(\tilde{R}^{max}\) in the blurred and non-blurred images, we generated blurred images with different blur parameters. Here, we have used the linear blur model mentioned in (2) with different blur parameters, i.e., blur lengths ranging from 10, 20,...,and 50 pixels, for each of the blur length we applied three blur angles (\(10^{\circ }\), \(30^{\circ }\), and \(60^{\circ }\)). By picking various pairs of blur lengths and blur angles, we created blur images. Subsequently, considered 100,000 sub-images for window size ranging \(10 \times 10 \) to \(30 \times 30\) from random locations and \(\tilde{R}^{max}\) is calculated for each sub-images. Moreover, the average value of \(\tilde{R}^{max}\) is compared between blurred and non-blurred images which are displayed in Figs. 6 and 7. Here non-blur image is considered as original image. The wide gap in \(\tilde{R}^{max}\) values of blurred and non-blurred images is observed from both the test images which are shown in Fig. 6(b-g) and Fig. 7(b-g). This phenomena are used effectively for segmenting blurred and non-blurred region. Moreover, it is seen that \(\tilde{R}^{max}\) of blurred image is always greater than of non-blurred image for a given window size, which can be seen from Figs. 6(b-g) and 7(b-g). The optimal window size should be above 10 pixels according to [18]. Therefore, we have chosen 10\(\times \)10 to 16\(\times \)16 pixels, window size for computation. For clarity, the comparison of \(\tilde{R}^{max}\) values from blur and nonblur images are calculated for two test images - Lena and Mandrill, which is shown in Figs. 6(c),(e) & (g) and 7(c),(e) & (g) for blur angles \(10^\circ \), \(30\circ \) & \(60^\circ \), respectively. The function \(\tilde{R}^{max}\) is segregating blurred and non blurred region effectively and therefore using the value of \(\tilde{R}^{max}\), we constructed local blur estimator. Next, we discuss \(\tilde{\theta }^{l}({\textbf {z}})\) and the proposed estimator \(\tilde{B}({\textbf {z}})\) along with two weight functions \(k_{1}({\textbf {z}})\) and \(k_{2}({\textbf {z}})\). From Fig. 9(b), it is observed that \(\tilde{\theta }^{l}({\textbf {z}})\) produces uniform blur information in blurred region, whereas in a non-blurred region it gives nonuniform blur information. The same can be observed in other test image displayed in Fig. 10(b). To overcome this problem, we used a new blur estimator \(\tilde{B}({\textbf {z}})\) as mentioned in (8). This is tested on both grayscale and colour images taken from datasets of [32], http://www.cse.cuhk.edu.hk/~leojia/projects/dblurdetect/dataset. From Fig. 9(e), it is seen that the new blur estimator in the proposed method produces uniform output in the non-blurred regions, unlike the method proposed in [18]. The final segmentation result of proposed method is compared with [10, 18, 32] along with ground truth results which is seen in Fig. 9(f-j). By subjective observation, it can be seen that the outcomes from the proposed method is better than other existing methods. Subsequently, quantitative analysis has been done by computing various performance measures after segmentation. For segmentation, we have used Ostu’s method. The results are discussed in Section 4.2.

Fig. 12
figure 12

Accuracy measures

Full size image
Fig. 13
figure 13

(a) Input image: Boy-640\(\times \)426;(b) Ground truth, (c) Blur information and using method from [18], (d) Segmented object [18], (e-f) Blur information and segmented object using method in [10], resp. (g-h) Blur information and segmented object using [32] method, resp. (i-j) Blur information and segmented object using proposed method, resp

Full size image

Further, we have analysed weight functions \(k_{2}({\textbf {z}})\) and \(k_{2}^{'}({\textbf {z}})\) for different scenarios. Here, we observed that the geodesic distance based function is better in comparison to local variance based function. Fig. 8(a) & (b) shows Jaccard’s similarity index for \(k_{2}({\textbf {z}})\) and \(k_{2}^{'}({\textbf {z}})\) derived over different window sizes ranging from 4\(\times \)4 to 30\(\times \)30 pixels. Here, we observed that any window size in the range greater than 4\(\times \)4 for the function \(k_{2}({\textbf {z}})\) produces a desirable result for the test image shown in Fig .9(a). Whereas for second test image shown in Fig. 10, the window size greater than 10\(\times \)10 produces a better result. This is due to the low contrast in the image. The third weight function \(k_{2}^{''}(z)\) mentioned in (13) is fully dependent on \(\epsilon \) which can differ from image to image as mentioned previously.

Table 1 Average of all accuracy measures
Full size table
Table 2 Computation time (in seconds)
Full size table

4.2 Quantitative performance

To assess the quantitative performance of our method, we compare our approach with M1, M2, and M3 methods described in [10, 18, 32], respectively. Here, M1 means method from [32], M2 means method from [10] and M3 means method from [18]. We determined various performance measures like; Dice index, Jaccard index, Accuracy, Sensitivity (Recall), Precision, Matthews Correlation Coefficient (MCC), and Specificity for three test images to find the similarity between the segmented image and the ground truth mask provided with the dataset. We have used a confusion matrix comprised of four values true positive (TP), true negative (TN), false positive (FP) and false-negative (FN), to determine these measures, and calculated as follows:

$$\begin{aligned} \text {Dice}= & {} \frac{2\text {TP}}{(2\text {TP}+\text {FP}+\text {FN})}, ~~~~ \text {Jaccard}=\frac{\text {TP}}{(\text {TP}+\text {FP}+\text {FN})},\\ \text {Accuracy}= & {} \frac{\text {TP}+\text {TN}}{(\text {TP}+\text {TN}+\text {FP}+\text {FN})},\\ \text {Sensitivity}= & {} \frac{\text {TP}}{(\text {TP}+\text {FN})}, \text {Precision}=\frac{\text {TP}}{(\text {TP}+\text {FP})},~~~ \text {Specificity}=\frac{\text {TN}}{(\text {TN}+\text {FP})} ~ \text {and} \\ \text {MCC}= & {} \frac{\text {TP}\times \text {TN} - \text {FP} \times \text {FN}}{\sqrt{(}\text {TP}+\text {FP})(\text {TP}+\text {FN})(\text {TN}+\text {FP})(\text {TN}+\text {FN})}. \end{aligned}$$

The values of these measures are closer to 1 indicates superior performance. The calculated values for three images are shown in Fig. 12. For the test image shown in Fig. 9, 5 out of 7 measures-accuracy, Jaccard, MCC, Dice, and sensitivity, are highest for the proposed method among all methods, which can be seen from Fig. 12(a). Values of other measures for the proposed method are also better. Though the M3 method gives the highest precision and specificity. For the test image shown in Fig. 10, 4 out of 7 measures- accuracy, precision, Jaccard, and Dice are highest for the proposed method, which can be seen from Fig. 12(b). M2 techniques are likewise delivering the most noteworthy estimations of MCC. At the same time, the M1 method produces the highest sensitivity, and M3 produces the highest specificity. For the test image shown in Fig. 11, 3 out of 7 measures- accuracy, Jaccard, and MCC are highest for the proposed method, which can be seen from Fig. 12(a). Whereas Dice are highest in the M2 method, and sensitivity is highest from the M1 method. In contrast, precision and specificity are maximum in the M3 method. From the test image displayed in Fig. 13, 5 out of 7 measures- accuracy, Dice, Jaccard, MCC, and precision are highest for the proposed method, which can be seen from Fig. 12(d). Overall, the proposed method gives 80 % (in 17 out of 21) highest values across all measures in all test images. Averages performance of segmentation measures for all test images is presented in Table 1 shows the superior performance of the proposed method. The computational expense for all test images is recorded in Tables 2, and 3 and the proposed method takes extra computational time compared to other existing methods. The extra computational expense of the proposed method is because of LBAE, which is a time-consuming operation. Moreover, geodesic distance-based weight function \(k_{2}({\textbf {z}})\) is also time taking operation. To reduce time complexity, other weight functions can be used, but it will deteriorate blur/nonblur segmentation accuracy. However, clearly visible that the performance of the proposed method is superior to other existing methods in terms of segmentation accuracy. We have used MATLAB software to implement the algorithm on a 2.0 GHz processor with 4GB RAM.

Table 3 The value of parameters for proposed method
Full size table

5 Conclusion

In this paper, a novel method to detect a partial blur region is proposed which facilitates object restoration, information retrieval, blur increment, etc., by segmenting blurred / non-blurred regions. In the proposed method, we have developed a new estimator with the help of the Radon transform and Laplacian of Gaussian operators. This estimator comprises of LBAE and \(\tilde{R}^{max}\) (see, (10)) along with two new weight functions (see, (11)). The experimental results carried out in this paper conclude the following: (i) As compared to other existing methods, the method proposed here is effective in detection & segmentation of the blurred region. (ii) Also, using various accuracy measures, the method proposed is better matched quantitatively to the ground truth result. (iii) The two-weight functions play an essential role in deciding the proportionality of index and maximum value of Radon transform. (iv) The proposed method is helpful in segregating blurred and non-blurred regions effectively, which further can be used as input for deblurring techniques. (v) It is more time-consuming than other existing methods, and we will attempt to find approaches to reduce the computational expense in the future.