A new image/video encryption scheme based on fractional discrete Tchebichef transform and singular value decomposition

Abstract

One of the major application areas of the fractional-order discrete transform (FrDTs) is in signal and information security, particularly in signal and image/video encryption. Recently, many researchers proposed techniques that implemented not only the fractional transforms, but also various randomized versions of the FrDTs, which add more security features to signal’s encryption. In this paper, we propose a new image/video encryption scheme based on fractional-order discrete Tchebichef transform (FrDTT) using singular value decomposition. The FrDTTs are derived algebraically using the spectral decomposition of discrete Tchebichef polynomials, then the singular value decomposition technique in order to build a basic set of orthonormal eigenvectors which help to develop FrDTTs. Finally, we implement and apply the scheme proposed in this paper for encrypting test images and video sequences. Moreover, we methodically perform the security evaluation in terms of brute force and statistical attacks as well as comparisons with the existing methods in terms of secret key sensitivity and space. The promising experiment results demonstrate the effectiveness and efficiency of our proposed FrDTTs based image encryption techniques.

1 Introduction

With the rapid development of network and multimedia technologies, the acquisition and transmission of information has become increasingly fast and convenient. Images and videos are widely distributed on the Internet because of their intuitive and vivid nature and their wealth of information. However, many images do not want to be acquired by illegal users due to multiple privacy and interests. Therefore, how to transmit images and videos safely on the network has become a very important issue. Image and video encryption technology can encrypt before propagation to hide the original information, which is an effective method to solve the image security problem. There are various techniques like Steganography, watermarking, cryptography available for the security of information from the invaders. Among these techniques, Steganography is used to embed the text into another image for the protection of text [4]. In watermarking, the original image is applied as watermarked image on cover image [27]. In cryptography, the whole image is transformed in such a form that is difficult for the interloper to comprehend it, so used for the protection of images [29] and videos [40]. Every security technique has its own significance and applications. But, encryption is one of the best methods used in cryptography for security of images and videos. This method is performed to create confusion and diffusion in the images and videos (or frames of videos). Due to presence of chaos in the ciphered information, hacker will consider information as random noise. The appearance of encrypted form will protect information from getting stolen. Further, encryption can be performed with different algorithms to hide actual data from hackers. The several techniques available for encryption algorithm are chaotic mapping [14], matrix transformation [1], scrambling [46], compressive sensing [60] and encryption using wavelet transform [7] etc. At present, image encryption can be performed in the spatial domain and the transform domain. The spatial domain mainly uses image scrambling, substitution, and diffusion to complete the encryption operation. The initial image scrambling is mostly based on Arnold transform, magic square transform, etc. In recent years, some space-domain image encryption algorithms combined with chaos theory have been proposed [32, 55]. Due to their strong key sensitivity and scrambling characteristics, these similar algorithms have high research value and important research significance. The transform domain encryption algorithm starts from the characteristics of the image transformation matrix and uses the key to generate a new transformation matrix to transform the image, thereby transforming the original clearly identifiable image into random noise information. This encryption method has a higher encryption efficiency. High, anti-interference characteristics, and easy to achieve compression. The characteristics of consideration in any encryption systems are perceptual transparency, capacity, and tamper resistance. Perceptual transparency is the ability to mask the existence of secret data from human visual system [13, 42, 69]. Capacity is the basic concern of any encryption algorithm that allows to increase the amount of secret data hidden into cover video by considering the perceptual transparency. Larger the amount of data hiding capacity, the algorithm is considered better. An encryption method is tampered resistant if the receiver gets the secret data exactly in the same way sent by the sender.

Different components of information security are (Fig. 1):

• (i) Cover Video: Envelope video that holds the secret data.

• (ii) Secret data: Important information concealed from the intruder.

• (iii) Stego Video: Video after encryption data.

• (iv) Encryption and Decryption algorithm: Strategy followed to conceal secret data by sender and extracted by the receiver.

Fig. 1

Layout of steganography

Although several techniques are discussed in literature that are used for the security of images and videos, but in most of the techniques in the spatial domain require a large amount of computations, so alternative solution is needed. To fulfill this requirement, two different keys (fractional parameter and random phase code) keys are introduced on each block. By operating in frequency domain, the amount of computation can be reduced, and more efficient processes can be used, for example, digitally encrypted processing in the frequency domain using fractional discrete Tchebichef transform. Secondly, the use of fractional transforms based on Singular Value Decomposition (SVD) has improved the performance of several applications, by providing an extra degree of freedom [22, 36, 37, 66]. It attracts security systems, so many fractional transforms have been implemented for the encryption of images and videos, but still the use of modified fractional transform (like dual parameter based) is required for more improvement. Another motivation is to enhance the performance parameters (like PSNR, MSE etc.) of existing techniques in order to provide better security to the images and videos from hackers. As, discussed in literature the use of fractional transform and random phase keys in combination provides better results. In this paper, we present three contributions in the field of image/video encryption based on FrDTTs. In the first contribution, we develop a new fractional transform for data security based on FrDTTs and the decomposition (SVD) technique in order to build a basic set of orthonormal eigenvectors. In the second contribution, we introduce a new encryption and decryption algorithm for one or various images simultaneously based on proposed FrDTTs, our algorithm has good encryption effect, larger secret key space, and high sensitivity to the secret key. In the third contribution, we propose a novel method for video sequences encryption by introducing a bloc based FrDTTs encryption structure. Finally, we implement and apply the scheme proposed in this work for the encryption of standard test images and video sequences. A methodical security evaluation in terms of brute force and statistical attacks has been followed for each of the proposed scheme. We also verified their resistance against additive noise and transmission errors in the communication channel. The simulation results have demonstrated the considerable contribution of the proposed scheme compared to the existing methods as well as the interest of their uses.

The rest of this paper is structured as follows: Section 2 introduces a related work. Section 3, the definition, and properties of the classical DTTs. Section 4 then provides details of the procedure for deriving FrDTTs. Section 5, an encryption and decryption algorithm for images and video by the proposed FrDTTs. The results of simulations that prove the efficiency of the proposed encryption algorithm based FrDTTs in Section 5. Finally, closing remarks of the paper are available in Section 6.

2 Related work

Information security has become a significant issue for protecting the secret information during transmission in practical applications in the era of information. In recent years, a raft of information security schemes has been used in image encryption, researchers have made some related achievements in the field of image analysis in the encrypted domain. These works can be roughly categorized into two types.

One category focused on the image/video encryption in the space domain. In the literature and in image encryption, several algorithms are developed according to the so-called permutation-diffusion architecture [34, 35, 54]. This architecture includes two important operations, the permutation and the diffusion, the combination between the two is also possible. Algorithms based on the parallel computing system [59] and on piecewise coupled map lattice [53] have shown exceptionally good properties in many aspects regarding security, complexity, speed, computational overhead, etc. Wang et al. [50, 51] suggested an image encryption algorithm based on matrix semi-tensor product theory and the image encryption algorithm based on fractal sorting matrix [64, 65]. The encryption of digital images by using chaotic system is mainly based on the excellent randomness of this system, the chaotic system is usually combined with image encryption methods based on spatial domain. The chaotic system was proposed for data encryption, Fridrich [14] first proposed image encryption scheme based on chaotic system. Wang et al. [52], proposed another image encryption method based on full chaos coupled mapping lattice, then a novel chaotic block image encryption algorithm based on dynamic random growth technique [57]. This encryption algorithm combined the dynamic random growth technique and chaotic system to effectively enhance the key space. Batham, et al. [3], a secure video encryption algorithm which uses an efficient compression technique called as hybrid video codec and encrypts the compressed video frames bitstreams along with motion vectors of each frames using indexed based chaotic sequence. A novel chaotic image encryption scheme using DNA sequence operations was proposed by Xing-Yuan Wang et al. [58].

The other category mainly paid attention to the image/video encryption in the frequency domain. Image encryption algorithm based on frequency domain encrypts the frequency coefficients based on the characteristics of human visual system, it can encrypt important data which is called selective encryption or partial encryption, so that the amount of encryption data is significantly reduced and the encryption efficiency is improved. At present, there are many research on digital image encryption algorithms based on fractional Fourier transform [6, 28, 45, 49]. For example, Unnikrishnan et al. [49] proposed a double random phase encoding scheme, which uses two independent random phase masks to encrypt the image Smooth white noise; Joshi et al. [18] proposed an image encryption algorithm combining Fourier transform and radial Hilbert transform; Lang et al. [28] proposed image encryption based on multi-parameter discrete fractional storage transform and chaos algorithm. Chen et al. [6], proposed an image encryption algorithm was proposed using singular value decomposition and Arnold transform.

One of the major limitations of these image encryption algorithms is that the encrypted image is a complex-valued image, which also contains amplitude and phase information, which is very unfavorable for transmission and storage. Especially as people have higher and higher requirements for real-time transmission, it is very necessary to propose an image encryption technology that meets real-number transformation, high encryption security, strong noise resistance, and fast calculation speed. The fractional transforms are mostly used for several purposes such as encryption, compression, noise reduction, filtering, watermarking etc. Recently, a number of fractional transforms have been exploited for image and video security in the real domain, such as image encryption based on fractional Fourier transform (FrFT) [28, 31], image/video encryption algorithms based on fractional discrete cosine transform [26, 41, 63], image encryption with fractional sine transform (FrST) [43], image encryption based on fractional discrete Meixner moments (FrDMM) [22], discrete fractional Krawtchouk transform and its application in image encryption and watermarking (FrKT) [36, 37], color image encryption scheme based on fractional Hartley transform (FrHT) [24, 25], fractional Mellin transform (FrMT) [71, 72], encryption of video main frames in the field of DCT transform [2], image and video processing using discrete fractional transforms [17] and secure video steganography using Framelet transform and singular value decomposition [47].

3 Discrete Tchebichef transform

Discrete Tchebichef polynomials were introduced by Pafnuty Chebyshev in [5], and first used in image analysis by Mukundan et al. [39] as a basis function for image moments. The classical Tchebichef orthogonal polynomials of order n are defined from the hypergeometric function 3F₂(∙) as follows:

$$ {t}_n(x)=\sum \limits_{k=0}^{N-1}{a}_{k,n}{x}^k={\left(1-N\right)}_n{{}_3F}_2\left(-n,-x,1+n,1,1-N,1\right) $$

(1)

where ₃F₂(.) is the hypergeometric function, defined as:

$$ {{}_3F}_2\left(a,b,c,d,e,z\right)=\sum \limits_{k=0}^n\frac{(a)_k{(b)}_k{(c)}_k}{(d)_k{(e)}_k}\frac{z^k}{k!} $$

(2)

and (a)_kis the Pochhammer symbol given by:

$$ {(a)}_k=\frac{\Gamma \left(a+k\right)}{\Gamma (a)}=a\left(a+1\right)\dots \left(a+k-1\right) $$

(3)

The orthogonal Tchebichef polynomial of order n can be written explicitly as follows:

$$ {t}_n(x)=n!\sum \limits_{k=0}^n{\left(-1\right)}^{n-k}\left(\begin{array}{c}N-1-k\\ {}n-k\end{array}\right)\left(\begin{array}{c}n+k\\ {}n\end{array}\right)\left(\begin{array}{c}x\\ {}k\end{array}\right) $$

(4)

Tchebichef polynomials satisfy the orthogonality condition with norm squared:

$$ \rho (n)=(2n)!\left(\begin{array}{c}N+n\\ {}2n+1\end{array}\right),n=0,1,\cdots, N-1, $$

(5)

with the binomial coefficient noted $\left(\begin{array}{c}n\\ {}k\end{array}\right)=\frac{n!}{k!\left(n-k\right)!}$.

For reasons of numerical stability and limited dynamic range, normalized Tchebichef polynomials are introduced by Mukundan [39], as follows:

$$ \tilde{t}_n\left(x,N\right)=\frac{t_n\left(x,N\right)}{\rho (n)} $$

(6)

where ρ(n) is an appropriate constant independent of x that serves as a scaling factor, such that Nⁿ.

The scaled Discrete Tchebichef polynomials obey a general three-term recursive relation [9]:

$$ {t}_n(x)=\frac{\left( Ax+B\right)}{n}{t}_{n-1}(x)+\frac{C}{n}{t}_{n-2}(x) $$

(7)

with

$$ {\displaystyle \begin{array}{c}A=\frac{2}{n}\sqrt{\frac{4{n}^2-1}{N^2-{n}^2}},B=\frac{1-N}{n}\sqrt{\frac{4{n}^2-1}{N^2-{n}^2}},\\ {}C=\frac{1-n}{n}\sqrt{\frac{2n+1}{2n-3}}\sqrt{\frac{N^2-{\left(n-1\right)}^2}{N^2-{n}^2}}\end{array}} $$

(8)

$$ {t}_0(x)=\frac{1}{\sqrt{N}},{t}_1(x)=\frac{2x+1-N}{N}\sqrt{\frac{3}{N\left({N}^2-1\right)}} $$

(9)

where n, x = 2, 3, …, N − 1,

For a digital image f(x, y) its DTT can be defined as

$$ {T}_{nm}=\sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{N-1}{t}_n(x){t}_m(y)f\left(x,y\right)n,m=0,1,.\dots N-1 $$

(10)

The corresponding discrete Tchebichef transform (iDTTs, inverse DTTs) is

$$ f\left(x,y\right)=\sum \limits_{n=0}^{N-1}\sum \limits_{m=0}^{N-1}{t}_n(x){t}_m(y){T}_{nm} $$

(11)

In practical applications, the DTTs of an image can be expressed as a matrix:

$$ \mathrm{T}={\mathrm{C}}^T\mathrm{fC} $$

(12)

where $\mathrm{T}={\left\{{T}_{nm}\right\}}_{n=0,m=0}^{n=N-1,m=N-1}$, $\mathrm{C}={\left\{{t}_n(x)\right\}}_{n=0,x=0}^{n=N-1,x=N-1}$ and $\mathrm{f}={\left\{f\left(x,y\right)\right\}}_{x,y=0}^{x,y=N-1}$.

Similarly, the inverse moment transform can be represented using the matrix as follows [10]:

$$ \mathrm{f}={\mathrm{CTC}}^T $$

(13)

The DTTs introduced into the literature are calculated for integer orders. In the following sections, we propose the calculation of the DTTs for fractional order (real) in order to generalize their calculation and to benefit other properties for non-integer orders.

4 Proposed fractional-order discrete Tchebichef transform

In this section, we provide a framework for deriving FrDTTs by the decomposition the properties of the eigenvalues and eigenvectors of the DTTs matrix which help to develop the new fractional discrete Tchebichef polynomials. In the following subsections, analysis regarding the decomposition of the polynomial’s matrices and important properties of FrDTTs are provided.

4.1 Eigenvalues and eigenvectors of the discrete Tchebichef polynomials

For a DTTs matrix $\mathrm{C}={\left\{{t}_n(x)\right\}}_{n,x=0}^{n,x=N-1}$ of the order N will be noted C in the following. The matrix C checks the following properties [8]:

• Property (i): It is real matrix.

• Property (ii): It is unitary, i.e., C^HC = CC^H = I, where C^H is the transposed matrix of C and I is the identity matrix.

• Property (iii): It is orthogonal,

• Property (iv): It is symmetrical, so C = C^T.

• Property (v): It has the following two eigenvalues: λ_k = (−1)^kk = 0, 1.

• The proof of property (v) is given in Appendix A.

The characteristic of the unitary matrix makes the eigenvalues of C, λ_k distributed on the unit circle, that is, ${\lambda}_k={e}^{j{\varphi}_k}$ (φ_k is a real number). Perform eigenvalue decomposition on the DTT matrix to obtain the corresponding eigenvalue matrix D and eigenvector matrix V, satisfying

$$ \mathrm{C}={\mathrm{VDV}}^H=\sum \limits_{n=1}^N{\mathrm{U}}_n{e}^{-j{\varphi}_n}=\sum \limits_{n=1}^N{\mathrm{U}}_n{\lambda}_n $$

(14)

where, V is the unitary matrix, which is composed of N eigenvectors nu of C, V^H is the conjugate transpose matrix of V, satisfying ${\mathrm{U}}_n\triangleq {u}_n{u}_n^H$, D is the diagonal matrix whose diagonal is the eigenvalue λ_k.

According to the above properties of C, the eigenvalue multiplicities of the matrix C can be given by the following Table 1:

Table 1 Multiplicities of the eigenvalues for matrix C

where N is the size of Discrete Tchebichef polynomial matrix.

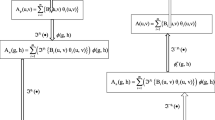
According to the spectral theorem [61]:

$$ \mathrm{C}=\sum \limits_{k=0}^1{\lambda}_k{\mathrm{P}}_k={\lambda}_0{\mathrm{P}}_0+{\lambda}_1{\mathrm{P}}_1 $$

(15)

where P_k denotes the spectral projector for Cassociated with the eigenvalueλ_k. Also, for any integerm, has the following spectral decomposition [61]:

$$ {\mathrm{C}}^m={\lambda}_0^m{\mathrm{P}}_0+{\lambda}_1^m{\mathrm{P}}_1 $$

(16)

we write the equation above for m = 0, 1 on the matrix form, to obtain the two matrices P₀ and P₁.

$$ \left(\begin{array}{c}\mathrm{I}\\ {}\mathrm{C}\end{array}\right)=\sum \limits_{k=0}^1{\lambda}_k^m\left(\begin{array}{c}{\mathrm{P}}_0\\ {}{\mathrm{P}}_1\end{array}\right)=\mathrm{H}\left(\begin{array}{c}{\mathrm{P}}_0\\ {}{\mathrm{P}}_1\end{array}\right)\kern0.24em \;\;\mathrm{with}\;\;\;\;\mathrm{H}=\left(\begin{array}{cc}\mathrm{I}& \mathrm{I}\\ {}{\lambda}_0\mathrm{I}& {\lambda}_1\mathrm{I}\end{array}\right) $$

(17)

Using the Eq. (17), the expression HH^H = 2I, to prove the relation between the inverse of H and transpose of H we find H⁻¹ = 0.5H^T.

By multiplying the H⁻¹ = 0.5H^T relation of the two left sides of Eq. (17), we obtain the following expressions for the projection matrices P₀ and P₁:

$$ {\mathrm{P}}_0=0.5\left(\mathrm{I}+\mathrm{C}\right)\ \boldsymbol{and}\ {\mathrm{P}}_1=0.5\left(\mathrm{I}-\mathrm{C}\right) $$

(18)

In the following, we will study the eigenvalues and the eigenvectors of the two spectral projector matrices P₀ and P₁., then we will present their properties.

From Eq. (18), we can get some properties of P₀ and P₁:

• Property (a): ${\mathrm{P}}_{\mathrm{i}}^T={\mathrm{P}}_{\mathrm{i}}\ \boldsymbol{and}\ {\mathrm{P}}_{\mathrm{i}}^2={\mathrm{P}}_{\mathrm{i}},i=0,1$.

• Property (b): P₀P₁ = 0, where 0 denotes the zero matrix.

• Property (c): The eigenvalues of a projection matrix P₀ and P₁ are only 0 and 1 [44].

• The multiplicity of eigenvalue 1 for P₀ is equal to the multiplicity of eigenvalue 1 of C.

• The multiplicity of eigenvalue 1 for P₁ is equal to the multiplicity of eigenvalue −1 of C.

The proof of properties (a)-(b) and (c) is given in Appendix B.

Lemma 1

The eigenvectors of P₀ are orthogonal to those of P₁, for the non-zero eigenvalues.

Lemma 2

For the non-zero eigenvalues: the eigenvectors of P₀ and P₁ are the eigenvectors of C, corresponding to eigenvalues λ₀ = 1, λ₁ =  − 1 of C, respectively.

The proofs of both Lemmas 1 and 2 are given in Appendix C.

In the following, by performing the SVD decomposition of P₀ and P₁, we have derive a set of orthonormal eigenvectors of C by using the decomposition SVD of its orthogonal projection matrices on its eigenspaces [16, 44].

SVD of its orthogonal projection matrices on its eigenspaces [16, 44].

The SVD decomposition of P₀ and P₁, are given as:

$$ {\mathrm{P}}_0={\mathrm{U}}_0{\mathrm{S}}_0{\mathrm{V}}_0^T\ \boldsymbol{and}\ {\mathrm{P}}_1={\mathrm{U}}_1{\mathrm{S}}_1{\mathrm{V}}_1^T $$

(19)

where U_i and V_i, (i = 1, 2) are unitary matrices and S_i a diagonal matrix with real and positive coefficient. Since the singular values of P₀ and P₁ are square root of non-negative eigenvalues of ${\mathrm{P}}_0{\mathrm{P}}_0^T$ and ${\mathrm{P}}_1{\mathrm{P}}_1^T$, respectively, using properties (a), (b) and (c), we can easily rewrite the Eqs. (19) as follows:

$$ {\mathrm{P}}_0={\mathrm{P}}_0^T{\mathrm{P}}_0={\mathrm{V}}_0{\mathrm{S}}_0{\mathrm{V}}_0^T;{\mathrm{P}}_1={\mathrm{P}}_1^T{\mathrm{P}}_1={\mathrm{V}}_1{\mathrm{S}}_1{\mathrm{V}}_1^T $$

(20)

It can be observed from Eqs. (20) that:

$$ {\mathrm{P}}_0{\mathrm{V}}_0={\mathrm{V}}_0{\mathrm{S}}_0;{\mathrm{P}}_1{\mathrm{V}}_1={\mathrm{V}}_1{\mathrm{S}}_1 $$

(21)

The above equation shows that V₀ and V₁ are a set of orthonormal eigenvectors of P₀ and P₁, respectively.

According to Table 1 and propriety (c), the multiplicities of the non-zero eigenvalues for P₀ and P₁ are summarized for an N × N transform as follows:

According to the Table 2 and Lemma 2, we are now ready to derive a set of orthonormal eigenvectors of C.

Table 2 Multiplicities of the non-zero eigenvalues for P₀ and P₁

Taking u_i and v_j be the i^th and j^th column of V₀ and V₁,respectively, a set of orthonormal eigenvectors V of C can be written as follows:

$$ \mathrm{V}=\left\{\begin{array}{c}\left[{u}_1,{u}_2,.\dots, {u}_{\frac{N}{2}},{v}_1,{v}_2,.\dots, {v}_{\frac{N}{2}}\right],\mathrm{if}\ \mathrm{N}\mathrm{is}\ \mathrm{even}\\ {}\left[{u}_1,{u}_2,.\dots, {u}_{\frac{N-1}{2}},{u}_{\frac{N+1}{2}},{v}_1,{v}_2,.\dots, {v}_{\frac{N-1}{2}}\right],\mathrm{if}\ \mathrm{N}\mathrm{is}\mathrm{odd}\end{array}\right. $$

(22)

4.2 Definition of fractional-order discrete Tchebichef polynomials

In this section, traditional DTTs are extended to FrDTTs in order to effectively improve their performance in image reconstruction. Such extension mainly involves the modification of Fractional-order Discrete Tchebichef Polynomials (FrDTPs) matrix that also satisfies the properties of the polynomial matrices in the DTTs, these polynomials replace the eigenvalues ${\lambda}_k={e}^{j{\varphi}_k}$ with its α^th power $\alpha \mathfrak{\in}\mathfrak{R}$ on the basis of matrix eigen-decomposition, that is The diagonal matrix D is replaced by its power of α, so that the definition of FrDTPs matrix C^α is:

$$ {\mathrm{C}}^{\alpha }={\mathrm{V}\mathrm{D}}^{\alpha }{\mathrm{V}}^H=\sum \limits_{k=0}^{N-1}{\lambda}_k^{\alpha }{v}_k{v}_k^H,k=0,\cdots, N-1 $$

(23)

where V = [v₀, v₁, .………, v_N − 1] with v_k (k = 0, 1, ………, N − 1) is the C eigenvector obtained from (Eq. 15), and D^α is defined as:

$$ {\mathrm{D}}^{\alpha }=\boldsymbol{Diag}\left\{1,{e}^{- j\alpha},{e}^{-j2\alpha },\dots \dots \dots, {e}^{-j\left(N-1\right)\alpha}\right\} $$

(24)

The main mathematical properties of FrDTPs are shown in Table 3 [22, 36, 38]. In addition, we will show in detail the steps of this proposed algorithm to calculate the coefficients of the matrix of fractional discrete Tchebichef polynomials. Algorithm 1 summarizes the steps for calculating the FrDTPs matrix.

Table 3 Main mathematical properties of FrDTPs

It should be noted that the eigenvalue decomposition of the Tchebichef transformation matrix will be used to define the discrete FrDTPs. The eigenvalues and vectors of FrDTPs are derived and some properties of FrDTPs are also studied. However, the proposed algorithm satisfies exactly the property of orthogonality up to the last order of FrDTPs (n = 4000) which shows the numerical stability of the values of FrDTPs calculated by the algorithm proposed. Therefore, the orthogonality of the FrDTPs polynomial matrix can be destroyed due to a numerical approximation in the calculation process. Indeed, the following Fig. 2 shows the distribution of the polynomial coefficients of the FrDTPs up to the order n = 4000. We can see that the FrDTPs values are well calculated, stable and verified all properties ((iii) end (iv)) of orthogonality and symmetry. It is important to also note that the proposed stability condition can be easily adapted for the stabilization of computation of other types of discrete orthogonal polynomials of high orders.

Fig. 2

a 2D plot of FrDTPs, b 3D plot of FrDTPs and c all polynomial curves of FrDTPs using algorithm 1 with α = 1

Algorithm 1

Computation of the Fractional Discrete Tchebichef Polynomials with respect to the order n

It is worth mentioning that when α is an unnatural number, (±1)^α = e^±j2πα is a complex number, so the matrix C^α is also a complex matrix. In order to obtain a FrDTTs matrix that always satisfies the real matrix, the eigenvalues of the matrix should not include ±1. Compared with DCTs, when the signal length N of the matrix dimension is a multiple of 4, it does not contain the eigenvalue ±1. DTTs has certain advantages. It satisfies that when the matrix dimension is even, that is, N = 2N₀ does not contain the eigenvalue ±1. It is more flexible and convenient in practical applications [11, 12, 21].

4.3 Proposed fractional-order discrete Tchebichef transform

The generalized FrDTTs are obtained from the FrDTPs. It can be seen from Eq. (23) that the inverse matrix of C^α can be obtained by its negative order matrix C^−α. The FrDTTs are obtained from the FrDTPs presented in the previous subsection. Thus, the 1D forward FrDTTs of signal f(x) of length N with fractional order α can be defined as follows:

$$ {\mathrm{F}}^{\alpha }={\mathrm{C}}^{\alpha }f $$

(25)

The reconstruction of the signal f(x)can be found from its transform by using the following expression:

$$ f={\mathrm{F}}^{\alpha }{\mathrm{C}}^{-\alpha } $$

(26)

In 2D case, the FrDTTs in terms of polynomials matrices C^α with fractional order (α, β), for an image with intensity function f(x, y), can be defined as follows:

$$ {\mathrm{F}}^{\alpha, \beta }={\mathrm{C}}^{\alpha }{\mathrm{fC}}^{\beta } $$

(27)

The Eq. (27) leads to the following inverse reconstruction procedure:

$$ \mathrm{f}={\mathrm{C}}^{-\alpha }{\mathrm{F}}^{\alpha, \beta }{\mathrm{C}}^{-\beta } $$

(28)

5 Proposed image/video encryption scheme using FrDTTs

In the several applications of image/video processing like business conferencing, military communication, secure transfer of images, Medical imaging, Road safety, Electronic signature, Remote monitoring [15, 30] etc., the content of image/video is required to be preserved. So, for the preservation of image/video information security techniques are required. To meet this requirement several techniques had been invented. Recently, a number of fractional transform based image/video encryption methods have been widely studied in recent years [19, 20, 22, 62, 67, 73]. In this section, an FrDTTs based image/video encryption and decryption scheme is proposed. Offering good security quality, resistance against image processing and large key space and high robustness against various kinds of attacks. The proposed scheme is a real-value-toreal-value mapping in encryption and decryption processes. In summary, different fractional orders will generate different FrDTTs matrices. Such characteristics can be well applied to image/video encryption. This section introduces a new image/video encryption method based on FrDTTs and gives detailed steps of the encryption and decryption process. Figure 3 illustrates the flowchart of the image/video encryption and decryption processes, and details are given in the following.

Fig. 3

The flowchart of the proposed scheme

5.1 Encryption process

As mentioned above, different fractional orders (α_k, β_k) result in different ${\mathrm{C}}^{\alpha_k}$ and ${\mathrm{C}}^{\beta_k}$. This property can be used for image encryption efficiently. Let a sequence of video frames have R frames of size N×M, which we note I_r, r = 1,2, ⋯, R. Each frame I_r is divided at the beginning into K blocks B_k, k = 1,2, ⋯, K ∈ ℕ∗ of width n and length m. Thus, each B_k block is encrypted separately as shown in Fig. 4. Let ${\mathrm{C}}^{\alpha_{x_k}}$, ${\mathrm{C}}^{\alpha_{y_k}}$, ${\mathrm{C}}^{\beta_{x_k}}$ and ${\mathrm{C}}^{\beta_{y_k}}$ be real FrDTTs matrices of size n×m constructed according to Eq. (27) with ${\alpha}_{x_k},{\alpha}_{y_k},{\beta}_{x_k}$ and ${\beta}_{y_k}$ being fractional orders. Thus, for each value of k = 1, 2, ⋯, K, the block B_k is encrypted in the following steps:

• Step 1. This step alters the image in the transverse direction, the original image I_r divided into sub-blocks B_k of size 8 × 8 pixels. Then each of these image blocks B_k undergoes a Jigsaw Transform (JT) [22]: B_k = {b_k(i, j), 0 ≤ i, j < 7} (k = 1, 2, …, N²/64).

• Step 2. The two-dimensional FrDTTs of the fractional order ${\alpha}_{x_k},{\alpha}_{y_k}$ are computed for each block B_k by using the following equation: ${\mathrm{F}}_{B_k}^{\alpha_{x_k},{\alpha}_{y_k}}={\mathrm{C}}^{\alpha_{x_k}}{\mathrm{B}}_k{\mathrm{C}}^{\alpha_{y_k}}$. The transform matrix of one block is denoted by ${\mathrm{F}}_{B_k}^{\alpha_{x_k},{\alpha}_{y_k}}$. with ${\mathrm{C}}^{\alpha_{x_k}}$ and ${\mathrm{C}}^{\alpha_{y_k}}$ the matrix generated from the fractional discrete Tchebichef matrix defined in Eq. (27).

• Step 3. To ensure the security of each block B_kwe secretly select the blocks (8 × 8) in image f(x, y). The secret key FrDTTs (Key1) of fractional order ${\alpha}_{x_k},{\alpha}_{y_k}$ corresponds to the position of the selected blocks.

• Step 4. Perform data masking on each block of the original image, then the pixels of the output of each block are multiplied by a random phase code R(x, y) (Key2). With R(x, y)is chosen to be a phase function e^iφ(x, y), where φ(x, y) is a random function uniformly distributed over [0, 2π].

• Step 5. For the last step of the encryption procedure, introduces the last security key FrDTTs (Key3) of fractional order ${\beta}_{x_k},{\beta}_{y_k}$ into the f(x, y) image to produce the encrypted final image I_r.

Fig. 4

Scheme of the encryption and decryption system based on FrDTTs

5.2 Decryption process

The decryption process is the inverse transformation of the encryption process. Based on FrDTTs satisfying exponential additivity, the fractional orders ${\alpha}_{x_k},{\alpha}_{y_k},{\beta}_{x_k}$ and ${\beta}_{y_k}$ can be selected. Figure 4 shows the main steps of decryption procedure which can be described in the following:

• Step 1. The first step of the decryption procedure, an inverse FrDTTs of order $-{\beta}_{x_k},-{\beta}_{y_k}$ is performed on the encrypted image I_r then divide the image into small non-overlapping blocks (B_k)^∗ of size 8 × 8 pixels. ${\left({\mathrm{B}}_k\right)}^{\ast }=\left\{{b}_k^{\ast}\left(i,j\right),0\le i,j<7\right\}\left(k=1,2,\dots, {N}^2/64\right)$.

• Step 2. The FrDTTs matrix ${\left({\mathrm{F}}_{B_k}^{\alpha_{x_k},{\alpha}_{y_k}}\right)}^{\ast }$ is computed for each decryption block (B_k)^∗ by ${\left({\mathrm{F}}_{B_k}^{\alpha_{x_k},{\alpha}_{y_k}}\right)}^{\ast }={\mathrm{C}}^{-{\alpha}_{x_k}}{\left({\mathrm{B}}_k\right)}^{\ast }{\mathrm{C}}^{-{\alpha}_{y_k}}$.

• Step 3. Perform the inverse FrDTTs on each block, for one block coefficients (B_k)^∗ multiplied with the conjugate of the random phase mask R^∗(x, y).

• Step 4. For the last step of the decryption procedure, introduce the inverse FrDTTs of fractional order $-{\alpha}_{x_k},-{\alpha}_{y_k}$ in each frame blocks, then we undergo an inverse Jigsaw transformation (IJT) to produce the final decrypted frame I_r.

The main advantage of the proposed method is that for a single frame I_r we use 4×퐾 fractional orders ${\alpha}_{x_k},{\alpha}_{y_k},{\beta}_{x_k}$ and ${\beta}_{y_k}$ instead of 4 fractional orders in the method FrDTTs, which significantly improves the secret key space. In addition, the use of the real FrDTTs transform and block random phase makes the proposed video image sequence encryption algorithm more efficient in terms of transmission rate and computational complexity. The process can be defined as a sequence of images presented at a certain rate expressed in the number of frames per second (FPS) (Fig. 5).

Fig. 5

Picture of a video sequence

6 Simulation results

In this section, we first analyze the fractional-order transformation performance of various encryption methods from the perspective of sensitivity analysis, key space analysis and robustness to the noise attack. In the experiments, we use “Lena” and “Peppers” images of different sizes. Then, we present simulation results of applying the proposed block-based encryption method on a few test video image sequences [48, 68] of standard CIF (352 × 288) and gray level (8bits) format.

6.1 Histogram analysis

The histogram is a very important analysis method used to describe the number of pixels in the image with different gray levels and their frequency of occurrence. The histograms of the original images usually are different, while those of encrypted images obey a uniform distribution, by which the attackers cannot obtain useful information. Mathematically, the variances of histograms are calculated by [70]:

$$ Var(Y)=\frac{1}{n^2}\sum \limits_{i=1}^n\sum \limits_{j=1}^n\frac{1}{2}{\left({Y}_i-{Y}_j\right)}^2 $$

(29)

where Y is the vector of the histogram values and Y = {Y₁, Y₂, …, Y₂₅₆}, Y_i and Y_j are the numbers of pixels which gray values are equal to i and j respectively.

The variance of the histogram reflects the histogram uniform distribution for the encrypted video sequence, where both are inversely proportional. Low variance means a uniform histogram. Table 4 shows the variances of histograms for the test video sequence. The variances of the encrypted video sequence are smaller than the variances of the original video sequence. Figure 6a, b, c and d shows the histograms and pixel distributions of the original images Lena and Peppers. Although the histograms and pixel distributions of the two original images are different from each other, the histograms of encrypted images are almost the same, following a nearly uniform distribution. Thus, one believes that the attackers cannot obtain any useful information by histogram analysis.

Table 4 Variances of histograms for both Original and encrypted video sequence

Fig. 6

Histograms and pixel distributions before and after image encryption

To evaluate the security of the proposed method against statistical histogram analysis. Let a sequence of video images in CIF format composed of 100 frames and Q a secret key which is defined by: fractional orders $\left({\alpha}_{x_k},{\alpha}_{y_k},{\beta}_{x_k},{\beta}_{y_k}\right)$ and the width n and length m of the block. Suppose we have four frames randomly drawn from a sequence of Tennis video images.

Figure 7 shows the encryption of these frames using the proposed method with the secret key Q defined earlier. We notice that the histograms of the encrypted frames are entirely different from those of the original frames, and they are generally identical regardless of the original frame. This reduces the risk of statistical attacks based on collecting information about the original frames by analyzing the histograms of the encrypted frames. Figure 7a, b show different frames from the Tennis video sequence along with their corresponding histograms, and then Fig. 7e, f shows the histograms and pixel distributions of corresponding encrypted frames. Consequently, the proposed method is robust against statistical analysis by histogram.

Fig. 7

Histograms and pixel distributions of some frames of the Tennis video sequence (a) original frames, (b) histograms of original frames, (c) pixel distributions of original frames, (d) encrypted frames, (e) histograms of encrypted frames and (f) pixel distributions of encrypted frames

6.2 Correlation of adjacent pixels

The correlation coefficient is another useful indicator to evaluate the performance of image/video encryption and decryption scheme. To test the correlation of the encrypted image/video obtained by the FrDTTs based method proposed in this paper, 1000 pairs of neighboring pixels are randomly selected as samples from the horizontal, vertical, and diagonal directions of the original image and the encrypted image and calculate the correlation coefficient for the three directions. The correlation coefficient, R_{x, y}, can be obtained using the following equation [23].

$$ {R}_{x,y}=\frac{E\left[\left(x-E(x)\right)\left(y-E(y)\right)\right]}{\sqrt{D(x)\times D(y)}} $$

(30)

where

$$ E(x)=\frac{1}{N}\sum \limits_{i=1}^N{x}_i,D(x)=\frac{1}{N}\sum \limits_{i=1}^N{\left({x}_i-E(x)\right)}^2 $$

(31)

x and y are gray-scale values of the adjacent pixels in the image. Figure 8 shows the correlation analysis between the pixels of “Lena” images before and after the encryption in three directions (horizontal, vertical and diagonal) to evaluate the performance of the proposed scheme, and the results are listed in Table 5 with a comparison with recent published results. The Table 5, we can see that the correlation coefficients of adjacent pixels in the three directions of the original image are close to 1, while the correlation coefficients of the encrypted image are close to 0. This shows that the proposed encryption algorithm can reduce the correlation between pixels very well and can resist the attack using image correlation.

Fig. 8

The correlation plots of the Lena image and the corresponding encrypted image of Lena (a) horizontal; (b) vertical; (c) diagonal; (d) horizontal of the encrypted image; (e) vertical of the encrypted image; (f) diagonal of the encrypted image

Table 5 Correlation coefficients of different images using the proposed method and other similar methods

Figure 9 shows the correlation analysis between the pixels of some CoastGuard frames of the video sequence before and after encryption in three directions (horizontal, vertical and diagonal) in order to evaluate the performance of the proposed scheme, Table 6 shows the correlation coefficients of the Tennis frames of the video sequence in the horizontal, vertical and diagonal directions respectively. From these results, we can see that there are strong neighborhood correlations between the adjacent pixels of each frame of the original video sequence, while those of the encrypted video sequence. Consequently, the proposed algorithm can effectively realize the confusion and diffusion of image information, which shows a capability against the correlation analysis attack.

Fig. 9

Correlation distributions of two adjacent pixels in original and encrypted video sequence. a Correlation of two adjacent pixels in frame 1 of the video sequence b Correlation of two adjacent pixels in frame 2 of the video sequence c Correlation of two adjacent pixels in frame 3 of the video sequence d Correlation of two adjacent pixels in frame 1 of the video sequence

Table 6 Correlation coefficients of tennis video sequence using the proposed method and other similar methods

6.3 Robustness differential attack

In this attack, the attacker encrypts the plain image with the proposed method. Then, the attackers penetrate the cryptosystem by tracing the difference between two encrypted images. The number of pixels change rate (NPCR) and the unified averaged changed intensity (UACI) are commonly used to evaluate the strength of any encryption process. The NPCR is the change rate of the number of pixels of the cipher-image when only one pixel of the plain image is modified. The UACI calculate the average intensity of differences between the plain and the encrypted images. They are calculated as follows [33].

$$ \boldsymbol{NPCR}=\frac{1}{N\times M}\left(\sum \limits_{i=1}^N\sum \limits_{j=1}^MD\left(i,j\right)\right)\times 100\% $$

(32)

$$ \boldsymbol{UACI}=\frac{1}{N\times M}\left[\sum \limits_{i=1}^N\sum \limits_{j=1}^M\frac{\left|{C}_2\left(i,j\right)-{C}_1\left(i,j\right)\right|}{255}\right]\times 100\% $$

(33)

where $D\left(i,j\right)=\left\{\begin{array}{c}1,\mathrm{if}{C}_1\left(i,j\right)\ne {C}_2\left(i,j\right)\\ {}0,\mathrm{if}{C}_1\left(i,j\right)={C}_2\left(i,j\right)\end{array}\right.$ and N, M is the image dimensions, L = 255 for image intensity. To get the best encryption strength against the diferential attack, NPCR and UACI must be higher and in the range of >99% and >33%, respectively. Tables 7 and 8 shows the results according to the proposed method of NPCR and UACI and compares the NPCR and UACI average of different encryption method for Lena image and tennis video sequence. From this table, we know that the proposed method has a larger NPCR average compared with other method, which show that the proposed method has excellent robustness against differential attack than the other method.

Table 7 The comparison results of average NPCR and UACI in proposed method and similar method

Table 8 The comparison results of average NPCR and UACI in proposed method and similar method

6.4 Sensitivity analysis to keys

The analysis of key space is required to calculate the space of key that is used for the encryption process. It should be as large as possible for good encryption technique. The fractional parameters of Tchebichef are involved in the proposed encryption algorithm, namely are served as the private keys for the cryptosystem. We analyze the influence of the number of erroneous fractional orders for image/video encryption. Next, we will check the sensitivity of our algorithm to the keys. To further validate the sensitivity of the key, this paper quantifies the mean square error (MSE) between the decrypted image and the original image by computing the MSE as follows:

$$ MSE=\frac{1}{N\times M}\sum \limits_{i=1}^N\sum \limits_{j=1}^M{\left|{I}_O\left(i,j\right)-{I}_D\left(i,j\right)\right|}^2 $$

(34)

The PSNR is defined by:

$$ \boldsymbol{PSNR}=10\times {\mathit{\log}}_{10}\left(\frac{255^2}{MSE}\right)(db) $$

(35)

where I_O(i, j) denotes the original image pixel, I_D(i, j) is the pixel of the decrypted image, N × M are the size of original and decrypted images.

Figures 10 and 11 show that even if the deviation of the correct keys and fractional-orders parameters are adjusted down to (δ_x, δ_y), no useful information can still be obtained from the decrypted image/video. We assume that incorrect keys locate in the vicinity of the correct key values, and then the relations between the keys used for decryption and encryption are ${\alpha}_x^{\prime }={\alpha}_x+{\delta}_x,{\alpha}_y^{\prime }={\alpha}_y+{\delta}_y$.

Fig. 10

Decrypted images with different fractional order deviations: (a) Original image (b) δ = 0.0005, (c) δ = 0.0003, (d) δ = 0.0025, (e) δ = 0.001 and (f) δ = 0.01

Fig. 11

Decrypted Tennis video sequence with different fractional order deviations: (a) Original video sequence (b) δ = 0.0005, (c) δ = 0.0003, (d) δ = 0.0025, (e) δ = 0.001 and (f) δ = 0.01

Figure 12a and 13a display the MSE with changes of fractional orders. The x-axis δ represents the deviation distance (in the interval [−0.05, 0.05] with step size 0,002) to the correct fractional orders. From the simulation results, we learn that the decrypted image/video has very distinct difference even if a very small deviation occurs in the fractional orders. When the deviation is up to 0.0003, the decrypted image/video is fuzzy and when the deviation is larger than 0.0003, one has difficulty in recovering the original image/video from the encrypted one.

Fig. 12

The MSE between the plain and encrypted image with the variation of deviation distance δ = δ_x = δ_y. a the images Lena and Peppers b comparison of MSEs of cryptosystems based on proposed method, FrDCTs [62] , FrDFTs [31], FrMTs [73], DFrST [43], DFrKT [37] and FrHT [24]

Fig. 13

The MSE between the plain and encrypted video sequence with the variation of deviation distance δ = δ_x = δ_y. a The CoastGuard and Tennis video sequence. b Comparison of MSEs of cryptosystems based on proposed method, FrDCTs [62] , FrDFT [17], DFrKT [37] and FrHT [24]

Figures 12b and 13b compares the security between the fractional transform of different encryption algorithms FrDTT, FrDCTs [62] , FrDFTs [31], FrMTs [73], DFrST [43], DFrKT [37] and FrHT [24], from the results of the MSE for grayscale image. The x-axis δ represents the deviation distance (in the interval [−0.1, 0.1] with step size 0,002) to the correct transform order parameters. This result demonstrates the effectiveness and performances of the proposed scheme in terms of its ability to secure image/video and sensitivity to Keys. It should be noted that when the keys are all correct, the original image/video can be completely decrypted with MSE = 0 for all compared algorithms.

6.5 Robustness detection

6.5.1 Robustness to the noise attack

Since the encrypted image/video are easily affected by noise and data loss during transmission and processing, it is necessary to measure the robustness of the proposed image/video encryption algorithm. Therefore, it is necessary to measure the quality of an image/video encryption method to verify its anti-noise ability. In this paper, the Gaussian white noise with the mean value of 0 and variance of 1 is added to the encrypted image/video of “Lena” and tennis video sequence by Eq. (36) for noise interference.

$$ {E}^{\prime }=E\left(1+\sigma G\right) $$

(36)

where Eand E^′ represent of the ideal encrypted image and the noise-affected encrypted image, respectively. Parameter σ is a coefficient on noise strength or intensity, and G represents Gaussian random data with zero-mean and identity standard deviation.

To see the resistance of the proposed method against noise, Fig. 15 shows four frames of a tennis video sequence along with their PSNRs when decrypted with an additive white Gaussian noise of variable power coefficient σ we notice that the frames remain identifiable despite the presence of noise. In the same way, Fig. 14 shows the encrypted images of the proposed method in this paper at Gaussian noise intensity σ correctly decrypted image at 0.05, 0.10, 0.20, 0.50, 0.80, 1.00.

Fig. 14

Decrypted image with different Gaussian noise intensities

As can be seen in Figs. 14 and 15, although the quality of the decrypted image/video gradually increases as the intensity of the Gaussian noise added to the decryption increases, the image/video quality after decryption is also decreasing. The noise intensity drops, but at 0.10 the image/video is clearly visible, and even when the intensity is increased to 1.00, the image is still visible. The original image/video information is vaguely recognizable, thus it can be seen that the encryption method proposed in this paper has good anti-noise performance. In order to deepen the comparison with current classical methods of image encryption, experiments were carried out to calculate the PSNR values of the decrypted images of proposed method, FrDCTs [62] , FrDFTs [31], FrMTs [73], DFrST [43], DFrKT [37] and FrHT [24]. From Table 9, we can see that, although the PSNR values of images decrypted by FrDFTs under different noise intensities of 0.80 and 1.00.

Fig. 15

Decrypted tennis video sequence with different Gaussian noise intensities σ

Table 9 The PSNR values of the decrypted images “Lena” after different intensities of Gaussian noise interference using the proposed method and other similar methods

Figure 16 shows the computed MSE between a decrypted tennis video sequence and the corresponding original video sequence as a function of the variable power coefficient σ. In this experiment, the MSE curves between the original video sequence and decrypted one with different σ of FrDCTs [62] , FrDFTs [17], DFrKT [37] and the proposed method are shown in Fig. 16a. This Figure shows the decrypted video performance of FrDCTs [62] , FrDFT [17], DFrKT [37] encrypted Tennis frame and the proposed method after Gaussian noise interference of different intensity. However, the FrDTTs based video sequence encryption method proposed in this article is better than the other in most cases has a better robustness.

Fig. 16

a Robustness performance decrypted tennis video sequence of FrDCTs [62] , FrDFT [17], DFrKT [37] and proposed method after different intensity Gaussian noise interference. b Robustness performance of the proposed method against noise perturbation with different σ

6.5.2 Classical types of attacks

The proposed scheme for the image/video encryption is robust; it protects image/video from several attacks that are applied by the intruder, for the data extraction from encrypted image/video. There are four classical types of attacks [56]:

• (i) ciphertext only attack (COA): the intruder doesn’t have any idea about the key used for encryption. Attacker tries to calculate the key to hack information. The encrypted image/video in proposed scheme is free from COA because of the use of fractional parameter keys, so attacker won’t be able to calculate it, without the presence of original fractional parameter. It is also called as replacement attacks.

• (ii) known plaintext attack (KPA): the attacker has some plaintexts and their corresponding ciphertext also, with use of them unauthorized person tries to calculate the relation between original and encrypted information. In proposed scheme fractional parameter and random phase code two asymmetric keys are applied alternatively on each frame of video. So, even if the hacker gets the information about public key, he won’t be able to extract original information, without the presence of private key. In this way proposed scheme is free from KPA attacks.

• (iii) chosen ciphertext attack (CCA): only ciphertext or encrypted data is used to hack the information, by doing little change in encrypted information and observing variation from image/video. Due to use of two different keys (fractional parameter and random phase code) for different image/video, the observation between two ciphered image/video will not facilitate hacker to deduce relation between them. So, the image/video is secured from chosen ciphertext attacks.

• (iv) chosen plaintext attack (CPA): the opponent has obtained temporary access to the encryption machinery. Hence, he can choose a plaintext string, and construct the corresponding ciphertext string.

In this way due to use of two different keys (fractional parameter and random phase code) for the encryption of image/video, the information is highly secure from the invaders. So, the proposed scheme can resist the chosen plaintext/ciphertext attack.

6.6 Computational complexity analysis

The complexity of the proposed algorithm is the sum of the complexities needed to implement the proposed algorithm. We count the main operations used in each step, and the total number represents the cipher’s complexity. Step 1 is to compute the 8 × 8 FrDTTs of a frame block using the matrix given by Eq. (27). The video sequence encryption process with secret keys is mainly implemented by times two-dimensional FrDTTs for each block of the frame. So the time complexity in Step 1 is (n_f × M × N), with n_f the number of frames. The time complexity in Step 2 is (n_f × M × N) since the time-consuming part is the number of the FrDTTs for each block. Therefore, considering that a block of an M × N frame

has to be transformed at most 8 times. Similar to Step 2, the mathematical complexity for the random phase mask can also be computed along similar lines for each block. The complexity of the random phase block in Step 3 is also (8 × n_f × M × N). In the last stage, four key streams with size of M × N are used to modify the image pixels. Therefore, the total time complexity of the presented encryption scheme is (8 × n_f × M × N)

. This will increase the security of the encryption process by many orders of magnitude in addition to the security provided by the FrDTTs and the random phase codes. However, our proposed algorithm can be executed in a parallel mode, which can accelerate the operation speed.

6.7 NIST statistical tests

NIST tests were performed on 100 encrypted Lena 256 × 256 Gy-scale images, each encrypted with hundred different keys. Table 10 below shows the obtained results of NIST tests. As it can be observed, all the tests were passed with a minimum passing rate of 98%.

Table 10 NIST Results for 100 Encrypted Lena 256 × 256 Images

7 Conclusion

In this paper, we have proposed an efficient method for the encryption of video image sequences. This method makes it possible to individually encrypt each frame of a video sequence using fractional-order discrete Tchebichef transform, which is advantageous in terms of transmission rate and in complexity of calculations. In addition, a block encryption scheme has been adopted and introduced in order to improve the sensitivity and space of the key. The method proposed in this paper extends the fractional-order discrete Tchebichef transform to the fractional-order vector in the real domain. Moreover, the use of fractional-orders parameters settings increases the key space for image/video encryption and has high key sensitivity. In addition, the encrypted image/video is a real-value image/video, and its size is the same as the original image/video size, which is convenient for display, transmission, and storage. Finally, the simulation results clearly show the feasibility of the proposed method as well as its resistance against statistical, brute force and noise attacks. Therefore, the image/video encryption method proposed in this paper can have a good application scenario in the field of image/video encryption communication.

Appendices

Appendix A

Proof of property (v)

Let λ be an eigenvalue of Tchebichef polynomial matrix and u the corresponding eigenvector, then Cu = λu, using the properties (iii) and (iv), we have:

$$ u=\mathrm{CC}u=\lambda \mathrm{C}u={\lambda}^2u $$

(A1)

thus. {Key1, Key2}

$$ \left({\lambda}^2-1\right)u=0 $$

(A2)

The matrix C has only two eigenvalues {1, −1}, The proof of Eq. (19) has been completed

Appendix B

Proof of properties (a)-(b)

Let C ∈ ℂ^N × Nbe Tchebichef polynomial matrix, with their eigenvalues on the diagonal of a diagonal matrix Λ =  diag (λ₁, ……λ_N) ∈ ℂ^N × N and the corresponding eigenvectors forming the columns of a matrix V = [u₁, ……, u_N] ∈ ℂ^N × N, we have:

$$ \mathrm{C}=V\Lambda {V}^{-1} $$

(B.1)

where, the orthonormal vectors u₁, ……u_N are eigenvectors of C, corresponding to eigenvalues λ₁, ……λ_N.

$$ \mathrm{C}=\left[{u}_1\cdots \cdots {u}_N\right]\left(\begin{array}{ccc}{\lambda}_1& & \\ {}& \ddots & \\ {}& & {\lambda}_N\end{array}\right)\left[\begin{array}{c}{u}_1^T\\ {}\vdots \\ {}{u}_N^T\end{array}\right]=\left[{\lambda}_1{u}_1\cdots \cdots {\lambda}_N{u}_N\right]\left[\begin{array}{c}{u}_1^T\\ {}\vdots \\ {}{u}_N^T\end{array}\right] $$

(B.2)

$$ \mathrm{C}={\lambda}_1{u}_1{u}_1^T\cdots \cdots {\lambda}_N{u}_N{u}_N^T $$

(B.3)

Notice that the matrices

$$ {\mathrm{P}}_j:= {u}_j{u}_j^T\in {\mathbb{C}}^{N\times N} $$

(B.4)

are orthogonal projectors, since ${\mathrm{P}}_j^T={\mathrm{P}}_j$and ${\mathrm{P}}_j^2:= {u}_j\left({u}_j^T{u}_j\right){u}_j^T={u}_j{u}_j^T={\mathrm{P}}_j$

$$ \mathrm{C}=\sum \limits_{j=1}^N{\lambda}_j{\mathrm{P}}_j $$

(B.5)

if j ≠ k, then the orthogonality of the eigenvectors implies

$$ {\mathrm{P}}_j{\mathrm{P}}_k={u}_j{u}_j^T{u}_k{u}_k^T=0 $$

(B.6)

The proof of properties (a) and (b) has been completed.

Proof of propriety (c)

Let γ, η and λ be respectively the eigenvalues of the matrices P₀,P₁ and C of size N × N, using Eq. (18), we have:

$$ {\displaystyle \begin{array}{c}\mid \gamma I-{\mathrm{P}}_0\mid =\mid \gamma I-0.5\left(\mathrm{C}+I\right)\mid =\mid \left(\gamma -0.5\right)I-0.5\mathrm{C}\mid \\ {}=\mid \left(\gamma -0.5\right)I-0.5\mathrm{C}\mid ={0.5}^N\mid \left(2\gamma -1\right)I-\mathrm{C}\mid \\ {}=0\end{array}} $$

(B.7)

Similarly, we have

$$ \mid \eta I-{\mathrm{P}}_1\mid ={0.5}^N\mid \left(2\eta -1\right)I-\mathrm{C}\mid =0,\boldsymbol{and}\mid \lambda I-\mathrm{C}\mid =0 $$

(B.8)

From (B.7) and (B.8), we have

$$ 2\gamma -1=\lambda, \boldsymbol{and}-\left(2\eta -1\right)=\lambda $$

(B.9)

Hence, if λ = 1, there is γ = 1, η = 0, and if λ =  − 1, then γ = 0, η = 1.

The proof of propriety (c) has been completed.

Appendix C

Let P₀ and P₁ the spectral projection matrices of Tchebichef polynomial matrix C ∈ ℂ^N × N, and u,v be their eigenvectors corresponding to λ = 1, respectively.

Proof of Lemma 1

From Table 1 and Property (c), we have:

$$ {\mathrm{P}}_0u=u,\boldsymbol{and}\ {\mathrm{P}}_1v=v $$

(C.1)

using (C.1) and Property (b), we have:

$$ {u}^Tv={\left({\mathrm{P}}_0u\right)}^T\left({\mathrm{P}}_1v\right)={u}^T{{\mathrm{P}}_0}^T{\mathrm{P}}_1v=0 $$

(C.2)

The proof of Lemma 1 has been completed.

Proof of Lemma 2

From Eq. (15), Lemma 1 and property (b) we have:

$$ {\displaystyle \begin{array}{c}\mathrm{C}u=\left({\lambda}_0{\mathrm{P}}_0+{\lambda}_1{\mathrm{P}}_1\right)u={\lambda}_0{\mathrm{P}}_0u+{\lambda}_1{\mathrm{P}}_1u\\ {}={\lambda}_0{\mathrm{P}}_0u+{\lambda}_1{\mathrm{P}}_1{\mathrm{P}}_0u={\lambda}_0{\mathrm{P}}_0u+{\lambda}_1{\mathrm{P}}_1^T{\mathrm{P}}_0u\\ {}={\lambda}_0{\mathrm{P}}_0u={\lambda}_0u\end{array}} $$

(C.3)

$$ {\displaystyle \begin{array}{c}\mathrm{C}v=\left({\lambda}_0{\mathrm{P}}_0+{\lambda}_1{\mathrm{P}}_1\right)v={\lambda}_0{\mathrm{P}}_0v+{\lambda}_1{\mathrm{P}}_1v\\ {}={\lambda}_0{\mathrm{P}}_0{\mathrm{P}}_1v+{\lambda}_1{\mathrm{P}}_1v={\lambda}_1{\mathrm{P}}_1v={\lambda}_1v\end{array}} $$

(C.4)

The proof of Lemma 2 has been completed.