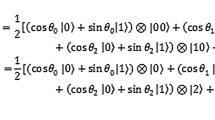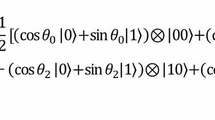1 Introduction

Quantum computers use the principles of quantum mechanics such as superposition and entanglement to solve problems more efficiently than classical computers [15]; i.e., they store and process data in a novel way to solve problems faster than classical computers [1, 13]. Digital image processing (DIP) [4] is a field in computer science that has many applications in remote sensing [2], traffic [21], machine learning [22], medicine [34], astronomy [16], and agriculture [25]. Storing, transmitting, and processing large images are challenging problems. One way to solve these challenges is to use quantum computers, this give rise to the field of quantum image processing (QIP). QIP offers a better performance as it could improve the storage requirements, the transmission speed and the computational complexity. Using quantum algorithms [5], the image can be captured, stored and processed on quantum computers. The first task in QIP is to represent digital images on quantum computers. Two types of image representations have been proposed in literature, amplitude representation and basis state representation.

In the amplitude representation, the values of the pixels are stored in the amplitude of the qubits such as in [24] which uses qubit lattice to store images, it stores the frequency of the colors in the amplitudes of a set of qubits, this model stores several copies of the same image in a qubit lattices to be able to retrieve the image. The method in [7] uses a real kit of Hilbert space to store \(2^n\times 2^n\) gray images so that the color value is stored in the amplitude of n-qubits and the basis state is used to label the pixels, the number of qubits required in this model increases logarithmically as the size of the image increases. Flexible representation of quantum images (FRQI) [8] uses the amplitude of a single qubit to store the gray value of the pixels for \(2^n\times 2^n\) image using rotation gates, this qubit is entangled with a qubit sequence to store the position of the pixels, unlike the previous models in literature, this model stores the pixels in a normalized superposition so that any operation can be applied on all the pixels simultaneously. Multi-channel representation for images on quantum computers using the RGB\(\alpha\) color space (MCRQI) [20] which is inspired by the FRQI model to store color images instead of gray images using the amplitude of three qubits to encode the R, G, B, and the \(\alpha\) channels for a \(2^n\times 2^n\) image. Flexible representation of quantum color images (FRQCI) [10] offers an improvement for the FRQI model to store the values of the pixels for color images in the amplitude of a single qubit using rotation gates instead of using three qubits as in the MCRQI model. Order-encoded quantum image model and parallel histogram specification (OQIM) [30] stores the gray value of pixels for \(2^n\times 2^n\) images in the amplitude of a single qubit and stores the position of the pixels in the amplitude of another qubit using rotation gates, these two qubits are entangled with a qubit sequence to store the ascending order of each pixel according to the magnitude of their gray values.

In the basis state representation, the values of the pixels are stored in the basis state of a qubit sequence such as in [23] which stores binary geometrical shapes with n vertices in the basis of n-qubits. Novel enhanced quantum representation (NEQR) [32] is inspired by the FRQI model to store the values of the pixels and the corresponding position in the basis of two entangled qubit sequences for a \(2^n\times 2^n\) gray image, it uses 2n-CNOT gates to store the gray value of the pixels in \(2n+8\) qubits, this model stores gray images instead of binary images as in the previous model. Improved NEQR (INEQR) [6] is an improvement for the NEQR model to store \(2^n\times 2^m\) images in the basis state of two entangled qubit sequences instead of storing \(2^n\times 2^n\) images as in the NEQR model. Novel quantum representation for log-polar images (QUALPI) [33] uses the basis of three entangled qubit sequences to store the gray value of the pixels, log-radius, and angular orientations of log-polar images, this model stores images sampled in log-polar coordinates instead of images sampled in Cartesian coordinates as in the previous models so that complex transformations such as rotation and scaling can be performed. Novel quantum representation of color digital images (NCQI) [18] which is inspired by the NEQR model for storing color digital images using the basis of two entangled qubit sequences to store the color value of the pixels and its corresponding position in a \(2n+24\) qubits. Optimized quantum representation for color digital images (OCQR) [11] uses the basis of three qubit sequences to store color images, this model uses \(2n+10\) qubits which is less qubits when compared with the NCQI model so it is considered an improvement for the NCQI model. Quantum representation of multi wavelength images (QRMW) [17] uses the basis of three qubit sequences to store the color value, the wavelength, and the position for \(2^n\times 2^m\) multi-channel images. Quantum image representation based on bitplanes (BRQI) [19] decomposes the gray image into 8 binary images and stores them in the basis state using the generalized model of NEQR (GNEQR) [9] which stores 2D integer signals. A new quantum representation model of color digital images (QRCI) [28] which uses two entangled qubit sequences to store a \(2^n\times 2^n\) color images, it stores the value of the pixels in the basis state of the first qubit sequence and stores the corresponding bit-plane and the position of the pixels in the second qubit sequence, this model uses \(2n+6\) qubits which is less qubits when compared with the NCQI and the OCQR models. Quantum block image encryption based on arnold transform and sine chaotification model (QBIR) [12] which is inspired by the NEQR model to store a \(2^n\times 2^n\) gray images, it divides the image into blocks and store them in two entangled qubit sequences, the values of the pixels are stored in the first qubit sequence while the position of the blocks and the position of the pixels in each block are stored in the second qubit sequence. Double quantum color images encryption scheme based on DQRCI [27] which is based on the QRCI model, it uses the QRCI method to store two color images of size \(2^n\times 2^n\) simultaneously in \(2n+9\) qubits. Quantum representation of indexed images and its applications (QIIR) [26] which stores \(2^n\times 2^n\) indexed images, it uses the NQER method to store the data matrix in \(2n+q\) qubits and stores the palette matrix in \(24+q\) qubits.

In this paper, two enhanced quantum image representations will be proposed to improve the FRQI and the NEQR models and also to improve the models that have been inspired by these models. The first enhanced quantum representation based on the FRQI model (EFRQI) is an amplitude representation that uses the partial negation operator [31] to store the gray value of the pixels in the amplitudes of the qubits, and the second enhanced quantum representation based on the NEQR model (ENEQR) is a basis state representation that uses the CNOT gate to store the gray value of the pixels. The comparison of the proposed models with the FRQI and the NEQR shows enhancements as follows:

  1. 1.

    The time complexity of the proposed EFRQI for representing a \(2^n\times 2^n\) gray image is decreased by a factor of \(\frac{2^{2n-1}}{n}\) when compared with the FRQI model, but with the same quantum cost.

  2. 2.

    The time complexity of the proposed ENEQR for representing a \(2^n\times 2^n\) gray image is decreased by a factor of 8, and the cost of the quantum circuit is decreased to be less than half when compared with the NEQR model.

The paper is organized as follows. Section 2 discusses the related work. Section 3 explains the two proposed enhanced quantum image representations, and describes the algorithms of quantum image representation. Section 4 shows the analysis of performance. Finally, Sect. 5 concludes the paper.

2 Related work

2.1 The FRQI model

In flexible representation of quantum images for polynomial preparation (FRQI) [8], the gray value of a pixel is stored in the amplitude of a single qubit using the quantum rotation gates and the position information of the corresponding pixel is stored in the basis state of a qubit sequence which is entangled to the color qubit. The quantum representation for this model is expressed in Eqn (1)

$$\begin{aligned} |{\Psi _1}\rangle = \dfrac{1}{2^n} \sum _{Y=0}^{2^n-1}\sum _{X=0}^{2^n-1}(cos \theta _{YX}|{0}\rangle + sin \theta _{YX}|{1}\rangle )|{YX}\rangle ,\qquad \theta _{YX} \in \Big [0,\dfrac{\pi }{2}\Big ], \end{aligned}$$
(1)

where \(\theta _{YX}\) is the phase of the color qubit which encodes the gray value of pixel (Y, X). An example of a \(2\times 2\) image and its representation with the FRQI model is shown in Fig. 1. The time complexity of the preparation process is \(O(2^{4n})\) for a \(2^n\times 2^n\) image.

2.2 The NEQR model

Instead of using the amplitude of a qubit to store the gray value of images as in the FRQI [8], a novel enhanced quantum representation for digital images (NEQR) [32] is proposed. The NEQR utilizes the basis state of a qubit sequence to store the gray value of images, it uses two entangled qubit sequences to store the gray value of each pixel and its corresponding position, and stores the whole image in the superposition. Assume that the binary sequence \(C^0_{YX}C^1_{YX}...C^{q-1}_{YX}\) encodes the gray value for a pixel P(Y, X) at position (Y, X) where the gray range is \([0,2^q-1]\) as in Eqn (2), therefore the NEQR needs \(2n+q\) qubits for storing \(2^n\times 2^n\) image with gray range \(2^q\).

$$\begin{aligned} P(Y,X) = C^0_{YX}C^1_{YX}...C^{q-1}_{YX}, C^i_{YX} \in [0,1], P(Y,X)\in [0,2^q-1]. \end{aligned}$$
(2)

Equation (3) shows the expression for storing \(2^n\times 2^n\) gray image with the NEQR model and Fig. 1 shows the NEQR representation for a \(2\times 2\) gray image,

$$\begin{aligned} |{\Psi _2}\rangle = \dfrac{1}{2^n} \sum _{Y=0}^{2^n-1}\sum _{X=0}^{2^n-1}|{P(Y,X)}\rangle |{YX}\rangle , \end{aligned}$$
(3)

where \(|{P(Y,X)}\rangle\) is the gray value of a pixel and \(|{YX}\rangle\) is the horizontal and vertical coordinates for the corresponding pixel. The time complexity of the preparation process is \(O(2qn2^{2n})\) for a \(2^n\times 2^n\) image and the cost of the quantum circuit for the image is \(c \,q\,2^{2n}\), where c is the quantum cost for the 2n-CNOT gate according to reversible benchmarks [14].

Fig. 1
figure 1

An example of \(2\times 2\) image and its representation with (a) the FRQI model and (b) the NEQR model

Full size image

2.3 The partial negation operator RX

Let X be the Pauli-X gate which is the quantum equivalent to the NOT gate as follows,

$$\begin{aligned} X = \begin{bmatrix} 0 &{} 1\\ 1 &{} 0 \end{bmatrix}, \\ X|{0}\rangle \rightarrow |{1}\rangle , \nonumber \\ X|{1}\rangle \rightarrow |{0}\rangle . \end{aligned}$$
(4)

The X gate is a negation gate that acts on one qubit, it flips the qubit state from \(|{0}\rangle\) to \(|{1}\rangle\) and vice-versa. The partial negation operator RX [31] is the \(k^{th}\) root of the X gate and can be calculated using the following matrix,

$$\begin{aligned} RX = \root k \of {X} = \dfrac{1}{2} \begin{bmatrix} 1+t &{} 1-t\\ 1-t &{} 1+t \end{bmatrix}, \end{aligned}$$
(5)

where \(t = \root k \of {-1}\). The RX operator negates the state partially as follows,

$$\begin{aligned} RX|{0}\rangle \rightarrow \dfrac{1+t}{2}|{0}\rangle + \dfrac{1-t}{2}|{1}\rangle , \nonumber \\ RX|{1}\rangle \rightarrow \dfrac{1-t}{2}|{1}\rangle + \dfrac{1+t}{2}|{0}\rangle . \end{aligned}$$
(6)

Applying the RX gate for d times on a qubit can be calculated as follows,

$$\begin{aligned} RX^d = \dfrac{1}{2} \begin{bmatrix} 1+t^d &{} 1-t^d\\ 1-t^d &{} 1+t^d \end{bmatrix}, \end{aligned}$$
(7)

and the state after applying \(RX^d\) is as follows,

$$\begin{aligned} RX^d|{0}\rangle \rightarrow \dfrac{1+t^d}{2}|{0}\rangle + \dfrac{1-t^d}{2}|{1}\rangle , \nonumber \\ RX^d|{1}\rangle \rightarrow \dfrac{1-t^d}{2}|{1}\rangle + \dfrac{1+t^d}{2}|{0}\rangle , \end{aligned}$$
(8)

such that if \(d = k\), then \(RX^d = X\).

3 Enhanced representations for quantum images

In this section, the two enhanced quantum representations will be proposed. The first representation is to improve the time complexity of the FRQI model, the second one is to improve the time complexity and the quantum cost of the NEQR model.

3.1 Enhanced quantum representation based on the FRQI model (EFRQI)

This representation employs \(2n+1\) qubits to store gray images, it uses the partial negation operator RX [31] to enhance the time complexity of the FRQI model [8]. As explained in Sect. 2.3, the RX operator is equivalent to \(\root k \of {X}\), so in this representation the RX operator is equivalent to \(\root 255 \of {X}\). The RX operator is applied according to the gray value of the pixel. For example, if the gray value of a pixel at position (Y, X) is 200, then 200 RX operators are applied on the qubit at that position which is equivalent to a single operator \(X^{\frac{200}{255}}\), and if the gray value is 255, then 255 RX operators are applied which is equivalent to a single operator \(X^{\frac{255}{255}}\) that is equivalent to the X gate, and so on. So, basically only one gate is applied to set the gray value of a pixel.

Inspired by the FRQI model, for a \(2^n\times 2^n\) gray image, the EFRQI uses a single qubit to store the gray value entangled with qubit sequence to store the corresponding position, the gray value of the pixel is stored in the amplitudes of the state as follows,

$$\begin{aligned} |{\Psi _3}\rangle =\dfrac{1}{2^n} \sum _{Y=0}^{2^n-1}\sum _{X=0}^{2^n-1}(a_{YX}|{0}\rangle +b_{YX}|{1}\rangle )|{YX}\rangle , \end{aligned}$$
(9)

where a and b are the amplitudes of the state as explained in Sect. 2.3.

The quantum image preparation using the EFRQI algorithm starts with the initial state \(|{\psi _0}\rangle\) which is a quantum register with \(2n+1\) qubits all initialized to \(|{0}\rangle\).

$$\begin{aligned} |{\psi _0}\rangle = |{0}\rangle ^{\otimes 2n+1}. \end{aligned}$$
(10)

The quantum image preparation is divided into two steps:

Step 1: Storing the position of the pixels of a black image by transforming the initial state \(|{\psi _0}\rangle\) into the intermediate state \(|{\psi _1}\rangle\) using the single qubit gates I and H, with a quantum operation \(V_1\) which is expressed as follows,

$$\begin{aligned} V_1 = H^{\otimes 2n}\otimes I. \end{aligned}$$
(11)

The position of the pixels is stored in the quantum state \(|{\psi _1}\rangle\) after applying \(V_1\) on the initial state \(|{\psi _0}\rangle\).

$$\begin{aligned} |{\psi _1}\rangle= & {} V_1{|{\psi _0}\rangle }\nonumber \\ \nonumber \\= & {} (H|{0}\rangle )^{\otimes {2n}} \otimes (I|{0}\rangle )\nonumber \\= & {} \dfrac{1}{2^n}\sum _{i=0}^{2^{2n}-1}|{i}\rangle \otimes |{0}\rangle \nonumber \\= & {} \dfrac{1}{2^n} \sum _{Y=0}^{2^n-1}\sum _{X=0}^{2^n-1} |{0}\rangle |{YX}\rangle . \end{aligned}$$
(12)

Step 2: To complete the image preparation, a quantum sub operation \(V_{YX}\) which consists of \(2^{2n}\) sub operations to set the gray value for every pixel in the image. For pixel (Y, X), the quantum sub operation is expressed as \(V_{YX}\),

$$\begin{aligned} V_{YX} = \Bigg ( I \otimes \sum _{j=0}^{2^n-1}\sum _{i=0,ji\ne {YX}}^{2^n-1} |{ji}\rangle \langle {ji}| \Bigg ) + \Gamma _{YX} \otimes |{YX}\rangle \langle {YX}|, \end{aligned}$$
(13)

where \(\Gamma _{YX}\) is the quantum setting operation for pixel (Y, X). The quantum setting operation consists of \(\prod _{i=1}^{d}\tau ^i_{YX}\) for setting the gray value as follows,

$$\begin{aligned} \Gamma _{YX}=\prod _{i=1}^{d}\tau ^i_{YX}, \qquad \qquad \qquad \qquad \nonumber \\ \qquad \tau ^i_{YX} : |{0}\rangle |{YX}\rangle = RX(|{YX}\rangle ,|{0}\rangle ) = (X^{\frac{d}{255}}|{0}\rangle )|{YX}\rangle , \end{aligned}$$
(14)

where d is the number of partial negation operators, if the pixel is not black, \(\tau ^i_{YX}\) is a partial negation operator, where \(RX(|{YX}\rangle ,|{0}\rangle )\) is a (\(2n+1\))-qubit controlled gate with \(|{YX}\rangle\) as 2n control qubits and \(|{0}\rangle\) as target qubit, otherwise it is the quantum identity gate as follows,

$$\begin{aligned} \tau _{YX}|{0}\rangle |{YX}\rangle = \prod ^{d}_{i=1}(\tau ^i_{YX}|{0}\rangle |{YX}\rangle ) = \prod ^{d}_{i=1} RX^i_{YX}(|{YX}\rangle ,|{0}\rangle ) = X_{YX}^{\frac{d}{255}}|{0}\rangle |{YX}\rangle = (a_{YX}|{0}\rangle +b_{YX}|{1}\rangle )|{YX}\rangle . \end{aligned}$$
(15)

So the operation of setting the gray value for the pixel at position (Y, X) is,

$$\begin{aligned} \Gamma _{YX}|{0}\rangle |{YX}\rangle= & {} \prod _{i=1}^{d}RX^i_{YX}(|{YX}\rangle ,|{0}\rangle )\nonumber \\= & {} X^{\frac{d}{255}}|{0}\rangle |{YX}\rangle = (a_{YX}|{0}\rangle +b_{YX}|{1}\rangle )|{YX}\rangle . \end{aligned}$$
(16)

By applying \(V_{YX}\) on the quantum state \(|{\psi _1}\rangle\), the state is transformed into:

$$\begin{aligned} V_{YX}|{\psi _1}\rangle= & {} V_{YX}\Bigg (\dfrac{1}{2^n}\sum _{j=0}^{2^n-1}\sum _{i=0}^{2^n-1}|{0}\rangle |{ji}\rangle \Bigg )\nonumber \\= & {} \dfrac{1}{2^n}V_{YX}\Bigg ( \sum _{j=0}^{2^n-1}\sum _{i=0,ji\ne {YX}}^{2^n-1}|{0}\rangle |{ji}\rangle + |{0}\rangle |{YX}\rangle \Bigg )\nonumber \\= & {} \dfrac{1}{2^n}\Bigg (\sum _{j=0}^{2^n-1}\sum _{i=0,ji\ne {YX}}^{2^n-1}|{0}\rangle |{ji}\rangle + \Gamma _{YX}|{0}\rangle |{YX}\rangle \Bigg )\nonumber \\= & {} \dfrac{1}{2^n}\Bigg (\sum _{j=0}^{2^n-1}\sum _{i=0,ji\ne {YX}}^{2^n-1}|{0}\rangle |{ji}\rangle + (a_{YX}|{0}\rangle +b_{YX}|{1}\rangle )|{YX}\rangle \Bigg ). \end{aligned}$$
(17)

The sub operation \(V_{YX}\) sets the gray value for only one pixel, therefore the quantum operation \(V_2\) is used to set the gray value for all the pixels in the image, it consists of all the required sub operations as follows,

$$\begin{aligned} V_2 = \prod _{Y=0}^{2^{n-1}}\prod _{X=0}^{2^{n-1}}V_{YX},\qquad \qquad \qquad \qquad \end{aligned}$$
(18)

and applying \(V_2\) on \(|{\psi _1}\rangle\) gives,

$$\begin{aligned} |{\psi _2}\rangle= & {} V_2|{\psi _1}\rangle \nonumber \\= & {} \dfrac{1}{2^n} \sum _{Y=0}^{2^n-1}\sum _{X=0}^{2^n-1} \Gamma _{YX}|{0}\rangle |{YX}\rangle \nonumber \\= & {} \dfrac{1}{2^n} \sum _{Y=0}^{2^n-1}\sum _{X=0}^{2^n-1}(a_{YX}|{0}\rangle +b_{YX}|{1}\rangle )|{YX}\rangle . \end{aligned}$$
(19)

Figure 2 shows the probability distribution for the gray image in Fig. 1 with the EFRQI representation. In order to show the efficiency of the EFRQI algorithm, the time complexity and the cost of the quantum circuit are discussed in the following theorems.

Theorem 1

The time complexity of preparing a gray image of size \(2^n\times 2^n\) using the EFRQI is no more than \(O(2n2^{2n})\).

Proof

The process of image representation using the EFRQI consists of one main operation \(V_2\) which is used for setting the gray values for the whole image. The quantum operation \(V_2\) consists of \(2^{2n}\) sub operations \(V_{YX}\), the sub operation \(V_{YX}\) uses the quantum operation \(\Gamma _{YX}\) to performs d operations on the qubit of the pixel according to the gray value of that pixel. When the pixel is not black, \(\Gamma _{YX}\) applies the RX gate to set the gray value of the pixel. Applying the RX for d times on a qubit it still a single operator \(X^{\frac{d}{255}}\) with 2n control qubits. The time complexity is calculated according to the number of the control qubits which means that the sub operation \(V_{YX}\) has time complexity equals to O(2n).

For the operation \(V_2\), it applies \(2^{2n}\) sub operations which is the total number of pixels in a \(2^n\times 2^n\) gray image, therefore the time complexity of \(V_2\) is \(O(2n2^{2n})\), hence the time complexity of the EFRQI representation is \(O(2n2^{2n})\). \(\square\)

Theorem 2

The quantum cost of the circuit for representing a \(2^n\times 2^n\) gray image using the EFRQI is no more than \(c \, 2^{2n}\), where c is the cost of \(X^{\frac{d}{255}}\) with 2n control qubits which has the same cost of 2n-CNOT gate [14].

Proof

For constructing the circuit of a gray image using the EFRQI, every pixel uses d RX gates which is equivalent to a single operator \(X^{\frac{d}{255}}\) and if \(d=255\), then the operator becomes 2n-CNOT gate, therefore the quantum cost of a single pixel is c. Since a \(2^n\times 2^n\) gray image contains \(2^{2n}\) pixel, then the quantum cost of the circuit for the entire image using the EFRQI is \(c\,2^{2n}\).\(\square\)

For example, to prepare the image in Fig. 1 using the EFRQI algorithm, prepare a quantum register with 3 qubits all initialized to \(|{0}\rangle\),

$$\begin{aligned} |{\psi _0}\rangle =|{0}\rangle ^{\otimes 3}, \end{aligned}$$

then the position of the pixels will be stored as follows,

$$\begin{aligned} |{\psi _1}\rangle= & {} H|{0}\rangle ^{\otimes 2}\otimes I|{0}\rangle \\= & {} \dfrac{1}{2}\sum ^3_{i=0}|{i}\rangle \otimes |{0}\rangle \\= & {} \dfrac{1}{2}\sum ^1_{Y=0}\sum ^1_{X=0}|{0}\rangle |{YX}\rangle \\= & {} \dfrac{1}{2}(|{0}\rangle |{00}\rangle +|{0}\rangle |{01}\rangle +|{0}\rangle |{10}\rangle +|{0}\rangle |{11}\rangle ). \end{aligned}$$

To complete the image preparation, the value of the pixels will be stored using the RX operator as follows,

$$\begin{aligned} |{\psi _2}\rangle= & {} \dfrac{1}{2}(X^{\frac{0}{255}}|{0}\rangle |{00}\rangle +X^{\frac{70}{255}}|{0}\rangle |{01}\rangle +X^{\frac{120}{255}}|{0}\rangle |{10}\rangle +X^{\frac{255}{255}}|{0}\rangle |{11}\rangle )\\= & {} \dfrac{1}{2}(|{0}\rangle |{00}\rangle +(a_{01} |{0}\rangle + b_{01} |{1}\rangle )|{01}\rangle +(a_{10} |{0}\rangle + b_{10} |{1}\rangle )|{10}\rangle +|{1}\rangle |{11}\rangle ). \end{aligned}$$
Fig. 2
figure 2

A probability distribution for a \(2\times 2\) gray image with the EFRQI representation

Full size image

3.2 Enhanced quantum representation based on the NEQR model (ENEQR)

In order to improve the time complexity and the quantum cost of the NEQR model [32], the ENEQR representation will be proposed to store and process digital image with less time complexity and less cost for the quantum circuit. The proposed enhancement is also applicable to the NCQI [18] and the OCQR [11] models for color digital images.

Inspired by the NEQR model, for a \(2^n\times 2^n\) image with gray range \(2^q\), the ENEQR uses two entangled qubit sequences to store the gray value of the pixel and its corresponding position as follows,

$$\begin{aligned} |{\Psi _4}\rangle = \dfrac{1}{2^n} \sum _{Y=0}^{2^n-1}\sum _{X=0}^{2^n-1}|{P(Y,X)}\rangle |{0}\rangle |{YX}\rangle , \end{aligned}$$
(20)

therefore, the representation employs \(2n+q+1\) qubits to store gray images. This representation uses an auxiliary qubit to load the position of the pixel to be changed. Instead of using q 2n-CNOT gates to set the gray value of every pixel, it uses only one 2n-CNOT gate to load the position to the auxiliary qubit and q CNOT gates to set the gray value for the pixel then resets the auxiliary qubit to be used for the next pixel and so on which improves the time complexity and the quantum cost of the circuit.

To prepare the quantum image using the proposed algorithm, assume the initial state \(|{\psi _0}\rangle\) is a quantum register prepared with \(2n+q+1\) qubits all initialized to \(|{0}\rangle\).

$$\begin{aligned} {|{\psi _0}\rangle } = {|{0}\rangle }^{\otimes {2n+q+1}}. \end{aligned}$$
(21)

The image preparation is divided into two steps:

Step 1: The single qubit gates I and H are used to transform the initial state \(|{\psi _0}\rangle\) into the intermediate state \(|{\psi _1}\rangle\) which is the position of the pixels of a black image, with a quantum operation \(U_1\) which is expressed as follows,

$$\begin{aligned} U_1=I^{\otimes {q+1}} \otimes H^{\otimes {2n}}. \end{aligned}$$
(22)

After applying \(U_1\) on the initial state \(|{\psi _0}\rangle\), the position information of the pixels is stored in the quantum state \(|{\psi _1}\rangle\).

$$\begin{aligned} |{\psi _1}\rangle= & {} U_1{|{\psi _0}\rangle } \nonumber \\= & {} (I|{0}\rangle )^{\otimes {q+1}} \otimes (H|{0}\rangle )^{\otimes {2n}} \nonumber \\= & {} \dfrac{1}{2^n}|{0}\rangle ^{\otimes {q+1}} \otimes \sum _{i=0}^{2^{2n}-1}|{i}\rangle \nonumber \\= & {} \dfrac{1}{2^n} \sum _{Y=0}^{2^n-1}\sum _{X=0}^{2^n-1} |{0}\rangle ^{\otimes {q+1}}|{YX}\rangle . \end{aligned}$$
(23)

Step 2: To complete the image preparation, it is required to set the gray value for every pixel. This step is divided into \(2^{2n}\) sub operations to set the gray value for every pixel. For pixel (Y, X), the quantum sub operation is expressed as \(U_{YX}\).

$$\begin{aligned} U_{YX} = \Bigg ( I \otimes \sum _{j=0}^{2^n-1}\sum _{i=0,ji\ne {YX}}^{2^n-1} |{ji}\rangle \langle {ji}| \Bigg ) + \varpi _{YX} \otimes |{YX}\rangle \langle {YX}|, \end{aligned}$$
(24)

where \(\varpi _{YX}\) is the quantum setting operation for pixel (Y, X). The quantum setting operation consists of two parts: \(\omega _{YX}\) for loading the pixel position to the auxiliary qubit and resetting the auxiliary qubit and \(\otimes _{i=0}^{q-1}\acute{\omega }^i_{YX}\) for setting the gray value.

$$\begin{aligned} \varpi _{YX} = \Bigg (\omega _{YX}\Bigg )\Bigg (\bigotimes _{i=0}^{q-1}\acute{\omega }^i_{YX}\Bigg )\Bigg (\omega _{YX}\Bigg ), \nonumber \\ \omega _{YX} : |{aux}\rangle \rightarrow |{0 \oplus YX}\rangle , \qquad \nonumber \\ \acute{\omega }^i_{YX} : |{0}\rangle \rightarrow |{0 \oplus aux}\rangle . \qquad \quad \end{aligned}$$
(25)

If the pixel is not black, \(\omega _{YX}\) is a 2n-CNOT gate and \(\acute{\omega }^i_{YX}\) is a CNOT gate, otherwise it is the quantum identity gate.

$$\begin{aligned} \acute{\omega }_{YX}|{0}\rangle ^{\otimes q} = \otimes ^{q-1}_{i=0}(\acute{\omega }^i_{YX}|{0}\rangle ) = \otimes ^{q-1}_{i=0}|{0^i \oplus aux}\rangle = \otimes ^{q-1}_{i=0}|{C^i_{YX}}\rangle = |{P(Y,X)}\rangle , \end{aligned}$$
(26)

so the operation of setting the gray value for the pixel at position YX is as follows,

$$\begin{aligned} \varpi _{YX}|{0}\rangle ^{\otimes q+1}= & {} \otimes _{i=0}^{q}(\varpi _{YX}^i|{0}\rangle ) = |{0 \oplus {YX}}\rangle \otimes _{i=0}^{q-1}|{0^i \oplus aux}\rangle |{YX \oplus YX}\rangle \nonumber \\= & {} |{YX}\rangle \otimes _{i=0}^{q-1} |{C_{YX}^i}\rangle |{0}\rangle = |{P(Y,X)}\rangle |{0}\rangle . \end{aligned}$$
(27)

By applying \(U_{YX}\) on the quantum state \(|{\psi _1}\rangle\), the state is transformed into:

$$\begin{aligned} U_{YX}|{\psi _1}\rangle= & {} U_{YX}\Bigg (\dfrac{1}{2^n}\sum _{j=0}^{2^n-1}\sum _{i=0}^{2^n-1}|{0}\rangle ^{\otimes q+1}|{ji}\rangle \Bigg )\nonumber \\= & {} \dfrac{1}{2^n}U_{YX}\Bigg ( \sum _{j=0}^{2^n-1}\sum _{i=0,ji\ne {YX}}^{2^n-1}|{0}\rangle ^{\otimes q+1}|{ji}\rangle + |{0}\rangle ^{\otimes q+1} |{YX}\rangle \Bigg )\nonumber \\= & {} \dfrac{1}{2^n}\Bigg (\sum _{j=0}^{2^n-1}\sum _{i=0,ji\ne {YX}}^{2^n-1}|{0}\rangle ^{\otimes q+1}|{ji}\rangle + \varpi _{YX}|{0}\rangle ^{\otimes q+1} |{YX}\rangle \Bigg )\nonumber \\= & {} \dfrac{1}{2^n}\Bigg (\sum _{j=0}^{2^n-1}\sum _{i=0,ji\ne {YX}}^{2^n-1}|{0}\rangle ^{\otimes q+1}|{ji}\rangle + |{P(Y,X)}\rangle |{0}\rangle |{YX}\rangle \Bigg ). \end{aligned}$$
(28)

The sub operation \(U_{YX}\) sets the gray value for only one pixel at a specific position, therefore the quantum operation \(U_2\) consists of all the sub operations that is used to set the gray value for the whole image as follows,

$$\begin{aligned} U_2 = \prod _{Y=0}^{2^{n-1}}\prod _{X=0}^{2^{n-1}}U_{YX}, \end{aligned}$$
(29)

and applying \(U_2\) on \(|{\psi _1}\rangle\) gives,

$$\begin{aligned} |{\psi _2}\rangle= & {} U_2|{\psi _1}\rangle \nonumber \\= & {} \dfrac{1}{2^n} \sum _{Y=0}^{2^n-1}\sum _{X=0}^{2^n-1} \varpi _{YX}|{0}\rangle ^{\otimes {q+1}}|{YX}\rangle \nonumber \\= & {} \dfrac{1}{2^n} \sum _{Y=0}^{2^n-1}\sum _{X=0}^{2^n-1}|{P(Y,X)}\rangle |{0}\rangle |{YX}\rangle . \end{aligned}$$
(30)

Figures 3 and 4 show the quantum circuits for the image in Fig. 1 with the NEQR and the ENEQR representations respectively. In order to show the efficiency of the ENEQR algorithm, the time complexity of the preparation process and the cost of the quantum circuit are discussed in the following two theorems.

Theorem 3

The time complexity of preparing a \(2^n\times 2^n\) gray image using the ENEQR is no more than \(O(2n2^{2n})\).

Proof

The process of image representation using the ENEQR consists of one main operation \(U_2\) which is used for setting the gray values for every pixel in the image.

The operation \(U_2\) is divided into \(2^{2n}\) sub operations \(U_{YX}\) which uses the quantum operation \(\varpi _{YX}\) to perform \(q+1\) operations on the qubits of the pixel according to the gray value of that pixel. When \(C^i_{YX} = 1\), \(\varpi _{YX}\) applies 2n-CNOT gate to store the position information in the auxiliary qubit, then applies the CNOT gate to invert the \(i^{th}\) qubit and finally resets the auxiliary qubit. Therefore, the sub operation \(U_{YX}\) applies one 2n-CNOT gate and q CNOT gates. The time complexity increases according to the number of the controls used to apply the 2n-CNOT gates on the position qubits, therefore the time complexity of the sub operation \(U_{YX}\) is O(2n).

For the main operation \(U_2\), it applies \(2^{2n}\) sub operations which is the total number of pixels in a \(2^n\times 2^n\) gray image, therefore the time complexity of \(U_2\) is \(O(2n2^{2n})\), hence the time complexity of the ENEQR representation is \(O(2n2^{2n})\).\(\square\)

Theorem 4

The cost of the quantum circuit for representing a \(2^n\times 2^n\) gray image using the ENEQR is no more than \((c+q) \,2^{2n}\), where c is the cost of a 2n-CNOT gate [14].

Proof

For constructing the circuit of a gray image, every pixel uses one 2n-CNOT gate and q CNOT gates. Therefore, the quantum cost of a single pixel is \(c+q\). Since a \(2^n\times 2^n\) gray image contains \(2^{2n}\) pixel, then the quantum cost of the circuit for the whole image using the ENEQR is \((c+q)\,2^{2n}\).

For example, to prepare the image in Fig. 1 using the ENEQR algorithm, prepare a quantum register with 11 qubits all initialized to \(|{0}\rangle\),

$$\begin{aligned} |{\psi _0}\rangle =|{0}\rangle ^{\otimes 11}, \end{aligned}$$

then the position of the pixels will be stored as follows,

$$\begin{aligned} |{\psi _1}\rangle= & {} I|{0}\rangle ^{\otimes 9}\otimes H|{0}\rangle ^{\otimes 2}\\= & {} \dfrac{1}{2}|{0}\rangle ^{\otimes 9}\otimes \sum ^3_{i=0}|{i}\rangle \\= & {} \dfrac{1}{2}\sum ^1_{Y=0}\sum ^1_{X=0}|{0}\rangle ^{\otimes 9}|{YX}\rangle \\= & {} \dfrac{1}{2}(|{00000000}\rangle |{0}\rangle |{00}\rangle +|{00000000}\rangle |{0}\rangle |{01}\rangle \\& +|{00000000}\rangle |{0}\rangle |{10}\rangle +|{00000000}\rangle |{0}\rangle |{11}\rangle ). \end{aligned}$$

To complete the preparation process, the value of the pixels will be stored using the CNOT gate as follows,

$$\begin{aligned} |{\psi _2}\rangle= & {} \dfrac{1}{2}(|{00000000}\rangle |{0}\rangle |{00}\rangle +|{00000000}\rangle |{0\oplus \overline{0}\wedge 1}\rangle |{01}\rangle \\& +|{00000000}\rangle |{0}\rangle |{10}\rangle +|{00000000}\rangle |{0}\rangle |{11}\rangle )\\= & {} \dfrac{1}{2}(|{00000000}\rangle |{0}\rangle |{00}\rangle +|{0,0\oplus 1,000,0\oplus 1,0\oplus 1,0}\rangle |{1}\rangle |{01}\rangle \\& +|{00000000}\rangle |{0}\rangle |{10}\rangle +|{00000000}\rangle |{0}\rangle |{11}\rangle )\\= & {} \dfrac{1}{2}(|{00000000}\rangle |{0}\rangle |{00}\rangle +|{01000110}\rangle |{1\oplus \overline{0}\wedge 1}\rangle |{01}\rangle \\& +|{00000000}\rangle |{0}\rangle |{10}\rangle +|{00000000}\rangle |{0}\rangle |{11}\rangle )\\= & {} \dfrac{1}{2}(|{00000000}\rangle |{0}\rangle |{00}\rangle +|{01000110}\rangle |{0}\rangle |{01}\rangle \\ &+|{00000000}\rangle |{0}\rangle |{10}\rangle +|{00000000}\rangle |{0}\rangle |{11}\rangle ). \end{aligned}$$

The final \(|{\psi _2}\rangle\) after applying the previous operations on each pixel is as follows,

$$\begin{aligned} |{\psi _2}\rangle= & {} \dfrac{1}{2}(|{00000000}\rangle |{0}\rangle |{00}\rangle +|{01000110}\rangle |{0}\rangle |{01}\rangle \\ & +|{01111000}\rangle |{0}\rangle |{10}\rangle +|{11111111}\rangle |{0}\rangle |{11}\rangle ). \end{aligned}$$
Fig. 3
figure 3

A quantum circuit for the NEQR model of a \(2\times 2\) gray image

Full size image
Fig. 4
figure 4

A quantum circuit for the ENEQR representation of a \(2\times 2\) gray image

Full size image

4 Analysis of performance

This section compares the proposed enhancements with the existing models in the aspect of time complexity and quantum cost. The FRQI model uses a single rotation gate with a 2n control qubits for each pixel. However, The EFRQI uses a single operator \(X^{\frac{d}{255}}\) with a 2n control qubits for each pixel to store the gray value, when \(d=255\) the operator becomes a 2n-CNOT gate which has time complexity lower than the rotation gate as explained in [3], the proposed EFRQI algorithm is also applicable to store color images using \(2n+3\) qubits and this will be referred as EFRQCI in Table 1. The ENEQR uses only one 2n-CNOT gate and q CNOT gates for each pixel which has time complexity lower than the NEQR model that uses q 2n-CNOT gates for each pixel, the proposed ENEQR algorithm is also applicable to the NCQI model [18] and this will be referred as ENCQI in Table 1 which shows a comparison between the time complexity of the proposed algorithms and the other models. The comparison shows that the time complexity of the EFRQI and the EFRQCI models are linear in the size of the image and can achieve a quadratic speedup in the preparation process when compared with the other models. The comparison also shows an improvement in the time complexity of the ENEQR and the ENCQI models when compared with the other models which leads to image preparation speedup.

The quantum cost of the 2n-CNOT gate used in the NEQR, ENEQR, NCQI, and ENCQI models are calculated according to the number of control qubits as shown in [14]. The proposed models uses only one 2n-CNOT gate for each pixel for both gray and color images, while the NEQR model uses q 2n-CNOT gates for gray images and the NCQI model uses 3q 2n-CNOT gates for color images which requires more quantum cost. Table 2 shows a comparison for the quantum cost between the proposed algorithms and the other models, the comparison is made using real images from the standard database [29], it shows that the quantum cost of gray images prepared by the ENEQR model is less than the quantum cost of the NEQR model, and the quantum cost of color images prepared by the ENCQI model is less than the quantum cost of the NCQI model.

Table 1 Comparison between the time complexity of the proposed algorithms and the other models for \(2^n\times 2^n\) images
Full size table
Table 2 Comparison of the quantum cost for \(2^n\times 2^n\) images between the proposed algorithms and the other models
Full size table

5 Conclusion

Two types of image representation on quantum computers have been considered in this paper, amplitude representation which stores the values of the pixels in the amplitude of the qubits, and the basis state representation which stores the values of the pixels in the basis state of qubit sequence. This paper introduced two enhanced representations for storing and processing digital images. The first enhanced quantum representation based on the FRQI model (EFRQI) is an amplitude representation that improved the FRQI model, it stores the values of the pixels using the partial negation operator in a single qubit, this qubit is entangled with a qubit sequence to store the position information of the pixels, the analysis showed that the EFRQI has less time complexity when compared with the FRQI model and also, can be used to store color images with less time complexity. The second enhanced quantum representation based on the NEQR model (ENEQR) is a basis state representation that improved the NEQR model, it stores the values of the pixels in a qubit sequence using one 2n-CNOT gate and q CNOT gates, this qubit sequence is entangled with another qubit sequence to store the position information of the pixels, the analysis showed that the ENEQR has less time complexity and less quantum cost when compared with the NEQR model, the algorithm is also applicable to the NCQI model to store color images with less time complexity and less quantum cost. The work in this paper can be extended by using the proposed image representations to enhance the efficiency of the operations of the quantum image processing.