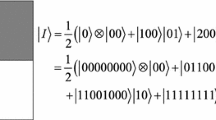1 Introduction

Along with the continuous development of quantum computation, the power of quantum mechanics has attracted the interest of many researchers in recent years. Since Feynman presented the concept of quantum computations in 1982, many quantum algorithms have been proposed such as the quantum integer factoring algorithm [1] and Grover search algorithm [2].

At present, some researchers try to apply quantum computing to the field of image processing. There are many quantum methods concerning quantum image representation such as Qubit Lattice [3], Entangled Image [4], Real Ket [5], Flexible Representation of Quantum Images (FRQI) [6], Improved Flexible Representation of Quantum Images (IFRQI) [7], Multi-Channel Quantum Images (MCQI) [8], Novel Enhanced Quantum Representation of Digital Images (NEQR) [9], the Generalized Quantum Image Representation (GQIR) [10] and Novel Quantum Representation of Color Digital Images (NCQI) [11]. In these models, only MCQI and NCQI refer to quantum color image.

MCQI model is designed based on FRQI, which uses the probability amplitude to represent the channels information. Although channel swapping operation and one channel operation can be performed on MCQI model, the quantum image preparation of this model is too complicated, whose complexity is O (4 × 24(n+ 1) − 6 × 22(n+ 1) + 2(n + 1) for the image with size 2n × 2n according to the discussion in [11]. In order to resolve this problem, NCQI model is proposed to achieve a quadratic speedup in preparation procedure. Based on NCQI, some color image processing operations can be executed conveniently. However, it needs 2n + 3q qubits to represent the RGB color image with size 2n ∗ 2n and every channel ranged [0,2q − 1], which does not make full use of quantum superposition to represent pixel values.

In this paper, an optimized quantum representation for color digital images is proposed to improve storage performance of NCQI model. The new representation model uses three-dimensional quantum sequence to store the channel index, channel information and position information of all pixels. Therefore, OCQR model only apply nearly one-third times the qubits to store the pixel value compared with NCQI. And these two models have almost the same complexity of preparation. On the other hand, any image operations performed on an NCQI model can be implemented on OCQR model and some operations based on OCQR can also be executed more conveniently.

The rest of this paper is organized as follows: Section 2 discusses the most relevant works in this field. Then Section 3 describes the newly storage model OCQR and introduces the process of model preparation. In Section 4, some basic operations based on OCQR are discussed. Next, the OCQR is compared with other models in Section 5. Finally, conclusion and prospects about the future work are presented in Section 6.

2 Related Work

In order to improve the flexible representation model (FRQI), a novel enhanced quantum representation (NEQR) is proposed which uses the basis state to store the gray-scale information of every pixel. In this model, one image is represented by a two-dimensional quantum sequence, one indicated the pixel position information, while the other described the pixel value. Since this model uses the basis state to store the pixel value for the first time, some quantum image processing algorithms can be implemented very conveniently such as image restoration algorithm [12,13,14], quantum watermarking algorithm [15,16,17], and other algorithms [18,19,20,21,22]

For an image with size 2n ∗ 2n and gray range [0,2q − 1], the representative expression of NEQR model is defined as in (1) where 2 ∗ n + q qubits are needed.

$$\begin{array}{@{}rcl@{}} \left| I \right\rangle = \frac{1}{{{2^{n}}}}\sum\limits_{y = 0}^{{2^{n}} - 1} {\sum\limits_{x = 0}^{{2^{n}} - 1} {\left| {f(x,y)} \right\rangle \otimes \left| {yx} \right\rangle } } \quad f(x,y) \in [0,{2^{q}} - 1] \end{array} $$
(1)

Inspired by the NEQR model, a novel quantum representation of color digital images (NCQI) is proposed to store and process quantum color image. Suppose the value range of each channel (R,G,B) is [0,2q − 1] in the quantum image with size 2n ∗ 2n, the NCQI model can be indicated as the following equation, where C(x,y) represents the pixel value of RGB channels. And the number of qubits employed in this model is 2 ∗ n + 3q.

$$\begin{array}{@{}rcl@{}} \left| I \right\rangle &=& \frac{1}{{{2^{n}}}}\sum\limits_{y = 0}^{{2^{n}} - 1} {\sum\limits_{x = 0}^{{2^{n}} - 1} {\left| {C(x,y)} \right\rangle \otimes \left| {yx} \right\rangle } } \\ \left| {C(x,y)} \right\rangle &=& \left| {\underbrace {R_{q - 1} {\cdots} R_{0}}_{{\text{Re}} d}\underbrace{G_{q - 1} {\cdots} G_{0}}_{Green}\underbrace{B_{q - 1} {\cdots} B_{0}}_{Blue}} \right\rangle \end{array} $$
(2)

For a 2 × 2 color image example with every channel R,G,B ranged [0,28 − 1] as shown in Fig. 1, two qubits are used to store the coordinate information and 24 qubits are utilized to store the color information. Therefore, if fewer qubits are used to represent the color information for every pixel, more computing resources will be saved.

Fig. 1
figure 1

A 2*2 color image example represented by NCQI model

Full size image

3 Optimized Representation for Color Quantum Images

In this section, an optimized quantum representation for color digital images will be proposed to improve the performance of storage. And the preparation procedures of OCQR model will also be introduced in details.

3.1 Quantum Image Representation Model-OCQR

Based on the model NCQI, we proposed an optimized quantum representation for color digital images. This model uses a three-dimensional quantum sequences to store the color quantum image, one represents the channel value, another indicates the channel index, and the other introduces the position information. Equation (3) shows the details of this model.

$$\begin{array}{@{}rcl@{}} \left| I \right\rangle &=& \frac{1}{{{2^{n + 1}}}}\sum\limits_{y = 0}^{{2^{n}} - 1} {\sum\limits_{x = 0}^{{2^{n}} - 1} {\left| {c(x,y)} \right\rangle \left| {ch\_index} \right\rangle \left| {yx} \right\rangle } } \\ &=& \frac{1}{{{2^{n + 1}}}}\sum\limits_{y = 0}^{{2^{n}} - 1} {\sum\limits_{x = 0}^{{2^{n}} - 1} {\left( {\begin{array}{ll} {\left| {{r_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \left| {{g_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + }\\ {\left| {{b_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle } \end{array}} \right)\left| {yx} \right\rangle } } \\ &&\left\{ {\begin{array}{ll} {\left| {{r_{yx}}} \right\rangle = \left| {r_{yx}^{q - 1} {\cdots} r_{yx}^{0}} \right\rangle ,\left| {{g_{yx}}} \right\rangle = \left| {g_{yx}^{q - 1} {\cdots} g_{yx}^{0}} \right\rangle ,}\\ {\left| {{b_{yx}}} \right\rangle = \left| {b_{yx}^{q - 1} {\cdots} b_{yx}^{0}} \right\rangle ,\left| {{s_{yx}}} \right\rangle = \left| {{0^{q - 1}} {\cdots} {0^{0}}} \right\rangle } \end{array}} \right\} \end{array} $$
(3)

The |ch_index〉 indicates the index of channel. It is usually encoded by the two qubits for RGB channel index, where |00〉 is red channel index, |01〉 stands for green channel index, |10〉 means blue while |11〉 represents a spare channel index. Although the spare channel will not be used in this article, it can be utilized to store other pixel information such as transparency discussed in [8].

For a 2n ∗ 2n color image with every channel ranged between 0 and 2q − 1, q qubits are used to represent the channel value, 2 qubits to indicate the channel index, and the other 2 ∗ n qubits to store the coordinate information. Therefore the total number of qubits used in OCQR model is 2 ∗ n + q + 2. Compared with the NCQI model that need 2n + 3q qubits to store the same size image, new representation OCQR can save the resource of storage through applying nearly one-third times the qubits to store the pixel value.

Figure 2 shows a 2 ∗ 2 color image and its representative expression in OCQR model. Because three channels ranged [0, 28 − 1], eight qubits are needed to represent the channel value. As a result, OCQR model totally utilizes 12 qubits to store this image which is much smaller than the number of qubits required in NCQI model.

Fig. 2
figure 2

A 2*2 color image example represented by OCQR model

Full size image

3.2 Quantum Image Preparation

To apply the quantum mechanics to image processing, the image information should be stored in a quantum superposition state at first. In this subsection, the preparation procedures for OCQR model will be discussed.

At the beginning, 2n + q + 2 qubits are initialized for a 2n ∗ 2n color image with each channel ranged [0,2q − 1]. The initial state can be shown in the (4).

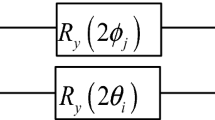
$$ {\left| I \right\rangle_{0}} = {\left| 0 \right\rangle^{\otimes q + 2 + 2n}} $$
(4)

Figure 3 depicts workflow of preparation about the new quantum image model. In this figure, the whole procedure can be divided into two steps.

  • Step 1: an empty quantum image is constructed through transforming the initial state |I〉0 to the middle state |I〉1

Fig. 3
figure 3

The workflow of preparation process for OCQR model

Full size image

In this step, the common single quantum gate I and H are used to construct the whole quantum operation as in (6)

$$\begin{array}{@{}rcl@{}} I = \left[ \begin{array}{ll} 1&0\\ 0&1 \end{array} \right] \quad H = \frac{1}{{\sqrt 2 }}\left[\begin{array}{ll} 1&1\\ 1&{ - 1} \end{array} \right] \end{array} $$
(5)
$$ {U_{1}} = {I^{\otimes q + 2}} \otimes {H^{\otimes 2n}} $$
(6)

Equation (7) interprets the quantum transformation from the initial state |I〉0 to the intermediate state |I〉1. After this step, the position information of each pixel is stored in the OCQR quantum model and the color value is set 0 for every pixel.

$$\begin{array}{@{}rcl@{}} {\left| I \right\rangle_{1}} &=& {U_{1}}({\left| I \right\rangle_{0}}) \\ &=& {I^{\otimes q}} \otimes {H^{\otimes 2n + 2}}({\left| 0 \right\rangle^{q + 2 + 2n}}) \\ &=& \frac{1}{{{2^{n + 1}}}}\sum\limits_{y = 0}^{{2^{n}} - 1} {\sum\limits_{x = 0}^{{2^{n}} - 1} {\left( {{{\left| 0 \right\rangle }^{q}} \otimes \left( {\left| {00} \right\rangle + \left| {01} \right\rangle + \left| {10} \right\rangle + \left| {11} \right\rangle } \right) \otimes \left| {yx} \right\rangle } \right)} } \end{array} $$
(7)

  • Step 2: To prepare the quantum image, we should set the color value of every pixel in the middle state |I〉1. Because the color image resolution is 2n ∗ 2n, this step must be divided into 22n sub-operations.

For pixel (x,y), the quantum sub-operation for color value setting is shown as (8). It consists of three parts that are Ryx, Gyx, Byx. These three operations contain q quantum oracles respectively. Taking Ryx as example, every qubit in the red channel quantum sequence is processed according to the binary code of the channel value. For ri= 1, a controlled gate 2n + 2-CNOT is needed. Otherwise, nothing will be done on the quantum state.

$$\begin{array}{@{}rcl@{}} &&{{\Omega}_{yx}}=\overset{3}{\underset{i = 1}{\otimes}} {\Omega}_{yx}^{i}\\ &&{\Omega}_{yx}^{1}={R_{yx}},\quad{\Omega}_{yx}^{2} = {G_{yx}},\quad{\Omega}_{yx}^{3} = {B_{yx}} \\ &&{R_{yx}} =\overset{q}{\underset{i = 1}{\otimes}} R_{yx}^{i},\quad{G_{yx}} =\overset{q}{\underset{i = 1}{\otimes}} G_{yx}^{i},\quad {B_{yx}} =\overset{q}{\underset{i = 1}{\otimes}} B_{yx}^{i} \\ &&R_{yx}^{i}:\;\left| 0 \right\rangle \to \left| {0 \oplus r_{yx}^{i}} \right\rangle ,\quad G_{yx}^{i}:\left| 0 \right\rangle \to \left| {0 \oplus g{{{~}_{yx}^{i}}_{i}}} \right\rangle ,\quad B_{yx}^{i}:\left| 0 \right\rangle \to \left| {0 \oplus b_{yx}^{i}} \right\rangle \end{array} $$
(8)

It is obvious that every sub-operation Ωyx only set the color value of its corresponding pixel. Therefore, we can use Uyx to express the unitary operation for every sub-operation as (9)

$$\begin{array}{@{}rcl@{}} {U_{yx}} = \left( {{I^{q + 2}} \otimes \sum\limits_{j = 0}^{{2^{n}} - 1} {\sum\limits_{i = 0,ji \ne yx}^{{2^{n}} - 1} {\left| {ji} \right\rangle \left\langle {ji} \right|} } } \right) + {{\Omega}_{yx}} \otimes \left| {yx} \right\rangle \left\langle {yx} \right| \end{array} $$
(9)

After applying sub-operation Uyx, the middle state |I1〉 is transformed as in (10)

$$\begin{array}{@{}rcl@{}} {U_{yx}}\left( {{{\left| I \right\rangle }_{1}}} \right) &= &\left[ {\left( {{I^{q + 2}} \otimes \sum\limits_{j = 0}^{{2^{n}} - 1} {\sum\limits_{i = 0,ji \ne yx}^{{2^{n}} - 1} {\left| {ji} \right\rangle \left\langle {ji} \right|} } } \right) + {{\Omega}_{yx}} \otimes \left| {yx} \right\rangle \left\langle {yx} \right|} \right] \\&&\times \left( {\frac{1}{{{2^{n + 1}}}}\sum\limits_{j = 0}^{{2^{n}} - 1} {\sum\limits_{i = 0}^{{2^{n}} - 1} {\left( {{{\left| 0 \right\rangle }^{q}} \otimes \left( {\left| {00} \right\rangle + \left| {01} \right\rangle + \left| {10} \right\rangle + \left| {11} \right\rangle } \right) \otimes \left| {ji} \right\rangle } \right)} } } \right) \\ &= &\left( {\frac{1}{{{2^{n + 1}}}}\sum\limits_{j = 0}^{{2^{n}} - 1} {\sum\limits_{i = 0,ji \ne yx}^{{2^{n}} - 1} {\left( {{{\left| 0 \right\rangle }^{q}} \otimes \left( {\left| {00} \right\rangle + \left| {01} \right\rangle + \left| {10} \right\rangle + \left| {11} \right\rangle } \right) \otimes \left| {ji} \right\rangle } \right)} } } \right) \\&&+ \frac{1}{{{2^{n + 1}}}}{{\Omega}_{yx}} \otimes \left| {yx} \right\rangle \\ &=&\left( {\frac{1}{{{2^{n + 1}}}}\sum\limits_{j = 0}^{{2^{n}} - 1} {\sum\limits_{i = 0,ji \ne yx}^{{2^{n}} - 1} {\left( {{{\left| 0 \right\rangle }^{q}} \otimes \left( {\left| {00} \right\rangle + \left| {01} \right\rangle + \left| {10} \right\rangle + \left| {11} \right\rangle } \right) \otimes \left| {ji} \right\rangle } \right)} } } \right) \\ && + \frac{1}{{{2^{n + 1}}}}\left( \begin{array}{ll} \left| {{r_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \left| {{g_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + \\ \left| {{b_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle \end{array} \right) \otimes \left| {yx} \right\rangle \end{array} $$
(10)

Through the operation introduced in (10), the color value of relevant pixel is stored. For the sake of setting the color value for every pixel, the operation U2 is performed according to the following equation as in (11)

$$ {U_{2}} = \prod \limits_{y = 0}^{{2^{n}} - 1} \prod \limits_{x = 0}^{{2^{n}} - 1} {U_{yx}} $$
(11)
$$\begin{array}{@{}rcl@{}} {U_{2}}\left( {{{\left| I \right\rangle }_{1}}} \right) &=& \prod \limits_{y = 0}^{{2^{n}} - 1} \prod \limits_{x = 0}^{{2^{n}} - 1} {U_{yx}}\left( {{{\left| I \right\rangle }_{1}}} \right) \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} & =&\left( {\frac{1}{{{2^{n + 1}}}}\sum\limits_{y = 0}^{{2^{n}} - 1} {\sum\limits_{x = 0}^{{2^{n}} - 1} {\left( {\left( \begin{array}{ll} {\left| {{r_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \left| {{g_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + }\\ {\left| {{b_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle } \end{array}\right) \otimes \left| {yx} \right\rangle } \right)} } } \right) \\ &=& \left| I \right\rangle \end{array} $$

After the above two steps, the quantum image stored in OCQR model has been prepared. Then we will show the validity of OCQR model through discussing the time complexity of preparation procedures.

Theorem 1

The whole preparation of OCQR model will cost no more thanO(q + 2 + 2n + 3q(2n + 2)22n) for a color image with size 2n ∗ 2n and every channel (R, G, B) ranged [0,2q − 1].

Proof

The whole preparation consists of two steps. The time complexities of every step will be discussed as follows. □

Firstly, there are q + 2 + 2n single quantum gates in the quantum operator U1. Therefore, step1 will cost O(q + 2 + 2n).

Secondly, the function of step2 is to set the color value for every pixel in the quantum image. The whole operation is consisted of 22n sub-operations as shown in (11).

Every sub-operation Uyx contains three quantum operations to set color value of the relevant channel. For every channel, q qubits are applied by a controlled quantum gate in the most complex situation. It is known that all the controlled quantum gates are (2n + 2)-CNOT which can be decomposed into at most O(2n + 2) single quantum gate at most according to the discussion in [9]. Therefore the time complexity of the operation Uyx is O(3q(2n + 2)). And the whole time complexity of step2 is no more than O(3q(2n + 2)22n).

Based on the above analyses, for a color image with size 2n ∗ 2n and each channel ranged [0, 2q − 1], the time complexity of preparing OCQR model is no more than O(q + 2 + 2n + 3q(2n + 2)22n), which is approximately linear to the resolution of image.

4 Quantum Image Processing Operation Based on OCQR

In this section, some fundamental operations on OCQR model will be discussed. Because of the particular properties of this model, these operations can be performed flexibly and efficiently.

4.1 Channel Swapping Operation

The Channel Swapping Operation (CS) can be divided into three types CSRG, CSRB and CSGB, which achieve the swap of value in channel R and G, R and B, G and B respectively. If we have a quantum image represented by (3), the specific implementation processes of channel swapping operations are described as follows.

$$\begin{array}{@{}rcl@{}} C{S_{RG}}\left( {\left| I \right\rangle } \right) = \frac{1}{{{2^{n + 1}}}}\sum\limits_{y = 0}^{{2^{n}} - 1} {\sum\limits_{x = 0}^{{2^{n}} - 1} {\left( {\left( \begin{array}{ll} \left| {{r_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + \left| {{g_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \\ \left| {{b_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle \end{array} \right) \left| {yx} \right\rangle } \right)} } \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} C{S_{RB}}\left( {\left| I \right\rangle } \right) =\frac{1}{{{2^{n + 1}}}}\sum\limits_{y = 0}^{{2^{n}} - 1} {\sum\limits_{x = 0}^{{2^{n}} - 1} {\left( {\left( \begin{array}{ll} \left| {{r_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \left| {{g_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + \\ \left| {{b_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle \end{array} \right) \left| {yx} \right\rangle } \right)} } \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} C{S_{GB}}\left( {\left| I \right\rangle } \right) =\frac{1}{{{2^{n + 1}}}}\sum\limits_{y = 0}^{{2^{n}} - 1} {\sum\limits_{x = 0}^{{2^{n}} - 1} {\left( {\left( \begin{array}{ll} \left| {{r_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \left| {{g_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \\ \left| {{b_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle \end{array} \right) \left| {yx} \right\rangle } \right)} } \end{array} $$
(15)

From the equations above, it can be seen that only channel index qubits are transformed. The examples of three CS operations are shown in Fig. 4. We can conclude from the examples that only simple quantum operations is needed to complete the this operation. Therefore the computation complexity of every channel swapping operation is O(1).

Fig. 4
figure 4

The examples of channel swapping operation and methods to realize in quantum circuit. a The original image. b–d The output images and realization methods about CSRG, CSRB and CSGB operations

Full size image

4.2 One Channel Operation

One Channel Changing Operation (OC) can also be divided into three types OCr, OCg and OCb, which achieve the change of value in channel R, G and B respectively. The specific implementation processes of them are described as (16–18).

$$\begin{array}{@{}rcl@{}} O{C_{R}}\left( {\left| I \right\rangle } \right) &=& O{C_{R}}\left( {\frac{1}{{{2^{n + 1}}}}\sum\limits_{j = 0}^{{2^{n}} - 1} {\sum\limits_{i = 0}^{{2^{n}} - 1} {\left( \begin{array}{ll} {\left| {{r_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \left| {{g_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + }\\ {\left| {{b_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle } \end{array} \right) \otimes \left| {yx} \right\rangle } } } \right)\\ &=& \frac{1}{{{2^{n + 1}}}}\sum\limits_{j = 0}^{{2^{n}} - 1} {\sum\limits_{i = 0}^{{2^{n}} - 1} {\left( {\left( \begin{array}{ll} {\left| {{{r^{\prime}}_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \left| {{g_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + }\\ {\left| {{b_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle } \end{array}\right) \otimes \left| {yx} \right\rangle } \right)} } \\ \left| {{{r^{\prime}}_{yx}}} \right\rangle &=& \left| {r_{yx}^{\prime q - 1} {\cdots} r_{yx}^{\prime 0}} \right\rangle \end{array} $$
(16)
$$\begin{array}{@{}rcl@{}} O{C_{G}}\left( {\left| I \right\rangle } \right) &=& O{C_{G}}\left( {\frac{1}{{{2^{n + 1}}}}\sum\limits_{j = 0}^{{2^{n}} - 1} {\sum\limits_{i = 0}^{{2^{n}} - 1} {\left( \begin{array}{ll} {\left| {{r_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \left| {{g_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + }\\ {\left| {{b_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle } \end{array} \right) \otimes \left| {yx} \right\rangle } } } \right)\\ &=& \frac{1}{{{2^{n + 1}}}}\sum\limits_{j = 0}^{{2^{n}} - 1} {\sum\limits_{i = 0}^{{2^{n}} - 1} {\left( {\left( \begin{array}{ll} {\left| {{r_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \left| {{{g^{\prime}}_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + }\\ {\left| {{b_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle } \end{array} \right) \otimes \left| {yx} \right\rangle } \right)} } \\ \left| {{{g^{\prime}}_{yx}}} \right\rangle &=& \left| {g_{yx}^{\prime q - 1} {\cdots} g_{yx}^{\prime 0}} \right\rangle \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} O{C_{B}}\left( {\left| I \right\rangle } \right) &=& O{C_{B}}\left( {\frac{1}{{{2^{n + 1}}}}\sum\limits_{j = 0}^{{2^{n}} - 1} {\sum\limits_{i = 0}^{{2^{n}} - 1} {\left( \begin{array}{ll} {\left| {{r_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \left| {{g_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + }\\ {\left| {{b_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle } \end{array} \right) \otimes \left| {yx} \right\rangle } } } \right)\\ &=& \frac{1}{{{2^{n + 1}}}}\sum\limits_{j = 0}^{{2^{n}} - 1} {\sum\limits_{i = 0}^{{2^{n}} - 1} {\left( {\left( \begin{array}{ll} {\left| {{r_{yx}}} \right\rangle \otimes \left| {00} \right\rangle + \left| {{g_{yx}}} \right\rangle \otimes \left| {01} \right\rangle + }\\ {\left| {{{b^{\prime}}_{yx}}} \right\rangle \otimes \left| {10} \right\rangle + \left| {{s_{yx}}} \right\rangle \otimes \left| {11} \right\rangle } \end{array}\right) \otimes \left| {yx} \right\rangle } \right)} } \\ \left| {{{r^{\prime}}_{yx}}} \right\rangle &=& \left| {r_{yx}^{\prime q - 1} {\cdots} r_{yx}^{\prime 0}} \right\rangle \end{array} $$
(18)

For every OC operation, some (2n + 2) − Cnot gates (this quantum gate can be decomposed to O(2n + 2) Toffoli gates at most [23]) are utilized to change the information of every channel. In the most complex case, every qubit used to represent color value will be changed. Therefore the complexity of one channel operation is no more than O (q (2n + 2))

Because of the unique coding method for color information, the operations that simultaneously changing the value of three channels can be realized in OCQR model with low computation complexity. Figure 5 shows an example of color reversal operation. After applying the quantum NOT gate in every qubit presenting the channel value, the original image (a) is transformed to image (b). And (c) is the quantum circuit about realizing this operation. It can be seen that the complexity of color reversal operation is O (q).

Fig. 5
figure 5

The examples of color reversal operation. a The original image. b The output image after applying this operation. c the realization method about this operation

Full size image

4.3 Geometric and Color Transformation on OCQR Quantum Image

Similar to the NEQR model, OCQR image also uses an entangled qubit sequence to represent the position information of all the pixels. Therefore some geometric transformations on NEQR model are also advisable in OCQR image, such as cycle shift operation and so on. The cycle shift operation based on OCQR can be designed using the same method described in [24] and the complexity of this operation on OCQR is also O(n2).

On the other hand, since OCQR utilizes a qubit sequence to encode color information instead of angles like MCRQI, most color transformations such as addition operation, subtraction operation and halving operation are applicable in OCQR image. Because q qubits are used to represent the color value in OCQR, the specific implementation processes of these color transformation can follow the way designed in NEQR model [24]. For addition operation, subtraction operation and halving operation in OCQR model, the complexity of them is same which is O(q).

5 Performance Comparison with Latest Models

In this section, the performance comparison is discussed among the models (OCQR and NCQI).

Firstly, as shown in Table 1, the entangled qubits used in NCQI model is more than that used in OCQR model. NCQI utilized 3q qubits to represent the color information, but the OCQR only makes use of q + 2 qubits which apply nearly one-third times the qubits to store the pixel value. As we all know, qubits are very valuable computing resources. Therefore, OCQR has higher storage efficiency compared with the NCQI model.

Table 1 The comparison of qubit number used in two quantum representation models
Full size table

On the other hand, since both NCQI and OCQR use the basis state of a qubit sequence to represent the pixel information, any image transformations performed on an NCQI model can also be implemented on OCQR model. Table 2 shows the complexity comparison about some image processing methods. It can be seen that OCQR is more efficient to conduct some quantum image color transformations.

Table 2 Complexity comparison about some image processing methods among OCQR and NCQI model
Full size table

6 Conclusion and Future Work

In this paper, an optimized quantum representation for color digital images is proposed based on the quantum superposition and entanglement properties. The OCQR model uses a three-dimensional quantum sequences to represent the channel value, the channel index, and position information respectively. Compared with the latest model NCQI, OCQR not only uses less qubits to save computing resources but is more efficiency to conduct some color transformations. Hence, OCQR is more suitable to store and process the quantum color image.

The storage of image is the basic part of the quantum image processing. In the future, we will try our best to design some quantum image processing methods based on OCQR model.