1 Introduction

With rapid development of Internet, security in data transmission is of critical importance. As a visualized information transmission medium, image becomes the most prevalent kind of data in the secure domain. Different from text encryption, images have some unique characteristics such as high correlation between adjacent pixels and bulk data capacity. Therefore, classical cryptographic techniques such as Data Encryption Standard (DES), Advance Encryption Standard (AES), and International Data Encryption Algorithm (IDEA) are not up to image encryption. To accommodate the requirements, many image encryption algorithms are proposed based on different technologies, including DNA code [7, 45], wavelet transmission [8, 26], vector quantization [10, 28], cellular automata [35, 38], digital signature or digital watermarking [13, 22, 31], attribute-based searchable encryption [30], and chaotic systems [2, 9, 11, 12, 14, 17, 21, 25, 34, 37, 40,41,42,43, 48, 50,51,52, 56, 57]. Additionally, steganography is another effective solution for information privacy and has been widely studied [1, 54].

Chaos has numerous good distinctive characteristics, including sensitivity to initial conditions, intrinsic stochasticity, aperiodicity and ergodic property, which are exactly analogous to the cryptographic properties of confusion and diffusion. Therefore, the chaos-based encryption algorithms are more popular than other schemes. Some simple chaotic maps are considered to propose novel image encryption schemes, such as tent map [25] and Logistic map [17]. Actually, complex chaotic systems are more commonly used for image encryption. Wang and Teng [40] proposed a bit-level image encryption scheme based on a spatiotemporal chaotic system. Tong et al. [41] utilized a perturbed high-dimensional chaotic map to improve security. Even in some other kinds of schemes, chaotic system exists as an indispensable component. Hanis and Amutha [17] proposed a double image compression and encryption scheme, which performs permutation and confusion based on Logistic map and cellular automata, respectively. Khan and Ahama [21] utilized block division technique for plaintext image to achieve light-weight encryption. They also used the tent map to generate random numbers. Chai et al. [9] proposed a novel visually secure image encryption scheme based on compressive sensing. In their scheme, the skew tent map is also used to improve security. Gong et al. [52] proposed a new multi-image encryption scheme based on quaternion discrete fractional Hartley transform and use chaotic systems to enhance the security of the algorithm.

At present, chaotic maps in most encryption algorithms can be classified into two categories, which are one-dimensional (1D) and high-dimensional (HD) chaotic maps. Higher-dimensional systems can exhibit hyperchaos [14] and spatiotemporal chaos [42]. In addition, 1D system with time delay may turn to be an infinite-dimensional chaotic system [15]. 1D chaotic maps generally have simple structure with low implementation costs and fast processing, however, followed by small key space and simple dynamical behaviors. Therefore, directly using 1D dimensional chaotic maps in the cryptosystem may lead to safety defects. To solve the trouble, some remedies are proposed to enhance the 1D dimensional chaotic map [2, 23, 55]. While these methods still increase the implementation cost to some extent. On the other hand, HD chaotic maps have more variables, larger key space, and more complex dynamical behaviors, and even hidden chaotic attractors [16], which can achieve better security. Even so, there is a flaw that complex structures of HD chaotic maps increase their computation costs. Hence, Chaos-based cryptosystems should take a combination of the advantages of both 1D and HD chaotic maps. Continuous chaotic systems as HD chaotic systems have more complex structure. It has been claimed that proposals based on continuous chaotic systems are more difficult to break [32]. Moreover, compared with HD chaotic maps, the encryption algorithms based on continuous chaotic systems perform faster processing.

Chaotic systems, especially low dimensional (LD) chaotic systems, are vulnerable to the finite precision effect. Then those good characteristics of chaos disappear, which leads to short cycle, strong correlation, poor distribution and loss of ergodicity. This phenomenon is call chaos degradation. Actually, most of chaos-based encryption schemes have been triumphantly cryptanalyzed [4,5,6, 20, 24, 27, 36] due to finite computing precision. The reason is that chaos degradation leads to short cycles of key streams thus makes cipher images vulnerable to attacks. Aiming at counteracting chaos degradation, assorted methods have been put forward as remedies and solutions. (1) Improving computing precision [46]. This method just increases the average period, and the computing precision is generally predetermined. (2) Integrating multiple chaotic systems by different techniques such as cascading [55], switching [19], and combination [3]. This method extends the cycle length but is difficult to satisfy other properties. The integrated chaotic systems still show periodic behaviors when those seed chaotic maps are all in short cycle orbits. (3) HD chaotic systems [44, 49] are more capable of resisting chaos degradation than LD chaotic systems. (4) Perturbing the chaotic systems [29, 39]. The perturbation sources can be classified into true random perturbation and pseudorandom perturbation. The perturbed objects are system variables and parameters. (5) Analog-digital hybrid chaotic systems [18, 53]. In this method, chaotic dynamical behaviors of digital chaotic map can be effectively recovered from degradation, and more complex dynamical behaviors can be obtained.

This paper proposes a novel chaos-based cryptosystem with analog-digital hybrid model based on the mechanism for chaos degradation (HMMCD) and a parameter selection mechanism (PSM). Without loss of generality, the typical permutation-diffusion architecture is adopted in this paper. In HMMCD of our proposed scheme, the continuous Chen chaotic system is introduced to control the Logistic map. The controlled Logistic map can resist chaos degradation under low computing precision. Meanwhile, except that one state variable of continuous chaotic systems is used for control, the other two state variables with high complexity are used to dynamically vary parameters of the controlled Logistic map. To overcome the drawbacks of traditional chaos-based cryptosystems, the pixels of cipher image will be involved in PSM one by one. Then the generated key streams are applied to permutation and diffusion stages, respectively. Overall, this cryptosystem can satisfy the security requirements by employing innovations in three aspects. (1) Introduction of continuous chaotic system has two advantages. One is that more excellent chaotic sequences can be obtained to counteract chaos degradation under low computing precision. The other is that the corresponding cryptosystem has larger key space and more complex structure. At the same time, the control process is straightforward, which guarantees the processing speed. (2) The PSM in the proposed scheme is equivalent to a two-level dynamic encryption of the secret key, which greatly increases security. Besides, with the participation of cipher pixels, the key stream is plain image related. When plain images are different, distinct key streams will be produced in both permutation and diffusion stages even if the same secret key is adopted. It ensures the ability to resist known/chosen-plaintext attacks. (3) The HMMCD and PSM are universal to nearly all continuous chaotic systems, digital chaotic maps and chaos-based encryption algorithms. Experiment results indicate that the controlled digital chaotic map has wonderful dynamical characteristics. Moreover, the proposed cryptosystem has a high security level and satisfactory effects for practical secure image applications. However, compared with those lightweight image encryption algorithm, the proposed cryptosystem is less cost-effective.

The rest sections of this paper are organized as follows. In section 2, the hybrid chaotic model based on the mechanism for chaos degradation is presented and its dynamical behaviors are analyzed. Section 3 provides a detailed description of PSM and the proposed encryption and decryption algorithms, followed by an analysis of its performance and security in Section 4. Conclusions are drawn in Section 5.

2 Hybrid model based on the mechanism for chaos degradation

2.1 The hybrid chaotic model

In Ref. [53], a mechanism based on space extending and symbolic dynamics is proposed for designing effective schemes to counteract the dynamical degradation of digital chaos. Moreover, the authors put forward an analog-digital hybrid scheme, in which continuous chaotic system perturbs digital chaotic system under finite computing precision. Here the Chen chaotic system and the Logistic map are employed to distinctly illustrate HMMCD. The Chen chaotic system is modeled:

$$ \Big\{{\displaystyle \begin{array}{c}\dot{u}(t)=a\left(v(t)-u(t)\right)\\ {}\dot{v}(t)=\left(c-a\right)u(t)-u(t)w(t)+ cv(t),\\ {}\dot{w}(t)=u(t)v(t)- bw(t)\end{array}}, $$
(1)

where a, b and c are system parameters. When a = 35, b = 3 and c ∈ [20, 28.4], the system is chaotic. The fourth order Runge-Kutta method is used to transform the Chen chaotic system into the Chen chaotic map. As shown in Fig. 1, chaotic behavior comes from the chaotic trajectory composed of discrete dots. The Logistic map can be described as

$$ {x}_{i+1}=k{x}_i\left(1-{x}_i\right), $$
(2)

where k is the control parameter. When k = 4, the Logistic map exhibits full chaos. In order to enhance the Logistic map and extend the system parameter range. The state of the Chen chaotic map is used to perturb the Logistic map. The perturbed Logistic map is given as

$$ {x}_{i+1}=\left(k{x}_i\left(1-{x}_i\right)+\alpha {u}_i\right)\operatorname{mod}1, $$
(3)

where α is the strength of perturbation. And x mod y denotes x modulo y operation.

Fig. 1
figure 1

Chaotic behavior of Chen chaotic map

Full size image

2.2 Chaotic model analysis

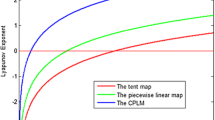
In this section, the dynamical behaviors of the HMMCD are appraised by phase diagram, bifurcation diagram and Lyapunov exponent. Figure 2(a) shows the phase diagram of the perturbed Logistic map. Compared with the parabolic attractor of the original Logistic map as shown in Fig. 2(b), the new attractor varies considerably and almost covers the entire phase space. This result indicates that the perturbed Logistic map can generate more random and uniform chaotic sequences with system features hidden. In addition, the system parameter range of Logistic map has been greatly extended. In this paper, the parameters are set at k ∈ [0.01, 10], α ∈ [0.01, 10] for study. The 2-D and 1-D bifurcation diagrams of the perturbed Logistic map are shown in Fig. 3, which indicate that the perturbed Logistic map has continuous chaotic ranges along with parameters k and α. Actually, the perturbed Logistic map has a much wider range of parameters. This means that the HMMCD can enhance chaotic performance of the digital maps. Lyapunov exponent is another important indicator to evaluate the dynamical characteristics of chaotic systems. Figure 4 plots the Lyapunov exponents of the perturbed Logistic map. One can see that the perturbed Logistic map has positive Lyapunov exponents in nearly all the parameter ranges with k, α ∈ [0.01, 10] except for a very small ranges. This result also confirms that in Fig. 3.

Fig. 2
figure 2

Phase diagrams of (a) the perturbed Logistic map in HHMCD with k = 4, α = 6; (b) Logistic map with classical parameter k = 4

Full size image
Fig. 3
figure 3

Bifurcation diagrams of the perturbed Logistic map (a) 2-D bifurcation diagram with two variable parameters, (b) 1-D bifurcation diagram with α = 0.01

Full size image
Fig. 4
figure 4

Lyapunov exponents of the perturbed Logistic map in HHMCD with parameters k ∈ [0.01, 10] and α ∈ [0.01, 10]

Full size image

2.3 The ability to counteract the dynamical degradation

Furthermore, we investigate the ability of the perturbed Logistic map to counteract the dynamical degradation. The perturbed Logistic map realized on the finite precision device can be modeled as:

$$ {x}_{i+1}=\left({G}_p\left(k{x}_i\left(1-{x}_i\right)\right)+{G}_p\left(\alpha {u}_i\right)\right)\operatorname{mod}1, $$
(4)

where Gp denotes the precision function. Next, we perform the analyses of trajectories, phase diagrams, autocorrelation and frequency distribution to compare the perturbed Logistic map Eq. (4) with the classical Logistic map Eq. (2) under low precision of 2−16. Initial values and parameters are fixed. Set x0 = 0.1, k = 4, α = 6.

Figure 5 shows the degraded chaotic characteristics of the Logistic map. Figure 5(a) shows that the trajectory of Eq. (2) eventually falls into a cycle. By observing the data, the critical point occurs after 116 iterations. The phase diagram in Fig. 5(b) depicts the visible parabolic attractor of the Logistic map, which is fragmentary. This result also reflects that Eq. (2) finally enters a periodic orbit. Figure 5(c) shows that the correlation of the adjacent orbits generated by Eq. (2) becomes very strong. Besides, the distribution of the states of Eq. (2) are concentrated at several periodic points as shown in Fig. 5(d).

Fig. 5
figure 5

Different indicators of the Logistic map with precision 2−16 (a) Trajectory. (b) Phase diagram. (c) Autocorrelation function. (d) Frequency distribution

Full size image

Comparatively, the improved characteristics of the perturbed Logistic map are shown in Fig. 6. The trajectory of Eq. (4) appears random. The phase space of Eq. (4) is uniformly covered with similar noise pattern. The correlation of outputs is driven to be delta-like, which implies accept randomness. The frequency distribution of Eq. (4) is more homogeneous than Eq. (2).

Fig. 6
figure 6

Different indicators of the perturbed Logistic map with precision 2−16 (a) Trajectory. (b) Phase diagram. (c) Autocorrelation function. (d) Frequency distribution

Full size image

To sum up, the discussions suggest that the perturbed Logistic map can effectively counteract the dynamical degradation.

3 The proposed cryptosystem

3.1 Parameter selection mechanism

In this section, the PSM is proposed for dynamically varying system parameters in the key stream generation, which can be applied to any chaotic system to improve security of cryptosystems. In the PSM, the parameter selection strategy is critical. Namely, how we change the system parameters with certain rules after each iteration of the dynamical system makes sense. For example, we can randomly or chaotically choose parameters for every iteration. On the other hand, the PSM should be plain-image related for the image encryption scenario. The key stream differs for different plain image, which can effectively resist the known-plaintext and chosen-plaintext attacks. In this model, two state variables of Chen chaotic system are underutilized. Therefore, the chaotic state variables and plain image are used for designing parameter selection strategy.

As shown in Fig. 7, V = {v1, v2, ⋯, vn, ⋯} is a chaotic sequence, and C = {C1, C2, ⋯, Cn, ⋯} is the set of pixels of cipher image by the order from top to bottom column by column. Suppose that x0 and k are initial values (parts of secret key). {x0, x1, x2, ⋯, xn, ⋯} that are used for the key stream generation are obtained under a defined strategy f. The parameter selection strategy that is equivalent to secondary encryption of the secret key will be expatiated in image encryption algorithm. Based on the PSM, the plain image will spill over into all state variables. Then, the slightly different plain images will bring about totally different key streams.

Fig. 7
figure 7

The structure of PSM

Full size image

3.2 Secret key structure and selection

The secret key has seven parts, which is denoted by (u, v, w, A, x, K, L). (u, v, w) and A are used to initialize the initial values (u0, v0, w0) and parameter c of the Chen chaotic system, respectively. x and K are used to initialize the initial values x0 and parameter k of the Logistic map, respectively. The perturbation strength α is obtained by L. In our scheme, according the chaotic characteristics analysis, the ranges of all parts of the key are set as u ∈ [−20, 20], v ∈ [−20, 20], w ∈ [10, 40], A ∈ [20,28.4], x ∈ [0, 1], K ∈ [4, 10], L ∈ [1, 10]. Then, we randomly select the secret key for encryption. The representation of the key is different as different platforms store the key. Specific coding method is not considered in this paper.

3.3 Image encryption algorithm

The overall architecture of the cryptosystem and encryption algorithm is shown in Fig. 8. The core components have two parts: the hybrid chaotic model based on HHMCD and parameter selection operation based on PSM. In the hybrid chaotic model, one state variable of Chen chaotic system is sampled to perturb the Logistic map. The perturbing method solves the problem of chaotic dynamical degradation when using Logistic map to generate key stream. On the other hand, the remaining two state variables of Chen chaotic system and cipher pixels are involved in PSM. Then two parameter selection rules are designed for the perturbed Logistic map. In this part, with the participation of cipher pixels, the key stream is plain image related, which ensures the ability to resist known/chosen-plaintext attacks. Besides, the state variables of Chen chaotic system are adequately used to increase complexity. At last, the perturbed Logistic map generates two key streams to shuffle the pixel positions and change the pixel values on permutation and confusion stages, respectively.

Fig. 8
figure 8

The architecture of the encryption process

Full size image

The plain image with M × N pixels is expanded to a sequence represented by P = {P1, P2, ⋯, PM × N} from top to bottom column by column. The corresponding cipher image is expressed as C = {C1, C2, ⋯, CM × N}. The detailed encryption algorithm is as follow:

  • Step 1: The initial values and system parameters are obtained from the randomly generated secret keys (u, v, w, A, x, K, L). The initial values (u0, v0, w0) and parameter c are obtained by (u, v, w) and A, respectively. The initial values x0 and parameter k are obtained by x and K, respectively. The perturbation strength α is obtained by L. Eq. (1) is iterated for 1000 times to avoid the effects for transient phase.

  • Step 2: The u-dimensional state variable is used to perturb the Logistic map as Eq. (3) described. Eq. (3) is pre-iterated for 1000 times with x0 and k. The last value of state variable is chosen to be the initial value (a new x0).

  1. (1)

    Permutation stage

  • Step 3: Set i = 1. An integer is generated from the initial value x0.

\( {Z}_x^1(i)=\left(\left\lfloor {x}_i^1\times {10}^{14}\right\rfloor \operatorname{mod}M\times N\right) \), M × N is the size of the image, \( {x}_i^1={x}_0 \).

  • Step 4: The pixels of the permutated image are denoted by B = {B1, B2, ⋯, BM × N}. For each pixel of plain image in P, the location of the corresponding permutated pixel is calculated as

    $$ {\displaystyle \begin{array}{c}{B}_i={P}_j,j=\left({Z}_x^1(i)\oplus i\right)\operatorname{mod}\left(M\times N+1-i\right)\\ {} permute\left({P}_j,{P}_i\right)\end{array}} $$
  1. (2)

    Confusion stage

  • Step 5: Another integer is generated from the initial value x0 \( {Z}_x^2(i)=\left(\left\lfloor {x}_i^2\times {10}^{14}\right\rfloor \operatorname{mod} Gray\right) \), Gray is the gray level of image, \( {x}_i^2={x}_0 \).

  • Step 6: The pixels of the diffused image (cipher image) are denoted by C = {C1, C2, ⋯, CM × N}. For each pixel of the confused image in B, the diffused pixel is encrypted as

    $$ {C}_i=\left({B}_i+{Z}_x^2(i)\right)\operatorname{mod} Gray $$
  1. (3)

    Parameter selection stage

  • Step 7: The v-dimensional state variable and the cipher image pixels are used to select system parameter k for each iteration. The parameter selection rule is:

    $$ {k}_i^1=f\left(k,{C}_i,{v}_i\right)=k\times \left(\left({v}_i\times {C}_i\right)\operatorname{mod}1\right) $$

  • Step 8: The perturbed Logistic map (3) is iterated with new system parameters k1

\( {x}_{i+1}={k}_i^1{x}_i\left(1-{x}_i\right)+\alpha {u}_i\operatorname{mod}1 \), to get a state variable sequence \( \left\{{x}_i^1\right\} \).

  • Step 9: Another parameter sequence k2 is got by using the w-dimensional state variable and the plain image pixels in the same way.

    $$ {k}_i^2=f\left(k,{C}_i,{w}_i\right)=k\times \left(\left({w}_i\times {C}_i\right)\operatorname{mod}1\right) $$

  • Step 10: The perturbed Logistic map (3) is iterated with new system parametersk2 \( {x}_{i+1}={k}_i^2{x}_i\left(1-{x}_i\right)+\alpha {u}_i\operatorname{mod}1 \), to get a state variable sequence \( \left\{{x}_i^2\right\} \).

  • Step 11: Set i = i + 1, and repeat steps 3 to 10 until i = M × N, namely, all pixels are encrypted.

3.4 Image decryption algorithm

Suppose that the receiver gets the secret keys (u, v, w, A, x, K, L) transmitted through secure channel. The overall architecture of the decryption algorithm is shown in Fig. 9. The core components and execution phases are similar. The defined symbols remain unchanged. The clear decryption algorithm is as follow:

  • Step 1 and Step 2 are the same as encryption process.

  1. (1)

    Parameter selection stage

  • Step 3: The v-dimensional state variable and the cipher image pixels are used to select system parameter k for each iteration. The parameter selection rule is:

Fig. 9
figure 9

The architecture of the decryption process

Full size image
$$ {k}_i^1=f\left(k,{C}_i,{v}_i\right)=k\times \left(\left({v}_i\times {C}_i\right)\operatorname{mod}1\right) $$

  • Step 4: The perturbed Logistic map (3) is iterated with new system parametersk1

$$ {x}_{i+1}={k}_i^1{x}_i\left(1-{x}_i\right)+\alpha {u}_i\operatorname{mod}1, $$

to get a state variable sequence \( \left\{{x}_i^1\right\} \).

  • Step 5: Another parameter sequence k2 is got by using the w-dimensional state variable and the plain image pixels in the same way.

    $$ {k}_i^2=f\left(k,{C}_i,{w}_i\right)=k\times \left(\left({w}_i\times {C}_i\right)\operatorname{mod}1\right) $$

  • Step 6: The perturbed Logistic map (3) is iterated with new system parameters k2

$$ {x}_{i+1}={k}_i^2{x}_i\left(1-{x}_i\right)+\alpha {u}_i\operatorname{mod}1, $$

to get a state variable sequence \( \left\{{x}_i^2\right\} \).

  1. (2)

    Confusion stage

  • Step 7: Set i = M × N. An integer is generated from \( {x}_i^2 \) \( {Z}_x^2(i)=\left(\left\lfloor {x}_i^2\times {10}^{14}\right\rfloor \operatorname{mod} Gray\right) \), Gray is the gray level of image.

  • Step 8: For each pixel in B, the diffused pixel is decrypted as

    $$ {B}_i=\left({C}_i+256-{Z}_x^2(i)\right)\operatorname{mod} Gray $$
  1. (3)

    Permutation stage

  • Step 9: Another integer is generated from \( {x}_i^1 \) \( {Z}_x^1(i)=\left(\left\lfloor {x}_i^1\times {10}^{14}\right\rfloor \operatorname{mod}M\times N\right) \), M × N is the size of the image.

  • Step 10: For each pixel of plain image in P, the location of the corresponding original is calculated as

    $$ {\displaystyle \begin{array}{c}{P}_i={B}_j,j=i+\left({Z}_x^1(i)\oplus i\right)\operatorname{mod}\left(M\times N+1-i\right)\\ {} permute\left({B}_j,{B}_i\right)\end{array}} $$

  • Step 11: Set i = i − 1, and repeat steps 7 to 10 until i = 1, namely, all pixels are decrypted.

4 Performance and security analysis

The proposed algorithm and related simulations are performed on Matlab R2019a with Intel Core i7-6700HQ CPU @ 2.60GHz and 12.0 GB RAM on Windows 10 (64bit).

4.1 Statistical analysis

4.1.1 Histogram analysis

An image histogram plotting the frequency of pixels at every color level illustrates the distribution of pixels in an image. To prevent attackers from getting some useful information by statistical methods, the histogram of the encrypted image must be as uniform as possible. Taking the 512 × 512 Lena image as an illustration, the secret key is set as (u = 1.1, v = 2.2, w = 3.3, A = 28, x = 0.1, K = 4, L = 1). It can be concluded that he encryption and decryption algorithms are effective from Fig. 10(a)-(c). The encrypted image in Fig. 10(b) provides no information about the plain image. The histograms of the 512 × 512 Lena image and the corresponding cipher image are given in Fig. 10(d)-(e). As shown in Fig. 10(e), the encrypted image has a nearly uniform distribution and completely hides the statistical characteristics of the plain image. Obviously, the histogram of the cipher image shows that encryption removes certain pattern that the plain image has.

Fig. 10
figure 10

Encryption and decryption results, (a) plain image, (b) cipher image, (c) recovered image; Histograms results, (d)-(f) are the corresponding histograms

Full size image

4.1.2 Correlation analysis

The adjacent pixels of the meaningful plain image have close values, so the correlation between two adjacent pixels is always high. The ability to efficiently reduce the correlation between adjacent pixels shows the performance of encryption algorithm. The correlation coefficient is calculated as.

$$ {r}_{uv}=\frac{\operatorname{cov}\left(u,v\right)}{\sqrt{D(u)}\sqrt{D(v)}}, $$
(5)
$$ \operatorname{cov}\left(u,v\right)=\frac{1}{N}\sum \limits_{i=1}^N\left({u}_i-E(u)\right)\left({v}_i-E(v)\right), $$
(6)
$$ E(u)=\frac{1}{N}\sum \limits_{i=1}^N{u}_i,D(u)=\frac{1}{N}\sum \limits_{i=1}^N{\left({u}_i-E(u)\right)}^2, $$
(7)

where u and v are two sequences.

10,000 pairs of adjacent pixels are randomly selected from the Lena image and its corresponding cipher image in the horizontal, vertical and diagonal directions. The distributions are shown in Fig. 11. Obviously, the Lena image has strong correlation between adjacent pixels in three directions as Fig. 11(a)-(c) shown. For cipher image, the whole space are covered with the adjacent pixels pairs, which means random distribution. Moreover, the correlation coefficients of adjacent pixels in the plain image and cipher image are listed in Table 1. For different images, the calculated correlation coefficients of adjacent pixels in the plain image and cipher image are close to one and zero, respectively. This result demonstrates that the correlation of pixel values between two adjacent points is greatly reduced and no correlation in cipher image. Both of them verify that the proposed cryptosystem can resist correlation attack.

Fig. 11
figure 11

Correlation distribution in different directions of plain image (first row) and cipher image (second row) of Lena, (a) and (d) horizontal direction coefficient; (b) and (e) vertical direction coefficient; (c) and (f) diagonal direction coefficient

Full size image
Table 1 Correlation coefficients of different images
Full size table

4.1.3 Information entropy

Information entropy is an indicator that is used to evaluate the randomness and indeterminacy of the information source. The entropy of a message source is defined as

$$ H(s)=-\sum \limits_{i=0}^{L-1}p(i){\log}_2p(i). $$
(8)

In this paper s is the message source generated by an image, L represents grey level, p(i) denotes the probability of occurrence of gray value i. For an ideal random message source with L symbols, the maximum entropy should theoretically be log2L. Therefore, for 256 Gy-level encrypted images, the ideal entropy should be 8. Four different 512 × 512 test images with pixel values from 0 to 255 are encrypted with the proposed cryptosystem. The calculated information entropies are given in Table 2. Compared with the four plain images, all the entropies of the cipher images are so close to 8 that information leakage can be negligible in the encryption process, which means that it is almost impossible to obtain useful information from encrypted images.

Table 2 Information entropies of different images
Full size table

4.2 Security analysis

A good cryptosystem should have excellent statistical performance as well as the ability to resist various attacks, such as brute-force attack, known-plaintext attack, chosen-plaintext attack, and differential attack. Some security analyses are conducted on the proposed image encryption algorithm in this section.

4.2.1 Secret key analysis

Large key space is a necessary condition for a secure cryptosystem. When the key space is no smaller than 2256, brute-force attack is infeasible even with quantum computers that run some quantum computing algorithms [33]. In general, the key space should be more than 2128. The proposed cryptosystem based on HHMCD has more parameters for secret key generation and a larger range of parameters, which is demonstrated in section 2.

The secret key consists of seven parameters: the initial values (u0, v0, w0) and parameter c of Chen chaotic system, the initial values x0 and parameter k of the Logistic map, and perturbation strength α. As the computing precision is set at 10−14, the total number of candidate values of the secret key is about key ≈ 1014 × 7 ≈ 2325. The key is large enough to resist brute-force attack under the computing power today. Even if the computing precision is very limited (set at 2−10), the continuous chaotic system that is the perturbation source will not be affected by a low precision. The key space is approximately 1014 × 4 × 210 × 3 ≈ 2216. Further, if the continuous chaotic system is implemented on analog devices, the key space will be much more elusive.

Moreover, extreme key sensitivity is an essential feature of an effective cryptosystem. Taking the Lena image as an example, its cipher image is obtained with the secret key (u = 1.1, v = 2.2, w = 3.3, A = 28, x = 0.1, K = 4, L = 1). To evaluate the key sensitivity, a slight change 10−14 is set for every parameter in turn while the others remain constant to repeat the encryption and decryption processes, respectively. The corresponding cipher images and deciphering images are given in Figs. 12 and 13. It is evident that the decryption fails when a secret key is slightly changed even by the minimal precision 10−14. The differences between any two cipher images and any two deciphering images are computed and shown in Table 3. The tests demonstrate that the cipher images with a slightly different secret key exhibit no similarity. There is no significant correlation that can be observed from the deciphering images as well. Both results indicate that the proposed image encryption algorithm is highly sensitive to secret key. Notably, the sufficiently large key space and PSM make the number of key collisions rare and attacks based on key collisions with high computational complexity.

Fig. 12
figure 12

Key sensitivity tests in encryption process. (a) 512×512 Lena image. Cipher images with slightly changed secret keys (b) u = 1.1, v = 2.2, w = 3.3, A = 28, x = 0.1, K = 4, L = 1, (c) x = 0.1 + 10−14, (d) K = 4 + 10−14, (e) L = 1 + 10−14, (f) A = 28 + 10−14, (g) u = 1.1 + 10−14, (h) v = 2.2 + 10−14, (i) w = 3.3 + 10−14

Full size image
Fig. 13
figure 13

Key sensitivity tests in decryption process. Deciphering images with slightly changed secret keys (a) u = 1.1, v = 2.2, w = 3.3, A = 28, x = 0.1, K = 4, L = 1, (b), x = 0.1 + 10−14, (c) K = 4 + 10−14, (d) L = 1 + 10−14, (e) A = 28 + 10−14, (f) u = 1.1 + 10−14, (g) v = 2.2 + 10−14, (h) w = 3.3 + 10−14

Full size image
Table 3 Differences between any two cipher images and any two deciphering images generated by slightly different secret keys
Full size table

4.2.2 Ability for resisting differential attack

By making a slight change to plain image (e.g., change one pixel value), attackers may find some patterns between plain image and cipher image. This kind of attacks is called differential attack. When a significant change happens in the cipher image under the slight change in the plain image, then the differential attack becomes largely useless. To evaluate the ability to resist differential attack, two common indicators are adopted: number of pixels change rate (NPCR) and unified average changing intensity (UACI) [47]. Two cipher images are obtained by changing the 1 bit of plain images. The NPCR and UACI of C1 and C2 are calculated by:

$$ NPCR\left({C}_1,{C}_2\right)=\frac{1}{MN}\sum \limits_{i=1}^M\sum \limits_{j=1}^N\mid \mathit{\operatorname{sign}}\left({C}_1\left(i,j\right)-{C}_2\left(i,j\right)\right)\mid \times 100\%, $$
(9)
$$ \mathit{\operatorname{sign}}(x)=\Big\{{\displaystyle \begin{array}{c}0,x=0\\ {}1,x\ne 0\end{array}}, $$
(10)
$$ UACI\left({C}_1,{C}_2\right)=\frac{1}{MN}\sum \limits_{i=1}^M\sum \limits_{j=1}^N\frac{\mid {C}_1\left(i,j\right)-{C}_2\left(i,j\right)\mid }{255}\times 100\%, $$
(11)

In order to improve the algorithm performance for resisting differential attack, two-round encryption is conducted. In this test, a pixel of the plain image is randomly selected. Then its value is changed by just 1 bit. Two plain images are encrypted. We choose different 512 × 512 images with standard 256 Gy scale and repeat the test 100 times. The corresponding NPCR and UACI are calculated. The minimum, maximum and mean values of each pair of images are given in Table 4. Consistent with [47], the critical values of NPCR and UACI have been calculated with respect to the significance level α = 0.05 as NPCR ≥ 99.5893 and UACI ∈ [33.3730, 33.5541]. Results show that the proposed cryptosystem can pass NPCR and UACI tests, and further can effectively withstand differential attacks.

Table 4 Values of NPCR and UACI of different plain images
Full size table

4.2.3 Ability for resisting chosen-plaintext and known-plaintext attacks

In order to identify the relationship between plain images and cipher images, adversaries often use specific type of images to cryptanalyze encryption algorithms then obtain key-related information via observing the cipher images. In the proposed cryptosystem, because of introduction of the PSM, the plain image plays a critical role in key stream generation. Thus totally different key streams are obtained for different plain images. Some specific images, such as all-black and all-white images, are adopted as powerful tools for adversaries to decipher cryptosystems. To depict the ability of the proposed cryptosystem for resisting chosen-plaintext and known-plaintext attacks, all-black and white images are encrypted. The resulting cipher images and corresponding histograms are displayed in Fig. 14. It can be seen that all-black and all-white images are totally random after encryption. The cryptosystem is effective to eliminate the patterns in plain images. Moreover, correlation coefficients, information entropy of the cipher images as well as difference ratio between plain images and cipher images are also tested. As shown in Table 5, all the results are close to the ideal values. Adversaries cannot obtain any useful information from the encrypted known-plain image or chosen-plain image for the proposed algorithm. Therefore it can be concluded that chosen-plaintext and known-plaintext attacks can be effectively resisted in the proposed encryption algorithm.

Fig. 14
figure 14

Encryption and histograms of all black and white images. (a) all black image, (b)cipher image of all black image, (c) histogram of all black image, (d) all white image, (e) cipher image of all white image, (f) histogram of all white image

Full size image
Table 5 The test results of cipher all-black and all-white images
Full size table

4.3 Comparisons with some exiting chaos-based encryption algorithms

The previously conducted tests indicate that our proposed algorithm are competent. Furthermore, a necessary comparison is given. The comparative objects are chosen from some typical researches, which are based on classical chaotic maps [25], complex chaotic system [40] (such as spatiotemporal chaos and hyperchaos), and some high performance cryptosystems which are recently published [2, 12]. To ensure rationality, the plain image is selected as 256 × 256 Lena image. The results of correlation coefficients, information entropy, NPCR, UACI, size of key space and encryption time are given in Table 6. The average encryption time for 100 times encryption is 0.4244 s. Moreover, the required time for two rounds of encryption is 0.9115 s. All indicators of the proposed cryptosystem are in good places that means our cryptosystems are surely secure and efficient.

Table 6 Comparisons of the proposed algorithm against other different algorithms
Full size table

5 Conclusion

This paper proposed a novel image cryptosystem based on an analog-digital hybrid chaotic system and a parameter selection mechanism. The chaotic dynamics analyses show that the perturbed Logistic map has uniform distribution, better chaotic complexity and wider chaotic parameter range. The proposed hybrid model based on the mechanism for chaos degradation can be used to greatly improve the dynamical characteristics of any chaotic map under finite computing precision. Meanwhile, the PSM introduced in key stream generation process can enhance security and resist known-plaintext and chosen-plaintext attacks. With cipher image involved in PSM, a tiny change in the plain image will bring about totally different key stream sequences even though the same secret key is used. Based on the proposed chaotic system and PSM, a new cryptosystem has been designed. Simulation results of extensive performance and security analyses show that the statistical properties, information entropy and ability to resist various attacks of the proposed cryptosystem are very satisfactory. All these results justify the advantageous security and complexity of our scheme, which is suitable for practical applications. In the future, laser chaotic system or high-speed chaotic oscillator can be used to design the continuous chaotic system for high speed and light weight.