A delay coupling method to reduce the dynamical degradation of digital chaotic maps and its application for image encryption

Abstract

In this study, a novel delayed coupled chaotic model to reduce the dynamical degradation of digital chaotic maps is firstly proposed. In this model, we introduce the delayed state variables in digital maps and use the state variable of one map to vary the control parameter of the other map. Numerical experimental results demonstrate that the delayed coupled system can effectively reduce the dynamical degradation of digital chaotic maps, and retain the phase space structure of the original system. Furthermore, we propose a simple image encryption algorithm based on the coupled model as a simple application. Numerical experiments show that our algorithm has high security level and can resist various attacks, which is competitive with some other chaotic image encryption algorithms.

1 Introduction

On the basis of certain complex dynamics characteristics, including sensitivity to initial conditions and parameters, topological transitivity, unpredictability, aperiodicity, and pseudo-randomness, chaotic systems/maps are widely used in various scientific and social fields, including communications, economics, chemistry, networking, and cryptography [5, 10, 27]. Particularly, chaos-based cryptography has received considerable attention from researchers since the 1990s due to its consistency of chaotic characteristics and cryptographic requirements [9, 22, 24, 25, 30]. Although various chaotic encryption algorithms have been proposed to date, their security is usually not as high as indicated.

The chaos theory is defined on a real number field. However, the computer is a finite precision device. When chaotic systems/maps are implemented on a computer, their state space will be finite and their dynamics will suffer degradation [11]. Therefore, the chaotic maps are no longer mathematically chaotic. We call them digital chaotic maps. The trajectory of digital chaotic maps will finally enter a cycle due to the finite state space, and other ideal performances of chaos, including sensitivity, transitivity, unpredictability, and ergodicity, will degenerate simultaneously, thereby no longer satisfying the requirements of cryptography. In most chaotic encryption algorithms, the chaotic maps are implemented on a computer; hence, security may be at risk. Therefore, the chaotic dynamics of digital chaotic maps should be improved to enhance the security of chaotic algorithms. In other words, the dynamical degradation of digital chaotic maps must be reduced.

Attempts to reduce the dynamical degradation of digital chaotic maps have been widely studied [3, 4, 13, 14, 16,17,18,19, 26, 30, 32]. [30] used high precision to extend the period of digital chaotic maps and improve their dynamics. [3, 32] cascaded multiple chaotic maps to extend the period of digital chaotic maps. [18, 26] reduced the dynamical degradation of digital chaotic maps by switching multiple chaotic maps. [13, 16, 19] improved the dynamics of chaotic maps by (pseudo)-random perturbation. [4, 17] introduced an analog chaotic system to improve the dynamics of digital chaotic maps. Recently, [14] extended the period of digital chaotic maps by using delayed state variables. Although these methods can reduce the dynamical degradation to some extent, they still possess limitations. Using a high precision will certainly increase the implementation cost. Cascading or switching multiple chaotic maps can extend the period of digital chaotic maps. However, the dynamical complexity of the remedied system is completely determined by the cascading or switching rules, which are always ignored and difficult to control. The perturbation method is better than the first three methods. Introducing a good perturbation source will considerably improve the dynamics of digital chaotic maps. The analog–digital mixed control method is a novel method in this field. However, the introduction of analog chaotic system constantly warrants additional resources, and the hybrid system is difficult to realize. The delay-introducing method proposed in [14] is a novel and feasible method; however, its dynamical complexity and universality should be further improved.

These past studies have motivated us to propose a novel delayed coupled chaotic model that reduces the dynamical degradation of digital chaotic maps. In our model, two digital chaotic maps are coupled. We use the state variable of one map to vary the control parameter of the other map. Therefore, the coupled system is time varying, and the output trajectories are non-stationary, resulting in high complexity. Furthermore, we introduce the delayed state variables in digital maps to extend the periods. As far as we know, combining both delay introducing method and coupling method to reduce the dynamical degradation of digital chaotic maps has not been studied yet. While improving these characteristics, this method still retains the phase space structure of the original system rather than constructing a new random source. The advantages of our model can be described as follows.

• 1) The model can greatly reduce the dynamical degradation of digital chaotic maps.

• 2) The model introduces a delay state, which relates the output of the system not only to the current state but also to the previous state.

• 3) The model couples two systems. The parameters of each sub-system are affected by the output of the other sub-system and are constantly varying.

• 4) This method can be applied to all digital chaotic systems.

We take two examples to show the effectiveness of our delayed coupling method. The trajectories, phase diagrams, auto-correlation function, and complexity, including approximate entropy (ApEn) and permutation entropy (PE), are analyzed in each example. Simulation results show that the coupled model can considerably improve the dynamical complexity of original digital chaotic maps, which implies the effectiveness of our delayed coupling method. As chaos-based encryption algorithm has been widely used in several areas [9, 22, 24, 25, 28,29,30], therefore, in this paper, we also apply the delayed coupled digital chaotic model to a simple image encryption algorithm as an application. Several numerical experiments show that our algorithm has high security level and can resist various attacks, which is competitive with some other chaotic image encryption algorithms.

The rest of this paper is organized as follows. The new delayed coupled chaotic model is introduced in Section 2. The logistic–logistic coupled model and logistic–Chebyshev coupled model with their complexity analysis are shown in Sections 3 and 4, respectively. In Section 5, we apply a simple image encryption algorithm based on the delayed coupled model. Finally, Section 6 concludes the paper.

2 Delayed coupled chaotic model

The general chaotic map can be described as follows:

$$ {x}_{i+1}=f\left({x}_i,p\right) $$

(1)

where x is the state variable, and p is the control parameter. Once the parameter p is selected in the suitable chaotic region, the map f will be chaotic. However, when this chaotic map is simulated on a computer (or other finite precision device), its dynamics will suffer degradation due to the finite phase space. In order to improve the dynamics of digital chaotic map, we provide the following delayed coupled model:

$$ \left\{\begin{array}{c}{x}_{i+1}={F}_1\left({x}_i,{x}_{i-1},\dots, {x}_{i-k},{h}_1\left({y}_i\right)\right)\\ {}{y}_{i+1}={F}_2\left({y}_i,{y}_{i-1},\dots, {y}_{i-k},{h}_2\left({x}_i\right)\right)\end{array}\right. $$

(2)

where h₁ and h₂ are parameter control functions. The chaotic functions F₁ and F₂ are two chaotic maps. In this model, the control parameter of each sub-system is controlled by the state from other sub-systems, and the delayed state is introduced to construct functions F₁ and F₂. These two functions can reduce the dynamical degradation of the delayed coupled chaotic model. The following two conditions should be satisfied in this model:

• 1) The parameter of a map should be in a particular region called the chaotic region to make the map chaotic. In our model, the parameter is affected by the coupled state variable, which is continuously varied. Therefore, the valued field of parameter control functions h₁ and h₂ should be a subset of the chaotic region. The varied parameter not only can improve the dynamics of digital chaotic map but also make the output sequence non-stationary, thereby resisting such statistical attacks.

• 2) In the original chaotic map, its current state x_i is completely determined by its previous state x_i − 1. Therefore, the digital chaotic sequence will fall into a cycle if two states x_p and x_q are identical. We introduce more delayed state variables in the chaotic map of our model to extend the period. In this case, state x_i is not completely determined by x_i − 1 but by vector (x_i − 1, x_i − 2,  … , x_i − k). Therefore, the digital chaotic sequence will not fall into a cycle unless the previous k states x_p − 1, x_p − 2, … , x_p − k and x_q − 1, x_q − 2, … , x_q − k are identical. A large k implies that the digital chaotic sequence has a large resistibility to enter a cycle. We consistently select k = 2 to reduce the implementation cost; thus, state x_i is determined by its previous two states x_i − 1 and x_i − 2. Furthermore, with the introduction of delayed states, the chaotic attractor should not be destroyed completely. Similar to other studies [4, 17], the digital chaotic attractors are entirely different from their original chaotic maps, which cannot be regarded as dynamical degradation remedies but methods of constructing new random sources.

Here, we propose a delayed coupling method to reduce the dynamical degradation of digital chaotic maps. The delayed state coupling and parameter control functions are uncertain, which are selected due to different chaotic maps. We recommend using simple linear functions to reduce implementation costs.

Remark 1

Our method is effective for all chaotic maps. We can couple any two identical chaotic maps, as well as two different chaotic maps. Moreover, the dimensions of these two maps can be different. All digital chaotic systems can apply our coupling method as long as the above construction rules are followed. We take two examples to show the effectiveness of our delayed coupling method in the subsequent sections.

Remark 2

Reducing the dynamical degradation of digital chaotic systems should not completely disturb the phase space of original systems. Some methods, such as [4, 17], have completely disrupted the structure of original chaotic map, which cannot be regarded as a remedy, but rather to generate new random sources.

3 Example 1

In this example, we couple two identical logistic maps, the mathematical model of which can be described as

$$ {x}_{i+1}=F\left({x}_i,{r}_1\right)={r}_1{x}_i\left(1-{x}_i\right) $$

(3)

where r₁ is the control parameter, which should be in the interval (3.5699, 4) to make the map chaotic. Here, we select the following delayed state coupling and parameter control functions:

$$ \left\{\begin{array}{c}X=a{x}_i+\left(1-a\right){x}_{i-1}\\ {}Y=a{y}_i+\left(1-a\right){y}_{i-1}\end{array}\right. $$

(4)

$$ \left\{\begin{array}{c}{h}_1\left({y}_i\right)={r}_1+\left(4-{r}_1\right){y}_i\\ {}{h}_2\left({x}_i\right)={r}_1+\left(4-{r}_1\right){x}_i\end{array}\right. $$

(5)

Then, the delayed coupled model can be written as

$$ \left\{\begin{array}{c}{x}_{i+1}={F}_1\left(X,{h}_1\left({y}_i\right)\right)={F}_1\left({x}_i,{x}_{i-1},{h}_1\left({y}_i\right)\right)\\ {}{y}_{i+1}={F}_2\left(Y,{h}_2\left({x}_i\right)\right)={F}_2\left({y}_i,{y}_{i-1},{h}_2\left({x}_i\right)\right)\end{array}\right. $$

$$ \left\{\begin{array}{c}{x}_{i+1}=\left({r}_1+\left(4-{r}_1\right){y}_i\right)\cdotp \left(a{x}_i+\left(1-a\right){x}_{i-1}\right)\cdotp \left(1-a{x}_i-\left(1-a\right){x}_{i-1}\right)\\ {}{y}_{i+1}=\left({r}_1+\left(4-{r}_1\right){x}_i\right)\cdotp \left(a{y}_i+\left(1-a\right){y}_{i-1}\right)\cdotp \left(1-a{y}_i-\left(1-a\right){y}_{i-1}\right)\end{array}\right. $$

(6)

In this model, the parameters of sub-systems X and Y are coupled and controlled by the states of Y and X, respectively. Thus, the coupled model is parameter varied. Next, we analyze certain characteristics to validate the efficiency of our method.

3.1 Trajectories and phase diagrams

The trajectory of an ideal chaotic system should be random-like and without any regular structural features. Let the largest precision be 2⁻¹². Set a = 0.999, r₁ = 3.99, and the initial values x₁ = 0.23245, x₂ = 0.512242109, y₁ = 0.30863, and y₂ = 0.41074 for Eqs. (6) and (3), respectively. The trajectories of the two maps are shown in Fig. 1. Figure 1(a) represents the trajectories of x-dimensional sequences of Eq. (6), whereas Figs. 1(b) and 1(c) represent the y-dimensional sequences of Eqs. (6) and (3), respectively. Figure 1 indicates that the trajectory of Eq. (3) quickly falls into a cycle after approximately 110 iterations, whereas that of Eq. (6) appears randomly after 400 iterations; no apparent period can be detected, which implies that the original system has a regular structure, whereas the improved system has none. Therefore, the period of delayed coupled digital chaotic maps has been extended with good randomness. Figures 2(a) and 2(b) plot the phase diagrams of Eqs. (3) and (6), respectively. The points of the improved chaotic sequences are denser than the original points, which indicates that the improved map is remarkably similar to the traditional logistic map and is active in the phase space.

Fig. 1

Trajectories of the (a) x-dimensional sequence of Eq. (6) and of the (b) y-dimensional sequences of Eqs. (6) and (c) (3)

Fig. 2

Phase diagrams of (a) Eq. (3) and (b) Eq. (6)

3.2 Auto-correlation analysis

Auto-correlation function is an important measure of randomness. The auto-correlation of an ideal chaotic sequence should be delta function. Let the largest precision be 2⁻¹⁶. The auto-correlation functions of sequences generated by Eqs. (6) and (3) are shown in Figs. 3(a) and 3(b), respectively. The waveform of auto-correlation function of a good performance sequence should be sharp needle-like without prominent side lobe, which can be used to detect and identify the signal accurately. As shown in Fig. 3, the main peak of auto-correlation function of the original system sequence is thick, and the side lobe is extremely high. However, the improved system sequence’s auto-correlation function has a small main peak, and the side lobes are rarely low and virtually invisible, which implies that the improved system has good randomness.

Fig. 3

Auto-correlation functions of (a) x-dimensional sequences of Eqs. (6); (b) Eqs. (3)

3.3 Complexity analysis and comparison

ApEn and PE are widely applied in measuring the complexity of time series. Here, we use these two complexity measures to evaluate and compare the complexity of our proposed model (Eq. (6)) and the original chaotic model (Eq. (3)).

3.3.1 ApEn analysis

ApEn was first proposed by Pincus to measure the complexity of time series [20]. ApEn measures the probability of the new pattern generated in sequences with an embedding dimension growth. A greater probability of generating a new pattern implies greater ApEn. In this test, we set a = 0.999 and r₁ = 3.99 to calculate the ApEn of sequences generated by Eqs. (6) and (3), as shown in Fig. 4. From the figure, the ApEn of the sequence generated by Eq. (6) (red line) is always larger than that by Eq. (3) (blue line) under the same precision, which indicates that our coupled model (Eq. (6)) is relatively more complex than the original chaotic model (Eq. (3)). This finding indicates that the proposed method (Eq. (6)) can enhance the complexity of the traditional logistic map without disrupting its structure and even improve the dynamic degradation to a certain extent. In comparison with other proposed methods, the ApEn of Eq. (6) is also larger than the methods in [7, 12, 16], whose ApEn is approximately 0.479, 0.613, and 0.615 under the same parameters, respectively. While comparing with the methods in [4, 17], the ApEn in these studied are larger than 1, which are both larger than our method. That is because the methods in [4, 17] completely disrupt the phase space structure of the original digital systems. Therefore, these methods can not be regarded as the method to reduce the dynamical degradation of digital chaotic maps, but to construct new random sources.

Fig. 4

ApEn of sequences generated by the x-dimension of Eqs. (6) and (3)

3.3.2 PE analysis

PE is another widely used complexity measure for time series [2]. This measure compares the size of certain consecutive values in the time series, sums up different order types, and then uses Shannon’s entropy to measure the uncertainty of the order. As suggested in [2], we set the ordinal pattern length L = 6 and the embedding delay D = 2 in this test. We measure the PE of sequences generated by Eqs. (6) and (3) with the method of changing the precision. The parameters are selected to be the same as those in Section 3.3.1, and the PE of sequences generated by Eqs. (6) and (3) under the same precision are shown in Fig. 5, where −logp starts at 12 and increases by 4; thus, the PE of the sequence generated by Eq. (6) (red line) is larger than that by Eq. (3) (blue line) with one accord. The complexity measure fully demonstrates that the proposed model has a higher complexity and stronger anti-jamming capabilities, such as applying to the encryption algorithm, compared with the original chaotic model. Furthermore, under the same precision, the PE complexity of the systems in [7, 12, 16] are 0.813, 0.882, and 0.885, respectively; hence, our method is competitive in improving the complexity of digital chaotic maps.

Fig. 5

PE of sequences generated by the x-dimension of Eqs. (6) and (3)

4 Example 2

In this example, we couple two different chaotic maps, namely, logistic and Chebyshev maps, to demonstrate the effectiveness of our method. The Chebyshev map model can be described as follows:

$$ {y}_{i+1}=\cos \left(r\times \operatorname{arccos}\left({y}_i\right)\right) $$

(7)

where r is the control parameter. In this example, the delayed state coupling functions are the same as Eq. (4), and the parameter control functions are selected as follows:

$$ \left\{\begin{array}{c}{h}_1\left({y}_i\right)={r}_1+\left(4-{r}_1\right){y}_i\\ {}{h}_2\left({x}_i\right)=2+{x}_i\kern4em \end{array}\right. $$

(8)

Then, the delayed coupled model can be written as

$$ \left\{\begin{array}{c}{x}_{i+1}=\left({r}_1+\left(4-{r}_1\right){y}_i\right)\cdotp \left(a{x}_i+\left(1-a\right){x}_{i-1}\right)\cdotp \left(1-a{x}_i-\left(1-a\right){x}_{i-1}\right)\\ {}{y}_{i+1}=\cos \left(\left(2+{x}_i\right)\mathit{\operatorname{arccos}}\left(a{y}_i+\left(1-a\right){y}_{i-1}\right)\right)\kern11.25em \end{array}\right. $$

(9)

Certain numerical simulations are provided in this study to present the characteristics of Eq. (9).

4.1 Trajectories and phase diagrams

Given that the second model couples the traditional logistic map and the Chebyshev map, we compare the performances of different characteristics. For the sake of guaranteeing the persuasiveness of the numerical experiment, we select the same precision, parameters, and initial values as those in Section 3.1 for Eqs. (9), (3), and (7), respectively. The trajectories of the three maps are shown in Fig. 6; Figs. 6(a) and 6(b) are the trajectories of Eqs. (3) and (7), respectively, and Figs. 7(c) and 7(d) are the trajectories of the x- and y-dimensional sequences of Eq. (9). Figure 6(a) shows the same result as that in Section 3.1. However, Fig. 6(b) reveals that the trajectories of Eq. (7) quickly fall into a cycle after approximately 120 iterations, which manifests a regular structure. The x- and y-dimensional sequences of Eq. (9) have no cycles after 400 iterations and no regular structure. Therefore, the period of the improved delayed coupled digital chaotic model is extended with good randomness. Similarly, Figs. 7(a)–7(d) plot the phase diagrams of Eqs. (3), (7), and (9). In comparison, the results in Figs. 7(a) and 7(c) are similar to those of Section 3.1, whereas the points in Fig. 7(d) are denser and more widely distributed than those in Fig. 7(b). Hence, the period of Eq. (9) is further improved.

Fig. 6

The trajectories of (a) Eq. (3); (b) Eq. (7); (c) x-dimensional of Eq. (9); (d) y-dimensional of Eq. (9)

Fig. 7

The phase diagrams of (a) Eq. (3); (b) Eq. (7); (c) x-dimensional of Eq. (9); (d) y-dimensional of Eq. (9)

4.2 Auto-correlation analysis

The auto-correlation functions are shown in Fig. 8; Figs. 8(a) and 8(b) represent the auto-correlation functions of the x- and y-dimensional sequences of Eq. (9), respectively, and Fig. 8(c) is the auto-correlation function of Eq. (7). From the figure, the side lobes generated by Eq. (9) are almost absent. The main peak is extremely thin, whereas the characteristics of Eq. (7) are the opposite. Moreover, the auto-correlation functions of the sequence generated by Eq. (9) are closer to delta function and more random than those by Eqs. (3) and (7).

Fig. 8

Auto-correlation functions of (a) x-dimensional of Eq. (9); (b) y-dimensional of Eq. (9); (c) Eq. (7)

4.3 Complexity analysis and comparison

4.3.1 ApEn analysis

We select the y-dimensional state variables in the following experiments because the results of the x-dimensional variables are similar to Section 3, which we omitted to avoid redundancy. Furthermore, we set the same precision, parameters, and initial values as those in Section 3.1. The results shown in Fig. 9 indicate that the ApEn of the sequence generated by Eq. (9) (red line) under the same precision is consistently larger than that of the sequence generated by Eq. (7) (blue line). Therefore, our method can greatly improve the complexity of the digital Chebyshev map.

Fig. 9

ApEn of sequences generated by the y-dimension of Eqs. (9) and (7)

4.3.2 PE analysis

PE analysis is used for this numerical experiment to compare the complexity of sequences generated by Eqs. (9) and (7). Figure 10 shows that the PE of the y-dimensional sequence generated by Eq. (9) (red line) is consistently larger than that of the sequence generated by Eq. (7) (blue line) under the same precision. Hence, our model is more complex than the traditional Chebyshev map.

Fig. 10

PE of sequences generated by Eqs. (9) and (7)

5 Simple image encryption algorithm based on example 1

In this section, we propose a simple image encryption algorithm based on logistic–logistic coupled model (Eq. (6)) to show the practicability of our delayed coupled chaotic model. The model (Eq. (6)) has a high complexity and good randomness. Thus, we do not need to design a tedious encryption algorithm to ensure its security. Here, the encryption algorithm is relatively simple, and the numerical analysis shows that the algorithm is comparatively secure and competitive with other algorithms.

5.1 New image encryption algorithm

5.1.1 Shuffling algorithm

The purpose of the shuffling algorithm is to scramble the pixel position of the plaint image. Its core idea is to arrange the generated chaotic sequence according to a certain algorithm and then rearrange the plaint image in this order to achieve the result of scrambling. Our simple shuffling algorithm can be described as follows. First, we convert a plain image into A_ij, which is the M × N pixel matrix. Then B_ij, which is the pixel matrix of the grayscale image, is transformed by A_ij into the pixel sequence {B}, whose length corresponds to M × N.

Our shuffling algorithm is based on a shuffling sequence. Suppose that {C_y} is the y-dimensional chaotic sequence generated by Example 1. Our method is to rearrange {C_y} into $\left\{\overset{\acute{\mkern6mu}}{C_y}\right\}$ in ascending order, and the sequence {B} of the plaint image is disturbed accordingly by the subscript of $\left\{\overset{\acute{\mkern6mu}}{C_y}\right\}$. Thus, we can obtain sequence {$\overset{\acute{\mkern6mu}}{B}$} after shuffling. The specific process is as follows:

The purpose of the shuffling algorithm is to scramble.

The shuffled image matrix $\overset{\acute{\mkern6mu}}{B}$ reshaped by {$\overset{\acute{\mkern6mu}}{B}$} can be written as follows:

$$ {\overset{\acute{\mkern6mu}}{B}}_{ij}=\left(\begin{array}{c}{p}_{11}\\ {}{p}_{21}\\ {}{p}_{31}\\ {}\vdots \\ {}{p}_{M1}\end{array}\ \begin{array}{c}{p}_{12}\\ {}{p}_{22}\\ {}{p}_{32}\\ {}\vdots \\ {}{p}_{M2}\end{array}\ \begin{array}{c}{p}_{13}\\ {}{p}_{23}\\ {}{p}_{33}\\ {}\vdots \\ {}{p}_{M3}\end{array}\ \begin{array}{c}\cdots \\ {}\cdots \\ {}\cdots \\ {}\ddots \\ {}\cdots \end{array}\ \begin{array}{c}{p}_{1N}\\ {}{p}_{2N}\\ {}{p}_{3N}\\ {}\vdots \\ {}{p}_{MN}\end{array}\right)\ \left({p}_{11}={q}_{k_1},{p}_{12}={q}_{k_2},{p}_{13}={q}_{k_3},\dots, {p}_{MN}={q}_{k_{M\times N}}\right) $$

5.1.2 New image encryption algorithm

The steps of our encryption algorithm are described in detail as follows.

• Step 1: Read the plain image A, supposing that the size of plain image A is M × N and B_ij is the grayscale pixel matrix of image A.

• Step 2: Calculate the average value (Ave) of all the pixels in the matrix B_ij and obtain the fractional part (b) as follows:

$$ b=\left(\sum \limits_{i=1}^M\sum \limits_{j=1}^N{B}_{ij}\right)/(MN) $$

• Step 3: Set initial values and parameters ($\overset{\acute{\mkern6mu}}{x_1\ }\overset{\acute{\mkern6mu}}{,{x}_2},\overset{\acute{\mkern6mu}}{y_1}\ \overset{\acute{\mkern6mu}}{,{y}_2},{r}_1,\mathrm{and}\ a$) of Eq. (6), where the initial values assigned and the b in Step 2 are added to the final initial values, such that the generated chaotic sequence is associated with the plain image-related information.

$$ \left\{\begin{array}{c}{x}_1=\left(\overset{\acute{\mkern6mu}}{x_1}+b\right)\left(\mathit{\operatorname{mod}}\ 1\right)\\ {}{x}_2=\left(\overset{\acute{\mkern6mu}}{x_2}+b\right)\left(\mathit{\operatorname{mod}}\ 1\right)\\ {}{y}_1=\left(\overset{\acute{\mkern6mu}}{y_1}+b\right)\left(\mathit{\operatorname{mod}}\ 1\right)\\ {}{y}_2=\left(\overset{\acute{\mkern6mu}}{y_2}+b\right)\left(\mathit{\operatorname{mod}}\ 1\right)\end{array}\right. $$

• Step 4: Generate x- and y-dimensional chaotic sequences based on Example 1 by iteration M × N times with the initial values obtained in Step 3. Then, the chaotic sequences of {C_x} and {C_y} can be obtained.

$$ \left\{\begin{array}{c}\left\{{C}_x\right\}=\left\{{x}_1,{x}_2,{x}_3,\dots, {x}_{M\times N}\right\}\\ {}\left\{{C}_y\right\}=\left\{{y}_1,{y}_2,{y}_3,\dots, {y}_{M\times N}\right\}\end{array}\right. $$

• Step 5: Use {C_y} as the shuffling sequence. According to Section 5.1, B will be disordered into matrix $\overset{\acute{\mkern6mu}}{B}$.

• Step 6: {C_x} will be normalized to (0, 255) and then converted to M × N matrix E. The specific conversion method is as follows:

• Step 7: Use chaotic matrix E to obtain the encrypted image D by executing XOR with $\overset{\acute{\mkern6mu}}{B}$.

$$ D=E\oplus \overset{\acute{\mkern6mu}}{B} $$

The flowchart of our algorithm is shown in Fig. 11. The initial values and parameters (x₁, x₂, y₁, y₂, r₁, and a) can be used as the security keys. The decryption of image is the inverse process of using the security keys to encrypt the chaotic matrix, and the steps are described as follows.

• Step 1: Read the encrypted image D, supposing that the size of encrypted image D is M × N and G_ij is the grayscale pixel matrix of image D.

• Step 2: Generate x- and y-dimensional chaotic sequences based on Example 1 by iteration M × N times with the secret keys (x₁, x₂, y₁, y₂, r₁, and a). Then, the chaotic sequences of {C_x} and {C_y} can be obtained.

Fig. 11

Flowchart of our image encryption algorithm

$$ \left\{\begin{array}{c}\left\{{C}_x\right\}=\left\{{x}_1,{x}_2,{x}_3,\dots, {x}_{M\times N}\right\}\\ {}\left\{{C}_y\right\}=\left\{{y}_1,{y}_2,{y}_3,\dots, {y}_{M\times N}\right\}\end{array}\right. $$

• Step 3: {C_x} will be normalized to (0, 255) and then converted to M × N matrix E. The specific conversion method is as follows:

• Step 4: Use chaotic matrix E to obtain the decrypted image $\overset{\acute{\mkern6mu}}{B}$ by executing XOR with D.

$$ \overset{\acute{\mkern6mu}}{B}=E\oplus D $$

• Step 5: Use {C_y} as the reverse shuffling sequence. According to Section 5.1, $\overset{\acute{\mkern6mu}}{B}$ will be restored into sequence B.

Then the {C_y} will be sorted in ascending order.

• Step 6: At last, convert the {B} to the B_ij, which is the grayscale pixel matrix of plain image A.

5.2 Security performances

In this section, different types of security analysis methods are used to demonstrate the security performance of our algorithm. The experimental image is a 256 × 256 “Lena” image. All the tests are produced by Matlab R2016a on a computer with 2.40 GHz CPU and 8.00 GB memory. The initial values and parameters are selected as follows: x₁ = 0.43245, x₂ = 0.51224, y₁ = 0.30863, y₂ = 0.41074, r₁ = 3.9901563, and a = 0.00321. The average value of all pixels of the original image is 99.8142. After adding the information of the original image, the security keys are as follows: x₁ = 0.2466, x₂ = 0.3264, y₁ = 0.1228, y₂ = 0.2249, r₁ = 3.9901563, and a = 0.00321. The precision is 10⁻¹⁴ in our numerical experiments.

5.2.1 Encryption and decryption experiment tests

The encryption and decryption results of the plain image, the encrypted image by the x-dimensional sequence of Eq. (6), the decrypted Lena with correct keys, and the decrypted Lena with wrong keys are shown in Figs. 12(a)–12(d), respectively. A comparison of these four images shows that the Lena becomes unrecognizable and extremely noisy after encryption. When decrypting with the wrong key, the plain image cannot be recognized unless the key is properly restored.

Fig. 12

Encryption and decryption results by the proposed scheme (a) Lena image; (b) encrypted Lena image (c) decrypted with correct keys; (d) decrypted with wrong keys

5.2.2 Histogram analysis

The distribution of the ciphered image is a major concern. Figs. 13(a) and 13(b) show the statistical histograms of Lena and the x-dimensional sequence of Eq. (6), respectively. The histogram of the original image is unevenly distributed and has special features, whereas that of the encrypted image is almost uniformly distributed, whose horizontal distribution is advantageous in resisting statistical and ciphertext-only attacks.

Fig. 13

Statistical histograms (a) Lena image; (b) Encrypted Lena image

5.2.3 Key space analysis

The key space should be sufficiently large to resist brute force attacks for a strong encryption algorithm. In our proposed encryption algorithm, initial values (x₁, x₂, y₁, y₂) and the parameter r₁ can be security keys. Let the precision of a real number be 10⁻¹⁴ and the key space be approximately 0.4 × 10¹⁴ × 10¹⁴ × 10¹⁴ × 10¹⁴ × 10¹⁴ = 0.4 × 10⁷⁰ ≈ 2²³¹, which is considerably larger than 2¹²⁸, and is also larger than 2¹⁶⁰ of [25], 2¹⁴⁰ of [23], and 2¹⁸⁴ of [15] under the same precision. Therefore, our proposed algorithm with such a large key space can sufficiently resist all types of brute force attacks.

5.2.4 Correlation analysis

For a good image encryption algorithm, the correlation coefficient of the encrypted image should be considerably weaker than that of the original image. The correlation coefficient between adjacent pixels of an image can be obtained as follows:

$$ \mathrm{C}=\frac{\sum_{i=1}^N\left({x}_i-\frac{1}{N}{\sum}_{i=1}^N{x}_i\right)\left({y}_i-\frac{1}{N}{\sum}_{i=1}^N{y}_i\right)}{\sqrt{\sum_{i=1}^N{\left({x}_i-\frac{1}{N}{\sum}_{i=1}^N{x}_i\right)}^2\times {\sum}_{i=1}^N{\left({y}_i-\frac{1}{N}{\sum}_{i=1}^N{y}_i\right)}^2}} $$

(10)

where x_i and y_i are two data sequences, and N is the length of the sequences. If two sequences have high correlation, then their correlation values are close to 1; if they are close to 0, then the correlation between the two sequences is weak.

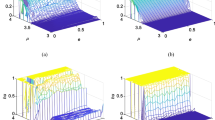
The distribution results of the pixel sequence pairs are shown in Fig. 14. In this test, 2704 pairs of two adjacent pixels along with the horizontal, vertical, and diagonal directions are selected randomly from the original and the encrypted images. Figures 14(a)–14(c) show the distributions of the pixel sequence pairs of the plain image in the horizontal, vertical, and diagonal directions, respectively. The figures indicate that these points are clustered around the diagonal; thus, the correlation between adjacent pixels in the original image is extremely strong. Figures 14(d)–14(f) show the distribution of the pixel sequence pairs of the encrypted image by the x-dimensional sequence of Eq. (6) in the horizontal, vertical, and diagonal directions, respectively. The figures imply that all points are randomly distributed within the range; thus, after breaking the mutuality between the adjacent pixels of the plain image, no correlation exists between the adjacent pixels of the encrypted image.

Fig. 14

Distributions of adjacent pixel sequence pairs (a) horizontal of plain image; (b) vertical of plain image; (c) diagonal of plain image; (d) horizontal of encrypted image; (e) vertical of encrypted image; (f) diagonal of encrypted image

The value of Eq. (10) for each pair is shown in Table 1. The correlation coefficients of the original image are all close to 1 in each direction, and the correlation coefficients of the encrypted image are all smaller than 0.01. This finding implies that our method successfully breaks the correlations between adjacent pixels of the plain image. The absolute values of the correlation coefficients of the encrypted image with our algorithm in the horizontal, vertical, and diagonal directions are far less than those of other proposed algorithms [1, 6, 8, 15, 23, 25], which implies that our algorithm is more competitive to a certain extent.

Table 1 Correlation analysis

5.2.5 Key sensitivity analysis

A secure encryption algorithm should have extreme key sensitivity, which is divided into two aspects,

• 1) The security keys should be sensitive in the encryption process. The encrypted images for the same plain image should be entirely different with a small change of the key.

• 2) The security keys should be sensitive in the decryption process. The decrypted images for the same encrypted images should be entirely different with a small change of the key.

We introduce the mean square error (MSE) to measure key sensitivity and make the results more intuitive. The MSE between two images can reflect their degree of difference, as shown as follows:

$$ \mathrm{MSE}=\frac{\sum_{x=1}^M{\sum}_{y=1}^N{\left[f\left(x,y\right)-\overline{f}\left(x,y\right)\right]}^2}{M\times N} $$

(11)

where f(x, y) and $\overline{f}\left(x,y\right)$ are the pixel values at point (x, y) of two test images. M × N denotes the image size. The MSE is extremely large with a slight deviation from the correct keys and is extremely small only when the main keys are completely correct. Figure 15 shows the MSE curves between the encrypted images generated by correct and wrong keys. Figure 16 shows the MSE curves between the decrypted images generated by correct and wrong keys. These results show that all the security keys have sensitivity in the encryption and decryption processes.

Fig. 15

Key sensitivity analysis in the encryption process (a) x₁, (b) x₂, (c) y₁, (d) y₂, (e) r₁, and (f) a

Fig. 16

Key sensitivity analysis in the decryption process (a) x₁, (b) x₂, (c) y₁, (d) y₂, (e) r₁, and (f) a

5.2.6 Resistance to differential attack analysis

The differential attack, also called the chosen-plaintext attack, is an effective image analysis method. A good image encryption algorithm should have good performance to resist the differential attack.

The number of changing pixel rate (NPCR) and the unified average changing intensity (UACI) are important factors in evaluating the performance against differential attacks of an image encryption algorithm.

$$ NPCR=\frac{\sum_{i=1}^M{\sum}_{j=1}^N{D}_{i,j}}{X\times Y}\times 100\% $$

(12)

$$ UACI=\frac{1}{X\times Y}\left(\sum \limits_{i=1}^M\sum \limits_{j=1}^N\frac{E\left(i,j\right)-\overset{\acute{\mkern6mu}}{E}\left(i,j\right)}{255}\right)\times 100\% $$

(13)

NPCR and UACI represent the percentage and the degree of change in the number of encrypted image pixel values after randomly changing a certain pixel value of the original image, respectively. If a pixel change can cause a complete change in the cipher image, then this algorithm has a good performance against a differential attack.

For the random grayscale image, the ideal values of NPCR and UACI are 0.9961 and 0.3346, respectively. We randomly add 1 pixel to the original image. The NPCR and UACI generated by Eq. (6) are shown in Table 2. From the table, the cipher image completely changes after randomly changing a certain pixel value of the original image. Thus, this algorithm exhibits good performance against differential attack, and is competitive to other recent proposed chaos-based encryption algorithms.

Table 2 Sensitivity analysis to plaintext

5.2.7 Information entropy analysis

Information entropy is the most significant measure of disorder, or unpredictability. The information entropy can be calculated as

$$ \mathrm{H}(x)=-\sum \limits_i^np\left({x}_i\right){\mathit{\log}}_2p\left({x}_i\right) $$

(14)

where, n is the total number of symbols, and p(x_i) is the probability of the symbol x_i. For a completely random image with 256 Gy levels, its entropy should ideally be 8.

The information entropies of the original and encrypted images are shown in Table 3. From the table, the entropy of the encrypted image using our method is extremely close to the ideal value of 8; thus, the pixels of the encrypted image are extremely random. Table 3 also indicates that the information entropy of our encrypted image is competitive compared with other proposed encryption algorithms.

Table 3 Information entropy analysis

5.2.8 Robustness analysis

Images will be destroyed due to various reasons in the process of spreading. Therefore, a good algorithm should have strong robustness against noise and data loss; hence, the cipher image can also be decoded even if some information is lost. Figure 17 shows the robustness analysis results of our algorithm against noise and data loss. The results demonstrate that the damaged cipher image can still be decoded and that the decrypted image can still be recognized with some noise. Therefore, our method is robust enough to resist the attack of noise and data loss.

Fig. 17

Robustness analysis (a₁) Ciphertext image with 0.5% speckle noise; (a₂) Decrypted result with 0.5% speckle noise; (b₁) Ciphertext image with 1% speckle noise; (b₂) Decrypted result with 1% speckle noise; (c₁) Ciphertext image with 1% data loss; (c₂) Decrypted result with 1% data loss; (d₁) Ciphertext image with 5% data loss; (d₂) Decrypted result with 5% data loss

6 Conclusions

On the basis of previous research, this study proposes a new delayed coupled chaotic model to reduce the dynamical degradation of digital chaotic maps. The characteristic analysis implies that the coupled system is time varying and that the output sequences are non-stationary with high complexity. In comparison with other methods, the proposed method has simple coupling rules that can be applied to all chaotic systems. The results confirm that our method has greater future potential in the area of information encryption. Furthermore, the proposed method is applied to image encryption. The image encryption algorithm is considerably simple, and the security of the encrypted image completely depends on the selected delayed coupled digital chaotic system. The experimental tests demonstrate that the image encryption algorithm has high security and is more competitive than other algorithms.