Introduction

The asymptotic averaging method was created in 1970 (see, for example, [1, 2]). It is widely used to determine the elastic moduli of composites [2]. Application of the method to determining the pore pressure transfer tensor (Biot’s tensor parameter) for natural composites is offered in [3,4,5].

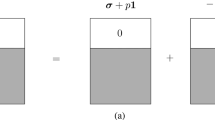
The pore pressure transfer tensor αij is a parameter that is included in the formula for the effective stresses \( \left\langle {\sigma}_{ij}^{\mathrm{eff}}\right\rangle \) [6]:

$$ \left\langle {\sigma_{ij}}^{\mathrm{eff}}\right\rangle =\left\langle {\sigma}_{ij}^{\mathrm{full}}\right\rangle +{\alpha}_{ij}\left\langle p\right\rangle . $$
(1)

In formula (1), the pressure 〈p〉of a liquid is a positive quantity at compression. The angular brackets mean averaging over a volume, for example,

$$ \left\langle {\sigma_{ij}}^{\mathrm{full}}\right\rangle =\frac{1}{V}\underset{V}{\int }{\sigma}_{ij}(x) dV. $$
(2)

The effective stresses (1) are connected with macroscopical strains by governing relations. At a zero pressure, the effective stresses, according to formula (2), are the averaged full stresses.

For isotropic rocks, α is a scalar factor varying from 0 to 1, depending on ground properties (porosity, pore form, and the Poisson ratio of the solid phase of ground) and the pressure applied. For the first time, the factor α appeared already in work [7] in 1941, but up to now, there is no a settled term for it as yet. In the literature, it is named “Biot’s parameter,” “Biot’s coefficient,” “Biot–Willis coefficient,” “coefficient α ,” “pore pressure transfer coefficient,” and “effective stress coefficient.” Later [8,9,10], a formula was offered for calculating the isotropic pore pressure transfer coefficient α in terms of compressibility βs of the matrix material and the effective compressibility βeff of a porous material (or in terms of the coefficient Ks of volumetric expansion of the matrix material and the effective coefficient Keff of volumetric expansion):

$$ \alpha =1-{\beta}_s/{\beta}^{\mathrm{eff}}=1-{K}^{\mathrm{eff}}/{K}_s. $$
(3)

A rigorous mathematical deduction of formula (3) for α is given in [11, 12].

From formula (3), it is seen that Biot’s coefficient α is close to unity if the effective compressibility of a rock strongly exceeds that of the solid matrix material. On the contrary, α ≈ 0ifβeff ≈ βs. Such a situation can take place in low-porosity materials. The value α is strongly affected by pore form, which determines the contact area between the liquid and solid components of ground [12]. The more the pore form differs from the round one and the more tortuous is the pore space, the greater is the contact area between the solid and liquid phases and, hence, the greater is the area of the rock skeleton surface on which the pore pressure operates, i.e. , the greater the coefficient α.

Many researchers offer experimental ways for determining the effective stress coefficient α (in the case of isotropic materials) on the basis of static [13,14,15,16] or dynamic [16,17,18,19] experiments on rock samples. All these ways use relation (3) and are based on calculating the compressibility of matrix material and the effective compressibility. The static methods suggest three-axial compression tests on ground samples in high-pressure installations allowing one to independently create an external hydrostatic pressure on a rock sample enclosed in a shell and the pore pressure inside the sample. The dynamic way to determine α includes the measurement of speeds of longitudinal and transverse waves in rock samples and in the solid ground material, from which (with account of the effective density and density of the matrix material) Keff and Ks are calculated by the known formulas of elasticity theory. In other words, laboratory experiments for determining Biot’s coefficient α are rather labor-consuming.

For anisotropic materials, a formula for calculating the tensor αij in terms of the effective elastic moduli Cijkl and components \( {S}_{mnpq}^s \) of the compliance tensor of matrix material are deduced in [20], namely,

$$ {\alpha}_{ij}={\delta}_{ij}-{C}_{ij kl}{S}_{klmm}^s. $$

In [21], Biot’s tensor parameters are deduced separately in pores and cracks in so-called materials of “double porosity.” However, a practical determination of Biot’s tensor parameter has been offered in the literature only for special cases of structural anisotropy of rocks (for example, orthotropy and transverse isotropy) [20,21,22,23], for which the components Cijkl and \( {S}_{mnpq}^s \) have been found experimentally.

An alternative is the application of a calculation method which allows one to determine Biot’s tensor parameter αij in the case of general anisotropy of a porous natural composite, whose matrix can be nonuniform.

In the present work, the calculation technique for determining Biot’s tensor parameter αij is presented by the example of dolomite and volcanic rocks (hyaloclastites), and the elastic moduli for these types of rocks are calculated and compared with experimental data.

1. Calculation of the Effective Elastic Moduli and Biot’s Tensor Parameter by the Asymptotic Averaging Method

The averaging method to determine the effective elastic moduli and the pore pressure transfer tensor (parameter Biot’s) leads to the solution of local problems in the representative volume of the material [3,4,5]. For its application, the structure of the pore and the elastic properties of matrix components have to be known. The pore structure and the mineral composition of ground are investigated microscopically on thin sections, and, to specify the mineral composition, the X-ray diffractometry is employed. The elastic properties of minerals can be found in the literature.

1.1. The local boundary-value problem for determining the elastic moduli

The local boundary-value problem for determination of the elasticity moduli [5] following from the averaging method agrees with the general definition of effective moduli, well known in the mechanics of composites [2].

To find the effective elastic moduli of the porous medium in its representative volume VRVE , it is necessary to solve a problem with a special boundary condition in the form of a linear function of coordinates on the external border ΣRVE of VRVE and a zero pressure p on the border Σint of pores and on ΣRVE [5]:

$$ {\displaystyle \begin{array}{l}{\left[{C}_{ijkl}\left(\mathrm{x}\right){u}_{k,l}^1\left(\mathrm{x}\right)\right]}_{,j}=0,\mathrm{x}\in {V}_{\mathrm{RVE}},\\ {}\kern2em {u}_k^1={\varepsilon}_{kq}^0{x}_q,\mathrm{x}\in \sum {}_{\mathrm{RVE}},\\ {}{C}_{ijkl}\left(\mathrm{x}\right){u}_{k,l}^1\left(\mathrm{x}\right){n}_j=0,\mathrm{x}\in \sum {}_{\mathrm{int}}.\end{array}} $$
(4)

Here, Cijkl (x) are the elastic moduli dependent on coordinates x; \( {u}_k^1 \) are displacements (the superscript numbers the local boundary-problems; \( {\varepsilon}_{kq}^0 \) are constant strains; nj are components of the normal to ΣRVE or Σint .

The numerical solution of problem (4) by the finite-element method does not cause difficulties if the 3D geometrical structure of the material is known. However, a vague arises if there are only 2D images of some number of microsections. Here, two approaches were employed. First, using a 2D digitalized structure of inhomogeneities of the material and the pore form, a 2D problem (4) in the case of plane strain state, schematically shown on Fig. 1a, was considered. This allowed us to calculate the elastic moduli \( {C}_{\alpha \alpha \alpha \alpha}^{\mathrm{eff}},{C}_{\beta \beta \alpha \alpha}^{\mathrm{eff}} \) and \( {C}_{\alpha \beta \alpha \beta}^{\mathrm{eff}},\alpha, \beta =1,2,\alpha \ne \beta \), in the image plane of material structure by the formulas

Fig. 1.
figure 1

Boundary conditions of the local boundary-value problem on determination of the effective elastic moduli of isotropic (а) and anisotropic (b) samples.

Full size image
$$ {C}_{\alpha \alpha \alpha \alpha}^{\mathrm{eff}}=\frac{\left\langle {\sigma}_{\alpha \alpha}\right\rangle }{\varepsilon_{\alpha \alpha}^0},{C}_{\beta \beta \alpha \alpha}^{\mathrm{eff}}=\frac{\left\langle {\sigma}_{\beta \beta}\right\rangle }{\varepsilon_{\alpha \alpha}^0},{C}_{\alpha \beta \alpha \beta}^{\mathrm{eff}}=\frac{\left\langle {\sigma}_{\alpha \beta}\right\rangle }{\varepsilon_{\alpha \beta}^0}. $$

For convenience, the integral in the expression of σαα (see (2)) was transformed to an integral along the border with the help of Gauss–Ostrogradski formula.

Further, for a material, a priori known as isotropic, the elastic modulus Eeff and Poisson ratio νeff were calculated (for simplicity, the superscript “eff” was omitted:

$$ {C}_{\alpha \alpha \alpha \alpha}=\uplambda +2\mu, {C}_{\beta \beta \alpha \alpha}=\lambda, v=\frac{\lambda }{2\left(\lambda +\mu \right)},E=2\mu \left(1+v\right). $$

Here, λ and μ are the Lamé moduli.

Second, the local problem can be solved in the case of plane stress state (see Fig. 1b). Here, the upper and lower borders of the model can deform freely. Young’s modulus in the tension direction of sample is calculated as

$$ {E}_{\alpha}^{\mathrm{eff}}=\frac{1}{\varepsilon_{\alpha \alpha}^0{l}_{\beta }}\underset{l\beta}{\int }{\sigma}_{\alpha \alpha}d{l}_{\beta }. $$

The use of the two approaches allows one to compare results, and, at their good enough agreement, to conclude that calculation results are reliable.

For anisotropic samples, numerical experiments were carried out only in the case of plane stress state, i.e., the problem shown on Fig. 1b was solved. Such numerical experiments allow one to investigate Young’s modulus as a function of orientation of extended pores.

1.2. Local boundary-values problem for determination of Biot’s tensor parameter

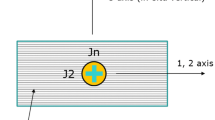
To determine components αijof the pore pressure transfer tensor in the representative volume VRVE , a boundary-value problem was formulated, where the boundary ΣRVE of the representative volume is fixed rigidly and a constant pressure p0 of liquid is given on the pore boundary Σint (Fig. 2) [5]:

Fig. 2.
figure 2

Boundary conditions of the local boundary-value problem on determination of components of the pore pressure transfer tensor.

Full size image
$$ {\displaystyle \begin{array}{l}\kern1em {\left[{C}_{ijkl}\left(\mathrm{x}\right){u}_{k,l}^2\right]}_{,j}=0,\mathrm{x}\in {V}_{\mathrm{RVE}},\\ {}{C}_{ijkl}\left(\mathrm{x}\right){u}_{k,l}^2{n}_j=-{p}_0{n}_i\left(\mathrm{x}\right),\mathrm{x}\in {\sum}_{\mathrm{int}},\\ {}\kern3em {u}_k^2=0,\mathrm{x}\in \sum {}_{\mathrm{RVE}}.\end{array}} $$
(5)

Problem (5) was solved in the case of plane strain state, and the components of Biot’s parameter were calculated as

$$ {\alpha}_{11}=\frac{1}{p_0{l}_2}\underset{l_2}{\int }{\sigma}_{11}d{l}_2,{\alpha}_{22}=\frac{1}{p_0{l}_1}\underset{l_1}{\int }{\sigma}_{22}d{l}_1. $$

It this case [5],

$$ {\alpha}_{ij}=\frac{\left\langle {C}_{ij kl}{u}_{k,l}^2\right\rangle }{p_0}. $$

2. Analysis of the Effective Properties of Soils Determined Experimentally and by Numerical Methods

2.1. Analysis of the effective properties of dolomite

A comparison of values of the effective elastic moduli found experimentally and by numerical methods and the research of elastic moduli and Biot’s tensor as functions of porosity and pore orientation were carried out by the example of a porous one-component material — pure dolomite (> 95% CaMg(CO3)2 — according to the data of X-ray diffractometry). The dolomite samples were selected in the territory of the Southeast part of Moscow from wells at an interval of depth from 15 to 38 m. According to the microscopic investigations of microsections, dolomite has structures from micro- to fine-crystalline ones. The bulk of dolomite consists of its rhombohedral grains. The texture of dolomite is porous. The pores are distributed nonuniformly; sometimes they are accumulated in strips, which makes dolomite anisotropic.

Experimentally investigated were 18 dolomite samples in the form of cube with 2.5-cm edges. For each sample, its density ρ and the density of its solid phase, ρs , were determined. The porosity n was calculated by the formula n = ((ρs − ρ)/ρs) ⋅ 100%. The elastic properties of the samples were determined by the technique of ultrasonic raying. From the measured values of speeds of longitudinal, Vp and transverse, Vs , waves, Young’s modulus Ed and the Poisson ratio ν were calculated:

$$ E=\frac{\rho {V}_s^2\left(3{V}_p^2-4{V}_s^2\right)}{V_p^2-{V}_s^2},v=\frac{0,5\left({V}_p^2-2{V}_s^2\right)}{V_p^2-{V}_s^2}. $$

On Fig. 3, Young’s modulus of dolomite Ed as a function of porosity n found in experiments is shown. As is seen, this relation is linear in the given range of porosities (from 13 to 37%). However, as calculations of the effective elastic moduli by the numerical method suggested showed, this linear relation cannot be extrapolated to lower values of porosity.

Fig. 3.
figure 3

Experimental elastic modulus Ed of dolomite vs. porosity n and the linear trend line (---).

Full size image

To create models for calculations, the porous structure of dolomite was digitalized on the photos of microsections manually in the AutoCAD program (student’s version). An example of the photo of a dolomite microsection and of its model created as a result of digitalization is shown on Fig. 4. The very fine pores that could not be digitalized, were taken into account in calculations in the properties of matrix material of the model. For this purpose, in the STIMAN program [24], the values of porosity were found by the model nmod and from the photo of a small section nsect , and then on the porosity nm of the solid matrix was calculated as

Fig. 4.
figure 4

Photograph of a microsection of dolomite (а) and its modeling image (b) (the black color indicates pores and the white — the solid matrix).

Full size image
$$ {n}_m=\frac{V_{\mathrm{por}\ \mathrm{m}}}{V_{\mathrm{m}}}\cdot 100\%=\frac{n_{\mathrm{sect}}-{n}_{\mathrm{m}\mathrm{od}}}{\gamma }. $$

where Vpor m is the volume of pores in the matrix; Vm is the volume of matrix material; γ is the fraction of matrix material in the model. The quantity nm takes into account the fine pores which had not been digitalized, but were actually present in the matrix material. According to calculations, it turned out that nm ≈ 3% for all the samples investigated. Thus, the matrix material will be dolomite with a porosity of 3%.

Properties of the matrix material for calculations in the finite-element program were taken from [25,26,27] (as also for dolomite with a 3% porosity): Ed = 90 GPa and ν = 0.33.

Calculations were carried out in the finite-element program. Altogether, 18 dolomite models with a porosity from 7 to 35% were calculated. For isotropic samples (see Fig. 4), Young’s modulus, the Poisson ratio, and the pore pressure transfer coefficient (Biot’s coefficient) were obtained. For anisotropic samples, Young’s modulus and pore pressure transfer coefficients in two perpendicular directions were deter mined.

Calculations showed that Young’s modulus of isotropic dolomite samples in plane strain and plane stress states differed (at the same porosity) by 2-3% for samples with a low porosity (7-15%) and by 7-10% — for highly porous (20-25%) samples. A sufficiently good agreement for Young’s modulus obtained using the two approaches described earlier is a necessary condition of the reliability of calculation results.

On Fig. 5, Young’s modulus as a function of porosity, constructed from the results of calculations by the averaging method for isotropic samples, for experimental data ultrasonic raying, and from the experimental results for the elastic properties of pure dolomite with a very low porosity (0-2%) described in [27], is illustrated. It is seen that the calculated, experimental, and literature data agree well — all points lay on one curve. This confirms the reliability of the calculation technique considered. The point corresponding to the given properties of matrix material of dolomite model also lays on this curve. Thus, during experiments and calculations, it was possible to found the relation for the elastic modulus of pure dolomite as a function of porosity for a wide range of porosities (from 0 to 38%) (see Fig. 5). It turned out that this relation was not linear, which was seen only from experimental data. The relation between Young’s modulus and porosity was almost linear at high porosities (> 15%), but its graph gradually steepened when the porosity decreased from 13-15 to 0%.

Fig. 5.
figure 5

The elastic modulus Ed of pure dolomite vs. porosity n : ● -— experimental data; ▲ — data from [27]; ■ — calculations by the averaging method; ♦ — data for the matrix of model; (---) —polynomial trend line according to all available information.

Full size image

Let us consider Biot’s coefficient. On Fig. 6, the relation for the pore pressure transfer coefficient (Biot’s coefficient) a for isotropic dolomite samples as a function of porosity is shown. The effective stress coefficient naturally grows with porosity. At low porosities, the graph is steeper, but with increase in porosity, it flattens out.

Fig. 6.
figure 6

Pore pressure transfer coefficient (Biot’s coefficient) α of dolomite vs. porosity n ; (---) —polynomial trend line.

Full size image

The calculated Poisson ratio also agreed with the experimental one. From the results of calculations and experiments, it was revealed that the higher the porosity, the smaller the Poisson ratio, other things being equal. For example, an increase in porosity from 8.8 to 25%, in different dolomite samples, reduced the Poisson ratio from 0.31 to 0.23.

The use of calculation technique allows one to investigate the elastic modulus and Biot’s parameter in relation to

the orientation extended pores. The dolomite sample on Fig. 7a contains a chain of pores extended in the horizontal direction, but in the dolomite sample on Fig. 7b, pores are oriented mainly vertically. Calculation results for the anisotropic materials are shown in Tab. 1, where the following designations are used: E1 is Young’s modulus, and α11 is the Biot’s coefficient in direction 1 (horizontally), and E2 and α22 are the corresponding quantities in direction 2 (vertically). As is seen from data of Table 1, Young’s modulus along the elongation direction of pores is higher, but the pore pressure transfer coefficient, on the contrary, is lower than across the pore orientation.

Fig. 7.
figure 7

Modeling images of anisotropic dolomite samples with pores oriented horizontally (а) and mainly vertically (b). The black color indicates pores and the white — the solid matrix.

Full size image
Table 1. The Elastic Modulus E and Biot’s Parameter α vs. the Orientation of Extended Pores
Full size table

2.2. Analysis of the effective properties of hyaloclastites

Let us consider natural composites having an inhomogeneous matrix. As an example of such a material, the volcanic rocks — hyaloclastites from the southern and southwest areas of Iceland can serve, whose structure includes the volcanic glass of basalt structure — palagonite, smectite, pyroxenes, and plagioclases. The specificity of these materials is that, owing to the features of their origin, hyaloclastites can have pores of very different form — round and angular (Fig. 8). By the example of such geomaterials, it is possible to investig ate the influence of pore form on their effective properties.

Fig. 8.
figure 8

Photographs of microsections and modelling images of the 1-st type hyaloclastite with angular (а) and round (b) pores. The white color indicates pores.

Full size image

According to the degree of palagonization, hyaloclastite samples were divided into two types: 1) slightly modified (with a contact and film-type cement) (see Fig. 8) and 2) greatly modified (with a film-pore type of cement) (Fig. 9) ones. For hyaloclastite samples of both types, the effective elastic properties and pore pressure transfer tensor (Biot’s parameter) were calculated by the averaging method in the finite-element program. The properties of the minerals and rocks composing hyaloclastites used in calculations were specified according to data given in [28, 29], and they are given in Tab. 2. As an example, the calculation results for the samples illustrated on Figs. 8 and 9 are given in Tab. 3.

Fig. 9.
figure 9

Photograph of a microsection and the modeling image of a sample of 2-nd type hyaloclastite. The white color indicates pores.

Full size image
Table 2. The Elastic Properties of the Minerals and Rocks Composing Hyaloclastites and Used in Calculations (Fig. 8 and 9)
Full size table
Table 3. The Effective Properties of Hyaloclastites Calculated by the Averaging Method
Full size table

On Fig. 8, the photographs of cuts of hyaloclastite samples with pores of different form — extended angular (Fig. 8a) and round (Fig. 8b), are presented. By the example of these samples, let us analyze the pore form-dependence of Biot’s parameter. In works [3,4,5], it is shown, that, at the same porosity, the effective stress coefficient in samples with round pores is much smaller than in the case with angular extended ones. This is explained by fact that the contact area of pores and the solid phase for round pores is smaller than for extended ones. As is seen from Tab. 3, for hyaloclastite samples with round (see Fig. 8b) and angular (see Fig. 8a) pores, the pore pressure transfer coefficients are equal (α = 0.67), though the porosity of the first sample is 33%, but only 15% for the second one. It is known [3,4,5] that the pore pressure transfer coefficient is the greater the higher the porosity. But in this case, the influence of porosity on α is compensated by the influence of pore form.

The investigation of the effective elastic properties of 10 hyaloclastite samples of the 1st type by calculation showed that, at the same porosity, Young’s modulus of samples with round pores was by about 12-17% higher than with angular pores (in the 10-40% range of porosity).

As is seen from the data in Tab. 3, the smallest pore pressure transfer coefficient and the highest Young’s modulus showed sample 3 (see Fig. 9), having a low porosity because pores were filled with palagonite to a great degree. Samples 1 and 2 (see Fig. 8b, a) had close values of elastic modulus, though their porosity differed more than two times. Here, the influence of pore form on Young’s modulus had shown up: for samples with a higher porosity, the pores were round.

Conclusions

The averaging method gives the general way for calculating Biot’s tensor parameter of porous composites, including the case of general anisotropy, when the matrix is nonuniform. Knowing the true pore pressure transfer tensor is necessary to correctly determine the effective stresses.

As objects of application, two types of materials — dolomite and hyaloclastites — were chosen in this work. It is shown that the effective stress coefficient strongly varies depending on the porosity and the structure of pore space.

Calculation results for the elastic moduli of dolomite agreed with experimental data, which confirmed the possibility of using averaging method to determine the effective elastic properties of soils by using digitalized two-dimensional photographs of microsections. Young’s modulus of dolomite calculated in the cases of plane strain and plane stress states turned out to be close (at identical values of porosities), which also pointed to the reliability of calculation results.

Besides, it is shown that the calculation technique used allows one to rather easily study the influence of porosity and pore form and orientation on the elastic modulus and Biot’s parameter. With increase in porosity, the elastic modulus decreased, but Biot’s parameter increased. At the same porosity, for samples with round pores, Young’s modulus was higher, but the pore pressure transfer coefficient was smaller than that in the case of angular pores with a complex branched form. For anisotropic samples, Biot’s parameter in the pore extension direction was smaller than across this direction (contrary the elastic modulus).