Quasi-isotropic Biot’s Tensor for Anisotropic Porous Rocks: Experiments and Micromechanical Modelling

Abstract

Several experimental studies, carried out on anisotropic rocks, have evidenced that even though strains, due to isotropic loading and/or internal fluid pressure, are strongly anisotropic, the resulting Biot’s tensor is almost isotropic. Those results were found on two different rocks: a clay rock (France—Bure argillite) and a sandstone from the Vosges region (France). Such (a priori) surprising results led us to develop micromechanical modelling in which anisotropy comes either from an anisotropic solid matrix (and isotropic pore space) or from an anisotropic pore space (and isotropic solid matrix). The obtained results have shown that for both cases the Biot’s tensor is virtually isotropic or presents a very weak anisotropy. This unambiguously supports the fact that a strongly anisotropic porous material is compatible with experimental measurements of isotropic (or quasi isotropic) Biot’s tensor.

1 Introduction

Poromechanical behavior of rocks, which accounts for couplings between fluid pressure(s) and material deformation, is crucial to be identified in many practical situations such as petroleum engineering and radioactive waste storage fields. The Biot’s poroelastic theory (Biot 1955) is usually recognized as the relevant theoretical approach for describing these poromechanical couplings. The latter is a generalization of Terzaghi’s theory to the case of a compressible solid matrix. The concept of elastic effective stress, initially introduced by Terzaghi, is then generalized. The Biot’s coefficient is introduced to calculate effective stresses for isotropic materials. For non-isotropic materials, a Biot’s second-rank tensor must be used, which makes tricky the experimental measurements of its components. For example, a simple transverse isotropic porous material needs eight poromechanical properties to be identified (Cheng 1997). As a consequence, there is a lack of laboratory measurements of the latter. One can nevertheless mention the comprehensive work of Wong (2017) who gathered many results on cracked Berea sandstone. The results are diverse as the anisotropy induced by cracks may sometimes lead to significant Biot’s components anisotropy or not. Other results on shales can also be found in Suarez-Rivera and Fjær (2013) but they are very disperse and strongly dependent on the stress levels and on the methodology used to measure the Biot’s components.

The present study mainly focuses on this particular point for two isotropic transverse materials, such as the COx argillite and a Vosges sandstone. As it will be detailed further, this case involves two independent components to be identified $b_1=b_2=b$ and $b_3$ according to the material structural axes.

This paper is organized into two parts: the first part sums up experimental measurements, carried out in the LaMCube Laboratory on argillite and sandstone, for which (quasi)-identical values of b and $b_3$ were obtained. This important result was found despite a strong anisotropic effect of the internal pore pressure on the material strains. A theoretical approach has been derived to assess this a priori counterintuitive result. The latter constitutes the second part of the present study. It relies on microporomechanic approaches (Dormieux et al. 2006) applied here in the context of poroelasticity. This methodology allows to relate the tensorial Biot’s coefficient to the material anisotropy. This modeling unambiguously shows that, despite a strong modeled anisotropy, the Biot’s components can virtually be identical.

2 Experimental Part

2.1 Materials Used

In this part are presented typical results obtained in a clay rock (Bure argillite) and in a high-porosity sandstone from the Vosges region in France. The argillite samples were originally drilled from the Callovo-Oxfordian stratum of the Meuse–Haute Marne (MHM) site in France, by URL of the French organization Andra. This argillite is mainly composed of a clay matrix, quartz and carbonate. The average proportions of these components are approximately $45\pm 7\%$ clay matrix, $23\pm 4\%$ quartz, $27\pm 9\%$ carbonate (calcite) and 5$\%$ feldspars, pyrite, and iron oxides (Song et al. 2015). However, the exact mineralogical composition of argillite varies significantly with depth. The clay matrix includes approximately 40$\%$ illite, 30$\%$ kaolinite, 5$\%$ chlorite and 25$\%$ swelling minerals (such as interstratified and smectite). Such a material has a swelling capacity that can modify its pore structure during the dehydration and/or hydration processes, which leads to porosity variations depending on its water content. These variations in porosity have a significant effect on the poroelastic properties of argillite during a hydro-mechanical loading process (Yang et al. 2012).

• Argillite has long been identified as a transverse isotropic material (Mohajerani et al. 2011). Axes 1 and 2 will characterize the plan of isotropy, which is related to the plan of horizontal layers at great depth in the Bure site. The vertical axis is, therefore, the revolution axis 3. On a practical point of view the ratio between Young’s moduli $E_1(=E_2)/E_3$ is around 2, which is already a pronounced anisotropy. The material porosity is often measured between 15 and 18$\%$ whereas its water permeability is generally less that $10^{-20}$ m$^2$. This low value makes it difficult to perform poromechanical experiments with water as the porous fluid since a long time is necessary, between each loading step, for the fluid pressure (or the strain values) to be stable. This also requires the use of small samples to shorten the experimental time. Both gas and water have been used to measure some poromechanical properties of the argillite but, in the results presented throughout this study, only experiments conducted with water are analyzed. The interested reader may find the results obtained with gas in Yuan et al. (2018) that give the same conclusions as with water.

• The sandstone used in the present study was obtained from a depleted gas reservoir in Vosges Mountain in the east of France (Hu et al. 2018). The initial porosity measured with distilled water is around 19.4$\%$. The microstructure of this sandstone was observed with X-ray tomography. Several horizontal sedimentary bands were detected from the CT scanning image (see Fig. 2). This structure leads to a slight anisotropy as it will be seen in the following. The material gas permeability is as high as 10$^{-12}$ to 10$^{-13}$ m$^2$. This makes it easy to perform poromechanical experiments with water or with gas as the pore fluid. In the results presented hereafter for the sandstone, all the experiments were conducted with gas.

Fig. 1

Schematic representation of the argillite sample with its bedding plane and equipped with crossed strain gages

Fig. 2

Microscopic picture and scheme of sandstone sample equipped with gages

2.2 Experimental Methods and Procedure for Argillite

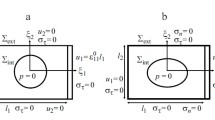
As mentioned before, the COx argillite from Bure is a transverse isotropic material. As shown in Fig. 1, the isotropic plane is the bedding plane containing the structural axes 1 and 2, and axis 3 is the in situ vertical axis. The samples used for the poromechanical tests were obtained from a ‘$T_1$ cell’ which is 80-mm-diameter, 250-mm-long cylindrical core. These cylinders are often cored in the horizontal direction, i.e. with a horizontal coring axis (axis 1 or 2). It is thus very difficult to accurately identify axis 3 (see Fig. 2) as the bedding plane is not visible at that scale. Cylindrical samples 20 mm in diameter and 40 mm in height were cored from ‘$T_1$ cell’ for the tests. These sample dimensions satisfy the standard requirement of the usual ratio (length-to-diameter ratio = 2), thus avoiding end effects and reducing the time needed to complete the poromechanical tests. Each sample was polished and verified, to ensure that it had parallel end surfaces within a tolerance of less than 0.05 mm. Four strain gauges were glued onto the surface of each sample : two longitudinal (1 or 2 axis), and two transverse (n-axis) gauges were used, as shown in Fig. 1. The strain values were measured with a Labview system having an accuracy of $\pm 10^{-6}$ m/m.

Within the framework of Biot’s theory, the transverse isotropic poroelastic behavior of the tested material can be expressed with respect to its material axis using the following relation:

$$\begin{aligned} \left( \begin{array}{c} \varepsilon _{11}\\ \varepsilon _{22}\\ \varepsilon _{33}\\ \gamma _{12}\\ \gamma _{13}\\ \gamma _{23} \end{array}\right) =\left( \begin{array}{cccccc} \frac{1}{E_1}&{} -\frac{\nu }{E_1}&{} -\frac{\nu '}{E_1}&{} 0 &{}0 &{}0\\ -\frac{\nu }{E_1}&{} \frac{1}{E_1}&{}-\frac{\nu '}{E_1}&{} 0 &{}0 &{}0\\ -\frac{\nu '}{E_1}&{} -\frac{\nu '}{E_1}&{}\frac{1}{E_3}&{} 0 &{}0 &{}0\\ 0 &{}0 &{}0 &{}\frac{2(1+\nu )}{E_1} &{}0 &{}0\\ 0 &{}0 &{}0 &{} 0 &{}\frac{1}{G_{13}} &{}0\\ 0 &{}0 &{}0 &{} 0 &{}0 &{}\frac{1}{G_{13}} \end{array}\right) \left( \begin{array}{c} \sigma _{11}+bp\\ \sigma _{22}+bp\\ \sigma _{33}+b_3p\\ \sigma _{12}\\ \sigma _{13}\\ \sigma _{23} \end{array}\right) , \end{aligned}$$

(1)

where tensile stresses are positive, and b, $b_3$ are the coefficients accounting for the Biot’s tensor in the transverse isotropic case. A convenient approach to the identification of these components relies on the application of a hydrostatic loading $P_c$ and/or a pore pressure p. One interesting case arises when $b=b_3$. When this specific case is verified, the following expressions for the three strain terms can be derived:

$$\begin{aligned} \begin{array}{l} \varepsilon _{11}=\varepsilon _{11}(P_c)(1-\alpha b)\\ \varepsilon _{22}=\varepsilon _{22}(P_c)(1-\alpha b)\\ \varepsilon _{33}=\varepsilon _{33}(P_c)(1-\alpha b)\\ \gamma _{ij}=0 \end{array}, \end{aligned}$$

(2)

where $\alpha =p/P_c$, and

$$\begin{aligned} \varepsilon _{11}(P_c)=\varepsilon _{22}(P_c)=\dfrac{-P_c}{E_1}(1-(\nu +\nu ')) ;\quad \varepsilon _{33}(P_c)=-P_c\left( \dfrac{1}{E_3}-\dfrac{2\nu '}{E_1}\right) . \end{aligned}$$

(3)

A gauge $J_n$, glued in any direction ${\varvec{n}}$, will give $\varepsilon _{nn}={\varvec{n}}\cdot {\varvec{\varepsilon }}\cdot {\varvec{n}}$. This yields (${\varvec{n}}=n_i\,{\varvec{e}}_i$):

$$\begin{aligned} \varepsilon _{nn}=(1-\alpha b)\left( n_1^2\varepsilon _{11}(P_c)+n_2^2\varepsilon _{22}(P_c)+n_3^2\varepsilon _{33}(P_c)\right) . \end{aligned}$$

(4)

Equation (4) shows that, whatever the gauge direction, the Biot’s coefficient b can be derived from two measurements, which may be combined: hydrostatic loading with a confining pressure $P_c$ and a change in pore pressure p. This is useful when the direction 3 is not accurately known as it is the case for Cox argillite samples. It can also be underlined that an “isotropic” Biot’s coefficient does not mean that a change in pore pressure would lead to isotropic strain state [see relations (2) and (3)].

Another modulus denoted by $H_i$ is sometimes used to analyze the different experiments. This modulus is related to a change in pore pressure p according to (no summation on i):

$$\begin{aligned} \varepsilon _{ii}(p)=\dfrac{p}{H_i}. \end{aligned}$$

(5)

While relation (1) is only relevant for poroelastic behavior, initial experiments on argillite have shown that, due to plastic strain effects and/or micro-cracking, its behavior is not reversible. The following method was thus used to identify Biot’s coefficient for a given value of $P_c$:

• Step 1 is a hydrostatic loading phase during which confining pressure is increased from $P_c^1$ to $P_c^2=P_c^1+\varDelta P_c$. Since this step is generally nonlinear and irreversible, unloading steps are needed to obtain elastic values of strain.

• Step 2 is a p loading phase, with confining pressure being increased up to $P_c^2$, following which an increase in pore pressure $\varDelta p$ is applied, with $\varDelta p = \varDelta P_c$. This loading is elastic since it is equivalent to hydrostatic pressure unloading. The strain values $\varepsilon _{22}(\varDelta p)$ and $\varepsilon _{nn}(\varDelta p)$ are measured after this process. The pore pressure p is then decreased down its initial value.

• Step 3 is a hydrostatic unloading phase, with confining pressure being reduced from $P_c^2$ to $P_c^2-\varDelta P_c=P_c^1$, allowing $\varepsilon _{22} (\varDelta P_c)$ and $\varepsilon _{nn}(\varDelta P_c)$ to be measured.

• Step 4 involves comparing $\varepsilon _{22}(\varDelta Pc)$ and $\varepsilon _{nn}(\varDelta P_c)$ with $\varepsilon _{22}(\varDelta p)$ and $\varepsilon _{nn}(\varDelta p)$, therefore, allowing Biot’s coefficient b to be identified.

When b is not equal to $b_3$, further tests, such as axial loading, must be carried out to produce new conditions allowing b and $b_3$ to be determined. This approach was not required in the present study since the first results confirmed that $b=b_3$.

2.3 Experimental Methods and Procedure for Sandstone

Contrary to argillite, the structural axis identification is easier for sandstone as the sedimentary layers are clearly visible (see Fig. 2). Two couples of crossed gages are diametrically glued on the cylindrical sample, which dimensions are 37 mm diameter and 70 mm height. They will allow to measure the axial strain $\varepsilon _a (=\varepsilon _{33})$ and the lateral strain $\varepsilon _l (=\varepsilon _{11}$ or $\varepsilon _{22}$). The measurement method used to obtain the strains due to $\varDelta P_c$ and $\varDelta p$ are the same than those previously described in Sect. 2.2.

2.4 Experimental Device

The device used is composed of a hydrostatic cell that allows both confining pressure and pore pressure to be controlled (see Fig. 3). This system is used either for water or gas injection. A Labview system is connected to this system to get the strain measurements and, more specifically, to follow the strain evolution when a long time is needed to assess their stability (see the case for argillite in the following).

Fig. 3

Scheme of the experimental device

2.5 Results for Argillite

Numerous tests have been performed on this material but the presentation of the whole series is not the purpose of this study. Hence, only typical and representative results are selected and given in Fig. 4. Four gages were glued on the sample as drawn in Fig. 1. These are crossed gages such as $J_2$ and $J_n$, and they are therefore located at the same point (or position); two crossed disposals were diametrically opposed: the (axial) average values of the two “$J_2$” are plotted in green, while the (transverse) average values of the two “$J_n$” are in black. A complete cycle of loading–unloading operations, described in Sect. 2.2, is represented in Fig. 4, which also gives the selected values of $P_c$ and p.

Fig. 4

Typical results for argillite

The total duration of this cycle is around 20 days. This long time comes from the low water permeability of argillite and is necessary to get a complete strain value stabilization. The difference between strains from A to B (or $A'$ to $B'$) and from D to E (or $E'$ to $D'$) is due to the $P_c$ loading or unloading (5–12–5 MPa) whereas $B-C$ ($B'-C'$) and $C-D$ ($C'-D'$) comes from the p loading or unloading (2–9–2 MPa). In the following, the writing (MN) will indicate the strain difference $\varepsilon (N)-\varepsilon (M)$. The strong material anisotropy is clearly visible as (AB) is almost twice higher than $(A'B')$, which is also confirmed by the comparison (DE) and $(D'E')$, or (BC) and $(B'C')$, etc. It is also interesting to underline that (AB) or $(A'B')$ and (ED) or $(E'D')$ are virtually the same. This simply means that the first $P_c$ loading step led to elastic strains. $(BC)=(DC)$ and $(B'C')=(D'C')$ were expected results as they are due to an increase in p, which was already assumed to lead to elastic strains (cf. Sect. 2.2). Another crucial information is given by the ratios: ((AB) or (ED))/((CB) or (CD)) and ($(A'B')$ or $(E'D')$)/($(C'B')$ or $(C'D')$) that are all virtually identical to 1. This unambiguously means that $b=b_3=1$ [see relation (2) in Sect. 2.2 when $\alpha =1$].

2.6 Results for Sandstone

The whole set of results obtained for five different samples are summed up in Table 1. Four samples were used at confining pressure of 5, 10, 20 and 30 MPa, respectively. The Biot’s coefficients were measured with the same methodology as for argillite. Then these samples were conducted up to the failure under increasing deviatoric stress (this is why the samples are not the same).

The last column 8, in italic letters, is related to the same 5th sample that was successively submitted to an increasing hydrostatic stress only (P_c = 5, 10, 20 and 30 MPa). The ‘b’ coefficient was therefore directly calculated by the ratio of volumetric strains $\varDelta \varepsilon _{v}(\varDelta p = \varDelta P_{c})/\varDelta\varepsilon_{v}(\varDelta P_{c})$. The second and third columns give the ratio of mean lateral strain over mean axial strain, respectively, for a decreasing confining pressure or an increasing pore gas pressure. Both indicate a slight material anisotropy (10–20$\%$), which can also be observed in columns 6 and 7. In columns 4 and 5, the ‘apparent’ Biot’s tensor components are calculated from the ratio $\varDelta \varepsilon _l^g/\varDelta \varepsilon _l^c$ (resp. $\varDelta \varepsilon _a^g/\varDelta \varepsilon _a^c$) for $b_1$ (resp. $b_3$). The term apparent is chosen here as these ratios are the real ‘$b_i$’ components only in the case where they are equal. As $b_1$ and $b_3$ are very close to each other, generally by a difference that is less than 5$\%$, it can be admitted that they are virtually identical. It can be finally observed that these $b_1$ and $b_3$ values are also very close to the ‘b’ values obtained on the same sample at different confining pressures. Once again, despite a (slight) material anisotropy, it is found that the Biot’s tensor is virtually composed of a unique component b.

Table 1 Initial anisotropic properties under hydrostatic stress and before failure test (except for the results in column 8 that are related to the same sample)

As a partial conclusion, two set of experimental results indicate that a (quasi)-isotropic Biot’s tensor, despite a more or less strong material anisotropy, can be obtained. This result can a priori be surprising, or non-logical, but it must be reminded here that this result does not mean that the pore pressure effect leads to isotropic strains. The next section raises the issue of this a priori surprising result from a theoretical point of view through a microporomechanics point of view (Dormieux et al. 2006).

3 Anisotropy of the Poromechanical Coupling: A Micromechanical Model

The purpose of this section is to propose a micromechanical model that supports the fact that a strong material anisotropy is compatible with a quasi-isotropic Biot tensor. The anisotropy of the poromechanical coupling will be examined through three indicators:

• Biot’s tensor ${\varvec{B}}$;

• the strain tensor ${\varvec{\varepsilon }}_1$ induced by a change of the confining pressure;

• the strain tensor ${\varvec{\varepsilon }}_2$ induced by a change of the pore pressure.

From a computational point of view, the starting point is the first state equation of poroelasticity in the form :

$$\begin{aligned} {\varvec{\sigma }}=\mathbb {C}^{dr}:{\varvec{\varepsilon }}-{\varvec{B}}p, \end{aligned}$$

(6)

which is the generalized formulation of (1). $\mathbb {C}^{dr}$ is the drained stiffness tensor of the porous material. For the unit change of pore (resp. confining) pressure, this yields:

$$\begin{aligned} {\varvec{\varepsilon }}_1=-{\mathbb {C}^{dr}}^{-1}:{\varvec{\delta }}\quad ;\quad {\varvec{\varepsilon }}_2={\mathbb {C}^{dr}}^{-1}:{\varvec{B}}. \end{aligned}$$

As regards the drained stiffness tensor, it is convenient to introduce the following anisotropy indicators:

$$\begin{aligned} \rho =\dfrac{C_{1111}^{dr}}{C_{3333}^{dr}}\quad ;\quad \chi =\dfrac{C_{1212}^{dr}}{C_{1313}^{dr}}. \end{aligned}$$

(7)

For a second rank tensor ${\varvec{T}}$ such as ${\varvec{B}}$, ${\varvec{\varepsilon }}^{(1)}$ and ${\varvec{\varepsilon }}^{(2)}$, the relevant anisotropy indicator is

$$\begin{aligned} r_{_{T}}=T_{11}/T_{33}. \end{aligned}$$

(8)

In the sequel, we propose to determine the drained stiffness tensor $\mathbb {C}^{dr}$ and Biot’s tensor ${\varvec{B}}$ of a theoretical porous material (acronym TPM) in the framework of an upscaling process. The scale at which the drained stiffness tensor and the Biot tensor are defined and can be measured is referred to as the macroscopic scale: it is the uppermost scale of the upscaling process. This way suggests two options that we shall consider successively:

• 1. The solid matrix itself is anisotropic. This option is considered in Sect. 3.1.

• 2. The porous material has an isotropic solid matrix and the anisotropy of $\mathbb {C}^{dr}$ and ${\varvec{B}}$ is the consequence of the anisotropy of the geometry of the pore space. This option is considered in Sect. 3.2

It is assumed in the sequel that the Mori–Tanaka scheme is appropriate for all forthcoming upscaling operations.

3.1 The Anisotropic Matrix

In this section, we shall consider a porous material having a transversely isotropic solid matrix (symmetry direction along ${\varvec{e}}_3$). We shall assume that the geometry of the pore space is isotropic, so that the porous material itself will be also transversely isotropic along ${\varvec{e}}_3$.

In fact, a transversely anisotropic matrix (symmetry axis along ${\varvec{e}}_3$) can a priori be defined by any appropriate choice of a set of the five constants $C^m_{1111}$, $C^m_{1122}$, $C^m_{1133}$, $C^m_{3333}$ and $C^m_{2323}$, chosen in such a way that the condition of definite positiveness of the elastic stiffness tensor $\mathbb {C}^m$ is satisfied. In this paper, a more physical approach is preferred, in which a micromechanical interpretation of the anisotropy of the matrix is provided.

We shall use the standard terminology of homogenization and introduce three levels of geometrical analysis, respectively, referred to as microscopic, mesoscopic and macroscopic, associated with increasing length scales: the lowest scale reveals the heterogeneity of the matrix. It will be termed the microscopic scale. At this scale, a representative elementary volume (rev) $\omega$ of matrix is regarded as an heterogeneous structure, comprising a solid subdomain and pores. In contrast, at the scale above, referred to as mesoscopic scale, this structure reduces to a material point which mechanical behavior is characterized by the matrix stiffness tensor $\mathbb {C}^m$. The latter can be derived by appropriate averaging techniques from the response of the rev ($\omega$) to a mechanical boundary value problem defined at the microscopic scale on $\omega$. In turn, the mesoscopic scale reveals the heterogeneity of the TPM. This means that a rev $\varOmega$ of the TPM at the mesoscopic scale is a heterogenous structure comprising an elastic solid domain (the matrix with elastic stiffness tensor $\mathbb {C}^m$) and a pore space filled by a pressurized fluid (pressure p). Eventually, the rev of the TPM reduces to a material point at the macroscopic scale. Again, the macroscopic state equation (6) can be derived by averaging techniques from the solution to a boundary value problem defined at the mesoscopic scale on $\varOmega$ by the macroscopic strain tensor ${\varvec{\varepsilon }}$ and the fluid pressure p (Dormieux et al. 2006). More precisely, the Hashin type boundary conditions consist in prescribing the displacement ${\varvec{\varepsilon }}\cdot {\varvec{z}}$ at any point ${\varvec{z}}$ on the boundary $\partial \varOmega$, while the pressure p is applied on the whole boundary of the mesoscopic pore space (see Fig. 5).

Fig. 5

Representative elementary volumes: at the mesoscopic scale (left), at the microscopic scale (right)

The first step consists in defining an anisotropic matrix characterized by a stiffness tensor $\mathbb {C}^m$, as the result of a micro $\rightarrow$ meso scale transition. Depending on assumptions on the pore space at the mesoscopic scale, we shall afterwards compute the macroscopic elastic stiffness ($\mathbb {C}^{dr}$) and the three indicators of the poromechanical coupling (${\varvec{B}}$, ${\varvec{\varepsilon }}_1$ and ${\varvec{\varepsilon }}_2$).

3.1.1 Definition of the Matrix

At the microscopic scale, a rev $\omega$ of matrix is made up of an isotropic linear elastic solid (elastic stiffness tensor $\mathbb {C}^s$) in which a set of homothetic spheroidal inclusions (same aspect ratio X) is embedded. The volume fraction of the microscopic inclusions in the rev $\omega$ is denoted by $\varphi$. The symmetry axis of the spheroids is along ${\varvec{e}}_3$.

As regards the numerical determination of $\mathbb {C}^m$, these inclusions will be interpreted as empty pores ($\mathbb {C}\rightarrow 0$). It should be emphasized that the role of this inclusionary phase is solely to provide an explanation to the anisotropy of the matrix behavior. Many other strategies could have been used alternatively for the same purpose including spheroidal rigid inclusions ($\mathbb {C}\rightarrow \infty$). Consequently, $\varphi$ may be interpreted as a microscopic occlusive porosity. As such, it will not be taken into account in the determination of the effective porosity that will only consider the mesoscopic pore space.

The homogenized elastic stiffness $\mathbb {C}^{m}$ of the matrix is determined by means of the Mori–Tanaka homogenization scheme that is dedicated to the particulate composite morphology:

$$\begin{aligned} \mathbb {C}^{m}=(1-\varphi )\mathbb {C}^s:\left( (1-\varphi )\mathbb {I}+\varphi \left( \mathbb {I}-\mathbb {P}^s(X):\mathbb {C}^s\right) ^{-1} \right) ^{-1}, \end{aligned}$$

(9)

where $\mathbb {P}^s(X)$ is the Hill tensor of a spheroid (aspect ratio X, symmetry axis along ${\varvec{e}}_3$) embedded in the elastic medium with stiffness $\mathbb {C}^s$ (see section “Appendix”). The fourth-rank identity tensor $\mathbb {I}$ is defined by

$$\begin{aligned} I_{ijkl}=\dfrac{1}{2}\left( \delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}\right) . \end{aligned}$$

The Young modulus $E^s$ of the isotropic solid phase is taken as reference unit ($E^s=1$). The Poisson coefficient is arbitrarily fixed: $\nu ^s=0.3$ and the matrix porosity is $\varphi =0.5$. Two numerical simulations, respectively, with an aspect ratio $X=5$ (prolate spheroids) and an aspect ratio $X=0.4$ (oblate spheroids) are performed. The set of elastic moduli derived from (9) are given in Table 2.

Table 2 Matrix moduli for pore aspect ratios $X=5$ and $X=0.4$

In the following, the subscripts 5 and 0.4 are used; hence, $\mathbb {C}^m_5$ and $\mathbb {C}^m_{0.4}$ are, respectively, associated with $X=5$ and $X=0.4$.

3.1.2 Macroscopic Poroelastic Behavior

The material determined at Sect. 3.1.1 from the micro$\rightarrow$meso transition is now the (anisotropic) solid phase at the mesoscopic scale (see Fig. 5). The next step is the meso$\rightarrow$macro transition. We again implement the Mori–Tanaka scheme. For the same value f of the mesoscopic porosity (numerical value $f=0.15$), two different isotropic geometries of the mesoscopic pore space are tested:

• (case a) The pore space is made up of spheres. In this case, the drained macroscopic stiffness tensor is

  $$\begin{aligned} \mathbb {C}^{dr}_a=(1-f)\mathbb {C}^m:\left( (1-f)\mathbb {I}+f\left( \mathbb {I}-\mathbb {P}^m_{sph}:\mathbb {C}^m\right) ^{-1} \right) ^{-1}, \end{aligned}$$

  where $\mathbb {P}^m_{sph}$ is the Hill tensor of a sphere embedded in the elastic medium with stiffness $\mathbb {C}^m$.

• (case b) The pore space is made up of a set of spheroidal pores (aspect ratio $X=3$), the distribution of the orientations of the symmetry axes being isotropic. The expression of the macroscopic drained stiffness tensor then reads:

  $$\begin{aligned} \mathbb {C}^{dr}_b=(1-f)\mathbb {C}^m:\left( (1-f)\mathbb {I}+f\overline{\left( \mathbb {I}-\mathbb {P}^m(\theta ,\phi ,X):\mathbb {C}^m\right) ^{-1}} \right) ^{-1}, \end{aligned}$$

  where $\mathbb {P}^m(\theta ,\phi ,X)$ is the Hill tensor of a spheroid embedded in the elastic medium with stiffness $\mathbb {C}^m$, having a symmetry axis along the radial vector ${\varvec{e}}_r(\theta ,\phi )$ in the system of spherical coordinates in which $\theta$ is the angle between ${\varvec{e}}_r$ and ${\varvec{e}}_3$) (see Sect. 1). $\overline{\mathbb {A}}$ is the averaging operator over the unit sphere applied on the fourth-rank tensor $\mathbb {A}$:

  $$\begin{aligned} \overline{\mathbb {A}}=\dfrac{1}{4\pi }\int _0^{2\pi }{\text {d}}\phi \left( \int _0^\pi \mathbb {A}(\theta ,\phi )\sin \theta \,{\text {d}}\theta \right) . \end{aligned}$$

In both cases, Biot’s tensor is given by the same relation:

$$\begin{aligned} {\varvec{B}}={\varvec{\delta }}:\left( \mathbb {I}-{\mathbb {C}^{m}}^{-1}:\mathbb {C}^{dr}\right) . \end{aligned}$$

3.1.3 Numerical Results

The set of the elastic moduli defining $\mathbb {C}^{dr}$ are given in Tables 3 and 6, respectively, for a microscopic pore aspect ratio $X=5$ and $X=0.4$. The anisotropy indicators are gathered in Tables 5 and 8.

• matrix elastic stiffness $\mathbb {C}^m_5$ (Tables 4, 5):

  It appears that the numerical results concerning cases a and b (spherical pores or isotropic distribution of spheroidal prolate pores) are very close. The anisotropy of Biot’s tensor is very weak (see. Table 4) while the anisotropy of the drained stiffness tensor is pronounced (see Table 3). The anisotropy of the characteristic strain tensors ${\varvec{\varepsilon }}_1$ and ${\varvec{\varepsilon }}_2$ are significant as well and similar (see Table 4).

• matrix elastic stiffness $\mathbb {C}^m_{0.4}$ (Table 6).

  The conclusions in the case $X=0.4$ are qualitatively identical to those formulated previously in the case $X=5$: strong elastic anisotropy and very weak anisotropy of Biot’s tensor. Interestingly, the anisotropy indicators are essentially inverted w.r.t. the previous case. It is, therefore, reasonable to hope that the similar conclusions drawn in the two considered cases are, in fact, general (Tables 7, 8).

Fig. 6

Anisotropy of the drained stiffness tensor. X is the aspect ratio of the microscopic porosity

Table 3 Drained stiffness moduli (microscopic aspect ratio $X=5$)

Table 4 Biot’s tensor and strain tensors ${\varvec{\varepsilon }}^{(1)}$ and ${\varvec{\varepsilon }}^{(2)}$ (microscopic aspect ratio $X=5$)

Table 5 Anisotropy scalar indicators (microscopic aspect ratio $X=5$)

Table 6 Drained stiffness moduli (microscopic aspect ratio $X=0.4$)

Table 7 Biot’s tensor and strain tensors ${\varvec{\varepsilon }}^{(1)}$ and ${\varvec{\varepsilon }}^{(2)}$ (microscopic aspect ratio $X=0.4$)

Table 8 Anisotropy scalar indicators (microscopic aspect ratio $X=0.4$)

For illustrative purposes, the case of an anisotropic matrix of the previous type (see Sect. 3.1.1) with spherical pores (same porosity $f=0.15$) is finally considered for the range of values of $X\in [0.4,5]$. The anisotropy indicators of the drained stiffness tensors thus generated are presented at Fig. 6. The corresponding anisotropy indicators of ${\varvec{\varepsilon }}^{(1)}$, ${\varvec{\varepsilon }}^{(1)}$ and ${\varvec{B}}$ are plotted against X at Fig. 7. The latter emphasizes that the Biot’s tensor is almost isotropic on the whole range of material anisotropy considered herein.

Fig. 7

Anisotropy indicators of ${\varvec{\varepsilon }}^{(1)}$, ${\varvec{\varepsilon }}^{(2)}$ and ${\varvec{B}}$. X is the aspect ratio of the microscopic porosity

3.2 The Anisotropic Pore Space

In the second morphological option, it is assumed that the solid matrix of the porous material is a linear elastic isotropic solid (isotropic elastic stiffness tensor $\mathbb {C}^m$). The macroscopic anisotropy is, therefore, due to the anisotropic shape of the pores. More precisely, we consider a pore space with volume fraction f made up of a set of homothetic spheroids (same symmetry axis along ${\varvec{e}}_3$ and same aspect ratio X). This second model is very simple in so far as it considers only two scales: the microscopic scale reveals the heterogeneity of the rev, which comprises a solid domain and a pore space, while the same material is homogenized at the macroscopic scale. The quantitative transition micro$\rightarrow$macro is again carried out with the help of the Mori–Tanaka scheme:

$$\begin{aligned} \mathbb {C}^{dr}=(1-f)\mathbb {C}^m:\left( (1-f)\mathbb {I}+f\left( \mathbb {I}-\mathbb {P}^m(X):\mathbb {C}^m\right) ^{-1} \right) ^{-1}, \end{aligned}$$

(10)

where $\mathbb {P}^m(X)$ is the Hill tensor of a spheroid (aspect ratio X, symmetry axis along ${\varvec{e}}_3$) embedded in the elastic medium with stiffness $\mathbb {C}^m$ (see “Appendix”).

As regards numerical simulations, the value of the porosity f is identical to the mesoscale porosity of the first model (see Sect. 3.1.2), that is, $f=0.15$. Figure 8 provides, through the anisotropy indicators $\rho$ and $\chi$ (see 7), an estimate of the anisotropy induced for a given pore aspect ratio.

Fig. 8

Anisotropy of the drained stiffness tensor. X is the aspect ratio of the mesoscopic porosity

Figure 9 presents the anisotropy indicators $r_{_1}$, $r_{_2}$ and $r_{_B}$, respectively, related to ${\varvec{\varepsilon }}^{(1)}$, ${\varvec{\varepsilon }}^{(2)}$ and ${\varvec{B}}$ (see 8). With this micromechanical model in which the anisotropy is induced by the geometry of the pore space, it appears that the strain ${\varvec{\varepsilon }}^{(2)}$ induced by a pore pressure change is the most sensitive anisotropy indicator. Again, Biot’s tensor exhibits the weakest anisotropy. Nevertheless, it is only slightly below the anisotropy of the strain ${\varvec{\varepsilon }}^{(1)}$ induced by a change in confining pressure. As opposed to the first model, ${\varvec{\varepsilon }}^{(1)}$ and ${\varvec{\varepsilon }}^{(2)}$ have very different sensitivities to the material anisotropy.

Fig. 9

Anisotropy indicators of ${\varvec{\varepsilon }}^{(1)}$, ${\varvec{\varepsilon }}^{(2)}$ and ${\varvec{B}}$. X is the aspect ratio of the mesoscopic porosity

4 Conclusion

This study, involving both experimental and theoretical considerations, was first motivated by poromechanical experiments intended for the measurements of Biot’s tensor components of transversely isotropic porous materials. As it is highlighted in the first part of this paper, a priori surprising results were found that showed an isotropic (or quasi-isotropic) Biot’s tensor. This result does not mean that the pore pressure effect is isotropic as the strains due to a pore pressure variation revealed to be anisotropic. It was, therefore, very tempting to involve a modelling based on a micromechanical model, able to take in a wide sweep various anisotropic scenario.

Hence, two main options were chosen: case 1—the solid matrix is transversely isotropic and the pore space is isotropic or case 2—the solid matrix is isotropic and the pore space is anisotropic, i.e. designed to obtain a transversely isotropic behavior of the skeleton. The strains calculated with those modellings, either for a confining pressure or for a pore pressure loading, were always indicative of a (sometime) strong anisotropic behavior. Conversely, for both cases, the Biot’s tensor always exhibited the weakest anisotropy. The anisotropy indicator for this tensor never exceeded $11\%$ in case 1 (and for some extreme case only). As a consequence, the Biot’s tensor is quasi isotropic. It is slightly different for case 2 but, in a large range of anisotropic pore space geometries, the Biot’s tensor can be seen as virtually isotropic.

On an experimental point of view, and taken into account the difficulties to measure the Biot’s coefficient, 10$\%$ variation (or errors) are very few and can be included into the experimental uncertainties. Hence, the obtained differences in the Biot’s tensor components are not significant for case 1, which in our opinion is likely to represent more in situ cases than the case 2.

To conclude, the micro-modelling calculations evidence that an isotropic Biot’s tensor is compatible with an anisotropic porous medium behavior.

Appendix: Hill Tensor of an Ellipsoid

Consider an ellipsoid defined by the equation:

$$\begin{aligned} {\varvec{z}}\cdot {\varvec{S}}\cdot {\varvec{z}}=1, \end{aligned}$$

where ${\varvec{S}}$ is a positive definite symmetric second-rank tensor. This ellipsoid is embedded in an infinite linear elastic medium with elastic stiffness tensor $\mathbb {C}$. Let ${\varvec{\xi }}$ denote some vector on the unit sphere: $|{\varvec{\xi }}|=1$. The associated acoustic tensor is ${\varvec{K}}={\varvec{\xi }}\cdot \mathbb {C}\cdot {\varvec{\xi }}$. The coefficient $P_{ijkl}$ of the Hill tensor reads:

$$\begin{aligned} P_{ijkl}=\dfrac{\sqrt{\mathrm{det}\,{\varvec{S}}}}{4\pi }\int _{|{\varvec{\xi }}|=1}\dfrac{\left( \xi _j\xi _k\left( K^{-1}({\varvec{\xi }})\right) _{i\ell }\right) _{(ij),(k\ell )}}{\left( {\varvec{\xi }}\cdot {\varvec{S}}\cdot {\varvec{\xi }}\right) ^{3/2}}\,{\text {d}}S_\xi . \end{aligned}$$

(11)

In the above expression, the integral is taken with respect to ${\varvec{\xi }}$ over the unit sphere. The subscript $(ij),(k\ell )$ means that the expression is symmetrized w.r.t. the subscripts i and j, and w.r.t. the subscripts k and $\ell$:

$$\begin{aligned} (A_{ijk\ell })_{(ij),(k\ell )}=\dfrac{1}{4}\left( A_{ijk\ell }+A_{jik\ell }+A_{ij\ell k}+A_{ji\ell k} \right) . \end{aligned}$$

In Sect. 3.1.2, the Hill tensor $\mathbb {P}^m(\theta ,\phi ,X)$ refers to a spheroid with aspect ratio X, and a symmetry axis along the radial unit vector ${\varvec{e}}_r(\theta ,\phi )$:

$$\begin{aligned} {\varvec{e}}_r(\theta ,\phi )=\sin \theta \left( \cos \phi {\varvec{e}}_1+\sin \phi {\varvec{e}}_2\right) +\cos \theta {\varvec{e}}_3. \end{aligned}$$

It is recalled that the matrix is transversely isotropic (symmetry axis along ${\varvec{e}}_3$). In the spherical basis $({\varvec{e}}_r,{\varvec{e}}_\theta ,{\varvec{e}}_\phi )$, the tensor ${\varvec{S}}(\theta ,\phi ,X)$ of this spheroid reads:

$$\begin{aligned} {\varvec{S}}={\varvec{e}}_\theta \otimes {\varvec{e}}_\theta +{\varvec{e}}_\phi \otimes {\varvec{e}}_\phi +X^2{\varvec{e}}_r\otimes {\varvec{e}}_r. \end{aligned}$$

The integration variables in (11) are the two angles x and y that define the unit vector ${\varvec{\xi }}$:

$$\begin{aligned} {\varvec{\xi }}=\sin x\left( \cos y\,{\varvec{e}}_1+\sin y\,{\varvec{e}}_2\right) +\cos x\,{\varvec{e}}_3, \end{aligned}$$

where ${\text {d}}S_\xi =\sin x\,{\text {d}}x{\text {d}}y$.