Introduction

At the present time, in investigating the stress-strain state (SSS) close to singular points (vertices of wedges, cones, cracks, spatial ribs, etc.), the asymptotic approach proposed in [1, 2] prevails. A local solution is sought in the form of expansion into series in terms of eigenforms with a power factor \( {r}^{\lambda_k} \), where r is the distance to the singular points and λ k is an eigenvalue [3,4,5,6,7,8]. Also, expansions into series in terms of arbitrary complete system of functions with power-logarithmic factors of the type r λ ln r [9, 10] and other representations of solution [11, 12] are used. The parameter r can be arbitrarily small. At a numerical construction of solution, for example, in studying the SSS in the vicinity of singular points by the finite-element method (see, for example, [13,14,15]), the mesh can be arbitrarily fine. The possibility of unlimitedly approaching a singular point means that its model in the methods used is a mathematical point (with no linear dimensions). The concept of SSS is not applicable to such a point, therefore, conditions which a solution have to satisfy are not given at this point. According to the postulates of continuum mechanics, point is the representative volume of the material of which the structural element investigated is made. Such a representative volume has a finite characteristic (linear) size and is the smallest body particle for which the concept of SSS has a meaning. The methods admitting an unlimited approach to a singular point allow one to construct a reliable solution only outside its small vicinity. Really, such a solution is not coordinated with the constraints set for the representative volume (singular point), as they are neglected in the statement of the problem. Besides, with approach to such a point at a distance commensurable with the characteristic size of the representative volume, the use of macroscopic physical equations becomes incorrect, because, at a lower structural level of a material, its behavior obeys different physical laws. From solutions constructed at a singular point and in its vicinity, in view of the constraints set at it [16, 17], it follows that the vicinity of the singular point outside which an asymptotic solution describes the SSS reliably has a radius of 5-10 characteristic sizes of the representative volume of the body.

The identification of a singular point with the representative volume of a body makes it possible to consider the constraints set at it. The formulation of such constraints is an independent problem. They are given by algebraic equalities whose number usually exceeds the number of conditions specified at an ordinary point. This makes the problem for a body containing a singular point nonclassical. Studying the constraints assigned by a singular point enables one to adequately pose a problem of the mechanics of deformable bodies with a singular point and to reveal the critical combinations of material and geometrical parameters. In the present work, the approach developed in [18, 19] is applied to studying constraints on the parameters of state at an internal singular point of plane and spatial compound structures. Internal singular points are characteristic, in particular, of composite materials filled with elements having angular points and ribs. The investigations of SSS at such points are topical, because, under certain conditions, an internal singular point can be a significant concentrator of stresses, which, in particular, is shown in [20], where tension of a compound strip is examined by the method of photoelasticity.Behavior of the stress field in the plane problem near to an internal angular point by using classical methods is examined, for example, in [12,22,23,, 21–24].

1. Statement of a Plane Problem

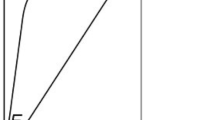
Let us consider two plane isotropic wedges 1 and 2, with a common with the vertex A, continuously connected together along their generatrix (Fig. 1). The mechanical and thermal loads on the body with this singularity create a plane stress state in the vicinity of the point A. The vertex angles of wedges are designated as 2α and 2β (with 0 < α < π, 0 < β < π, α + β = π), the external normals to the generatrix of wedge 1 — as \( \overline{n} \) and \( \overline{m} \), and the unit vectors perpendicular to them — as \( \overline{n}\hbox{'} \) and \( \overline{m}\hbox{'} \). Along the bisector of the wedges, the axis x 1 of a Cartesian orthogonal system of coordinates is directed. The axis x 2 is directed so that the system of coordinates Ax 1 x 2 is right-handed. The following designations are assumed: σ (k) ij and ε (k) ij are stresses and strains; E k are Young’s moduli; ν k are Poisson ratios; G k are shear moduli; ω k are coefficients of thermal expansion (i, j = 1, 2, k = 1, 2); ∆T is a homogeneous increment of temperature. The index k hereinafter specifies a constituent wedge. According to the concept assumed, two singular points are considered in the vicinity of the point A — the representative volume of body 1 containing the point A and the representative volume of body 2 containing the same point. These volumes are in a homogeneous SSS and interact along the demarcation line between both bodies. This interaction is characterized by the following conditions:

  • equality of normal stresses

    $$ {\sigma}_n^{(1)}={\sigma}_{-n}^{(2)},\kern1em {\sigma}_m^{(1)}={\sigma}_{-m}^{(2)}, $$
    (1.1)

  • equality of shear stresses

    $$ {\tau}_{n\prime}^{(1)}={\tau}_{-n\prime}^{(2)},\kern1em {\tau}_{m\prime}^{(1)}={\tau}_{-m\prime}^{(2)}, $$
    (1.2)

  • equality of relative lengthenings along the common generatrices

    $$ {\eta}_{n\prime}^{(1)}={\eta}_{-n\prime}^{(2)},\kern1em {\eta}_{m\prime}^{(1)}={\eta}_{-m\prime}^{(2)}, $$
    (1.3)

  • equality to zero of the sum of variations in vertex angles

    $$ \varphi +\psi =0, $$
    (1.4)

    where φ and ψ are variations in the angles 2α and 2β, respectively.

Fig. 1
figure 1

Internal singular point in a plane problem.

Full size image

With designations

$$ {\zeta}_{ij}={\sigma}_{ij}^{(1)}-{\sigma}_{ij}^{(2)},{\zeta}_{ij}={\varepsilon}_{ij}^{(1)}-{\varepsilon}_{ij}^{(2)} $$
(1.5)

Eqs. (1.1) and (1.2) can be written as the system of four linear homogeneous equations

$$ \begin{array}{c}\hfill {\zeta}_{11}{ \sin}^2\alpha +2{\zeta}_{12} \sin \alpha \cos \alpha +{\zeta}_{22}{ \cos}^2\alpha =0,\hfill \\ {}\hfill {\zeta}_{11}{ \sin}^2\alpha -2{\zeta}_{12} \sin \alpha \cos \alpha +{\zeta}_{22}{ \cos}^2\alpha =0,\hfill \\ {}\hfill -{\zeta}_{11} \sin \alpha \cos \alpha +{\zeta}_{12}\left({ \sin}^2\alpha -{ \cos}^2\alpha \right)+{\zeta}_{22} \sin \alpha \cos \alpha =0,\hfill \\ {}\hfill {\zeta}_{11} \sin \alpha \cos \alpha +{\zeta}_{12}\left({ \sin}^2\alpha -{ \cos}^2\alpha \right)-{\zeta}_{22} \sin \alpha \cos \alpha =0,\hfill \end{array} $$
(1.6)

and Eqs. (1.3) and (1.4), provided that α ≠ π/2, — as the system of three homogeneous equations

$$ \begin{array}{c}\hfill {\xi}_{11}{ \cos}^2\alpha -{\xi}_{12} \sin 2\alpha +{\xi}_{22}{ \sin}^2\alpha =0,\hfill \\ {}\hfill {\xi}_{11}{ \cos}^2\alpha +{\xi}_{12} \sin 2\alpha +{\xi}_{22}{ \sin}^2\alpha =0,\hfill \\ {}\hfill {\xi}_{11}{ \cos}^2\alpha -{\xi}_{22}{ \sin}^2\alpha =0.\hfill \end{array} $$
(1.7)

In constructing the third of Eqs. (1.7), we used the formula

$$ \varphi \sin \gamma =\left[2{\varepsilon}_{rp}-\left({\eta}_k+{\eta}_{\upiota}\right){\delta}_{rp}\right]{k}_r{l}_p, $$
(1.8)

Which determines the shift φ at an any point of the continuous medium between linear elements with directions \( \overline{k} \) and \( \overline{l} \) and the angle γ between them. In formula (1.8), η k and η l are the relative lengthenings at a point of the continuous medium in the directions of unit vectors \( \overline{k} \) and \( \overline{l} \), respectively; δ rp are components of the unit tensor. At α = π/2, the angles 2α and 2β become straight. At deformation of a continuous medium, in a small vicinity of its point, straight lines remain straight, and the shear deformation between the linear elements making a straight angle vs zero. Therefore, condition (1.4) is obeyed automatically, and the necessity for the third equation of system (1.7) falls off.

The problem consists in investigating the properties of solutions of the system of equations (1.6) and (1.7) in relation to the material parameters of elements of the compound wedge.

2. Investigating the Properties of Solutions of the System of Equations ( 1.6 ) and ( 1.7 )

The rank of the system of Eqs. (1.6) at α ≠ π/2 is equal to three. In this case, the only its solution is zero, and therefore the stress tensor at the wedge vertex is continuous:

$$ {\sigma}_{11}^{(1)}={\sigma}_{11}^{(2)}={\sigma}_{11},\kern1em {\sigma}_{12}^{(1)}={\sigma}_{12}^{(2)}={\sigma}_{12},\kern1em {\sigma}_{22}^{(1)}={\sigma}_{22}^{(2)}={\sigma}_{22}, $$
(2.1)

Under the same condition (α ≠ π/2), the rank of the system of equations (1.7) is also equal to three, from which it follows that

$$ {\varepsilon}_{11}^{(1)}={\varepsilon}_{11}^{(2)}={\varepsilon}_{11},\kern1em {\varepsilon}_{12}^{(1)}={\varepsilon}_{12}^{(2)}={\varepsilon}_{12},\kern1em {\varepsilon}_{22}^{(1)}={\varepsilon}_{22}^{(2)}={\varepsilon}_{22}, $$
(2.2)

i.e., stresses at the singular point are also continuous. We should note that the condition α = π/2 means that there are no internal angular points.

Equality (2.2), with the use of physical equations, can be written in terms of stresses:

$$ \begin{array}{c}\hfill \left(\frac{1}{E_1}-\frac{1}{E_2}\right){\sigma}_{11}-\left(\frac{\nu_1}{E_1}-\frac{\nu_2}{E_2}\right){\sigma}_{22}=Q,\hfill \\ {}\hfill -\left(\frac{\nu_1}{E_1}-\frac{\nu_2}{E_2}\right){\sigma}_{11}+\left(\frac{1}{E_1}-\frac{1}{E_2}\right){\sigma}_{22}=Q,\hfill \\ {}\hfill \left(\frac{1}{G_1}-\frac{1}{G_2}\right){\sigma}_{12}=0,\hfill \end{array} $$
(2.3)

where Q = (ω 1 − ω 2)∆T.

First two equations of (2.3) form an independent system. Its determinant

$$ \Delta =\frac{1}{E_1{E}_2}\left[\left({E}_2\left(1-{\nu}_1\right)-{E}_1\left(1-{\nu}_2\right)\right)\left({E}_2\left(1+{\nu}_1\right)-{E}_1\left(1+{\nu}_2\right)\right)\right] $$
(2.4)

becomes zero under the conditions

$$ \begin{array}{c}\hfill \left.1\right)\kern0.5em {E}_2\left(1-{v}_1\right)={E}_1\left(1-{v}_2\right),\hfill \\ {}\hfill \left.2\right)\kern0.5em {E}_2\left(1+{v}_1\right)={E}_1\left(1+{v}_2\right),\;\mathrm{i}.\mathrm{e}.,\;{G}_1={G}_2.\hfill \end{array} $$
(2.5)

Therefore, the following solutions of Eqs. (2.3) are possible.

  1. 1.

    Conditions (2.5) are not satisfied. Equations (2.3) have the only solution

    $$ {\sigma}_{11}={\sigma}_{22}=\frac{\left({\omega}_1-{\omega}_2\right)\Delta T\;{E}_1{E}_2}{\left({E}_2\left(1-{v}_1\right)-{E}_1\left(1-{v}_2\right)\right)},\kern1em {\sigma}_{12}=0, $$
    (2.6)

    and the stress state at the wedge vertex is completely determined.

  2. 2.

    Satisfied is only the first of Eqs. (2.5). In this case the solution depends on the value of Q.

    1. a)

      Q ≠ 0. The first two equations of system (2.3) are incompatible. The wedge vertex is the point of singular behavior of solution.

    2. b)

      Q = 0 (either ∆T = 0 or ω 1 = ω2). From Eqs. (2.3), it follows that

      $$ {\sigma}_{11}={\sigma}_{22},\kern1em {\sigma}_{12}=0, $$
  3. 3.

    Satisfied is only the second of Eqs. (2.5). The first two of Eqs. (2.3) are compatible, from which it follows that

    $$ {\sigma}_{11}+{\sigma}_{22}=\frac{Q{E}_1{E}_2}{\left({E}_2-{E}_1\right)}. $$

    From the third equation, σ 12 cannot be determined, because G 1 = G 2 in this case.

  4. 4.

    Both conditions (2.5) are satisfied. The rank of the matrix of the system of the first two equations of (2.3) is equal to zero, because E 1 = E 2 and v 1 = v 2. Equations (2.3) are compatible only at Q = 0. If Q ≠ 0, the singular point is the point of singularity for stresses.

As is seen, depending on the combination of material parameters at the singular point, various constraints are imposed on stress components. These constraints follow not only from the conditions assumed in the classical statement of the problem (the conditions of continuity for displacements and the normal and shear stresses on the connection lines of bodies 1 and 2). The dependence of constraints at a singular point on physical equations indicates that they need not be satisfied in the classical solution of the problem. Therefore, in the cases where such constraints exist, the problem of the mechanics of deformation of solids for a body with an internal singular point is not classical. The constraints caused by physical equations have to be considered as independent.

3. Statement of a Spatial Problem

Let us consider two isotropic deformable bodies fastened along their surfaces in such a manner that an internal rib Г (Fig. 2) is formed. At an arbitrary point A of the rib Г, we construct its normal section and introduce an orthonormal basis \( {\overline{r}}_1,{\overline{r}}_2,{\overline{r}}_3 \) whose unit vector \( {\overline{r}}_1 \) is directed along the bisector of the angle 2α at the vertex of body 1 toward body 2. In the normal section of rib Г, the unit vector \( {\overline{r}}_3 \) is perpendicular to \( {\overline{r}}_1 \) and \( {\overline{r}}_2 \) and is directed along the tangent to the rib Г so that the three vectors \( {\overline{r}}_1,{\overline{r}}_2,{\overline{r}}_3 \) make the right-hand basis of an orthonormal system of coordinates Ax 1, x 2, x 3. We assume that the vectors of normals \( \overline{n} \) and \( \overline{m} \) to the surfaces of bodies 1 and 2 at the point A lay in the normal section of rib Г. The designations accepted in Sect. 1 are retained, but i, j = 1, 2, 3.

Fig. 2
figure 2

Normal section of the internal rib.

Full size image

At the point A of the rib Г, for the representative volumes containing the singular point of bodies 1 and 2, the following conditions are satisfied:

  • equality of normal stresses

    $$ {\sigma}_n^{(1)}={\sigma}_{-n}^{(2)},\kern1em {\sigma}_m^{(1)}={\sigma}_{-m}^{(2)}, $$
    (3.1)

  • equality of shear stresses

    $$ {\tau}_{n,n\ \prime}^{(1)}={\tau}_{-n,-n\prime}^{(2)},\kern1em {\tau}_{m,m\ \prime}^{(1)}={\tau}_{-m,-m\prime}^{(2)},\kern1em {\tau}_{n,{r}_2}^{(1)}={\tau}_{-n,-{r}_2}^{(2)},\kern1em {\tau}_{m,{r}_2}^{(1)}={\tau}_{-m,-{r}_2}^{(2)}, $$
    (3.2)

    (the first subscript specifies the area element and the second one — the direction of action),

  • equality of relative lengthenings and shear strains is the tangent planes to the surface of fastening of the bodies at the point A

    $$ \begin{array}{c}\hfill {\eta}_{n\prime}^{(1)}={\eta}_{n\prime}^{(2)},\kern1em {\eta}_{m\prime}^{(1)}={\eta}_{m\prime}^{(2)},\kern1em {\eta}_{r,2}^{(1)}={\eta}_{r_2}^{(2)},\hfill \\ {}\hfill {\eta}_{n\prime {r}_2}^{(1)}={\eta}_{n\prime {r}_2}^{(2)},\kern1em {\eta}_{m\prime y}^{(1)}={\eta}_{m\prime, y}^{(2)},\hfill \end{array} $$
    (3.3)

    (the parameters marked with one subscript are the relative lengthenings and those with two subscripts — the shear strains.)

  • equality to zero of the sum of variations in the angles 2α and 2β

    $$ \varphi +\psi =0. $$
    (3.4)

In a small vicinity of a point, during deformation, planes remain plane. This fact is also true at the point A — the vertex of the compound wedge in the plane x 1 x 3, therefore, the total angle with the center at the point A is also retained. With designations (1.5), conditions (3.1) and (3.2) can be written in the form

$$ \begin{array}{c}\hfill {\zeta}_{11}{ \sin}^2\alpha +{\zeta}_{13} \sin 2\alpha +{\zeta}_{33}{ \cos}^2\alpha =0,\hfill \\ {}\hfill {\zeta}_{11}{ \sin}^2\alpha -{\zeta}_{13} \sin 2\alpha +{\zeta}_{33}{ \cos}^2\alpha =0,\hfill \\ {}\hfill -{\zeta}_{11} \sin \alpha \cos \alpha -{\zeta}_{13} \cos 2\alpha +{\zeta}_{33} \sin \alpha \cos \alpha =0,\hfill \\ {}\hfill {\zeta}_{11} \sin \alpha \cos \alpha -{\zeta}_{13} \cos 2\alpha -{\zeta}_{33} \sin \alpha \cos \alpha =0.\hfill \end{array} $$
(3.5)
$$ \begin{array}{c}\hfill {\zeta}_{12} \sin \alpha +{\zeta}_{23} \cos \alpha =0,\hfill \\ {}\hfill {\zeta}_{12} \sin \alpha -{\zeta}_{23} \cos \alpha =0,\hfill \end{array} $$
(3.6)

and the kinematic relations (3.3) and (3.4) — in the form

$$ \begin{array}{c}\hfill {\xi}_{11}{ \cos}^2\alpha -{\xi}_{13} \sin 2\alpha +{\xi}_{33}{ \sin}^2\alpha =0,\hfill \\ {}\hfill {\xi}_{11}{ \cos}^2\alpha +{\xi}_{13} \sin 2\alpha +{\xi}_{33}{ \sin}^2\alpha =0,\hfill \\ {}\hfill {\xi}_{22}=0,-{\xi}_{11} \cos \alpha +{\xi}_{32} \sin \alpha =0,\hfill \\ {}\hfill {\xi}_{11} \cos \alpha +{\xi}_{32} \sin \alpha =0,{\xi}_{11}{ \cos}^2\alpha -{\xi}_{33}{ \sin}^2\alpha =0.\hfill \end{array} $$
(3.7)

The last equality is valid at sin 2α ≠ 0 (α ≠ π/2) and have been found using Eq. (1.8).

The problem consists in investigating the properties of solutions of the system of equations (3.5)-(3.7) in relation to the material parameters of elements of the compound wedge.

4. Investigating the Properties of the Systems of Equations ( 3.5 )-( 3.7 )

If α ≠ π/2, i.e., in the absence of an angular point, the ranks of the systems of equations (3.5) and (3.6) are equal to three and two, respectively. Hence, they have only zero solutions, and the stresses σ (k) ij at the singular point are continuous:

$$ {\sigma}_{ij}^{(1)}={\sigma}_{ij}^{(2)}\kern1em \left(i,j=1,2,3\right). $$
(4.1)

The system of equations (3.7) at α ≠ π/2 has also only a zero solution, hence

$$ {\varepsilon}_{ij}^{(1)}={\varepsilon}_{ij}^{(2)}\kern1em \left(i,j=1,2,3\right), $$
(4.2)

which means that continuous are all strains at the internal singular point.

With the use of physical equations, Eqs. (4.2) can be written in terms of stresses:

$$ \begin{array}{c}\hfill \left(\frac{1}{E_1}-\frac{1}{E_2}\right){\sigma}_{11}-\left(\frac{v_1}{E_1}-\frac{v_2}{E_2}\right){\sigma}_{22}-\left(\frac{v_1}{E_1}-\frac{v_2}{E_2}\right){\sigma}_{33}=Q,\hfill \\ {}\hfill -\left(\frac{v_1}{E_1}-\frac{v_2}{E_2}\right){\sigma}_{11}+\left(\frac{1}{E_1}-\frac{1}{E_2}\right){\sigma}_{22}-\left(\frac{v_1}{E_1}-\frac{v_2}{E_2}\right){\sigma}_{33}=Q,\hfill \\ {}\hfill -\left(\frac{v_1}{E_1}-\frac{v_2}{E_2}\right){\sigma}_{11}-\left(\frac{v_1}{E_1}-\frac{v_2}{E_2}\right){\sigma}_{22}+\left(\frac{1}{E_1}-\frac{1}{E_2}\right){\sigma}_{33}=Q,\hfill \\ {}\hfill \left(\frac{1}{G_1}-\frac{1}{G_2}\right){\sigma}_{12}=0,\kern1em \left(\frac{1}{G_1}-\frac{1}{G_2}\right){\sigma}_{13}=0,\kern1em \left(\frac{1}{G_1}-\frac{1}{G_2}\right){\sigma}_{23}=Q,\hfill \end{array} $$
(4.3)

The first three of Eqs. (4.3) form an independent system in the stresses σ 11, σ 22, and σ 33. The determinant of this system

$$ \Delta =\frac{1}{E_1{E}_2}{\left[{E}_2\left(1+{\nu}_1\right)-{E}_1\left(1+{\nu}_2\right)\right]}^2\left[{E}_2\left(1-2{\nu}_1\right)-{E}_1\left(1-2{\nu}_2\right)\right] $$

becomes zero under the conditions

$$ {E}_2\left(1+{v}_1\right)-{E}_1\left(1+{v}_2\right)=0\kern1em \left({G}_1={G}_2\right), $$
(4.4)
$$ {E}_2\left(1-2{v}_1\right)-{E}_1\left(1-2{v}_2\right)=0. $$
(4.5)

Therefore the following solutions of Eqs. (4.3) are possible.

  1. 1)

    None of conditions (4.4) and (4.5) is satisfied. The system of Eqs. (4.3) has the only solution

    $$ \begin{array}{c}\hfill {\sigma}_{11}={\sigma}_{22}={\sigma}_{33}=\frac{Q{E}_1{E}_2}{E_2\left(1-2{v}_1\right)-{E}_1\left(1-2{v}_2\right)},\hfill \\ {}\hfill {\sigma}_{12}={\sigma}_{13}={\sigma}_{23}=0.\hfill \end{array} $$

    The SSS at rib points is completely determined.

  2. 2)

    Satisfied is only condition (4.4). The ranks of the system of the first three Eqs. (4.3) and of its expanded matrix are equal to unity. The equations are compatible and give the relation

    $$ {\sigma}_{11}+{\sigma}_{22}+{\sigma}_{33}=\frac{Q{E}_1{E}_2}{E_2-{E}_1}. $$

    Equations (4.3) do not impose any restrictions on the stresses σ ij (i ≠ j).

  3. 3)

    Satisfied is only condition (4.5). The solution of Eqs. (4.3) depends on the value of Q.

    1. a)

      Q = 0. The first three equations of system (4.3) are compatible. Valid are the equalities

      $$ {\sigma}_{11}={\sigma}_{22}={\sigma}_{33}. $$

      From the three last equations of (4.3), it follows that

      $$ {\sigma}_{12}=0,\kern1em {\sigma}_{13}=0,\kern1em {\sigma}_{23}=0. $$
    2. b)

      Q ≠ 0. The system of Eqs. (4.3) is incompatible. The combination of material parameters (4.5) is critical, because stresses at the singular point are infinite.

  4. 4)

    Satisfied are both conditions (4.4) and (4.5). In this case, E 1 = E 2 and v 1 = v 2. The rank of the system of Eqs. (4.3) is equal to zero. If Q = 0, the equations are compatible, but no restrictions on stresses follow. If Q ≠ 0, Eqs. (4.3) are incompatible. The singular point is the point of singular behavior of stresses.

The data presented indicate that restrictions at an internal singular point following from physical equations (depending on material parameters) are absent only if the fastened bodies have identical material characteristics. Otherwise, at the singular point, restrictions are formulated which make the problem of investigation of SSS in its vicinity nonclassical, because the number of constraints in this case exceeds that at border points in the classical problem.

Conclusion

An approach to constructing constraints on the parameters of state at an internal singular point of a flat compound wedge and a compound spatial rib is offered. The approach is based on identification of the singular point of a deformable body with its representative volume, which agrees with the postulates of continuum mechanics. It is shown, that, at an angular internal point, stresses and strains are continuous both in the plane and spatial cases. It is revealed, that in addition to the constraints considered in the classical approach, at an internal special point, there are restrictions dependent on physical equations (in the elastic case — on material constants). These additional constraints make the problem of mechanics of a deformable body with a singular point nonclassical. To each set of constraints there correspond its own statements of the problem. Combinations of material parameters of fastened bodies determine the number of additional constraints and the critical SSS at the singular point. The dependence of the number of constraints on material parameters of connected bodies makes the statement of the problem of continuum mechanics for bodies with singular points ambiguous. The approach suggested can be extended to the research of constraints in internal singular points of compound bodies with other physical properties. Results of the investigation can be used in the mechanics of composite materials for studying the SSS near the vertices and ribs of reinforcing elements and in fracture mechanics for studying stress concentrations in structures made by welding or gluing.