Introduction. One of the main tasks of material mechanics is the prediction of deformation processes, analysis, and comparison of the dependencies between stresses and strains under different kinds of loads. These dependencies are easily obtained for the case of uniaxial tension or compression. However, in the case of a complex stress state, this problem encounters significant difficulties due to the mutual influence of deformations. This problem is solved approximately by introducing the concept of equivalent stresses and strains and, accordingly, the following relation between them:

$$ {\upsigma}_{eq}=f\left({\upvarepsilon}_{eq}\right), $$
(1)

where σeq and εeq are equivalent stress and strain values, respectively. In this case, the equivalent stress is considered a conditional value of stress, which corresponds to the basic diagram of loading according to the adopted criterion of equivalence of the stress state. There is a similar understanding of the concept of equivalent strains. In mechanical engineering, it is customary to reduce the current relationship between stress and strain to a uniaxial tensile diagram.

Among the most common definitions of equivalent stresses, the following dependencies are used in the form of formulas (2)–(5):

$$ {\upsigma}_{eq}=\frac{1}{\sqrt{2}}\sqrt{{\left({\upsigma}_1-{\upsigma}_2\right)}^2+{\left({\upsigma}_2-{\upsigma}_3\right)}^2+{\left({\upsigma}_1-{\upsigma}_3\right)}^2}, $$
(2)
$$ 2{\upsigma}_{eq}=\left(\upeta +1\right){\upsigma}_i+\left(1-\upeta \right)3{\upsigma}_0, $$
(3)
$$ {\upsigma}_{eq}=\upxi {\upsigma}_i+\left(1-\upxi \right)\left({\upsigma}_1-{\upsigma}_3\right), $$
(4)
$$ {\upsigma}_{eq}=\upchi {\upsigma}_i+\left(1-\upchi \right){\upsigma}_1, $$
(5)

Here η, ξ, and χ are proportionality coefficients, which are determined from basic tensile and compression diagrams, σ1, σ2, and σ3 are principal stresses, and σ0 is average stress. In the literature, relations (2) are called stress intensity, and are denoted by the symbol σi.

From the geometrical point of view, in the stress space, the dependences (2)–(5) represent some surfaces, which are commonly called loading surfaces. The loading surfaces expand, approaching their limiting definitions – the limiting fracture surfaces. It is assumed that their shape and orientation remain unchanged [1].

To construct the relationship between stress and strain in the form of expression (1), in addition to determining the equivalent stresses, it is necessary to determine the value of equivalent strains. Thus, for expression (2), the equivalent amount of strain is defined as expression:

$$ {\upvarepsilon}_{eq}=\frac{1}{\sqrt{2}\left(1+\upmu \right)}\sqrt{{\left({\upvarepsilon}_1-{\upvarepsilon}_2\right)}^2+{\left({\upvarepsilon}_2-{\upvarepsilon}_3\right)}^2+{\left({\upvarepsilon}_1-{\upvarepsilon}_3\right)}^2}, $$
(6)

where is the transverse strain coefficient, and ε1, ε2, and ε3 are the principal deformations.

It is assumed that it will not be a big mistake to take the transverse strain coefficient equal to 0.5. As a result, we obtain an expression that determines the value of strain intensity εi:

$$ {\upvarepsilon}_i=\frac{\sqrt{2}}{3}\sqrt{{\left({\upvarepsilon}_1-{\upvarepsilon}_2\right)}^2+{\left({\upvarepsilon}_2-{\upvarepsilon}_3\right)}^2+{\left({\upvarepsilon}_1-{\upvarepsilon}_3\right)}^2}. $$
(7)

Attempts were made to similarly determine the value of equivalent deformations for expressions (3)–(5). However, due to the volumetric influence of the strain components, the problem has never been solved.

Thus, to date, the relationship between stress and strain in a complex stress state is calculated as a relationship between stress intensity (2) and strain intensity (8).

$$ {\upsigma}_i=f\left({\upvarepsilon}_i\right). $$
(8)

Relationship between Stresses and Strains. In general, the relationship between stresses and strains, both in the elastic and plastic strain region, for materials whose properties may be assumed to be isotropic can be described by expression (9) in the following form:

$$ \left\{\begin{array}{c}{\upvarepsilon}_1=\frac{1}{E_s}\left[{\upsigma}_1-\upmu \left({\upsigma}_2+{\upsigma}_3\right)\right],\\ {}{\upvarepsilon}_2=\frac{1}{E_s}\left[{\upsigma}_2-\upmu \left({\upsigma}_1+{\upsigma}_3\right)\right],\\ {}{\upvarepsilon}_3=\frac{1}{E_s}=\frac{1}{E_s}\left[{\upsigma}_3-\upmu \left({\upsigma}_1+{\upsigma}_2\right)\right],\end{array}\right. $$
(9)

where ε1, ε2, and ε3 are the principal deformations, σ1, σ2, and σ3 are the principal stresses, is the transverse strain coefficient, and Es is the secant module (Fig. 1).

Fig. 1.
figure 1

Conditional relationship between tensile stress and strain.

Full size image

Figure 1 shows the conditional relationship between tensile stress and strain.

For the case of elastic linear deformation, when the secant coincides with the modulus of elasticity, the system of equations (9) turns into a generalized Hooke’s law.

The transverse strain coefficient, which appears in the system of equations (9), is physically a volume coefficient and characterizes the compressibility of the material under loading [2]. As part of the solution of the problem formulated in this article, we will limit ourselves to the assumption that, during elastic deformation, the transverse strain factor is equal to the table value of the Poisson’s ratio, and, during plastic deformation, it is equal to 0.5.

Introduction of the Concept of “Nominal Strain”. There is an idea that if there is a stress surface and a basic relationship between the stress and strain, it is possible to determine the corresponding strain surface. However, this problem is greatly complicated due to the volumetric influence of deformations on the effective stress, and, consequently, the impossibility of substituting the components of equations (9) directly into the expressions of equivalent stresses.

The problems of constructing the deformation surface and determining the relationship between the stress and strain surfaces can be solved by introducing the value of “nominal deformations” εσ. The nominal deformation is the deformation only from the action of the directly applied force, without taking into account the mutual influence of the deformations.

The proposed nominal strain εσ is determined as follows:

$$ {\upvarepsilon}_{\upsigma_1}=\frac{\upsigma_1}{E_s},\kern1.5em {\upvarepsilon}_{\upsigma_2}=\frac{\upsigma_2}{E_s},\kern1.5em {\upvarepsilon}_{\upsigma_3}=\frac{\upsigma_3}{E_s}, $$
(10)

where σ1, σ2, and σ3 are principal stresses, and Es is the secant module.

The meaning of using the replacement of variables (10) is to isolate the deformation of the directly acting stress from the volumetric effects of deformations. It is also obvious that the direction of action of the applied force and the direction of action of the nominal strain will coincide, and there will be a clear linear relationship between them in the form of expression (10). Accordingly, we can assume that, in case of representation of the stress surface in the form of some geometric figure, we can similarly set a similar surface of nominal deformations.

By substituting the corresponding parameter values from equations (10) into the system of equations (9), we obtain the relation of mutual influence of deformations:

$$ \left\{\begin{array}{c}{\upvarepsilon}_1={\upvarepsilon}_{\upsigma_1}-\upmu \left({\upvarepsilon}_{\upsigma_2}+{\upvarepsilon}_{\upsigma_3}\right),\\ {}{\upvarepsilon}_2={\upvarepsilon}_{\upsigma_2}\upmu \left({\upvarepsilon}_{\upsigma_1}+{\upvarepsilon}_{\upsigma_3}\right),\\ {}{\upvarepsilon}_3={\upvarepsilon}_{\upsigma_3}\upmu \left({\upvarepsilon}_{\upsigma_1}+{\upvarepsilon}_{\upsigma_2}\right),\end{array}\right. $$
(11)

Thus, given certain values of nominal deformations and transverse strain coefficient, it is possible to calculate the value of normal deformations as well. As noted above, in this paper, it is assumed that for elastic deformation, the transverse strain factor is equal to the table value of Poisson’s ratio, while for plastic deformation, it is equal to 0.5.

The general relationship between the stress and nominal strain for the case of complex stress state in elasticplastic deformation is defined as the relationship between the Euclidean norms of the stress and nominal strain tensors in the form of expression (12):

$$ {\left\Vert {T}_{\upvarepsilon_{\upsigma}}\right\Vert}_2=\frac{1}{E_s}{\left\Vert {T}_{\upsigma}\right\Vert}_2, $$
(12)

where ‖Tσ‖2 is the Euclidean norm of the stress tensor and \( {\left\Vert {T}_{\upvarepsilon_{\upsigma}}\right\Vert}_2 \) is the Euclidean norm of the nominal strain tensor.

When representing the stress state in principal stresses, the Euclidean norms of the stress and nominal strain tensors have the following expression:

$$ {\left\Vert {T}_{\upsigma}\right\Vert}_2=\sqrt{\upsigma_1^2+{\upsigma}_2^2+{\upsigma}_3^2},\kern0.75em {\left\Vert {T}_{\upvarepsilon_{\upsigma}}\right\Vert}_2=\sqrt{\upvarepsilon_{\upsigma_1}^2+{\upvarepsilon}_{\upsigma_2}^2+{\upvarepsilon}_{\upsigma_3}^2}. $$
(13)

Interestingly, in the case of uniaxial loading (tension or compression), the dependence diagrams σ = f (ε) and σ = f (εσ) will be the same. And, if the loading diagram σ = f (ε) for the case of a complex stress state is meaningless, due to its distortion by the mutual influence of deformations and, accordingly, the impossibility of comparative analysis with uniaxial loading, the dependence σ = f (εσ) preserves the dynamics of secant modulus change relative to the effective stress and can be compared with other similar loading diagrams.

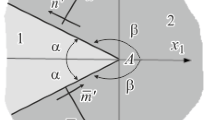
Selection of Loading Surface. As mentioned above, the loading surface in the stress space represents a certain geometric figure, the type and shape of which are determined by the differential conditions imposed on this surface and the presence of a sufficient number of points necessary for its construction. One of the conditions imposed on the type of surface is the Drucker postulate, which determines the convexity of the loading surface. Another unequivocal fact is the absence of plastic deformation in the case of equiaxial tension. Accordingly, there is no expansion of the surface in the direction σh due to hardening in the case of plastic deformation. In this case, the loading surface, expanding, approaches the fracture surface. Accordingly, the loading surface should not cross the fracture surface.

In [3], it was proposed to use the loading surface in the form of an elliptic paraboloid. For its construction, it is necessary to conduct four basic experiments. From a practical point of view, such criterion is more theoretical than practical, because conducting a such number of experiments, from a technological point of view, is quite a complicated procedure. Therefore, as a simplification, we propose to use a criterion in the form of a circular paraboloid, which will have only three unknown quantities, presented in the following form:

$$ {\upsigma}_{\uprho}=A{\left(f-{\upsigma}_h\right)}^{\upalpha}, $$
(14)

where A and α are the internal coefficients, which are determined on the basis of two basic experiments – for compression, and for tension. The third value f is found by fitting under the condition of convergence of the two surfaces – the flow surface and the fracture surface at F, as shown in Fig. 2.

Fig. 2.
figure 2

Flow surface (1) and fracture surface (2), for the conditional material. (The segment OAB is the direction of loading under uniaxial tension, OCD – under uniaxial compression.)

Full size image

In Fig. 2, the coordinate axes have the following definitions [4]: σh is the hydrostatic axis and σρ is the radial stress axis,

$$ {\displaystyle \begin{array}{c}{\upsigma}_h=\frac{1}{\sqrt{3}}\left({\upsigma}_1+{\upsigma}_2+{\upsigma}_3\right),\\ {}{\upsigma}_{\uprho}=\frac{1}{\sqrt{3}}\sqrt{{\left({\upsigma}_1-{\upsigma}_2\right)}^2+{\left({\upsigma}_2-{\upsigma}_3\right)}^2+{\left({\upsigma}_2-{\upsigma}_3\right)}^2}.\end{array}} $$

When the material hardens as a result of plastic deformation, the surface of the beginning of the flow (surface 1 in Fig. 2) expands, approaching the fracture surface (surface 2 in Fig. 2). In this case, the internal coefficients of the equation A and α will change from their initial values, designated as A' and α', which correspond to the beginning of the plastic flow, to their final values A” and α”, determined at material failure. A description of the variation of the internal parameters A and α will be given below.

The Surface of the Nominal Strain. In order to be able to determine the predicted relationship between stress and strain using loading surfaces, it is necessary to define a strain surface in addition to a defined stress surface. The construction of the strain surface due to the volumetric effects of deformations currently remains an uncertain task. However, by introducing a value of nominal strain, the issue of volumetric effects of deformations can be bypassed.

As mentioned above, the surface of the beginning of the plastic flow is defined by expression (14), which is presented in the following form:

$$ {\upsigma}_{\uprho}^y={A}^{\prime }{\left(f-{\upsigma}_h\right)}^{\upalpha^{\prime }}, $$
(15)

where A' and α' are internal coefficients of the beginning of plastic flow and f is the internal parameter described in expression (14).

According to the assumptions introduced (10), the surface of the beginning of plastic flow in nominal strains for the case of active loading is described by expression (16):

$$ {\upvarepsilon}_{\upsigma_{\uprho}^y}=\frac{\upsigma_{\uprho}^y}{E}=\frac{A^{\prime }{\left(f-{\upsigma}_h\right)}^{\upalpha^{\prime }}}{E}, $$
(16)

where E is the elastic modulus.

After some transformations, expression (16) can be presented in the following form:

$$ {\upvarepsilon}_{\upsigma_{\uprho}^y}={A}^{\prime }{E}^{\upalpha^{\prime }-1}{\left(\frac{f}{E}-\frac{\upsigma_h}{E}\right)}^{\upalpha^{\prime }}, $$
(17)

From the geometric point of view, the surface described in expressions (16) and (17) is a circular paraboloid represented as a rotation surface 1 in Fig. 3. As active loading continues, surface (1) will change, approaching surface 2, as shown in Fig. 3.

Fig. 3.
figure 3

The surface of the beginning of plastic flow (1) and the surface of complete strain (2) of the material (OB' is the direction of deformation under uniaxial tension and OD' – in uniaxial compression).

Full size image

Thus, the limiting surface of the nominal deformations can be represented as a circular paraboloid of the following form:

$$ {\upvarepsilon}_{\upsigma_{\uprho}}=B{\left(q-{\upvarepsilon}_{\upsigma_h}\right)}^{\upbeta}, $$
(18)

where \( {\upvarepsilon}_{\upsigma_{\uprho}} \) is the radial component of the nominal strain, \( {\upvarepsilon}_{\upsigma_h} \) is the hydrostatic component of the nominal strain, B and β are internal coefficients, q is the parameter that is determined by expression (19):

$$ q=\frac{f}{E}. $$
(19)

In Fig. 3, the coordinate axes have the following definitions [4]: \( {\upvarepsilon}_{\upsigma_{\uprho}} \) is the hydrostatic axis of nominal strain and \( {\upvarepsilon}_{\upsigma_h} \) is the radial axis of nominal strain.

As stated earlier, the principal axes of nominal deformations coincide with the principal axes of stresses. Accordingly, the direction of loading in the stress space coincides with the direction of deformation in the nominal strain space.

Determination of the Elastic and Plastic Component of the Nominal Strain. The nominal strain, similar to the usual strain, can be decomposed into its components – elastic and plastic parts:

$$ {\upvarepsilon}_{\upsigma}={\upvarepsilon}_{\upsigma}^e+{\upvarepsilon}_{\upsigma}^p, $$
(20)

where \( {\upvarepsilon}_{\upsigma}^e \) and \( {\upvarepsilon}_{\upsigma}^p \) are the elastic and plastic components of the nominal strain, respectively.

As noted above, for the case of a complex stress state, the value of the total nominal strain, as well as the value of the total stress, is defined as the Euclidean norms of the stress and nominal strain tensors. In cylindrical coordinates for the case of active loading, they have the following form:

$$ \upsigma ={\left\Vert {T}_{\upsigma}\right\Vert}_2=\sqrt{\upsigma_h^2+{\upsigma}_{\uprho}^2},\kern0.5em {\upvarepsilon}_{\upsigma}={\left\Vert {T}_{\upvarepsilon_{\upsigma}}\right\Vert}_2=\sqrt{\upvarepsilon_{\upsigma_h}^2+{\upvarepsilon}_{\upsigma_{\uprho}}^2}. $$
(21)

There is a relationship between the stress and the nominal strain in the form of a relationship:

$$ {\upvarepsilon}_{\upsigma}=\frac{\upsigma}{E_s}\kern1.5em \textrm{or}\kern1.5em {\left\Vert {T}_{\upvarepsilon_{\upsigma}}\right\Vert}_2=\frac{{\left\Vert {T}_{\upsigma}\right\Vert}_2}{E_s}. $$
(22)

The elastic component of the nominal strain will have the appropriate form:

(23)

The plastic part of the nominal strain, respectively, will have the following form:

$$ {\upvarepsilon}_{\upsigma}^{\uprho}={\upvarepsilon}_{\upsigma}-{\upvarepsilon}_{\upsigma}^e=\frac{\upsigma}{E_s}-\frac{\upsigma}{E}=\upsigma \left(\frac{1}{E_s}-\frac{1}{E}\right), $$

or

$$ {\left\Vert {T}_{\upvarepsilon_{\upsigma}^{\uprho}}\right\Vert}_2=\left(\frac{1}{E_s}-\frac{1}{E}\right){\left\Vert {T}_{\upsigma}\right\Vert}_2. $$
(24)

Determination of Internal Constants of Loading Surfaces. As noted above, when the material is loaded, the loading surface under elastic deformation expands uniformly, approaching the surface of the beginning of plastic deformation. Further expansion of the loading surface, due to the action of plastic deformation, occurs from surface 1 to surface 2, as shown in Fig. 2. The surface of nominal strains expands in a similar way (Fig. 3).

To determine the predicted relationship between stress and nominal strain in a complex stress state, the following algorithm is proposed.

The internal constants of expressions (15) and (18) are determined on the basis of the two basic relations between stress and strain – in compression and tension. It should be noted that for the case of uniaxial loading (compression, tension), the values of normal strain and nominal strain will coincide.

Figure 4 shows two arbitrary material hardening trajectories under loading: one for uniaxial tension, and the other for uniaxial compression.

Fig. 4.
figure 4

Arbitrary trajectories of material loading. (σ+ and σ- are tensile and compressive stresses, εp+ , εe+ , and ε+ are plastic, elastic, and total tensile strains, and εp-, εe-, and ε- are plastic, elastic, and total compressive strains.

Full size image

Since the values of the limiting deformations for both cases are different, let us introduce some normalizing factor ξ:

$$ \upxi =\frac{\upvarepsilon^p}{\upvarepsilon_b^p}, $$
(25)

where εp is the plastic strain and \( {\upvarepsilon}_b^p \) is the limit value of plastic strain.

Figure 5 shows a reduced diagram of material hardening during plastic deformation as a function of the normalizing factor ξ.

Fig. 5.
figure 5

Summary diagram of material strengthening. (ξ is the normalizing factor, ξ = [0; 1].)

Full size image

The internal variables A and α for the loading surface are determined step-by-step for each value of ξ by solving equation (14) for the corresponding compressive and tensile stress values. In [3], a detailed definition of the internal coefficients was shown. As a result, we obtain the dependence of the parameters A and α on ξ, as shown in Fig. 6.

Fig. 6.
figure 6

General view of the change in the internal parameters of Eq. (15) from the normalizing coefficient ξ.

Full size image

Similarly, the surface constants of nominal tensile strains are determined from the basic compression and tension experiments by substituting the corresponding values into Eq. (18). It should be noted here that, in order to determine the relationship between the stress and nominal strain in an arbitrary loading direction, the dynamics of changes in the coefficients B and β in Eq. (18) are not important, since only the finite values of these parameters are needed.

Methodology for Constructing the Predicted Relationship between Stress and Nominal Strain for an Arbitrary Direction of Loading. The essence of the definition of the loading criteria is the possibility of predicting the relationship between stress and strain for an arbitrary direction of loading in the stress space.

First, for the chosen direction of loading, determine the limiting values of the nominal strain \( {\upvarepsilon}_{\upsigma_b} \) and the corresponding stress σb. Then the limit value of plastic strain is determined:

$$ {\upvarepsilon}_{\upsigma_b}^p={\upvarepsilon}_{\upsigma_b}-\frac{\upsigma_b}{E}. $$
(26)

According to expression (26) and the graph in Fig. 6, for each step ξ, there are corresponding values \( {\upvarepsilon}_{\upsigma}^p \), A, and α. We find the stress that corresponds to a given nominal plastic strain.

By setting each new value ξ, we build the dependence \( {\upvarepsilon}_{\upsigma}^p=f\left(\upsigma \right) \), step by step and reconstruct the obtained dependence into the graph of the function εσ = f(σ).

CONCLUSIONS

1. By introducing the concept of nominal strain, the possibility of determining complete strain diagrams for an arbitrary direction of loading in a complex stress state is shown. The obtained strain diagrams can be compared with each other.

2. The defined deformation surface and its expansion during loading are demostrated.

3. The possibility of using multiparametric strength criteria to determine the predicted relationship between stresses and strains in a complex stress-strain state is proved.