Introduction

A voice source is understood by experts as a signal of excitation of acoustic vibration in the vocal tract of the speaker in the production of voiced speech sounds, especially vowels [1,2,3]. As an object of acoustic analysis, voice sources serve as interesting objects for the researchers in various fields of activity: from the digital speech processing and synthesis to biomedical systems and technologies [3,4,5,6]. The general system problem of these and similar studies is connected with the time instability of the fine structure of speech signal under the influence of numerous random (uncontrollable) factors [7, 8]. The general problem explains and, at the same time, stimulates the development of various theories and experimental tools aimed the analysis of voice speech [9,10,11].

The aim of the present paper is to develop a rapid method that can be used for the real-time voice analysis.

Analysis of voice sources

The acoustic theory of speech formation [12] and its model of a voice source in the form of a quasiperiodic (or periodic for bounded time intervals) sequence of excitation pulses of the vocal tract of a speaker [13] are now extensively used in the field of information speech technologies. The parameters of the indicated sequence, namely, the repetition rate F0 and the shape of pulses, specify the fundamental tone and the fine structure of vocalized segments of the speech signal. Various values of the parameters correspond to different speech sounds and the indicated correspondence has a strictly individual (speaker-dependent) character. Therefore, the analysis of vocal source is both a nontrivial problem and an urgent task [14,15,16].

As a widespread procedure used to solve the posed problem, we can mention voice inverse filtering of the speech signal [17, 18]. The idea of filtering is to decompose the model of the observed signal into two independent components, namely, the voice source and the vocal tract [19]. In this case, the vocal tract is modeled by a linear recursive filter of relatively low order \(p_{1}=8\ldots 12\) [12, 20].There are two known approaches to the realization of this decomposition [21, 22]. They differ by the procedure of acoustic measurements.

In the first approach, the sequence of observations (readings) of the speech signal is synchronized with its fundamental tone [12, 16]. In this case, the frequency of the fundamental tone F0 is regarded as a priori specified or preliminarily measured, and the shape of excitation pulses is computed within the period of synchronous observations with duration \(\tau =T_{0}\) of a single period \(T_{0}={F}_{0}^{-1}\) of the fundamental tone. However, under the conditions of a priori uncertainty, this task is practically unsolvable, at least for the real-time voice analysis of speech [22,23,24].

The second approach is based on simulation of speech signals in the frequency region [25]. In particular, the autoregressive model [13, 15] is used fairly extensively. This model is based on the description of stationary segments of speech signals of relatively large length \(\tau \gg T_{0}\) and, therefore, does not require synchronization with the fundamental tone. In this case, we encounter the problem of proper choice of the order p of the autoregressive model [20]. Under the conditions of a priori uncertainty in the fine structure of the speech signal, the order \(p\gg 1\) should be sufficiently large [26]. However, in the case of application of a high-order autoregressive model as a tool for the statistical data processing, we get a general system problem of small samples of the data of observations [27, 28]. In the analyzed case, this problem is strongly complicated by the conditions of finite duration τ of the period of observations in which the speech signal can be regarded as stationary [8].

Thus, the problem of development of a rapid method for the asynchronous analysis of the voice source of speech aimed at the real-time application proves to be quite urgent. For this purpose, the authors of the present paper propose to apply a two-level autoregressive model of speech signals [29]. Its order (p1,p2) is determined by a pair of noticeably different values \(p_{2}\gg p_{1}\), which enables us to expect the possibility of combination, within a single method, of the advantages of both methods of acoustic measurements, namely, synchronous characterized by the potential accuracy of the results of analysis and asynchronous capable of decreasing the computational costs required for its realization.

Statement of the problem

Let x(t) be a vocalized speech signal given by a sequence \(\{x(n)\}\) of x(n) readings at discrete times \(n=0,1,\ldots ,N-1\) within the interval of observations \(t\leq \tau\) of finite length \(\tau =NT\), where T is the period of time sampling of the signal. The Fourier spectrum of the sequence \(\{x(n)\}\) as a function of linear frequency f is given by the formula [30]:

$$S_{x}\left(\mathrm{j}f\right)=T\sum_{n=0}^{N-1}x(n)\exp \left(-\mathrm{j}2\pi nfT\right),\quad|f| \leq 0.5F,$$
(1)

where \(F=T^{-1}\) is a sampling rate and j is the imaginary unit.

In the linear model of vocal tract [8] specified by the complex transmission coefficient K(jf), we get the following equality:

$$S_{x}(\mathrm{j}f)=K(\mathrm{j}f)S_{z}(\mathrm{j}f),\quad | f| \leq 0.5F,$$

where Sz(jf) is a frequency spectrum of the sequence of excitation pulses \(z(n),n=0,1,\ldots ,N-1\), and

$$S_{z}(\mathrm{j}f)=K^{-1}(\mathrm{j}f)S_{x}(\mathrm{j}f),\quad| f| \leq 0.5F.$$
(2)

As a result of the inverse Fourier transformation, we obtain

$$z(n)=\int_{-0.5F}^{0.5F}S_{z}(\mathrm{j}f)\exp (\mathrm{j}2\pi nfT)df,\quad n=0,1,\ldots ,N-1,$$
(3)

In integral form, we can write

$$y(n)=y(n-1)+z(n),\quad n=0,1,\ldots ,N-1$$
(4)

The set of expressions (2)–(4) determines the vocal source of speech by the method of inverse filtering [31]. In this case, Eq. 3 describes the sequence of excitation pulses of the vocal tract, while Eq. 4 specifies the volumetric velocity of the airflow passing through the glottis. The problem is thus reduced to the determination of the right-hand side of expression (2). In this case, it is necessary to explicitly determine the complex transmission coefficient of the vocal tract filter and substitute it in expression (3). Under the conditions of a priori uncertainty of the fine structure of speech signal, this is a nontrivial problem, and its solution requires the application of a universal probability-theory approach [13].

Statistical model of the vocal tract

The main difficulty encountered in solving the posed problem is connected with the acoustic variability of speech signal [8]. Due to the influence of various random (uncontrollable) factors on the speaker in the process of speech production, the signal x(t) cannot be regarded as stationary or stable with respect to its parameters even for relatively small observation periods \(\tau =(3\ldots 5)T_{0}\).

In the work [24] devoted to the analysis of voice timbre, the author justified the procedure of modeling the vocal tract by using a scheme of recursive filter with complex transmission factor

$$K(\mathrm{j}f)=\left(1+\sum_{i=1}^{p_{1}}a_{{p_{1}}}(i)\exp \left(-\mathrm{j}2\pi ifT\right)\right)^{-1},\quad|f| \leq 0.5F$$
(5)

The order of this filter p1 is comparable with the double number of formants L1 in the spectrum of speech signal [20]. Thus, within the frequency band of a standard telephone channel 4 kHz in width, for the vowel speech sounds, we have \(L_{1}=4\ldots 6\) [32] and, hence, \(p_{1}=8\ldots 12\). At the same time, the vector of filter coefficients (5) is determined by the p-vector of coefficients from the autoregressive equation

$$y(n)=-\sum_{i=1}^{p}a_{p}(i)y\left(n-i\right)+\eta (n),\quad n=0,1,\ldots$$
(6)

of the same order \(p=p_{1}\). Here, \(\{y(n)\}\) is a random (hypothetical) time series simulating the speech signal in discrete time \(n;\{\eta (n)\}\) is the generating white noise with variance \({\sigma }_{\eta }^{2}=\) const. Assume that the preliminary autoregressive coefficients {ap(i)} are adapted to the speech signal x(t) according to a vector of its readings \(\{x(n)\}\) of finite dimension N. In the theory of parametric estimation, there exists a specially developed mathematical procedure [33]. In particular, we can mention Berg’s methodFootnote 1 widely used in practice and based on the Levinson recursion [30]:

$$\forall q=\overline{1,p}\colon a_{q}(i)=a_{q-1}(i)+c_{q}a_{q-1}\left(q-i\right),\quad i=1,2,\ldots ,q$$
(7)
$$\begin{aligned} c_{q}&=-2{S}_{q}^{-2}\sum_{n=q+1}^{N}\eta_{q-1}(n)v_{q-1}(n-1), \\ S_{q}^{2}&=\sum_{n=q+1}^{N}\left[{\eta}_{q-1}^{2}(n)+{v}_{q-1}^{2}(n-1)\right] \\ \eta_{q}(n)&=\eta_{q-1}(n)+c_{q}v_{q-1}(n-1), \\ v_{q}(n)&=v_{q-1}(n-1)+c_{q}\eta_{q-1}(n) \end{aligned}$$

in the case of its initialization by the system of equalities \(v_{0}(n)=\eta_{0}(n)=x(n-1)\) for all \(n\leq N\). The final values of recursion (7) for \(q=p_{1}\) determine the adaptive autoregressive model (5) of the vocal tract in the frequency region, which should be substituted in expression (2). However, this is only the first step in solving the posed problem.

Statistical model of speech signal

The problem is connected with the fact that not only the complex transmission factor of the vocal tract but also the spectral density Sx(jf) of the speech signal x(t) on the right-hand side of Eq. 3 are not completely determined by expression (1) due to the insufficient volume \(N=\tau F\) of the sample of observations \(\{x(n)\}\). Note that the duration of frames in the systems of digital processing and transmission of speech does not exceed \(\tau =30-\)40 msec (see GOST R 53556.3-2012Footnote 2). Thus, by using a standard telephone communication line and a sampling frequency of speech signal \(F=8\) kHz for substitution in expression (1), we get at most \(N=240\)–320 readings of observations. A frequency resolution \(\delta f=\tau^{-1}=25{-}30\) Hz attained in this case is comparable with the lower limit of the fundamental tone frequency \(F_{0}=80{-}100\) Hz in male speech. However, this contradicts the requirements imposed on the accuracy of voice analysis in the frequency domain because the spectral density (2) has a linear form and consists of amplitude-modulated quasiharmonics with frequencies \(F_{0},2F_{0},\ldots ,LF_{0}\), where \(L=0.5F/F_{0}\gg 1\) [29]. Thus, for the sampling frequency \(F=8\) kHz, there are \(L=40\) quasiharmonics within the working frequency band with relative shifts (with respect to each other) by a frequency \(F_{0}=100\) Hz. In order to significantly decrease the value of δf in these conditions, it is necessary to additionally determine (extrapolate [30]), within the framework of the posed problem (2)–(4), not only the vocal tract but also the speech signal itself outside the interval of its observations. For this purpose, a special mathematical apparatus of parametric methods of statistical analysis was theoretically developed in [33]. The methods of this kind are based on the statistical simulation of the time series \(\{x(n)\}\) with the help of a hypothetical (imaginary) random process \(\{y(n)\}\). For this purpose, it is customary to use the linear autoregressive process (6) of order p2≫1 [25, 26]. The power spectral density of this process is given by the expression

$$G(f)=\sum_{\eta}^{2}T\left| 1+\sum_{i=1}^{p}\:a_{p}(i)\exp \left(-\mathrm{j}2\pi ifT\right)\right|^{-2},\quad | f| \leq 0.5F$$
(8)

where the coefficients {ap(i)} are computed according to recursive relation (7) with \(p=p_{2}\). The order of autoregression \(p_{2}\geq 2L\) is determined with regard for the double (but less than a half of the sample volume N) number of quasiharmonics L in the spectrum of speech signal [20]. Under the conditions of the previous example, we obtain \(80\leq p_{2}< 120\). In the general case, p2 is much greater than the order of the vocal tract filter (5), namely, \(p_{2}\gg p_{1}\).

From expression (8), by the method of spectral factorization [30], we obtain an autoregressive model of speech signal in the frequency domain:

$$S_{x}\left(\mathrm{j}f\right)=c_{0}\left(1+\sum_{i=1}^{p_{2}}a_{{p_{2}}}(i)\exp \left(-\mathrm{j}2\pi ifT\right)\right)^{-1},\quad | f| \leq 0.5F,$$
(9)

where c0 = const is an adjustable scaling factor.

The problem of resolving power \(\delta f\ll F_{0}\) in model (9) can be overcome due to the effect of superresolution in frequency [28, 34]. According to (2), by using (9), we can write

$$S_{z}\left(\mathrm{j}f\right)=c_{0}\frac{1+\sum_{i=1}^{p_{1}}a_{{p_{1}}}(i)\exp \left(-\mathrm{j}2\pi ifT\right)}{1+\sum_{i=1}^{p_{2}}a_{{p_{2}}}(i)\exp \left(-\mathrm{j}2\pi ifT\right)};\quad | f| \leq 0.5F$$
(10)

Expression (10) defines the general system autoregressive moving-average (ARMA) model in the theory of statistical analysis of random time series [30]. In the analyzed case, this model describes the voice source in the frequency domain (2). Substituting (10) in expression (3), in the time domain, we obtain

$$\begin{aligned} z(n)&=c_{0}\int_{-0.5F}^{0.5F}\frac{1+\sum_{i=1}^{p_{1}}a_{{p_{1}}}(i)\exp \left(-\mathrm{j}2\pi ifT\right)}{1+\sum_{i=1}^{p_{2}}a_{{p_{2}}}(i)\exp \left(-\mathrm{j}2\pi ifT\right)}\exp \left(\mathrm{j}2\pi nfT\right)df= \\ & =c_{0}\int_{-0.5F}^{0.5F}\frac{FT_{N}\left\{\boldsymbol{b}_{1}\right\}}{FT_{N}\left\{\boldsymbol{b}_{2}\right\}}\exp \left(\mathrm{j}2\pi nfT\right)df= \\ & =c_{0}IFT_{n}\left\{\frac{FT_{N}\left\{\boldsymbol{b}_{1}\right\}}{FT_{N}\left\{\boldsymbol{b}_{2}\right\}}\right\}\triangleq z_{N}(n),\quad n=0,1,\ldots ,N-1. \end{aligned}$$
(11)

In (11), we have used the following notation:

$$FT_{N}\left\{\boldsymbol{b}_{r}\right\}\triangleq T\sum_{i=0}^{N}b_{r}(i)\exp (-\mathrm{j}2\pi ifT)=T\left[1+\sum_{i=1}^{p_{r}}a_{{p_{r}}}(i)\exp (-\mathrm{j}2\pi ifT)\right]$$

is the operator of Fourier transform, \(\boldsymbol{b}_{r}=\left\{b_{r}(i),i\leq J\right\}=\left[1,a_{{p_{r}}}(1),a_{{p_{r}}}(2),\ldots ,a_{{p_{r}}}\left(p_{r}\right),0{,}0,\ldots ,0\right]\)is the vector of coefficients with dimension N + 1, where \(r=1.2\); \(IFT_{n}\{\}\) is the operator of inverse Fourier transform of the spectral density \(S_{z,N}(\mathrm{j}f)={K}_{N}^{-1}(\mathrm{j}f)S_{x,N}(\mathrm{j}f),\ | f| \leq 0.5F\) of the excitation signal of vocal tract {zN(n)}; \(\mathrm{and}\:K_{N}\left(\mathrm{j}f\right)=F{T}_{N}^{-1}\left\{\boldsymbol{b}_{1}\right\}\mathrm{and}\:S_{x,N}(\mathrm{j}f)=c_{0}F{T}_{N}^{-1}\left\{\boldsymbol{b}_{2}\right\}\) are the autoregressive models of the vocal tract (5) and speech signal (9), respectively, formed according to the results of recurrent processing (7) of the sequence of observations \(\{x(n)\}\) of finite volume N.

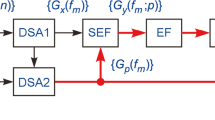
Expression (11), together with (7) and (10) specifies a method intended for the asynchronous analysis of a vocal speech source within the general formulation of the form (3). This method is based on the two-level autoregressive model aimed at the description of speech signals for two different levels of autocorrelation within the period of the fundamental tone (if the orders are equal \(p=p_{1}\)) and in the interval of several consecutive periods (for \(p=p_{2}\)). The problem of small samples in the proposed method is overcome due to the high rate of convergence of the Berg-Levinson recursion [31]. The problem of speed is solved by combining two computation procedures of different kinds within the framework of the common recurrence scheme (7). These procedures are aimed at the estimation, according to a sample {x(n)}, of the autoregressive coefficients \(\left\{a_{{p_{2}}}(i)\right\}\) and moving average \(\left\{a_{{p_{1}}}(i)\right\}\) as parameters of the ARMA model of the voice source (10). The efficiency of the proposed method was experimentally investigated by using the software specially developed by the authorsFootnote 3.

Program and experimental results

As the object of the experimental investigations, we used the signals of six Russian vowel phonemes pronounced by a control speaker (one of the authors of the present paper): “a”, “i”, “o”, “u”, “y”, and “é”. A sufficiently large (3.5–4.0 sec) duration of these signals was chosen with an aim to be able to perform automatic partition of signals with a period of 16 msec into stationary segments of speaker’s oral speech of the same duration equal to \(\tau =128\) msec. For the sampling frequency of speech signal \(F=8\) kHz, the volume of experimental database for each vowel was not smaller than \(R=(3.5-0.128)/0.016\approx 210\) frames of speech of the control speaker with dimensions \(N_{0}=8\cdot 128=1024\). For each frame, we formed four single-phoneme sound files x(t) of different duration τ: 128, 64, 32 and 16 msec. In this case, the dimensions of N vectors of the same name \(\{x(n)\}\) were equal to \(N_{1}=1024;\ N_{2}=512;\ N_{3}=256,\ \mathrm{and }N_{4}=128\) readings, respectively. All sound files of the frame of vowel speech sound “a” are depicted in Fig. 1. It is easy to see that any kind of synchronization of the data of observations with the fundamental tone of speech signal is excluded.

Fig. 1
figure 1

Signal of the Russian vowel phoneme “a” for the observation intervals equal to N = 1024, 512, 256, and 128, regions 1–4, respectively

Full size image

The software implementation of the voice source (11) with parameters \(p_{1}=10\) and \(p_{2}=90\) was experimentally investigated. In this case, the operators of direct and inverse Fourier transforms are realized on the basis of rapid algorithms of Fourier transformations with dimension \(M=2^{10}\) and the frequency selectivity \(\Updelta f=FM^{-1}=7.8125\) Hz. The purpose and principle of action of both operators are illustrated in Figs. 2, 3 and 4.

Fig. 2
figure 2

Amplitude spectrum of the speech signal (1) and the amplitude-frequency response of the vocal tract filter (2) according to the results of processing of the data of observations with a volume \(N=1024\)

Full size image
Fig. 3
figure 3

Amplitude spectrum of the model of voice source of the Russian vowel phoneme “a” for the sample size \(N=1024\)

Full size image
Fig. 4
figure 4

Model of voice source of the Russian vowel phoneme “a” based on the results of processing of the data of observations with a volume \(N=1024\) in two versions of the description: excitation pulses (1) and pulses of the volumetric velocity of air flow (2) at the entrance of the vocal tract

Full size image

In Fig. 2, we present the amplitude spectrum \(S_{x,N}(f)=\left| S_{x,N}\left(\mathrm{j}f\right)\right|\) of the Russian vowel phoneme “a” signal and the amplitude-frequency characteristic \(K_{N}(f)=\left| K_{N}(jf)\right|\) of the vocal tract filter (5) for \(c_{0}=\sqrt{10}\) constructed according to the results of processing the data of observations \(\{x(n)\}\) with the following volume: \(N=1024\). In Fig. 3, we display the corresponding amplitude spectrum \(S_{z,N}(f)=\left| S_{Z,N}\left(\mathrm{j}f\right)\right|\) of the model of voice source (11). The envelope of the amplitude spectrum characterizes the shape of the excitation pulses zN(n), whereas the repetition period of its quasiharmonics characterizes the frequency of the fundamental tone of the signal x(t). In the analyzed case, it is approximately equal to \(F_{0}\approx 132\) Hz. This fact is confirmed by the results of the profile work [29].

The same source (for the volume of observations \(N=1024\)) in the time domain is presented in Fig. 4 by two impulsive sequences: excitation of the vocal tract (11) and volumetric velocity of the air flow:

$$y_{N}(n)=y_{N}(n-1)+z_{N}(n),\quad n=0,1,\ldots ,N-1$$

The shape of excitation pulses on the enlarged scale is shown in Fig. 5 and compared with an impulsive sequence {zN(n)} obtained for \(N=256\). It follows from Fig. 5 that both the shape and repetition frequency \(F_{0}\approx 131.5\) Hz of the pulses of voice source (11) are stable with respect to the duration of the speech signal x(t) within a broad range \(\tau =32\ldots 128\) msec. This conclusion is used as a foundation of the second (final) stage of the experimental investigation of the efficiency of the proposed method of voice analysis.

Fig. 5
figure 5

Model of the voice source in the interval of the first two periods of the fundamental tone of speech signal according to the results of processing of the data of observations with sample sizes N = 1024 and 256; marks 1 and 2 respectively

Full size image

As a parameter of efficiency, we use the objective measure of stability of the ARMA model of the voice source (10) regarded as a function of the sample size N of the data of observations \(\{x(n)\}\):

$$\rho (N)\triangleq \sqrt{F^{-1}\int_{-0.5F}^{0.5F}S_{z,N}^{2}(f){\overline{S}}_{z}^{-2}(f)df} \times \sqrt{F^{-1}\int_{-0.5F}^{0.5F}\overline{S}_{z}^{2}(f){S}_{z,N}^{-2}(f)df-1\geq 0}$$
(12)

Here, \(\overline{S}_{z}(f)\triangleq 0.25\sum_{i=1}^{4}S_{z,{N_{i}}}(f)\) is the mean value of the amplitude spectrum SZ,N(f) of the speech signal on the set of four versions \(S_{z,{N_{i}}}(f),i=\overline{1.4},\) considered in the experiment. In [35], the authors showed the invariance of measure (12) to the scale of the excitation signal {zN(n)}. The lower the value of ρ(N), the higher the stability of the considered model in the dynamics [36]. Moreover, the stability of the ARMA model (10) guarantees the validity of the proposed method of voice analysis [7].

The obtained results are presented in Fig. 6 in the form of a family of plots of the function ρ(N) for six Russian vowel phonemes pronounced by the control speaker. The vertical segments at the control points of these plots specify the boundaries of the confidence interval of parameter (12) according to the results of multiple (R-fold) measurements. In this case, the relative length of the confidence interval \(\varepsilon =1.65/\sqrt{R}\) [29] for a confidence level equal to 0.9 does not go beyond \(165\cdot 210^{-\frac{1}{2}}=11.38\mathrm{{\%}}\). The plots presented in Fig. 6 differ from each other only in details. However, they are similar in the main: in all versions, the optimal choice of the size of sample {x(n)} lies within the range \(N=256{-}512\). This volume corresponds to the length of the interval of observations \(\tau =32{-}64\) msec. This is, in fact, the requirement of the proposed method to the duration of the speech signal x(t) in the problem of voice analysis (2)–(4). Moreover, the lower boundary \(\tau =32\) msec of the acceptable signal duration is directly related to the period T0 of its fundamental tone [29]. In the experiments, for different vowels, it varied within the range 7–8 msec. At the same time, the upper boundary \(\tau =64\) msec of acceptable duration reflects a natural requirement of the proposed method (7), (10), and (11) to the stability of fine structure of the speech signal in the interval of observations.

Fig. 6
figure 6

Dependence of the parameter of accuracy of the ARMA model of voice source (11) on the duration of Russian vowel phonemes: “a” (1), “i” (2), “o” (3), “u” (4), “y” (5), and “é” (6)

Full size image

Discussion of the obtained results

We now consider the speed of the developed method for the analysis of voice sources determined by the two factors: the duration τ of the speech frame characterizing the period of updating the results of the voice analysis of speech in formulation (11) and the computational complexity of the proposed method caused by the total amount of calculations \(W_{\tau }=W_{7}+W_{10}\) performed according to relations (7) and (11). For relations (7), we have about \(W_{7}=3Np_{2}=3\tau Fp_{2}\) elementary operations of multiplication and division of real numbers [30]. The cost of simulation of the vocal tract by the autoregressive model (5) of order \(p_{1}< p_{2}\) is not taken into account in this case because, in the recurrence computational scheme, they are included in the computation cost of modeling of the speech signal (9) [36]. In the case of relation (11), the volume of computations includes the threefold cost of performing the M-point rapid Fourier transform for \(M\geq N\), which correspond to \(W_{10}=3M\log_{2}M\) elementary operations. In total, we get \(W_{\tau }=3\left(Np_{2}+M\log_{2}M\right)\) elementary operations within the interval of observations of length τ or \(W=W_{\tau }/\tau =3F\left(p_{2}+N^{-1}M\log_{2}M\right)\) operations per second. Thus, under the conditions of the performed experiment, for \(p_{2}=90;F=8\) kHz; \(\tau =2^{5}\) msec; \(N=2^{8}; \mathrm{ and }M=2^{10},\) we get \(W=3\cdot 8000\left(90+2^{-8}\cdot 2^{10}\cdot 10\right)=3.12\cdot 10^{6}c^{-1}\), which gives, as a result of recalculation to the clock frequency of the computing device, 3.12 MHz. This result, with a significant margin (by an order of magnitude or more) corresponds to the efficiency of modern speech systems operating under the conditions of soft (with delays for the duration of a single frame) real-time mode [37].

Conclusions

The proposed method for the analysis of voice sources of speech makes it possible to model the excitation signal (3) of the vocal tract of a speaker in real time. Its sufficiently high speed is explained by the use of a high-speed recurrence procedure (7) used to adjust the parameters of the ARMA model (10) for a sequence of excitation pulses (11) according to a speech signal x(t) of finite duration τ. The proposed method does not require synchronization of the sequence of observations \(\{x(n)\}\) with the fundamental tone of the speech signal and is characterized by relatively small calculation costs required for the technical implementation. The performed full-scale experiment confirmed the high speed of the proposed method and, at the same time, allowed us to formulate the requirements to the duration of speech signals.

The obtained results are intended for applications in the development and investigation of modern systems of digital speech communication, voice control, biometrics, biomedicine, and other speech systems [7] in which the specific voice features of speaker’s speech are of primary importance.