1 Introduction and motivation

Many modern engineering systems, which include lightweight, thin, and flexible elements as essential parts, are often called upon to meet high, if not extreme, performance. Therefore, cables, ropes, pipes, and beams have countless applications and a widespread presence in structural design. Similarly, natural systems, such as cellular cilia and flagella, tree branches, mammalian long bones or insect legs, to name a few, have shapes that allow us to consider them, with some accuracy, as ropes or beams. The behavior of each of these types of elements can be described using an appropriate beam theory. Noteworthy, the formulation of a beam includes many modeling assumptions that are difficult to capture in their wide diversity, leading the definition itself of a beam to represent a challenge [1]. One of the key aspects concerns constitutive assumptions, whose definitions can be given with or without reference to a three-dimensional beam theory, as induced or intrinsic theories do, respectively. In this respect, a delicate point is the choice of the curvature to be adopted as the flexural deformation in formulating the constitutive relation for the bending moment.

Basically, there are different, though equivalent, definitions of what must be said the curvature of a plane curve in a point. Roughly speaking we can say that the curvature of a plane curve in a point is the rate of change of direction (of the tangent vector to the curve) with arc length at that point measured along the curve. As reported in [2], such a concept was already stated in 1758 by Kästner in his book “Foundations of Mathematics”, where the curvature of a curve at a point is defined as the ratio of the angle subtended between two tangents to the curve at two points, in the limit of their coincidence, and the length of the arc of the curve between them. However, the Cartesian form of the curvature was derived by Newton even before 1671, year during which his “Method of fluxions” was finished (although published in 1736, when Newton was already passed away), by using for the first time the concept of “fluxion”, kind of kinematic notion of derivative.

Lamb, in two articles of his book [3], namely Art. 127, p. 275, “The capillary curve” and Art. 150, p. 323, “Finite flexure of a rod”, claims that the two problems are essentially equivalent and both described through the Young-Laplace equation. Indeed, the latter states that the pressure jump at the interface between two fluids at different pressures is proportional to the surface tension times the curvature of the interface. To use the same equation for the beam problem, it is necessary to multiply both the pressure jump and the surface tension for a quantity having dimensions of a volume. Thus, they take dimensions of a bending moment and a bending stiffness, respectively, leaving unchanged dimensions of curvature, which now refers to the beam axis. Indeed, as reported by Love [4], already Bernoulli and Euler stated that the bending moment is proportional to the curvature of the deformed beam axis (see also [5, p. 123]). However, such a seemingly innocuous statement actually has subtle consequences, at least from a purely theoretical point of view. Since they are worthy of further study, in the following we will try to illuminate these aspects from the ground up.

We know that, in general, in a beam bent in a plane, without shearing deformation, two different cross sections exhibit different rotations. Let us consider cross sections at a mutual reference distance which is approaching zero and measure the variation of rotation with respect to the undeformed element. If the length of the element remains unchanged during the deformation process, the local extrinsic curvature has same value of the derivative of the rotation with respect to the reference configuration. If, on the other hand, the bending is accompanied by stretching, the geometric curvature has instead value equal to that of the derivative of the rotation with respect to the deformed arclength.

Therefore, there are two notable choices for the derivative of the rotation, which we call from now on “mechanical” and “geometrical” curvatures, of course both having dimensions of inverse of a length and both, at least in principle, could be considered as candidates for the strain to set up a one-dimensional constitutive assumption for the bending moment.

There is a long history of formulations to describe large deformations of beams and there is in parallel a large amount of papers accepting, sometimes implicitly, the constitutive assumption of Bernoulli and Euler (i.e. the moment is proportional to the geometrical curvature), or even the moment is whatever function of the geometrical curvature. A short, not exhaustive list of contributions in this direction includes [3, 5,6,7,8,9,10,11,12,13,14,15]. In some cases, the geometrical curvature is considered for the general case, although only the inextensible one is analyzed, making the two curvatures identical [16,17,18,19,20]. In addition, the geometrical curvature in the Cartesian form is explicitly adopted sometimes [21,22,23,24], although it is observed in [25] that it has no physical meaning for the problem of the bending of a beam in terms of the axial coordinate, unless derivatives are redefined to be with respect to the shortened axis, thus achieving the relation found by Koiter [26] (having, from a purely formal perspective, the same structure of a curvature in parametric form).

In contrast, there are many contributions assuming that the mechanical curvature (possibly adopting different names) is the right flexural strain related to the bending moment, as in [27,28,29,30,31,32,33,34,35,36,37,38,39,40], to cite a few.

There are also attempts to unravel the issue as in [41, 42], where it is concluded that it is better to use the mechanical curvature, although it is recalled that in intrinsic beam theories constitutive assumptions are introduced in axiomatic way and therefore, at least in principle, both geometrical and mechanical curvature may be legitimate choices.

The definition of the problem also seems to be complicated by reasons of nomenclature, to the point that [43] feels the need to explicitly warn that the quantity measuring the bending does not coincide with the curvature of the beam, apparently in the sense that the bending strain should differ from the curvature seen in the geometric sense.

Therefore, two questions arise. Why is the choice of curvature so important? Is there one, in any sense, that is correct?

The answer to the former question, besides the above cited purely theoretical interest, could be relevant also from a practical point of view. In fact, the choice of the strain measure to adopt in formulating a constitutive relationship for the bending moment for beams undergoing large deflections and rotations may influence the accuracy and reliability of results, in comparison with experiments, unless specific conditions are met. To cite a few, if the inextesibility assumption of the beam centerline is enforced (as already stated before), or the beam does not experience any extension due to loads or boundary conditions, or the curvature is expanded in power series and only linear terms are retained, the two curvatures, still different in principle, are quantitatively coincident. In these cases, choosing one or the other curvature does not affect the practical results, but this is no longer true if these conditions are not met, and the issue regains possible moderate relevance in practical terms as well. In fact, in [44] it is shown that the use of the two definitions of curvature does not affect the linear frequency, while it has an effect on the nonlinear correction coefficient of the backbone curve, which becomes negligible for slender beams.

The answer to the second question given above is more complicated to figure out and requires a comparative approach. Staying in an abstract setting, provided a beam can be defined in some way and the fields involved have appropriate smoothness properties, the balance equations can be derived in differential form by exploiting the Newton approach, also in case the constitutive assumptions are left undefined. Indeed, basically equations of motion in Newtonian form state that the rate of the total linear momentum of the constrained system is the total resultant acting on the system [45].

On the other hand, using a variational principle, the equations of motion can be obtained directly from a scalar functional, the Lagrangian, whose existence is sometimes axiomatically assumed to be basic, to the extent that equations not derivable from such a principle would be considered in certain circles hardly reliable or acceptable. [46, 47].

Therefore, we may argue that the “correct” curvature is that allows deriving the same equations of motion when written in differential form as Newtonian equations and derived from a variational principle. Both definitions of curvature could, in principle, satisfy this basic request. However, we will show in this work - and this is our principal finding - that only the mechanical curvature can have this property, by an adequate choice of the constitutive laws. On the contrary, the geometrical curvature does not have it, whatever is the constitutive law, and thus it is less “robust” from a theoretical point of view, even if of course one can decide in any case to use it, if that is convenient from a different point of view.

In trying to satisfy the previous property, we underline that our unique “degree of freedom”, i.e., the sole part we can choose or modify to obtain the results, is the constitutive law, since the balance law is derived from basic principles and kinematic relations are exact, so both cannot be changed. Therefore, the play now moves to understanding how the constitutive laws should be made so that the balance equations obtained by the Newton approach can also be derived from the stationarity of a Lagrangian function. In other words, when the differential equations are given, one needs to find out whether they are variational or not [48]. Additionally, in the affirmative case any Lagrange function for these equations must be constructed. Indeed, the Lagrangian in not unique and it can be either natural (that is, equal to the difference between the kinetic and potential energy of the system [49]) or virtual (also called nonstandard or unnatural, that cannot be split into kinetic and potential energy [50]).

This is the inverse problem of the calculus of variations [51], which is of considerable interest, since the variational formulation provides compact descriptions of dynamical systems, also giving natural means of approximating or finding solutions [52], to the point that numerical methods using discrete Lagrangians often have significant advantages over other integration methods such as, for instance, Runge–Kutta algorithms [50].

General conditions for the existence of Lagrangians were first obtained by Helmholtz [53] (and therefore referred to as the Helmholtz conditions) and then generalized by Boehm [54]. In agreement with what was previously stated, the goal of this contribution is indeed to verify, by exploiting Helmholtz conditions, which notion of curvature gives rise to a variational system of equations of motion.

The paper is organized as follows. The exact kinematics of the beam, with no a priori assumption on the order of magnitude of displacements and rotations, is introduced in Sect. 2. The balance written by means of the Newton approach is reported in Sect. 3 and the constitutive assumptions are detailed in Sect. 4. The variational form of the equations of motion is introduced in Sect. 5 and Helmholtz conditions are summarized in Sect. 6. The existence of a Lagrangian under the condition that one or another definition of the curvature is chosen as bending strain is discussed in Sects. 7 and 8, which are indeed the main core of this work. Some conclusive remarks are finally reported in Sect. 9.

2 The exact kinematics and the strain measures

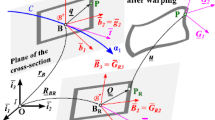
Let us consider a plane beam that in general, both in its initial and deformed configuration, has a curved shape. Given a generic frame of reference, the beam configurations can be conveniently represented in parametric form by expressing the components of the vectors from the origin to points with coordinates X, Y (initial configuration) and x, y (current configuration) as functions of a space parameter z and time t. For convenience, the parameter z can be taken as a coordinate along one of the reference axes. Therefore, the initial configuration, which is assumed to be stress-free, is remapped to a straight reference configuration, as shown in Fig. 1. By calling \(\text {d}S\) the length of an infinitesimal beam element in initial configuration, we may state

$$\begin{aligned} \text {d}S=\sqrt{\text {d}X^2+\text {d}Y^2} \quad \rightarrow \quad S'=\sqrt{X'^2+Y'^2} \,, \end{aligned}$$
(1)

where prime means derivative with respect to z.

Fig. 1
figure 1

The beam element in its three relevant configurations (reference, initial stress-free and deformed)

Full size image

The angle between the tangent to the initial configuration and the reference one is

$$\begin{aligned} \Phi =\arctan \left( \frac{\text {d}Y}{\text {d}X}\right) = \arctan \left( \frac{ Y'}{ X'}\right) . \end{aligned}$$
(2)

The geometrical curvature of the initial configuration is defined as

$$\begin{aligned} K_g=\frac{\text {d}\Phi }{\text {d}S}=\frac{\text {d}\Phi }{\text {d}z}\frac{\text {d}z}{\text {d}S}=\frac{\Phi ^\prime }{S^\prime }, \end{aligned}$$
(3)

where the angle \(\text {d}\Phi\) is also

$$\begin{aligned} \text {d}\Phi =\frac{\text {d}S}{R}, \end{aligned}$$
(4)

R being the radius of the osculans circle at the infinitesimal initial element (see Fig. 1).

We note that the curvature given by Eq. (3) can be seen as the product of \(\Phi ^\prime\) times the ratio between the length \(\text {d}z\) of the reference beam-element and the length \(\text {d}S\) of the initial one.

We call \(\Phi ^\prime\) the initial mechanical curvature,

$$\begin{aligned} K_m=\frac{\text {d}\Phi }{\text {d}z}=\Phi ^\prime =K_g S' , \end{aligned}$$
(5)

in agreement with the definition adopted in [41] (although using a slight different symbology) and we observe that the quantity

$$\begin{aligned} \lambda _R=\frac{\text {d}S}{\text {d}z}=S^\prime \end{aligned}$$
(6)

represents the fictitious stretch relating initial and reference configurations, which however has no physical meaning.

Once the beam element is deformed, its infinitesimal length is

$$\begin{aligned} \text {d}s=\sqrt{\text {d}x^2+\text {d}y^2} \quad \rightarrow \quad s'=\sqrt{x'^2+y'^2} \,, \end{aligned}$$
(7)

and the angle \(\text {d}\varphi\) is

$$\begin{aligned} \text {d}\varphi =\frac{\text {d}s}{r}, \end{aligned}$$
(8)

r being the radius of the osculans circle at the infinitesimal deformed element (see Fig. 1). The current (i.e. deformed) mechanical curvature, coherently with Eq. (5), is expressed as

$$\begin{aligned} k_m=\frac{\text {d}\varphi }{\text {d}z}=\varphi ^\prime =\left( \arctan \left( \frac{y^\prime }{x^\prime }\right) \right) ^\prime = \frac{x^\prime y^{\prime \prime }-y^\prime x^{\prime \prime }}{{x^\prime }^2+{y^\prime }^2}, \end{aligned}$$
(9)

and the current geometrical curvature is

$$\begin{aligned} k_g=\frac{k_m}{s^\prime } = \frac{x^\prime y^{\prime \prime }-y^\prime x^{\prime \prime }}{\left( {x^\prime }^2+{y^\prime }^2\right) ^{3/2}} . \end{aligned}$$
(10)

Similarly to what was observed above, the stretch the element undergoes when passing from the reference configuration to the current one is given by

$$\begin{aligned} \lambda =\frac{\text {d}s}{\text {d}z}=s^\prime . \end{aligned}$$
(11)

By comparing initial and current configurations, we may define the deformation of the beam-element along its tangent direction as

$$\begin{aligned} \varepsilon =\frac{\text {d}s}{\text {d}S}-1=\frac{\lambda }{\lambda _R}-1=\frac{s^\prime }{S^\prime }-1 = \frac{\sqrt{x^{\prime 2}+y^{\prime 2}}}{S^\prime }-1 , \end{aligned}$$
(12)

and the changes of mechanical and geometrical curvatures respectively as

$$\begin{aligned} \Delta k_m =k_m-K_m{=\varphi ^\prime -\Phi ^\prime =\left( \varphi -\Phi \right) ^\prime =\left( \Delta \varphi \right) ^\prime } \end{aligned}$$
(13)

and

$$\begin{aligned} \Delta k_g =k_g-K_g{=\frac{\varphi ^\prime }{s^\prime }-\frac{\Phi ^\prime }{S^\prime }}. \end{aligned}$$
(14)

In the following we consider Euler-Bernoulli beams only. Accordingly, the rotation \(\varphi\) of two adjacent cross sections is equal to the tangent angle of the deformed configuration, and there is no shear strain. Therefore, the axial strain given in Eq. (12) and the flexural strain, alternatively given by Eq. (13) or Eq. (14), are enough to describe the deformation of the beam. Notice that, in the Euler-Bernoulli beam theory, \(k_g\) is quantitatively equivalent to the curvature 1/r of the deformed beam line. On the contrary, in the stress-free configuration, it should be recognized that \(K_g=1/R\) holds.

2.1 Additional remarks on kinematics

A number of further relationships among the kinematic quantities can be found. We report here some of them.

From Eq. (12),

$$\begin{aligned} s^\prime =S^\prime (1+\varepsilon ) \end{aligned}$$
(15)

straightforwardly follows. It is also easily recognized that

$$\begin{aligned}&\sin {\varphi } = \frac{y^\prime }{s^\prime } = S^\prime \frac{\partial \varepsilon }{\partial y^\prime } = -\frac{\partial \Delta k_m}{\partial x^{\prime \prime }} S^\prime (1+\varepsilon )\nonumber \\&= -\frac{\partial \Delta k_g}{\partial x^{\prime \prime }}\left( S^\prime (1+\varepsilon )\right) ^2\,, \end{aligned}$$
(16)
$$\begin{aligned}&\cos {\varphi } = \frac{x^\prime }{s^\prime }= S^\prime \frac{\partial \varepsilon }{\partial x^\prime } \nonumber \\&= \frac{\partial \Delta k_m}{\partial y^{\prime \prime }} S^\prime (1+\varepsilon )= \frac{\partial \Delta k_g}{\partial y^{\prime \prime }}\left( S^\prime (1+\varepsilon )\right) ^2\, \end{aligned}$$
(17)

hold, and from these it also attained

$$\begin{aligned} \tan {\varphi }= \frac{y^\prime }{x^\prime }=\frac{\displaystyle \frac{\partial \varepsilon }{\partial y^\prime }}{\displaystyle \frac{\partial \varepsilon }{\partial x^\prime }}= -\frac{\displaystyle \frac{\partial \Delta k_m}{\partial x^{\prime \prime }}}{\displaystyle \frac{\partial \Delta k_m}{\partial y^{\prime \prime }}}= -\frac{\displaystyle \frac{\partial \Delta k_g}{\partial x^{\prime \prime }}}{\displaystyle \frac{\partial \Delta k_g}{\partial y^{\prime \prime }}}. \end{aligned}$$
(18)

We also emphasize that \(\varepsilon\) here and the one in [41] have different meanings: here \(\varepsilon\) is, indeed, the Biot strain of the beam axis [34], whereas \(\varepsilon\) in [41] is the Euler–Lagrange strain in the direction and at the height of the beam axis.

It is important to observe that the displacements along the global directions \(x(z,t)-X(z)\) and \(y(z,t)-Y(z)\) (X and Y independent of time) are related to the tangential displacement u(z, t) (i.e. along the axis of the initial configuration) and the radial displacement v(z, t) (i.e. transversal to the axis of the initial configuration) by

$$\begin{aligned} x-X&= u \cos {\Phi } - v \sin {\Phi }\,, \end{aligned}$$
(19)
$$\begin{aligned} y-Y&= u \sin {\Phi } + v \cos {\Phi } \,, \end{aligned}$$
(20)

and that \(\varphi (z,t)\) is the rotation of the section with respect to the fictitious straight configuration, being \(\Delta \varphi (z,t)=\varphi (z,t)-\Phi (z)\) (\(\Phi\) independent of time) the actual rotation with respect to the initial configuration.

2.2 Nesting between nonlinear strains

There is a number of possible definitions of strains relevant in a beam theory. The strains used in this work are the axial strain \(\varepsilon\) defined in Eq. (12) and the flexural strains \(\Delta k_m\) and \(\Delta k_g\) defined in Eq. (13) and Eq. (14), respectively.

The three different strains depend on z,  in a direct way, being functions of \(S^\prime\) or \(\Phi ^\prime\) or both, and in nested way being functions of the derivatives of the placements x and y.

Actually, only two of the three measures are independent on each other, as shown by the simple relation

$$\begin{aligned} \Delta k_g = \frac{\Delta k_m -\varepsilon \Phi ^\prime }{S^\prime \left( 1+\varepsilon \right) }, \end{aligned}$$
(21)

that is obtained by exploiting Eq. (3), Eq. (5), Eq. (10), Eq. (13), Eq. (14), and Eq. (15). More precisely, from a theoretical point of view it is necessary to assume that the axial strain \(\varepsilon\) and one of the two flexural strains are independent of each other, while the other flexural strain follows from (21).

By virtue of Eqs. (16) and (17), from Eq. (13), it can be achieved

$$\begin{aligned} \Delta k_m =S^\prime \left( \frac{\partial \varepsilon }{\partial x^\prime } \left( S^\prime \frac{\partial \varepsilon }{\partial y^\prime } \right) ^\prime -\frac{\partial \varepsilon }{\partial y^\prime } \left( S^\prime \frac{\partial \varepsilon }{\partial x^\prime } \right) ^\prime \right) -\Phi ^\prime , \end{aligned}$$
(22)

which is another relation between derivatives of strains, that could be useful in the sequel. Note that it does not imply that \(\Delta k_m\) is a function of the local value of \(\varepsilon ,\) but of the whole function \(\varepsilon (z,t)\) that varies from case to case.

3 The balance with Newton approach

The balance equations can be obtained through the Newton approach by requiring that the sum of forces and bending moments, including inertial ones, vanish on the deformed configuration, see Fig. 2. By calling N,  T and M the generalized internal forces and moments, \(q_x,\) \(q_y\) the distributed external loads, c the distributed external moments, the equations of motion projected along the global axes take the form

$$\begin{aligned} \left( N\cos \varphi + T\sin \varphi \right) ^\prime + q_x = \rho A \ddot{x} , \end{aligned}$$
(23)
$$\begin{aligned} \left( N\sin \varphi - T\cos \varphi \right) ^\prime + q_y = \rho A \ddot{y} , \end{aligned}$$
(24)

and the equation of rotary motion (written about the right end of the beam element, i.e., the end with the greater value of the abscissa) is

$$\begin{aligned} M^\prime - T s' + c = \rho J \ddot{\varphi } . \end{aligned}$$
(25)

In Eqs. (23) to (25), A and J are the cross-sectional area and second moment of area, respectively, \(\ddot{x}\) and \(\ddot{y}\) are the accelerations along the global directions and \(\ddot{\varphi }\) is the rotary acceleration. Superimposed dots stand for the time derivative, where prime, as already stated, means derivative with respect the space parameter z. It is noteworthy that \(q_x,\) \(q_y,\) c,  \(\rho A\) and \(\rho J\) are intensities per unit length of the axis in the reference configuration. In addition, it must be emphasized that N and T in the present work have \(F_a\) and \(F_t\) as counterparts in [41] (therefore, N and T here have a slightly different meaning compared to N and T there).

Fig. 2
figure 2

Internal and external forces and moments in the deformed configuration

Full size image

The inertial terms appear linearly in Eqs. (23)–(25) and so in the following it is convenient to define (see Fig. 2)

$$\begin{aligned} {\hat{q}}_x =q_x -\rho A \ddot{x}, \quad {\hat{q}}_y = q_y -\rho A \ddot{y}, \quad {\hat{c}} = c -\rho J \ddot{\varphi }, \end{aligned}$$
(26)

i.e. to use a d’Alembert’s approach, in a reversed way, by collecting inertial terms and external loads. Indeed, d’Alembert’s principle formally generalizes static equations to dynamics by including the inertia forces as part of the body forces [55], thus extending the principle of virtual work from the statics to dynamics. It is worth noting that applying virtual work to statics results in algebraic equations between forces, whereas d’Alembert’s principle applied to dynamics gives differential equations [56]. The use of Eqs. (26) strongly simplifies the formulation (for example transforms the PDEs in ODEs, which are easier to manage), and allow us to focus on our main results by considering a dynamical problem through its static counterpart, with advantages in terms of computations and understanding. It is worth to underline that this is not a restrictive hypothesis, just a way to simplify the developments.

In Euler-Bernoulli beam model, the shear force T is an internal reaction and not a constitutive force, the rotary inertia \(\rho J \ddot{\varphi }\) can be assumed negligible and the distributed external moment c is typically null. With these assumptions behind Eq. (25), T can be written as

$$\begin{aligned} T = \frac{M'}{s'} = \frac{M^\prime }{S^\prime (1+\varepsilon )} , \end{aligned}$$
(27)

and thus it can be eliminated from Eq. (23) and Eq. (24), which, using Eq. (16) and Eq. (17), then take the form

$$\begin{aligned} \left( N \frac{x'}{s'} + \frac{M'}{s'} \frac{y'}{s'} \right) ^\prime + {\hat{q}}_x = 0, \end{aligned}$$
(28)
$$\begin{aligned} \left( N \frac{y'}{s'} - \frac{M'}{s'} \frac{x'}{s'} \right) ^\prime + {\hat{q}}_y = 0, \end{aligned}$$
(29)

or

$$\begin{aligned}&\left( N S^\prime \frac{\partial \varepsilon }{\partial x^\prime } + \frac{M^\prime }{1+\varepsilon }\frac{\partial \varepsilon }{\partial y^\prime }\right) ^\prime + {\hat{q}}_x = 0\,, \end{aligned}$$
(30)
$$\begin{aligned}&\left( N S^\prime \frac{\partial \varepsilon }{\partial y^\prime } - \frac{M^\prime }{1+\varepsilon }\frac{\partial \varepsilon }{\partial x^\prime }\right) ^\prime + {\hat{q}}_y = 0 \,, \end{aligned}$$
(31)

which are the equations we deal with in the following.

4 The constitutive relations

To complete the set of equations, the constitutive relations must be added to the kinematic and balance equations obtained in the previous sections. Assuming an elastic behavior, of local nature, they can be abstractly described by

$$\begin{aligned} N=\overline{N}(\varepsilon ,\Delta k_m)\quad \text{ and }\quad M=\overline{M}(\varepsilon ,\Delta k_m), \end{aligned}$$
(32)

or

$$\begin{aligned} N=\widehat{N}(\varepsilon ,\Delta k_g)\quad \text{ and }\quad M=\widehat{M}(\varepsilon ,\Delta k_g), \end{aligned}$$
(33)

depending on whether one alternately assumes mechanical or geometrical curvature as the measure of bending strain. We assume that constitutive relationships for N and M do not directly depend on t and z, i.e. the beam is assumed to be homogeneous. The case of non-homogeneous beams, that could be very interesting, is left for future works.

If the constitutive laws are assumed to be smooth enough, as it commonly happens, we have that both \(\overline{N}\) and \(\overline{M}\) can be defined as

$$\begin{aligned}&\overline{N}(\varepsilon ,\Delta k_m) = \sum \limits _{i=0}^\infty \sum \limits _{j=0}^\infty a_{ij}\, \varepsilon ^i\,\Delta k_m^j\,, \end{aligned}$$
(34)
$$\begin{aligned}&\overline{M}(\varepsilon ,\Delta k_m) = \sum \limits _{i=0}^\infty \sum \limits _{j=0}^\infty b_{ij}\,\varepsilon ^i\,\Delta k_m^j\,, \end{aligned}$$
(35)

where \(a_{ij},\) and \(b_{ij},\) \(i,j\in {\mathbb {N}},\) are stiffness terms and where \(a_{00}\) and \(b_{00}\) are the pre-tension. In the linear elastic case without pre-tension we have

$$\begin{aligned}&\overline{N}(\varepsilon ,\Delta k_m) = a_{10} \varepsilon + a_{01} \Delta k_m \,, \end{aligned}$$
(36)
$$\begin{aligned}&\overline{M}(\varepsilon ,\Delta k_m) = b_{10} \varepsilon + b_{01} \Delta k_m \,. \end{aligned}$$
(37)

Similar expressions for \(\widehat{N}\) and \(\widehat{M}\) are easily obtained.

It is worth to the remark that smoothness is not really needed, and non-smooth constitutive relations can be considered as well.

5 Equations of motion

The equations of motion can be derived in a number of different ways, depending whether Newton, Lagrange or Hamilton mechanics are considered (see, e.g. [49]). In the following we consider Newton and Lagrange approaches, and the final goal is to show how and when they are equivalent.

The Newtonian approach consists of combining kinematics, balance and constitutive equations obtained in the previous sections, in such a way to have two equations in the two unknowns x(z, t) and y(z, t). It will be detailed in forthcoming Sects. 7 and 8.

The Lagrange (or variational) approach, on the other hand, is illustrated in the following subsection.

5.1 The variational problem

The Lagrange approach consists of assuming the existence of the Lagrangian functional

$$\begin{aligned} {\mathbb {L}}=\int \limits _0^L\mathcal {L} \,\text {d}z, \end{aligned}$$
(38)

where \(\mathcal {L}\) is the Lagrangian density, that depends on the kinematics unknowns and their derivatives, and on z (the dependence on t is not necessary since we are using the d’Alembert approach, see (26)). It incorporates the constitutive relations and kinematic equations. Since the case of homogeneous beam is considered, it is consistently assumed that \(\mathcal {L}\) also does not depend explicitly on z.

In our problem the unknowns are x and y and the highest derivative is the second (see Eq. (9) or Eq. (10)). Therefore

$$\begin{aligned} \mathcal {L}=\mathcal {L}( x,y,x^\prime ,y^\prime ,x^{\prime \prime }, y^{\prime \prime }). \end{aligned}$$
(39)

The equations of motion, that substituted the missing balance equations, are obtained by assuming the stationarity of the functional in Eq. (39) with respect to any possible variation of the kinematic unknowns. This leads to the Euler–Lagrange equations, which take the form

$$\begin{aligned}&-\frac{\text {d}^2}{\text {d}z^2}\frac{\partial \mathcal {L}}{\partial x^{\prime \prime }} +\frac{\text {d}}{\text {d}z}\frac{\partial \mathcal {L}}{\partial x^\prime }-\frac{\partial \mathcal {L}}{\partial x}=0\,, \end{aligned}$$
(40)
$$\begin{aligned}&-\frac{\text {d}^2}{\text {d}z^2}\frac{\partial \mathcal {L}}{\partial y^{\prime \prime }} +\frac{\text {d}}{\text {d}z}\frac{\partial \mathcal {L}}{\partial y^\prime }-\frac{\partial \mathcal {L}}{\partial y}=0\,, \end{aligned}$$
(41)

together with appropriate boundary conditions, that however are not used in this work and thus are not reported for the sake of conciseness.

For the problem we are dealing with a natural Lagrangian density is of the form

$$\begin{aligned} \mathcal {L}=\mathcal {U}-\mathcal {W}, \end{aligned}$$
(42)

where \(\mathcal {U}=\mathcal {U}(x^\prime ,y^\prime ,x^{\prime \prime }, y^{\prime \prime })\) is the internal energy density and \(\mathcal {W}=\mathcal {W}(x,y)\) is the density of work of the external loads, that in the present case is simply given by

$$\begin{aligned} \mathcal {W}= {\hat{q}}_x\,x +{\hat{q}}_y\,y , \end{aligned}$$
(43)

so that

$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial x}=-{\hat{q}}_x, \quad \frac{\partial \mathcal {L}}{\partial y}=-{\hat{q}}_y, \end{aligned}$$
(44)

and the loads are easily obtained in Eqs. (28)–(31).

If Eq. (42) can be written, the balance given by Eqs. (40) and (41) are rewritten as

$$\begin{aligned}&\frac{\text {d}}{\text {d}z}\left( \frac{\partial \mathcal {U}}{\partial x^\prime }-\frac{\text {d}}{\text {d}z}\frac{\partial \mathcal {U}}{\partial x^{\prime \prime }}\right) + {\hat{q}}_x=0\,, \end{aligned}$$
(45)
$$\begin{aligned}&\frac{\text {d}}{\text {d}z}\left( \frac{\partial \mathcal {U}}{\partial y^\prime }-\frac{\text {d}}{\text {d}z}\frac{\partial \mathcal {U}}{\partial y^{\prime \prime }}\right) + {\hat{q}}_x=0\,. \end{aligned}$$
(46)

While \(\mathcal {W}\) is easy, more complicated is to achieve \(\mathcal {U}.\) If indeed \(\mathcal {U}\) exists, its form cannot be independent of the choice of the constitutive assumptions, so that two different forms of \(\mathcal {U}\) should be expected, namely \(\mathcal {U}=\overline{\mathcal {U}}\) somehow related to Eq. (32), and \(\mathcal {U}=\widehat{\mathcal {U}}\) to Eq. (33).

6 Conditions for the existence of a Lagrangian

A fundamental problem is related to finding the conditions to be satisfied by Eq. (30) and Eq. (31) to be obtained from the stationarity of whatever Lagrangian functional, not necessarily with a physical meaning, i.e. the condition for Eq. (30) and Eq. (31) being equal to Eq. (40) and Eq. (41). This is the inverse problem of the calculus of variations [51].

In a more general setting, given the functions \(P_i=P_i\left( p_j,p_j^\prime ,\ldots ,p_j^{(2n)}\right) ,\) with \(p_j=p_j(z)\) and \(i,j=1,2,\ldots ,m,\) the necessary and sufficient conditions for the existence of a given function \(\mathcal {L}\) of the first n derivatives of the coordinates \(p_i\) such that

$$\begin{aligned} -\left( \frac{\partial \mathcal {L}}{\partial p_i}-\frac{\text {d}}{\text {d}z}\left( \frac{\partial \mathcal {L}}{\partial p^\prime _i}\right) +\cdots +(-1)^n\frac{\text {d}^n}{\text {d}z^n}\left( \frac{\partial \mathcal {L}}{\partial p^{(n)}_i}\right) \right) =P_i, \end{aligned}$$
(47)

were reported by Boehm [54] for \(n=2\) (i.e. fourth order derivatives in the equations), which generalized the work by Helmoltz [53] holding for \(n=1\) (i.e. second order derivatives in the equations). Both are also reported by Kot\(\mathring{{\textrm{u}}}\)lek in [57, 58]. Such conditions state that \(2n+1\) equations written as

$$\begin{aligned} \frac{\partial P_i}{\partial p^{(k)}_j}-\left( {\begin{array}{c}k+1\\ 1\end{array}}\right) \frac{\text {d}}{\text {d}z}\frac{\partial P_i}{\partial p^{(k+1)}_j} +\left( {\begin{array}{c}k+2\\ 2\end{array}}\right) \frac{\text {d}^2}{\text {d}z^2}\frac{\partial P_i}{\partial p^{(k+2)}_j}-\cdots \nonumber \\ +(-1)^{2 n-k}\left( {\begin{array}{c}2n\\ 2n-k\end{array}}\right) \frac{\text {d}^{2n-k}}{\text {d}z^{2n-k}}\frac{\partial P_i}{\partial p^{(2n)}_j}=(-1)^k\frac{\partial P_j}{\partial p^{(k)}_i}, \end{aligned}$$
(48)

with k spanning from 0 to 2n,  must be satisfied.

The case of interest for us is \(n=2\), and Eqs. (48) explicitly become

$$\begin{aligned}{} & {} \frac{\partial P_1}{\partial p_2^{(4)}} = \frac{\partial P_2}{\partial p_1^{(4)}}, \end{aligned}$$
(49)
$$\begin{aligned}{} & {} \frac{\partial P_1}{\partial p_2^{\prime \prime \prime }}+\frac{\partial P_2}{\partial p_1^{\prime \prime \prime }} = 2\frac{\text {d}}{\text {d}z}\left( \frac{\partial P_1}{\partial p_2^{(4)}} + \frac{\partial P_2}{\partial p_1^{(4)}}\right) , \end{aligned}$$
(50)
$$\begin{aligned}{} & {} \frac{\partial P_1}{\partial p_2^{\prime \prime }}-\frac{\partial P_2}{\partial p_1^{\prime \prime }} = \frac{3}{2}\frac{\text {d}}{\text {d}z}\left( \frac{\partial P_1}{\partial p_2^{\prime \prime \prime }} - \frac{\partial P_2}{\partial p_1^{\prime \prime \prime }}\right) , \end{aligned}$$
(51)
$$\begin{aligned}{} & {} \frac{\partial P_1}{\partial p_2^{\prime }}+\frac{\partial P_2}{\partial p_1^{\prime }} = \frac{\text {d}}{\text {d}z}\left( \frac{\partial P_1}{\partial p_2^{\prime \prime }} + \frac{\partial P_2}{\partial p_1^{\prime \prime }}\right) \nonumber \\{} & {} - \frac{\text {d}^3}{\text {d}z^3}\left( \frac{\partial P_1}{\partial p_2^{(4)}} + \frac{\partial P_2}{\partial p_1^{(4)}}\right) , \end{aligned}$$
(52)
$$\begin{aligned}{} & {} \frac{\partial P_1}{\partial p_2} - \frac{\partial P_2}{\partial p_1} = \frac{1}{2}\frac{\text {d}}{\text {d}z}\left( \frac{\partial P_1}{\partial p_j^{\prime }} - \frac{\partial P_2}{\partial p_1^{\prime }}\right) \nonumber \\{} & {} - \frac{1}{4}\frac{\text {d}^3}{\text {d}z^3}\left( \frac{\partial P_1}{\partial p_2^{\prime \prime \prime }} - \frac{\partial P_2}{\partial p_1^{\prime \prime \prime }}\right) . \end{aligned}$$
(53)

In what follows, for symbolic computations, we remind that

$$\begin{aligned} \varepsilon =&\,\varepsilon (x^\prime ,y^\prime ,S^\prime )\,, \end{aligned}$$
(54)
$$\begin{aligned} \Delta k_m=&\,\Delta k_m(x^\prime ,y^\prime ,x^{\prime \prime },y^{\prime \prime },\Phi ^\prime )\,, \end{aligned}$$
(55)
$$\begin{aligned} \Delta k_g=&\,\Delta k_g(x^\prime ,y^\prime ,x^{\prime \prime },y^{\prime \prime },\Phi ^\prime ,S^\prime )\,, \end{aligned}$$
(56)

in agreement with \(\varepsilon ,\) \(\Delta k_m,\) and \(\Delta k_g\) given by Eqs. (12), (13) and (14), respectively.

In addition, because of the cumbersome nature of the calculations required in the following, we will combine manual and computer-aided simplifications. For the latter, we will use symbolic manipulation software.

7 The mechanical curvature as bending strain

Let us now assume that the constitutive laws are those symbolically given by Eqs. (32).

Recalling that by virtue of Eqs. (16) and  (17)

$$\begin{aligned} \frac{1}{1+\varepsilon }\frac{\partial \varepsilon }{\partial y^\prime }=-\frac{\partial \Delta k_m}{\partial x^{\prime \prime }}\quad \text{ and }\quad \frac{1}{1+\varepsilon }\frac{\partial \varepsilon }{\partial x^\prime }=\frac{\partial \Delta k_m}{\partial y^{\prime \prime }} \end{aligned}$$
(57)

hold, Eq. (30) and Eq. (31) can be rewritten, after some algebra, as

$$\begin{aligned} \left( \overline{N}S^\prime \frac{\partial \varepsilon }{\partial x^\prime }- \overline{M}^\prime \frac{\partial \Delta k_m}{\partial x^{\prime \prime }}\right) ^\prime + {\hat{q}}_x = 0, \end{aligned}$$
(58)
$$\begin{aligned} \left( \overline{N}S^\prime \frac{\partial \varepsilon }{\partial y^\prime } -\overline{M}^\prime \frac{\partial \Delta k_m}{\partial y^{\prime \prime }}\right) ^\prime + {\hat{q}}_y = 0\,, \end{aligned}$$
(59)

or, alternatively,

$$\begin{aligned} \left( \overline{N}\frac{x'}{\sqrt{x'^2 + y'^2}} + \overline{M}' \frac{y'}{x'^2+y'^2} \right) ' + {\hat{q}}_x = 0 \,, \end{aligned}$$
(60)
$$\begin{aligned} \left( \overline{N}\frac{y'}{\sqrt{x'^2 + y'^2}} - \overline{M}' \frac{x'}{x'^2+y'^2} \right) ' + {\hat{q}}_y = 0 \,. \end{aligned}$$
(61)

It turns out that Eq. (49) is automatically satisfied, while the condition

$$\begin{aligned} S^\prime \frac{\partial \overline{N}}{\partial \Delta k_m} = \frac{\partial \overline{M}}{\partial \varepsilon }\, \end{aligned}$$
(62)

is got by developing Eq. (50). From Eq. (51), by taking into account Eq. (62) and its first derivatives with respect to both \(\varepsilon\) and \(\Delta k_m,\) we attain

$$\begin{aligned} S^{\prime \prime }\frac{\partial \overline{M}}{\partial \varepsilon }=0. \end{aligned}$$
(63)

Since the constitutive assumptions we consider are Eqs. (32), \(\partial \overline{M}/\partial \varepsilon \ne 0\) is expected to hold in general. Therefore, in order Eq. (63) be satisfied, \(S^{\prime \prime }=0\) must hold, that is \(S^\prime\) does not explicitly depend on z,  so that

$$\begin{aligned} S^{(k)}(z)=0,\quad k\ge 2. \end{aligned}$$
(64)

In fact, the condition \(S^{\prime \prime }=0\) can already be determined from Eq. (62): since we have assumed that \(\overline{N}\) and \(\overline{M}\) do not explicitly depend on z, and since Eq. (62) must hold for every \(\Delta k_m\) and every \(\varepsilon ,\) it follows that \(S^\prime\) must not depend on z,  namely \(S^{\prime \prime }=0\).

By developing Eqs. (51)– (53) we see that the obtained expressions, which are too long to be written here, are automatically satisfied taking in account Eq. (62) and its derivatives and Eq. (64).

In summary, we see that Eq. (62) and \(S''=0\) are the only conditions to be met for the existence of a Lagrangian whose stationarity leads to Eqs. (58) and (59).

7.1 Symmetry conditions

Inspecting Eq. (62), it could be noted that it is a symmetry condition. To argue this concept, let us assume that the potential density \(\mathcal {U}=\overline{\mathcal {U}}\) exists and is at least twice continuously differentiable, so that the Schwarz theorem on second derivatives holds.

Comparing Eq. (45) with Eq. (58), and Eq. (46) with Eq. (59), we can see that

$$\begin{aligned}&\frac{\partial \overline{\mathcal {U}}}{\partial x^\prime }-\frac{\text {d}}{\text {d}z}\frac{\partial \overline{\mathcal {U}}}{\partial x^{\prime \prime }} =\overline{N}S^\prime \frac{\partial \varepsilon }{\partial x^\prime }- \overline{M}^\prime \frac{\partial \Delta k_m}{\partial x^{\prime \prime }}\,, \end{aligned}$$
(65)
$$\begin{aligned}&\frac{\partial \overline{\mathcal {U}}}{\partial y^\prime }-\frac{\text {d}}{\text {d}z}\frac{\partial \overline{\mathcal {U}}}{\partial y^{\prime \prime }} =\overline{N}S^\prime \frac{\partial \varepsilon }{\partial y^\prime } -\overline{M}^\prime \frac{\partial \Delta k_m}{\partial y^{\prime \prime }}\,, \end{aligned}$$
(66)

where the constant of integration is set equal to 0 since this is enough to obtain the desired results. Developing the left hand sides of such equations, and remembering that \(\varepsilon =\varepsilon (x^\prime ,y^\prime ,S^\prime )\) and \(\Delta k_m=\Delta k_m(x^\prime ,y^\prime ,x^{\prime \prime },y^{\prime \prime },\Phi ^\prime )\), we get

$$\begin{aligned}&\frac{\partial \overline{\mathcal {U}}}{\partial x^\prime }-\frac{\text {d}}{\text {d}z}\frac{\partial \overline{\mathcal {U}}}{\partial x^{\prime \prime }} =\frac{\partial \overline{\mathcal {U}}}{\partial \varepsilon }\frac{\partial \varepsilon }{\partial x^\prime }-\left( \frac{\text {d}}{\text {d}z}\frac{\partial \overline{\mathcal {U}}}{\partial \Delta k_m}\right) \frac{\partial \Delta k_m}{\partial x^{\prime \prime }}\nonumber \\&+\frac{\partial \overline{\mathcal {U}}}{\partial \Delta k_m}\left( \frac{\partial \Delta k_m}{\partial x^{\prime }}-\frac{\text {d}}{\text {d}z}\frac{\partial \Delta k_m}{\partial x^{\prime \prime }}\right) \,, \end{aligned}$$
(67)
$$\begin{aligned}&\frac{\partial \overline{\mathcal {U}}}{\partial y^\prime }-\frac{\text {d}}{\text {d}z}\frac{\partial \overline{\mathcal {U}}}{\partial y^{\prime \prime }} =\frac{\partial \overline{\mathcal {U}}}{\partial \varepsilon }\frac{\partial \varepsilon }{\partial y^\prime }-\left( \frac{\text {d}}{\text {d}z}\frac{\partial \overline{\mathcal {U}}}{\partial \Delta k_m}\right) \frac{\partial \Delta k_m}{\partial y^{\prime \prime }}\nonumber \\&+\frac{\partial \overline{\mathcal {U}}}{\partial \Delta k_m}\left( \frac{\partial \Delta k_m}{\partial y^{\prime }}-\frac{\text {d}}{\text {d}z}\frac{\partial \Delta k_m}{\partial y^{\prime \prime }}\right) \,. \end{aligned}$$
(68)

Inserting Eq. (67) in Eq. (65), and Eq. (68) in Eq. (66), and knowing that

$$\begin{aligned}{} & {} \frac{\partial \Delta k_m}{\partial x^{\prime }}=\frac{\text {d}}{\text {d}z}\frac{\partial \Delta k_m}{\partial x^{\prime \prime }}\,\quad \text{ and }\quad \frac{\partial \Delta k_m}{\partial y^{\prime }}=\frac{\text {d}}{\text {d}z}\frac{\partial \Delta k_m}{\partial y^{\prime \prime }}, \end{aligned}$$
(69)

as seen by virtue of Eq. (9), we achieve

$$\begin{aligned}&\frac{\partial \overline{\mathcal {U}}}{\partial \varepsilon }\frac{\partial \varepsilon }{\partial x^\prime }-\left( \frac{\text {d}}{\text {d}z}\frac{\partial \overline{\mathcal {U}}}{\partial \Delta k_m}\right) \frac{\partial \Delta k_m}{\partial x^{\prime \prime }} =N S^\prime \frac{\partial \varepsilon }{\partial x^\prime }-\overline{M}^\prime \frac{\partial \Delta k_m}{\partial x^{\prime \prime }}\,, \end{aligned}$$
(70)
$$\begin{aligned}&\frac{\partial \overline{\mathcal {U}}}{\partial \varepsilon }\frac{\partial \varepsilon }{\partial y^\prime }-\left( \frac{\text {d}}{\text {d}z}\frac{\partial \overline{\mathcal {U}}}{\partial \Delta k_m}\right) \frac{\partial \Delta k_m}{\partial y^{\prime \prime }} =N S^\prime \frac{\partial \varepsilon }{\partial y^\prime } - \overline{M}^\prime \frac{\partial \Delta k_m}{\partial y^{\prime \prime }}\,, \end{aligned}$$
(71)

or reordering side by side

$$\begin{aligned}&\left( \frac{\partial \overline{\mathcal {U}}}{\partial \varepsilon }-\overline{N}S^\prime \right) \frac{\partial \varepsilon }{\partial x^\prime } =\frac{\text {d}}{\text {d}z}\left( \frac{\partial \overline{\mathcal {U}}}{\partial \Delta k_m}-\overline{M}\right) \frac{\partial \Delta k_m}{\partial x^{\prime \prime }}\,, \end{aligned}$$
(72)
$$\begin{aligned}&\left( \frac{\partial \overline{\mathcal {U}}}{\partial \varepsilon }-\overline{N}S^\prime \right) \frac{\partial \varepsilon }{\partial y^\prime } =\frac{\text {d}}{\text {d}z}\left( \frac{\partial \overline{\mathcal {U}}}{\partial \Delta k_m}-\overline{M}\right) \frac{\partial \Delta k_m}{\partial y^{\prime \prime }}\,. \end{aligned}$$
(73)

The latter are satisfied if

$$\begin{aligned}{} & {} \frac{\partial \overline{\mathcal {U}}}{\partial \varepsilon }=\overline{N}S^\prime \end{aligned}$$
(74)

and

$$\begin{aligned}{} & {} \frac{\partial \overline{\mathcal {U}}}{\partial \Delta k_m}=\overline{M}, \end{aligned}$$
(75)

provided that \(\partial \varepsilon /\partial x^\prime ,\) \(\partial \varepsilon /\partial y^\prime ,\) \(\partial \Delta k_m/\partial x^{\prime \prime }\) and \(\partial \Delta k_m/\partial y^{\prime \prime }\) are not null in general. Then,

$$\begin{aligned}{} & {} S^\prime \frac{\partial \overline{N}}{\partial \Delta k_m}=\frac{\partial ^2\overline{\mathcal {U}}}{\partial \Delta k_m\partial \varepsilon }=\frac{\partial ^2\overline{\mathcal {U}}}{\partial \varepsilon \partial \Delta k_m}=\frac{\partial \overline{M}}{\partial \varepsilon }, \end{aligned}$$
(76)

which is in fact Eq. (62).

We observe that, as confirmed by Eq. (75), \(\Delta k_m\) is work-conjugated to \(\overline{M},\) which is expected, while interestingly \(\varepsilon\) is in correspondence to \(\overline{N}S^\prime ,\) instead of \(\overline{N},\) as a consequence of Eq. (74).

7.2 Construction of the internal energy density

By virtue of Eqs. (74), (75) and (76), it is possible to obtain the internal energy density as

$$\begin{aligned} \overline{\mathcal {U}}&= \int \limits _0^\varepsilon {\frac{\partial \overline{\mathcal {U}}}{\partial \varepsilon ^\star }\text {d}\varepsilon ^\star }+ \int \limits _0^{\Delta k_m}{\frac{\partial \overline{\mathcal {U}}}{\partial \Delta k_m^\star }\text {d}\Delta k_m^\star }- \int \limits _0^{\Delta k_m}\int \limits _0^\varepsilon {\frac{\partial ^2\overline{\mathcal {U}}}{\partial \Delta k_m^\star \partial \varepsilon ^\star }\text {d}\varepsilon ^\star \text {d}\Delta k_m^\star }\nonumber \\&=\int \limits _0^\varepsilon {\overline{N}S^\prime \text {d}\varepsilon ^\star }+ \int \limits _0^{\Delta k_m}{\overline{M}\text {d}\Delta k_m^\star }-\int \limits _0^{\Delta k_m}\int \limits _0^\varepsilon {\frac{\partial \overline{M}}{\partial \varepsilon ^\star }\text {d}\varepsilon ^\star \text {d}\Delta k_m^\star }, \end{aligned}$$
(77)

where \(\varepsilon ^\star\) and \(\Delta k_m^\star\) are dummy variables introduced for formal reasons. We must observe that Eq. (77) has only an abstract nature, since at this stage Eqs. (32) are not explicitly written. An example is reported in the forthcoming Eq. (92).

7.3 Some further remarks

We observe that satisfying Eq. (64) implies that \(S(z)=c_1 z+c_2,\) with \(c_1\) and \(c_2\) two constants to be chosen, the former dimensionless, the latter with dimension of a length. This, indeed, could be interpreted as a condition stating that an appropriate reference configuration must be chosen for the existence of the Lagrangian or, in different words, that the stationarity depends also on the reference configuration. In addition, Eq. (6) allows to observe that the fictitious stretch \(\lambda _R\) plays a role only in the transformation of the initial configuration into the reference one. Therefore, it defines a remapping rule. Noteworthy, whenever the initial length and the reference one are in a fixed ratio, \(S^\prime\) is constant. This simple choice is indeed convenient and rational.

Equation (62) extends to the nonlinear realm a results that is well-known in linear elasticity, namely that a material is conservative if and only if its elasticity tensor is symmetric, i.e. \(a_{01}=b_{10}\) in Eqs. (36) and (37).

A further remark pertains to the uncoupled case of constitutive assumptions, i.e.

$$\begin{aligned} N=\overline{N}(\varepsilon )\quad \text{ and }\quad M=\overline{M}(\Delta k_m). \end{aligned}$$
(78)

In such a case, Eqs. (49) to (53) are automatically satisfied, being Eq. (62) an identity with both sides vanishing, leading to the symmetry which is trivially satisfied and the condition stated by Eq. (64) is not anymore required.

Finally, an apparently not obvious relationship between the derivatives of \(\overline{M},\) standing the abstract nature of Eq. (32), descends from Eq. (49), which is automatically satisfied, as stated before. In fact both sides of Eq. (49) take the same value, i.e.,

$$\begin{aligned} \frac{\partial P_1}{\partial p_2^{(4)}} = -\frac{1}{S^\prime }\frac{\partial \overline{M}}{\partial \Delta k_m} \frac{\partial \Delta k_m}{\partial y^{\prime \prime }} \frac{\partial \Delta k_m}{\partial x^{\prime \prime }} = \frac{\partial P_2}{\partial p_1^{(4)}}. \end{aligned}$$
(79)

To further manipulate Eq. (79), we use Eqs. (57) and

$$\begin{aligned} \frac{\partial \overline{M}}{\partial x^{\prime \prime }}= \frac{\partial \overline{M}}{\partial \Delta k_m} \frac{\partial \Delta k_m}{\partial x^{\prime \prime }}\quad \text{ and }\quad \frac{\partial \overline{M}}{\partial y^{\prime \prime }}= \frac{\partial \overline{M}}{\partial \Delta k_m} \frac{\partial \Delta k_m}{\partial y^{\prime \prime }}, \end{aligned}$$
(80)

following from the chain rule. Thus, we are led to recognize that

$$\begin{aligned} \frac{\partial \varepsilon }{\partial y^{\prime }}\frac{\partial \overline{M}}{\partial y^{\prime \prime }}=-\frac{\partial \varepsilon }{\partial x^{\prime }}\frac{\partial \overline{M}}{\partial x^{\prime \prime }} \end{aligned}$$
(81)

holds. It appears as the static counterpart of the kinematic relationship

$$\begin{aligned} \frac{\partial \varepsilon }{\partial y^{\prime }}\frac{\partial \Delta k_m}{\partial y^{\prime \prime }}=- \frac{\partial \varepsilon }{\partial x^{\prime }}\frac{\partial \Delta k_m}{\partial x^{\prime \prime }}, \end{aligned}$$
(82)

taken from Eq. (18).

7.4 An example of Lagrangian density

Let us consider no pre-tension and only terms at most cubic in \(\varepsilon ,\) \(\Delta k_m\) and their mutual products in Eq. (34) and Eq. (35), obtaining

$$\begin{aligned}&\overline{N}(\varepsilon ,\Delta k_m)=a_{10}\,\varepsilon +a_{20}\,\varepsilon ^2+a_{30}\,\varepsilon ^3\nonumber \\&+a_{01}\,\Delta k_m+a_{02}\,\Delta k_m^2+a_{03}\,\Delta k_m^3\nonumber \\&+a_{11}\,\varepsilon \,\Delta k_m+a_{12}\,\varepsilon \,\Delta k_m^2+a_{21}\,\varepsilon ^2\,\Delta k_m\,, \end{aligned}$$
(83)
$$\begin{aligned}&\overline{M}(\varepsilon ,\Delta k_m)= b_{10}\,\varepsilon +b_{20}\,\varepsilon ^2+b_{30}\,\varepsilon ^3 \nonumber \\&+b_{01}\,\Delta k_m+b_{02}\,\Delta k_m^2+b_{03}\,\Delta k_m^3\nonumber \\&+b_{11}\,\varepsilon \,\Delta k_m+b_{12}\,\varepsilon \,\Delta k_m^2+b_{21}\,\varepsilon ^2\,\Delta k_m\,. \end{aligned}$$
(84)

By virtue of Eq. (62) it can be recognized that

$$\begin{aligned} \begin{matrix} a_{01}=\displaystyle \frac{b_{10}}{S^\prime }, &{} a_{02}=\displaystyle \frac{1}{2}\frac{b_{11}}{S^\prime }, &{} a_{03}=\displaystyle \frac{1}{3}\frac{b_{12}}{S^\prime },\\ \\ a_{11}=2\displaystyle \frac{b_{20}}{S^\prime }, &{} a_{12}=\displaystyle \frac{b_{21}}{S^\prime }\ , &{} a_{21}=3\displaystyle \frac{b_{30}}{S^\prime }. \end{matrix} \end{aligned}$$
(85)

In addition, by introducing \(K_\ell ,\) \((\ell =0,\ldots ,4),\) which are the products of the longitudinal elastic modulus times the moment of area of \(\ell\)th order, the dimensional analysis allows to set

$$\begin{aligned} \begin{matrix} a_{10}=K_0\,\alpha _{10}, &{} a_{20}=K_0\,\alpha _{20}, &{} a_{30}=K_0\,\alpha _{30},\\ b_{10}=K_1\,\beta _{10}, &{} b_{20}=K_1\,\beta _{20}, &{} b_{30}=K_1\,\beta _{30},\\ b_{01}=K_2\,\beta _{01}, &{} b_{02}=K_3\,\beta _{02}, &{} b_{03}=K_4\,\beta _{03},\\ b_{11}=K_2\,\beta _{11}, &{} b_{21}=K_2\,\beta _{21}, &{} b_{12}=K_3\,\beta _{12},\\ \end{matrix} \end{aligned}$$
(86)

where \(\alpha _{ij}\) and \(\beta _{ij},\) \((i,j=0,\ldots ,3)\) are real numbers.

Therefore, generalized internal forces in Eqs. (83) and (84) can be rewritten as

$$\begin{aligned} \overline{N}&=K_0\,\varepsilon \left( 1+\alpha _{20}\,\varepsilon +\alpha _{30}\,\varepsilon ^2\right) +K_1\frac{\Delta k_m}{S^\prime }\left( 1+2\,\beta _{20}\,\varepsilon +3\,\beta _{30}\,\varepsilon ^2\right) \nonumber \\&+K_2\frac{\Delta k_m^2}{S^\prime }\left( \frac{\beta _{11}}{2}+\beta _{21}\,\varepsilon \right) + K_3\frac{\beta _{12}\,\Delta k_m^3}{3\,S^\prime }\,, \end{aligned}$$
(87)
$$\begin{aligned} \overline{M}&=K_1\,\varepsilon \left( 1+\beta _{20}\,\varepsilon +\beta _{30}\,\varepsilon ^2\right) +K_2\,\Delta k_m\left( 1+\beta _{11}\,\varepsilon +\beta _{21}\,\varepsilon ^2\right) \nonumber \\&+K_3\,\Delta k_m^2\left( \beta _{02}+\beta _{12}\,\varepsilon \right) +K_4\,\beta _{03}\,\Delta k_m^3\,, \end{aligned}$$
(88)

in a frame of reference whose axes, in general, do not pass through the cross-sectional centroid and are not principal. In addition, in Eqs. (87) and (88), \(\alpha _{10}=\beta _{10}=\beta _{01}=1\) is conveniently accepted in order the linearized versions of Eqs. (87) and (88) agree with the standard linear model, that is

$$\begin{aligned} \overline{N}&=K_0\,\varepsilon +K_1 \,\Delta k_m\,, \end{aligned}$$
(89)
$$\begin{aligned} \overline{M}&=K_1\,\varepsilon +K_2\,\Delta k_m\,, \end{aligned}$$
(90)

with reference and initial configurations having the same length (\(S^\prime =1\)). In the centroidal principal axes (\(K_1=0\)), Eqs. (87) and (88) are coupled, while Eqs. (89) and (90) not.

It is straightforward to recognize that Eqs. (87) and (88) include different models, depending on the values of real constants. For instance, to recover the model in [34], written with respect the centroidal principal axes for a straight beam, whose stress-free configuration is used as reference, then again \(S^\prime =1,\) it is enough to set

$$\begin{aligned} \begin{matrix} \alpha _{20}=\beta _{21}=\displaystyle \frac{3}{2},&\alpha _{30}=\beta _{03}=\displaystyle \frac{1}{2},&\beta _{11}=3. \end{matrix} \end{aligned}$$
(91)

7.4.1 The potential energy density

As they are constructed, Eqs. (87) and (88) satisfy the symmetry condition and inserted in Eq. (77) allow obtaining

$$\begin{aligned}{} & {} \overline{\mathcal {U}}_0=\frac{K_0}{2}\,S^\prime \,\varepsilon ^2\left( 1+\frac{2\,\alpha _{20}}{3}\,\varepsilon +\frac{\alpha _{30}}{2}\,\varepsilon ^2\right) \nonumber \\{} & {} + K_1\,\varepsilon \,\Delta k_m\left( 1+\beta _{20}\,\varepsilon +\beta _{30}\,\varepsilon ^2\right) \nonumber \\{} & {} +\frac{K_2}{2}\,\Delta k_m^2 \left( 1+\beta _{11}\,\varepsilon +\beta _{21}\,\varepsilon ^2\right) + \frac{K_3}{3}\,\Delta k_m^3\left( \beta _{02}+\beta _{12}\,\varepsilon \right) \nonumber \\{} & {} + \frac{K_4}{4}\,\beta _{03}\,\Delta k_m^4. \end{aligned}$$
(92)

7.4.2 The equations from Newton and Lagrange approaches

We conclude this section emphasizing that Eqs. (58) and (59), obtained according the Newton approach, i.e. directly from the balance of an infinitesimal beam element, become explicit in terms of functions x and y and their derivatives by virtue of generalized forces given by Eqs. (87) and (88) and strains from Eqs. (12) and (13).

On the other hand, following the Lagrange approach, as stated before, we insert Eqs. (43) and Eq. (92) in Eqs. (45) and (46).

After long, but straightforward, calculations, the two set of equations result identical, as expected being satisfied the Helmholtz-Boehm conditions.

8 The geometrical curvature as bending strain

Let us now assume that the constitutive laws are those symbolically given by Eqs. (33).

As done before, we transform Eqs. (30) and (31) recalling Eqs. (16) and  (17) and, after some algebra, attain

$$\begin{aligned} \left( \widehat{N}S^\prime \frac{\partial \varepsilon }{\partial x^\prime }- \widehat{M}^\prime S^\prime (1+\varepsilon )\frac{\partial \Delta k_g}{\partial x^{\prime \prime }}\right) ^\prime +{\hat{q}}_x = 0, \end{aligned}$$
(93)
$$\begin{aligned} \left( \widehat{N}S^\prime \frac{\partial \varepsilon }{\partial y^\prime } -\widehat{M}^\prime S^\prime (1+\varepsilon )\frac{\partial \Delta k_g}{\partial y^{\prime \prime }}\right) ^\prime +{\hat{q}}_x = 0, \end{aligned}$$
(94)

or, equivalently,

$$\begin{aligned} \left( \widehat{N}\frac{x'}{\sqrt{x'^2 + y'^2}} + \widehat{M}' \frac{y'}{x'^2+y'^2} \right) ' + {\hat{q}}_x = 0 \,, \end{aligned}$$
(95)
$$\begin{aligned} \left( \widehat{N}\frac{y'}{\sqrt{x'^2 + y'^2}} - \widehat{M}' \frac{x'}{x'^2+y'^2} \right) ' + {\hat{q}}_y = 0 \,. \end{aligned}$$
(96)

Similarly to the case of Eqs. (32), recalling Eqs. (12) and (21), Eq. (49) is satisfied, with results similar to Eq. (80) and Eq. (81), provided that \(\widehat{M}\) and \(\Delta k_g\) are used in place of \(\overline{M}\) and \(\Delta k_m,\) respectively.

From Eq. (50) we now get

$$\begin{aligned} \frac{\partial \widehat{N}}{\partial \Delta k_g}=(1+\varepsilon )\frac{\partial \widehat{M}}{\partial \varepsilon }-\left( \Delta k_g+\frac{\Phi ^\prime }{S^\prime }\right) \frac{\partial \widehat{M}}{\partial \Delta k_g}, \end{aligned}$$
(97)

which is more complicated than Eq. (62).

Developing Eq. (51), the resulting equation contains \(\partial \widehat{N}/\partial \Delta k_g,\) \(\partial ^2 \widehat{N}/\partial \Delta k_g^2\) and \(\partial ^2 \widehat{N}/\partial \Delta \varepsilon \partial \Delta k_g.\) The former is given by Eq. (97) and allows computing the others, also making use of the chain rule, as

$$\begin{aligned} \begin{aligned} \frac{\partial ^2 \widehat{N}}{\partial \Delta k_g^2}=&(1+\varepsilon )\frac{\partial ^2 \widehat{M}}{\partial \varepsilon \partial \Delta k_g} -\left( \Delta k_g+\frac{\Phi ^\prime }{S^\prime }\right) \frac{\partial ^2 \widehat{M}}{\partial \Delta k_g^2} -\frac{\partial \widehat{M}}{\partial \Delta k_g}, \end{aligned} \end{aligned}$$
(98)
$$\begin{aligned} \begin{aligned} \frac{\partial ^2 \widehat{N}}{\partial \varepsilon \partial \Delta k_g}=&(1+\varepsilon )\frac{\partial ^2 \widehat{M}}{\partial \varepsilon ^2}+\frac{\partial \widehat{M}}{\partial \varepsilon } -\left( \Delta k_g+\frac{\Phi ^\prime }{S^\prime }\right) \frac{\partial ^2 \widehat{M}}{\partial \varepsilon \partial \Delta k_g} . \end{aligned} \end{aligned}$$
(99)

Inserting Eq. (97), Eq. (98) and Eq. (99) in Eq. (51) allows us attaining the relation between the first derivative of \(\widehat{M}\) with respect to its arguments as

$$\begin{aligned} \left( \Delta k_g + \frac{\Phi ^\prime }{S^\prime }\right) ^\prime \frac{\partial \widehat{M}}{\partial \Delta k_g}=\varepsilon ^\prime \frac{\partial \widehat{M}}{\partial \varepsilon }\,, \end{aligned}$$
(100)

or

$$\begin{aligned} k_g^\prime \frac{\partial \widehat{M}}{\partial \Delta k_g}=\varepsilon ^\prime \frac{\partial \widehat{M}}{\partial \varepsilon }. \end{aligned}$$
(101)

This requires heavy and long computations, that are omitted for the sake of conciseness.

Equation (100) inserted in Eq. (97) gives

$$\begin{aligned} \frac{\partial \widehat{N}}{\partial \Delta k_g}= \left( 1+\varepsilon - \frac{\varepsilon ^\prime \,S^\prime \left( \Delta k_g\,S^\prime +\Phi ^\prime \right) }{S^\prime \left( {\Delta k_g}^\prime \,S^\prime +\Phi ^{\prime \prime }\right) -S^{\prime \prime }\, \Phi ^\prime }\right) \frac{\partial \widehat{M}}{\partial \varepsilon } , \end{aligned}$$
(102)

provided that \(\Delta k_g^\prime \ne -(\Phi ^\prime /S^\prime )^\prime\) holds (i.e. \(k_g^\prime \ne 0\)), which is the counter part of (62).

Inspecting Eqs. (97) and (100), we note that they explicitly depend on the space variable z,  because of the term \(\Phi ^\prime /S^\prime .\) However, observing that \(\widehat{N}\) and \(\widehat{M}\) in Eqs. (33) do not depend directly on z, since we have assumed that the beam is homogeneous, their derivatives with respect to \(\varepsilon\) and \(\Delta k_g\) do likewise. Therefore, in order left and right hand sides of both Eqs. (97) and (100) are mutually consistent, they cannot explicitly depend on z. In Eq. (97) this requires \(\Phi ^\prime /S^\prime =c_3\), namely \(\Phi (z)=c_3 S(z) + c_4\), being \(c_3\) and \(c_4\) two constants to be freely chosen. Once the initial shape is given, i.e. \(\Phi (z)\) is known, this relation can be used to properly select S(z). We note again that to (hope to) have stationarity, the reference configuration cannot be chosen freely.

The four case-examples in Fig. 3 show that this implies that equidistant cross sections on the initial configuration do not correspond to equidistant cross sections on the reference configuration unless \(\Phi ^\prime\) is constant, i.e., if the beam is initially straight or a circular arch. Therefore a configurational stretching (without physical effects) is needed to be applied to the reference configuration.

We observe that also assuming \(\Phi ^\prime /S^\prime =c_3\) is not sufficient to make Eq. (100), rewritten as

$$\begin{aligned} \frac{\Delta k_g^\prime }{\varepsilon ^\prime } \frac{\partial \widehat{M}}{\partial \Delta k_g}=\frac{\partial \widehat{M}}{\partial \varepsilon }, \end{aligned}$$
(103)

independent of z. In fact, this would require to find a function f such that

$$\begin{aligned} \Delta k_g^\prime = f(\varepsilon , \Delta k_g) \varepsilon ^\prime . \end{aligned}$$
(104)

This is an ODE in the two unknown functions \(x^\prime (z)\) and \(y^\prime (z)\) (the dependence on t is irrelevant here). Since \(\Delta k_g^\prime\) contains \(x^{\prime \prime \prime }\) and \(y^{\prime \prime \prime }\), see Eq. (10), that are not present on the right hand side, where there are only \(x^{\prime \prime }\) and \(y^{\prime \prime }\), we conclude that it is not possible to find an f such that Eq. (104) is valid for any possible deformation \(x^\prime\) and \(y^\prime\), which is indeed what we are looking for.

This means that independence of z cannot be achieved. Therefore, the Helmholtz-Boehm condition given by Eq. (51) cannot be satisfied, and we must conclude that a \(\widehat{\mathcal {U}},\) which would imply that \(\widehat{N}\) and \(\widehat{M}\) in Eqs. (33) are potentials, does not exist. Being no longer necessary at this point, we skip to test Eqs. (52) and (53).

This, which is the main result of this work and is valid for beams of any initial shape, marks a fundamental difference between geometrical and mechanical curvature when used as strain measures of bending. It extends a preliminary result already cited in [59] for straight Timoshenko beams. See also [41] for further developments on this topic.

Fig. 3
figure 3

Four case-examples of initially curved beams with reference configurations stretched accordingly to the curvature \(\Phi ^{\prime }\): circular (a), parabolic (b), sinusoidal (c) and Jacobi’s elliptic \(\vartheta _1\) arches. Notice that cross sections equally spaced on the initial configuration remains equally spaced in the reference configuration only for the case (a) of constant curvature

Full size image

8.1 An additional observation

As shown before, Eqs. (33) are not potential, in the sense that it is not possible to find a \(\widehat{\mathcal {U}}\) from which to derive suitable Eqs. (33) to recover Eqs. (93) and (94), not even in the uncoupled case \(N=\widehat{N}(\varepsilon )\) and \(M=\widehat{M}(\Delta k_g)\). In fact, in Eq. (97), \(\partial \widehat{N}/\partial \Delta k_g=0\) leads to

$$\begin{aligned} \frac{\partial \widehat{M}}{\partial \varepsilon }=\frac{S^\prime \Delta k_g+\Phi ^\prime }{S^\prime \left( 1+\varepsilon \right) }\frac{\partial \widehat{M}}{\partial \Delta k_g}, \end{aligned}$$
(105)

but accepting the left hand side vanishes, i.e. \(\partial \widehat{M}/\partial \varepsilon =0,\) would imply also \(\partial \widehat{M}/\partial \Delta k_g=0,\) provided that, in the general case, \(\Delta k_g\ne -\Phi ^\prime /S^\prime\) must hold. Of course, having \(\widehat{M}\) independent of \(\Delta k_g,\) after requiring the independence of \(\varepsilon\) for the uncoupled case, is a contradiction. However, also if a mixed case is considered, that is \(N=\widehat{N}(\varepsilon )\) and \(M=\widehat{M}(\varepsilon ,\Delta k_g),\) it is still not possible to make both Eq. (100) and Eq. (105) independent of z.

8.2 An alternative verification

In Sect. 7.1, by the direct comparison of Eq. (45) with Eq. (58), and Eq. (46) with Eq. (59), we recovered Eq. (62), which is the symmetry condition for Hessian matrix of \(\overline{\mathcal {U}}\) and one out of two conditions to be required in order \(\overline{N}\) and \(\overline{M}\) be potential.

The fact that, as stated before, Eq. (51) is not fulfilled in the case \(\Delta k_g\) is adopted as the bending strain implies that there is no \(\widehat{\mathcal {U}}\) from which both \(\widehat{N}\) and \(\widehat{M}\) can be derived. Then, a question arises: what kind of result do we get in comparing the Euler–Lagrange equations for some arbitrary \(\widehat{\mathcal {U}}\) with Eqs. (93) and (94) written according to the Newton approach? We argue about this question here.

Let us assume a certain \(\widehat{\mathcal {U}}\) is chosen, from which we may develop, coherently with Eq. (45),

$$\begin{aligned}{} & {} \frac{\partial \widehat{\mathcal {U}}}{\partial x^\prime }-\frac{\text {d}}{\text {d}z}\frac{\partial \widehat{\mathcal {U}}}{\partial x^{\prime \prime }}\nonumber \\{} & {} =\frac{\partial \widehat{\mathcal {U}}}{\partial \varepsilon }\frac{\partial \varepsilon }{\partial x^\prime }\nonumber \\{} & {} +\frac{\partial \widehat{\mathcal {U}}}{\partial \Delta k_g}\frac{\partial \Delta k_g}{\partial x^{\prime }} -\left( \!\frac{\text {d}}{\text {d}z}\frac{\partial \widehat{\mathcal {U}}}{\partial \Delta k_g}\!\right) \frac{\partial \Delta k_g}{\partial x^{\prime \prime }}-\frac{\partial \widehat{\mathcal {U}}}{\partial \Delta k_g}\left( \!\frac{\text {d}}{\text {d}z}\frac{\partial \Delta k_g}{\partial x^{\prime \prime }}\!\right) \nonumber \\{} & {} =\frac{\partial \widehat{\mathcal {U}}}{\partial \varepsilon }\frac{\partial \varepsilon }{\partial x^\prime }\nonumber \\{} & {} -{S^\prime }^3(1+\varepsilon )^3\left( \!\frac{\partial \Delta k_g}{\partial x^{\prime \prime }}\!\right) ^2\!\frac{\text {d}}{\text {d}z}\!\left( \!\frac{\partial \widehat{\mathcal {U}}}{\partial \Delta k_g}\left( \!{S^\prime }^3(1+\varepsilon )^3\frac{\partial \Delta k_g}{\partial x^{\prime \prime }}\!\right) ^{-1}\!\right) , \end{aligned}$$
(106)

and, similarly for Eq. (46),

$$\begin{aligned}{} & {} \frac{\partial \widehat{\mathcal {U}}}{\partial y^\prime }-\frac{\text {d}}{\text {d}z}\frac{\partial \widehat{\mathcal {U}}}{\partial y^{\prime \prime }}\nonumber \\{} & {} =\frac{\partial \widehat{\mathcal {U}}}{\partial \varepsilon }\frac{\partial \varepsilon }{\partial y^\prime }\nonumber \\{} & {} -{S^\prime }^3(1+\varepsilon )^3\left( \!\frac{\partial \Delta k_g}{\partial y^{\prime \prime }}\!\right) ^2\!\frac{\text {d}}{\text {d}z}\!\left( \!\frac{\partial \widehat{\mathcal {U}}}{\partial \Delta k_g}\left( \!{S^\prime }^3(1+\varepsilon )^3\frac{\partial \Delta k_g}{\partial y^{\prime \prime }}\!\right) ^{-1}\!\right) . \end{aligned}$$
(107)

Assuming that \(\partial \varepsilon /\partial x^\prime \ne 0\) and \(\partial \varepsilon /\partial y^\prime \ne 0\) hold in general, comparing Eq. (106) with Eq. (93) and Eq. (107) with Eq. (94) we achieve

$$\begin{aligned} \frac{\partial \widehat{\mathcal {U}}}{\partial \varepsilon }=\widehat{N}S^\prime , \end{aligned}$$
(108)

analogous and formally equivalent to Eq. (74). Comparing Eq. (106) with Eq. (93) it is obtained

$$\begin{aligned} \frac{\widehat{M}^\prime }{{S^\prime }^2(1+\varepsilon )^2}=\frac{\partial \Delta k_g}{\partial x^{\prime \prime }}\frac{\text {d}}{\text {d}z}\left( \frac{\partial \widehat{\mathcal {U}}}{\partial \Delta k_g}\left( {S^\prime }^3(1+\varepsilon )^3\frac{\partial \Delta k_g}{\partial x^{\prime \prime }}\right) ^{-1}\right) , \end{aligned}$$
(109)

while comparing Eq. (107) with Eq. (94) gives

$$\begin{aligned} \frac{\widehat{M}^\prime }{{S^\prime }^2(1+\varepsilon )^2}=\frac{\partial \Delta k_g}{\partial y^{\prime \prime }}\frac{\text {d}}{\text {d}z}\left( \frac{\partial \widehat{\mathcal {U}}}{\partial \Delta k_g}\left( {S^\prime }^3(1+\varepsilon )^3\frac{\partial \Delta k_g}{\partial y^{\prime \prime }}\right) ^{-1}\right) , \end{aligned}$$
(110)

provided that \(\partial \Delta k_g/\partial y^{\prime \prime }\ne 0\) and \(\partial \Delta k_g/\partial x^{\prime \prime }\ne 0\) hold in general.

Dividing, side by side, Eq. (109) by Eq. (110), after some algebra, we achieve

$$\begin{aligned} \frac{\Delta k_g\,S^\prime +\Phi ^\prime }{x^\prime y^\prime }\frac{\partial \widehat{\mathcal {U}}}{\partial \Delta k_g}=0, \end{aligned}$$
(111)

which is satisfied only if \(\partial \widehat{\mathcal {U}}/\partial \Delta k_g=0,\) provided that the other terms are not null, in general.

We must therefore conclude that, besides the fact that having \(\widehat{\mathcal {U}}\) independent of \(\Delta k_g\) seems quite contradictory, it also implies that \(\widehat{M}\) is not potential, in perfect agreement with what we deduced using Helmholtz-Boehm conditions.

8.2.1 A naïve derivation of the equations of motion

The arguments shown above led us to the conclusion that a Lagrangian admitting Eqs. (93) and (94) as Euler–Lagrange equations does not exist. As stated before, this is related to the fact that it is not possible to find an elastic potential \(\widehat{\mathcal {U}}\) from which to derive suitable Eqs. (33) to recover Eqs. (93) and (94).

If we relax the request and naïvely assume that there is some \(\widetilde{\mathcal {U}}\) that allows the axial force and the bending moment to be derived similarly to Eqs. (74) and (75), i.e.

$$\begin{aligned} \frac{\partial \widetilde{\mathcal {U}}}{\partial \varepsilon }=\widetilde{N}S^\prime \end{aligned}$$
(112)

and

$$\begin{aligned} \frac{\partial \widetilde{\mathcal {U}}}{\partial \Delta k_g}=\widetilde{M}, \end{aligned}$$
(113)

what would the equations of motion look like? How do they differ from Eqs. (93) and (94)?

The answers to these questions are found by replacing \(\widehat{\mathcal {U}}\) with \(\widetilde{\mathcal {U}}\) in Eqs. (106) and (107) and then making use of Eqs. (112) and (113). Therefore, after some algebra, we achieve

$$\begin{aligned} \left( \!\widetilde{N}\!S^\prime \frac{\partial \varepsilon }{\partial x^\prime }- \widetilde{M}^\prime \frac{\partial \Delta k_g}{\partial x^{\prime \prime }}+\widetilde{M}\!\left( 3\frac{\partial \Delta k_g}{\partial x^{\prime \prime }}\frac{S^{\prime \prime }}{S^\prime }+\frac{\text {d}}{\text {d}z}\frac{\partial \Delta k_g}{\partial x^{\prime \prime }}\right) \!\right) ^{\!\!\prime }\! + {\hat{q}}_x= 0 , \end{aligned}$$
(114)
$$\begin{aligned} \left( \!\widetilde{N}\!S^\prime \frac{\partial \varepsilon }{\partial y^\prime }- \widetilde{M}^\prime \frac{\partial \Delta k_g}{\partial y^{\prime \prime }}+\widetilde{M}\!\left( 3\frac{\partial \Delta k_g}{\partial y^{\prime \prime }}\frac{S^{\prime \prime }}{S^\prime }+\frac{\text {d}}{\text {d}z}\frac{\partial \Delta k_g}{\partial y^{\prime \prime }}\right) \!\right) ^{\!\!\prime }\! + {\hat{q}}_y = 0 , \end{aligned}$$
(115)

having inserted \(\widetilde{\mathcal {U}}\) and Eqs. (43) in Eq. (42).

A direct comparison between Eq. (93) and Eq. (114), and between Eq. (94) and Eq. (115), shows the differences. In particular, \(\widehat{M}\) cannot be written in terms of \(\widetilde{M},\) because of \(\partial \Delta k_g/\partial x^{\prime \prime }\) in the former comparison and \(\partial \Delta k_g/\partial y^{\prime \prime }\) in the latter. Therefore, as expected, the two sets of equations cannot be made equivalent.

9 Conclusions

This work is devoted to understanding what conditions must be satisfied by the constitutive relations in order for the equations of motion obtained by the Newton approach to be obtained also by the variational Euler–Lagrange approach.

Indeed, in the scientific literature, two different notions of curvature are adopted, sometimes without making explicit the reasons behind the choice. With the aim of unraveling the problem on a definitional basis (i.e., from definitions and nomenclature), the balance equations of beams satisfying the Euler-Bernoulli assumptions and with a generic initial configuration are written using the Newton approach before introducing the constitutive assumptions. Then, the equations are particularized to the two cases of the bending moment as a function of the mechanical or the geometrical curvature, i.e. the derivative of the cross-sectional rotation with respect to the reference length and the arc length, respectively. By means of the Helmholtz conditions, the two systems of differential equations have been checked to see if they are variational or not.

It has been found that the equations based on the constitutive assumption relating the bending moment to the mechanical curvature satisfy the Helmholtz conditions and therefore can be derived from a Lagrangian. In such a case, an example of Lagrangian, among the infinitely many, has been constructed as well. In particular, such a Lagrangian is of the natural type, i.e. it can be expressed in terms of the difference between the kinetic and the potential energy of the system.

On the other hand, it has been argued that the equations containing the geometrical curvature do not allow the Helmholtz conditions to be satisfied, nullifying the possibility that there is a Lagrangian that allows such equations to be derived. To emphasize such a fact, we proceeded ignoring it and naïvely derived a natural Lagrangian, essentially based on what one would straightforwardly expect from a mechanical system. This led us to clearly see the ineradicable differences between Newtonian and variational set of equations in this case.

We finally observe that, while the evaluation of the quantitative effect of using one or the other curvature are not considered here, with some comments found in the cited literature, the obtained results are definitely important from the theoretical standpoint. Furthermore, we remark that we considered a direct 1D approach, where the constitutive laws can be freely chosen (and we provided conditions on them for the existence of the Lagrangian). Actually, it is possible to derive them from a 3D approach, i.e. considering the beam as a 3D body, along the lines developed in [41]. Of course, the generality of the 3D constitutive law will give the generality of the derived 1D constitutive law.