Classical Nonlinear Beam Theories

Abstract

Classical nonlinear beams from the point of view of an induced theory are continuous bodies with a constrained position field which are described by the motion of a centerline and the motion of plane rigid cross sections attached to every point at the centerline. This restricted kinematics allows to determine resultant forces at each cross section and to reduce the equations of motion of a three-dimensional continuous body to a partial differential equation with only one spatial variable. The present chapter is partly based on the publication of Eugster et al. [1]. First, in Sect. 5.1, the kinematical assumptions are stated. Subsequently, in Sect. 5.2, the virtual work contributions of the internal forces, the inertia forces and the external forces are reformulated by the application of the restricted kinematics to the virtual work of the continuous body. In Sects. 5.3–5.5 we present the generalized constitutive laws of the geometrically nonlinear and elastic theories of Timoshenko, Euler–Bernoulli and Kirchhoff in the form of a semi-induced beam theory. Lastly, Sect. 5.6 closes the chapter with a concise literature survey of numerical implementations of nonlinear classical beam theories.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Classical nonlinear beams from the point of view of an induced theory are continuous bodies with a constrained position field which are described by the motion of a centerline and the motion of plane rigid cross sections attached to every point at the centerline. This restricted kinematics allows to determine resultant forces at each cross section and to reduce the equations of motion of a three-dimensional continuous body to a partial differential equation with only one spatial variable. The present chapter is partly based on the publication of Eugster et al. [1].

First, in Sect. 5.1, the kinematical assumptions are stated. Subsequently, in Sect. 5.2, the virtual work contributions of the internal forces, the inertia forces and the external forces are reformulated by the application of the restricted kinematics to the virtual work of the continuous body. In Sects. 5.3–5.5 we present the generalized constitutive laws of the geometrically nonlinear and elastic theories of Timoshenko, Euler–Bernoulli and Kirchhoff in the form of a semi-induced beam theory. Lastly, Sect. 5.6 closes the chapter with a concise literature survey of numerical implementations of nonlinear classical beam theories.

1 Kinematical Assumptions

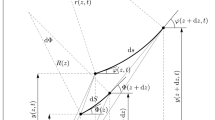
For the derivation of the classical beam theory, it is convenient to think of a slender continuous body with an isotropic material behavior as depicted in Fig. 5.1. First, we assume at a given instant of time $t$ a placement of the slender body in $\mathbb {E}^3$, at which the body covers the subset $\overline{\varOmega }_t\subset \mathbb {E}^3$. We identify the characteristic direction of the slender isotropic body with an arbitrarily chosen centerline $\mathbf r$ which propagates along the largest expansion of the body. The property that the configuration ${\varvec{\xi }}(\cdot ,t)$ at time $t$ is an embedding, enables us to identify every point of the continuous body in $\overline{\varOmega }_t$ with a unique point in the set . Subsequently, we choose the body chart $\theta$ such that the centerline $\mathbf r$ is parametrized by only. For a classical beam we assume the existence of a motion given by the constrained position field of the form

$$\begin{aligned} {\varvec{\xi }}(\theta ^\alpha ,\nu ,t)= \mathbf x(\mathbf q(\cdot ,t))(\theta ^\alpha ,\nu ) = \mathbf r(\nu ,t)+\theta ^\alpha \mathbf d_\alpha (\nu ,t), \end{aligned}$$

(5.1)

where the generalized position functions $\mathbf q(\cdot ,t)$ are recognized as $\mathbf r(\cdot ,t)$, $\mathbf d_1(\cdot ,t)$ and $\mathbf d_2(\cdot ,t)$. The centerline is given by the space curve $\mathbf r(\cdot ,t) = {\varvec{\xi }}(0,0,\cdot ,t)$ and is bounded by its ends $\nu = \nu _1$ and $\nu =\nu _2$ for $\nu _2>\nu _1$. A customary choice of $\nu$ is the arc length parametrization $s$ of the centerline $\mathbf r$. Since the arc length parametrization comes along with an additional constraint and may change under deformation from one instant of time to another, we do not want to restrict us to this special case. At every material point $\nu$ of the centerline $\mathbf r$ a positively oriented orthonormal director triad $(\mathbf d_1(\nu ,t),\mathbf d_2(\nu ,t),\mathbf d_3(\nu ,t))$ is attached. The two directors $\mathbf d_\alpha$ span the plane cross section of the beam. The current state of the cross section ${\varvec{\xi }}(\bar{A}(\nu ),\nu ,t)$ is parametrized by the cartesian coordinates $(\theta ^1,\theta ^2) \in \bar{A}(\nu )$, where . The restriction to cartesian coordinates is implied by the parametrization of the cross section by two orthonormal directors. For specific problems, e.g. computation of the cross section area, appropriate local reparametrizations can be performed. One could think of different descriptions of the plane which do allow for more general coordinates, but such a generalization is outside the scope of this book. The director triad $(\mathbf d_1,\mathbf d_2,\mathbf d_3)$ can be related to an inertial orthonormal basis $(\mathbf e_1,\mathbf e_2,\mathbf e_3)$ by introducing for the rotation tensor $\mathbf R(\nu ,t) \in SO(3)$ such that

$$\begin{aligned} \mathbf d_k(\nu ,t) = \mathbf R(\nu ,t) \mathbf e_k, \qquad \mathrm {with} \; \mathbf R= \mathbf d_k \otimes \mathbf e_k. \end{aligned}$$

(5.2)

For orthonormal vector triads, we do not distinguish here between co- and contravariant vectors. In (5.1) we have identified the generalized position functions $\mathbf q(\cdot ,t)$ with $\mathbf r(\cdot ,t)$, $\mathbf d_1(\cdot ,t)$, $\mathbf d_2(\cdot ,t)$ and have constrained the directors $\mathbf d_1(\cdot ,t)$ and $\mathbf d_2(\cdot ,t)$ by (5.2) to remain orthonormal. Hence, the evaluation at $\nu$ of the generalized position functions $\mathbf q(\cdot ,t)$ can be considered as a point on the 6-dimensional manifold $\mathbb {E}^3 \times SO(3)$.

Fig. 5.1

Reference and current configuration of the beam

Since a beam in an induced theory is treated as a continuous body with a constrained position field, one has to guarantee that the motion always requires the conditions of an embedding . As long as the density of the volume form $g^{1/2}>0$ does not vanish for every point $\theta ^k$ and the function remains injective, the permanence of matter and the principle of impenetrability are fulfilled and the motion is an embedding. As an example of how extreme such deformations can be, we assume a beam with circular cross sections of radius $r$ where the cross sections remain orthogonal to the tangent vector of the centerline. As depicted in Fig. 5.2, the beam is bent in-plane up to a bending radius $R$. As long as the bending radius is larger than the radius of the beam $R \ge r$, no interpenetration of the cross sections may appear. This restriction seems to be reasonable for the example at hand. Ultimately, at the configuration where the bending radius coincides with the cross section radius $r=R$, the lateral surfaces of the beam come into contact. Because of the impenetrability condition $R \ge r$, beam theories are generally limited to slender bodies (among other reasons).

Fig. 5.2

Maximal allowed deformation of a beam with cross section radius $r$ and limit bending radius $R$

In the classical beam theory, the cross section deformation is considered to be irrelevant for the deformation of the body. Consequently, the cross section is rigidified by the choice of the constrained position field (5.1). This implies that material points which are on the same cross section stay on the same cross section throughout the whole motion of the body. The choice of the body chart together with the current configuration can be denominated as a fibration of the continuous body. In the remainder of this section the kinematical expressions which are necessary for the formulation of the virtual work (4.3) of the constrained continuous body are derived.

To begin with the effective curvature, the angular velocity and the virtual rotation, which all describe the change of the directors when changing a single parameter, e.g. the parameter $\nu$. Using (5.2), we derive

(5.3)

in which we recognize the effective curvature ${\tilde{\mathbf k}}=\mathbf R'\mathbf R^{\mathop {\mathrm {T}}}$ and denote the partial derivative with respect to $\nu$ by a superposed prime $(\cdot )'$. The effective curvature $\tilde{\mathbf k}$ only coincides with the curvature of a spatial curve $\mathbf r(\nu ,t)$ when $\nu$ corresponds to the arc length parametrization $s$ of the spatial curve at a given instant of time $t$. The skew-symmetry of $\tilde{\mathbf k}$ can easily be shown using the ${ SO}(3)$ properties of the rotation tensor $\mathbf R$:

$$\begin{aligned} \mathbf R\mathbf R^{\mathop {\mathrm {T}}}= 1\!\!1 \; \mathop {\Rightarrow }\limits ^{(\cdot )'} \; \tilde{\mathbf k} \mathop {=}\limits ^{(5.3)}\mathbf R'\mathbf R^{\mathop {\mathrm {T}}}= -\mathbf R(\mathbf R^{\mathop {\mathrm {T}}})'=-(\mathbf R'\mathbf R^{\mathop {\mathrm {T}}})^{\mathop {\mathrm {T}}}= -\tilde{\mathbf k}^{\mathop {\mathrm {T}}}. \end{aligned}$$

Hence, the skew-symmetric effective curvature $\tilde{\mathbf k}$ has an associated axial vector $\mathbf k(\nu ,t) \in \mathbb {E}^3$ such that

$$\begin{aligned} (\mathbf d_k)' = \tilde{\mathbf k} \mathbf d_k = \mathbf k\times \mathbf d_k, \qquad \mathrm {with} \; \tilde{\mathbf k} = \mathbf R' \mathbf R^{\mathop {\mathrm {T}}}= (\mathbf d_i)' \otimes \, \mathbf d_i. \end{aligned}$$

(5.4)

The tilde-operator will be used to denote the skew-symmetric tensor to an associated axial vector. The components of the effective curvature can be written using the alternating symbols $\varepsilon _{ijk}$ as

$$\begin{aligned} k_i = \frac{1}{2}\varepsilon _{ijk}(\tilde{\mathbf k})_{kj} = \frac{1}{2}\varepsilon _{ijk} (\mathbf d_k \cdot (\mathbf d_j)'). \end{aligned}$$

Similar to (5.4) we introduce the angular velocity $\tilde{{\varvec{\omega }}}(\nu ,t)$ and its associated axial vector ${\varvec{\omega }}(\nu ,t)$ as

$$\begin{aligned} \dot{\mathbf d}_k = \tilde{{\varvec{\omega }}} \mathbf d_k = {\varvec{\omega }}\times \mathbf d_k, \qquad \mathrm {with} \; \tilde{{\varvec{\omega }}} = \dot{\mathbf R}\mathbf R^{\mathop {\mathrm {T}}}= \dot{\mathbf d}_i \otimes \, \mathbf d_i. \end{aligned}$$

(5.5)

Likewise, we obtain the virtual rotation $\delta \tilde{{\varvec{\phi }}}(\nu ,t)$ and its associated axial vector $\delta {\varvec{\phi }}(\nu ,t)$ by considering virtual variations of the directors $\mathbf d_k$, i.e. through derivation with respect to the variation parameter $\varepsilon$,

$$\begin{aligned} \delta \mathbf d_k = \delta \tilde{{\varvec{\phi }}} \mathbf d_k =\delta {\varvec{\phi }}\times \mathbf d_k, \quad \mathrm {with} \; \delta \tilde{{\varvec{\phi }}} = \delta \mathbf R\mathbf R^{\mathop {\mathrm {T}}}= \delta \mathbf d_i \otimes \mathbf d_i. \end{aligned}$$

(5.6)

The velocity and acceleration fields are introduced by taking the total time derivative of the position field (5.1) and the kinematical relation introduced in (5.5)

$$\begin{aligned} \dot{\mathbf x}&= \dot{\mathbf r} + {\varvec{\omega }}\times (\mathbf x- \mathbf r) = \dot{\mathbf r} + {\varvec{\omega }}\times {\varvec{\rho }}, \qquad \mathrm {with} \; {\varvec{\rho }}= \mathbf x- \mathbf r= \theta ^\alpha \mathbf d_\alpha , \nonumber \\ \ddot{\mathbf x}&= \ddot{\mathbf r} + \dot{{\varvec{\omega }}} \times {\varvec{\rho }}+ {\varvec{\omega }}\times ({\varvec{\omega }}\times {\varvec{\rho }}). \end{aligned}$$

(5.7)

Using (5.1) and (5.4), the partial derivatives of the constrained position field take the form

$$\begin{aligned} \mathbf x,_\alpha = \mathbf d_\alpha , \qquad \mathbf x' = \mathbf r' + \, \mathbf k\times {\varvec{\rho }}. \end{aligned}$$

(5.8)

The variation of the constrained position field and insofar the admissible virtual displacement field is, in accordance with (5.1) and (5.6), given by

$$\begin{aligned} \delta \mathbf x= \delta \mathbf r+ \delta {\varvec{\phi }}\times {\varvec{\rho }}. \end{aligned}$$

(5.9)

The variation of the partial derivatives (5.8) are reformulated to

$$\begin{aligned} \delta \mathbf x,_{\alpha } = \delta {\varvec{\phi }}\times \mathbf x,_\alpha , \quad \delta \mathbf x' = \delta \mathbf r' + \,\delta \mathbf k\times {\varvec{\rho }}+ \mathbf k\times (\delta {\varvec{\phi }}\times {\varvec{\rho }}). \end{aligned}$$

(5.10)

Since cartesian coordinates are chosen, the derivative with respect to $\nu$ and the variation commute, i.e. $(\delta \mathbf d_k)' = \delta ((\mathbf d_k)') = \delta \mathbf d_k'$. By (5.4) and (5.6) we write this identity as

$$\begin{aligned} (\delta {\varvec{\phi }}\times \mathbf d_k)' = \delta (\mathbf k\times \mathbf d_k). \end{aligned}$$

Applying the product rule and using again (5.4) and (5.6) yields

$$\begin{aligned} \delta {\varvec{\phi }}' \times \, \mathbf d_k + \delta {\varvec{\phi }}\times (\mathbf k\times \mathbf d_k) = \delta \mathbf k\times \mathbf d_k + \mathbf k\times (\delta {\varvec{\phi }}\times \mathbf d_k). \end{aligned}$$

By subtracting the left-hand side from the right-hand side, and by applying the skew-symmetric property of the cross product and the Jacobi identity (B.1), one obtains

$$\begin{aligned} \begin{aligned} 0&\mathop {=}\limits ^{} \delta \mathbf k\times \mathbf d_k + \mathbf k\times (\delta {\varvec{\phi }}\times \mathbf d_k) + \delta {\varvec{\phi }}\times (\mathbf d_k \times \mathbf k) - \delta {\varvec{\phi }}' \times \mathbf d_k \\&\mathop {=}\limits ^{(\mathrm{B.1})} \delta \mathbf k\times \mathbf d_k - \mathbf d_k \times (\mathbf k\times \delta {\varvec{\phi }}) - \delta {\varvec{\phi }}' \times \, \mathbf d_k \\&\mathop {=}\limits ^{} (\delta \mathbf k- \delta {\varvec{\phi }}\times \mathbf k- \delta {\varvec{\phi }}') \times \mathbf d_k. \end{aligned} \end{aligned}$$

Since the right-hand side of (5.1) has to vanish for all directors $\mathbf d_k \in \mathbb {E}^3$ we retrieve the important identity

$$\begin{aligned} \delta {\varvec{\phi }}' = \delta \mathbf k- \delta {\varvec{\phi }}\times \mathbf k. \end{aligned}$$

(5.11)

For the formulation of constitutive laws or for the determination of mass densities it is convenient to introduce a special configuration, called reference configuration . Let $\mathbf r_0$ and $\mathbf D_\alpha$ be the reference generalized position functions of $\mathbf Q$, then the reference configuration of the beam corresponds to the constrained position field

$$\begin{aligned} {\varvec{\Xi }}(\theta ^\alpha ,\nu ) = \mathbf X(\mathbf Q)(\theta ^\alpha ,\nu )= \mathbf r_0(\nu ) + \theta ^\alpha \mathbf D_\alpha (\nu ). \end{aligned}$$

(5.12)

We call the space curve $\mathbf r_0 = {\varvec{\Xi }}(0,0,\cdot )$ the reference curve of the beam. At each material point of the reference curve $\mathbf r_0$ we have attached a positively oriented orthonormal director triad $(\mathbf D_1(\nu ),\mathbf D_2(\nu ),\mathbf D_3(\nu ))$ which is related to the basis $(\mathbf e_1,\mathbf e_2,\mathbf e_3)$ by introducing the rotation tensor $\mathbf R_0(\nu ) \in { SO}(3)$ such that

$$\begin{aligned} \mathbf D_k(\nu ) = \mathbf R_0(\nu ) \mathbf e_k, \qquad \mathrm {with} \; \mathbf R_0 = \mathbf D_k \otimes \mathbf e_k. \end{aligned}$$

The directors $\mathbf D_\alpha$ describe the reference state of the cross section ${\varvec{\Xi }}(\bar{A}(\nu ),\nu )$. In the formulation of constitutive laws, the reference configuration is often defined as the stress free configuration of the body.

2 Virtual Work Contributions

In an induced theory, the classical nonlinear beam is a continuous body with the constrained position field (5.1). The dynamics of a continuous body with such a restricted kinematics can be described by the principle of virtual work (4.3) with the total stress field (4.7). The constraint position field (5.1) which defines the constraint manifold $\mathcal {C}\subset \mathcal {K}$ corresponds to the embedding (4.10) determining an induced theory. The admissible virtual displacements (5.9) are directly obtained by the variation of the constrained position field. Using the constrained kinematics (5.1), in the following section, the contributions of the virtual work (4.3) due to the admissible virtual displacements (5.9) are determined. Since the constraint stresses are assumed to be perfect, by the principle of d’Alembert–Lagrange (4.8), they do not contribute to the virtual work and the weak variational form of the classical nonlinear beam is obtained. By further continuity assumptions on the involved functions, the strong variational form and the corresponding boundary value problem of the classical nonlinear beam is determined.

It is important to notice, that within this formulation we lose all information about the constraint stresses which rigidify the cross sections. The fact that the constraint stresses do not appear in the equations of motion does not imply that no stresses act in the cross section.

2.1 Virtual Work Contributions of Internal forces

Using (4.1), (5.10) and the property of the cross product of (B.2), the internal virtual work density can be written as

$$\begin{aligned} {\mathbf t}^i \cdot \delta \mathbf x,_{i} = \delta {\varvec{\phi }}\cdot (\mathbf x,_{\alpha } \times {\mathbf t}^\alpha ) +{\mathbf t}^3 \cdot \delta \mathbf r' + \, \delta \mathbf k\cdot ({\varvec{\rho }}\times {\mathbf t}^3) + {\mathbf t}^3 \cdot (\mathbf k\times (\delta {\varvec{\phi }}\times {\varvec{\rho }})). \end{aligned}$$

(5.13)

Employing the symmetry condition (4.5), we can rewrite the first term in (5.13) as follows:

$$\begin{aligned} \delta {\varvec{\phi }}\cdot (\mathbf x,_{\alpha } \times {\mathbf t}^\alpha ) \mathop {=}\limits ^{(4.5)} - \delta {\varvec{\phi }}\cdot (\mathbf x' \times \, {\mathbf t}^3) \mathop {=}\limits ^{(5.8,B.2)} -{\mathbf t}^3 \cdot (\delta {\varvec{\phi }}\times \mathbf r' + \, \delta {\varvec{\phi }}\times (\mathbf k\times {\varvec{\rho }})). \end{aligned}$$

Using the above derived relation and the Jacobi identity (B.1), we can manipulate (5.13) further and obtain

$$\begin{aligned} \begin{aligned} {\mathbf t}^i \cdot \delta \mathbf x,_{i}&\mathop {=}\limits ^{} -{\mathbf t}^3 \cdot (\delta {\varvec{\phi }}\times \mathbf r' + \, \delta {\varvec{\phi }}\times (\mathbf k\times {\varvec{\rho }})) +{\mathbf t}^3 \cdot \delta \mathbf r' +\,\delta \mathbf k\cdot ({\varvec{\rho }}\times {\mathbf t}^3) \\&\quad + {\mathbf t}^3 \cdot (\mathbf k\times (\delta {\varvec{\phi }}\times {\varvec{\rho }})) \\&\mathop {=}\limits ^{}\, {\mathbf t}^3 \cdot (\delta \mathbf r' - \delta {\varvec{\phi }}\times \mathbf r' ) + \delta \mathbf k\cdot ({\varvec{\rho }}\times {\mathbf t}^3) \\&\quad + {\mathbf t}^3 \cdot (\mathbf k\times (\delta {\varvec{\phi }}\times {\varvec{\rho }}) + \delta {\varvec{\phi }}\times ({\varvec{\rho }}\times \mathbf k)) \\&\mathop {=}\limits ^{(\mathrm{B.1})} {\mathbf t}^3 \cdot (\delta \mathbf r' - \delta {\varvec{\phi }}\times \mathbf r' ) + \delta \mathbf k\cdot ({\varvec{\rho }}\times {\mathbf t}^3) + {\mathbf t}^3 \cdot ({\varvec{\rho }}\times (\delta {\varvec{\phi }}\times \mathbf k))\\&\mathop {=}\limits ^{(\mathrm{B.2})} {\mathbf t}^3 \cdot (\delta \mathbf r' - \delta {\varvec{\phi }}\times \mathbf r' ) + ({\varvec{\rho }}\times {\mathbf t}^3)\cdot (\delta \mathbf k- \delta {\varvec{\phi }}\times \mathbf k). \end{aligned} \end{aligned}$$

(5.14)

Since the kinematical quantities $\delta \mathbf r' - \delta {\varvec{\phi }}\times \mathbf r'$ and $\delta \mathbf k- \delta {\varvec{\phi }}\times \mathbf k$ depend merely on $(\nu ,t)$, we split the integration over $\overline{\mathrm {B}}$ in an integration over the cross section in the body chart $\bar{\mathrm {A}}(\nu )$ and an integration along $\nu \in (\nu _1,\nu _2)$

$$\begin{aligned} \begin{aligned} \delta W^\mathrm {int}&\mathop {=}\limits ^{} \int _{\overline{\mathrm {B}}} {\mathbf t}^i \cdot \delta \mathbf x,_{i} \, \mathrm {d}^3 \theta \\&\mathop {=}\limits ^{(5.14)} \int _{\nu _1}^{\nu _2} \left\{ \mathbf n\cdot (\delta \mathbf r' - \delta {\varvec{\phi }}\times \mathbf r' )+ \mathbf m\cdot (\delta \mathbf k- \delta {\varvec{\phi }}\times \mathbf k) \right\} \mathrm {d}\nu . \end{aligned} \end{aligned}$$

(5.15)

Herein, the integrated kinetic quantities $\mathbf n$ and $\mathbf m$ are the resultant contact forces and the resultant contact couples of the current configuration defined by

(5.16)

with abbreviation of the area element $\mathrm {d}^2 \theta = \mathrm {d}\theta ^1 \mathrm {d}\theta ^2$. Due to the surface integral, the resultant contact forces and couples are independent of the cross section coordinates $\theta ^\alpha$. Although not explicitly expressed in the notation, the stress distributions under the surface integral are mapped from the Euclidean cotangent space to the cotangent space of the beams configuration manifold. Nevertheless, in an induced theory, we still have the connection to the stress distribution of the Euclidean space. In order to make the connection to an intrinsic theory, it is necessary to introduce an equivalence class of forces. Force distributions in the Euclidean space which have the same resultant contact forces and contact couples are considered to be equivalent. The representatives of the equivalence class are then identified with the internal generalized forces of an intrinsic beam theory which postulates the right-hand side of (5.15) as its internal virtual work of the generalized one-dimensional continuum. By the definition of an equivalence class, we decouple our induced theory from the theory of a constrained three-dimensional continuous body and arrive at an intrinsic theory.

2.2 Virtual Work Contributions of Inertia Forces

For convenience, the mass density is introduced in the bodies reference configuration as a real valued field $\rho _0:\mathbf X(\mathbf Q)(\overline{B}) \subset \mathbb {E}^3 \rightarrow \mathbb {R}$ which to every point of the body in the Euclidean space assigns a local mass per volume. Together with a volume element $\mathrm {d}V = \mathrm {d}x^1\,\mathrm {d}x^2\,\mathrm {d}x^3$ we obtain the mass distribution $\mathrm {d}m = \rho _0 \, \mathrm {d}x^1\,\mathrm {d}x^2\,\mathrm {d}x^3$. The pullback of the mass distribution to the domain $\overline{B}$ with respect to the reference configuration leads to the local description of the mass distribution as

$$\begin{aligned} \mathrm {d}m = \rho _0 \,G^{1/2} \,\mathrm {d}^3 \theta , \quad G^{1/2}=\mathbf X,_{1}\,\,\cdot \,\,(\mathbf X,_{2}\,\,\times \,\,\mathbf X,_{3}). \end{aligned}$$

Considering the virtual work (4.3) and the virtual displacements (5.9) we can transform the virtual work contributions of the inertia terms. For the manipulation of the inertia terms we introduce some abbreviations of integral expressions which have their analogous expressions in rigid body dynamics. The cross section mass density per unit of $\nu$ is defined as

(5.17)

When the centerline does not coincide with the line of centroids $\mathbf r_c(\nu ,t)$, e.g. when the centerline is determined by the shear centers and the shear centers do not coincide with the centroids of the cross sections, a coupling term remains, which we introduce as the integrated quantity

(5.18)

The cross section inertia density is introduced as

(5.19)

Furthermore, it is convenient to express the time derivatives of the coupling term by the angular velocity. Using (5.5) and (5.18), the second time derivative of the coupling term is expressed by

$$\begin{aligned} \ddot{\mathbf c} = ({\varvec{\omega }}\times A_{\rho _0} (\mathbf r_c - \mathbf r))\dot{} = \dot{{\varvec{\omega }}} \times A_{\rho _0}(\mathbf r_c-\mathbf r) + {\varvec{\omega }}\times ({\varvec{\omega }}\times A_{\rho _0} (\mathbf r_c - \mathbf r)). \end{aligned}$$

(5.20)

Another quantity which is going to occur, is the product of the cross section inertia density and the angular velocity

In the basis $\mathbf d_i\otimes \mathbf d_j$ the moment of inertia $\mathbf I_{\rho _0}$ is constant with respect to time $t$. Using a coordinate description it can easily be shown that

$$\begin{aligned} \begin{aligned} \dot{\mathbf h}&= ((\mathbf I_{\rho _0})_{ij} \omega _j \mathbf d_i)\dot{} = (\mathbf I_{\rho _0})_{ij} \dot{\omega }_j \mathbf d_i + (\mathbf I_{\rho _0})_{ij} \omega _j \dot{\mathbf d}_i \\&=(\mathbf I_{\rho _0})_{ij}\mathbf d_i \otimes \mathbf d_j (\dot{\omega }_k \mathbf d_k + {\varvec{\omega }}\times \omega _k \mathbf d_k) + {\varvec{\omega }}\times (\mathbf I_{\rho _0})_{ij} \omega _j \mathbf d_i \\&= \mathbf I_{\rho _0} \dot{{\varvec{\omega }}} + {\varvec{\omega }}\times \mathbf I_{\rho _0} {\varvec{\omega }}. \end{aligned} \end{aligned}$$

(5.21)

Substitution of the admissible virtual displacements (5.9) and the accelerations (5.7) of the restricted kinematics into the virtual work expression (4.2) yields:

$$\begin{aligned} \delta W^\mathrm {dyn} = \int _{\overline{\mathrm {B}}} \delta \mathbf x\cdot \ddot{\mathbf x} \, \mathrm {d}m = \int _{\overline{\mathrm {B}}} \left\{ (\delta \mathbf r- \tilde{{\varvec{\rho }}}\delta {\varvec{\phi }}) \cdot (\ddot{\mathbf r}- \tilde{{\varvec{\rho }}}\,\dot{{\varvec{\omega }}}+\tilde{{\varvec{\omega }}}\tilde{{\varvec{\omega }}}{\varvec{\rho }}) \right\} \rho _0\, G^{1/2} \, \mathrm {d}^3 \theta . \end{aligned}$$

Similar to the internal virtual work contribution, the integration over $\overline{\mathrm {B}}$ is split in an integration over the cross section in the body chart $\bar{\mathrm {A}}(\nu )$ and an integration along $\nu \in (\nu _1,\nu _2)$. Together with the definitions (5.17), (5.18) and (5.19) and the property (B.5) of the cross product we obtain

$$\begin{aligned} \begin{aligned} \delta W^\mathrm {dyn}&= \int _{\nu _1}^{\nu _2} \left\{ \delta \mathbf r\cdot \left( A_{\rho _0} \ddot{\mathbf r} + A_{\rho _0} ({\tilde{\mathbf r}_c} - {\tilde{\mathbf r}})^{\mathop {\mathrm {T}}}\, \dot{{\varvec{\omega }}} + {\tilde{{\varvec{\omega }}}}{\tilde{{\varvec{\omega }}}} A_{\rho _0} (\mathbf r_c-\mathbf r) \right) \right. \\&\quad + \left. \delta {\varvec{\phi }}\cdot \left( A_{\rho _0} ({\tilde{\mathbf r}_c} - {\tilde{\mathbf r}}) \, \ddot{\mathbf r} + \mathbf I_{\rho _0} \, {\dot{{\varvec{\omega }}}} + {\tilde{{\varvec{\omega }}}} \mathbf I_{\rho _0} {\varvec{\omega }}\right) \right\} \mathrm {d}\nu . \end{aligned} \end{aligned}$$

Using (5.20) and (5.21) the virtual work contribution of the inertia terms is rewritten in an even more compact form

$$\begin{aligned} \delta W^\mathrm {dyn} = \int _{\nu _1}^{\nu _2} \left\{ \delta \mathbf r\cdot \left( A_{\rho _0} \ddot{\mathbf r} + \ddot{\mathbf c} \right) + \delta {\varvec{\phi }}\cdot \left( \mathbf q\times \ddot{\mathbf r} + \dot{\mathbf h} \right) \right\} \mathrm {d}\nu . \end{aligned}$$

(5.22)

As for the internal virtual work expression, we have two possible points of view. Either we consider the cross section mass density, the coupling term and the cross section inertia as integrated quantities from a mass distribution of a three-dimensional continuous body or we identify them as constitutive parameters of an intrinsic theory which relate the generalized inertia forces from (5.22) with the time derivatives of the generalized position functions.

2.3 Virtual Work Contributions of External Forces

There is a vast amount of possibilities how external forces can be impressed on the beam. Forces may occur as volume or surface forces and even point forces applied somewhere at the beam are common in engineering problems. An elegant way to be short in notation is, if we allow the force contribution $\mathrm {d}\mathbf f$ to contain Dirac-type contributions. Since the forces may also contribute on the boundaries, it is essential that we integrate over the closed set of the body. Using the same split of the integration as above and the admissible virtual displacements (5.9), we obtain

$$\begin{aligned} \delta W^\mathrm {ext} = \int _{\overline{\mathrm {B}}} \delta \mathbf x\cdot \mathrm {d}\mathbf f\mathop {=}\limits ^{(5.9)} \int \limits _{[\nu _1,\nu _2]} \left\{ \delta \mathbf r\cdot \mathrm {d}\overline{\mathbf n} + \delta {\varvec{\phi }}\cdot \mathrm {d}\overline{\mathbf m} \right\} , \end{aligned}$$

where the resultant external force distribution $\mathrm {d}\overline{\mathbf n}$ and the resultant external couple distribution $\mathrm {d}\overline{\mathbf m}$ are the integrated quantities

With the same equivalence class argument as for the resultant contact forces and couples, we can identify the resultant external force and couple distributions with external generalized force distributions of an intrinsic theory. In order to avoid cumbersome derivations, we only allow the discontinuities in the force distributions at the boundaries $\nu _1$ and $\nu _2$. This leads to the virtual work contribution

$$\begin{aligned} \delta W^\mathrm {ext} = \int _{\nu _1}^{\nu _2} \left\{ \delta \mathbf r\cdot \overline{\mathbf n} + \delta {\varvec{\phi }}\cdot \overline{\mathbf m} \right\} \mathrm {d}\nu + \sum _{i=1}^2\left\{ \delta \mathbf r\cdot \overline{\mathbf n}_i + \delta {\varvec{\phi }}\cdot \overline{\mathbf m}_i \right\} |_{\nu =\nu _i}. \end{aligned}$$

(5.23)

The resultant external forces and couples $\overline{\mathbf n}_i$ and $\overline{\mathbf m}_i$, respectively, are the resultant external forces which are impressed at $\nu _1$ and $\nu _2$. Whereas the unit of $\overline{\mathbf n}$ is $[\mathrm {N}]$ per unit of $\nu$, the unit of $\overline{\mathbf n}_i$ is $[\mathrm {N}]$. For the couples we argue in a similar way.

2.4 The Boundary Value Problem

Taking all the transformed contributions of the virtual work for admissible virtual displacements (5.15), (5.22) and (5.23), the principle of virtual work (4.3) with the total stress (4.7), together with the principle of d’Alembert–Lagrange (4.8) leads directly to the weak variational form of the classical beam

$$\begin{aligned} \begin{aligned} \delta W&= \int _{\nu _1}^{\nu _2} \left\{ \mathbf n\cdot (\delta \mathbf r' - \delta {\varvec{\phi }}\times \mathbf r') + \mathbf m\cdot (\delta \mathbf k- \delta {\varvec{\phi }}\times \mathbf k) \right. \\&\quad \left. + \delta \mathbf r\cdot \left( A_{\rho _0} \ddot{\mathbf r} + \ddot{\mathbf c} - \overline{\mathbf n} \right) + \delta {\varvec{\phi }}\cdot \left( \mathbf c\times \ddot{\mathbf r} + \dot{\mathbf h} - \overline{\mathbf m} \right) \right\} \mathrm {d}\nu \\&\quad \ - \sum _{i=1}^2\left\{ \delta \mathbf r\cdot \overline{\mathbf n}_i + \delta {\varvec{\phi }}\cdot \overline{\mathbf m}_i \right\} |_{\nu =\nu _i} = 0 \quad \forall \delta \mathbf r,\delta {\varvec{\phi }}, t. \end{aligned} \end{aligned}$$

(5.24)

Using the identity (5.11) and integration by parts, the virtual work is expressed as

$$\begin{aligned} \begin{aligned} \delta W&= -\left\{ \delta \mathbf r\cdot (\mathbf n+ \overline{\mathbf n}_1) + \delta {\varvec{\phi }}\cdot (\mathbf m+\overline{\mathbf m}_1)\right\} |_{\nu =\nu _1} \\&\quad + \int \limits _{\nu _1}^{\nu _2} \left\{ \delta \mathbf r\cdot \left( A_{\rho _0} \ddot{\mathbf r} + \ddot{\mathbf c} - \overline{\mathbf n} - \mathbf n' \right) + \delta {\varvec{\phi }}\cdot \left( \mathbf c\times \ddot{\mathbf r} + \dot{\mathbf h} - \overline{\mathbf m} - \mathbf m' - \mathbf r' \times \, \mathbf n\right) \right\} \mathrm {d}\nu \; \\&\quad + \left\{ \delta \mathbf r\cdot (\mathbf n- \overline{\mathbf n}_2) + \delta {\varvec{\phi }}\cdot (\mathbf m-\overline{\mathbf m}_2)\right\} |_{\nu =\nu _2} = 0 \quad \forall \delta \mathbf r,\delta {\varvec{\phi }},t, \end{aligned} \end{aligned}$$

which corresponds to the strong variational form of the classical beam. When the functions in the round brackets are continuous and when the virtual displacements $\delta \mathbf r$ and the virtual rotations $\delta {\varvec{\phi }}$ are smooth enough, then by the Fundamental Lemma of Calculus of Variation, the former terms have to vanish pointwise. This leads to the complete boundary value problem with the equations of motion of the classical beam which are valid for $\nu \in (\nu _1,\nu _2)$

$$\begin{aligned} \begin{aligned} \mathbf n' + \, \overline{\mathbf n}&= A_{\rho _0} \ddot{\mathbf r} + \ddot{\mathbf c},\\ \mathbf m' + \, \mathbf r' \times \, \mathbf n+\overline{\mathbf m}&= \mathbf c\times \ddot{\mathbf r} + \dot{\mathbf h}, \end{aligned} \end{aligned}$$

(5.25)

together with the boundary conditions $\mathbf n(\nu _1) = -\overline{\mathbf n}_1$, $\mathbf m(\nu _1) = -\overline{\mathbf m}_1$ and $\mathbf n(\nu _2) = \overline{\mathbf n}_2$, $\mathbf m(\nu _2) = \overline{\mathbf m}_2$. If we allow discontinuities of the force distributions at countable many points inside the beam, the domain $(\nu _1,\nu _2)$ has to be divided into sets where the force distributions are continuous. The integration by parts can then only be performed on the differentiable parts. Consequently, this leads to an equation of motion (5.25) for the differentiable parts, to boundary conditions at the boundaries and to transition conditions at the points of the discontinuities.

To summarize, we have seen that the restricted kinematics of the beam allows us reducing the virtual work of the continuous body in such a way, that the equations of motion (5.25) correspond to partial differential equations with only one spatial variable. As mentioned several times, we have two different viewpoints. In an induced theory, the force contributions in (5.25) are interpreted as resultant forces, i.e. weighted surface integrals of forces and stresses of the Euclidean space mapped to the cotangent space of the beams configuration manifold. In an intrinsic theory the forces are considered as generalized forces which lose their connection to force and stress distributions of the Euclidean space.

3 Nonlinear Timoshenko Beam Theory

Constitutive laws for the resultant contact forces $\mathbf n$ and the resultant contact couples $\mathbf m$ are required to complete the equations of motion (5.25). In an induced theory, it is customary to choose a three-dimensional material law with an appropriate three-dimensional strain measure and integrate the corresponding stress contributions (5.16) over the cross sections. Here, however, we propose a semi-induced approach for the formulation of constitutive laws in three-dimensional beam theories. Henceforth, we interpret the resultant contact forces and couples as generalized internal forces and formulate a constitutive law between generalized strains and generalized internal forces. The generalized strains are directly determined by the generalized position functions $\mathbf q$. When proposing an elastic constitutive behavior, we have to show, that the variation with respect to the generalized strain measures leads to the same form of the internal virtual work (5.15) of the induced theory. This shows the compatibility between an induced and an intrinsic beam formulation. In classical beam theories, the generalized constitutive laws relate the generalized position functions of the beam, i.e. the motion of the centerline and the rotation of the cross sections, with the internal generalized forces $\mathbf n$ and $\mathbf m$. As in the three-dimensional theory, we allow the generalized internal forces to consist of an impressed and of a constraint part

$$\begin{aligned} \mathbf n= \mathbf n_I + \mathbf n_C, \qquad \mathbf m= \mathbf m_I + \mathbf m_C. \end{aligned}$$

(5.26)

The subscripts $(\cdot )_I$ and $(\cdot )_C$ stand for impressed forces and constraint forces , respectively. Whereas the constitutive laws of impressed internal generalized forces are formulated by single valued force laws, the constitutive law of the constraint internal generalized forces are given by the principle of d’Alembert–Lagrange (4.8) which can be considered to be a set-valued force law .

Even though in Timoshenko [2, 3] only the linear and plane case is treated, we call the beam theory of this section, in which no further constraints are impressed on the beam, the nonlinear Timoshenko beam theory. Accordingly, the constraint parts of internal generalized forces vanish, i.e.

$$\begin{aligned} \mathbf n_C = 0, \quad \mathbf m_C = 0. \end{aligned}$$

(5.27)

There exists a multitude of other names for the same beam theory. Ballard and Millard [4] call the beam “poutre naturelle”, Antman [5] denotes it as “special Cosserat rod” and as “geometrically exact beam”. With reference to Reissner [6] and Simo [7], it is also called “Simo–Reissner beam”. In our genealogy of beam theories, we denote a beam with the same constraints by the same name. We distinguish further between a nonlinear theory, a linearized theory and a plane linearized theory.

The most basic constitutive law for a nonlinear Timoshenko beam is an elastic force law being expressed by an elastic potential $\hat{W}(\nu ,t)$ for the impressed part of the generalized internal forces , such that

$$\begin{aligned} \delta W^\mathrm {int}_I = \delta \int _{\nu _1}^{\nu _2} \hat{W}(\nu ,t) \, \mathrm {d}\nu . \end{aligned}$$

We assume the elastic potential to depend on the generalized strain measures $\gamma _i$ and  $\kappa _i$

$$\begin{aligned} \tilde{W}(\nu ,t) = W(\gamma _i(\nu ,t), \kappa _i(\nu ,t)). \end{aligned}$$

(5.28)

The generalized strain

(5.29)

measures the difference between the deformation of the centerline in the direction $\mathbf d_i$ and the deformation of the reference curve in the direction $\mathbf D_i$. The effective reference curvature is defined as $\tilde{\mathbf k}_0(\nu ) = \mathbf R_0'\mathbf R_0^{\mathop {\mathrm {T}}}= (\mathbf D_i)' \otimes \, \mathbf D_i$. When measuring the difference between the effective curvature and the effective reference curvature in the direction $\mathbf d_k,\mathbf d_j$ and $\mathbf D_k,\mathbf D_j$, respectively, we obtain the components $\tilde{k}_{kj}-(\tilde{k}_0)_{kj}$. Since these components are skew-symmetric, there is an associated axial vector with the components

(5.30)

In the following we demonstrate the compatibility of the intrinsic generalized strain measures with the induced theory, thereby showing that the internal virtual work expression (5.15) is obtained when varying the elastic potential (5.28), i.e. that

$$\begin{aligned} \delta W^\mathrm {int}_I = \int _{\nu _1}^{\nu _2} \left\{ \frac{\partial W}{\partial \gamma _i} \delta \gamma _i + \frac{\partial W}{\partial \kappa _i}\delta \kappa _i \right\} \mathrm {d}\nu \end{aligned}$$

holds. Using (5.6) and (B.2), the variation of $W$ with respect to $\gamma _i$ takes the form

$$\begin{aligned} \frac{\partial W}{\partial \gamma _i}\delta \gamma _i \mathop {=}\limits ^{(5.29)} \frac{\partial W}{\partial \gamma _i}(\delta \mathbf r' \cdot \, \mathbf d_i + \mathbf r' \cdot \, \delta \mathbf d_i) = \mathbf n_I \cdot (\delta \mathbf r' - \delta {\varvec{\phi }}\times \mathbf r'), \end{aligned}$$

(5.31)

where we have recognized the resultant contact force . By expansion with the orthonormality condition $\delta _{ij} = \mathbf d_i \cdot \mathbf d_j$ and using (5.6), the variation with respect to $\kappa _i$ yields

$$\begin{aligned} \frac{\partial W}{\partial \kappa _i}\delta \kappa _i = \frac{\partial W}{\partial \kappa _i} \mathbf d_i \cdot \delta \kappa _j \mathbf d_j = \mathbf m_I \cdot (\delta \mathbf k- \delta {\varvec{\phi }}\times \mathbf k) \;, \end{aligned}$$

(5.32)

in which the resultant contact couple as has been identified. Comparison of (5.31) and (5.32) with (5.15) demonstrates the compatibility of the chosen generalized strain measures and their corresponding elastic potential.

Let $E$ and $G$ be the Young’s and shear modulus, respectively, and let $A_\alpha$ be the area of the cross sections $A$ multiplied by a shear correction factor. Let $I_1$, $I_2$ and $J$ be the second moments of area and polar moment, respectively. In the following we assume that the elastic potential takes the quadratic form

$$\begin{aligned} W(\gamma _i,\kappa _i) = \frac{1}{2} \, \gamma _i \, (\hat{\mathbf D}_1)_{ij} \, \gamma _j + \frac{1}{2} \, \kappa _i \, (\hat{\mathbf D}_{2})_{ij} \, \kappa _j, \end{aligned}$$

(5.33)

with

$$\begin{aligned}{}[\hat{\mathbf D}_1] = \mathrm {Diag}[GA_1,GA_2,EA], \quad [\hat{\mathbf D}_2] = \mathrm {Diag}[EI_1,EI_2,GJ], \end{aligned}$$

where $[\hat{\mathbf D}_1]$ and $[\hat{\mathbf D}_2]$ contain the collection of the stiffness components $(\hat{\mathbf D}_1)_{ij}$ and $(\hat{\mathbf D}_2)_{ij}$, respectively. In the elastic potential (5.33) the directors $\mathbf d_\alpha$ have been chosen such that they correspond to the principle axes of the cross section surfaces. Consequently, the constitutive laws for the generalized internal forces are given as

$$\begin{aligned} \mathbf n= \mathbf n_I = n_{Ii} \mathbf d_i = (\hat{\mathbf D}_1)_{ij} \gamma _j \mathbf d_i, \quad \mathbf m= \mathbf m_I = m_{Ii} \mathbf d_i = (\hat{\mathbf D}_2)_{ij} \kappa _j \mathbf d_i. \end{aligned}$$

which coincide with the impressed part, since the constraint parts (5.27) vanish.

4 Nonlinear Euler–Bernoulli Beam Theory

The nonlinear Euler–Bernoulli beam (or Navier–Bernoulli beam) can be regarded as a Timoshenko beam on which additional constraints have been imposed. The cross sections, and insofar the directors $\mathbf d_\alpha$, have to remain orthogonal to the tangent vectors $\mathbf r'$ of the centerline. These constraints are formulated for every instant of time $t$ by the two constraint functions

$$\begin{aligned} g_\alpha (\nu ,t) = \mathbf d_\alpha \cdot \mathbf r' = 0. \end{aligned}$$

It is convenient to let the reference configuration also to satisfy the orthonormality condition. In this case, the constraints coincide with vanishing shear deformation , i.e.

$$\begin{aligned} g_\alpha = \gamma _\alpha = \mathbf d_\alpha \cdot \mathbf r' - \mathbf D_\alpha \cdot \mathbf r_0' = 0. \end{aligned}$$

(5.34)

The bilateral constraints are guaranteed by the constraint forces $n_{C\alpha }$. Using (5.6) and properties of the cross product, the generalized constraint forces $\mathbf n_C = n_{C\alpha } \mathbf d_\alpha$ contribute to the virtual work of the beam as

$$\begin{aligned} \delta W^{\mathrm {int}}_C = \delta g_\alpha n_{C\alpha } = (\mathbf d_\alpha \cdot \delta \mathbf r' + \delta \mathbf d_\alpha \cdot \mathbf r') n_{C\alpha } = \mathbf n_C \cdot (\delta \mathbf r' - \delta {\varvec{\phi }}\times \mathbf r'). \end{aligned}$$

(5.35)

Fig. 5.3

Bilateral constraint as set-valued force law

The generalized constraint forces contribute in the same way as the generalized internal forces in (5.15). This is in accordance with the decomposition of the internal generalized forces (5.26) into an impressed and a constraint part. The force law of the generalized constraint forces, which are considered to be perfect, can only be formulated variationally by the principle of d’Alembert–Lagrange , which states that (5.35) vanishes for all virtual displacements which are admissible with respect to (5.34). Such a variational force law is described by a set-valued force law as depicted in Fig. 5.3. The force law at hand may be cast in a normal cone inclusion $n_{C\alpha } \in \mathcal {N}_{\{0\}}(\gamma _\alpha )=\mathbb {R}$, where the normal cone, cf. [8, 9], to the convex set $\{0\}$ is defined as

$$\begin{aligned} \mathcal {N}_{\{0\}}(x) = \left\{ y \in \mathbb {R} \,| \, y(x^*-x) \le 0, x \in 0, \; \forall x^* \in 0 \right\} =\mathbb {R}. \end{aligned}$$

By setting $(x^*-x)= \delta g_\alpha$ and $y=n_{C\alpha }$ in the normal cone inclusion, we readily recognize the principle of d’Alembert–Lagrange in inequality form.

For the impressed part, we assume the same quadratic form (5.33) as its elastic potential. Since the constraint forces do not allow any shear deformation $\gamma _\alpha$, the corresponding shear stiffness components are immaterial and

$$\begin{aligned}{}[\hat{\mathbf D}_1] = \mathrm {Diag}[*,*,{ EA}], \quad [\hat{\mathbf D}_2] = \mathrm {Diag}[EI_1,EI_2,GJ]. \end{aligned}$$

The generalized shear forces $n_{I\alpha }$ of the underlying Timoshenko beam theory have become bilateral generalized constraint forces $n_{C\alpha }$ in the Euler–Bernoulli beam theory. Hence, an elastic material law of the Euler–Bernoulli beam is given by

$$\begin{aligned} \mathbf n= \mathbf n_I + \mathbf n_C, \quad \mathbf m= \mathbf m_I, \end{aligned}$$

where the impressed parts are represented by

$$\begin{aligned} \mathbf n_I = n_{Ii} \mathbf d_i = (\hat{\mathbf D}_1)_{ij} \gamma _j \mathbf d_i, \quad \mathbf m_I = m_{Ii} \mathbf d_i = (\hat{\mathbf D}_2)_{ij} \kappa _j \mathbf d_i\; \end{aligned}$$

and the generalized constraint forces are formulated by the normal cone inclusions

$$\begin{aligned} \mathbf n_C = n_{C\alpha } \mathbf d_\alpha , \qquad \mathrm {with} \; n_{C\alpha } \in \mathcal {N}_{\{0\}}(\gamma _\alpha ) =\mathbb {R}. \end{aligned}$$

Using further concepts of convex analysis, e.g. the indicator function and the concept of the subdifferential, it is possible to also include the set-valued part in the potential (5.33), cf. [10]. This allows an alternative interpretation, that the bilateral generalized constraint forces $n_{C\alpha }$ are obtained by the limit to infinity of the shear stiffnesses ${ GA}_1$ and ${ GA}_2$.

5 Nonlinear Kirchhoff Beam Theory

The nonlinear Kirchhoff beam (or nonlinear inextensible Navier–Bernoulli beam) is an Euler–Bernoulli beam with additional inextensibility constraints. Hence, in the Kirchhoff beam theory the cross sections remain orthogonal to the tangent vectors of the centerline and the centerline is not allowed to stretch. When also the reference configuration satisfies these constraints, the set of constraints for every instant of time $t$ is described by three bilateral constraint functions on the longitudinal and the shear strains

$$\begin{aligned} g_i(\nu ,t) = \gamma _i = \mathbf d_i \cdot \mathbf r' - \mathbf D_i \cdot \mathbf r_0' = 0. \end{aligned}$$

The contribution of the generalized constraint forces $\mathbf n_C = n_{Ci} \mathbf d_i$ to the virtual work is similar to the Euler–Bernoulli beam

$$\begin{aligned} \begin{aligned} \delta W^{\mathrm {int}}_C&= \delta g_i n_{Ci} = (\mathbf d_i \cdot \delta \mathbf r' + \delta \mathbf d_i \cdot \mathbf r') n_{Ci} = \mathbf n_C \cdot (\delta \mathbf r' - \delta {\varvec{\phi }}\times \mathbf r'). \end{aligned} \end{aligned}$$

For the impressed part, we assume the same quadratic form (5.33) as its elastic potential. Since the generalized constraint forces do not allow any deformation $\gamma _i$, the corresponding stiffness components are immaterial and

$$\begin{aligned}{}[\hat{\mathbf D}_1] = \mathrm {Diag}[*,*,*], \quad [\hat{\mathbf D}_2] = \mathrm {Diag}[{ EI}_1,{ EI}_2,{ GJ}]. \end{aligned}$$

Hence, an elastic constitutive law of the nonlinear Kirchhoff beam is given by

$$\begin{aligned} \mathbf n= \mathbf n_C, \quad \mathbf m= \mathbf m_I, \end{aligned}$$

where the impressed parts are represented by

$$\begin{aligned} \mathbf m_I = m_{Ii} \mathbf d_i = (\hat{\mathbf D}_2)_{ij} \kappa _j \mathbf d_i. \end{aligned}$$

and the generalized constraint forces are formulated by the normal cone inclusions

$$\begin{aligned} \mathbf n_C = n_{Ci} \mathbf d_i, \qquad \mathrm {with} \; n_{Ci} \in \mathcal {N}_{\{0\}}(\gamma _i)=\mathbb {R}, \end{aligned}$$

representing the bilateral constraints.

6 Literature Survey of Numerical Implementations

The benefit of the procedure proposed in Sect. 5.2 is that the derivation of the beam equations results directly in the weak variational form (5.24) which is the starting point of any one-field beam finite element formulation. The numerical implementation of the nonlinear Timoshenko beam with a hyperelastic constitutive law (5.33) is treated in the celebrated papers of Simo and Vu-Quoc [7, 11]. These two papers have been the starting point of a wealth of new discussions about the numerical implementation of the Timoshenko beam, often cited as “geometrically exact beam” or “Simo–Reissner beam”. The configuration space of the Timoshenko beam requires the parametrization of the positions of the centerline and the parametrization of the rotations of the cross sections. Whereas the positions of the centerline constitute a linear space, the space of rotations is given by the ${ SO}(3)$-group whose parametrization is not straight forward. Formulations which employ rotation vectors to parametrize the rotations can be found in Iura and Atluri [12, 13] and in Pimenta and Yojo [14]. An overview of different rotation parameterizations is given by Ibrahimbegović [15]. A formulation suitable for arbitrary cross section geometry is treated in Gruttmann and Sauer [16]. Crisfield and Jelenić [17, 18] have recognized that several discretization procedures using additive updates of the approximate rotations lead to a lack of objectivity and path dependent solutions and eliminated the problem by an interpolation of the local rotations. Another approach to remedy this problem are director interpolations originally proposed by Romero and Armero [19] and by Betsch and Steinmann [20, 21]. A further improvement of the director approach which accounts for the lack of orthonormality in the Gauss points is given by Eugster et al. [1]. Furthermore, the director approach facilitates the design of structure-preserving time integrators as has been shown in Betsch and Steinmann [22], Armero and Romero [23], and Leyendecker et al. [24].

A drawback of the one-field finite element formulation, where position vectors and rotations are interpolated, is on the one hand problems with shear locking [25, 26], and on the other hand the occurrence of stress discontinuities across element boundaries [27]. In order to overcome these problems more extensive more-field formulation has been developed. By augmenting the weak variational form (5.24) Zupan and Saje [28, 29], Pimenta [30] and Santos et al. [27, 31] present recent development where displacements, stresses and strains are interpolated. An excellent overview of the whole numerical development of the nonlinear Timshenko beam in the last three decades is given by Santos et al. [27].

Beside the vast amount of contributions to the nonlinear Timoshenko beam the amount of publications on the numerical treatment of the spatial Euler–Bernoulli beam is rather moderate. The crucial point is, that for the spatial Euler–Bernoulli beam the non-holonomic constraints (5.35) have to be guaranteed. These constraints require higher continuity of the shape functions which are fulfilled e.g. by hermite polynomials as shown in Boyer and Primault [32]. Due to the popularity of the isogeometric analysis [33], where B-splines and NURBS can guarantee higher continuity assumptions, more contributions may be expected as the recent publications of Greco and Cuomo [34, 35] show.

The Kirchhoff beam as an inextensible Euler–Bernoulli beam incorporates the same difficulties. Here very recently a finite element formulation by Meier et al. [36] is given. In the context of computer graphics the super helix approach by Bertails [37] is another approach.