The propagation of the multi-physical fields coupled Rayleigh wave on the half-space with a gradient piezoelectric semiconductor layer

Abstract

In this paper, the propagation characteristics of a multi-physical fields coupled Rayleigh surface wave in a semi-infinite piezoelectric medium covering with a functionally gradient piezoelectric semiconductor layer are investigated. First, we can get state transfer equation of piezoelectric semiconductor material from constitutive and governing equations. The transfer and stiffness matrices in the piezoelectric semiconductor material and the piezoelectric material based on the state vector can be got by solving state transfer equation. Furthermore, by combining these matrices of the functionally gradient piezoelectric semiconductor covering layer and the homogeneous piezoelectric half-space, it can be obtained that the total surface stiffness matrix of the Rayleigh wave. Last, it can be obtained that the dispersion curve relation from electrical boundary conditions and mechanical stress freedom. The velocity equations of Rayleigh surface waves propagating along $x$-direction under different electrical boundary conditions and five types of gradient profiles of piezoelectric semiconductor layers are presented. The effects of gradient variation, stable carrier concentration, bias electric fields, and surface boundary conditions on Rayleigh surface waves are investigated. The wave propagation characteristics obtained in this paper have certain theoretical guiding significance for the development of the surface wave devices made of semiconductor materials.

1 Introduction

The widespread adoption of surface acoustic wave (SAW) devices in electronic, information, communication media, and various other fields has resulted in a surge in demand. These devices offer numerous advantages, including ease of production, high sensitivity, and compact size [1,2,3,4]. Among these devices, those equipped with a piezoelectric half-space or overlayer stand out as particularly significant. These acoustic devices utilize piezoelectric materials as their primary covering layers, making them a focal point of extensive research and investigation. Sharma [5] studied the characteristics of the Bleustein–Gulyaev wave propagating in a nonlocal piezoelectric layered structure. Mansfel'd [6] researched selection of modes of a piezoelectric layer in a composite acoustic resonator using bulk acoustic waves. Xu and Fu [7] studied enhanced coupling coefficient in dual-mode ZnO/SiC surface acoustic wave devices with partially etched piezoelectric layer. Xu and Fang et al. [8] researched effect on coupling coefficient of diamond-based surface acoustic wave devices using two layers of piezoelectric materials of different widths. In addition, the propagation of surface waves in piezoelectric media has received more attention from scholars, this includes propagation in piezoelectric half-spaces as well as propagation in piezoelectric overlays. Singh et al. [9] studied propagation characteristics of transverse surface wave in a heterogeneous layer cladded with a piezoelectric stratum and an isotropic substrate. Jin et al. [10] researched the propagation of love waves with the influence of imperfect interface in piezoelectric layered structures. Manna [11] studied the propagation characteristics of love wave in a structure composed of a piezoelectric cover layer and an inhomogeneous elastic half space. Chaudhary et al. [12] researched the propagation of Rayleigh wave in piezoelectric layer overlying in a orthotropic substratum. Liu[13] et al. researched propagation of shear horizontal surface waves in a layered piezoelectric half space with an imperfect interface. Chen [14] studied surface effect on Bleustein-Gulyaev wave in a piezoelectric half-space. Yang and Kong[15] studied love waves in a piezoelectric half-space with an anisotropic elastic layer. All these studies have been made to improve the accuracy of the SAW devices.

During the research process, it is found that some piezoelectric materials exhibit obvious semiconductor properties, which affect the accuracy of the research results. In 1962, White [16] discussed the propagation characteristics of the surface elastic waves in the piezoelectric semiconductor, and firstly predicted the increase or decrease effect of bias electric field on elastic waves. This shows that, the wave propagation in the piezoelectric semiconductor materials does have obvious unique characteristics compared with that in the piezoelectric materials. Yang and Zhou [17] studied the wave propagation characteristics in a piezoelectric ceramic slab sandwiched by two semiconductor layers, and found that the semiconductor properties of piezoelectric materials can cause the loss of dispersion and harmony. Gu and Jin [18] investigated the shear-horizontal surface waves propagating in a piezoelectric semiconductor half space, and found that semiconductor effects have influence on the wave velocity, and cause dispersion or attenuation of waves. Jiao and Wei [19] studied the wave propagating in a piezoelectric semiconductor plate sandwiched between two piezoelectric half spaces. Sharma et al. [20] studied the propagation characteristics of thermoelastic diffusive surface waves in a semiconductor half-space. The adoption of the piezoelectric semiconductor in SAW devices and so on can provide some new ideas for the development of novel surface acoustic wave devices.

As a composite structure, there are two completely different materials are bonded together in the overlay structure, which leads to a mismatch of physical properties at the interface. Tian et al. [21] researched the effect of the imperfect interface on the SH wave propagation in multilayered piezoelectric semiconductor layers. A pn-junction will appear at the interface when a p-type semiconductor and an n-type semiconductor bonded [22], and a Schottky junction will appear at the interface when a metal and a semiconductor are bonded [23]. The accuracy and stability of the devices will be damaged. Due to the gradual gradient of material properties, the functionally gradient material is an optional direction to eliminate the mismatch. Lakshman [24] studied the propagation characteristics of love wave in functionally graded piezoelectric layered structure. Li and Wei [25, 26] discussed the Rayleigh and Love wave propagation in a functionally gradient piezoelectric overlay, and found that the wave velocity can be affected by the carefully designed gradient profiles of the overburden. Long and Fan[27] investigated the propagation of the SH surface wave in a strain-gradient half space, and found that the wave characteristics are much richer than those in the classical elastic materials. Less work on the functionally gradient piezoelectric semiconductor overlays in these structures is reported, which is the origin and highlight of this paper.

It is investigated in this paper that the propagation characteristics of the Rayleigh wave in a semi-infinite space with a functionally gradient piezoelectric semiconductor (FGPS) layer at the intact interface. In order to avoid additional interface effects, the transfer and stiffness matrices of the gradient piezoelectric semiconductor overlay are directly obtained by geometric integration instead of dividing the layer into multiple sub-layers. The total surface stiffness matrix is obtained by combining the stiffness matrix of the overlay with that of the substrate. Furthermore, the dispersion equation of the Rayleigh surface wave is derived. Based on the numerical results in Sect. 5, the influences of the steady-state carrier concentration, bias electric fields, gradient variation of overburden and surface boundary conditions on Rayleigh wave velocity are discussed.

2 State transfer equation of the Rayleigh wave

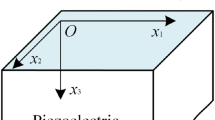
Consider a homogeneous, anisotropic, and piezoelectric half space covering with a functionally gradient piezoelectric semiconductor (FGPS) layer, as shown in Fig. 1. A Rayleigh wave propagates along the positive $x$-axis, and the material properties of the FGPS layer are changing along $z$-direction. The thickness of the FGPS layer is $h$.

Fig. 1

A piezoelectric half space coating with a FGPS layer

The constitutive equations of piezoelectric semiconductor materials are [19, 25]

$${\sigma }_{ij}={c}_{ijkl}{S}_{kl}-{e}_{kij}{E}_{k},$$

(1a)

$${D}_{i}={e}_{ikl}{S}_{kl}+{\varepsilon }_{ik}{E}_{k},$$

(1b)

$${J}_{i}=q\overline{p}{\mu }_{ij}{E}_{j}+qp{\mu }_{ij}{\overline{E} }_{j}-q{d}_{ij}{p}_{,j},$$

(1c)

where ${\sigma }_{ij}$ is the stress tensor, ${S}_{kl}$ is the strain tensor, ${E}_{k}$ is the electric field vector, ${D}_{i}$ is the electric displacement vector, ${J}_{i}$ is the electric current vector, $p$ is the perturbation of the carrier concentration. ${c}_{ijkl}$, ${e}_{kij}$ and ${\varepsilon }_{ik}$ are the elastic, piezoelectric and dielectric parameters, respectively. ${\overline{E} }_{j}$ is the biasing electric field, $q$ is the carrier charge, and $\overline{p }$ is the steady carrier concentration. ${\mu }_{ij}$ and ${d}_{ij}$ are the carrier mobility and diffusion constants, respectively.

The governing equations of piezoelectric semiconductor materials consist of the equations of motion, electrostatics, and the charge conservation, that is [19]

$${\sigma }_{ij,j}=\rho {\ddot{u}}_{i}, {D}_{i,i}=qp, q\dot{p}+{J}_{i,i}=0,$$

(2a,b,c)

where $\rho$ and ${u}_{i}$ are the mass density and the displacement component, respectively. The dot above the variable represents derivative of time. The strain tensor ${S}_{ij}$ with respect to ${u}_{i}$ and the electric field vector ${E}_{i}$ with respect to the electric potential scalar $\varphi$ are given, respectively,

$${S}_{ij}=\frac{{u}_{i,j}+{u}_{j,i}}{2}, {E}_{i}=-{\varphi }_{,i}.$$

(3)

In the wave motion problem of Rayleigh wave, the mechanical displacement ${\varvec{u}}$, the electric potential $\varphi$, and the carrier concentration perturbation $p$ are all functions of the variables $x$ and $z$. That is,

$${\varvec{u}}=\left\{{u}_{1},0,{u}_{3}\right\}\left(x,z,t\right), \varphi =\varphi \left(x,z,t\right), p=p\left(x,z,t\right).$$

(4)

It is widely assumed that the form of the components ${u}_{1},{u}_{3}, \varphi$ and $p$ in Eq. (4) is as

$$\psi \left(x,z,t\right)=f\left(z\right){e}^{\mathrm{i}\left(\omega t-kx\right)}, $$

(5)

where $\omega$ and $k$ are the angular frequency and wave number, respectively.

Let $\mathbf{U}=[{u}_{1}, {u}_{3}, \varphi ,p]$ and $\mathbf{T}=[{\sigma }_{13},{\sigma }_{33},{D}_{3},{J}_{3}]$, and the state vector is defined as ${\varvec{\upxi}}{=(\mathbf{U},\mathbf{T})}^{\mathrm{T}}$.Then, when the parameters of the piezoelectric semiconductor material gradiently changes, the state vector of the covering layer will satisfy the following first-order matrix differential equation with variable coefficient,

$$\frac{d{\varvec{\upxi}}}{dz}= \mathrm{i}\mathbf{A}(z){\varvec{\upxi}}$$

(6)

where the detailed description of $\mathbf{A}(z)$ in the FGPS layer can be found in Appendix A.

Equation (6) is the state transfer equation of the piezoelectric or functionally gradient piezoelectric semiconductor material. In fact, it is a reduced-dimension form of second-order wave motion.

3 The total surface stiffness matrix of the Rayleigh wave

Firstly, the stiffness matrices of the overlay and the substrate are derived, respectively. And then the total surface stiffness matrix is obtained by further combined. At last, the dispersion equation of the Rayleigh wave is derived.

3.1 Stiffness matrix of the FGPS covering layer

For the FGPS material, the state vectors ${\varvec{\upxi}}\left({z}_{0}\right)$ and ${\varvec{\upxi}}(z)$ are combined by a transfer matrix $\mathbf{B}(z,{z}_{0})$ as

$${\varvec{\upxi}}\left(z\right)=\mathbf{B}\left(z,{z}_{0}\right){\varvec{\upxi}}\left({z}_{0}\right).$$

(7)

Substituting Eq. (7) into Eq. (6), the following differential equation with respect to $\mathbf{B}(z,{z}_{0})$ can be gotten

$$\frac{d\mathbf{B}\left(z,{z}_{0}\right)}{dz}=\mathrm{i}\mathbf{A}\left(z\right)\mathbf{B}\left(z,{z}_{0}\right), \mathbf{B}\left({z}_{0},{z}_{0}\right)=\mathbf{I},$$

(8)

where $\mathbf{I}$ indicates the unit matrix. The solution of Eq. (8) is of an exponential form by using Magnus expansion [20]. Let $\mathbf{B}(h)$ denotes the transfer matrix of the FGPS covering layer, where $h$ is the thickness of the layer. It can be expressed as

$$\mathbf{B}\left(h\right)=\mathbf{B}\left(h,0\right)={e}^{{\varvec{\Lambda}}\left(h,0\right)},$$

(9)

where [25]

$$ \begin{aligned} {{\varvec{\Lambda}}}\left( {h,0} \right) & = \mathop \smallint \limits_{0}^{h} {\text{i}} {\mathbf{A}}\left( \tau \right){\mathbf{d}}\tau + \frac{1}{2}\mathop \smallint \limits_{0}^{h} {\mathbf{d}}\tau_{1} \mathop \smallint \limits_{0}^{{\tau_{1} }} {\mathbf{d}}\tau_{2} \left[ {{\text{i}}{\mathbf{A}}\left( {\tau_{1} } \right),{\text{i}}{\mathbf{A}}\left( {\tau_{2} } \right)} \right] \\ { } & \quad + \frac{1}{12}\mathop \smallint \limits_{0}^{h} {\mathbf{d}}\tau_{1} \mathop \smallint \limits_{0}^{{{\uptau }_{1} }} {\mathbf{d}}\tau_{2} \mathop \smallint \limits_{0}^{{{\uptau }_{1} }} {\mathbf{d}}\tau_{3} \left( {\left[ {{\text{i}}{\mathbf{A}}\left( {\tau_{3} } \right),\left[ {{\text{i}}{\mathbf{A}}\left( {\tau_{2} } \right),{\text{i}}{\mathbf{A}}\left( {\tau_{1} } \right)} \right]} \right]} \right){ } \\ { } & \quad + \frac{1}{4}\mathop \smallint \limits_{0}^{h} {\mathbf{d}}\tau_{1} \mathop \smallint \limits_{0}^{{{\uptau }_{1} }} {\mathbf{d}}\tau_{2} \mathop \smallint \limits_{0}^{{{\uptau }_{2} }} {\mathbf{d}}\tau_{3} \left( {\left[ {\left[ {{\text{i}}{\mathbf{A}}\left( {\tau_{3} } \right),{\text{i}}{\mathbf{A}}\left( {\tau_{2} } \right)} \right],{\text{i}}{\mathbf{A}}\left( {\tau_{1} } \right)} \right]} \right) + \cdots \\ \end{aligned} $$

(10a)

is the Magnus series and

$$\left[\mathrm{i}\mathbf{A}({\tau }_{m}),\mathrm{i}\mathbf{A}({\tau }_{n})\right]=\mathrm{i}\mathbf{A}\left({\tau }_{m}\right)\mathrm{i}\mathbf{A}\left({\tau }_{n}\right)-\mathrm{i}\mathbf{A}\left({\tau }_{n}\right)\mathrm{i}\mathbf{A}\left({\tau }_{m}\right).$$

(10b)

To simplify the calculation of multiple integrals, the integral of the univariate [20]

$${\mathbf{M}}_{j} =\frac{1}{{h}^{j}}{\int }_{{z}_{0}}^{h}{\left(\tau -\left({z}_{0}+\frac{h}{2}\right)\right)}^{j}\mathrm{i}\mathbf{A}\left(\tau \right)\mathbf{d}\tau , j=0,1,2\cdots ,$$

(11)

is introduced. A sixth-order approximation of a Magnus series can be written as [25]

$${ {\varvec{\Lambda}}}^{\left(6\right)} ={\mathbf{M}}_{0}+\frac{1}{240}\left[-20{\mathbf{b}}_{1}-{\mathbf{b}}_{3}+{\mathbf{s}}_{1},{\mathbf{b}}_{1}+{\mathbf{s}}_{2}\right],$$

(12a)

where

$$ \begin{aligned} & {\mathbf{s}}_{1} = \left[ {{\mathbf{b}}_{1} ,{\mathbf{b}}_{2} } \right],{ }{\mathbf{s}}_{2} = - \frac{1}{60}\left[ {{\mathbf{b}}_{1} ,2{\mathbf{b}}_{3} + {\mathbf{s}}_{1} } \right], \\ & {\mathbf{b}}_{1} = \frac{3}{4}\left( {3{\mathbf{M}}_{0} - 20{\mathbf{M}}_{2} } \right),{ }{\mathbf{b}}_{2} = 12{\mathbf{M}}_{1} ,{ }{\mathbf{b}}_{3} = - 15\left( {{\mathbf{M}}_{0} - 12{\mathbf{M}}_{2} } \right). \\ \end{aligned} $$

(12b)

Then, based on the the diagonal Padé approximation [26], the asymptotic solution of the transfer matrix $\mathbf{B}(h)$ can be obtained with an eight order Padé approximation as

$$\mathbf{B}\left(h\right)=\left[\begin{array}{cc}{\mathbf{B}}_{11}& {\mathbf{B}}_{12}\\ {\mathbf{B}}_{21}& {\mathbf{B}}_{22}\end{array}\right]={\left({\mathbf{P}}_{4}\left(-{\varvec{\Lambda}}\right)\right)}^{-1}\left({\mathbf{P}}_{4}\left({\varvec{\Lambda}}\right)\right),$$

(13a)

where

$$ \begin{aligned} & {\mathbf{P}}_{0} \left( {{\varvec{\Lambda}}} \right) = {\mathbf{I}} , {\mathbf{P}}_{1} \left( {{\varvec{\Lambda}}} \right) = 2{\mathbf{I}} + {{\varvec{\Lambda}}}, \\ & {\mathbf{P}}_{m} \left( {{\varvec{\Lambda}}} \right) = 2\left( {2m - 1} \right){\mathbf{P}}_{m - 1} \left( {{\varvec{\Lambda}}} \right) + {{\varvec{\Lambda}}}^{2} {\mathbf{P}}_{m - 2} \left( {{\varvec{\Lambda}}} \right). \\ \end{aligned} $$

(13b)

The stress vector consisted of $\mathbf{T}(h)$ and $\mathbf{T}(0)$ and the displacement vector consisted of $\mathbf{U}(h)$ and $\mathbf{U}(0)$ are connected by a matrix $\mathbf{K}\left(h\right)$, called stiffness matrix, as

$$\left[\begin{array}{c}\mathbf{T}\left(h\right)\\ \mathbf{T}\left(0\right)\end{array}\right]=\mathbf{K}\left(h\right)\left[\begin{array}{c}\mathbf{U}\left(h\right)\\ \mathbf{U}\left(0\right)\end{array}\right],$$

(14)

Comparing Eq. (7) and Eq. (14), the stiffness matrix $\mathbf{K}\left(h\right)$ of the FGPS overlay is derived as

$$\mathbf{K}\left(h\right)=\left[\begin{array}{cc}{\mathbf{K}}_{11}& {\mathbf{K}}_{12}\\ {\mathbf{K}}_{21}& {\mathbf{K}}_{22}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{B}}_{22}{\left({\mathbf{B}}_{12}\right)}^{-1}& {\mathbf{B}}_{21}{-{\mathbf{B}}_{22}\left({\mathbf{B}}_{12}\right)}^{-1}{\mathbf{B}}_{11}\\ {\left({\mathbf{B}}_{12}\right)}^{-1}& -{\left({\mathbf{B}}_{12}\right)}^{-1}{\mathbf{B}}_{11}\end{array}\right].$$

(15)

3.2 Surface stiffness matrix of the piezoelectric half space

The state vector ${{\varvec{\upxi}}}^{\mathrm{e}}=\left[{u}_{1},{u}_{3},{\varphi ,\sigma }_{13},\right.{\sigma }_{33},{{D}_{3}]}^{\mathrm{T}}$ in the piezoelectric material satisfies Eq. (6), that is

$$\frac{\mathrm{d}{{\varvec{\upxi}}}^{e}}{\mathrm{d}z}=\mathrm{i}{\mathbf{A}}^{e}{{\varvec{\upxi}}}^{e}.$$

(16)

The elements of matrix ${\mathbf{A}}^{e}$ in Eq. (16) are all constants.

Meanwhile, the vector ${{\varvec{\upxi}}}^{\mathrm{e}}$ in Eq. (16) satisfies that

$${{\varvec{\upxi}}}^{e}(z)={\mathbf{B}}^{e}(z,{z}_{0}){{\varvec{\upxi}}}^{e}\left({z}_{0}\right).$$

(17)

Substituting Eq. (17) into Eq. (16), the following matrix differential equation of constant coefficient can be gotten

$$\frac{\mathrm{d}{\mathbf{B}}^{e}\left(z,{z}_{0}\right)}{\mathrm{d}z}=\mathrm{i}{\mathbf{A}}^{e}{\mathbf{B}}^{e}\left(z,{z}_{0}\right),{\mathbf{B}}^{e}\left({z}_{0},{z}_{0}\right)=\mathbf{I}.$$

(18)

The solution of ${\mathbf{B}}^{e}\left(z,{z}_{0}\right)$ in Eq. (18) with the constant matrix ${\mathbf{A}}^{e}$ can be obtained

$${\mathbf{B}}^{e}\left(z,{z}_{0}\right)={e}^{\mathrm{i}{\mathbf{A}}^{e}(z-{z}_{0})}.$$

(19)

Then, by combining Eqs. (17) and (19), the state vector ${{\varvec{\upxi}}}^{e}$ of the piezoelectric material can be expressed as

$${{\varvec{\upxi}}}^{e}\left(z\right)={e}^{\mathrm{i}{\mathbf{A}}^{e\left(z-{z}_{0}\right)}} {{\varvec{\upxi}}}^{e}({z}_{0})$$

(20)

Let ${\lambda }_{n}(n=\mathrm{1,2},\cdots ,6)$ be the eigenvalues of matrix ${\mathbf{A}}^{e}$. They are separated into two groups ${\lambda }_{1}{,\lambda }_{2}{,\lambda }_{3}$ ($\mathrm{Im}\left({\lambda }_{n}\right)<0$) and ${\lambda }_{4},{\lambda }_{5}{,\lambda }_{6}$ ($\mathrm{Im}\left({\lambda }_{n}\right)>0$). Let ${{\varvec{\beta}}}_{z}^{-}=\mathrm{diag}\left({\uplambda }_{1}{,\uplambda }_{2}{,\uplambda }_{3}\right)$ and ${{\varvec{\beta}}}_{z}^{+}=\mathrm{diag}\left({\uplambda }_{4},{\uplambda }_{5}{,\uplambda }_{6}\right)$. The eigenvectors can form a matrix, and we can define this matrix as $\mathbf{W}$ and its two submatrices are ${{\varvec{\beta}}}_{z}^{-}$ and ${{\varvec{\beta}}}_{z}^{+}$. Let ${\mathbf{W}} = \left[ {\begin{array}{*{20}c} {{\mathbf{Y}}^{ - } } & {{\mathbf{Y}}^{ + } } \\ {{\mathbf{D}}^{ - } } & {{\mathbf{D}}^{{ + { }}} } \\ \end{array} } \right] = [{\mathbf{W}}^{ - } { }{\mathbf{W}}^{ + } ]$. Then, the matrix ${\mathbf{A}}^{e}$ can be rewritten as

$${\mathbf{A}}^{e}=\mathbf{W}{{\varvec{\beta}}}_{z}{\mathbf{W}}^{-1} =\left[\begin{array}{cc}{\mathbf{Y}}^{-}& {\mathbf{Y}}^{+}\\ {\mathbf{D}}^{-}& {\mathbf{D}}^{+}\end{array}\right]\left[\begin{array}{cc}{{\varvec{\beta}}}_{z}^{-}& 0\\ 0& {{\varvec{\beta}}}_{z}^{+}\end{array}\right]{\left[\begin{array}{cc}{\mathbf{Y}}^{-}& {\mathbf{Y}}^{+}\\ {\mathbf{D}}^{-}& {\mathbf{D}}^{+}\end{array}\right]}^{-1}$$

(21)

The inverse of the matrix $\mathbf{W}$ is expressed as

$${\mathbf{W}}^{-1}={\left[\begin{array}{cc}{\mathbf{Y}}^{-}& {\mathbf{Y}}^{+}\\ {\mathbf{D}}^{-}& {\mathbf{D}}^{+}\end{array}\right]}^{-1}=\left[\begin{array}{c}{\mathbf{M}}^{-}\\ {\mathbf{M}}^{+}\end{array}\right]$$

(22)

For a homogeneous piezoelectric half-space, as shown in Fig. 1, wave functions in Eq. (3) gradually decrease to zero as $z\to -\infty$. Therefore, only ${{\varvec{\beta}}}_{z}^{-}$, in which the imaginary parts of the three elements are negative, are retained. Let

$${\mathbf{A}}_{0}^{e}={\mathbf{W}}^{-}{{\varvec{\beta}}}_{z}^{-}{\mathbf{M}}^{-}$$

(23)

Thus, by inserting Eq. (23) into Eq. (19), it is obtained that the transfer matrix of the piezoelectric half space

$${\mathbf{B}}_{0}^{e}\left(z,{z}_{0}\right)=\left[\begin{array}{c}{{\mathbf{Y}}^{-}\left({\mathbf{H}}^{-}\right)}^{-1}\\ {{\mathbf{D}}^{-}\left({\mathbf{H}}^{-}\right)}^{-1}\end{array}\right]{\mathbf{M}}^{-}$$

(24)

where ${\mathbf{H}}^{-}=\mathrm{diag}\left({\mathrm{e}}^{-\mathrm{i}{\lambda }_{1}\left(z-{z}_{0}\right)},{\mathrm{e}}^{-\mathrm{i}{\lambda }_{2}\left(z-{z}_{0}\right)},{\mathrm{e}}^{-\mathrm{i}{\lambda }_{3}\left(z-{z}_{0}\right)}\right)$.

In addition, inserting Eq. (24) into Eq. (17), namely

$$\left[\begin{array}{c}{\mathbf{U}}_{0}^{e}\left(z\right)\\ {\mathbf{T}}_{0}^{e}\left(z\right)\end{array}\right]=\left[\begin{array}{c}{{\mathbf{Y}}^{-}\left({\mathbf{H}}^{-}\right)}^{-1}\\ {{\mathbf{D}}^{-}\left({\mathbf{H}}^{-}\right)}^{-1}\end{array}\right]{\mathbf{F}}_{0}$$

(25)

where ${\mathbf{M}}^{-}{{\varvec{\upxi}}}_{0}^{e}\left({z}_{0}\right)={\mathbf{F}}_{0}$ is a constant matrix. Then, it can be derived that

$${\mathbf{T}}_{0}^{e}\left(z\right)={\mathbf{K}}_{S}^{e}{\mathbf{U}}_{0}^{e}\left(z\right)$$

(26)

where the surface stiffness matrix ${\mathbf{K}}_{S}^{e}$ of the piezoelectric half space satisfies that

$${\mathbf{K}}_{S}^{e}={\mathbf{D}}^{-}{\left({\mathbf{Y}}^{-}\right)}^{-1}.$$

(27)

3.3 Total surface stiffness matrix

$\mathbf{B}$ And $\mathbf{K}$, which have been derived in Sect. 3.1, are the transfer and stiffness matrices of the FGPS overlay, respectively. In the piezoelectric substrate, let ${\mathbf{B}}^{e}$ denotes the transfer matrix and ${\mathbf{K}}^{e}$ denote the stiffness matrix. The thickness of the substrate is assumed to ${h}{\prime}$ (${h}{\prime}\gg h$). For the structure in Fig. 1, they can be rewritten as

$${\varvec{\upxi}}\left({h}^{-}\right)=\mathbf{B}(h){\varvec{\upxi}}\left({0}^{+}\right)$$

(28a)

$${{\varvec{\upxi}}}^{e}\left({0}^{-}\right)={\mathbf{B}}^{e}\left({h}{\prime}\right){{\varvec{\upxi}}}^{{\varvec{e}}}\left({-{h}^{\mathbf{^{\prime}}}}^{+}\right),$$

(28b)

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{T}}\left( {h^{ - } } \right)} \\ {{\mathbf{T}}\left( {0^{ + } } \right)} \\ \end{array} } \right] = {\mathbf{K}}\left[ {\begin{array}{*{20}c} {{\mathbf{U}}\left( {h^{ - } } \right)} \\ {{\mathbf{U}}\left( {0^{ + } } \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{11} } & {{\mathbf{K}}_{12} } \\ {{\mathbf{K}}_{21} } & {{\mathbf{K}}_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{U}}\left( {h^{ - } } \right)} \\ {{\mathbf{U}}\left( {0^{ + } } \right)} \\ \end{array} } \right], $$

(29)

$$\left[\begin{array}{c}{\mathbf{T}}^{e}\left({0}^{-}\right)\\ {\mathbf{T}}^{e}\left({-h\mathbf{^{\prime}}}^{+}\right)\end{array}\right]={\mathbf{K}}^{e}\left[\begin{array}{c}{\mathbf{U}}^{e}\left({0}^{-}\right)\\ {\mathbf{U}}^{e}\left({-{h}^{\mathbf{^{\prime}}}}^{+}\right)\end{array}\right]=\left[\begin{array}{cc}{\mathbf{K}}_{11}^{{\varvec{e}}}& {\mathbf{K}}_{12}^{{\varvec{e}}}\\ {\mathbf{K}}_{21}^{{\varvec{e}}}& {\mathbf{K}}_{22}^{{\varvec{e}}}\end{array}\right]\left[\begin{array}{c}{\mathbf{U}}^{e}\left({0}^{-}\right)\\ {\mathbf{U}}^{e}\left({-{h}^{\mathbf{^{\prime}}}}^{+}\right)\end{array}\right].$$

(30)

The displacements, the electric potential, the carrier concentration perturbation, the stresses, the normal electric displacement, and the normal electric current are continuous on the interface is required for the perfect interface conditions. That is, the state vectors at the two sides of the interface satisfy that

$${{\varvec{\upxi}}}^{{\varvec{e}}}\left({0}^{-}\right)={\varvec{\upxi}}\left({0}^{+}\right).$$

(31)

For the FGPS covering layer, the state vector ${\varvec{\upxi}}\left({0}^{+}\right)$ is 8 × 1 order in the cover $z={0}^{+}$ plane. But the substrate is piezoelectric material, and then, the state vector ${{\varvec{\upxi}}}^{e}\left({0}^{-}\right)$ at $z={0}^{-}$ plane should be turned to a 6 × 1 order matrix, denoted as ${{\varvec{\upxi}}}^{e}\left({0}^{-}\right)$. Therefore, Eq. (31) need to be amended. Because the electric displacement and electric current are nonexistent in the substrate (piezoelectric medium) and vacuum, the electrical displacement and electrical current in the FGPS covering layer should approach zero at the boundary, which means that ${J}_{3}=0$ at $z={0}^{+}$ and ${h}^{-}$. Then, Eq. (28a) is corrected to

$${{\varvec{\upxi}}}^{f}\left({h}^{-}\right)={\mathbf{B}}^{f}\left(h\right){{\varvec{\upxi}}}^{f}\left({0}^{+}\right).$$

(32)

Equation (29) can be corrected to

$$\left[\begin{array}{c}{\mathbf{T}}^{{\varvec{f}}}\left({h}^{-}\right)\\ {\mathbf{T}}^{{\varvec{f}}}\left({0}^{+}\right)\end{array}\right]={\mathbf{K}}^{f}\left(h\right)\left[\begin{array}{c}{\mathbf{U}}^{{\varvec{f}}}\left({h}^{-}\right)\\ {\mathbf{U}}^{f}\left({0}^{+}\right)\end{array}\right],$$

(33)

the stiffness matrix in Eq. (15) of the covering layer can be modified to ${\mathbf{K}}^{f}\left(h\right)$.

Where${{\varvec{\upxi}}}^{f}\left(x,z,t\right)={\left({\mathbf{U}}^{f},{\mathbf{T}}^{f}\right)}^{\mathrm{T}},{\mathbf{U}}^{f}={\left({u}_{1},{u}_{3},\varphi \right)}^{\mathrm{T}}$, ${{\mathbf{T}}^{f}=\left({\sigma }_{13 },{\sigma }_{33},{D}_{3}\right)}^{\mathrm{T}}$. The 8 × 8 order matrices $\mathbf{B}\left(h\right)$ and $\mathbf{K}\left(h\right)$ are amended to 6 × 6 order matrices ${\mathbf{B}}^{f}\left(h\right)$ and${\mathbf{K}}^{f}\left(h\right)$, respectively. The detailed expressions ${\mathbf{U}}^{f}$ and ${\mathbf{T}}^{f}$ are given in “Appendix A”. Then, the continuous condition, shown in Eq. (31), of the state vector is amended to

$${{\varvec{\upxi}}}^{e}\left({0}^{-}\right)={{\varvec{\upxi}}}^{f}\left({0}^{+}\right).$$

(34)

From Eqs. (28b), (32) and (34), it can be derived that

$${{\varvec{\upxi}}}^{f}\left({h}^{-}\right)=\overline{\mathbf{B}}{{\varvec{\upxi}} }^{e}\left({-{h}{\prime}}^{+}\right),$$

(35)

where

$$\overline{\mathbf{B} }={\mathbf{B}}^{f}\left(h\right){\mathbf{B}}^{e}\left({h}{\prime}\right).$$

(36)

$\overline{\mathbf{B} }$ is the total transfer matrix of the composite system with two layers. From Eqs. (55), (30), and (34), it can be obtained that

$$\left[\begin{array}{c}{\mathbf{T}}^{f}\left({h}^{-}\right)\\ {\mathbf{T}}^{e}\left({{-h}^{\prime}}^{+}\right)\end{array}\right]=\overline{\mathbf{K} }\left[\begin{array}{c}{\mathbf{U}}^{f}\left({h}^{-}\right)\\ {\mathbf{U}}^{e}\left({-{h}^{\prime}}^{+}\right)\end{array}\right],$$

(37a)

where

$$\overline{\mathbf{K} }=\left[\begin{array}{cc}{\mathbf{K}}_{11}^{f}+{\mathbf{K}}_{12}^{f}{\left({\mathbf{K}}_{11}^{e}-{\mathbf{K}}_{22}^{f}\right)}^{-1}{\mathbf{K}}_{21}^{f}& -{\mathbf{K}}_{12}^{f}{\left({\mathbf{K}}_{11}^{e}-{\mathbf{K}}_{22}^{f}\right)}^{-1}{\mathbf{K}}_{12}^{e}\\ {\mathbf{K}}_{21}^{e}{\left({\mathbf{K}}_{11}^{{\varvec{e}}}-{\mathbf{K}}_{22}^{f}\right)}^{-1}{\mathbf{K}}_{21}^{f}& {{\mathbf{K}}_{22}^{{\varvec{e}}}-{\mathbf{K}}_{21}^{e}\left({\mathbf{K}}_{11}^{e}-{\mathbf{K}}_{22}^{f}\right)}^{-1}{\mathbf{K}}_{12}^{e}\end{array}\right].$$

(37b)

$\overline{\mathbf{K} }$ is the total stiffness matrix of the system.

As shown in Eq. (27), ${\mathbf{K}}_{S}^{e}$ represents the surface stiffness matrix of the piezoelectric half space, and then, the substrate stiffness matrix can be expressed as:

$${\mathbf{K}}^{\mathbf{^{\prime}}}=\left[\begin{array}{cc}{\mathbf{K}}_{S}^{e}& {0}_{3\times 3}\\ {0}_{3\times 3}& {0}_{3\times 3}\end{array}\right]$$

(38)

From Eqs. (37b) and (38), the total stiffness matrix of the compound system consisted of a FGPS overlay and a piezoelectric half space is

$$\overline{\mathbf{K} }=\left[\begin{array}{cc}{\mathbf{K}}_{11}^{f}+{\mathbf{K}}_{12}^{f}{\left({\mathbf{K}}_{S}^{e}-{\mathbf{K}}_{22}^{f}\right)}^{-1}{\mathbf{K}}_{21}^{f}& 0\\ 0& 0\end{array}\right]. $$

(39)

Then, the total surface stiffness matrix is

$${\overline{\mathbf{K}} }_{\mathrm{S}}={\mathbf{K}}_{11}^{f}+{\mathbf{K}}_{12}^{f}{\left({\mathbf{K}}_{S}^{e}-{\mathbf{K}}_{22}^{f}\right)}^{-1}{\mathbf{K}}_{21}^{f}.$$

(40)

4 The velocity equation of Rayleigh wave

In this section, the wave velocity equations of the Rayleigh surface wave in a piezoelectric half space with a FGPS covering layer under two different electrical boundary conditions are given, respectively. The total surface stiffness matrix ${\overline{\mathbf{K}} }_{\mathrm{S}}$ is adopted to relate the generalized traction vector ${\mathbf{T}}_{\mathrm{S}}\left(h\right)$ with the generalized displacement vector ${\mathbf{U}}_{\mathrm{S}}\left(h\right)$ as

$${\mathbf{T}}_{\mathrm{S}}\left(h\right)={\overline{\mathbf{K}} }_{\mathrm{S}}{\mathbf{U}}_{\mathrm{S}}\left(h\right).$$

(41)

Two kinds of surface conditions at the top surface $z=h$ of the FGPS overlay are considered.

• (1) The mechanically traction is free, and the circuit is electrically open, that is

  $${\sigma }_{13}\left(h\right)=0,{\sigma }_{33}\left(h\right)=0,{D}_{3}\left(h\right)=0,{J}_{3}\left(h\right)=0.$$

  (42)

  A homogeneous algebraic equation is derived by inserting Eq. (43) into Eq. (42), and the existence of its nontrivial solution requires

  $$\mathrm{det}\left({\overline{\mathbf{K}} }_{\mathrm{S}}\right)=0.$$

  (43)

  Equation (43) is the dispersive relation of the Rayleigh wave based on the dielectrically open circuit surface condition.

• (2) The mechanically traction is free, and the circuit is electrically short, that is

  $${\sigma }_{13}\left(h\right)=0,{\sigma }_{33}\left(h\right)=0,\varphi \left(h\right)=0,p\left(h\right)=0.$$

  (44)

  Inserting Eq. (44) into Eq. (41), it is obtained that

  $$\left\{\begin{array}{c}0={\overline{k} }_{11}{u}_{1}+{\overline{k} }_{12}{u}_{3}\\ 0={\overline{k} }_{21}{u}_{1}+{\overline{k} }_{22}{u}_{3}\\ {D}_{3}={\overline{k} }_{31}{u}_{1}+{\overline{k} }_{32}{u}_{3}\end{array}\right.$$

  (45)

The nontrivial solution exists when

$$\left|\begin{array}{cc}{\overline{k} }_{11}& {\overline{k} }_{12}\\ {\overline{k} }_{21}& {\overline{k} }_{22}\end{array}\right|=0,$$

(46)

where ${\overline{\mathbf{K}} }_{\mathrm{S}}=\left({\overline{k} }_{ij}\right), i,j=\mathrm{1,2}.$ Eq. (46) is the dispersive equation of the Rayleigh wave based on the dielectrically short circuit surface condition.

5 Numerical results and discussions

It is considered that an isotropic, homogeneous, and piezoelectric half space with a functionally gradient piezoelectric semiconductor overlay, as shown in Fig. 1. The interface between the overlay and the substrate is mechanically and dielectrically perfect. The substrate (with thickness $h{\prime}$) adopts the material SiO₂ whose parameters are listed in Table 1. And the overlay is a functionally gradient, transversely isotropic, piezoelectric semiconductor material. Let ${P}_{A}$ and ${P}_{B}$ denote the material parameters at the bottom and top of the overlay, respectively. In this simulation, ${P}_{A}$ adopts ZnO, and its material parameters are shown in Table 2. In order to facilitate the calculation, the following dimensionless biased electric fields are introduced, ${\gamma }_{1}={\mu }_{11}{\overline{E} }_{1}\sqrt{\rho /{c}_{44}}$, ${\gamma }_{3}={\mu }_{11}{\overline{E} }_{3}\sqrt{\rho /{c}_{44}}$ and ${\varvec{\upgamma}}={\gamma }_{1}{\mathbf{e}}_{1}+{\gamma }_{3}{\mathbf{e}}_{3}$.

Table 1 Material parameters of the Substrate (SiO₂) [20]

Table 2 Material parameters at the bottom of the overlay (ZnO) [14, 16]

The material constants $P(z)$ in the FGPS overlay satisfy that

$$P\left(z\right)={P}_{A}V\left(z\right)+{P}_{B}\left(1-V\left(z\right)\right).$$

(47)

$P(z)$ represents the piezoelectric parameters ${c}_{ijkl}(z)$, the piezoelectric parameters ${e}_{kij}(z)$, the dielectric parameters ${\varepsilon }_{ik}(z)$, the carrier mobility constants ${\mu }_{ik}(z)$, the carrier diffusion constants ${d}_{ik}(z)$, or the mass density $\rho (z)$ at any given position $z$. Five types of gradient profile are considered in the numerical examples,

Case 1:

$$V(z)={ (1-\frac{z}{ h})}^{0.2}$$

(48a)

Case 2:

$$V(z)=1-\frac{z}{h}$$

(48b)

Case 3:

$$V(z)=(1-\frac{z}{h}{)}^{5}$$

(48c)

Case 4:

$$V\left(z\right)=\left\{\begin{array}{c}\frac{1}{2}+{\frac{1}{2}(1-2\frac{z}{ h})}^{0.2},z\le \frac{1}{2}h\\ \frac{1}{2}-{\frac{1}{2}\left(-1+2\frac{z}{ h}\right)}^{0.2},z\ge \frac{1}{2}h\end{array}\right.$$

(48d)

Case 5:

$$V\left(z\right)=\left\{\begin{aligned}&\frac{1}{2}+{\frac{1}{2}(1-2\frac{z}{ h})}^{5},z\le \frac{1}{2}h\\& \frac{1}{2}-{\frac{1}{2}\left(-1+2\frac{z}{ h}\right)}^{5},z\ge \frac{1}{2}h\end{aligned}\right.$$

(48e)

The five types of gradient profiles are shown in Fig. 2.

Fig. 2

The gradient profile of the overlay

For a gradient overlay, the material constant ${P}_{A}$ at the bottom can be larger or less than ${P}_{B}$ at the top, as shown in Fig. 2. Let $f=P/{P}_{A}$ denotes the ratio of the top parameter to the bottom one. $f<1$ indicates that the parameters at the bottom are much larger, while $f>1$ means that the parameters at the top are larger. In this paper, let $f=0.5$ or 2, respectively. The horizontal axis represents the change in position within the gradient layer; the vertical axis represents the ratio of the material parameter value $P$ at the current position to ${P}_{A}$ at the bottom of the covering layer. $P/{P}_{A}=1$ indicates that the material parameters are equal to ${P}_{A}$, while $P/{P}_{A}=f$ indicates that the material parameters are equal to ${P}_{B}$. Five gradient profiles were used in the layer, which represent five different material parameter variation rules, respectively. The curves in case 2, 4, and 5 converge together at $z/h=0.5$, which means the material parameters $P=\frac{1}{2}({P}_{A}+{P}_{B})$. In case 2, the material parameters change linearly from ${P}_{A}$ to ${P}_{B}$. In other cases, the convex curves represent that the values of $P$ are much closer to ${P}_{B}$, while the concave curves represent that the value of $P$ are much closer to ${P}_{A}$.

Figure 3 shows the effects of five different gradients on Rayleigh wave velocity with the steady carrier concentration $\overline{p }=6\times {10}^{16}\,\text{m}^{-3},$ the tangential bias electric field ${\gamma }_{1}=4$, the normal bias electric field ${\gamma }_{3}=4$ when ${P}_{B} = 0.5{P}_{A}$ (top-level parameters are smaller). In this case, the dispersion curves are insensitive to both the surface open circuit and short circuit boundary conditions. It can be observed that, in the low-frequency range, the wave velocity in case 3 is greater than that in case 1. However, an opposite result is gotten in the high-frequency region, that is, the wave velocity in case 1 is greater than that in case 3. In other words, the curves in case 1 and case 3 are symmetric with respect to those in case 2. The wave velocity in cases 4 and 5 are almost the same in the low-frequency region, but they show a significant difference in the high-frequency region.

Fig. 3

The influences of the five kinds of gradient profiles on the dispersive curves $v \sim kh$ and ${P}_{B} = 0.5{P}_{A}$ under a open circuit and b short circuit conditions

Figure 4 shows the effects of five different gradients on Rayleigh wave velocity with the steady carrier concentration $\overline{p }=6\times {10}^{16}\,\text{m}^{-3},$ the bias electric fields ${\gamma }_{1}=$ ${\gamma }_{3}=4$ when ${P}_{B} = 2{P}_{A}$ (top-level parameters are larger). The results are obviously different from those when ${P}_{B} =0.5{P}_{A}$. The wave velocity in case 3 is smaller than that in case 1 when propagating in the low-frequency region, but much larger in the high-frequency region. The wave velocities of case 4 and case 5 are almost identical in the low-frequency range but significantly different in the high-frequency region. When ${P}_{B} =0.5{P}_{A}$ and ${P}_{B} =2{P}_{A}$, the relative positions of the curves in cases 1 and 3 are diametrically opposed to those in cases 4 and 5. Meanwhile, the velocity curve is sensitive to the opening and short circuit surface conditions when ${P}_{B} =2{P}_{A}$, which is quite different from the result when ${P}_{B} =0.5{P}_{A}$. Under the short circuit surface condition, the curve for case 4 becomes flatter, and the curve for case 3 becomes much steeper. When ${P}_{B} =0.5{P}_{A}$, the influence of open circuit or short circuit on the velocity curve is not obvious. It also has been found that the steady carrier concentration and bias electric fields exhibit tiny influences at the studied frequency range in the figures. Therefore, the velocity curves under ${P}_{B} =2{P}_{A}$ are focused on at the following simulations.

Fig. 4

The influences of the five kinds of gradient profiles on the dispersive curves $v \sim kh$ and ${P}_{B} =2{P}_{A}$ under a open circuit and b short circuit conditions

Figure 5 shows the effects of the steady carrier concentration on the Rayleigh wave velocity when biasing fields ${\gamma }_{1}={\gamma }_{3}=4$ and the parameters of top overlayer ${P}_{B} = 2{P}_{A}$. Figures 5a–j exhibit the velocity curves under case 1 ~ case 5, respectively. And Fig. 5a, c, e, g and i are plotting based on the open circuit condition, while Fig. 5b, d, f, h and j are based on the short circuit condition. The same layout is still adopted in the following figures. The wave velocity for case 1 under both open and short circuit surface conditions decreases initially and then increases as the increasing wave number. Under the open circuit condition, the effect of increasing carrier concentration on wave velocity is not obvious when $kh<2$, while the wave velocity increases obviously as the increasing steady carrier concentration at the high-frequency region. Under the short circuit condition, the wave velocity increases obviously as the steady carrier concentration increases at the frequency region shown in the figure. It can be seen in Fig. 5a and b that the frequency-sensitive region expands when the carrier concentration increases, and the sensitivity under open circuit condition is much greater than that under short circuit one. Under open-circuit condition, the sensitivity of wave velocity to the steady carrier concentration gradually increases with the increase of frequency. Under short-circuit condition, it can be observed that the sensitivity of wave velocity to the steady carrier concentration increases firstly and then decreases as the frequency increases, which reaches its peak when $kh\approx 5$. In both the open and short circuit surface conditions for case 2, the change in wave velocity first increases and then decreases with the increasing wave number, and the change in steady-state carrier concentration will have a sensitive impact on the wave velocity. (There is a small insensitive region in the low-frequency region under the open-circuit condition). The sensitivity of wave velocity to the increase of the steady carrier concentration increases firstly and then decreases, which reaches the peak at $kh\approx 4$. In the low-frequency region, the higher the steady carrier concentration, the larger the wave velocity, which is opposite in the high-frequency region. In case 3, the wave velocity under the open-circuit condition presents a trend of first decreasing, then increasing, and again decreasing with the constantly increase of wave number, while that under the short circuit condition first decreases and then increases. Under both conditions, the wave velocity is sensitive to the steady carrier concentration, and consistently increases with it over the whole frequency region shown in the figure. Under the open-circuit condition, the wave velocity increases when the steady carrier concentration increases, and the sensitivity is higher in the mid-frequency region. However, the sensitivity reaches the peak when $kh\approx 4$ under the short circuit surface condition. For case 4, the wave velocity firstly increases and then decreases with the increasing wave number under the open circuit condition. But the curves are quite different under the short circuit surface condition. When the steady carrier concentration is smaller, the wave velocity decreases with the increasing wave number. When the steady carrier concentration increases, the wave velocity decreases first and then increases with the wave number. The wave velocity is sensitive to the steady carrier concentration regardless of open circuit condition or short one. With the increasing steady carrier concentration, the wave velocity increases first and then decreases, and the sensitive region also becomes slightly larger. In the mid-frequency region, the sensitivity is much higher. The sensitivity of the wave velocity to carrier concentration reaches the peak at $kh\approx 2.7$ under the open circuit condition, while it gets to its maximum at $kh\approx 3.6$ under the short one. In case 5, the propagation velocity of the Rayleigh wave first decreases, and then increases with the increase of wave number under the two electrically surface conditions. When the steady carrier concentration increases, the sensitive region increases. The wave velocity for the open circuit is sensitive to the steady carrier concentration in high-frequency region. In the short circuit condition, the sensitivity of wave velocity changes increases firstly and then decreases with the increasing steady carrier concentration. When $kh\approx 5.7$, the sensitivity gets the maximum.

Fig. 5

The influences of the steady carrier concentration on the dispersive curves $v \sim kh$ when ${P}_{B} =2 {P}_{A}$ in all the five gradient profiles

Figure 6 shows the effects of the tangential bias electric field ${\gamma }_{1}$ on Rayleigh wave velocity when the steady carrier concentration $\overline{p }=6\times {10}^{16}\,\text{m}^{-3}$ and the parameters of the top overlayer ${P}_{B} = 2{P}_{A}$. In case 1, Fig. 6a and b show that the effect of the tangential bias field ${\gamma }_{1}$ on wave velocity is tiny. When $kh\in (\mathrm{3,5})$, the increase of bias field ${\gamma }_{1}$ will exhibit a little effect, which makes the wave velocity smaller. In case 2, the bias electric field ${\gamma }_{1}$ still has little influence. When $kh\in (\mathrm{1,2})$ and $(\mathrm{6,7})$, the increase of the bias electric field ${\gamma }_{1}$ will have a weak effect, which makes the wave velocity increase. In case 3, the influence of ${\gamma }_{1}$ is more sensitive in the mid-frequency band. In the open circuit condition, the bias electric field ${\gamma }_{1}$ has a clearly visible on the wave velocity when $kh\in (\mathrm{3.5,6})$. When ${\gamma }_{1}$ increases, the wave velocity will gradually decrease, which get the maximum sensitivity when $kh\approx 4.1$. In the short circuit condition, the wave velocity will reduce with the increasing ${\gamma }_{1}$ when $kh\in (\mathrm{4,5})$, and, the bias electric field ${\gamma }_{1}$ get the maximum impact on the wave velocity when $kh\approx 4.2$. In case 4, the influence of bias field ${\gamma }_{1}$ is tiny. When $kh\in (\mathrm{1,2}),$ the wave velocity will increase with the increasing ${\gamma }_{1}$ as shown in Fig. 6g and h. In case 5, when $kh\in (\mathrm{2,6})$, the wave velocity increases firstly, and then decrease with the increasing ${\gamma }_{1}$ under both the open and short circuit conditions.

Fig. 6

The influences of the tangential biasing electric field ${\gamma }_{1}$ on the dispersive curves $v \sim kh$ in all the five gradient profiles with ${P}_{B} =2 {P}_{A}$

Figure 7 shows the effects of the bias electric field ${\gamma }_{3}$ on Rayleigh wave velocity when the carrier concentration $\overline{p }=6\times {10}^{16}\,\text{m}^{-3}$ and the parameters of the top overlayer ${P}_{B} = 2{P}_{A}$. In case 1, under the open circuit surface condition, the influence of the normal bias field ${\gamma }_{3}$ is not obvious when $kh<2$. With the increasing frequency, the wave velocity obviously increases with ${\gamma }_{3}$. Under the short circuit condition, the wave velocity increases obviously when ${\gamma }_{3}$ increases at the whole frequency region shown in the Fig. 7b. The wave velocity is sensitive to the bias electric field ${\gamma }_{3}$ in both conditions, and the sensitivity to open circuit condition is much greater than short circuit condition. The increasing ${\gamma }_{3}$ causes an expansion of sensitive areas. When the bias electric field ${\gamma }_{3}$ increases, the sensitivity of the wave velocity under the open circuit condition increases gradually with the increasing frequency, and the sensitivity of wave velocity under the short circuit condition, which reaches the maximum when $kh\approx$ 5, firstly increases and then decreases with the increasing frequency. Under the open circuit conditions for case 2 shown in Fig. 7c, the bias electric field ${\gamma }_{3}$ has no obvious effect on the wave velocity when $kh<1.5$, but the wave velocity increases obviously with ${\gamma }_{3}$ when $kh>1.5$. When the bias field ${\gamma }_{3}$ increases, the sensitive region increases and the wave velocity change is more sensitive in the high-frequency region. Under short circuit condition shown for case 2 in Fig. 7d, the wave velocity increases obviously when ${\gamma }_{3}$ increases. Meanwhile, the sensitivity of wave velocity change first increases and then decreases, it gets the maximum when $kh\approx 3.5$. In case 3, under both the open and short circuit surface conditions, the wave velocity is sensitive to ${\gamma }_{3}$, and the sensitive region increases gradually as the bias electric field ${\gamma }_{3}$ increases. Meanwhile, the sensitivity of the wave velocity under the condition of open circuit is more obvious at the mid-frequency region, while it under the short circuit condition reach the peak when $kh\approx 4$ and even the trend of the curve is changed if ${\gamma }_{3}$ is large enough. For case 4 in Fig. 7g, the increase of ${\gamma }_{3}$ under the open circuit has no obvious effect on the wave velocity when $kh<1.5$. With the increasing frequency, the wave velocity increases obviously with ${\gamma }_{3}$. Under the short circuit condition, the wave velocity increases obviously when ${\gamma }_{3}$ increases. It can be seen from Fig. 7g and h that, the sensitive area expands with the increasing ${\gamma }_{3}$, and the sensitivity is greater under the open circuit condition than short one. The sensitivity of wave velocity to the bias electric field ${\gamma }_{3}$ under the open circuit condition gradually increases with the increase of frequency, while under the short circuit condition firstly increases and then decreases with the increasing frequency, which get its peak as $kh\approx 3$. For case 5, under the open circuit condition, ${\gamma }_{3}$ has no obvious effect on the wave velocity when $kh<2$. With the increasing frequency, the wave velocity increases obviously with ${\gamma }_{3}$. Under the short circuit condition, the wave velocity obviously increases with the increasing ${\gamma }_{3}$. In both conditions, the wave velocity is sensitive to the normal bias field ${\gamma }_{3}$, and the sensitivity is greater for open circuit than short circuit. Under the open circuit condition, with the increase of frequency, the sensitivity of wave velocity to the bias electric field ${\gamma }_{3}$ gradually increases and then remains unchanged. Under the condition of short circuit, with the increase of frequency, it can be observed that the sensitivity of wave velocity to the bias field increases first and then decreases, and reaches the peak when $kh\approx 5.5$.

Fig. 7

The influences of the normal biasing electric field ${\gamma }_{3}$ on the dispersive curves $v \sim kh$ in all the five gradient profiles when ${P}_{B} =2 {P}_{A}$

6 Conclusions

In this paper, it is observed that the influence of the material properties of functionally gradient layer, the boundary conditions of open or short circuit, the steady carrier concentration, and the bias electric fields on Rayleigh wave velocity in a semi-infinite piezoelectric half space covering with a functionally gradient piezoelectric semiconductor layer. The following results can be found based on the theoretical analysis and numerical simulation.

• (1) Various transformations on the dispersive curves have occurred when the homogeneous covering layer is replaced by the gradient covering layer. The dispersive curves are more sensitive to the gradient profile under the surface short than the open circuit condition, which is similar to the results in the functionally gradient piezoelectric overlayer. Under both surface short and open circuit conditions, the dispersive curves are more sensitive to the gradient profile in the high-frequency range than the low- frequency one.

• (2) When the parameters at the top FGPS overlayer are larger than those at the bottom one, the influences of all the factors are more obvious than in the opposite case. The dispersive curves are more sensitive in the high-frequency region than in the low-frequency region.

• (3) For the five gradient profiles, the relative positions of the velocity curves in cases 1 and 3 and that in case 4 and case 5 are completely opposite about that in case 2 at the low-frequency region, which can be used as a basis to design the changing trends of material parameters in the overlay.

• (4) The increase of the steady carrier concentration has different effects on the wave velocity under different geometric profiles and open or short circuit boundary conditions, and it will make the wave velocity increase in the low-frequency region in all cases but more complex in the high-frequency region.

• (5) The normal biased electric field, which makes the sensitive region and the wave velocity increase, has a far greater influence on the wave velocity than the tangential biased electric field. It indicates that the normal biased electric field helps the propagation of the Rayleigh waves for the hole carrier.

All these conclusions provide theoretical support for the design of surface acoustic wave devices with FGPS layer.

Appendix A

The explicit expressions of $\mathbf{A}\left(z\right)$ in Eq. (6),

$$\mathbf{A}\left(z\right)=\left[\begin{array}{cc}{\mathbf{A}}_{11}\left(z\right)& -\mathrm{i}\mathbf{X}\left(z\right)\\ {\mathbf{A}}_{21}\left(z\right)& k{{\varvec{\Gamma}}}_{13}\left(z\right)\mathbf{X}\left(z\right)\end{array}\right]$$

(49)

where

$$ \begin{aligned} & {\mathbf{A}}_{\begin{subarray}{l} 11 \\ \end{subarray} } \left( z \right) = {\mathbf{X}}\left( z \right)\left( {k{{\varvec{\Gamma}}}_{31} \left( z \right) - {\text{i}}{\mathbf{M}}\left( z \right)} \right), \\ & {\mathbf{A}}_{21} \left( z \right) = - {\text{i}}k^{2} \left( {{{\varvec{\Gamma}}}_{11} \left( z \right) - {{\varvec{\Gamma}}}_{13} \left( z \right){\mathbf{X}}\left( z \right){{\varvec{\Gamma}}}_{31} \left( z \right)} \right) + {\text{i}}\rho \left( z \right)\omega^{2} {\mathbf{I^{\prime}}} \\ &\quad + k{{\varvec{\Gamma}}}_{13} \left( z \right){\mathbf{X}}\left( z \right){\mathbf{M}}\left( z \right) + {\mathbf{N}}\left( z \right), \\ & {{\varvec{\Gamma}}}_{ik} \left( z \right) = \left[ {\begin{array}{*{20}c} {c_{1i1k} \left( z \right)} & {c_{1i3k} \left( z \right)} & {e_{k1i} \left( z \right)} & 0 \\ {c_{3i1k} \left( z \right)} & {c_{3i3k} \left( z \right)} & {e_{k3i} \left( z \right)} & 0 \\ {e_{i1k} \left( z \right)} & {e_{i3k} \left( z \right)} & { - \varepsilon_{ik} \left( z \right)} & 0 \\ 0 & 0 & { - q\overline{p}\mu_{ik} \left( z \right)} & { - qd_{ik} \left( z \right)} \\ \end{array} } \right], \\ & {\mathbf{X}}\left( z \right) = [{{\varvec{\Gamma}}}_{33} \left( z \right)]^{ - 1} , \\ & {\mathbf{I}}^{\prime} = {\text{diag}}\left( {1,1,0,0} \right), \\ & {\mathbf{M}}\left( z \right) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ { - q\left( {\mu_{31} \left( z \right)\overline{E}_{1} + \mu_{33} \left( z \right)\overline{E}_{3} } \right)} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \\ & {\mathbf{N}}\left( z \right) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} { - {\text{i}}q} \\ { - q\left( {\omega - k\mu_{11} \left( z \right)\overline{E}_{1} - k\mu_{13} \left( z \right)\overline{E}_{3} } \right)} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \\ \end{aligned} $$

The explicit expressions of ${\mathbf{A}}^{e}$ in Eq. (16),

$${\mathbf{A}}^{e}=\left[\begin{array}{cc}k{\mathbf{X}}^{e}{{\varvec{\Gamma}}}_{31}^{e}& -\mathrm{i}{\mathbf{X}}^{e}\\ -{\mathrm{i}k}^{2}({{\varvec{\Gamma}}}_{11}^{e}-{{\varvec{\Gamma}}}_{13}^{e}{\mathbf{X}}^{e}{{\varvec{\Gamma}}}_{31}^{e})+\mathrm{i}\rho {\omega }^{2}{\mathbf{I}}^{e}& k{{\varvec{\Gamma}}}_{13}^{e}{\mathbf{X}}^{e}\end{array}\right]$$

(50)

where

$$ \begin{aligned} & {{\varvec{\Gamma}}}_{ik}^{e} = \left[ {\begin{array}{*{20}c} {c_{1i1k} } & {c_{1i3k} } & {e_{k1i} } \\ {c_{3i1k} } & {c_{3i3k} } & {e_{k3i} } \\ {e_{i1k} } & {e_{i3k} } & { - \varepsilon_{ik} } \\ \end{array} } \right] \\ & {\mathbf{X}}^{e} = \left( {{{\varvec{\Gamma}}}_{33}^{e} } \right)^{ - 1} \\ & {\mathbf{I}}^{e} = {\text{diag}}\left( {1,1,0} \right) \\ \end{aligned} $$

The state vectors ${\varvec{\upxi}}\left({0}^{+}\right)$ and ${\varvec{\upxi}}\left({h}^{-}\right)$ of the FGPS layer are connected by the transfer matrix $\mathbf{B}\left(h\right)$, that is,

$${\varvec{\upxi}}\left({h}^{-}\right)=\mathbf{B}\left(h\right){\varvec{\upxi}}\left({0}^{+}\right)$$

(51)

where

$$\mathbf{B}\left(h\right)={\left({b}_{ij}\right)}_{8\times 8}, i,j=1,\dots ,8$$

(52)

Let ${\mathbf{U}}_{1}^{f}=\left[\begin{array}{c}\begin{array}{c}{u}_{1}\\ {u}_{3}\end{array}\\ \varphi \end{array}\right],{\mathbf{U}}_{2}^{f}=\left[p\right],{\mathbf{T}}_{1}^{f}=\left[\begin{array}{c}\begin{array}{c}{\sigma }_{11}\\ { \sigma }_{13}\end{array}\\ {D}_{3}\end{array}\right],{\mathbf{T}}_{2}^{f}=\left[{J}_{3}\right].$ Due to the nonexistence of the electric current ${J}_{3}$, Eq. (50) can be rewritten as

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{1}^{f} \left( {h^{ - } } \right)} \\ {{\mathbf{U}}_{2}^{f} \left( {h^{ - } } \right)} \\ {{\mathbf{T}}_{1}^{f} \left( {h^{ - } } \right)} \\ {0\left( {h^{ - } } \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{D}}_{11} } \\ {\begin{array}{*{20}c} {{\mathbf{D}}_{21} } \\ {\begin{array}{*{20}c} {{\mathbf{D}}_{31} } \\ {{\mathbf{D}}_{41} } \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{D}}_{12} } \\ {\begin{array}{*{20}c} {{\mathbf{D}}_{22} } \\ {\begin{array}{*{20}c} {{\mathbf{D}}_{32} } \\ {{\mathbf{D}}_{42} } \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{D}}_{13} } \\ {\begin{array}{*{20}c} {{\mathbf{D}}_{23} } \\ {\begin{array}{*{20}c} {{\mathbf{D}}_{33} } \\ {{\mathbf{D}}_{43} } \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {{\mathbf{D}}_{14} } \\ {\begin{array}{*{20}c} {{\mathbf{D}}_{24} } \\ {\begin{array}{*{20}c} {{\mathbf{D}}_{34} } \\ {{\mathbf{D}}_{44} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{1}^{f} \left( {0^{ + } } \right)} \\ {{\mathbf{U}}_{2}^{f} \left( {0^{ + } } \right)} \\ {{\mathbf{T}}_{1}^{f} \left( {0^{ + } } \right)} \\ {0\left( {0^{ + } } \right)} \\ \end{array} } \right] $$

(53a)

From Eq. (52), it can be obtained that

$$ \begin{gathered} {\mathbf{U}}_{1}^{f} \left( {h^{ - } } \right) = {\mathbf{D}}_{11} {\mathbf{U}}_{1}^{f} \left( {0^{ + } } \right) + {\mathbf{D}}_{12} {\mathbf{U}}_{2}^{f} \left( {0^{ + } } \right) + {\mathbf{D}}_{13} {\mathbf{T}}_{1}^{f} \left( {0^{ + } } \right), \hfill \\ {\mathbf{U}}_{2}^{f} \left( {h^{ - } } \right) = {\mathbf{D}}_{21} {\mathbf{U}}_{1}^{f} \left( {0^{ + } } \right) + {\mathbf{D}}_{22} {\mathbf{U}}_{2}^{f} \left( {0^{ + } } \right) + {\mathbf{D}}_{23} {\mathbf{T}}_{1}^{f} \left( {0^{ + } } \right), \hfill \\ {\mathbf{T}}_{1}^{f} \left( {h^{ - } } \right) = {\mathbf{D}}_{31} {\mathbf{U}}_{1}^{f} \left( {0^{ + } } \right) + {\mathbf{D}}_{32} {\mathbf{U}}_{2}^{f} \left( {0^{ + } } \right) + {\mathbf{D}}_{33} {\mathbf{T}}_{1}^{f} \left( {0^{ + } } \right), \hfill \\ 0 = {\mathbf{D}}_{41} {\mathbf{U}}_{1}^{f} \left( {0^{ + } } \right) + {\mathbf{D}}_{42} {\mathbf{U}}_{2}^{f} \left( {0^{ + } } \right) + {\mathbf{D}}_{43} {\mathbf{T}}_{1}^{f} \left( {0^{ + } } \right).{ } \hfill \\ \end{gathered} $$

(53b)

Furthermore, it can be derived that

$$ { }\left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{1}^{f} \left( {h^{ - } } \right)} \\ {{\mathbf{T}}_{1}^{f} \left( {h^{ - } } \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{11} - {\mathbf{D}}_{12} {\mathbf{D}}_{42}^{ - 1} {\mathbf{D}}_{41} } & {{\mathbf{D}}_{13} - {\mathbf{D}}_{12} {\mathbf{D}}_{42}^{ - 1} {\mathbf{D}}_{43} } \\ {{\mathbf{D}}_{31} - {\mathbf{D}}_{32} {\mathbf{D}}_{42}^{ - 1} {\mathbf{D}}_{41} } & {{\mathbf{D}}_{33} - {\mathbf{D}}_{32} {\mathbf{D}}_{42}^{ - 1} {\mathbf{D}}_{43} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{1}^{f} \left( {0^{ + } } \right)} \\ {{\mathbf{T}}_{1}^{f} \left( {0^{ + } } \right)} \\ \end{array} } \right]. $$

(54)

Let ${{\varvec{\upxi}}}^{f}=\left[\begin{array}{c}{\mathbf{U}}_{1}^{f}\\ {\mathbf{T}}_{1}^{f}\end{array}\right]$, then, Eq. (28a) can be amended to

$${{\varvec{\upxi}}}^{f}\left({h}^{-}\right)={\mathbf{B}}^{f}\left(h\right){{\varvec{\upxi}}}^{f}\left({0}^{+}\right),$$

(55a)

where

$$ \begin{aligned} & {\mathbf{B}}^{f} \left( h \right) = \left( {{\mathbf{B}}_{ij}^{f} } \right),i,j = 1,2, \\ & {\mathbf{B}}_{11}^{f} = {\mathbf{D}}_{11} - {\mathbf{D}}_{12} {\mathbf{D}}_{42}^{ - 1} {\mathbf{D}}_{41} ,{\mathbf{B}}_{12}^{f} = {\mathbf{D}}_{13} - {\mathbf{D}}_{12} {\mathbf{D}}_{42}^{ - 1} {\mathbf{D}}_{43} , \\ & {\mathbf{B}}_{21}^{f} = {\mathbf{D}}_{31} - {\mathbf{D}}_{32} {\mathbf{D}}_{42}^{ - 1} {\mathbf{D}}_{41} ,{\mathbf{B}}_{22}^{f} = {\mathbf{D}}_{33} - {\mathbf{D}}_{32} {\mathbf{D}}_{42}^{ - 1} {\mathbf{D}}_{43} , \\ \end{aligned} $$

$$ \begin{aligned} {\mathbf{D}}_{11} & = \left[ {\begin{array}{*{20}c} {b_{11} } & {b_{12} } & {b_{13} } \\ {b_{21} } & {b_{22} } & {b_{23} } \\ {b_{31} } & {b_{32} } & {b_{33} } \\ \end{array} } \right],{\mathbf{D}}_{12} = \left[ {\begin{array}{*{20}c} {b_{14} } \\ {b_{24} } \\ {b_{34} } \\ \end{array} } \right],{\mathbf{D}}_{13} = \left[ {\begin{array}{*{20}c} {b_{15} } & {b_{16} } & {b_{17} } \\ {b_{25} } & {b_{26} } & {b_{27} } \\ {b_{35} } & {b_{36} } & {b_{37} } \\ \end{array} } \right] \\ {\mathbf{D}}_{31} & = \left[ {\begin{array}{*{20}c} {b_{51} } & {b_{52} } & {b_{53} } \\ {b_{61} } & {b_{62} } & {b_{63} } \\ {b_{71} } & {b_{72} } & {b_{73} } \\ \end{array} } \right],{\mathbf{D}}_{32} = \left[ {\begin{array}{*{20}c} {b_{54} } \\ {b_{64} } \\ {b_{74} } \\ \end{array} } \right],{\mathbf{D}}_{33} = \left[ {\begin{array}{*{20}c} {b_{55} } & {b_{56} } & {b_{57} } \\ {b_{65} } & {b_{66} } & {b_{67} } \\ {b_{75} } & {b_{76} } & {b_{77} } \\ \end{array} } \right] \\ {\mathbf{D}}_{41} & = \left[ {\begin{array}{*{20}c} {b_{81} } & {b_{82} } & {b_{83} } \\ \end{array} } \right],{\mathbf{D}}_{42} = \left[ {b_{84} } \right],{\mathbf{D}}_{43} = \left[ {\begin{array}{*{20}c} {b_{85} } & {b_{86} } & {b_{87} } \\ \end{array} } \right]. \\ \end{aligned} $$

(55b)

$$ {\mathbf{K}}^{f} \left( h \right) = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{11}^{f} } & {{\mathbf{K}}_{12}^{f} } \\ {{\mathbf{K}}_{21}^{f} } & {{\mathbf{K}}_{22}^{f} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{B}}_{22}^{f} \left( {{\mathbf{B}}_{12}^{f} } \right)^{ - 1} } & {{\mathbf{B}}_{21}^{f} - {\mathbf{B}}_{22}^{f} \left( {{\mathbf{B}}_{12}^{f} } \right)^{ - 1} {\mathbf{B}}_{11}^{f} } \\ {\left( {{\mathbf{B}}_{12}^{f} } \right)^{ - 1} } & { - \left( {{\mathbf{B}}_{12}^{f} } \right)^{ - 1} {\mathbf{B}}_{11}^{f} } \\ \end{array} } \right]. $$

(56)