1 Introduction

Since scientists found that piezoelectric properties exist in some semiconductor materials, they have drawn conclusion that both II–VI material alloys and III–V material alloys are piezoelectric semiconductors. Most of the early researches related to waves in piezoelectric semiconductor were reported on the bulk waves [11, 15]. Over the past decade, the research group of Prof. Wang Zhonglin have proposed the concept of piezotronics and have done much work on the basic theory, principals and devices of piezoelectric semiconductors [21,22,23]. To enhance the application of surface acoustic wave (SAW) devices and bulk acoustic wave devices, scientists have considered utilizing the coupling properties of piezoelectric-semiconductor materials to investigate the electric-elastic dynamics problems [10, 13, 28].

An early report regarding wave propagation in piezoelectric structures was a study on surface horizontal shear waves in the piezoelectric half space by Bleustein [1] and Gulyaev [1], and the wave was named the B–G wave. Subsequently, researchers have investigated different waves in various piezoelectric structures for application in acoustic wave device design and nondestructive evaluation. The structures include plane layered structures [12], cylindrical structures [31], spherical structures [33], and other curved surface structures [5]. The materials are not limited to homogenous piezoelectric material, and extend to functionally graded piezoelectric materials [16] and piezoelectric–piezomagnetic materials [4, 27]. The waves are related to plane strain surface waves in a half space [24], Lamb waves in a thin film or plate [4], and horizontal shear surface waves (Love waves or B–G waves) [14] and horizontal shear (SH) waves in a thin film or plate [19]. Many methods are employed for solving the governing equations of wave propagation problems, such as the exact analytical solution [7], the special function method [6], the power series method [3], the Legendre polynomials method [32], and so on.

When the electric field is accompanied with travelling acoustic waves in a piezoelectric semiconductor, carriers can be transported by the acoustic wave from one place to another. The phenomenon is called acoustic charge transport [2, 17]. Up to now, few studies have reported on semiconductor and piezoelectric coupling effects on wave propagation properties. Most of these studies, however, focus on structures in which one piezoelectric layer is compounded on another semiconductor layer [29, 30]. It was found that an acoustic wave propagating in these structures can be amplified by a dc electric field, which is named an acoustoelectric amplification phenomenon [8, 25, 26]. Few reports have been published on piezoelectric semiconductor structures. SH waves in a piezoelectric semiconductor half space have recently been investigated by Gu and Jin [9]. They found that semiconduction affects wave speed and causes wave dispersion and attenuation, and that waves can be amplified by the biasing electric field. Scientists aim the plain strain surface wave, also named Rayleigh surface wave, in a composite consisting of homogeneous isotropic semiconductor half space coated with a thin layer of homogeneous, transversely isotropic, piezoelectric material [18]. However, no report has been published on the Rayleigh waves in a half space made of the material which have both piezoelectric and semiconductor properties.

In this paper, we investigate the plane strain surface in a piezoelectric semiconductor half space. Based on the basic elastic-dynamic equations, we deduce the governing equations with respect to the displacement, the electric potential and the perturbation of the carrier density. By solving the governing equations analytically, we obtain a dispersion equation with complex variables. The influences of the steady-state carrier density \(\bar{n}\) and the biasing electric field on dispersion and attenuation are discussed.

2 Statement of the problem and basic equations

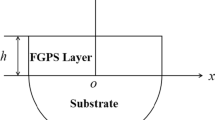
For a transversely isotropic piezoelectric semiconductor wafer, Cartesian coordinates are shown in Fig. 1. It is assumed that the x1–x2 coordinate plane is an isotropic plane; the direction of polling is the same as the positive direction of the x3-axis. It is under a uniform biasing electric field \(\bar{E}_{j}\), \(j = 1,2,3\). The carrier charge and steady-state carrier density are \(q\) and \(\bar{n}\), respectively.

Fig. 1
figure 1

A piezoelectric semiconductor wafer and Cartesian coordinates

Full size image

The piezoelectric semiconductor constitutive equations can be expressed as

$$\sigma_{ij} = c_{ijkl} S_{kl} - e_{kij} E_{k} ,\quad D_{i} = e_{ikl} S_{kl} + \varepsilon_{il} E_{l} ,\quad J_{i} = q\bar{n}\mu_{ij} E_{j} + qn\mu_{ij} \bar{E}_{j} - qd_{ij} n_{,j}$$
(1)

where \(i,j,k,l = 1,2,3\); \(\sigma_{ij}\) and \(S_{kl}\) are the stress and strain tensors; the perturbation of the carrier density is denoted by \(n\); \(D_{i} {\kern 1pt} {\kern 1pt} ,E_{k}\) and \(J_{i}\) are the electrical displacement, the electrical field intensity and electric current; \(c_{ijkl}\), \(e_{kij}\) and \(\varepsilon_{il}\) are the elastic, piezoelectric and dielectric coefficients, respectively; and \(\mu_{ij}\) and \(d_{ij}\) are the carrier mobility and diffusion constants, respectively.

The relationship between the mechanical displacement and the strain components is as follows:

$$S_{ij} = {{\left( {u_{i,j} + u_{j,i} } \right)} \mathord{\left/ {\vphantom {{\left( {u_{i,j} + u_{j,i} } \right)} 2}} \right. \kern-0pt} 2}$$
(2)

where \(u_{i}\) is the component of mechanical displacement in the ith direction, and the comma followed by an index denotes partial differentiation with respect to the coordinate associated with the index.

The electric field \(E_{k}\) is related to the electric potential \(\varphi\) by

$$E_{k} = - \varphi_{,k} .$$
(3)

The linear theory for the small and dynamic signals consists of the equations of motion, Gauss’ law of electrostatics and the conservation of charge, given by

$$\sigma_{ij,j} = \rho \ddot{u}_{i} ,\quad D_{i,i} = qn,\quad q\dot{n} + J_{i,i} = 0,$$
(4)

where \(\rho\) is the mass density, the dot ‘‘·” represents time differentiation, and the repeated index in the subscript implies summation with respect to that index.

Considering plane strain waves propagating along \(x_{1}\) direction in a piezoelectric semiconductor wafer, we suppose that the mechanical displacement components, the electrical potential and the perturbation of the carrier density can be expressed as

$$u_{1} = u_{1} \left( {x_{1} ,x_{3} ,t} \right),\quad u_{2} = 0,\quad u_{3} = u_{3} \left( {x_{1} ,x_{3} ,t} \right),\quad \varphi = \varphi \left( {x_{1} ,x_{3} ,t} \right),\quad n = n\left( {x_{1} ,x_{3} ,t} \right).$$
(5)

When the thickness of the wafer is much greater than the wavelength, the wafer can be considered a piezoelectric semiconductor half space. Therefore, the plane strain waves should be generalized Rayleigh surface waves.

Typically, for the transversely isotropic piezoelectric semiconductor material, substitution of Eq. (5) into Eqs. (2) and (3), and then substitution of these new equations into Eq. (1), leads to

$$\begin{aligned} & \sigma_{11} = c_{11} \frac{{\partial u_{1} }}{{\partial x_{1} }} + c_{13} \frac{{\partial u_{3} }}{{\partial x_{3} }} + e_{31} \frac{\partial \varphi }{{\partial x_{3} }},\quad \sigma_{22} = c_{12} \frac{{\partial u_{1} }}{{\partial x_{1} }} + c_{13} \frac{{\partial u_{3} }}{{\partial x_{3} }} + e_{31} \frac{\partial \varphi }{{\partial x_{3} }},\quad \sigma_{33} = c_{13} \frac{{\partial u_{1} }}{{\partial x_{1} }} + c_{33} \frac{{\partial u_{3} }}{{\partial x_{3} }} + e_{33} \frac{\partial \varphi }{{\partial x_{3} }}, \\ & \sigma_{12} = 0,\quad \sigma_{13} = c_{44} \left( {\frac{{\partial u_{1} }}{{\partial x_{3} }} + \frac{{\partial u_{3} }}{{\partial x_{1} }}} \right) + e_{15} \frac{\partial \varphi }{{\partial x_{1} }},\quad \sigma_{23} = 0, \\ & D_{1} = e_{15} \left( {\frac{{\partial u_{1} }}{{\partial x_{3} }} + \frac{{\partial u_{3} }}{{\partial x_{1} }}} \right) - \varepsilon_{11} \frac{\partial \varphi }{{\partial x_{1} }},\quad D_{2} = e_{15} \left( {\frac{{\partial u_{1} }}{{\partial x_{3} }} + \frac{{\partial u_{3} }}{{\partial x_{1} }}} \right),\quad D_{3} = e_{31} \frac{{\partial u_{1} }}{{\partial x_{1} }} + e_{33} \frac{{\partial u_{3} }}{{\partial x_{3} }} - \varepsilon_{33} \frac{\partial \varphi }{{\partial x_{3} }}, \\ & J_{1} = - q\bar{n}\mu_{11} \frac{\partial \varphi }{{\partial x_{1} }} + qn\mu_{11} \bar{E}_{1} - qd_{11} \frac{\partial n}{{\partial x_{1} }},\quad J_{2} = qn\mu_{11} \bar{E}_{2} ,\quad J_{3} = - q\bar{n}\mu_{33} \frac{\partial \varphi }{{\partial x_{3} }} + qn\mu_{33} \bar{E}_{3} - qd_{33} \frac{\partial n}{{\partial x_{3} }}. \\ \end{aligned}$$
(6)

By substituting Eq. (6) into Eq. (4), we obtain the governing equations expressed by \(u_{1}\), \(u_{3}\), \(\varphi\) and \(n\), providing the following equation:

$$\begin{aligned} & c_{11} \frac{{\partial^{2} u_{1} }}{{\partial x_{1}^{2} }} + c_{44} \frac{{\partial^{2} u_{1} }}{{\partial x_{3}^{2} }} + \left( {c_{13} + c_{44} } \right)\frac{{\partial^{2} u_{3} }}{{\partial x_{1} \partial x_{3} }} + \left( {e_{31} + e_{15} } \right)\frac{{\partial^{2} \varphi }}{{\partial x_{1} \partial x_{3} }} = \rho \ddot{u}_{1} \\ & c_{44} \left( {\frac{{\partial^{2} u_{1} }}{{\partial x_{3} \partial x_{1} }} + \frac{{\partial^{2} u_{3} }}{{\partial x_{1}^{2} }}} \right) + e_{15} \frac{{\partial^{2} \varphi }}{{\partial x_{1}^{2} }} + c_{13} \frac{{\partial^{2} u_{1} }}{{\partial x_{1} \partial x_{3} }} + c_{33} \frac{{\partial^{2} u_{3} }}{{\partial x_{3}^{2} }} + e_{33} \frac{{\partial^{2} \varphi }}{{\partial x_{3}^{2} }} = \rho \ddot{u}_{3} , \\ & \left( {e_{15} + e_{31} } \right)\frac{{\partial^{2} u_{1} }}{{\partial x_{3} \partial x_{1} }} + e_{15} \frac{{\partial^{2} u_{3} }}{{\partial x_{1}^{2} }} + e_{33} \frac{{\partial^{2} u_{3} }}{{\partial x_{3}^{2} }} - \varepsilon_{11} \frac{{\partial^{2} \varphi }}{{\partial x_{1}^{2} }} - \varepsilon_{33} \frac{{\partial^{2} \varphi }}{{\partial x_{3}^{2} }} = qn, \\ & \bar{n}\mu_{11} \frac{{\partial^{2} \varphi }}{{\partial x_{1}^{2} }} - \mu_{11} \bar{E}_{1} \frac{\partial n}{{\partial x_{1} }} + d_{11} \frac{{\partial^{2} n}}{{\partial x_{1}^{2} }} + \bar{n}\mu_{33} \frac{{\partial^{2} \varphi }}{{\partial x_{3}^{2} }} - \mu_{33} \bar{E}_{3} \frac{\partial n}{{\partial x_{3} }} + d_{33} \frac{{\partial^{2} n}}{{\partial x_{3}^{2} }} = \dot{n}. \\ \end{aligned}$$
(7)

The electrical potential \(\varphi_{0}\) in the air satisfies the Laplace equation, for \(z < 0,\)

$$\frac{{\partial^{2} \varphi_{0} }}{{\partial x_{3}^{2} }} + \frac{{\partial^{2} \varphi_{0} }}{{\partial x_{1}^{2} }} = 0.$$
(8)

Therefore, the third component of electrical displacement of the air should satisfy

$$D_{30} = - \varepsilon_{0} \frac{{\partial \varphi_{0} }}{{\partial x_{3} }}$$
(9)

where \(\varepsilon_{0}\) is the dielectric coefficient in the air.

For generalized Rayleigh surface waves propagating in an unelectroded piezoelectric semiconductor half space, the following boundary conditions, continuity conditions and attenuation conditions should be satisfied:

  1. (a)

    Traction free conditions

    $$\sigma_{33} = 0,\quad \sigma_{13} = 0,\quad {\text{at}}\;z = 0.$$
    (10)
  2. (b)

    Continuity condition

    $$\varphi = \varphi_{0} ,\quad \dot{D}_{3} + J_{3} = \dot{D}_{30} ,\quad {\text{at}}\;z = 0.$$
    (11)
  3. (c)

    The perturbation of the carrier density of the surface

    $$n = 0,\quad {\text{at}}\;z = 0.$$
    (12)
  4. (d)

    The attenuation conditions for generalized Rayleigh surface waves at \(z \to \pm \infty ,\)

    $$u_{1} \to 0,\quad u_{3} \to 0,\quad \varphi \to 0,\quad n \to 0,\quad {\text{as}}\;z \to + \infty ,$$
    (13)
    $$\varphi_{0} \to 0,\quad {\text{as}}\;z \to - \infty .$$
    (14)

3 Solution to the problem

For generalized Rayleigh surface waves propagating along \(x_{1}\) direction in an unelectroded piezoelectric semiconductor half space, as described above, the solution of the governing equations can be expressed as

$$\begin{aligned} & u_{1} = U_{1} \left( {x_{3} } \right)\exp \left[ {{\text{i}}k\left( {x_{1} - ct} \right)} \right],\quad u_{3} = U_{3} \left( {x_{3} } \right)\exp \left[ {{\text{i}}k\left( {x_{1} - ct} \right)} \right], \\ & \varphi = \mathcal{\varPhi }\left( {x_{3} } \right)\exp \left[ {{\text{i}}k\left( {x_{1} - ct} \right)} \right],\quad n = N\left( {x_{3} } \right)\exp \left[ {{\text{i}}k\left( {x_{1} - ct} \right)} \right], \\ \end{aligned}$$
(15)

where \({\text{i}} = \sqrt { - 1}\), \(k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0pt} \lambda }\) is the wave number, \(\lambda\) is the wave length, \(c\) is the wave speed, and \(U_{l} \left( {x_{3} } \right)\), \(\mathcal{\varPhi }\left( {x_{3} } \right)\), \(N\left( {x_{3} } \right)\) and \(\mathcal{\varPhi }_{0} \left( {x_{3} } \right)\) are undetermined functions of the mechanical displacement, the electrical potential of the piezoelectric semiconductor, the perturbation of the carrier density and the electrical potential of air, respectively, which are to be solved.

By substituting Eq. (15) into Eq. (7), we obtain a series of ordinary differential equations with respect to \(x_{3}\), as follows:

$$\begin{aligned} & c_{44} \frac{{{\text{d}}^{2} U_{1} }}{{{\text{d}}x_{3}^{2} }} + \left( {c_{13} + c_{44} } \right){\text{i}}k\frac{{{\text{d}}^{2} U_{3} }}{{{\text{d}}x_{3} }} + \left( {e_{31} + e_{15} } \right){\text{i}}k\frac{{{\text{d}}\varPhi }}{{{\text{d}}x_{3} }} + \left( {\rho c^{2} - c_{11} } \right)k^{2} U_{1} = 0 \\ & c_{33} \frac{{{\text{d}}^{2} U_{3} }}{{{\text{d}}x_{3}^{2} }} + {\text{i}}k\left( {c_{44} + c_{13} } \right)\frac{{{\text{d}}U_{1} }}{{{\text{d}}x_{3} }} + \left( {\rho c^{2} - c_{44} } \right)k^{2} U_{3} + e_{33} \frac{{{\text{d}}^{2} \varPhi }}{{{\text{d}}x_{3}^{2} }} - e_{15} k^{2} \varPhi = 0 \\ & \left( {e_{15} + e_{31} } \right){\text{i}}k\frac{{{\text{d}}U_{1} }}{{{\text{d}}x_{3} }} + e_{33} \frac{{{\text{d}}^{2} U_{3} }}{{{\text{d}}x_{3}^{2} }} - k^{2} e_{15} U_{3} + \varepsilon_{11} k^{2} \varPhi - \varepsilon_{33} \frac{{{\text{d}}^{2} \varPhi }}{{{\text{d}}x_{3}^{2} }} - qN = 0 \\ & \bar{n}\mu_{33} \frac{{{\text{d}}^{2} \varPhi }}{{{\text{d}}x_{3}^{2} }} - \bar{n}\mu_{11} k^{2} \varPhi + d_{33} \frac{{{\text{d}}^{2} N}}{{{\text{d}}x_{3}^{2} }} - \mu_{33} \bar{E}_{3} \frac{{{\text{d}}N}}{{{\text{d}}x_{3} }} - {\text{i}}k\mu_{11} \bar{E}_{1} N + {\text{i}}kcN - d_{11} k^{2} N = 0 \\ \end{aligned}$$
(16)

Suppose the solution of Eq. (16) is

$$U_{1} = A_{1} \exp \left( {\alpha x_{3} } \right),\quad U_{3} = A_{3} \exp \left( {\alpha x_{3} } \right),\quad \varPhi = A_{\varPhi } \exp \left( {\alpha x_{3} } \right),\quad N = A_{N} \exp \left( {\alpha x_{3} } \right),$$
(17)

where \(A_{1}\), \(A_{3}\), \(A_{\varPhi }\) and \(A_{N}\) are the coefficients, and \(\alpha\) describes the decay rate from the free surface \(x_{3} = 0\) which should have a negative real part. Substituting Eq. (17) into Eq. (16) and cancelling the common exponential factor, we obtain a series of homogeneous linear equations with respect to \(A_{1}\), \(A_{3}\), \(A_{\mathcal{\varPhi }}\) and \(A_{N}\), as follows:

$$\begin{aligned} & \left[ {c_{44} \alpha^{2} + \left( {\rho c^{2} - c_{11} } \right)k^{2} } \right]A_{1} + {\text{i}}\left( {c_{13} + c_{44} } \right)k\alpha A_{3} + {\text{i}}\left( {e_{31} + e_{15} } \right)k\alpha A_{\mathcal{\varPhi }} = 0, \\ & {\text{i}}\left( {c_{13} + c_{44} } \right)k\alpha A_{1} + \left[ {c_{33} \alpha^{2} + \left( {\rho c^{2} - c_{44} } \right)k^{2} } \right]A_{3} + \left( {e_{33} \alpha^{2} - e_{15} k^{2} } \right)A_{\mathcal{\varPhi }} = 0, \\ & {\text{i}}\left( {e_{31} + e_{15} } \right)k\alpha A_{1} + \left( {e_{33} \alpha^{2} - e_{15} k^{2} } \right)A_{3} + \left( {\varepsilon_{11} k^{2} - \varepsilon_{33} \alpha^{2} } \right)A_{\varPhi } - qA_{N} = 0, \\ & \left( {\bar{n}\mu_{33} \alpha^{2} - \bar{n}\mu_{11} k^{2} } \right)A_{\mathcal{\varPhi }} + \left( {d_{33} \alpha^{2} - \mu_{33} \bar{E}_{3} \alpha - ik\mu_{11} \bar{E}_{1} + ikc - d_{11} k^{2} } \right)A_{N} = 0. \\ \end{aligned}$$
(18)

For the homogeneous linear equations shown in Eq. (18), the sufficient and necessary condition for the existence of a non-trivial solution is that the determinant of the coefficient matrix has to vanish. Therefore, \(\alpha\) should satisfy:

$$\left| {\begin{array}{*{20}c} {c_{44} \alpha^{2} + \left( {\rho c^{2} - c_{11} } \right)k^{2} } & {{\text{i}}\left( {c_{13} + c_{44} } \right)k\alpha } & {{\text{i}}\left( {e_{31} + e_{15} } \right)k\alpha } & 0 \\ {{\text{i}}\left( {c_{13} + c_{44} } \right)k\alpha } & {c_{33} \alpha^{2} + \left( {\rho c^{2} - c_{44} } \right)k^{2} } & {e_{33} \alpha^{2} - e_{15} k^{2} } & 0 \\ {{\text{i}}\left( {e_{31} + e_{15} } \right)k\alpha } & {e_{33} \alpha^{2} - e_{15} k^{2} } & {\varepsilon_{11} k^{2} - \varepsilon_{33} \alpha^{2} } & { - \,q} \\ 0 & 0 & {\bar{n}\mu_{33} \alpha^{2} - \bar{n}\mu_{11} k^{2} } & {\left( \begin{aligned} d_{33} \alpha^{2} - \mu_{33} \bar{E}_{3} \alpha \hfill \\ - ik\mu_{11} \bar{E}_{1} + ikc - d_{11} k^{2} \hfill \\ \end{aligned} \right)} \\ \end{array} } \right| = 0$$
(19)

Equation (19) is an eighth-order equation with respect to \(\alpha\). Omitting the root with a positive real part, we should obtain four roots with a negative real part: \(\alpha_{j}\), \(j\) from 1 to 4. \(\alpha_{j}\) depends on the wave speed c and wave number k.

Once \(\alpha_{j}\) is known, by substituting \(\alpha_{j}\) into Eq. (18), we obtain the linear relationship between \(A_{1}\), \(A_{3}\), \(A_{\varPhi }\) and \(A_{N}\), which can be expressed as

$$A_{3j} = \beta_{1j} A_{1j} ,\quad A_{{\mathcal{\varPhi j}}} = \beta_{2j} A_{1j} ,\quad A_{Nj} = \beta_{3j} A_{1j} ,$$

where subscript \(j\) represents the case of different \(\alpha_{j}\), \(A_{1j}\) are the undetermined constants, and \(\beta_{1j}\), \(\beta_{2j}\), and \(\beta_{3j}\), which also depend on the wave speed c and wave number k, can be calculated based on Eq. (18) and \(\alpha_{j}\). \(U_{1} \left( {x_{3} } \right)\), \(U_{3} \left( {x_{3} } \right)\), \(\mathcal{\varPhi }\left( {x_{3} } \right)\), and \(N\left( {x_{3} } \right)\) in Eq. (15) can be rewritten as

$$\begin{aligned} & U_{1} \left( {x_{3} } \right) = \sum\limits_{j = 1}^{4} {A_{1j} \exp \left( {\alpha_{j} x_{3} } \right)} ,\quad U_{3} \left( {x_{3} } \right) = \sum\limits_{j = 1}^{4} {\beta_{1j} A_{1j} \exp \left( {\alpha_{j} x_{3} } \right)} , \\ & \mathcal{\varPhi }\left( {x_{3} } \right) = \sum\limits_{j = 1}^{4} {\beta_{2j} A_{1j} \exp \left( {\alpha_{j} x_{3} } \right)} ,\quad N\left( {x_{3} } \right) = \sum\limits_{j = 1}^{4} {\beta_{3j} A_{1j} \exp \left( {\alpha_{j} x_{3} } \right)} . \\ \end{aligned}$$
(20)

The solution of Eq. (8) can also be expressed as

$$\varphi_{0} = \mathcal{\varPhi }_{0} \left( {x_{3} } \right)\exp \left[ {{\text{i}}k\left( {x_{1} - ct} \right)} \right],$$
(21)

where

$$\mathcal{\varPhi }_{0} \left( {x_{3} } \right) = \sum\limits_{j = 1}^{4} {\beta_{2j} A_{1j} \exp \left( {kx_{3} } \right)} ,$$
(22)

and is deduced from continuity conditions, as shown in the first equation in Eq. (11), and attenuation conditions, as shown in Eq. (14).

Upon the following sequence of substitution: (1) Equations (20) and (22) into Eqs. (15) and (21), (2) the modified Eqs. (15) and (21) into Eq. (6), (3) the new equation into boundary condition Eqs. (10), (11), and (12), the linear homogeneous equations with respect to \(A_{1j}\), \(j\) from 1 to 4, can be obtained.

$$\begin{array}{*{20}l} {\sum\limits_{j = 1}^{4} {\left( {{\text{i}}kc_{13} + c_{33} \beta_{1j} \alpha_{j} + e_{33} \beta_{2j} \alpha_{j} } \right)A_{1j} } = 0,} \hfill \\ {\sum\limits_{j = 1}^{4} {\left( {c_{44} \alpha_{j} + {\text{i}}kc_{44} \beta_{1j} + {\text{i}}ke_{15} \beta_{2j} } \right)A_{1j} } = 0,} \hfill \\ {\sum\limits_{j = 1}^{4} {\beta_{3j} A_{1j} } = 0,} \hfill \\ {\sum\limits_{j = 1}^{4} {\left( \begin{aligned} k^{2} ce_{31} - {\text{i}}kc\beta_{1j} \alpha_{j} e_{33} + {\text{i}}kc\varepsilon_{33} \beta_{2j} \alpha_{j} - {\text{i}}k^{2} c\varepsilon_{0} \beta_{2j} \hfill \\ - q\bar{n}\mu_{33} \beta_{2j} \alpha_{j} + q\mu_{33} \bar{E}_{3} \beta_{3j} - qd_{33} \beta_{3j} \alpha_{j} \hfill \\ \end{aligned} \right)A_{1j} } = 0.} \hfill \\ \end{array}$$
(23)

For non-trivial solutions of \(A_{j}\), \(j\) from 1 to 4, the determinant of the coefficient matrix of Eq. (23) must vanish, which gives an equation that determines the wave speed c versus the wave number k, as follows:

$$\left| {Q_{ij} } \right| = 0$$
(24)

where \(\left[ {Q_{ij} } \right]\) is a \(4 \times 4\) matrix, and

$$\begin{aligned} & Q_{1j} = {\text{i}}kc_{13} + c_{33} \beta_{1j} \alpha_{j} + e_{33} \beta_{2j} \alpha_{j} ,\quad Q_{2j} = c_{44} \alpha_{j} + {\text{i}}kc_{44} \beta_{1j} + {\text{i}}ke_{15} \beta_{2j} ,\quad Q_{3j} = \beta_{3j} , \\ & Q_{4j} = k^{2} ce_{31} - {\text{i}}kc\beta_{1j} \alpha_{j} e_{33} + \left[ {{\text{i}}kc\left( {\varepsilon_{33} \alpha_{j} - \varepsilon_{0} k} \right) - q\bar{n}\mu_{33} \alpha_{j} } \right]\beta_{2j} + q\left( {\mu_{33} \bar{E}_{3} - d_{33} \alpha_{j} } \right)\beta_{3j} , \\ \end{aligned}$$

and each item depends on the wave speed c and the wave number k.

The relationship between the wave speed c and the wave number k can be obtained from Eq. (24). Furthermore, the relationship between the undetermined constants \(A_{1j}\) can be obtained from

$$\left[ {Q_{ij} } \right]\left[ {A_{1j} } \right] = 0.$$
(25)

4 Numerical results and discussion

For numerical analysis with the theoretical model developed above, we consider a half-space of ZnO with

$$\begin{aligned} & c_{11} = 210\,{\text{Gpa,}}\quad c_{13} = 105\,{\text{Gpa}},\quad c_{33} = 211\,{\text{Gpa}},\quad c_{44} = 4 3\,{\text{Gpa}},\quad e_{31} = - 0.57\,{\text{C/m}}^{ 2} , \\ & e_{33} = 1.32\,{\text{C/m}}^{ 2} ,\quad e_{15} = - 0.48\,{\text{C/m}}^{ 2} ,\quad \varepsilon_{0} = 8.854 \times 10^{ - 12} \,{\text{F/m,}}\quad \varepsilon_{11} = 7.61 \times 10^{ - 11} \,{\text{F/m}}, \\ {\kern 1pt} & \varepsilon_{33} = 8.85 \times 10^{ - 11} \,{\text{F/m,}}\quad \rho = 5700\,{\text{kg/m}}^{ 3} ,\quad q = 1.602 \times 10^{ - 19} \,{\text{C,}}{\kern 1pt} \quad {\kern 1pt} {\kern 1pt} \mu_{11} = \mu_{33} = 0.01\,{\text{m}}^{ 2} / {\text{Vs}}, \\ & d_{11} = d_{33} = \mu_{11} \,{\text{KT/q,}} \\ \end{aligned}$$

where \(K\) is the Boltzmann constant and \(T\) is the absolute temperature. At room temperature, KT/qe= 0.056 V, where qe= 1.602 × 10−19 C is the electric charge. For the carriers, we consider holes with q = qe. With present technology, \(\bar{n}\) might be any value from zero to 1019/m3. If the semiconductor is omitted, the phase velocity of Rayleigh waves propagating in the ZnO half space should be a constant which satisfies cR= 2689.3 m/s. In this study, we consider it as a normalizing speed.

Equation (24) is an equation with a complex number, and so the solution should include a complex number. If the surface wave is excited by a given load frequency, it means that the frequency, ω, is a real number, and both the wave speed, c, and the wave number, k, are complex numbers. Normally, for the attenuation waves, the imaginary part of the wave speed is negative and that of the wave number is positive. Based on Eq. (15), it can be deduced that the amplitude of the displacement and the potential should decrease with propagating direction. On the other hand, if the surface wave is excited by a given load wavelength, both the wavelength and the wave number, k, are real numbers. In this case, the wave speed is a complex number, in which the real part denotes the phase velocity and the imaginary part determines the attenuation. Hereafter, waves with real wave numbers are investigated, with the exception of Sect. 4.4. The product of wave speed c and the wave number k, defined as \(\mathcal{\varOmega }\), is also a complex number, expressed as

$${\varOmega} = \omega + i\tilde{\omega } = ck$$
(26)

where \(\omega\) and \(\tilde{\omega }\) are the real part and the imaginary part of \(\mathcal{\varOmega }\), respectively. For each item shown in Eq. (15), this can be rewritten as

$$f = F\left( {x_{3} } \right)\exp \left( {\tilde{\omega }t} \right)\exp \left[ {i\left( {kx_{1} - \omega t} \right)} \right],$$
(27)

where \(f\) represents an arbitrary function shown in Eq. (15) and \(F\left( {x_{3} } \right)\exp \left( {\tilde{\omega }t} \right)\) denotes the amplitude of \(f\). If \(\tilde{\omega }\) is negative, the amplitude of \(f\) should decrease as time increases. Here, we only consider that the wave number is a real number and discuss the dispersion behavior and the attenuation tendency through the numerical examples.

4.1 Influence of steady-state carrier density \(\bar{n}\) on dispersion and attenuation

Steady-state carrier density \(\bar{n}\) represents the semiconduction property of the piezoelectric material. To investigate the effect of semiconduction on wave speed, we first consider the case without a biasing electric field, i.e. \(\bar{E}_{1} = \bar{E}_{3} { = }0\). Both the real part and the imaginary part of the wave speed are plotted as functions of wavenumber, as shown in Fig. 2.

Fig. 2
figure 2

The relationship of wave speed and wave number for the generalized Rayleigh waves in a piezoelectric semiconductor wafer without a biasing electric field. a Real part of the wave speed. b Imaginary part of the wave speed

Full size image

If the semiconduction property is not considered, the Rayleigh wave in the unelectroded piezoelectric half space is a non-dispersion wave. The wave speed, also named the phase velocity, is a constant. For ZnO, the phase velocity of Rayleigh waves, defined as CR0 and also plotted in Fig. 2, is 2689.3 m/s. When the steady-state carrier density \(\bar{n}\) is smaller than 1015/m3, the variation of the phase velocity is too small to distinguish, and the imaginary part of the wave speed approaches zero. The real part of the wave speed represents the phase velocity, that is

$$c_{p} = \text{Re} \left( c \right).$$
(28)

By considering Eqs. (26) and (28), we have

$$\omega = c_{p} k,$$
(29)

where \(\omega\) is the frequency.

If we do not omit the semiconduction property, the steady-state carrier density \(\bar{n}\) should lead to decreased phase velocity, as shown in Fig. 2a. Larger steady-state carrier density causes larger decreases of phase velocity. When the wave number is small, the influence of the steady-state carrier density is obvious. With increasing wave number, the difference in phase velocity decreases and the phase velocity approaches a constant. This implies that the effect of the semiconduction property on the phase velocity is more obvious for lower frequencies and becomes slighter for higher frequencies, and the effect relies on the steady-state carrier density. For example, if the permission error of phase velocity is 0.1%, the minimum frequency should be 2.01 MHz when the steady-state carrier density is 1 × 1016/m3; and, when the steady-state carrier density reaches 1017/m3, the minimum frequency should be 9.40 MHz.

The dispersion property depends on the relationship between the phase velocity and the group velocity. The definition of the group velocity cg is the velocity of the wave energy, which is satisfied by

$$c_{g} = \frac{{{\text{d}}\omega }}{{{\text{d}}k}} = c_{p} + k\frac{{{\text{d}}c_{p} }}{{{\text{d}}k}}$$
(30)

If the phase velocity is larger than the group velocity, the wave has normal dispersion. Conversely, if the phase velocity is less than the group velocity, the dispersion is anomalous. It is shown in Fig. 2a that the phase velocity increases with wave number. In other words, the phase velocity is less than the group velocity. This means that the semiconduction property should lead to the generalized Rayleigh waves having anomalous dispersion.

Furthermore, the period of the oscillation of phase should be

$$T = \frac{2\pi }{{k\text{Re} \left( c \right)}}.$$
(31)

To evaluate the attenuation tendency, we define the damping coefficient \(\eta\), which represents the attenuation value in a period [20],

$$\eta = \exp \left[ { - 2\pi \frac{{\text{Im} \left( c \right)}}{{\text{Re} \left( c \right)}}} \right] = \exp \left( { - \frac{{2\pi \tilde{\omega }}}{\omega }} \right).$$
(32)

When \(\tilde{\omega }\) is negative and the damping coefficient \(\eta\) is larger than 1, the wave is an attenuation wave in which the amplitude should decrease along the propagating direction. The larger the damping coefficient, the faster the wave attenuates. Conversely, when \(\tilde{\omega }\) is positive and the damping coefficient \(\eta\) is less than 1, the amplitude of the wave should increase along the propagating direction. This case is discussed in the next section.

For the case without a biasing electric field, the damping coefficient \(\eta\) is larger than 1 and the generalized Rayleigh waves are attenuation waves, as shown in Fig. 3. For lower frequencies, the damping coefficient \(\eta\) reaches a maximum. For higher frequencies, the damping coefficient \(\eta\) decreases with the increase of frequency. A large steady-state carrier density should lead to the damping coefficient, \(\eta\), increasing for high frequencies. Especially for the piezoelectric semiconductor with higher steady-state carrier density, the permission frequency should be a higher frequency when the allowance for the damping coefficient \(\eta\) is selected. For example, if the allowance for the damping coefficient, \(\eta\), is 1.01, then the frequencies should be larger than 6.45 MHz for \(\bar{n} = {{2 \times 10^{16} } \mathord{\left/ {\vphantom {{2 \times 10^{16} } {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\) and 27.0 MHz for \(\bar{n} = {{1 \times 10^{17} } \mathord{\left/ {\vphantom {{1 \times 10^{17} } {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\).

Fig. 3
figure 3

The relationship between the damping coefficient \(\eta\) and the frequency \(\omega\)

Full size image

4.2 Influence of the biasing electric field \(\bar{E}_{1}\) on dispersion and attenuation

It is shown in Eqs. (19) and (23) that both electric field \(\bar{E}_{1}\) and electric field \(\bar{E}_{3}\) should affect dispersion curves. To investigate the effect of electric field \(\bar{E}_{1}\), we consider the case without a biasing electric field along x3 direction, i.e. \(\bar{E}_{3} = 0\). \(\bar{E}_{1}\) represents the biasing electric field in the plane parallel to the surface. Consequently, \(\bar{E}_{1}\) should be named as the in-plane biasing electric field intensity and we define the normalized in-plane biasing electric field intensity as

$$\tilde{E}_{1} { = }{{\mu_{11} \bar{E}_{1} } \mathord{\left/ {\vphantom {{\mu_{11} \bar{E}_{1} } {c_{{{\text{R}}0}} }}} \right. \kern-0pt} {c_{{{\text{R}}0}} }}.$$
(33)

The real part and the imaginary part of the wave speed, as functions of the wave number, are plotted in Figs. 4 and 5, respectively. It is found that the phase velocity and the dispersion curves show similarities when the normalized biasing electric field intensity equals 0 and 2. When the normalized biasing electric field intensity is 1, the phase velocity is less than in the other two cases. For the case without the biasing electric field, the imaginary part is negative, as shown in Fig. 5b, and the wave is damped. When the normalized biasing electric field intensity approaches 1, the imaginary part is positive, with \(k > 568\) at \(\bar{n} = {{2 \times 10^{16} } \mathord{\left/ {\vphantom {{2 \times 10^{16} } {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\) and \(k > 2684\) at \(\bar{n} = {{1 \times 10^{17} } \mathord{\left/ {\vphantom {{1 \times 10^{17} } {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\). When the normalized biasing electric field intensity is 2, all of the imaginary part is positive, and the generalized Rayleigh wave is amplified.

Fig. 4
figure 4

The relationship of the real part of the wave speed and the wave number for generalized Rayleigh waves in a piezoelectric semiconductor wafer with biasing electric field \(\bar{E}_{3} = 0\), \(\bar{E}_{1} \ne 0\). a\(\bar{n} = {{2 \times 10^{16} } \mathord{\left/ {\vphantom {{2 \times 10^{16} } {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\). b\(\bar{n} = {{1 \times 10^{17} } \mathord{\left/ {\vphantom {{1 \times 10^{17} } {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\)

Full size image
Fig. 5
figure 5

The relationship of the imaginary part of the wave speed and the wave number for the generalized Rayleigh waves in a piezoelectric semiconductor wafer with biasing electric field \(\bar{E}_{3} = 0\), \(\bar{E}_{1} \ne 0\). a\(\bar{n} = {{2 \times 10^{16} } \mathord{\left/ {\vphantom {{2 \times 10^{16} } {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\). b\(\bar{n} = {{1 \times 10^{17} } \mathord{\left/ {\vphantom {{1 \times 10^{17} } {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\)

Full size image

4.3 Influence of the biasing electric field \(\bar{E}_{3}\) on dispersion and attenuation

Similarly, to investigate the effect of the out-plane biasing electric field on the generalized Rayleigh waves, we also define the out-plane normalized biasing electric field intensity as

$$\tilde{E}_{3} = {{\mu_{11} \bar{E}_{3} } \mathord{\left/ {\vphantom {{\mu_{11} \bar{E}_{3} } {c_{{{\text{R}}0}} }}} \right. \kern-0pt} {c_{{{\text{R}}0}} }}.$$
(34)

We select the carrier charge and steady-state carrier density \(\bar{n} = {{1 \times 10^{17} } \mathord{\left/ {\vphantom {{1 \times 10^{17} } {{\text{m}}^{ 3} }}} \right. \kern-0pt} {{\text{m}}^{ 3} }}\) and plot the wave speed in Fig. 6, including the real part and the imaginary part, as a function of the wave number. Increased out-plane normalized biasing electric field intensity leads to decreased phase velocity, as shown in Fig. 6a. The variation in phase velocity is small and the dispersion remains anomalous. The minimum of the imaginary part of the wave speed increases with increase in the out-plane normalized biasing electric field intensity. However, the influence is so limited that the attenuation tendency of the generalized Rayleigh waves does not change.

Fig. 6
figure 6

The relationship of wave speed and wave number for the generalized Rayleigh waves in a piezoelectric semiconductor wafer with \(\bar{E}_{1} = 0\), \(\bar{E}_{3} \ne 0\), \(\bar{n} = {{1 \times 10^{17} } \mathord{\left/ {\vphantom {{1 \times 10^{17} } {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\). a Real part. b Imaginary part

Full size image

4.4 Propagation properties for the case of complex wave number

Consider that the frequency, \(\mathcal{\varOmega }\), is a real number, and that both the wave speed, c, and the wave number, k, are complex numbers. The dispersion curves, which plot the relationship between the real part of the wave speed and the frequency, are shown in Fig. 7a. The imaginary part of the wave speed versus frequency is plotted in Fig. 7b. The frequency, \(\mathcal{\varOmega }\), is selected from \(0.5\) to \(300\;{\text{MHz}}\), \(\bar{n} = {{1 \times 10^{17} } \mathord{\left/ {\vphantom {{1 \times 10^{17} } {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\) and \(\bar{E}_{3} = 0\). A similar conclusion should be obtained. The real part of phase velocity is smaller than the Rayleigh wave speed of the piezoelectric half space, increases gradually, and approaches a constant with the increase of frequency. The imaginary part of the wave speed is negative when the structure does not undergo the biasing electric field, and it is implied that the imaginary part of the wave number should be positive and that the wave should attenuate along the wave propagation direction. If the structure undergoes enough in-plane biasing electric field, then the imaginary part of the wave speed might be positive. Therefore, the imaginary part of the wave number should be negative and the amplitude of the generalized Rayleigh wave should increase along the wave propagation direction.

Fig. 7
figure 7

The relationship of wave speed and frequencies for the generalized Rayleigh waves in a piezoelectric semiconductor wafer with \(\bar{E}_{3} = 0\), \(\bar{n} = {{1 \times 10^{17} } \mathord{\left/ {\vphantom {{1 \times 10^{17} } {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}\). a Real part. b Imaginary part

Full size image

5 Conclusion

Plane strain surface waves, also named generalized Rayleigh waves, can propagate along the surface of an unelectroded piezoelectric semiconductor wafer. The mechanic–electric coupling governing equations are solved analytically in this study. Supposing that the wave length is real, and analyzing the complex wave speed, we find that the semiconductor should lead to phase velocity decreasing, and to the generalized Rayleigh waves showing anomalous dispersion and damping. The phase velocity changes with in-plane biasing electric field intensity, but the anomalous dispersion does not change. If the structure is subject to enough in-plane biasing electric field, the waves should increase rather than be damped. However, the influence of the out-plane biasing electric field is too limited to change the dispersion and attenuation properties. If we must select materials with large steady-state carrier densities and wish to omit the effects of semiconductors on the generalized Rayleigh waves, then high frequencies should be selected. Furthermore, enough in-plane biasing electric field can overcome the damping caused by semiconductors. The results obtained in the study may be used to provide theoretical guidance for the design of high-performance SAW devices.