1 Introduction

Nanoscale materials such as nanofilms, nanowires, nanobeams, nanotubes and nanoparticles, have attracted much interest thanks to their widely proposed applications in nano-electro-mechanical systems [1,2,3,4,5,6]. Piezoelectric nanostructures such as nanowires, nanobelts, or nanofilms have a lot of applications in nanotechnology [7,8,9,10,11]. They are applied as nanogenerators, diodes, field effect transistors, nanoresonators [12,13,14,15,16], and more. The size-dependent and surface modulated properties of piezoelectric nanostructures lead to a giant difference from their bulk counterparts [17, 18]. It is very important to understand nanostructure mechanical properties and the piezoelectric response to external force loading [19, 20]. The size-dependent mechanical properties of piezoelectric nanostructures have been researched by experimental measurements, atomistic simulations and theoretical methods [21,22,23,24]. The semiconducting and piezoelectric characteristics of ZnO nanostructures allow it to be ideal material for nanogenerators and nano-energy harvesters [25,26,27]. ZnO nanostructures, such as nanofilms, nanorods, nanobelts, nanorings and nanowires, have been widely applied in nanogenerators, biosensors, humidity/chemical nanosensors and so on [28,29,30]. ZnO nanowire based nanogenerators have attracted interests widely. It converts mechanical energy into electric energy by bending, compression or flexion. The voltage in the cross section of nanowires is committed step for nanogenerators [19, 20].

Gao and Wang gave a fundamental theory to interpret nanogenerator and nanopiezotronics which based on bent piezoelectric nanowires [19]. They estimated geometry and external force influences on equilibrium electrostatic potential of the nanowire cross section. Tong et al. researched piezoelectric potential by using a one-dimensional model, which gave the piezoelectric potential varies along length direction rather than cross section [31]. Yao et al. gave a continuum theory by considering surface elasticity effect. The surface effect was introduced by a modified core–shell model [20, 32]. The rigorous surface elasticity theory was developed by Gurtin and Murdoch in 1975 for pure elastic solids, in which the surface was treated as an ideal material surface without thickness [33, 34]. Based on the G-M surface model, many researchers established the surface model for piezoelectric structures. There are two popular types of surface elasticity model, core-surface model [35,36,37,38] and core–shell model [21, 39, 40], have been used to interpret the mechanical properties of nanowires. Both models separate the nanowire into two parts, surface area and bulk like core. There is obvious interface between surface area and bulk like core. Furthermore, there must be sudden sharp step of Young’s modulus at the interface [41, 42]. Yao et al. cleared up the Young’s modulus step by introducing a concept of gradient Young’s modulus within surface shell [20, 32]. But the step of Young’s modulus derivative appears at the interface. It can hardly be physical and reasonable to separate a nanowire into surface area and bulk like core [41]. Actually indeed, for a nanowire, the surface shell should be the same material as the bulk like core. The derivative of Young’s modulus within so-called surface area and within bulk like core should be also consistent. According to this train of thought, the interface within nanowire absents.

In this paper, a continuum theoretical model for describing nanowire mechanical and piezoelectric properties was established by considering exponentially decreased surface elasticity effect. In Sect. 2 the model for effective Young’s modulus and the piezoelectric properties of nanowires were established. In Sect. 3, our model was applied to the Young’s modulus and piezoelectric properties of ZnO nanowire, and the maximum effective deflection was also discussed. Finally, Sect. 4 summarized our conclusions.

2 Theory and model

At film surface, the bond outside the film absents. The dangling bonds combine together. This surface procedure moves surface atoms, and then the surface atoms depart from their traditional equilibrium position. The second surface layer is also influenced by the movement of outermost atoms via Van Der Waals force. The movement decays at the second surface layer compared to the outermost surface layer counterpart. One can deduce that the third, fourth surface layers and so on, are also influenced by surface effect. But the influence of surface effect fades off with depth (the distance from surface layer). Researchers pointed out that the elastic constants of crystal are very sensitive to interatomic distance [21]. Therefore, the elastic property near surface is different from bulk material counterpart. In our model, the Young’s modulus of nanowires was influenced by surface elasticity effect. Therefore, the effective Young’s modulus of nanowires can be constructed by bulk Young’s modulus and surface Young’s modulus. The influence of surface Young’s modulus decreases based on the distance from surface i.e. decreases with going deep into the inner area of the nanowire. And then, surface Young’s modulus is an additional elastic parameter but not the real Young’s modulus of nanowires. The real Young’s modulus of nanowires is constructed by bulk and surface Young’s moduli. This model can eliminate the interface between the so-called surface area and bulk like core, which is virtually non-existent.

Surface Young’s modulus varies within nanowire and can be expressed as

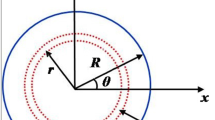
$${E}_{\text{s}}\left(r\right)={E}_{\text{s}}{e}^{-\alpha \left(R-r\right)}={E}_{\text{s}}{e}^{\alpha \left(r-R\right)}$$
(1)

where r ≤ R, R is the radius of the nanowire. Es(r) serves as the variational surface Young’s modulus of the nanowire. Es is the surface Young’s modulus at outermost atomic layer (surface layer). R-r is the distance between the consideration site and nanowire surface, see in Fig. 1. This theoretical model is similar to functionally graded materials. In this work, the gradient of elasticity is induced by surface effect and widely exists in any nanowire. The origin of elasticity gradient is different from artificial functionally graded materials. Equation (1) shows that the influence of surface elasticity effect decreases with distance from surface layer. And the exponential law was assumed in this paper. While α represents the degree of decrease and it is in unit of nm−1. Therefore, α can be called as decrease factor in this paper.

Fig. 1
figure 1

Schematic representation of the nanowire cross section

Full size image

The effective bending stiffness of nanowires is

$${E}_{\text{eff}}I={E}_{0}{I}_{0}+{E}_{\text{s}}\left(r\right){I}_{\text{s}}$$
(2)

where Eeff and E0 are the effective and the bulk Young’s moduli of nanowires.

The differential of nanowire inertia moment

$$dI=\underset{0}{\overset{2\pi }{\int }}\underset{r}{\overset{r+dr}{\int }}{\left(r\text{cos}\theta \right)}^{2}rd\theta dr=\pi {r}^{3}dr$$
(3)

as shown in Fig. 1.

$$I=\underset{0}{\overset{R}{\int }}\pi {r}^{3}dr=\frac{1}{4}\pi {R}^{4}$$
(4)

The bulk Young’s modulus keeps constant with position. Therefore, the bulk bending stiffness can be obtained by

$${E}_{0}{I}_{0}={E}_{0}\frac{1}{4}\pi {R}^{4}$$
(5)

directly.

Since surface Young’s modulus is an additional elastic parameter, the surface bending stiffness is also an additional parameter. The surface bending stiffness can be given by

$${E}_{\text{s}}\left(r\right){I}_{\text{s}}=\underset{0}{\overset{R}{\int }}{E}_{\text{s}}\left(r\right)\pi {r}^{3}dr$$
(6)

The effective bending stiffness is constructed by bulk stiffness and surface stiffness. Therefore, the effective bending stiffness of nanowires can be given by

$${E}_{\text{eff}}I={E}_{0}\frac{1}{4}\pi {R}^{4}+{E}_{\text{s}}\left(\frac{1}{\alpha }\pi {R}^{3}-\frac{3}{{\alpha }^{2}}\pi {R}^{2}+\frac{6}{{\alpha }^{3}}\pi R-\frac{6}{{\alpha }^{4}}\pi +\frac{6}{{\alpha }^{4}}\pi {e}^{-\alpha R}\right)$$
(7)

And the effective Young’s modulus of nanowires is

$${E}_{\text{eff}}={E}_{0}+4{E}_{\text{s}}\left(\frac{1}{\alpha R}-\frac{3}{{\alpha }^{2}{R}^{2}}+\frac{6}{{\alpha }^{3}{R}^{3}}-\frac{6}{{\alpha }^{4}{R}^{4}}+\frac{6}{{\alpha }^{4}{R}^{4}}{e}^{-\alpha R}\right)$$
(8)

The first and second terms are bulk Young’s modulus and the influence of surface effect, respectively. For surface effect term, the first surface modification is linear surface modification, the second, third and fourth surface modifications are nonlinear modifications. The fifth surface modification represents exponential modification. Equation (8) shows that surface Young’s modulus is independent from bulk Young’s modulus. If surface Young’s modulus is set to be zero, the surface effect on nanowires will disappear. On the other hand, if the radius of the nanowire is very large, \(R\to \infty \), the influence of surface effect will be also gone.

When decrease factor \(\alpha \) is relatively larger, the nonlinear terms as well as exponential term of Eqs. (7) and (8) can be neglected. The effective Young’s modulus will degenerate as

$${E}_{\text{eff}}={E}_{0}+\frac{4S}{R}$$
(9)

where \(S={E}_{\text{s}}/\alpha \) stands for surface elasticity. For piezoelectric nanowires, the surface layer may be very thin, in the order or 1 nm. For the piezoelectric nanowire with relatively larger radius (as well as relatively larger \(\alpha \)), in the order or 100 nm for example, the surface elasticity effect decreases quickly with distance from surface. In other words, the surface elasticity effect only works near surface area and vanishes quickly with depth. This condition suits for the core-surface model addressed [35,36,37].

According to the piezoelectric theory, the constitutive equations of the piezoelectric medium are given by [43]

$${\sigma }_{i}={l}_{ij}{\varepsilon }_{j}-{e}_{kj}{E}_{k}$$
(10a)
$${D}_{m}={e}_{mj}{\varepsilon }_{j}+{\kappa }_{mk}{E}_{k}$$
(10b)

where εj, σi, Ek, and Dm are strain, stress, electric field and electric displacement, respectively. κmk, ekj and cij stand for dielectric tensor, piezoelectric tensor and stiffness tensor, respectively. Theoretically, there should be multi-orders of electromechanical coupling. The piezoelectric field induced by mechanical deformation for example. Researchers pointed out that there is barely piezoelectric field influence on the nanowire stress or strain experimentally [19]. Therefore, the high-order electromechanical coupling can be ignored [19]. In other words, first-order i.e. direct piezoelectric effect (the stress or strain generates electric field directly) is accurate enough to interpret the piezoelectric effect of bending nanowires.

The matrix form of the effective stress and strain relationship is given by Hooke’s law [19]

$$ \left( {\begin{array}{*{20}l} {\varepsilon _{1}^{e} } \hfill \\ {\varepsilon _{2}^{e} } \hfill \\ {\varepsilon _{3}^{e} } \hfill \\ {\varepsilon _{4}^{e} } \hfill \\ {\varepsilon _{5}^{e} } \hfill \\ {\varepsilon _{6}^{e} } \hfill \\ \end{array} } \right) = \frac{1}{{E_{{{\text{eff}}}}^{{{\text{iso}}}} }}\left( {\begin{array}{*{20}c} 1 & { - v} & { - v} & 0 & 0 & 0 \\ { - v} & 1 & { - v} & 0 & 0 & 0 \\ { - v} & { - v} & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & {2\left( {1 + v} \right)} & 0 & 0 \\ 0 & 0 & 0 & 0 & {2\left( {1 + v} \right)} & 0 \\ 0 & 0 & 0 & 0 & 0 & {2\left( {1 + v} \right)} \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\sigma _{1}^{e} } \hfill \\ {\sigma _{2}^{e} } \hfill \\ {\sigma _{3}^{e} } \hfill \\ {\sigma _{4}^{e} } \hfill \\ {\sigma _{5}^{e} } \hfill \\ {\sigma _{6}^{e} } \hfill \\ \end{array} } \right) $$
(11)

where v is served as Poisson’s ratio. The isotropic effect Young’s modulus \(E_{{{\text{eff}}}}^{{{\text{iso}}}}\) was given by Eq. (8). For the sake of compactness of the notation, rr, θθ, zz, θz, rz and rθ are replaced by 1, 2, 3, 4, 5 and 6. For the sake of simplicity, the isotropic Young’s modulus of nanowires was used here [19]. According to the Saint–Venant bending theory [44], the effective stress expressions of ZnO nanowire can be obtained as follows

$$\left(\begin{array}{l}{\sigma }_{1}^{e}\\ {\sigma }_{2}^{e}\\ {\sigma }_{3}^{e}\\ {\sigma }_{4}^{e}\\ {\sigma }_{5}^{e}\\ {\sigma }_{6}^{e}\end{array}\right)=\left(\begin{array}{l}0\\ 0\\ -\frac{{f}_{x}}{{I}_{e}}\left(l-z\right)r\text{cos}\theta \\ -\frac{{f}_{x}}{8{I}_{e}}\frac{3+2v}{1+v}\left({R}^{2}-\frac{1-2v}{3+2v}{r}^{2}\right)\text{sin}\theta \\ \frac{{f}_{x}}{8{I}_{e}}\frac{3+2v}{1+v}\left({R}^{2}-{r}^{2}\right)\text{cos}\theta \\ 0\end{array}\right)$$
(12)

In Eq. (12), fx, Ie and l are external force, effective inertia moment and nanowire length, respectively. The external force fx is applied along lateral direction.

Since there is no free charge inside the nanowire, one can obtain the Gauss’s law of the electrostatic field as

$$ \nabla \cdot \left( {e_{{mj}} \varepsilon _{j} + \kappa _{{mk}} E_{k} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {i} _{m} = \nabla \cdot \left( {P + \kappa _{{mk}} E_{k} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {i} _{m} = 0 $$
(13)

The nanowire deformation induces polarization and enlarges dipoles. And then, polarized residual charges emerge. The residual body charge density can be given by

$$ \rho _{P} = - \nabla \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {P} $$
(14a)

and the residual surface charge density can be given by

$${\rho }_{\text{s}}=-\stackrel{\to}{n}\cdot \left(0-\stackrel{\to}{P}\right)=\stackrel{\to}{n}\cdot \stackrel{\to}{P}$$
(14b)

The Gauss’s law of the electrostatic field Eq. (13) can be transformed into Poisson’s equation as follows

$$\nabla \cdot \left({\kappa }_{mk}{E}_{k}{\stackrel{\to}{i}}_{m}\right)={\rho }_{P}$$
(15)

According to the first piezoelectric effect approximation, the matrix of effective piezoelectric polarization induced by the mechanical deformation of ZnO nanowire is

$$\left(\begin{array}{l}{P}_{1}^{e}\\ {P}_{2}^{e}\\ {P}_{3}^{e}\end{array}\right)=\left(\begin{array}{l}{e}_{15}{\varepsilon }_{5}\\ {e}_{15}{\varepsilon }_{4}\\ {e}_{31}{\varepsilon }_{1}+{e}_{31}{\varepsilon }_{2}+{e}_{33}{\varepsilon }_{3}\end{array}\right)$$
(16)

One can easily obtain the residual surface charge density of the nanowire as \(\rho_{{\text{s}}}^{{\text{e}}} = 0\), and then the body charge density of effective polarization can be derived as

$${\rho }_{P}=\frac{{f}_{x}}{{I}_{e}{E}_{\text{eff}}^{\text{iso}}}\left[2\left(1+v\right){e}_{15}+2v{e}_{31}-{e}_{33}\right]r\text{cos}\theta $$
(17)

Thereby, the piezoelectric equilibrium potential in the cross section of the nanowire can be solved by Poisson’s equation

$${\nabla }^{2}\varphi =-\frac{{\rho }_{P}}{{\kappa }_{\perp }}$$
(18)

where \(k_{ \bot } = k_{11} = k_{22}\), and \(k_{ \bot }\) is served as the dielectric constant of the nanowire cross-sectional plane. The piezoelectric potential can be obtained by using Eqs. (17) and (18).

$${\varphi }_{i}\left(r,\theta \right)=\frac{1}{8{k}_{\perp }}\frac{{f}_{x}}{I{E}_{\text{eff}}^{\text{iso}}}\left[2\left(1+v\right){e}_{15}+2v{e}_{31}-{e}_{33}\right]\times \left(\frac{3{k}_{\perp }+{k}_{0}}{{k}_{\perp }+{k}_{0}}{R}^{2}r-{r}^{3}\right)\text{cos}\theta , r\le R$$
(19a)
$${\varphi }_{o}\left(r,\theta \right)=\frac{1}{8{k}_{\perp }}\frac{{f}_{x}}{I{E}_{\text{eff}}^{\text{iso}}}\left[2\left(1+v\right){e}_{15}+2v{e}_{31}-{e}_{33}\right]\times \left(\frac{2{k}_{\perp }}{{k}_{\perp }+{k}_{0}}\frac{{R}^{4}}{r}\right)\text{cos}\theta , r>R$$
(19b)

The maximum effective deflection of nanowires is given by [45]

$${v}_{\text{e}}^{\text{max}}=\frac{{f}_{x}{l}^{3}}{3I{E}_{\text{eff}}^{\text{iso}}}$$
(20)

The piezoelectric potential can also be interpreted as

$${\varphi }_{i}\left(r,\theta \right)=\frac{1}{8{k}_{\perp }}\frac{3{v}_{\text{e}}^{\text{max}}}{{l}^{3}}\left[2\left(1+v\right){e}_{15}+2v{e}_{31}-{e}_{33}\right]\times \left(\frac{3{k}_{\perp }+{k}_{0}}{{k}_{\perp }+{k}_{0}}{R}^{2}r-{r}^{3}\right)\text{cos}\theta , r\le R$$
(21a)
$${\varphi }_{o}\left(r,\theta \right)=\frac{1}{8{k}_{\perp }}\frac{3{v}_{e}^{max}}{{l}^{3}}\left[2\left(1+v\right){e}_{15}+2v{e}_{31}-{e}_{33}\right]\times \left(\frac{2{k}_{\perp }}{{k}_{\perp }+{k}_{0}}\frac{{R}^{4}}{r}\right)\text{cos}\theta , r>R$$
(21b)

The piezoelectric potential is proportional to external force and inversely proportional to bending stiffness (or effective Young’s modulus), according to Eqs. (19a) and (19b). In other words, the piezoelectric potential is proportional to maximum effective deflection of the nanowire and inversely proportional to the third power of nanowire length, according to Eqs. (21a) and (21b). If surface effect can be neglected, Eq. (19b) will degenerate as

$${\varphi }_{i}\left(r,\theta \right)=\frac{{f}_{x}}{\pi \left({k}_{\perp }+{ k}_{0}\right)r{E}_{\text{b}}^{\text{iso}}}\left[2\left(1+v\right){e}_{15}+2v{e}_{31}-{e}_{33}\right]\text{cos}\theta , r>R$$
(22)

Equation (22) indicates that when surface effect is neglected and external force is given, nanowire radius has no effect on outside piezoelectric potential (i.e. r > R).

Since piezoelectric potential and body charge density are both independent from z direction, the electric potential energy calculation should only integrate r and \(\theta\) coordinates. And then multiply it by nanowire length. The charge element can be given by

$$dq={\rho }_{P}dS={\rho }^{R}rdrd\theta $$
(23)

And the corresponding electric potential energy element is

$$d{U}_{e}=dq\cdot {\Pi}_{\text{i}}\left({\text{r}},\,\theta\right) \left(r\le R\right)$$
(24)

The total electric potential energy can be given by integrating electric potential energy element within nanowires

$${U}_{e}=\frac{1}{96}l\frac{{\left({f}_{y}\right)}^{2}}{{\text{k}}_{\bot}{\left({I}_{xx}{E}_{\text{eff}}^{\text{iso}}\right)}^{2}}{\left[2\left(1+v\right){e}_{15}+2v{e}_{31}-{e}_{33}\right]}^{2}\left(\frac{{3}{\text{k}}_{\bot} + {\text{k}}_{0}}{{\text{k}}_{\bot} + {\text{k}}_{0}}3-2\right){\text{R}}^{6}\pi $$
(25)

The total input energy can be given by

$${U}_{i}={\int }_{0}^{v}{\text{f}}_{\text{x}}d{v}_{\text{e}}^{\text{max}}$$
(26)

According to Eq. (20), the external force

$${f}_{x}={v}_{\text{e}}^{\text{max}}\frac{3I{E}_{\text{eff}}^{\text{iso}}}{{l}^{3}}$$
(27)

The total input energy is

$${U}_{i}=\frac{{f}_{x}^{2} {l}^{3}}{6I{E}_{\text{eff}}^{\text{iso}}}$$
(28)

The ratio of electric potential energy is

$$k=\frac{{U}_{e}}{{U}_{i}}=\frac{1}{4}\frac{{R}^{2}}{{k}_{\perp }{E}_{\text{eff}}^{\text{iso}} {l}^{2}}\left(\frac{3{k}_{\perp }+{k}_{0}}{{k}_{\perp }+{k}_{0}}3-2\right){\left[2\left(1+v\right){e}_{15}+2v{e}_{31}-{e}_{33}\right]}^{2}$$
(29)

According to Eq. (29), the ratio of electric potential energy is dependent on nanowire effective Young’s modulus, radius and length.

3 Results and discussions

The atoms near surface are in the different environment comparing to the inner atoms. And the symmetry is also different from bulk materials. For the outermost surface atoms, the absence of bonding partners outside the film relaxes and moves atoms. In other words, the outermost surface atoms move away from their original equilibrium position. This surface procedure induces second surface atoms also move away from their original equilibrium position. But on the other hand, the movement of second surface atoms weakened (comparing with the outermost layer). Based on this reasoning, the third surface as well as the inner atoms are also moved. This influence of surface effect decays with depth (the distance from surface). The lattice structure and inter-atomic forces near surface are changed. Since Young’s modulus (elastic constant) is very sensitive to lattice structure and inter-atomic forces, the effective Young’s modulus near surface is different from bulk material counterpart. Therefore, there should be additional Young’s modulus to interpret this difference. The additional Young’s modulus is usually called as surface Young’s modulus. The surface effect affects Young’s modulus not only outermost surface atomic layer but also inward the nanowire. And the influence of surface effect degrades for the site being apart from surface (the inner atoms of nanowires). In order to examine the validity of our theoretical model, the size dependent Young’s modulus of ZnO nanowire was predicted in Fig. 2. The theoretical line was compared with experimental result and numerical calculation. Chen et al. measured the Young’s modulus of ZnO nanowire under bending mode. The nanowire diameters range from 17 to 550 nm [21]. When the diameter is smaller than about 17 nm, the experimental measurement is invalid and the simulated calculation i.e. molecular statistical thermodynamics (MST) is going to be used [22]. The theoretical line shows good agreement with experimental and calculated data. The fitting parameters Eb = 140 GPa, Es = 180 GPa, and α = 0.8 nm−1. The simplified isotropic bulk Young’s modulus 129 GPa [19] is used rather than 140 GPa of [0001] direction [46], and then surface Young’s modulus Es = 280 GPa and decrease factor α = 1.3 nm−1. In this paper, we take the same value of bulk Young’s modulus (129 GPa) as Ref. [19] for the sake of comparison. ZnO nanowire Young’s modulus behaves size dependent and surface modulated obviously. The positive surface Young’s modulus Es induces the larger effective Young’s modulus of ZnO nanowire than the bulk counterpart.

Fig. 2
figure 2

Size dependent Young’s modulus of ZnO nanowire

Full size image

Generally speaking, the lateral force is the main factor causing piezoelectric potential. Nanowire radius influences bending curvature and then influences the piezoelectric potential significantly. Nanowire effective Young’s modulus is another important factor influencing piezoelectric potential. With decreasing nanowire radius, the surface elasticity effect induces ZnO nanowire Young’s modulus to increase. And then, the deflection is smaller than the result given by classical theory without surface effect [19]. Therefore, the piezoelectric equilibrium potential in the cross section of the nanowire is smaller than Wang’s theory. In order to compare to Ref. [19], the isotropic bulk Young’s modulus \({\text{E}}_{\text{b}}^{\text{iso}}\) = 129 Gpa rather than 140 Gpa to predict piezoelectric potential. Poisson’s ratio v = 0.349, relative dielectric \({\text{k}}_{ \bot }^{\text{r}}{=7.77}\), piezoelectric coefficients e31 = -0.51 Cm−2, e15 = -0.45 Cm−2, e33 = 1.22 Cm−2. Since surface effect enhances the bending stiffness of ZnO nanowire, a weaker piezoelectric potential was obtained, as shown in Fig. 3. In Fig. 3, the nanowire radius is chosen as R = 25 nm and the external force f = 80 nN to compare with Ref. [19]. The nanowire length l = 600 nm in Ref. [19] has no any effect on the piezoelectric potential according to Eqs. (19a) and (19b). The largest potential values can be found as 0.222 V with surface effect and 0.284 V without surface effect in Fig. 3. Surface effect stiffens ZnO nanowire and hinders the nanowire bend, and then decreases the largest potential.

Fig. 3
figure 3

Potential distribution along x-axis in the cross section of the nanowire

Full size image

Figure 4 interprets the piezoelectric potential distribution inside and outside the nanowire along x-axis direction. The typical value of external force f = 80 nN allows us to contrast to Ref. [19]. Two typical nanowire radii R = 25 nm and R = 50 nm are chosen to interpret the piezoelectric potential distribution. The cases with and without surface effect were contrasted with each other in Fig. 4. Surface effect lowered the piezoelectric potential compared to the case without surface effect as discussed above. A larger nanowire radius induces a lowered piezoelectric potential. The radius effect is very obvious and is more important than surface effect when radius is dozens of nanometers. With decreasing nanowire radius, surface effect is of more importance and makes larger difference between the cases with and without surface effect. Surface elasticity effect plays an important impact not only on the mechanical property but also on the piezoelectric potential especially when the nanowire radius reduces below 100 nm. When surface effect is neglected, the outside piezoelectric potential is independent from nanowire radius, as shown in Fig. 4 and as shown in Eq. (22).

Fig. 4
figure 4

The influence of nanowire radius on the piezoelectric potential along x-axis direction. θ = 0 indicates x-axis positive direction while θ = π indicates x-axis negative direction. The external force f = 80 nN is applied along x-axis positive direction. The nanowire radii are R = 25 nm and R = 50 nm to display the piezoelectric potential properties

Full size image

In order to investigate the external force influence on piezoelectric potential, Fig. 5 exhibited the piezoelectric potential distribution under different external forces. The nanowire radius is kept as the typical magnitude R = 25 nm. If other conditions are all given, the piezoelectric potential is proportional to external force, as exhibited in Eqs. (19a) and (19b). Therefore, the influence of surface effect on piezoelectric potential is of more importance for the case with larger external force. A larger external force makes a larger mechanical deformation, hence a larger piezoelectric potential, as shown in Fig. 5. On the other hand, surface elasticity means additional modulus of a nanowire, and the larger mechanical deformation induces the larger additional resistance. Positive surface Young’s modulus arrests the deformation, and leads to a lower piezoelectric potential. Therefore, the larger external force enhances the surface effect on piezoelectric potential.

Fig. 5
figure 5

The influence of external force on the piezoelectric potential along x-axis direction. The nanowire radius R = 25 nm means surface effect strongly influences the piezoelectric potential. The external force is applied along x-axis positive direction

Full size image

Nanowire radius is an important factor not only theoretically but also experimentally. The nanowire radius effect on piezoelectric potential was predicted in Fig. 6. The larger the nanowire radius, the smaller the piezoelectric potential is. There are two factors to influence the radius effect. One is that the larger radius indicates larger inertia moment I, which certainly enlarges effective bending stiffness and impedes the nanowire bending curvature. This factor induces a smaller piezoelectric potential. Another is that surface elasticity effect decreases with increasing nanowire radius. Since surface elasticity effect enlarges the Young’s modulus of ZnO nanowire, the larger radius indicates the smaller Young’s modulus. Therefore, this factor induces the larger bending curvature and the larger piezoelectric potential. The effective radius effect depends on the completion between these two factors. There is obvious difference between the lines with surface effect and without surface effect when nanowire radius R < 100 nm. This fact indicates that the surface elasticity effect plays an important role when nanowire radius reduces below 100 nm.

Fig. 6
figure 6

Maximum piezoelectric potential as function of nanowire radius

Full size image

Surface Young’s modulus influences piezoelectric potential obviously when nanowire radius is smaller than 100 nm. In order to interpret the Es effect, Fig. 7 displayed largest potential when the decrease factor is set to be constant as α = 1.3 nm−1. For the condition that external force f = 80 N and nanowire radius R = 25 nm and R = 50 nm, the largest potential decreases with increasing surface Young’s modulus. Since ZnO surface Young’s modulus is positive, surface Young’s modulus Es stiffens the nanowire and finally decreases the largest potential. On the other hand, if we set the surface Young’s modulus to be constant as Es = 280 GPa, the largest potential (absolute value) increases with increasing decrease factor α, as shown in Fig. 8. The larger α indicates that surface elasticity effect on nanowires rapidly decreases with position depth (i.e. the distance between the considered atomic layer and surface layer). The atomic layer, which is far away from surface layer, is less influenced by surface effect. This fact induces a weakened surface elasticity effect and softens the nanowire (actually, it is also stiffer than the nanowire without surface effect). Since surface elasticity effect induces a smaller piezoelectric potential, the larger α weakens the surface effect and induces a larger piezoelectric potential (absolute value in Fig. 8).

Fig. 7
figure 7

Maximum piezoelectric potential as function of surface Young’s modulus Es

Full size image
Fig. 8
figure 8

Maximum piezoelectric potential as function of decrease factor α

Full size image

The maximum deflection versus decrease factor α was displayed in Fig. 9. As discussed above, the larger decrease factor indicates the rapid decay of surface effect. Since surface elasticity effect hardens ZnO nanowire, the larger decrease factor induces the larger maximum deflection. When α → ∞, which heralds the surface effect vanishes, the maximum deflection will be consistent with the result of Ref. [19]. The larger surface Young’s modulus indicates the larger effective Young’s modulus of ZnO nanowire, therefore a weaker maximum deflection was produced. When surface Young’s modulus Es = 0, surface effect also vanishes, the maximum deflection will be also consistent with the result of Ref. [19]. In special cases, when α → 0, the maximum deflection rapidity goes down to 0. The ultra-small α indicates a very large effective Young’s modulus. Actually, when α = 0, the effective Young’s modulus will be an indefinite quantity. The effective Young’s modulus should be influenced by other factors, symmetry lowering effect for example [41].

Fig. 9
figure 9

Maximum deflection as function of decrease factor α

Full size image

When external force was applied on nanowire free end, energy was also input into the nanowire. The input energy was stored within the nanowire as elastic energy and electric potential energy. The electric potential energy and input total energy were shown in Fig. 10a and b, respectively. With increasing nanowire radius, it is more difficult to bend the nanowire. Therefore, both electric potential energy and input total energy decrease with increasing nanowire radius. Figure 10a and b show that input total energy decreases faster than electric potential energy. This property was also exhibited in Fig. 11. With increasing the nanowire radius, the electric potential energy decreases but the ratio increases obviously, as shown in Fig. 11.

Fig. 10
figure 10

Electric potential energy and input total energy as function of nanowire radius. (a) Electric potential energy. (b) Input total energy

Full size image
Fig. 11
figure 11

Ratio of electric potential energy

Full size image

4 Conclusions

This work researched ZnO nanowire mechanical and piezoelectric properties by considering exponentially decreased surface elasticity effect. The effective Young’s modulus of nanowires was constructed by bulk Young’s modulus and surface Young’s modulus. ZnO nanowire Young’s modulus will be influenced by surface elasticity effect obviously when radius is below 100 nm. This surface effect induces piezoelectric potential to be very different from the counterpart without surface effect. Since surface elasticity effect stiffens ZnO nanowire, the largest piezoelectric potential decreases due to surface elasticity effect. If nanowire radius and external force are given, surface elasticity effect influences nanowire deflection and piezoelectric potential obviously. Larger nanowire radius certainly decreases piezoelectric potential. Larger surface Young’s modulus stiffens ZnO nanowire and decreases piezoelectric potential. Larger decrease factor means weaker surface effect and increases piezoelectric potential. If surface effect is neglected, the theory in this paper will degenerate into Wang’s theory. When nanowire radius R < 100 nm, surface effect is more important and cannot be neglected.