1 Introduction

Over the past decade, the mechanics of nanostructures has attracted a great deal of attention due to their widely proposed applications in nanoelectromechanical systems (NEMS) [1,2,3]. Nanostructures such as nanowires, nanobeams, and nanofilms differ significantly from bulk structures in their mechanical properties [4,5,6]. The nanostructures were used as nanosensors, nanoactuators, nanogenerators, and nanoresonators which are important components of NEMS [7,8,9,10,11]. With the rapid development of nanomaterial manufacture, NEMS has been an important research area in nanotechnology and nanoscience [12, 13]. Since the nanostructures have large surface-to-volume ratio, their mechanical properties are very different from their bulk counterparts [14,15,16]. The size-dependent and surface-modulated properties of nanostructures are the main mechanical difference from their bulk counterparts [17,18,19]. Miller and Shenoy gave a continuum mechanics theoretical scheme with effective elasticity for size-dependent and surface-modulated elastic properties of nanofilms [20]. Wang et al. introduced surface slice thickness concept in the natural frequency of nanofilm researching, but they let the surface slice thickness approach zero while keeping surface elasticity as a constant [21]. When the surface slice thickness was neglected, the result of theoretical scheme will be same as surface model [20]. In the surface model, a completely ideal slice with surface elastic coefficient (measured in N/m) but without thickness (i.e., the surface slice thickness is absolutely zero) ideally adheres to the bulk-like core of nanofilms. This surface model is very useful in solving many surface and mechanics problems of nanostructures [22, 23]. But this surface model is a completely ideal model that does not take surface slice thickness into consideration. The absence of surface slice thickness might lead to unrealistic physical images in some cases. And in application, their surface model works only on the condition that the size of nanostructures is relatively large, and the whole thickness of nanofilm is large enough comparing with surface slice thickness. Researchers found that the native oxide at surface may affect overall elastic response strongly and the native oxide layer thicknesses were reported in the literatures, ranging from 2 nm to 5 nm [24,25,26]. The surface slice is thick enough to influence overall film mechanical properties obviously and cannot be neglected. In consideration of the defects in surface model, another model was established to extract the overall mechanical response of nanowires, called as Core–Shell model [27, 28]. Core–Shell model modified surface model by considering surface slice thickness. Researchers pointed out that elastic constants of crystals are very sensitive to interatomic distance. This property of elastic constants indicates that surface slice elastic properties are strongly affected by surface relaxation effect [27,28,29,30]. On the other hand, the absence of bond at surface lowered the symmetry of surface slice. These surface effects extend into inner atomic layers of films. This extending should be a gradual process and fades off slowly. Surface slice can be seen as a uniform elastic slice for sake of simplicity. In nanowire Core–Shell model, cylindrical core has bulk modulus E0, while surface shell has surface modulus Es. This surface elasticity theoretical route is reasonable in application, but the concept of nanowire Core–Shell model implicates that surface shell seems to be a different elastic material compared with bulk-like core [28]. Actually indeed, surface shell should be the same material as bulk-like core but influenced by surface effect. Following this train of thought, bulk modulus should work on whole nanostructure area (including surface shell and so called bulk-like core), while surface modulus should work only on surface slice and should be seen as additional modulus.

In this paper, a continuum elasticity theoretical model for nanofilms was established by considering surface slice thickness. The bulk Young’s modulus works on whole nanofilm area and surface Young’s modulus (surface elastic coefficient) works only on surface slice. The relationship between present theory and surface model was established by distinguishing surface Young’s modulus and surface elastic coefficient. This paper is organized as follows. In Sect. 2 the model for effective Young’s modulus of nanofilms was established. In Sect. 3, our model was applied to Si nanofilm Young’s modulus, Au nanofilm biaxial modulus and Cu nanofilm biaxial modulus, and the influences of surface elastic coefficient and surface slice thickness were discussed. Finally, Sect. 4 summarized our conclusions.

2 Theory and models

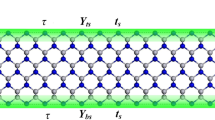
For a freestanding nanofilm with thickness t, the relative number of atoms that are bonded at surface of the film increases with decreasing thickness. The environment of atoms near surface is different from that of bulk counterparts. The missed bonding partners of atoms near surface relaxed the film. Thus, surface slice symmetry might differ from bulk counterpart. There should be additional Young’s modulus (or elastic coefficient) due to surface effect. The additional Young’s modulus (or elastic coefficient) can be called as surface Young’s modulus (or surface elastic coefficient). The surface effect affects the elasticity and symmetry of not only surface atomic layer but also inward near surface atomic layers. Hence, a surface slice with thickness ts should be reckoned in to interpret the elasticity of nanofilms. The hypothesis that the same thickness of top and bottom surface slices can be proposed for sake of simplicity, tts= tbs= ts, where tts and tbs are top and bottom surface slice thicknesses, respectively. The range of top and bottom surface slices in coordinate is t/2 − ts ~ t/2 and − t/2 + ts ~  − t/2, respectively, where t is total thickness of the nanofilm. Here we set the reference plane on the mid-plane of the nanofilm as shown in Fig. 1. Surface Young’s modulus within surface slice can be given by

$$ Y_{\text{s}} = \frac{1}{{t_{\text{s}} }}\int_{{t_{\text{s}} }} {Y_{\text{s}} \left( z \right){\text{d}}z} = \frac{1}{{t_{\text{s}} }}S , $$
(1)
Fig. 1
figure 1

Schematics of nanofilm with surface slice thickness ts and surface Young’s modulus Ys. The blue backdrop part near surface is surface slice with thickness ts. The reference plane was set on the mid-plane of the film (color figure online)

Full size image

where surface elastic coefficient

$$ S = \int_{{t_{\text{s}} }} {Y_{\text{s}} \left( z \right){\text{d}}z} $$
(2)

Equation (1) averaged the surface Young’s modulus within surface slice. Where Ys(z) is surface Young’s modulus which varies with position (z coordinate actually) within surface slice; and Ys is the average of Ys(z) within surface slice. The unit N/m of surface elastic coefficient S is different from Young’s modulus of bulk material (bulk Young’s modulus) Pa. While surface Young’s modulus Ys holds the same dimension as bulk Young’s modulus Pa. Surface Young’s modulus means surface elasticity effect on Young’s modulus of film (within surface slice), but not real or effective Young’s modulus within surface slice. Effective Young’s modulus within surface slice can be given by the sum of surface Young’s modulus and bulk Young’s modulus within surface slice via \( Y_{\text{eff}}^{\text{s}} = Y + Y_{\text{s}} \) (here surface slice thickness effect is not considered for sake of simplicity), but not pure surface Young’s modulus Ys. Bulk Young’s modulus works on the whole film, not only surface slice but also inner core. However, surface Young’s modulus works only on surface slice.

This surface elasticity theoretical scheme can be used as calculation programme for the overall elastic response, i.e., the overall effective Young’s modulus of nanofilms. Film bending modulus can be given by

$$ G_{\text{bent}} = \int\limits_{{ - \frac{1}{2}t}}^{{\frac{1}{2}t}} {Y\left( z \right)z^{2} {\text{d}}z} . $$
(3)

where Y(z) is film Young’s modulus varies with z coordinate and including bulk Young’s modulus and surface Young’s modulus. Film bending modulus can be obtained as

$$ G_{\text{bent}} = \frac{1}{12}Yt^{3} + \left( {\frac{1}{4}t^{2} t_{\text{s}} - \frac{1}{2}tt_{\text{s}}^{2} + \frac{1}{3}t_{\text{s}}^{3} } \right)\left( {Y_{\text{ts}} + Y_{\text{bs}} } \right) . $$
(4)

where Yts and Ybs are top and bottom surface Young’s moduli, respectively. The effective Young’s modulus under bending mode of nanofilms can be given by

$$ Y_{\text{bent}} = \frac{{G_{\text{bent}} }}{{\frac{1}{12}t^{3} }} $$
(5)

Submitting Eq. (4) into Eq. (5), the nanofilm effective Young’s modulus under bending mode can be given by

$$ Y_{\text{bent}} = \frac{{Yt^{3} + \left( {3t^{2} t_{\text{s}} - 6tt_{\text{s}}^{2} + 4t_{\text{s}}^{3} } \right)\left( {Y_{\text{ts}} + Y_{\text{bs}} } \right)}}{{t^{3} }} . $$
(6)

Submitting surface elastic coefficient

$$ S = t_{s} Y_{s} $$
(7)

into effective Young’s modulus under bending mode Eq. (6), one can obtain

$$ Y_{\text{bent}} = Y + \frac{3}{t}\left( {S_{\text{ts}} + S_{\text{bs}} } \right) - \frac{{6t_{s} }}{{t^{2} }}\left( {S_{\text{ts}} + S_{\text{bs}} } \right) + \frac{{4t_{s}^{2} }}{{t^{3} }}\left( {S_{\text{ts}} + S_{\text{bs}} } \right) . $$
(8a)

One can easily find that the first term is bulk Young’s modulus, the second, third and fourth terms are first-, second- and third-order surface modifications, respectively. This surface modification is similar to Core–Shell model about nanowires [27]. Compare with nanowire, nanofilm surface elasticity effect will not introduce fifth term (the fourth-order surface modification). This showed the difference between present theoretical scheme and nanowire Core–Shell model. In Eq. (8a), the first-order surface modification is independent from surface slice thickness and only dependent on surface elastic coefficient, and it is proportional to 1/t. In other words, the first-order surface modification is linear surface effect on effective Young’s modulus. It is a pure surface elastic coefficient modification. While the second- and third-order surface modifications are dependent on surface elastic coefficient and surface slice thickness. They are surface slice thickness modifications and proportional to 1/t2 and 1/t3, respectively, in other words, they are nonlinear surface effects on effective Young’s modulus. The first-order surface modification (linear surface effect) is same as theoretical scheme (surface model) in Ref. [20]. But the two-dimensional surface slice without thickness is just a completely ideal model. The existence of surface slice thickness requires researchers to introduce the second- and third-order surface modifications (nonlinear surface effects) to model the elastic response of nanofilms.

For the sake of convenient discussion of the higher order surface modifications, Eq. (8a) can be simply rewritten as

$$ Y_{\text{bent}} = Y + \frac{{S^{\left( 1 \right)} }}{t} + \frac{{S^{\left( 2 \right)} }}{{t^{2} }} + \frac{{S^{\left( 3 \right)} }}{{t^{3} }} $$
(8b)

where S(1) = 3(Sts + Sbs), S(2) = -6ts (Sts + Sbs), S(3) = 4t 2s (Sts + Sbs) are first-, second- and third-order surface modifications. There is no restriction on orientation of Young’s modulus in Eqs. (6) and (8), hence the limitation of present theoretical scheme covers any orientation. This theory can be used for researching the Young’s moduli Y(100), Y(110) and Y(111) of nanofilms with (100), (110) or (111) surface, as well as biaxial modulus under bending mode, respectively, for example.

Equations (8a) and (8b) provided the relationship between surface model and present theory. When the film is relatively thicker or the surface slice is relatively thinner, i.e., ts can be neglected compared with film thickness t, then ts → 0. Equation (8a) or (8b) reduces to

$$ Y_{\text{bent}} = Y + 3\frac{{\varSigma_{\text{s}} }}{t} , $$
(9)

where ∑s = (Sts + Sbs) is the sum of top surface elastic coefficient and bottom surface elastic coefficient. Equation (9) is just effective Young’s modulus of nanofilm under bending mode in surface model [20, 21]. Surface model can be treated as first approximation of the present theory in this paper.

For the extension mode, the overall Young’s modulus can be given by

$$ Y_{\text{extension}} = \frac{1}{t}\int_{t} {Y\left( z \right){\text{d}}z} , $$
(10)

The overall Young’s modulus under extension mode can be obtained as

$$ Y_{\text{extension}} = Y + \frac{{t_{s} \left( {Y_{ts} + Y_{bs} } \right)}}{t} = Y + \frac{{S_{ts} + S_{bs} }}{t} , $$
(11)

Equation (10) indicates that, for given surface elastic coefficient S, there is no difference between present theory and surface model under extension mode. Surface slice thickness has no contribution to the film effective Young’s modulus under extension mode.

3 Results and discussions

Bulk Young’s modulus is 169 GPa for [110] single-crystal silicon [24]. During fabrication of nanofilms, film surface will be inevitably affected by oxidation and molecule adsorption. Surface effects make surface slice elasticity to be very different from bulk or inner core counterpart. It is difficult to quantify these surface effects because they are always affected by experiment condition. Surface slice thickness of Si nanofilms under the condition that surface is obviously oxided have been reported by Refs. [24,25,26], ranging from 2 nm to 5 nm. And effective Young’s modulus within surface slice is also varies in the Refs. [24, 31, 32], ranging from 50 GPa to 75 GPa. Surface Young’s modulus induced by surface effect can be obtained here and is also varies, ranging from − 94 to − 119 GPa.

In Fig. 2, we chose surface slice thickness as 2 nm and 5 nm, and surface Young’s modulus as − 94 and − 119 GPa, respectively, to model effective Young’s modulus of Si nanofilm with (110) surface. The corresponding surface elastic coefficient S can be obtained using Eq. (7). For example, when surface slice thickness ts = 2 nm, surface Young’s modulus Ys = − 94 GPa and − 119 GPa, the corresponding surface elastic coefficient S = − 188 N/m and − 238 N/m, respectively. When surface slice thickness ts = 5 nm, surface Young’s modulus Ys = − 94 GPa and − 119 GPa, the corresponding surface elastic coefficient S = − 470 N/m and − 595 N/m, respectively. When surface slice thickness ts = 2 nm, present theory gives good agreement with experimental data for larger film thickness. And when ts = 5 nm, present theory gives good agreement with experimental data for smaller film thickness. In Fig. 2, it is observed that surface elasticity effect along with surface slice thickness effect partially explained the distinctive drops of Si nanofilm effective Young’s modulus, but not fully. This shows that there might be more dominant effects influencing the trend. A possible effect that caught our attention is the overall symmetry breaking of the nanofilm induced by surface relaxation [13, 33].

Fig. 2
figure 2

Si nanofilm effective Young’s modulus as function of film thickness t. For experiment details see Ref. [23] (color figure online)

Full size image

Figures 3 and 4 showed that present theory gives good agreement with simulated results about biaxial moduli of Au and Cu nanofilms. We used surface slice thickness ts = 0.25 nm to calculate biaxial moduli in Figs. 3 and 4. Bulk biaxial modulus of Au is given as Y0 = 66.75 GPa by embedded-atom method (EAM) while Y0 = 78.22 GPa by modified embedded-atom method (MEAM) [19]. For Cu bulk biaxial modulus, EAM gives the value as Y0 = 107.16 GPa while MEAM gives the value as Y0 = 116.30 GPa [19]. For surface elastic coefficient, different values are used to calculate biaxial moduli under different conditions. For Au nanofilms in Fig. 3, surface elastic coefficient is chosen as S = 25 N/m to conform to EAM result and is chosen as S = 8.5 N/m to conform to MEAM result. And for Cu nanofilms in Fig. 4, surface elastic coefficient is chosen as S = 25 N/m to conform to EAM result and is chosen as S = 2.5 N/m to conform to MEAM result. Both Au and Cu nanofilms as well as both EAM and MEAM calculations, present theoretical method can give good agreement with calculated results in Ref. [19].

Fig. 3
figure 3

Biaxial modulus of Au nanofilms as function of film thickness t. In the figure, bulk biaxial modulus is given as Y0 = 66.75 GPa by ESM and Y0 = 78.22 GPa by MEAM [19], surface slice thickness ts = 0.25 nm, surface elastic coefficient S = 25 N/m to conform to EAM and S = 8.5 N/m to conform to MEAM, respectively. The calculated data are from Ref. [19] (color figure online)

Full size image
Fig. 4
figure 4

Biaxial modulus of Cu nanofilms as function of film thickness t. In the figure, bulk biaxial modulus is given as Y0 = 107.16 GPa by ESM and Y0 = 116.30 GPa by MEAM [19], surface slice thickness ts = 0.25 nm, surface elastic coefficient S = 25 N/m to conform to EAM and S = 2.5 N/m to conform to MEAM, respectively. The calculated data are from Ref. [19] (color figure online)

Full size image

In Fig. 5, one can easily find that surface slice thickness increases effective Young’s modulus when surface elastic coefficient S is given. Minus surface elastic coefficient S certainly decreases effective Young’s modulus. This fact means that surface slice thickness weakens surface elasticity effect on the overall elastic character. This ts effect property can be interpreted by Eq. (3). There is z2 term in the integral formula of bending modulus, hence the different contribution of different position of surface elasticity modification. Surface elasticity modification with larger z coordination, i.e., farther from the reference plane (mid-plane of the film) and closer to film surface plane, gives larger contribution. For larger surface slice thickness, part of surface elasticity S embeds inner atomic layers to be closer to reference plane. This property weakened S effect on film effective Young’s modulus. Therefore, larger ts indicates weakened surface effect on film Young’s modulus when surface elastic coefficient S is given. On the other hand, effective Young’s modulus Eq. (8a) contains quadratic term of ts. Therefore, ts will enhance S effect when ts satisfies ts ≥ (3/2)t. But unfortunately, it is impossible to satisfy this condition. Since surface slice thickness ts cannot be larger than film thickness t. Figure 6 showed that effective Young’s modulus is strongly affected by surface slice thickness ts when surface Young’s modulus Ys is given. Larger ts enhanced surface Young’s modulus effect on film-effective Young’s modulus obviously. The relation between surface Young’s modulus and surface elastic coefficient Eq. (7) gives the reasonable commentation on surface slice thickness effect in Fig. 6. Larger surface slice thickness ts means larger surface elastic coefficient S. This effect enhanced surface effect obviously despite the weakened ts effect for given S.

Fig. 5
figure 5

Si nanofilm Young’s modulus as function of surface slice thickness ts. Surface elastic coefficient S is given in the figure

Full size image
Fig. 6
figure 6

Si nanofilm Young’s modulus as function of surface slice thickness ts. Surface Young’s modulus Ys is given in the figure (color figure online)

Full size image

4 Conclusions

This work researched nanofilm Young’s modulus (as well as biaxial modulus) by considering surface elasticity and surface slice thickness; and established nanofilm-effective Young’s modulus mathematic expression which contains surface elasticity effect as well as surface slice thickness effect. The present theory was used to compare with Si film experiment, Au and Cu film simulations. When film is very thick, surface effect should be neglected and bulk Young’s modulus is valid for the description of elastic response of the film. But when film thickness turns down nanaometers to form a nanofilm, surface effects become very important and cannot be neglected. Both Surface Young’s modulus (surface elastic coefficient) and surface slice thickness affect effective Young’s modulus of nanofilms strongly. For given surface Young’s modulus, surface slice thickness obviously enhanced surface elasticity effect on overall elastic property of nanofilm. While for given surface elastic coefficient, surface slice thickness weakened surface elasticity effect on overall elastic property. Surface elastic coefficient effect introduces the first-order surface modification, i.e., linear surface modification as surface model addressed; while surface slice thickness introduces higher terms of surface modification, i.e., nonlinear surface modifications. The effective Young’s modulus mathematic expression implied that previous surface model can be seen as the first approximation of present theoretical scheme. The influence of surface slice thickness effect is up to the relative thickness comparing with whole thickness of the film. If surface slice thickness is much smaller than whole thickness of the film, higher terms of surface modification can be neglected. But for ultrathin nanofilm with several nanometers thickness or for the film with obviously oxided surface, surface slice thickness and the corresponding higher terms of surface modification cannot be neglected anymore.