1 Introduction

Piezoelectric nanomaterials have attracted much interest due to their tremendous potential for device applications in nano-electro-mechanical systems (NEMS) [1,2,3]. They are widely applied in nanogenerators [4,5,6,7], nanosensors [8, 9], biosensors [10, 11], nanoactuators [12,13,14], and nanoresonators [15,16,17]. When dimension reduces to nanoscale, the properties of piezoelectric nanomaterials will be size-dependent and surface modulated [18,19,20]. There are many works to research the size-dependent properties of piezoelectric nanomaterials, such as experimental measurements, simulated calculations, and theory research [21, 22]. The mechanical properties of ZnO piezoelectric nanowire (NW) were found to vary with radius by experiment [23, 24]. Molecular statistical thermodynamics method also reported the size-dependent mechanical properties of piezoelectric nanomaterials [25]. The size-dependent piezoelectric coefficients of ZnO, GaN, and BaTiO3 nanowires were researched by using molecular dynamics as well as first principle approach [26,27,28,29]. The surface effect on electromechanical behavior of graphene-based nanobeams was investigated by using size-dependent Euler–Bernoulli theory [20]. Piezoelectricity property of piezoelectric nanomaterials was used to harvest nanoscale mechanical energy [30]. Wang and Song first demonstrated the piezoelectric nanogenerator prototype by using a single ZnO nanowire [7]. To explore the basic theory of nanogenerators, Gao and Wang gave a continuum theory to calculate the equilibrium electrostatic potential [31]. The theoretical interpretation of size-dependent piezoelectric properties was also researched in [17, 22, 32].

Surface elasticity effect is usually interpreted as a zero-thickness layer with elastic property ideally adhering to the bulk like core [33, 34]. The model of surface elasticity taking these features into account was first proposed by Gurtin and Murdoch [35]. This core-surface model was widely used to investigate nanomaterial mechanical properties [36,37,38]. In order to take the surface slice thickness into account, core–shell model was introduced to interpret the nanowire elastic property [23, 24]. Both core-surface and core–shell model meet the same problem that there is a sudden change of Young’s modulus at the interface between surface area and bulk like core. In order to eliminate this sudden change, a modified core–shell model was established by introducing a concept of inhomogeneity of Young’s modulus [39]. There is another problem of the modified core–shell model, that when eliminating sudden change of Young’s modulus, the sudden change of the derivation of Young’s modulus appears at interface. For a nanowire, the surface area and bulk like area are same material. They should hold same change rule of Young’s modulus. The sudden change of Young’s modulus is just assumed theoretically, it does not exist actually. Correspondingly, there is no essential difference between surface area and bulk like area (except core–shell structures with different materials between core and shell). Not only Young’s modulus, but also piezoelectric coefficient follows this continuum rule within nanowires. At surface, the outer bonding partner is absent. The dangling bonds combine together and outmost surface atom moves. This surface relaxation procedure changes lattice structure and symmetry at the surface. And then, Young’s modulus and piezoelectric coefficient also change and behave different from their bulk material counterparts. There one needs additional Young’s modulus and piezoelectric coefficient to interpret this difference. Therefore, surface Young’s modulus and surface piezoelectric coefficient come up. Since the outermost atoms move and leave their original equilibrium position, the secondary outer atomic layer and inner atomic layers are also influenced via van der Waals force. Therefore, the secondary outer atomic layer and inner atomic layers also change their lattice structure and symmetry but more weakly than outmost surface atomic layer. In other words, the surface effects on Young’s modulus and piezoelectric coefficient decrease with increasing distance from the surface layer [40]. The decrease rule was assumed to follow exponential law in this paper.

In this paper, a continuum theoretical model for describing nanowire mechanical and piezoelectric properties is established by considering exponentially decreasing surface effects. In Sect. 2 the model for effective Young’s modulus and effective piezoelectric coefficient of nanowires is established. The piezoelectric charge density and piezoelectric potential are also derived. In Sect. 3, our model is applied to Young’s modulus of ZnO nanowire and piezoelectric coefficients of ZnO and GaN nanowires. Piezoelectric charge density and piezoelectric potential are also discussed in this Section. Finally, Sect. 4 summarizes our conclusions.

2 Theory and model

Young’s modulus and piezoelectric coefficient are strongly influenced by surface effects. The surface Young’s modulus and surface piezoelectric coefficient were considered as additional parameters in the overall piezoelectric properties of nanowires. The influence of surface effects decreases with increasing distance from surface layer. The decrease rule is assumed to follow exponential law in this paper. The real Young’s modulus and real piezoelectric coefficient are constructed by bulk parameters and surface parameters. In the current model, there is no surface area, bulk like area as well as the corresponding interface concept. Nanowire mechanical and piezoelectric properties behave continuously within nanowires.

Various surface elasticity and surface piezoelectricity within nanowires can be interpreted as [40]

$${E}_{\mathrm{s}}\left(r\right)={E}_{\mathrm{s}}{e}^{-\alpha \left(R-r\right)},$$
(1.1)
$${e}_{kj}^{s}\left(r\right)={e}_{kj}^{s}{e}^{-\beta \left(R-r\right)}$$
(1.2)

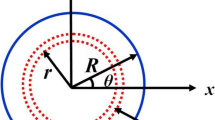
where r ≤ R, R is the radius of the nanowire. \({E}_{\mathrm{s}}\left(r\right)\) and \({e}_{kj}^{s}\left(r\right)\) serve as the variational surface Young’s modulus and surface piezoelectric coefficients of nanowires, respectively. \({E}_{\mathrm{s}}\) and \({e}_{kj}^{s}\) are surface Young’s modulus and surface piezoelectric coefficients at the outermost atomic layer, respectively. R-r stands for the distance between the consideration site and nanowire surface, see in Fig. 1. Equations (1.1) and (1.2) show that the influence of surface effects decreases with distance from the surface layer. And the exponential law was assumed in this paper, while α and β represent the degree of decrease and are in unit of \({\mathrm{nm}}^{-1}\). Therefore, α and β can be called as decrease factors of surface Young’s modulus and surface piezoelectric coefficients, respectively.

Fig. 1
figure 1

Schematic representation of the nanowire cross section

Full size image

The real Young’s modulus and real piezoelectric coefficients at the point with coordinate r are [40]

$$E={E}_{0}+{E}_{\mathrm{s}}{e}^{-\alpha \left(R-r\right)},$$
(2.1)
$${e}_{kj}={e}_{kj}^{0}+{e}_{kj}^{s}{e}^{-\beta \left(R-r\right)},$$
(2.2)

respectively.

The effective bending stiffness and bending piezoelectricity of nanowires are [23]

$${E}_{\mathrm{eff}}I={E}_{0}{I}_{0}+{E}_{\mathrm{s}}\left(r\right){I}_{\mathrm{s}},$$
(3.1)
$${e}_{kj}I={e}_{kj}^{0}{I}_{0}+{e}_{kj}^{s}\left(r\right){I}_{s}$$
(3.2)

where Eeff and E0 are the effective and bulk Young’s moduli, \({e}_{kj}\) and \({e}_{kj}^{0}\) are the effective and bulk piezoelectric coefficients of nanowires, respectively.

The differentiation of nanowire inertia moment [32] gives

$$dI=\underset{0}{\overset{2\pi }{\int }}\underset{r}{\overset{r+dr}{\int }}{\left(r\mathrm{cos}\theta \right)}^{2}rd\theta dr=\pi {r}^{3}dr$$
(4)

as shown in Fig. 1,

$$I=\underset{0}{\overset{R}{\int }}\pi {r}^{3}dr=\frac{1}{4}\pi {R}^{4}.$$
(5)

Both bulk Young’s modulus and bulk piezoelectric coefficients are consistent with the variable site. Therefore, the bulk bending stiffness and bulk bending piezoelectricity can be obtained by [23]

$${E}_{0}{I}_{0}={E}_{0}\frac{1}{4}\pi {R}^{4},$$
(6.1)
$${e}_{kj}^{0}{I}_{0}={e}_{kj}^{0}\frac{1}{4}\pi {R}^{4}.$$
(6.2)

Since surface Young’s modulus and surface piezoelectric coefficients are additional parameters, the surface bending stiffness and surface bending piezoelectricity are also additional parameters. They can be given by

$${E}_{\mathrm{s}}\left(r\right){I}_{\mathrm{s}}=\underset{0}{\overset{R}{\int }}{E}_{\mathrm{s}}\left(r\right)\pi {r}^{3}dr,$$
(7.1)
$${e}_{kj}^{s}\left(r\right){I}_{s}=\underset{0}{\overset{R}{\int }}{e}_{kj}^{s}\left(r\right)\pi {r}^{3}dr.$$
(7.2)

The effective bending stiffness and effective bending piezoelectricity are constructed by bulk parameters and surface parameters, respectively. Therefore, the effective bending stiffness and effective bending piezoelectricity of piezoelectric nanowires are given by

$${E}_{\mathrm{eff}}I={E}_{0}\frac{1}{4}\pi {R}^{4}+{E}_{\mathrm{s}}\left(\frac{1}{\alpha }\pi {R}^{3}-\frac{3}{{\alpha }^{2}}\pi {R}^{2}+\frac{6}{{\alpha }^{3}}\pi R-\frac{6}{{\alpha }^{4}}\pi +\frac{6}{{\alpha }^{4}}\pi {e}^{-\alpha R}\right),$$
(8.1)
$${e}_{kj}I={e}_{kj}^{0}\frac{1}{4}\pi {R}^{4}+{e}_{kj}^{s}\left(\frac{1}{\beta }\pi {R}^{3}-\frac{3}{{\beta }^{2}}\pi {R}^{2}+\frac{6}{{\beta }^{3}}\pi R-\frac{6}{{\beta }^{4}}\pi +\frac{6}{{\beta }^{4}}\pi {e}^{-\beta R}\right).$$
(8.2)

And the effective Young’s modulus and effective piezoelectric coefficients of nanowires are [40]

$${E}_{\mathrm{eff}}={E}_{0}+4{E}_{\mathrm{s}}\left(\frac{1}{\alpha R}-\frac{3}{{\alpha }^{2}{R}^{2}}+\frac{6}{{\alpha }^{3}{R}^{3}}-\frac{6}{{\alpha }^{4}{R}^{4}}+\frac{6}{{\alpha }^{4}{R}^{4}}{e}^{-\alpha R}\right),$$
(9.1)
$${e}_{kj}={e}_{kj}^{0}+4{e}_{kj}^{s}\left(\frac{1}{\beta R}-\frac{3}{{\beta }^{2}{R}^{2}}+\frac{6}{{\beta }^{3}{R}^{3}}-\frac{6}{{\beta }^{4}{R}^{4}}+\frac{6}{{\beta }^{4}{R}^{4}}{e}^{-\beta R}\right).$$
(9.2)

The first and second terms (of both effective Young’s modulus and piezoelectric coefficients) are bulk parameters and the influence of surface parameters, respectively. For the surface effect terms, the first surface modification is linear surface modification, and the second, third, and fourth surface modifications are nonlinear modifications. The fifth surface modification represents exponential modification. If the surface Young’s modulus (as well as surface piezoelectric coefficients) is set to be zero, the surface effects on nanowires will disappear. On the other hand, if the radius of the nanowire is very large, the influence of surface effects is also gone.

According to the piezoelectric theory, the constitutive equations of the piezoelectric medium can be given by [31, 32, 41]

$${\sigma }_{i}={c}_{ij}{\varepsilon }_{j}-{e}_{kj}{E}_{k},$$
(10.1)
$${D}_{m}={e}_{mj}{\varepsilon }_{j}+{\kappa }_{mk}{E}_{k}$$
(10.2)

where εj, σi, Ek, and Dm stand for strain, stress, electric field, and electric displacement, respectively. κmk, ekj and cij serve as dielectric tensor, piezoelectric tensor, and stiffness tensor, respectively. Theoretically, there should be multi-orders of electromechanical coupling. But there is barely piezoelectric field influence on the nanowire stress or strain [31, 32]. Therefore, the high-order electromechanical coupling was ignored in this paper. According to the first-order piezoelectric effect approximation, the piezoelectric polarization induced by strain can be interpreted by [31, 32]

$${P}_{m}=\sum_{j}{e}_{mj}{\varepsilon }_{j}$$
(11)

where \({P}_{m}\) (m = 1, 2, 3) serves as components of the piezoelectric polarization vector \(\mathop{P}\limits^{\rightharpoonup}\) and \({\varepsilon }_{j}\) (j = 1, 2, 3, 4, 5, 6) serves as the components of strain tensor. For Wurtzite structure ZnO, the matrices of the piezoelectric and dielectric tensors can be written as [31]

$${e}_{mj}=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ {e}_{13}& {e}_{31}& {e}_{33}\end{array} \begin{array}{ccc}0& {e}_{15}& 0\\ {e}_{15}& 0& 0\\ 0& 0& 0\end{array}\right)$$
(12)

and

$${\kappa }_{mk}=\left(\begin{array}{ccc}{\kappa }_{11}& 0& 0\\ 0& {\kappa }_{22}& 0\\ 0& 0& {\kappa }_{33}\end{array}\right),$$
(13)

respectively.

For the sake of compactness of the notation, rr, θθ, zz, θz, rz, and rθ are replaced by 1, 2, 3, 4, 5, and 6. According to the Saint–Venant bending theory [31, 32, 42, 43], the effective stress expressions of ZnO nanowire can be obtained as follows:

$$\left(\begin{array}{c}{\sigma }_{1}^{e}\\ {\sigma }_{2}^{e}\\ {\sigma }_{3}^{e}\\ {\sigma }_{4}^{e}\\ {\sigma }_{5}^{e}\\ {\sigma }_{6}^{e}\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ -\frac{{f}_{x}}{{I}_{e}}\left(l-z\right)r\mathrm{cos}\theta \\ -\frac{{f}_{x}}{8{I}_{e}}\frac{3+2v}{1+v}\left({R}^{2}-\frac{1-2v}{3+2v}{r}^{2}\right)\mathrm{sin}\theta \\ \frac{{f}_{x}}{8{I}_{e}}\frac{3+2v}{1+v}\left({R}^{2}-{r}^{2}\right)\mathrm{cos}\theta \\ 0\end{array}\right)$$
(14)

where \({f}_{x}\) serves as the external force which is applied along lateral direction. \({I}_{e}\) stands for the effective inertia moment of area of the whole nanowire. \(l\) is the nanowire length. Since ZnO crystal is transversely isotropic, for the sake of simplicity, the isotropic bulk Young’s modulus and Poisson’s ratio were used in this paper. The value can be calculated from ZnO nanowire elastic constant [31, 44]. Taking the surface Young’s modulus into account, the matrix form of the effective stress and strain relationship can be given by Hooke’s law [32],

$$\left( {\begin{array}{*{20}{c}} {\varepsilon _1^e}\\ {\varepsilon _2^e}\\ {\varepsilon _3^e}\\ {\varepsilon _4^e}\\ {\varepsilon _5^e}\\ {\varepsilon _6^e} \end{array}} \right) = \frac{1}{{E_{{\rm{eff}}}^{{\rm{iso}}}}}\left( {\begin{array}{*{20}{c}} 1&{ - v}&{ - v}&0&0&0\\ { - v}&1&{ - v}&0&0&0\\ { - v}&{ - v}&1&0&0&0\\ 0&0&0&{2\left( {1 + v} \right)}&0&0\\ 0&0&0&0&{2\left( {1 + v} \right)}&0\\ 0&0&0&0&0&{2\left( {1 + v} \right)} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\sigma _1^e}\\ {\sigma _2^e}\\ {\sigma _3^e}\\ {\sigma _4^e}\\ {\sigma _5^e}\\ {\sigma _6^e} \end{array}} \right),$$
(15)

where v serves as Poisson’s ratio. The isotropic effect Young’s modulus \({E}_{\mathrm{eff}}^{\mathrm{iso}}\) was given by Eq. (9.1).

Since there is no free charge within the nanowire, one can obtain the Gauss’s law of the electrostatic field as

$$\nabla \cdot \left( {e_{mj} \varepsilon_{j} + \kappa_{mk} E_{k} } \right)\mathop{i}\limits^{\rightharpoonup} _{m} = \nabla \cdot \left( {P_{m} + \kappa_{mk} E_{k} } \right)\mathop{i}\limits^{\rightharpoonup} _{m} = 0.$$
(16)

Within polarized piezoelectric nanowires, residual strain induces piezoelectric field. These enlarged dipoles induce residual charges to emerge. The density of remnant body charges can be described by

$$\rho_{P} = - \nabla \cdot \mathop{P}\limits^{\rightharpoonup},$$
(17)

and the density of remnant surface charges can be given by

$$\rho_{{\text{s}}} = - \mathop{n}\limits^{\rightharpoonup} \cdot \left( {0 - \mathop{P}\limits^{\rightharpoonup} } \right) = \mathop{n}\limits^{\rightharpoonup} \cdot \mathop{P}\limits^{\rightharpoonup}.$$
(18)

The Gauss’s law of the electrostatic field Eq. (16) can be transformed into Poisson’s equation as follows:

$$\nabla \cdot \left( {\kappa_{mk} E_{k} \mathop{i}\limits^{\rightharpoonup} _{m} } \right) = \rho_{P}.$$
(19)

According to the first piezoelectric effect approximation, the matrix of the effective piezoelectric polarization can be given by

$$\left(\begin{array}{c}{P}_{1}^{e}\\ {P}_{2}^{e}\\ {P}_{3}^{e}\end{array}\right)=\left(\begin{array}{c}{e}_{15}{\varepsilon }_{5}\\ {e}_{15}{\varepsilon }_{4}\\ {e}_{31}{\varepsilon }_{1}+{e}_{31}{\varepsilon }_{2}+{e}_{33}{\varepsilon }_{3}\end{array}\right)$$
(20)

where piezoelectric coefficients \({e}_{15}\), \({e}_{31}\), and \({e}_{33}\) are all size dependent and surface modulated. According to Eq. (2.2), \({e}_{33}\), \({e}_{15}\), and \({e}_{31}\) can be given by

$${e}_{33}={e}_{33}^{0}+{e}_{33}^{s}{e}^{-\beta \left(R-r\right)},$$
(21.1)
$${e}_{15}={e}_{15}^{0}+{e}_{15}^{s}{e}^{-\beta \left(R-r\right)},$$
(21.2)
$${e}_{31}={e}_{31}^{0}+{e}_{31}^{s}{e}^{-\beta \left(R-r\right)}.$$
(21.3)

Taking the strain components into Eq. (15), one can obtain the effective piezoelectric polarization as

$$\left(\begin{array}{c}{P}_{1}^{e}\\ {P}_{2}^{e}\\ {P}_{3}^{e}\end{array}\right)=\frac{1}{{E}_{\mathrm{eff}}^{\mathrm{iso}}}\left(\begin{array}{c}\frac{{f}_{x}}{4{I}_{e}}\left(3+2v\right){e}_{15}\left({R}^{2}-{r}^{2}\right)\mathrm{cos}\theta \\ -\frac{{f}_{x}}{4{I}_{e}}\left(3+2v\right){e}_{15}\left({R}^{2}-\frac{1-2v}{3+2v}{r}^{2}\right)\mathrm{sin}\theta \\ \frac{{f}_{x}}{{I}_{e}}\left(2v{e}_{31}-{e}_{33}\right)\left(l-z\right)r\mathrm{cos}\theta \end{array}\right).$$
(22)

We can easily get the remnant surface charge density of the nanowire as \(\rho_{{\text{s}}}^{{\text{e}}} = 0\). The remnant body charge density of effective polarization can be derived as

$${\rho }_{P}=\frac{1}{{E}_{\mathrm{eff}}^{\mathrm{iso}}}\frac{{f}_{x}}{{I}_{e}}\left[2\left(1+v\right){e}_{15}^{0}+2v{e}_{31}^{0}-{e}_{33}^{0}\right]r\mathrm{cos}\theta +\frac{1}{{E}_{\mathrm{eff}}^{\mathrm{iso}}}\frac{{f}_{x}}{{I}_{e}}\left\{\left[2\left(1+v\right){e}_{15}^{s}+2v{e}_{31}^{s}-{e}_{33}^{s}\right]r-\frac{\left(3+2v\right)}{4}{e}_{15}^{s}\beta \left({R}^{2}-{r}^{2}\right)\right\}\mathrm{cos}\theta {e}^{-\beta \left(R-r\right)}.$$
(23)

The first term is the contribution of bulk piezoelectric coefficients. The second term is induced by surface piezoelectric coefficients. Bulk piezoelectric coefficients induce charge density to vary with x (\(x=r\mathrm{cos}\theta\)) coordinate linearly, while surface piezoelectric coefficients contribution varies with r coordinate exponentially. These two terms (surface piezoelectric coefficients contribution and bulk piezoelectric coefficients contribution) are both influenced by surface Young’s modulus. They are both dependent on effective Young’s modulus \({E}_{\mathrm{eff}}^{\mathrm{iso}}\). The piezoelectric equilibrium potential in the cross section of the nanowire can be determined by solving Poisson’s equation,

$$\nabla^{2} \varphi = - \frac{{\rho_{P} }}{{\kappa_{ \bot } }},$$
(24)

where \(\kappa_{ \bot } = \kappa_{11} = \kappa_{22}\), and \(\kappa_{ \bot }\) stands for the dielectric constant of the nanowire cross-sectional plane. According to Eq. (24), the piezoelectric potential is independent from z coordinate (the length direction of the nanowire). The boundary conditions of Eq. (24) are:

$$\left. {\varphi_{i} } \right|_{r = 0} \;{\text{limited}},$$
(25.1)
$${\left.{\varphi }_{e}\right|}_{r\to \infty }=0,$$
(25.2)
$$\begin{gathered} \kappa_{ \bot } \left. {\frac{{\partial \varphi_{i} }}{\partial r}} \right|_{r = R} = \kappa_{0} \left. {\frac{{\partial \varphi_{e} }}{\partial r}} \right|_{r = R} , \hfill \\ \left. {\varphi_{i} } \right|_{r = R} = \left. {\varphi_{e} } \right|_{r = R} \hfill \\ \end{gathered}$$
(25.3)

where \({\varphi }_{i}\) and \({\varphi }_{e}\) are the piezoelectric potential inside and outside the nanowire, respectively.

The power exponent function \({e}^{\beta r}\) in Eq. (23) can be expanded into MacLaurin series as

$${e}^{\beta r}=\sum_{n=0}^{\infty }\frac{{\left(\beta r\right)}^{n}}{n!}.$$
(26)

Poisson’s equation becomes

$$\begin{gathered} \nabla^{2} \varphi = - \frac{{f_{x} }}{{E\kappa_{ \bot } I_{e} }}\left[ {2\left( {1 + v} \right)e_{15}^{0} + 2ve_{31}^{0} - e_{33}^{0} } \right]r\cos \theta \hfill \\ - \frac{{f_{x} }}{{E\kappa_{ \bot } I_{e} }}\left[ {2\left( {1 + v} \right)e_{15}^{s} + 2ve_{31}^{s} - e_{33}^{s} } \right]r\cos \theta e^{ - \beta R} \sum \limits_{n = 0}^{\infty } \frac{{\left( {\beta r} \right)^{n} }}{n!} \hfill \\ + \frac{{f_{x} }}{{E\kappa_{ \bot } I_{e} }}\frac{{\left( {3 + 2v} \right)}}{4}e_{15}^{s} \beta R^{2} \cos \theta e^{ - \beta R} \sum \limits_{n = 0}^{\infty } \frac{{\left( {\beta r} \right)^{n} }}{n!} \hfill \\ - \frac{{f_{x} }}{{E\kappa_{ \bot } I_{e} }}\frac{{\left( {3 + 2v} \right)}}{4}e_{15}^{s} \beta r^{2} \cos \theta e^{ - \beta R} \sum \limits_{n = 0}^{\infty } \frac{{\left( {\beta r} \right)^{n} }}{n!}, \hfill \\ \end{gathered}$$
(27)

The special solution of Poisson’s equation is

$${\varphi }_{p}=-\frac{1}{8}\frac{{f}_{x}}{E{\kappa }_{\perp }{I}_{e}}\left[2\left(1+v\right){e}_{15}^{0}+2v{e}_{31}^{0}-{e}_{33}^{0}\right]\mathrm{cos}\theta {r}^{3}-\frac{{f}_{x}}{E{\kappa }_{\perp }{I}_{e}}\left[2\left(1+v\right){e}_{15}^{s}+2v{e}_{31}^{s}-{e}_{33}^{s}\right]\mathrm{cos}\theta {e}^{-\beta R}\sum_{n=0}^{\infty }\frac{1}{\left(n+2\right)\left(n+4\right)}\frac{{\beta }^{n}{r}^{n+3}}{n!}+\frac{{f}_{x}}{E{\kappa }_{\perp }{I}_{e}}\frac{\left(3+2v\right)}{4}{e}_{15}^{s}\beta {R}^{2}\mathrm{cos}\theta {e}^{-\beta R}\sum_{n=0}^{\infty }\frac{1}{\left(n+1\right)\left(n+3\right)}\frac{{\beta }^{n}{r}^{n+2}}{n!}-\frac{{f}_{x}}{E{\kappa }_{\perp }{I}_{e}}\frac{\left(3+2v\right)}{4}{e}_{15}^{s}\beta \mathrm{cos}\theta {e}^{-\beta R}\sum_{n=0}^{\infty }\frac{1}{\left(n+3\right)\left(n+5\right)}\frac{{\beta }^{n}{r}^{n+4}}{n!}.$$
(28)

Considering the boundary conditions Eqs. (25.1), (25.2) and (25.3), and the special solution Eq. (28), the piezoelectric potential can be obtained as

$${\varphi }_{i}=\frac{1}{8}\frac{3{\kappa }_{\perp }+{\kappa }_{0}}{{\kappa }_{\perp }+{\kappa }_{0}}{R}^{2}{A}_{0}\mathrm{cos}\theta r-\frac{1}{8}{A}_{0}\mathrm{cos}\theta {r}^{3}+{\Omega }_{R1}\left(n\right)\mathrm{cos}\theta r-{\Omega }_{r}\left(n\right)\mathrm{cos}\theta r (r<R),$$
(29.1)
$${\varphi }_{e}=\frac{1}{4}\frac{{\kappa }_{\perp }}{{\kappa }_{\perp }+{\kappa }_{0}}{A}_{0}{R}^{4}\mathrm{cos}\theta {r}^{-1}+{\Omega }_{R2}\left(n\right)\mathrm{cos}\theta {r}^{-1} \left(r>R\right)$$
(29.2)

where

$${\Omega }_{R1}\left(n\right)=\frac{1}{{\kappa }_{\perp }+{\kappa }_{0}}\sum_{n=0}^{\infty }\left[{A}_{s}\frac{{\kappa }_{\perp }\left(n+3\right)+{\kappa }_{0}}{\left(n+2\right)\left(n+4\right)}-{B}_{s}\frac{{\kappa }_{\perp }\left(2n+6\right)+4{\kappa }_{0}}{\left(n+1\right)\left(n+3\right)\left(n+5\right)}R\right]\frac{{\beta }^{n}}{n!}{R}^{n+2},$$
$${\Omega }_{R2}\left(n\right)=\frac{{\kappa }_{\perp }}{{\kappa }_{\perp }+{\kappa }_{0}}\sum_{n=0}^{\infty }\left[{A}_{s}\frac{1}{\left(n+4\right)}-{B}_{s}\frac{2}{\left(n+3\right)\left(n+5\right)}R\right]\frac{{\beta }^{n}}{n!}{R}^{n+4},$$
$${\Omega }_{r}\left(n\right)=\sum_{n=0}^{\infty }\left[{A}_{s}\frac{1}{\left(n+2\right)\left(n+4\right)}r-{B}_{s}\frac{1}{\left(n+1\right)\left(n+3\right)}{R}^{2}+{B}_{s}\frac{1}{\left(n+3\right)\left(n+5\right)}{r}^{2}\right]\frac{{\beta }^{n}}{n!}{r}^{n+1},$$
$${A}_{0}=\frac{{f}_{x}}{{E}_{\mathrm{eff}}^{\mathrm{iso}}{\kappa }_{\perp }{I}_{e}}\left[2\left(1+v\right){e}_{15}^{0}+2v{e}_{31}^{0}-{e}_{33}^{0}\right],$$
$${A}_{s}=\frac{{f}_{x}}{{E}_{\mathrm{eff}}^{\mathrm{iso}}{\kappa }_{\perp }{I}_{e}}\left[2\left(1+v\right){e}_{15}^{s}+2v{e}_{31}^{s}-{e}_{33}^{s}\right]{e}^{-\beta R},$$
$${B}_{s}=\frac{{f}_{x}}{{E}_{\mathrm{eff}}^{\mathrm{iso}}{\kappa }_{\perp }{I}_{e}}\frac{\left(3+2v\right)}{4}{e}_{15}^{s}\beta {e}^{-\beta R}.$$

The coefficient \({A}_{0}\) stands for the contribution of bulk piezoelectric coefficients. \({A}_{s}\) and \({B}_{s}\) stand for contributions of surface piezoelectric coefficients. The contributions of surface piezoelectric coefficients are dependent on nanowire radius and decrease with R exponentially.

3 Results and discussion

The symmetry and lattice structure near surface are different from the bulk material counterparts. For the outmost atomic layer, the outer bonding partner absents and induces broken bond. The dangling bonds combine together. The symmetry and lattice structure are changed by this surface relaxation. This surface change procedure will influence the second outer atomic layer. The surface effect on second outer atomic layer is weaker than outmost atomic layer. The inner layers are also influenced by surface effect but weaker and weaker. Therefore, the influence of surface effect decreases with going deep into the inner core. Due to the influence of surface effect, Young’s modulus and piezoelectric coefficients are different from bulk materials. This difference was usually interpreted by surface Young’s modulus (surface elasticity) and surface piezoelectric coefficients. Surface Young’s modulus and surface piezoelectric coefficients are additional parameters which combine with bulk parameters to construct effective Young’s modulus and effective piezoelectric coefficients.

The ZnO nanowire effective Young’s modulus is predicted in Fig. 2. The theoretical line was compared with experimental result and numerical calculation. ZnO nanowire Young’s modulus was measured by Chen et. al. under bending mode [23]. The experimental measurement was invalid for a diameter being smaller than about 17 nm, and then the molecular statistical thermodynamics (MST) was going to be used [25]. The current theory gave good agreement with experimental and calculated data. The simplified isotropic bulk Young’s modulus 129 GPa [31] was used rather than 140 GPa of [0001] direction [44]. The surface Young’s modulus Es = 280 GPa and decrease factor α = 1.3 nm−1. Figure 2 shows that when nanowire diameter is smaller than 100 nm, surface Young’s modulus (surface elasticity) effect will influence the overall elastic property obviously.

Fig. 2
figure 2

Size-dependent Young’s modulus of ZnO nanowire

Full size image

The piezoelectric effect exhibits a diverse range of atomic structures and configurations. For piezoelectric nanomaterials with extremely large surface-to-volume ratio, the effective piezoelectric coefficients are strongly influenced by surface effect. As a result of surface effect, the size-dependent piezoelectric properties of piezoelectric nanomaterials were observed. The axial piezoelectric coefficient (e33) of ZnO and GaN as function of nanowire diameter is shown in Fig. 3a, b. It was shown that ZnO and GaN piezoelectric coefficient (e33) increase with decreasing nanowire diameter. This tendency means surface piezoelectric coefficient (\({e}_{33}^{s}\)) is positive for ZnO and GaN nanowires. Theoretical line was plotted by using Eq. (9.2) in this paper. The bulk piezoelectric coefficient was chosen as \({e}_{33}^{0}=1.22\) Cm−2 and \({e}_{33}^{0}=0.73\) Cm−2 for ZnO and GaN nanowires [21, 28], respectively. The surface piezoelectric coefficient was chosen as \({e}_{33}^{s}=2.2\) Cm−2 and \({e}_{33}^{s}=8\) Cm−2 for ZnO and GaN nanowires, respectively. Decrease factor \(\beta =9\) nm−1 and \(\beta =25\) nm−1 for ZnO and GaN nanowires, respectively. The molecular dynamics calculation of ZnO nanowire can be found in Ref. [27]. The first principles investigation of GaN nanowire can be found in Ref. [28]. Figure 3a, b shows that the effective piezoelectric coefficient (e33) is obviously affected by surface effect when nanowire diameter is smaller than 10 nm. Comparison between Figs. 2 and 3 gives the obvious result that surface piezoelectricity effect is remarkably weaker than surface elasticity effect, for ZnO nanowire.

Fig. 3
figure 3

The piezoelectric coefficient e33 of ZnO and GaN nanowires. a e33 of ZnO nanowire, the molecular dynamics calculation was from Ref. [27]. b e33 of GaN nanowire, the first principles investigation was from Ref. [28]

Full size image

The piezoelectric coefficient e33 of ZnO and GaN nanowires as function of surface piezoelectric coefficient \({e}_{33}^{s}\) is shown in Fig. 4a. The effective piezoelectric coefficient e33 varies linearly with \({e}_{33}^{s}\), as shown in Fig. 4a and Eq. (9.2). The slope of e33 line is dependent on nanowire diameter and decrease factor. Both larger diameter and larger decrease factor diminish the slope. In Fig. 4a, b, nanowire diameter was set as D = 5 nm, other parameters are same as in Fig. 3a, b. Larger \({e}_{33}^{s}\) enlarges the effective piezoelectric coefficient. When \({e}_{33}^{s}=0\), surface piezoelectricity effect absents. The piezoelectric coefficient e33 of ZnO and GaN nanowires as function of decrease factor \(\beta\) is shown in Fig. 4b. Except variable \(\beta\), other parameters were same as in Fig. 4a. In Fig. 4b, the effective piezoelectric coefficient decreases with increasing decrease factor \(\beta\). The larger decrease factor \(\beta\) means that the influence of surface piezoelectric coefficient decreases faster with distance from surface. For same surface piezoelectric coefficient \({e}_{33}^{s}\), the larger decrease factor \(\beta\) weakens surface influence on inner area of nanowires. Therefore, larger decrease factor \(\beta\) weakens the surface influence on the effective piezoelectric coefficient.

Fig. 4
figure 4

Piezoelectric coefficient e33 of ZnO and GaN nanowires. Nanowire diameter D = 5 nm. a e33 varies with surface piezoelectric coefficient \({e}_{33}^{s}\). b e33 varies with decrease factor \(\beta\)

Full size image

Traditionally, for piezoelectric materials, the residual strain induces piezoelectric effect. But the remnant body charges of effective polarization were induced by the gradient of residual strain, as shown in Eqs. (17) and (20). Without surface piezoelectricity effect, the remnant body charge density varies linearly with x coordinate (i.e., \(r\mathrm{cos}\theta\)). Surface piezoelectric coefficients induce additional charges, as shown in Eq. (23). Due to exponential decrease law, the surface piezoelectricity effect obviously influences the remnant body charge density only near surface area, the distance from surface is smaller than 0.5 nm (\(R-r\le 0.5\) nm), as shown in Fig. 5a, b. With going deep into the inner core, surface piezoelectricity effect decreases rapidly, and the influence becomes very weak. Therefore, charge density almost varies linearly with x coordinate when \(R-r\ge 0.5\) nm. In Fig. 5a, b, Poisson’s ratio of ZnO v = 0.349, bulk piezoelectric coefficients \({e}_{31}^{0}=-0.51\) Cm−2 and \({e}_{15}^{0}=-0.45\) Cm−2, surface piezoelectric coefficients \({e}_{31}^{s}=0\) Cm−2, \({e}_{15}^{s}=0\) Cm−2, Fig. 5a nanowire diameter D = 50 nm and external force fx = 80 nN, Fig. 5b nanowire diameter D = 5 nm and external force fx = 8 nN, other parameters are same as in Figs. 2 and 3.

Fig. 5
figure 5

Charge density within ZnO nanowire. a D = 50 nm, fx = 80 nN. b D = 5 nm, fx = 8 nN

Full size image

The comparison of piezoelectric potential distribution between with and without surface effects is shown in Fig. 6a, b. The representativeness was chosen at x axis (\(\theta =0\) and \(\theta =\pi\)). In Fig. 6a, b, \({k}_{\perp }=7.77\), \({k}_{0}=0.885\), Fig. 6a nanowire diameter D = 50 nm and external force fx = 80 nN, Fig. 6b nanowire diameter D = 5 nm and external force fx = 8 nN, other parameters are same as previous. In Fig. 6a, the potential value (absolute value) with surface effects is obviously smaller than the counterpart without surface effects. The positive surface piezoelectric coefficient \({e}_{33}^{s}=2.2\) Cm−2 means larger effective piezoelectric coefficient e33. The larger e33 induces larger piezoelectric potential, according to Eqs. (29.1) and (29.2). Due to the deficiency of the data of surface piezoelectric coefficients \({e}_{31}^{s}\) and \({e}_{15}^{s}\), we put \({e}_{33}^{s}\) as representative here. (The influence of \({e}_{31}^{s}\) and \({e}_{15}^{s}\) will be discussed later.) At the same time, the positive surface Young’s modulus induces the nanowire to be more difficult to be bent. The smaller bending curvature means smaller residual strain within the nanowire. Therefore, positive surface Young’s modulus induces smaller potential value (absolute value). The actual potential value is dependent on the comprehensive effect of surface elasticity and surface piezoelectricity (the competition between surface elasticity and surface piezoelectricity effects). The relative surface Young’s modulus value \({E}_{\mathrm{s}}/{E}_{0}=2.17\) has only a slim advantage compared with the relative surface piezoelectric value \({e}_{33}^{s}/{e}_{33}^{0}=1.80\). But the obvious smaller decrease factor \(\alpha =1.3\) nm−1, compared with \(\beta =9\) nm−1, means the influence of surface Young’s modulus decrease slower with going deep into inner core (compared to surface piezoelectricity). The surface Young’s modulus more obviously influences the inner core compared with surface piezoelectric coefficient. Therefore surface Young’s modulus makes larger contribution than surface piezoelectric coefficient.

Fig. 6
figure 6

Potential distribution along x direction in the cross section within nanowire. a D = 50 nm, fx = 80 nN. b D = 5 nm, fx = 8 nN

Full size image

Piezoelectric potential distribution has positive correlation with x coordinate within nanowire and negative correlation outside nanowire, as shown in Fig. 7a, b. The charge density has positive correlation with x coordinate within nanowire, hence the positive correlation of piezoelectric potential. The absence of remnant body charges outside nanowire causes negative correlation of piezoelectric potential. Generally speaking, the largest potential will appear at surface (and at x axis). Corresponding to x = -–5 and 25 nm in Fig. 7a, and x = -–2.5 nm and 2.5 nm in Fig. 7b.

Fig. 7
figure 7

Potential distribution along x direction in the cross section. a D = 50 nm, fx = 80 nN. b D = 5 nm, fx = 8nN

Full size image

The surface piezoelectricity effect was focused on \({e}_{33}^{s}\) previously. The \({e}_{33}^{s}\), \({e}_{31}^{s}\), and \({e}_{15}^{s}\) effects on maximum piezoelectric potential are shown in Fig. 8. It can be seen in Fig. 8 that the maximum piezoelectric potential varies linearly with surface piezoelectric coefficients, not only with \({e}_{33}^{s}\), but also with \({e}_{31}^{s}\) or \({e}_{15}^{s}\). The maximum piezoelectric potential (absolute value) decreases with increasing \({e}_{31}^{s}\) or \({e}_{15}^{s}\) and increases with increasing \({e}_{33}^{s}\). This linear dependence can also be found in Eq. (29.1) or Eq. (29.2). The nanowire diameter was set as D = 5 nm in Fig. 8. Surface piezoelectric coefficients were set as \({e}_{33}^{s}=2.2\), \({e}_{31}^{s}=-2.2\), and \({e}_{15}^{s}=-2.2\), except varying it.

Fig. 8
figure 8

Maximum piezoelectric potential at x = 2.5 nm (\(\theta =0\)) varies with surface piezoelectric coefficients \({e}_{31}^{s}\), \({e}_{15}^{s}\), \({e}_{33}^{s}\), respectively

Full size image

The maximum piezoelectric potential (absolute value), at x = R, as function of decrease factors \(\alpha\) and \(\beta\) is shown in Fig. 9. Surface piezoelectric coefficient \({e}_{33}^{s}\) enhances effective piezoelectricity due to its positive value. For ZnO nanowire with diameter D = 5 nm, surface piezoelectric coefficient influences piezoelectricity obviously, as shown in Fig. 3a. Smaller \(\beta\) means surface piezoelectric coefficient effect influences inner area obviously. When decrease factor \(\beta <15\), piezoelectric effect varies rapidly with \(\beta\). When \(\beta\) is relative larger, \(\beta >15\) for example, means surface piezoelectric coefficient effect decreases rapidly with distance from surface. If \(\beta\) is very large, inner area is hardly influenced by surface piezoelectric coefficient. In other words, larger decrease factor \(\beta\) weakens surface piezoelectric coefficient effect. And then, the result of exponentially decreasing model in this paper is close to core-surface model (when \(\beta\) is very large). The discussion about \(\alpha\) is similar to \(\beta\).

Fig. 9
figure 9

Maximum piezoelectric potential at x = 2.5 nm (\(\theta =0\)) varies with decrease factors \(\alpha\) and \(\beta\)

Full size image

4 Conclusions

This work researched piezoelectric nanowire mechanical and piezoelectric properties by considering exponentially decreasing surface elasticity and piezoelectricity effects. The effective Young’s modulus and effective piezoelectric coefficients of nanowires were constructed by bulk parameters and surface parameters. ZnO nanowire Young’s modulus was influenced obviously by surface elasticity effect when radius below 100 nm. The effective piezoelectric coefficient of ZnO and GaN nanowires was influenced obviously by surface piezoelectricity effect when radius below 10 nm. Surface effects induce the effective piezoelectric coefficient and piezoelectric potential to be very different from the bulk material counterparts. Surface elasticity effect stiffens ZnO nanowires, which induces piezoelectric potential to decrease. At the same time, the positive surface piezoelectric coefficient \({e}_{33}^{s}\) induces piezoelectric potential to increase. The positive surface piezoelectric coefficients \({e}_{31}^{s}\) and \({e}_{15}^{s}\) induce piezoelectric potential to decrease. The actual potential value is dependent on the comprehensive effect of surface elasticity and surface piezoelectricity. The relatively smaller surface Young’s modulus decrease factor \(\alpha\), compared with surface piezoelectric coefficient decrease factor \(\beta\), induces surface Young’s modulus to make larger contribution than surface piezoelectric coefficient. The larger decrease factor weakens surface effects obviously.