1 Introduction

The vibration resonance (VR), originally discovered by Linda and McClintock in a bistable system, is a dynamic characteristic induced by two different frequency signals which mainly reflects the phenomenon that the response amplitude of the system at the low-frequency \(\omega \) can be amplified excellently by adjusting the relatively high-frequency input signal [1]. After the seminal paper published by Linda and McClintock, the VR has attracted lots of attention and investigated in many practical systems [2,3,4,5].

Fractional differential equations have many applications in applied science and engineering since the dynamical variable of some complex media such as glasses, liquid crystals, polymers, and biopolymers often obeys fractional differential equations [6,7,8,9]. The traditional fractional-order forced damped vibration equation can be expressed as

$$\begin{aligned} \begin{aligned} mD^{2}x( t ) + \delta _{m} D^{\lambda }x( t ) + H_{m}( x ) = f(t), ~\lambda \in (0,2] \end{aligned} \end{aligned}$$
(1)

where m is the mass. \(mD^{2}x( t )\) represents the inertial force. \(\delta _m D^{\lambda }x(t)\) represents the external damping force received in the damping material, for example, it may result from friction. \(H_{m}( x )\) represents the potential field force received by the object, and f(t) represents the external excitation. The vibrator composed of viscoelastic materials will consume energy in the process of vibration so that the vibrator makes a damping vibration. The damping force generated by the vibrator itself is called internal damping force, fractional derivatives can be used to better describe the dynamic characteristics of internal damping [10,11,12], that is, \(mD^{2}x( t )\) is corrected to fractional derivative \(mD^{\alpha }x( t )\). When \(\alpha = 2, \lambda = 1\) and \(H_{m}( x )\) is Duffing oscillator, it can be expressed as a classical nonlinear physical model of hydraulic cylinder motion [13]. It is well known that VR can occur if the external forces on a mechanical structure exhibit fast harmonic excitation and slowly varying excitation. In [14], Zhang investigates the VR problem of a improved the Duffing oscillator, which is of the following form.

$$\begin{aligned} \begin{aligned}&mD^{\alpha }x( t ) + \delta _{m} D^{\lambda }x( t ) + H_{m}( x ) = f_{m}\cos ( \omega t ) \\&\quad + F_{m}\cos ( \Omega t), ~~~\alpha \in [1,2],\lambda \in (0,2] \end{aligned} \end{aligned}$$
(2)

where \(f\ll F\), \(\omega \ll \Omega , \beta >0\). Zhang’s contribution focus on the influence of the fractional orders of the system on VR [14]. In the present paper, we also consider a system of the form Eq. (2), but \(H_{m}(x)\) taken as a nonlinear function disturbed by time delay because there is a time lag between the instantaneous force applied to the object and the moment when the object actually moves [15]. It describes the transmission lag of oscillator motion.

Time delay can induce many rich dynamic behaviors, such as resonance, bifurcation, and chaos [16,17,18,19,20,21]. VR analysis of time delay Duffing system can reflect the characteristics of the actual system more accurately. Therefore, the investigation of the effecting of time delay on the VR is of great significance. To mention a few, for instance, Niu et al. investigate the forced vibration of the fractional single-degree-of-freedom gap oscillator and analyzed the influence of the fractional term and gap on the frequency response of the main resonance of the system [22]. Yan et al. investigate the vibration mechanism at arbitrary fraction-order harmonic resonance of the fractional Mathieu–Duffing system driven by multiple periodic excitations with distributed delay theoretically and numerically [23]. They verify in detail a novel transcritical bifurcation induced by the strength of the distributed delay, namely, with the variant of the fractional order of the derivative, the steady-state amplitude solutions can be converted from monostability to bistability, then to monostability, and finally to the bistability again. The primary and subharmonic simultaneous resonance of Duffing oscillator with fractional-order derivative is investigated in [24], the effect mechanism of fractional-order term on the system is revealed, and the result show that the focus and intensity of effect are determined by the order and coefficient of the fractional-order derivative, respectively. All of mentioned above only consider the case of external damping forces. Only a few investigations on double damping forces case are available in the literature [14].

To the best of our knowledge, fractional-order double damping duffing system with time delay does not been fully investigated yet. Inspired by the results in [23, 24], the bifurcation and VR of the fractional-order internal and external damping Duffing system with time delay are discussed in this note. Compared with some existing results this note has the following novelty and contribution.

  1. 1.

    When considering the fractional model with the internal damping force, the order of the fractional derivative can induce the occurrence of VR.

  2. 2.

    The critical bifurcation point of the considered system is derived by using direct separation of slow and fast motions and verified by means of numerical simulation.

  3. 3.

    The parameter conditions to the occurrence of three different types of VR are derived theoretically and verified by means of numerical simulation.

This paper is organized as follows: In Sect. 2, problem formulation and definition of the fractional derivative are presented. The bifurcation and VR theoretical analysis given in Sect. 3. The bifurcation characteristics and the conditions to the occurrence of VR, numerical simulation, and the affect of the system parameters on VR given in Sect. 4. The conclusion is given in Sect. 5.

2 Problem formulation

There are several definitions of fractional derivative, among which Riemann–Liouville (R–L) definition, Caputo definition, and Grunwald–Letnikow(G–L) definition are widely used. These definitions are explained in detail in Refs. [25]. The fractional derivative of R-L form of f(t) is defined as

$$\begin{aligned} \frac{d^{\alpha } f(t)}{dt^{\alpha }}=\frac{d^{m} f(t)}{dt^{m}}\left[ \frac{1}{\Gamma (m-\alpha )} \int _{0}^t\frac{f(\tau )}{(t-\tau )^{\alpha -m+1}}d\tau \right] \end{aligned}$$
(3)

where \(m-1<\alpha <m,m\in \mathbf{N}\), \(\Gamma (\cdot )\) is the Gamma function. Although R-L definition ensures some nice and useful mathematical properties, it receives many limitations in engineering applications. For example, the initial value is equal to zero, which has no practical significance in engineering applications. It is caused by the fact that the fractional derivative of a constant is not identically zero. To avoid these difficulties, an alternative definition is introduced by Caputo as

$$\begin{aligned} \frac{d^{\alpha } f(t)}{dt^{\alpha }}=\frac{1}{\Gamma (m-\alpha )} \int _{0}^t\frac{f^{(m)}(\tau )}{(t-\tau )^{\alpha -m+1}}d\tau \end{aligned}$$
(4)

Due to the existence of the integral and the gamma function, it is difficult to obtain the numerical solution of a fractional-order differential equation by the above derivative definitions. The G–L definition is well-known for its simplicity in the discretization of the fractional-order operators, and this definition is given by

$$\begin{aligned} D^{\alpha } f(t)|_{t=kh}=\lim \limits _{h \rightarrow 0} \frac{1}{h^{\alpha }}\displaystyle \sum ^{k}_{j=0}{\omega _{k}^{(\alpha )}f(kh-jh)} \end{aligned}$$
(5)

where \(\omega ^{(\alpha )}_{k}=(-1)\left( {\begin{array}{c}\alpha \\ k\end{array}}\right) = \frac{(-1)^{k}\Gamma (\alpha +1)}{\Gamma (k+1)\Gamma (\alpha -k+1)},\alpha >0\), h is the sampling step.

For the convenience, let \(\delta =\delta _{m}/m, H(x)=H_{m}(x)/m=\xi x(t)+\beta x^{3}(t)+\gamma x(t-\tau ), f=f_{m}/m, F=F_{m}/m\). Thus, Eq. (2) can be simplified to Eq. (6). The considered special type fractional Duffing system with time delay driven by dual-frequency periodic signals can be described as follows:

$$\begin{aligned} \begin{aligned}&D^{\alpha }x( t ) + \delta D^{\lambda }x( t ) + \xi x(t)+\beta x^{3}(t)+\gamma x(t-\tau )\\&\quad =f\cos ( \omega t ) +F\cos ( \Omega t),~~~~~\alpha \in [1,2],\lambda \in (0,2] \end{aligned} \end{aligned}$$
(6)

where the denotation of the operator\(D^{\alpha }x(t)\) and \(\delta D^{\lambda }x(t)\) are the same as in Eq. (5). \(\xi \) is the linear stiffness coefficient, \(\beta \) is the nonlinear stiffness coefficient, \(\gamma \) is the time delay feedback coefficient, \(\tau \) is time delay size, and the dual-frequency periodic signals are represented by \(f\cos ( \omega t )\) and \(F\cos ( \Omega t)\). Equation 2 reduces to classic under-damped case when \(\alpha =2,\lambda =1\) and classic over-damped case when \(\alpha =2,\lambda =0\). The potential of the system (6) satisfies the following form in the absence of \(\tau \), damping teams, and external excitation

$$\begin{aligned} V_{eff}=\frac{1}{2}(\xi +\gamma )x^{2}(t)+\frac{1}{4}\beta x^{4}(t) \end{aligned}$$
(7)

3 Theoretical analysis

The considered system is subjected to two periodic forces \(f \cos (\omega t)\) and \(F\cos (\Omega t)\) with \(\Omega \gg \omega \), so its movement will be a combination of a slow-motion X with frequency \(\omega \) and a fast-motion \(\Psi \) with frequency \(\Omega \). The approximated solution of Eq. (eq2) can be expressed as \(x(t)=X(t)+\Psi (t)\), where X shows the slow-motion with period \(2\pi /\omega \) and \(\Psi \) stands for the fast-motion with period \(2\pi /\Omega \), based on the method of direct separation of motions. Substituting \(x(t)=X(t)+\Psi (t)\) into the Eq. (6), the following equality can be obtained.

$$\begin{aligned} \begin{aligned}&D^{\alpha }(X(t)+\Psi (t))+\delta D^{\lambda }(X(t)+\Psi (t))+\xi (X(t)+\\&\quad \Psi (t))+\beta (X(t)+\Psi (t))^{3}+\gamma (X(t-\tau )+\Psi (t-\tau ))\\&\quad =f\cos (\omega t)+F\cos (\Omega t) \end{aligned} \end{aligned}$$
(8)

Now, searching for an approximate solution of \(\Psi \) in the following linear Eq. (9)

$$\begin{aligned} D^{\alpha }\Psi (t)+\delta D^{\lambda }\Psi (t)+\xi \Psi (t)+\gamma \Psi (t)=F\cos (\Omega t) \end{aligned}$$
(9)

And solving the Eq. (9), one obtains

$$\begin{aligned} \Psi (t)=\frac{F}{\mu _{\alpha ,\lambda }}\cos (\Omega t-\theta _{\alpha ,\lambda }) \end{aligned}$$
(10)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _{\alpha ,\lambda }^{2}=A^{2}_{\alpha ,\lambda }+B^{2}_{\alpha ,\lambda }, \\ \theta _{\alpha ,\lambda }=\arctan \frac{B_{\alpha ,\lambda }}{A_{\alpha ,\lambda }} \end{array}\right. } \end{aligned}$$
(11)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} A_{\alpha ,\lambda }&=\xi +\Omega ^{\alpha }\cos (\alpha \pi /2)+\delta \Omega ^{\lambda }\cos (\lambda \pi /2)\\ &{}\,+\,\gamma \cos (\Omega \tau ) \\ B_{\alpha ,\lambda }&=\gamma \sin (\Omega \tau )-\Omega ^{\alpha }\cos (\alpha \pi /2)\\ &{}\,-\,\delta \Omega ^{\lambda }\cos (\lambda \pi /2) \end{array}\right. } \end{aligned}$$
(12)

Substituting Eq. (10) into Eq. (8) and averaging all terms in the interval \([0,2\pi / \Omega ]\), one obtains the following equation of the slow variable

$$\begin{aligned} {\begin{matrix} &{}D^{\alpha }X+\delta D^{\lambda }X+C_{\alpha ,\lambda }X+\beta X^{3}+\gamma X(t-\tau )\\ &{}\quad =f\cos (\omega t) \end{matrix}} \end{aligned}$$
(13)

where \(C_{\alpha ,\lambda }=\xi +\frac{3\beta F^{2}}{2 \mu _{\alpha ,\lambda }^{2}}\). Hereto, the fast-motion disappears and only the slow-motion is retained. The potential of system (13) satisfies the following form:

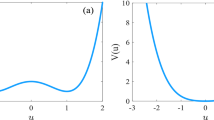
$$\begin{aligned} V_{\alpha ,\lambda }=\frac{1}{2} C_{\alpha ,\lambda } X^{2}+\frac{1}{2} \gamma X^{2} (t-\tau )+ \frac{1}{4} \beta X^{4} \end{aligned}$$
(14)

The different shapes of this potential, in the absence of time delay \(\tau \), depending on the values of the system parameters \(F,\Omega ,\alpha ,\lambda \) are given in Fig. 1. Figure 1a shows the transition of the potential function from a bistable system to a monostable system with the increases of F. Figure 1b–d show transition of the potential function from a monostable system to a bistable system with the increases of \(\Omega ,\alpha \) and \(\lambda \), respectively. The other parameters are assumed to be constant and taken as \(\xi =-1,\delta =1,\beta =1,\gamma =0.1\). The monostable state indicates that Eq. (7) has unique extreme value point.

Fig. 1
figure 1

The different shapes of the potential function in (14)

Full size image
Fig. 2
figure 2

Evolution of the bifurcation point \(F_c\) with the orders \(\lambda \) and \(\alpha \) [by Eqs. (16) and (17)]

Full size image
Fig. 3
figure 3

The pitchfork bifurcation is induced by F with different values of \(\lambda (\lambda =0.7,0.8,1.2,1.6)\), \(\alpha =1.8\) fixed [by Eqs. (15) and (24)]

Full size image

The equilibrium points of the potential function (14) are given by:

$$\begin{aligned} X^{*}_{0}=0,X^*_{1,2}=\pm \sqrt{-(C_{\alpha ,\lambda }+\gamma )/\beta } \end{aligned}$$
(15)

Now, let F be a control variable, it is fact that

$$\begin{aligned} C_{\alpha ,\lambda }+\gamma <0, ~~~~if~~F\ge F_{c}=\sqrt{\frac{-2\mu ^{2}_{\alpha ,\lambda }(\xi +\gamma )}{3\beta }} \end{aligned}$$
(16)

Equation (13) has two stable equilibrium points \(X_{1,2}^{*}\) and an unstable equilibrium point \(X_{0}^{*}\) with this case. Otherwise,

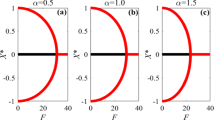
$$\begin{aligned} C_{\alpha ,\lambda }+\gamma \ge 0,~~~~if~~F< F_{c}=\sqrt{\frac{-2\mu ^{2}_{\alpha ,\lambda }(\xi +\gamma )}{3\beta }} \end{aligned}$$
(17)

in this case, Eq. (13) has unique stable equilibrium point \(X_{0}^{*}\). Therefore, \(F_c\) is a bifurcation point that makes the system transit from one stable state to another one. A subcritical pitchfork bifurcation will occur when the value of \(C_{\alpha ,\lambda }+\gamma \) transits from negative to positive, in other words, the system transits from the bistable one to the monostable one. On the contrary, the system occurs a supercritical pitchfork bifurcation. The evolution of the bifurcation point with the order of the fractional derivative shown in Fig. 2, where the area \(R_1\) stands for \(F>F_c\), and the area \(R_2\) stands for \(F<F_c\). From Fig. 2, where \(\alpha =1.1\) in Fig. 2a and \(\lambda =0.8\) in Fig. 2b, other parameters are \(f=0.1,\omega =1,\Omega =10,\xi =-1,\beta =1,\delta =1,\gamma =0.1\), it can be seen that the value of the bifurcation point \(F_c\) increases with the fractional-order \(\alpha \) or \(\lambda \) increases. The influence of the internal damping fractional-order \(\lambda \) and the external damping fractional-order \(\alpha \) on the bifurcation point is shown in Figs. 3 and 4, respectively. From here, it can be seen that the critical bifurcation point \(F_c\) gradually increases with fractional-orders \(\alpha \) and \(\lambda \) increases which are consistent with the theoretical analysis results, other parameters are \(f=0.1,\omega =1,\Omega =10,\xi =-1,\beta =1,\delta =1,\gamma =0.1\) in Figs. 3 and 4. The accuracy of the analytical result is verified by the high fitting degree between the analytical result and the numerical one. To perturb the system in its slow-motion, let \(Y=X-X^*\) with \(X^*\) is the equilibrium point of system (13), and substitute it into Eq. (13) to obtain:

$$\begin{aligned} \begin{aligned}&D^{\alpha }Y+\delta D^{\lambda }Y+3\beta X^*Y^2+\beta Y^{3}+\gamma Y(t-\tau )\\&\quad =f\cos (\omega t) \end{aligned} \end{aligned}$$
(18)

Let \(t\rightarrow \infty \), the response of the system at the low-frequency \(\omega \) can be obtained from the following linear equation

$$\begin{aligned} D^{\alpha }Y+\delta D^{\lambda }Y+\omega ^{2}_{\alpha ,\lambda }Y+\gamma Y(t-\tau )=f\cos (\omega t) \end{aligned}$$
(19)

where \(\omega ^{2}_{\alpha ,\lambda }=C_{\alpha ,\lambda }+3\beta X^{*2}\). For \(f\ll 1\), supposing that \(|Y|\ll 1\) and solving Eq. (19), one obtains \(Y=fQ\cos (\omega t+\vartheta )\) with

$$\begin{aligned} {\left\{ \begin{array}{ll} Q=\frac{1}{\sqrt{(\omega ^{2}_{\alpha ,\lambda }+\mu _{c,\alpha ,\lambda }+\gamma \cos (\omega \tau ))^2+(\gamma sin(\omega \tau )-\mu _{s,\alpha ,\lambda })^2}}\\ \vartheta =-\arctan {\frac{\gamma sin(\omega \tau )-\mu _{s,\alpha ,\lambda }}{\omega ^{2}_{\alpha ,\lambda }+\mu _{c,\alpha ,\lambda }+\gamma \cos (\omega \tau )}}\\ \end{array}\right. } \end{aligned}$$
(20)

where \(\mu _{c,\alpha ,\lambda }=\omega ^{\alpha } \cos (\alpha \pi /2)+\delta \omega ^{\lambda } \cos (\lambda \pi /2)\) and \(\mu _{s,\alpha ,\lambda }\) \(=\omega ^{\alpha } \sin (\alpha \pi /2)+\delta \omega ^{\lambda } \sin (\lambda \pi /2)\). Now, let F is a control parameter in Eq. (16), the necessary condition for vibrational resonance to occur is that d(F) is minimized, where \(d(F)=\omega ^{2}_{\alpha ,\lambda }+\mu _{c,\alpha ,\lambda }+\gamma \cos (\omega \tau )\). With this case, vibrational resonance occurs at point \(F_c\) or \(F_{VR}\), where \(F_c\) is the critical bifurcation point in where the system has a pitchfork bifurcation and \(F_{VR}\) is the real root of \(\frac{dQ}{dF}=0\), which can be expressed as

$$\begin{aligned} \begin{aligned}&F^{(1)}_{VR}=\sqrt{\frac{\mu ^{2}_{\alpha ,\lambda }}{3\beta }[-2\xi -3\gamma +\mu _{\alpha ,\lambda }+\gamma \cos (\omega \tau )]}\\&F^{(2)}_{VR}=\sqrt{-\frac{2\mu ^{2}_{\alpha ,\lambda }}{3\beta }[\xi +\gamma +\mu _{\alpha ,\lambda }+\gamma \cos (\omega \tau )]} \end{aligned} \end{aligned}$$

To analyze the characteristic of VR of the response amplitude Q. Three different cases are considered:

Case 1: \(\mu _{c,\alpha ,b}\le 2\xi +3\gamma -\gamma \cos (\omega \tau )\), with this case, there is unique stable equilibrium point in (6), VR occurs at point \(F=F_{VR}^{(2)}\) and it is a single-peak VR with the maximum value of Q is \(Q_{max}=\frac{1}{|\gamma \sin (\omega \tau )-\mu _{s,\alpha ,\lambda }|}\).

Case 2: \(2\xi +3\gamma -\gamma \cos (\omega \tau )<\mu _{c,\alpha ,\lambda }<\gamma -\gamma \cos (\omega \tau )\), with this case, there are two stable equilibrium points in (6), VR occurs at points \(F=F_{VR}^{(1)}\) and \(F=F_{VR}^{(2)}\) and it is a double-peak VR with the maximum value of Q is the same as case 1.

Case 3: \(\mu _{c,\alpha ,\lambda }\ge \gamma -\gamma \cos (\omega \tau )\), there is also a unique stable equilibrium point in (6), however, VR occurs at point \(F=F_c\) and it is a single-peak VR with the maximum value of Q is \(Q_{max}=\frac{1}{\sqrt{(-\tau +\mu _{c,\alpha ,\lambda }+\gamma \cos (\omega \tau ))^2+(\gamma sin(\omega \tau )-\mu _{s,\alpha ,\lambda })^2}}\).

It is worth noting that neither \(F=F_{VR}^{(1)}\) nor \(F=F_{VR}^{(2)}\) exists with this case.

4 Numerical simulation and Result analysis

For the sake of numerical simulation, Eq. (6) needs to be discretized, so (6) is first transformed into the equivalent form as follows

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} &{}D^{\lambda }x=y\\ &{}D^{\alpha }x=D^qy \\ &{}D^{q}y=-\delta y-\xi x(t)\\ &{}-\beta x^3(t)-\gamma x(t-\tau )+fcos(\omega t)+Fcos(\Omega t) \\ \end{array}\right. } \end{aligned} \end{aligned}$$
(21)

where \(q=|\alpha -\lambda |\). Next, to discrete (21) base on G-L fractional derivative algorithm, the following discretized formulations obtained

$$\begin{aligned} \begin{aligned} x_{k+1}=&-\sum \limits _{j=1}^{k}\omega _{j}^{\alpha _1}x_{k+1-j}+h^{\lambda }y_k \\ y_{k+1}=&-\sum \limits _{j=1}^{k}\omega _{j}^{\alpha _2}y_{k+1-j}+h^{q}\vartriangle \end{aligned} \end{aligned}$$
(22)

where \(\vartriangle =-\delta y_k-\xi x_{k}-\beta x_{k}^{3}-\gamma x_{k-N}+f\cos (\omega kh)+F\cos (\Omega k h)\), h is the same as one in (5), and \(N=\tau /h\) denotes the interval points caused by time delay. By utilizing the time response series, the formula of the equilibrium point is defined as

$$\begin{aligned} X^*=\frac{1}{nT}\int _0^{nT} x(t)dt \end{aligned}$$
(23)

the discretized form of the above formula is

$$\begin{aligned} X^*=\frac{1}{nT}\sum _{i=1}^{nT/h}x(t_{i})h \end{aligned}$$
(24)

The numerical expression of Q is necessary, which can be obtained directly from (22) as follows:

$$\begin{aligned} Q=\frac{\sqrt{Q^{2}_{A}+Q^{2}_{B}}}{f} \end{aligned}$$
(25)

with

$$\begin{aligned} \begin{aligned}&Q_A=\frac{2}{nT}\int _0^{nT} x(t)\sin (\omega t)dt, \\&Q_B=\frac{2}{nT}\int _0^{nT} x(t)\cos (\omega t)dt. \end{aligned} \end{aligned}$$
(26)

where n is a positive integer which should be chosen big enough. \(Q_A\) and \(Q_B\) are discreted as follows

$$\begin{aligned} \begin{aligned}&Q_A=\frac{2}{nT}\sum _{i=1}^{nT/h}x(t_{i})\sin (\omega t_{i}), \\&Q_B=\frac{2}{nT}\sum _{i=1}^{nT/h}x(t_{i})\cos (\omega t_{i}). \end{aligned} \end{aligned}$$
(27)

where \(T=2\pi /\omega \), \(n=200\) and \(x(t_{i})\) is given by (22).

Letting \(W=\mu _{\alpha ,\lambda },W_1=2\xi +3\gamma -\gamma \cos (\omega \tau )\) and \(W_2=\gamma -\gamma \cos (\omega \tau )\) where \(\mu _{\alpha ,\lambda },\gamma ,\xi ,\tau \) are the same as Sect. 3. Under each case discussed above, the areas where VR occurs and the types of VR are shown in Figs. 5, 6, 7, 8, 9, 10 and 11, in where F served as a control parameter.

Fig. 4
figure 4

The pitchfork bifurcation is induced by F with different values of \(\alpha (\alpha =1.1,1.4,1.6,1.8)\), \(\lambda =1.2\) fixed [by Eqs. (15) and (24)]

Full size image
Fig. 5
figure 5

The influence of parameter \(\lambda \) on VR types. a \(\lambda \) versus double-peak VR area, b–d the double-peak VR cases [by Eqs. (20) and (25)]

Full size image
Fig. 6
figure 6

The influence of parameter \(\alpha \) on VR types. a \(\alpha \) versus double-peak VR area. b the single-peak VR case, c, d the double-peak VR cases [by Eqs. (20) and (25)]

Full size image
Fig. 7
figure 7

The influence of parameter \(\lambda \) on VR types. a \(\lambda \) versus the double-peak VR area, b, c the double-peak VR case, d the single-peak VR case [by Eqs. (20) and (25)]

Full size image
Fig. 8
figure 8

The influence of parameter \(\alpha \) on VR types. a \(\alpha \) versus VR area, b, c the double-peak VR cases, d the single-peak VR case [by Eqs. (20) and (25)]

Full size image
Fig. 9
figure 9

The double-peak VR occurs are induced by the different \(\tau \) [by Eq. (20)]

Full size image
Fig. 10
figure 10

The influence of parameter \(\tau \) on VR types. a \(\tau \) versus VR area, b, d the single-peak VR cases. c The double-peak VR case [by Eq. (20)]

Full size image
Fig. 11
figure 11

Single-peak VR area and type. a \(\tau \) versus VR area, b single-peak VR occurs at point \(F_{VR}^{(2)}\) [by Eq. (20)]

Full size image
Fig. 12
figure 12

Periodic VR caused by \(\tau \) when \(\lambda \) and \(\alpha \) take different constants [by Eq. (20)]

Full size image
Fig. 13
figure 13

Periodic VR caused by \(\tau \) when F takes different values, a \(F=10\), b \(F=100\) [by Eq. (20)]

Full size image
Fig. 14
figure 14

\(\lambda \) versus Q with different \(F(F=10,50,100)\) [by Eqs. (20) and (25)]

Full size image
Fig. 15
figure 15

\(\alpha \) versus Q with different \(F(F=10,50,100)\) [(by Eqs. (20) and (25)

Full size image
Fig. 16
figure 16

\(\beta \) versus Q [by Eq. (20)]

Full size image

4.1 VR induced by the parameters \(\alpha \) and \(\lambda \)

Figure 5a shows the area where double-peak VR occurs in case 2. Figure 5b through Fig. 5d show the Q–F curve of double-peak VR at points \(F_{VR}^{(1)}\), \(F_{VR}^{(2)}\). It can be seen that the number of VR peaks of the system remains unchanged as the internal damping order \(\lambda \) increases, but the first VR peak of the system becomes more and more gentle. In Fig. 5, other parameters are \(f=0.1,\xi =-1,\beta =1,\gamma =0.1,\omega =1,\Omega =10,\delta =0.65,\tau =\pi /2,\alpha =1.5\). It is proved that if the control parameter \(\lambda \) satisfies \(W_1<W<W_2\)(see Fig. 5a), the double-peak VR will occur. From Fig. 5, it can be seen that the type of VR is consistent with that of case 2.

Figure 6 shows the change of VR type with the internal damping order \(\alpha \). For \(\alpha \in [1,\alpha _{c})\), a single-peak VR occurs at point \(F=F_c\) which shown in Fig. 6b (\(\alpha =1.1\)), just as discussed in case 3. For \(\alpha =[\alpha _c,2]\), the double-peak VR occurs at two points of F, namely, \(F_{VR}^{(1)}\), \(F_{VR}^{(2)}\) which shown in Figs. 6c (\(\lambda =1.6\)) and 6d (\(\lambda =1.8\)), as discussed in case 2. It can be seen from Fig. 6 that the type of resonance peak of the system changes from single-peak to double-peak with the increase of the internal damping order \(\alpha \). In Fig. 6 other parameters are \(f=0.1,\xi =-1,\beta =1,\gamma =0.1,\omega =1,\Omega =10,\delta =0.65,\tau =\pi /2,\lambda =0.4\). The analytical results are consistent with the numerical ones, which shows that the VR type of system (6) changes with the change of the parameter \(\alpha \). Apparently, Fig. 6b is consistent with that of case 3, and Fig. 6c, d are consistent with that of case 2, that is, with the increase of \(\alpha \), the VR type transitions from one of case 3 to that of case 2.

Figure 7 shows the change of VR types with the internal damping order \(\lambda \). For \(\lambda \in (0,\lambda _c)\), namely, \(W_1<W<W_2\), the double-peak VR occurs at points \(F=F_{VR}^{(1)}\) and \(F=F_{VR}^{(2)}\) as shown in Fig. 7 b (\(\lambda =0.7\)) and Fig. 7c (\(\lambda =1.0\)), respectively, which is consistent with that discussed in case 2. For \(\lambda \in (\lambda _c,2]\), a single-peak VR occurs at point \(F_{VR}^{(2)}\) as shown in Fig. 7d (\(\lambda =1.8\)), which is consistent with that discussed in case 1. Other parameters are \(f=0.1,\xi =-1,\beta =1,\gamma =0.1,\omega =1,\Omega =8,\delta =1,\tau =\pi /2,\alpha =1.8\). The analytical results is consistent with the numerical ones, which shows that the VR type of system (6) changes with the change of the parameter \(\lambda \). The VR type transitions from one of case 2 to that of case 1.

Figure 8 shows that the influence of parameter \(\alpha \) on VR types by means of analytical results and numerical ones respectively, (b) and (c) shows the double-peak VR occurs at points \(F=F_{VR}^{(1)}\) and \(F=F_{VR}^{(2)}\) with \(\alpha =1.2\) and \(\alpha =1.3\), respectively. (d) show the single-peak VR occurs at point \(F_{VR}^{(2)}\) with \(\alpha =1.9\). Other parameters are \(f=0.1,\xi =-1,\beta =1,\gamma =0.1,\omega =1,\Omega =10,\delta =0.5,\tau =\pi /2,\lambda =1.2\). The analytical results are consistent with the numerical ones, which shows that the VR type of system (2) changes with the change of the parameter \(\alpha \). Figure 8b is consistent with that of case 2, and Fig. 8c, d are consistent with that of case 1, that is, with the increase of \(\alpha \), the VR type transitions from one of case 2 to that of case 1.

4.2 The VR induced by the parameter \(\tau \)

For the parameters \(\alpha \) and \(\lambda \) fixed, the time delay \(\tau \) can induce different VR types as well. By Eq. (20), the double-peak VR types induced by \(\tau \) shown in Fig. 9. With \(W_1<W<W_2\) satisfied, \(\tau \in (0,2\pi /\omega ), f=0.1,\xi =-1,\beta =1,\gamma =0.1,\omega =1,\Omega =10,\delta =1.2,\alpha =1.2,\lambda =1.4\). Figure 9b–d shows that the double-peak VR occurs at points \(F=F_{VR}^{(1)}\) and \(F=F_{VR}^{(2)}\) with \(\tau =\frac{\pi }{2\omega },\tau =\frac{\pi }{\omega },\tau =\frac{2\pi }{\omega }\), respectively, where \(F_c\) is the minimum point of F. But when \(W>W_1\), there are types of VR since there exist two points of intersection between curves W and \(W_2\), as shown in Fig. 10a. For \(W>W_2>W_1\), there is unique single-peak VR at point \(F_c\), as shown in Fig. 10b, d. For \(W_1<W<W_2\), there are double-peak VR occur at points \(F=F_{VR}^{(1)}\) and \(F=F_{VR}^{(2)}\), as shown in Fig. 10c, which is the same as Fig. 9. For \(W_1>W\), there is another type of single-peak VR at point \(F_c\), as shown in Fig. 10b, d. Other parameters are \(f=0.1,\xi =-1,\beta =1,\gamma =0.35,\omega =1,\Omega =10,\delta =0.65,\alpha =1.3,\lambda =0.4\) in Fig. 10. In this case, VR occurs at point \(F=F_{VR}^{(2)}\), as shown in Fig. 11. Other parameters are \(f=0.1,\xi -1,\beta =1,\gamma =0.1,\omega =1,\Omega =10,\delta =1.5,\alpha =1.8,\lambda =1.5\) in Fig. 11.

Figure 12 shows the change of response amplitude Q with time delay \(\tau \) when \(\lambda \) and \(\alpha \) take different constant. It can be seen that the response amplitude Q is a periodic function in \(\tau \). The period of Q is a constant (\(Q=\frac{2\pi }{\omega }\)) regardless of the values of order \(\alpha \) and \(\lambda \). The other parameters are \(f=0.1,\xi =-1,\beta =1,\gamma =0.1,\omega =1,\Omega =10,\delta =1.2,F=100,\tau \in [0,40]\) in Fig. 12. For different constant F, the changing curve of the response amplitude Q with \(\tau \) is given in Fig. 13. It shows the amplitude Q also is a periodic function in \(\tau \), amd the period is equal to \(\frac{2\pi }{\omega }\) as well. The other parameters are \(f=0.1,\xi =-1,\beta =1,\gamma =0.1,\omega =1,\Omega =10,\delta =1.2,\alpha =1.2,\lambda =0.8\) in Fig. 13.

4.3 The effect of F on VR

Figures 14 and 15 show the effect of external damping order \(\lambda \) and internal damping order \(\alpha \) on the response amplitude Q, respectively. For \(\alpha \) fixed and \(\lambda \) viewed as a variable, the curve of the amplitude Q changes with \(\lambda \) shown in Fig. 14(\(\alpha =1.8\)) when F takes a different value. It can be seen that the VR occurs when \(F=100\). For \(\lambda \) fixed and \(\alpha \) viewed as a variable, the curve of the amplitude Q changes with \(\alpha \) shown in Fig. 15 (\(\lambda =0.8\)), where the VR occurs when \(F=50\). As a result, the high-frequency amplitude F is an important parameter to be considered when the VR is discussed. The other parameters are \(f=0.1,\xi =-1,\beta =1,\gamma =0.1,\omega =1,\Omega =10,\delta =1,\tau =\pi /2\). The analytical results is consistent with the numerical ones, which proves the correctness of the proposed results.

4.4 The effect of \(\beta \) on VR

Figure 16 shows the quantitative relationship between the parameter \(\beta \) and response amplitude Q. It can be seen from (6) that when \(\beta =0\), the denominator of \(F_c\) is 0 which indicates \(F_c\) is meaningless, through whole paper, (6) reduce to a linear equation. But when \(\beta \) take a very small number, the system will occur the single-peak VR. It can be seen from Fig. 16 that the analytic results fit well with numerical ones which verifies the effectiveness of the obtained results.

5 Conclusion

In this paper, the effect of the system parameters of a new fractional double damping Duffing oscillator, including internal and external fractional damping order \(\alpha \) and \(\lambda \), high-frequency response amplitude F, delay size \(\tau \) and \(\beta \) on VR are discussed, and some meaningful results are obtained: (1) The bifurcation characteristics of the system are analyzed theoretically. The results show that when F is the control variable, the critical bifurcation point of the system is affected by the size of \(\alpha \) or \(\lambda \), and it’s going to get bigger as increasing the number of \(\alpha \) or \(\lambda \). (2) Three types of VR are obtained by means of the analytic formula of response amplitude Q, from this the single-peak VR or double-peak VR is discussed by taking different system parameters. (3) The response amplitude Q appear periodic behavior as Q is viewed as a function of \(\tau \). (4) If \(\beta \) is used as a control variable, when \(\beta \) takes a very small number, the response amplitude Q reaches the peak. The results are verified by numerical simulation, which enable us to understand better the effects of the sizes of system parameters on VR of the fractional double damping Duffing oscillator.