1 Introduction

Smart materials complement regular construction materials and provide extraordinary capabilities, therefore, opening new perspectives for engineering applications [1]. Amongst various types of smart materials, shape memory alloys (SMA) are especially worth mentioning since they exhibit two shape memory effects, i.e., one-way, and two-way memory effects. SAM also exhibit high damping capability [2], and the ability to withstand large elastic deformations at the strain up to 8% [3,4,5,6,7]. The later property is also known as superelasticity or pseudoelasticity.

The two above-listed specific properties of SMA are allowed due to the involved thermomechanical effects. These effects may be observed when an SMA sample is subjected to a mechanical or thermal load. In that case the respective reversible solid phase transformation, also known as martensitic transformation, occurs. The resultant macroscale behavior of SMA reflects the two-way phase transformation and can be externally controlled. The capabilities of memorizing geometric shapes and the superelasticity effect are illustrated in Figs. 1, 2 and 3.

Fig. 1
figure 1

One-way memory effect in SMA—visualization of the mechanically and thermally induced phase transformation in the stress–temperature coordinate system. The numbers mark subsequent steps for mechanical and thermal loads and relaxations

Full size image
Fig. 2
figure 2

Effect of superelasticity in SMA—visualization of the mechanically induced phase transformation in the stress–temperature coordinate system. The numbers mark subsequent steps for mechanical loads and relaxation

Full size image
Fig. 3
figure 3

Effect of superelasticity in SMA—visualization of the hysteretic stress–strain relation

Full size image

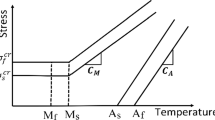
One-way memory effect stands for a reversible phase change within the following subsequent steps carried out for initially relaxed SMA sample, i.e., made of undeformed martensite (Fig. 1 for reference): (1) mechanical load leading to deformed mertensite, (2) mechanical relaxation resulting with a remembered macroscopic shape of the specimen, (3) thermal load (heating) leading to austenite that recovers the initial shape of the SMA sample, (4) final cooling—the recovered shape is maintained. Similarly, the reversible superelasticity effect is visualized in Fig. 2 where the two phase changes are marked: (1) from austenite to the deformed martensite for the increasing mechnical load and, respectively, (2) transformation from the deformed martensite to austenite performed during mechanical relaxation. As shown in Fig. 2 the martensitic transformation occurs if the ambient temperature is greater than \(A_{f}\) which is one of the four characteristic temperatures (material properties) of an SMA sample, i.e., \(A_{s}\), \(A_{f}\), \(M_{s}\), \(M_{f}\). These quantities specify the temperature limiting cases, i.e., marking initiation \(A(M)_{s}\) and finish \(A(M)_{f}\), for martensite to austente and austenite to martensite transformations respectively. It should be noted that kinetics of the above described phenomenon is governed by the change of ambient temperature which influences the stress level required to be achieved for phase transformation. This relationship is illustrated in Fig. 2 using the four skewed lines. Complementarily, Fig. 3 provides with an example of the hysteretic stress–strain curve which may be considered representative for an SMA sample.

The observable macroscopic behavior of SMA components results from the specific nature of microscale solid phase transformations conducted in their crystalline structure. Hence, modeling of the SMA properties is a challenging issue. In fact, kinetics of the thermally and mechanically activated changes between martensite and austenite phases is governed by both the internal and external factors. The former are e.g., variation of spatial orientations of the grains, complexity of contact effects between the grains, variations regarding alloy composition as well as the level of its purity. The later factors primarily cover the types and localizations of the applied loads. All these factors lead to high spontaneity of the phenomena observed in SMA. Effectively, even if the demanded dominant effects are clearly visible, which are the memory effects and superelasticity, the involved physical processes exhibit inherent randomness. This specificity results in the variation of the courses of phase transformations. In other words, the respective paths (trajectories) which describe the deformations of an SMA sample in a stress–strain–temperature coordinate system, as presented in Fig. 3, are subjected to irreducible variation.

There are known the following types of SMA models [8]: microscopic thermodynamics, micromechanics-based macroscopic models and macroscopic phenomenological models, including the approaches based on the free energy concept. Unfortunately, there is not yet proposed a modeling method which would holistically address the specificity of SMA in a computationally effective way [4, 5, 9, 10]. In fact, microscopic models are considered to be the most accurate due to an explicit handling the physics of phase transformations. These models allow to describe nucleation process in the crystalline structure as well as to track the course of phase change front observed within the SMA body undergoing mechanical or thermal activation. However, the microscopic approaches require significant amount of computational resources to be used for the engineering applications. The micromechanics-based macroscopic models make use of the representative volume element (RVE) approach [11]. The results obtained at macroscale are determined with the averaged properties found based on the calculations carried out for a single grain. The main advantage of the mentioned methods is their relatively high accuracy at acceptable level of the computational effort, also in case of macroscale-sized SMA components. However, identification of a high number of the so-called internal variables is required to build a constitutive model. Finally, the macroscopic phenomenological models may be used to effectively handle the global properties of SMA components, i.e., at macroscale [12, 13]. The simplified approach to thermodynamics and phenomenological modeling allow for a convenient introduction of the experimental data to elaborate the SMA constitutive relation. Lack of a direct link between the model properties and the characteristics of the microstructural behavior of SMA, however, states for a drawback of the referenced approach. Although macroscopic phenomenological models do not address the nano- and microscale phenomena in SMA accurately, there are known successful applications of this modeling approach to engineering problems. The authors of the study [2] investigate a non-linear dynamical response of an SMA-based oscillator. The developed thermomechanical model is capable of catching hysteretic stress–strain relation and correctly determine the restoring force required to model the proposed device functionality, making use of internal variables and the previously reported dissipation function [14]. In [15], an antagonistically operating SMA-based position control aeroelastic system is presented. The computational analysis was performed using a phenomenological model inspired by Tanaka [16], taking into account the phenomenon of heat convection for phase transformations in SMA. The work [17] reports the results of investigation conducted for a sliding mode control system elaborated for vibration control and angular positioning of a flexible link attached to the DC motor shaft. For the discussed technical solution which is equipped with SMA components, an analytical model was proposed following the phenomenological approach previously reported in [18]. A mesoscale finite element (FE) model based on Voronoi tessellation and microplane theory was investigated for porous SMA in [19].

The authors of the present work employ the free energy based macroscopic phenomenological approach to propose a peridynamic SMA model to capture the effect of superelasticity taking into account thermomechanical coupling. In reference to the authors’ previous work, the current study experiences an extended capability of the model allowing for non-isothermal phase transformations as well [5]. The present research should be also considered an extension of the recent paper reported at the DSTA2019 conference [12].

The authors’ motivation for the application of peridynamics to the SMA model has originated from various unique capabilities of the mentioned modeling method [20]. Peridynamics was primarily proposed for continuum mechanics [21]. Hence, it can be conveniently used to build a model for a given type of materials, including smart materials, operating using macroscopic parameters. This feature is especially important when developing macroscopic phenomenological models for SMA which is within the scope of the current study. Moreover, an integral based formulation of the governing equation allows to handle various types of model nonlinearities when solving problems numerically, including material nonlinearities, e.g., hysteretic stress–strain relations. Finally, a peridynamic model, due to its nonlocal formulation, may inherently offer efficient multiscale approach which is crucial when reflecting nano- and microscale phenomena in the modeled macroscale behavior. It is highly important that, due to the extraordinary properties of peridynamics, the results obtained for peridynamic models may converge to the outcomes of either local or other nonlocal computation approaches, e.g., classically formulated FE method or molecular dynamics, respectively, depending on the requirements of the stated problem. Amongst others, in the following fields of static and dynamic studies peridynamics confirmed its versatility [20]: material failure (damage, fracture, spontaneous crack growth and fatigue) [22, 23], constitutive models (elasticity, plasticity, viscoelasticity, viscoplasticity) [24], multiscale problems, multidomain (multiphysics) problems, including heat transfer, thermal diffusion [25], thermoelasticity [26], complex flow problems, impact problems, wave dispersion and numerical techniques, taking into account various types of materials (not necessarily metallic ones), e.g., composites [23] and polymers [27]. As experienced thus far by the authors of the present research, the field of peridynamic modeling for SMA-type materials is still not yet addressed.

As a demanded scope of the future application for the proposed peridynamic SMA model, the authors of the present work consider its use in the study of operational conditions for a gas foil bearing (GFB), primarily for reduction of mechanical vibrations [28,29,30,31]. GFB are a type of the journal bearings. In contrast to the standard journal bearings, however, GFB are lubricated using an air film of the thickness equal to tens of micrometers. By their nature GFB experience multidomain interactions between structural components, also involving fluid-structure interactions present between fluidic and structural components of the supporting layer in a bearing. The motivation of the work has originated from the perspective of more accurate, i.e., more physical, modeling of the structural components which employ SMA to stabilize the bearing operation. Both multiphysics (via thermomechanical coupling) and nonlocality (using integral based governing equation) are advantageously taken into account for future elaboration of a comprehensive model a GFB [21, 32, 33].

The paper is organized as follows. In present Sect. 1 the overall motivation of the work as well as fundamentals regarding SMA are addressed. Next, Sect. 2 introduces the mathematical formalism for the total specific Gibbs free energy required for elaboration of the SMA phenomenological model. Section 3 introduces the multiphysics model of SMA based on the theories of peridynamics and thermoelasticity, making the reference to the authors’ previous work. The property of the developed numerical model is discussed in Sect. 4, specifically making use of stability analysis. Section 5 reports exemplary numerical results for the developed peridynamic SMA model to visualize its fundamental computational capability, in terms of hysteretic stress–strain relation determination and adequate parametric study. Summary of the paper as well as concluding remarks are drowned in final Sect. 6.

2 Phenomenological model of SMA

The elaborated peridynamic SMA model takes into account the following theories:

  • Total specific Gibbs free energy—allows for introduction a phenomenological model of SMA which considers nonlinear (hysteretic) stress–strain relation required to model phase transformations. Advantageously, it operates based on the martensite phase contribution factor which is a macroscale model parameter;

  • Peridynamics—introduces nonlocality into the governing equation to handle the geometric and material nonlinearities more conveniently and accurately in a numerical model, especially for dynamics;

  • Thermoelasticity—enables thermomechanical coupling in an SMA material.

The total specific Gibbs free energy G for SMA is defined as follows [34]

$$\begin{aligned} \begin{aligned} G(\overline{\overline{\varvec{\sigma }}},T,\xi ,\overline{\overline{\varvec{\epsilon }^{t}}})&= -\frac{1}{2\rho }{\varvec{C}}_{\varvec{ijkl}} \varvec{\sigma }_{\varvec{ij}}\varvec{\sigma }_{\varvec{kl}}+\\&\quad -\, \frac{1}{\rho }{\varvec{\sigma }}_{\varvec{ij}} [\varvec{\alpha }_{\varvec{ij}}(T-T_{0})+\overline{\overline{\varvec{\epsilon }^{\varvec{t}}}}]+\\&\quad +\, c[T-T_{0}-T\text {ln}(T/T_{0})]+\\&\quad -\, s_{0}T+u_{0}+\frac{1}{\rho }f(\xi ) \end{aligned} \end{aligned}$$
(1)

where \(\overline{\overline{\varvec{\sigma }}}\)—second order Cauchy stress tensor, for \({\varvec{\sigma }}_{\varvec{ij}}\), \(\varvec{\sigma }_{\varvec{kl}}\) the Einstein summation notation is used, T—temperature, \(T_{0}\)—reference (ambient) temperature, \(\xi\)—martensite phase contribution factor, it can vary within the interval [0, 1], \(\overline{\overline{\varvec{\epsilon }^{\varvec{t}}}}\)—second-order transformation strain tensor, \(\rho\)—mass density, \(\varvec{C}_{\varvec{ijkl}}\)—fourth-order elastic compliance tensor, \(\varvec{\alpha }_{\varvec{ij}}\)—second-order thermal expansion coefficient tensor, c—specific heat, \(s_{0}\)—specific entropy at the reference state, \(u_{0}\)—specific internal energy at the reference state, \(f(\xi )\)—the transformation hardening function, it defines elastic strain energy for the interactions between various variants of the martensite phase, \(f(\xi )\) also considers the interactions with other surrounding phases.

For one-dimensional (1-D) case, Eq. (1) becomes

$$\begin{aligned} \begin{aligned} G(\sigma ,T,\xi ,\epsilon ^{t})&= -\frac{1}{2\rho }C\sigma ^{2}-\frac{1}{\rho }\sigma [\alpha (T-T_{0})+\epsilon ^{t}]+\\&\quad +\, c[T-T_{0}-T\text {ln}(T/T_{0})]-s_{0}T+u_{0}+\frac{1}{\rho }f(\xi ) \end{aligned} \end{aligned}$$
(2)

The SMA material properties declared in Eq. (2), except from the mass density \(\rho\), thermal expansion coefficient \(\alpha\) and specific heat c, are defined using linear combinations of the quantities attached to both phases with the weighting factor \(\xi\):

$$\begin{aligned} C &= C^{A}+\xi (C^{M}-C^{A})=C^{A}+\xi \varDelta C=\frac{1}{E^{A}}\nonumber+ \\&\quad +\, \xi \left( \frac{1}{E^{M}}-\frac{1}{E^{A}}\right) \end{aligned}$$
(3)
$$\begin{aligned} s_{0} &= s_{0}^{A}+\xi (s_{0}^{M}-s_{0}^{A})=s_{0}^{A}+\xi \varDelta s_{0} \end{aligned}$$
(4)
$$\begin{aligned} u_{0} &= u_{0}^{A}+\xi (u_{0}^{M}-u_{0}^{A})=u_{0}^{A}+\xi \varDelta u_{0} \end{aligned}$$
(5)

where \(\bullet ^{A}\) and \(\bullet ^{M}\) are the austenite and martensite properties respectively. \(E^{A}\) and \(E^{M}\) are the Young’s moduli.

The total strain \(\epsilon\) can be found as the sum of elastic linear material response \(\epsilon ^{E}=C\sigma\), the nonlinear (hysteretic) contribution \(\epsilon ^{t}\) and the thermal strain \(\epsilon ^{T}=\alpha (T-T_{0})\)

$$\begin{aligned} \epsilon =C\sigma +\epsilon ^{t}+\alpha (T-T_{0}) \end{aligned}$$
(6)

The contributing strains \(\epsilon ^{E}\) and \(\epsilon ^{t}\) appear due to mechanical load, whereas \(\epsilon ^{T}\) represents thermal expansion (Note, the coefficient \(\alpha\) declares the regular linear material expansion resulting from the temperature variation without reference to the phase change). The rate of the transformation strain \({{\dot{\epsilon }}}^{t}\) can be determined as a function of the parameter \(\varLambda\) and the rate of martensite contribution factor \({{\dot{\xi }}}\)

$$\begin{aligned} {{\dot{\epsilon }}}^{t}= \varLambda {{\dot{\xi }}} \text {, for } {{\dot{\xi }}} \ne 0 \end{aligned}$$
(7)

The parameter \(\varLambda\) is defined based on the maximum uniaxial transformation strain H

$$\begin{aligned} \varLambda =\sqrt{\frac{3}{2}}H \end{aligned}$$
(8)

Next, the Clausius–Planck inequality is introduced to assure non-decreasing entropy of the SMA model irrespectively form the sign of the rate of external mechanical load

$$\begin{aligned} \sigma {{\dot{\epsilon }}}^{t} - \rho \frac{\partial G}{\partial \xi } \dot{\xi }\ge 0 \end{aligned}$$
(9)

The derivative \(\frac{\partial G}{\partial \xi }\) can be determined using Eq. (2), (3), (4), (5) and (7)

$$\begin{aligned} \begin{aligned} \frac{\partial G}{\partial \xi }&= -\frac{1}{2\rho }\varDelta C\sigma ^{2}-\frac{1}{\rho }\varLambda \sigma -T\varDelta s_{0}+ \\&\quad +\, \varDelta u_{0}+\frac{1}{\rho }\frac{\partial f(\xi )}{\partial \xi } \end{aligned} \end{aligned}$$
(10)

Having introduced Eq. (10) and (8) into Eq. (9) one can obtain the following conditionally formulated formula

$$\begin{aligned} \varPi (\sigma , T, \xi , {{\dot{\xi }}}) {{\dot{\xi }}} \ge 0 \end{aligned}$$
(11)

with

$$\begin{aligned} \begin{aligned} \varPi&= \frac{1}{2} \varDelta C \sigma ^2 + \rho \varDelta s_{0} T + {\left\{ \begin{array}{ll} \varPi _{1},&{}\quad {{\dot{\xi }}} > 0\\ \varPi _{2},&{}\quad {{\dot{\xi }}} < 0 \end{array}\right. } \end{aligned} \end{aligned}$$
(12)
$$\begin{aligned} \begin{aligned} \varPi _{1}&=\sqrt{6} H \sigma + \rho \varDelta s_{0}(M_{s}-M_f)\xi +\\&\quad -\frac{1}{4}\rho \varDelta s_0 (3M_s+A_f+A_s-M_f) \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned} \begin{aligned} \varPi _{2}&=\sqrt{6} H \sigma + \rho \varDelta s_{0}(A_f-A_s)\xi +\\&\quad -\frac{1}{4}\rho \varDelta s_0 (M_s+3A_f-A_s+M_f) \end{aligned} \end{aligned}$$
(14)

Finally, phase transformations in an SMA sample are governed by the conditionally defined transformation function \(\varPhi\)

$$\begin{aligned} \varPhi = {\left\{ \begin{array}{ll} \varPi -Y,&{}\quad {{\dot{\xi }}} > 0\\ -\varPi -Y,&{}\quad {{\dot{\xi }}} < 0 \end{array}\right. } \end{aligned}$$
(15)

with

$$\begin{aligned} Y=\frac{1}{4}\rho \varDelta s_0 (M_s+M_f-A_f-A_s) \end{aligned}$$
(16)

When the external mechanical load grows, i.e., the stress \(\sigma\) increases, and the condition \(\varPhi ({{\dot{\xi }}}>0)>0\) is satisfied, the fraction \(\xi\) grows what expresses growing contribution of the martensite phase. Contrarily, an increase of austenite, i.e., reduction of \(\xi\), is observed if \(\varPhi ({{\dot{\xi }}} <0)>0\) and the stress \(\sigma\) gradually decreases.

In the following the SMA model based on the total specific Gibbs free energy is briefly presented making use of the theory of peridynamics and thermoelasticity.

3 Peridynamic model of SMA

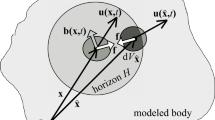
As already mentioned in Sect. 1, peridynamics constitutes an integral based description of statics and dynamics problems in physics. As shown in Fig. 4, a peridynamic model considers nonlocal interactions between the so-called particles within the space defined as the horizon H [21]. Hence, all the parts of the particles that are covered by the horizon are taken into account to determine the resultant reaction force acting on an actual central particle.

Fig. 4
figure 4

Peridynamic modeling of a continuum domain for a deformable body. Horizon defines the spatial range for nonlocal interactions between particles

Full size image

The advantageous properties of peridynamics originate from its nonlocal integral based formulation of the governing equation [21]

$$\begin{aligned} \begin{aligned} \rho {\ddot{u}} (x,t) =\int _H f(u({\hat{x}},t)-u(x,t),{\hat{x}}-x)dV_x +b(x,t) \end{aligned} \end{aligned}$$
(17)

Equation (17) can be then used to derive the numerical description of a 1-D model of an homogeneous and isotropic material [5]

$$\begin{aligned} \begin{aligned} m_i {\ddot{u}}_{i}^{t} = 2 \sum _{ \begin{array}{c} j=-N \\ j\ne 0 \end{array}}^{N} \left( \beta _{i,j}\gamma _i k\frac{u_{i+j}^t-u_i^t}{|j| N^2} \right) +F_i^t \end{aligned} \end{aligned}$$
(18)

with the stiffness coefficient

$$\begin{aligned} k=\frac{EA}{\varDelta x} \end{aligned}$$
(19)

The reader is kindly advised to study the work [5] to identify all the remaining model parameters included in Eq. (18).

The present paper is a continuation of the authors’ previous study conducted to combine nonlocality and the theory of thermoelasticity to elaborate the constitutive model of SMA [5, 12]. Particularly, the recently proposed peridynamic model allows for simulations of mechanically induced phase transformations observed for the superelasticity effect.

Below, the formulation of the peridynamic thermomechanical SMA model is presented. First, making use of the computational framework presented in [5] (Eq. (47)–(58)) the following governing equations can be found

$$\begin{aligned} \begin{aligned} m_i {\ddot{u}}_{i}^{t}&= 2 \sum _{ \begin{array}{c} j=-N \\ j\ne 0 \end{array}}^{N} \left( \beta _{i,j}\gamma _i \frac{k^A}{\alpha _E \xi _i + 1} \frac{u_{i+j}^t-u_i^t}{|j| N^2} \right) +\\&\quad +\, \frac{F_M^{*} \xi _i}{\alpha _E \xi _i +1} +F_i^t \end{aligned} \end{aligned}$$
(20)

Next, (1) making the adequate changes in Eq. (20) originated from the differences between the total strains defined via Eq. (6) in the present paper and Eq. (14) in [5] as well as (2) introducing the theory of thermoelasticity

$$\begin{aligned} \begin{aligned} \rho {\ddot{\mathbf {u}}}&= \mu \nabla ^2 {\mathbf {u}} + (\lambda + \mu ) \nabla \nabla {\mathbf {u}} + {\mathbf {f}} - \gamma \nabla T \\ \frac{1}{\kappa } {\dot{T}}&= \nabla ^2 T - \eta \nabla {\dot{\mathbf {u}}} + \frac{Q}{\kappa } \end{aligned} \end{aligned}$$
(21)

the 1-D thermomechanical peridynamic model of an SMA material can be derived to take the final form as follows [12]

$$\begin{aligned} \begin{aligned} m_i {\ddot{u}}_{i}^{t}&= 2 \sum _{ \begin{array}{c} j=-N \\ j\ne 0 \end{array}}^{N} \left( \beta _{i,j}\gamma _i \frac{k^A}{\alpha _E \xi _i + 1} \frac{u_{i+j}^t-u_i^t}{|j| N^2} \right) +\\&\quad +\, \frac{F_M^{*} \xi _i + \alpha E^A A}{\alpha _E \xi _i +1}\theta _i^t-\gamma A \varDelta x \nabla \theta _{i}^{t} +F_i^t \end{aligned} \end{aligned}$$
(22)

complemented by the thermal diffusion equation

$$\begin{aligned} {\dot{\theta }}_{i}^{t} = \kappa \nabla ^2 \theta _i^t - \kappa \eta \nabla {\dot{u}}_{i}^{t} + Q_i^t \end{aligned}$$
(23)

In the following the discussion on the stability criteria for the developed model is carried out.

4 Stability analysis

Below, stability analysis for the developed 1-D peridynamic model of SMA material (presented via Eqs. (22) and (23) in Sect. 3) is conducted to derive the requirements regarding the maximal time step \(\varDelta t\) (integration time) allowed to be used in numerical simulations.

First, the finite difference (FD) schemes are adequately introduced to substitute all the partial derivatives in Eq. (22) and (23) with numerical formulas:

$$\begin{aligned} {\ddot{u}}_{i}^{t} &= \frac{u_i^{t-1}-2u_i^t+u_i^{t+1}}{ \varDelta t^2} \end{aligned}$$
(24)
$$\begin{aligned} {\dot{u}}_{i}^{t} &= \frac{u_i^{t+1}-u_i^{t-1}}{2 \varDelta t} \end{aligned}$$
(25)
$$\begin{aligned} \nabla {\dot{u}}_{i}^{t} &= \frac{1}{4 \varDelta t \varDelta x} \left( u_{i+1}^{t+1} -u_{i+1}^{t-1} -u_{i-1}^{t+1} + u_{i-1}^{t-1} \right) \end{aligned}$$
(26)
$$\begin{aligned} {\dot{\theta }}_{i}^{t} &= \frac{\theta _i^{t+1}-\theta _i^{t}}{\varDelta t} \end{aligned}$$
(27)
$$\begin{aligned} \nabla \theta _{i}^{t} &= \frac{\theta _{i+1}^{t}-\theta _{i-1}^{t}}{2 \varDelta x} \end{aligned}$$
(28)
$$\begin{aligned} \nabla ^2 \theta _{i}^{t} &= \frac{\theta _{i-1}^{t}-2\theta _i^t+\theta _{i+1}^{t}}{ \varDelta x^2} \end{aligned}$$
(29)

Having introduced Eqs. (24) and (28) and skipping the external force excitation \(F_i^t\), Eq. (22) becomes

$$\begin{aligned} \begin{aligned}&m_i \frac{u_i^{t-1}-2u_i^t+u_i^{t+1}}{ \varDelta t^2}= \\&\quad = 2 \sum _{ \begin{array}{c} j=-N \\ j\ne 0 \end{array}}^{N} \left( \beta _{i,j} \frac{k^A}{\alpha _E \xi _i + 1} \frac{u_{i+j}^t-u_i^t}{|j| N^2} \right)+ \\&\qquad +\, \frac{F_M^{*} \xi _i + \alpha E^A A}{\alpha _E \xi _i +1}\theta _i^t -\gamma A \varDelta x \frac{\theta _{i+1}^{t}-\theta _{i-1}^{t}}{2 \varDelta x} \end{aligned} \end{aligned}$$
(30)

and then

$$\begin{aligned} \begin{aligned}&m_i \frac{u_i^{t-1}-2u_i^t+u_i^{t+1}}{ \varDelta t^2}= \\&\quad = 2 \frac{k_i^{*}}{N^2} \sum _{ \begin{array}{c} j=-N \\ j\ne 0 \end{array}}^{N} \left( \beta _{i,j} \frac{u_{i+j}^t-u_i^t}{|j| } \right)+ \\&\qquad +\, F_i^{**} \theta _i^t - \frac{\gamma A }{2} \left( \theta _{i+1}^{t}-\theta _{i-1}^{t} \right) \end{aligned} \end{aligned}$$
(31)

with:

$$\begin{aligned} k_i^{*} &= \frac{k^A}{\alpha _E \xi _i + 1} \end{aligned}$$
(32)
$$\begin{aligned} F_i^{**} &= \frac{F_M^{*} \xi _i + \alpha E^A A}{\alpha _E \xi _i +1} \end{aligned}$$
(33)

Note, the factor \(\gamma _i\) is not present in Eqs. (30) and (31) since the internal particles in the peridynamic modal are taken into account which means neither the condition \(i=1\) nor \(i=i_{MAX}\) is satisfied.

Next, the nonlocal case exhibiting the horizon declared using \(N=2\) is considered in Eq. (31) which leads to

$$\begin{aligned} \begin{aligned}&u_i^{t-1}-2u_i^t+u_i^{t+1}= \\&\quad = \frac{\varDelta t^2 k_i^{*}}{m_i} \left( \frac{1}{8} u_{i-2}^t + \frac{1}{2} u_{i-1}^t -\frac{5}{4} + \frac{1}{2} u_{i+1}^t + \frac{1}{8} u_{i+2}^t \right)+ \\&\qquad +\, \frac{\varDelta t^2 F_i^{**}}{m_i} \theta _i^t - \frac{\gamma A }{2} \left( \theta _{i+1}^{t}-\theta _{i-1}^{t} \right) \end{aligned} \end{aligned}$$
(34)

and then

$$\begin{aligned} \begin{aligned}&u_i^{t-1}-2u_i^t+u_i^{t+1} = r_2 \theta _i^t - \frac{\gamma A }{2} \left( \theta _{i+1}^{t}-\theta _{i-1}^{t} \right)+ \\&\quad +\, r_1 \left( \frac{1}{8} u_{i-2}^t + \frac{1}{2} u_{i-1}^t -\frac{5}{4} + \frac{1}{2} u_{i+1}^t + \frac{1}{8} u_{i+2}^t \right) \end{aligned} \end{aligned}$$
(35)

with

$$\begin{aligned} r_1 &= \frac{\varDelta t^2 k_i^{*}}{m_i} \end{aligned}$$
(36)
$$\begin{aligned} r_2 &= \frac{\varDelta t^2 F_i^{**}}{m_i} \end{aligned}$$
(37)

Similarly, introduction Eqs. (26), (27) and (29) into thermal diffusion equation (23) as well as skipping external thermal excitation \(Q_i^t\) yields

$$\begin{aligned} \begin{aligned} \frac{\theta _i^{t+1}-\theta _i^{t}}{\varDelta t}&= \kappa \frac{\theta _{i-1}^{t}-2\theta _i^t+\theta _{i+1}^{t}}{ \varDelta x^2}+ \\&\quad -\, \kappa \eta \frac{1}{4 \varDelta t \varDelta x} \left( u_{i+1}^{t+1} -u_{i+1}^{t-1} -u_{i-1}^{t+1} + u_{i-1}^{t-1} \right) \end{aligned} \end{aligned}$$
(38)

Next, Eq. (38) evolves to the form

$$\begin{aligned} \begin{aligned} \theta _i^{t}&= \theta _i^{t+1} -\kappa \varDelta t \frac{\theta _{i-1}^{t}-2\theta _i^t+\theta _{i+1}^{t}}{ \varDelta x^2}+ \\&\quad +\, \frac{\kappa \eta }{4 \varDelta x } \left( u_{i+1}^{t+1} -u_{i+1}^{t-1} -u_{i-1}^{t+1} + u_{i-1}^{t-1} \right) \end{aligned} \end{aligned}$$
(39)

Within the scope of the current work only the specific case of high thermal conductivity is considered. Hence, the following condition regarding the temperature distribution along an SMA rod remains satisfied

$$\begin{aligned} \forall t \in \left\{ 0,{\mathbb {N}} \right\} , \forall i,j \in {\mathbb {N}} \cap [1,i_{MAX}]: \theta _i^t \equiv \theta _j^t \end{aligned}$$
(40)

Taking into account the condition (40) in Eqs. (35) and (39) leads to:

$$\begin{aligned} \begin{aligned}&u_i^{t-1}-2u_i^t+u_i^{t+1} = r_2 \theta _i^t+ \\&\quad +\, r_1 \left( \frac{1}{8} u_{i-2}^t + \frac{1}{2} u_{i-1}^t -\frac{5}{4} + \frac{1}{2} u_{i+1}^t + \frac{1}{8} u_{i+2}^t \right) \end{aligned} \end{aligned}$$
(41)
$$\begin{aligned} \begin{aligned}&\theta _i^{t} = \theta _i^{t+1} + \frac{\kappa \eta }{4 \varDelta x } \left( u_{i+1}^{t+1} -u_{i+1}^{t-1} -u_{i-1}^{t+1} + u_{i-1}^{t-1} \right) \end{aligned} \end{aligned}$$
(42)

Finally, substituting \(\theta _i^t\) in Eq. (41) using the formula (42) yields the following combined numerical form for the two-domain case

$$\begin{aligned} \begin{aligned}&u_i^{t-1}-2u_i^t+u_i^{t+1}= \\&\quad = r_1 \left( \frac{1}{8} u_{i-2}^t + \frac{1}{2} u_{i-1}^t -\frac{5}{4} + \frac{1}{2} u_{i+1}^t + \frac{1}{8} u_{i+2}^t \right)+ \\&\qquad +\, r_2 \theta _i^{t+1} + \frac{r_3}{4 } \left( u_{i+1}^{t+1} -u_{i+1}^{t-1} -u_{i-1}^{t+1} + u_{i-1}^{t-1} \right) \end{aligned} \end{aligned}$$
(43)

with

$$\begin{aligned} r_3=\frac{r_2 \kappa \eta }{\varDelta x } \end{aligned}$$
(44)

Next, based on Eq. (43), stability conditions for numerical calculations can be derived via a numerical error equation which describes its propagation in the temporal and spatial domain. The adequate error equation can be defined taking into account the displacement and temperature errors, i.e., \(\epsilon\) and \(^{\theta }\epsilon\) respectively. Hence, Eq. (43) takes the form

$$\begin{aligned} \begin{aligned}&\epsilon _i^{t-1}-2\epsilon _i^t+\epsilon _i^{t+1}= \\&\quad = r_1 \left( \frac{1}{8} \epsilon _{i-2}^t + \frac{1}{2} \epsilon _{i-1}^t -\frac{5}{4} + \frac{1}{2} \epsilon _{i+1}^t + \frac{1}{8} \epsilon _{i+2}^t \right)+ \\&\qquad +\, r_2 {} ^{\theta }\epsilon ^{t+1} + \frac{r_3}{4 } \left( \epsilon _{i+1}^{t+1} -\epsilon _{i+1}^{t-1} -\epsilon _{i-1}^{t+1} + \epsilon _{i-1}^{t-1} \right) \end{aligned} \end{aligned}$$
(45)

The errors \(\epsilon\) and \(^{\theta }\epsilon\) take spatial and temporal terms:

$$\begin{aligned} \begin{aligned} \epsilon _{i+j}^{t+q}&=\exp {(a_{u}(t+q)\varDelta t)}\exp {(\sqrt{-1} \kappa _{u} (i+j)\varDelta x)}=\\&=\exp {(a_{u}t\varDelta t)}\exp {(\sqrt{-1} \kappa _{u} i\varDelta x)} \\&\quad \times \, \exp {(a_{u}q\varDelta t)}\exp {(\sqrt{-1} \kappa _{u} j\varDelta x)} \end{aligned} \end{aligned}$$
(46)
$$\begin{aligned} \begin{aligned} {}^{\theta }\epsilon _{i+j}^{t+q}&=\exp {(a_{\theta }(t+q)\varDelta t)}\exp {(\sqrt{-1} \kappa _{\theta } (i+j)\varDelta x)}=\\&=\exp {(a_{\theta }t\varDelta t)}\exp {(\sqrt{-1} \kappa _{\theta } i\varDelta x)} \\&\quad \times \, \exp {(a_{\theta }q\varDelta t)}\exp {(\sqrt{-1} \kappa _{\theta } j\varDelta x)} \end{aligned} \end{aligned}$$
(47)

Introduction Eqs. (46) and (47) in (43) leads to

$$\begin{aligned} R_A=r_1R_B+r_2 R_C + \frac{r_3}{4}R_D \end{aligned}$$
(48)

where

$$\begin{aligned} R_A &= R_u \left( \exp {(-a_u \varDelta t)} + \exp {(a_u \varDelta t) } -2 \right) \end{aligned}$$
(49)
$$\begin{aligned} R_B &= R_u \left( \frac{1}{8} \exp {(-2\sqrt{-1}\kappa _u \varDelta x)} \right. \nonumber+ \\&\quad +\, \left. \frac{1}{2} \exp {(-\sqrt{-1}\kappa _u \varDelta x)} -\frac{5}{4} \right. \nonumber+ \\&\quad +\, \left. \frac{1}{2} \exp {(\sqrt{-1}\kappa _u \varDelta x)} + \frac{1}{8} \exp {(2\sqrt{-1}\kappa _u \varDelta x)}\right) \nonumber= \\ &= R_u \left( \frac{1}{4} \cos {(2 \kappa _u \varDelta x)} + \cos {(\kappa _u \varDelta x)} - \frac{5}{4} \right) \end{aligned}$$
(50)
$$\begin{aligned} R_C &= \exp {(a_{\theta }t\varDelta t)}\exp {(\sqrt{-1} \kappa _{\theta } i\varDelta x)} \exp {(a_{\theta }\varDelta t)} \end{aligned}$$
(51)
$$\begin{aligned} R_D &= R_u ( \exp {(a_u \varDelta t)} \exp {(\sqrt{-1}\kappa _u \varDelta x)} \nonumber+ \\&\quad -\, \exp {(-a_u \varDelta t)} \exp {(\sqrt{-1}\kappa _u \varDelta x)} \nonumber+ \\&\quad -\, \exp {(a_u \varDelta t)} \exp {(-\sqrt{-1}\kappa _u \varDelta x)} \nonumber+ \\&\quad +\, \exp {(-a_u \varDelta t)} \exp {(-\sqrt{-1}\kappa _u \varDelta x)}) \nonumber= \\ &= 2\sqrt{-1} R_u ( \exp {(a_u \varDelta t)} - \exp {(-a_u \varDelta t)} ) \sin (\kappa _u \varDelta x) \end{aligned}$$
(52)

with

$$\begin{aligned} R_u=\exp {(a_{u}t\varDelta t)}\exp {(\sqrt{-1} \kappa _{u} i\varDelta x)} \end{aligned}$$
(53)

To avoid the displacement error growth the following condition must be satisfied which is also considered sufficient to prevent from increasing temperature error

$$\begin{aligned} \vert \frac{\epsilon _i^{t+1}}{\epsilon _i^{t}} \vert \le 1 \end{aligned}$$
(54)

which results in

$$\begin{aligned} \vert \exp {(a_u \varDelta t)} \vert \le 1 \end{aligned}$$
(55)

and

$$\begin{aligned} \vert \exp {(-a_u \varDelta t)} \vert \ge 1 \end{aligned}$$
(56)

Whichever condition of the two above stated, i.e., (55) or (56), is taken into account it allows to find the stability conditions. Based on (55) and (56) it can be assumed that the two exponential expressions present in \(R_A\), i.e., \(\exp {(a_u \varDelta t)}\) and \(\exp {(-a_u \varDelta t)}\), simultaneously converge to 1. Hence, Eq. (48) can be split into the two equivalent, i.e., equal, formulas allowing to explicitly and separately define the above mentioned exponential expressions. The respective equation derived for the expression \(\exp {(a_u \varDelta t)}\) takes the form

$$\begin{aligned} \exp {(a_u \varDelta t) } =\frac{r_1R_B}{2R_u} +\frac{r_2 R_C}{2R_u} + \frac{r_3 R_D}{8 R_u} +1 \end{aligned}$$
(57)

however, noticing that \(\exp {(a_u \varDelta t)} - \exp {(-a_u \varDelta t)}\) converges to 0, the parameter \(R_D\) cancels out.

Further simplification regarding Eq. (57) can be performed analyzing the fraction \(R_C/R_u\) which becomes

$$\begin{aligned} \begin{aligned} \frac{R_C}{R_u}&= \exp {((a_{\theta }-a_{u})t\varDelta t)}\exp {(\sqrt{-1} (\kappa _{\theta }-\kappa _{u}) i\varDelta x)} \\&\quad \times \, \exp {(a_{\theta }\varDelta t)} \end{aligned} \end{aligned}$$
(58)

Due to the previously assumed uniform distribution of the temperature the respective equivalent wave number for the temperature identified along a 1-D model \(\kappa _{\theta }\) converges to 0. Moreover, excluding the imaginary component \(-\sqrt{-1}\sin (\kappa _u i \varDelta x)\) from Eq. (58)—as it appears after introduction the Euler’s formula for the expression \(\exp {(\sqrt{-1} (-\kappa _{u}) i\varDelta x)}\)—Eq. (58) takes the form

$$\begin{aligned} \begin{aligned} \frac{R_C}{R_u}= \exp {((a_{\theta }-a_{u})t\varDelta t)} \exp {(a_{\theta }\varDelta t)}\cos (\kappa _u i \varDelta x) \end{aligned} \end{aligned}$$
(59)

Noticing that the most demanding case for numerical calculations references to the wave number \(\kappa _{u,MAX}=\varPi / \varDelta x\) (it is an equivalent description for the shortest wavelength \(\lambda _{MIN}=2 \varDelta x\)) the expression \(R_C/R_u\) becomes

$$\begin{aligned} \begin{aligned} \frac{R_C}{R_u}= \pm \exp {((a_{\theta }(t+1)-a_{u}t)\varDelta t)} \end{aligned} \end{aligned}$$
(60)

Similarly, based on the greatest wavelength criterion \(\kappa _{u,MAX}\) the expression \(R_B/R_u\) takes the form

$$\begin{aligned} \begin{aligned} \frac{R_B}{R_u}&= \frac{1}{4} \cos {(2 \kappa _{u,MAX} \varDelta x)} + \cos {(\kappa _{u,MAX} \varDelta x)}\\&\quad -\, \frac{5}{4} = -2 \end{aligned} \end{aligned}$$
(61)

Having considered Eqs. (60), (61) and \(R_D=0\) the formula (57) and the condition (55) take the following forms

$$\begin{aligned}&\exp {(a_u \varDelta t) } =-r_1 \pm \frac{r_2}{2} \exp {((a_{\theta }(t+1)-a_{u}t)\varDelta t)} +1 \end{aligned}$$
(62)
$$\begin{aligned}&\vert 1-r_1 \pm \frac{r_2}{2} \exp {((a_{\theta }(t+1)-a_{u}t)\varDelta t)} \vert \le 1 \end{aligned}$$
(63)

Now, the two cases of the exponential expression \(\exp {((a_{\theta }(t+1)-a_{u}t)\varDelta t)}\) may be considered not to violate validity of the condition (63), namely the above mentioned exponential expression should converge either to 0 or \(\pm 1\). Hence, the two complementary cases are derived

$$\begin{aligned}&\vert 1-r_1 \vert \le 1 \end{aligned}$$
(64)
$$\begin{aligned}&\vert 1-r_1 \pm \frac{r_2}{2} \vert \le 1 \end{aligned}$$
(65)

Taking into account the most demanding case of the greatest elastic wave velocity in an SMA sample \(c^A\), as observed for austenite (for \(\xi _i=0\), \(E^A>E^M\)), it can be found that

$$\begin{aligned}&r_1=\frac{\varDelta t^2 k_i^{*}}{m_i} =\frac{\varDelta t^2 E^A A}{m_i \varDelta x}= \frac{\varDelta t^2}{\varDelta x ^2} (c^A)^2 \end{aligned}$$
(66)
$$\begin{aligned}&r_2=\frac{\varDelta t^2 F_i^{**}}{m_i} =\frac{\varDelta t^2 \alpha E^A A}{m_i} = \frac{\varDelta t^2}{\varDelta x} \alpha (c^A)^2 \end{aligned}$$
(67)

since

$$\begin{aligned} c^A &= \sqrt{\frac{E^A}{\rho }} \end{aligned}$$
(68)
$$\begin{aligned} \rho &= \frac{m}{A\varDelta x} \end{aligned}$$
(69)

Finally, substitution of \(r_1\) and \(r_2\) in (64) and (65), respectively making use of (66) and (67), leads to the following stability conditions

$$\begin{aligned}&\varDelta t \le \sqrt{2} \frac{\varDelta x^2}{c^A} \end{aligned}$$
(70)
$$\begin{aligned}&\varDelta t \le \sqrt{2} \frac{\varDelta x}{c^A \sqrt{1+\alpha \varDelta x /2}} \end{aligned}$$
(71)

The derived stability conditions (70) and (71) allow for making a reliable choice on the time integration for numerical calculations \(\varDelta t\). The conditions should be satisfied simultaneously as they introduce both solely the mechanical property (the velocity \(c^A\)) and the thermomechanical one (coefficient of thermal expansion \(\alpha\)). As already mentioned the above stated conditions are valid for the presently studied specific case of uniform distribution of the temperature. An extension of the work considering the temperature variation along an SMA rod is scheduled by the authors to be the subject of the future research activity.

5 Numerical study: stress–strain relation and parametric analysis

In present section, exemplary numerical results are provided for the developed peridynamic SMA model to visualize its fundamental computational capability. First, the reference temperature \(T_{0}\) is arbitrarily assumed to take values from the range \([0^{\circ }{\hbox {C}},50^{\circ }{\hbox {C}}]\) for identification the changes regarding hysteretic stress–strain relationships observed for mechanical load. The following material properties are taken into account for an SMA wire: Young’s moduli for austenite and martensite \(E^{A}=160GPa\) and \(E^{M}=145GPa\), the characteristic solid phase transformations temperatures \(A_{s}=-8^{\circ }{\hbox {C}}, A_{f}=10^{\circ }{\hbox {C}}, M_{s}=-35^{\circ }{\hbox {C}}, M_{f}=-55^{\circ }{\hbox {C}},\) maximum transformation strain \(H=0.008\), specific heat \(c=329J/(kgK)\), mass density \(\rho =6450kg/m^3\), stress influence coefficient \(\rho \varDelta s_0=-0.2MPa/K\) and thermal expansion coefficient equals \(\alpha =22 \cdot 10^{-6}K^{-1}\). Figure 5 presents the results of numerical simulations.

Fig. 5
figure 5

Stress–strain relations obtained for various reference temperatures—numerical study

Full size image

Making use of the results visualized in Fig. 5, it can be found that hysteretic behavior—originating from the phenomenon of superelasticity—is not seen for each analyzed case. Within the scope of the assumed maximum level of the externally induced stress (arbitrarily set to be 700MPa), the above mentioned nonlinear material response is identified only when \(T_{0}<40^{\circ }{\hbox {C}}\). For positive values of stress, i.e., for uniaxial extension only, closed hysteretic loops are achieved for the cases when \(10^{\circ }{\hbox {C}}\leqslant T_{0} \leqslant 35^{\circ }{\hbox {C}}\). More specifically, the hysteretic subloops—resulting from incomplete phase transformations—are observed when \(T_{0}\in \{30^{\circ }{\hbox {C}},35^{\circ }{\hbox {C}}\}\). A linear elastic material behavior is found for \(T_{0}\geqslant 40^{\circ }{\hbox {C}}\). The two remaining case studies for \(T_{0}\in \{0^{\circ }{\hbox {C}},5^{\circ }{\hbox {C}}\}\) characterize non-zero residual strain in a modeled SMA sample after stress relieving.

Next, a parametric study regarding selected model properties is carried out to discuss the sensitivity of the simulation results for the uncertainty originating from experimental identification of the considered material properties [35]. To conduct an exemplary calculation on uncertainty propagation, the authors of the present work arbitrarily assume the level of \(5^{\circ }{\hbox {C}}\) variation for the previously introduced characteristic solid phase transformations temperatures \(A_{s}\), \(A_{f}\), \(M_{s}\) and \(M_{f}\). The introduced \(\pm 5^{\circ }{\hbox {C}}\) intervals of temperature uncertainty refer to the \(3\sigma\) levels for the four independent normally distributed components \({\tilde{X}}_{\bullet }={\mathcal {N}}(\mu =0,\,\sigma ^{2})\) being added to the nominal values of the transformations temperatures \(\bullet\), where \(\bullet \in \{ A_{s},A_{f},M_{s},M_{f} \}\). This allows for definition of adequate four random numbers \({\tilde{\bullet }}\) such that \({\tilde{\bullet }}=\bullet + {\tilde{X}}_{\bullet }\). Figure 6 presents the results of the conducted study on uncertainty propagation, i.e., the analysis of influence of parametric errors, for the reference temperature \(T_{0}=20^{\circ }{\hbox {C}}\).

Fig. 6
figure 6

Distribution of stress–strain relations obtained for parametric study—the results of uncertainty propagation for the selected material properties

Full size image

Latin hypercube sampling is applied to improve distribution of the randomly generated 1000 samples for the characteristic temperatures \({\tilde{\bullet }}\) according to the assumed uncertainty levels.

As visualized in Fig. 6, the above introduced type and level of model uncertainty leads to the adequate variation of the shape of stress–strain relation for the modeled SMA sample. Due to the assumed uncorrelated changes of the characteristic temperatures—which are considered to model the errors appearing during process of experimental identification of the mentioned material properties—the regions in the stress–strain coordinate systems where phase transformations are respectively initiated and finished randomly evolve. Consequently, there may be observed various slopes and localizations of the curves’ sections representing the courses of forward and reverse phase transformation processes (adequate sections are marked with ‘2’ and ‘4’ in Fig. 6). In contrast, no change regarding the hysteresis sections marked as ’1’ and ’3’ are noticed which is expected since the Youngs’ moduli (that govern the adequate curve slopes) are considered constant for the conducted numerical analysis. In reference to the determined uncertainty regarding the shape of stress–strain relationship, it may be also expected the respective variation of the amount of energy that can be dissipated in an SMA component for a single complete stretching and release cycle. The raised issue is of particular importance in case of SMA-based damping components [35].

6 Summary and final conclusions

The paper addresses the 1-D peridynamic thermomechanical model proposed to simulate the behavior of SMA components. The model is successfully formulated combining advantageous properties of both (1) integral based peridynamic governing equation and (2) phenomenological SMA model based on the concept of the total Gibbs free energy. The former approach allows for convenient modeling various types of model nonlinearities, e.g., those regarding material, geometry and boundary conditions, whereas the latter model enables handling the properties of an SMA material in a computationally efficient manner. Additionally, the classically formulated theory of thermoelasticity complements the newly developed SMA model with the temperature based contributors. The overall application scope for the developed model deals with simulations of the phenomena of superelasticity in SMA components subjected to mechanical loads under non-isothermal conditions. The above mentioned case study is scheduled by the authors to be performed for the models of GFB equipped with SMA parts used to reduce mechanical vibrations.

Unfortunately, there has not been yet proposed a holistic approach to reliably model all the phenomena observed in SMA at various geometric scales. There are many various models dedicated to study specific aspects of the SMA behavior. Continuously growing demands regarding simulation efficiency and accuracy result in contradictory objectives and conditions that cannot be satisfied simultaneously. In fact, microscopic models are reliable but require significant amount of computational resources. In contrast, running fast macroscopic codes cannot lead to very accurate outcomes. The model presented in the current work should be considered as a step towards more accurate modeling of SMA behavior making use of a phenomenological approach. The derived stability criteria allow for reasonable choice on the integration time to prevent from numerical errors effectively. The present work focuses entirely on the theoretical aspects of numerical modeling. Exemplary results of numerical analyses are provided to confirm fundamental computational capability of the developed SMA model. The formulated stability criteria will allow to conduct numerical simulations which are scheduled by the authors for the future research as the continuation of the present work.