1 Introduction

The characteristic of wave propagation in elastic solids has been an attractive topic for decades. Intensive research about the characteristic of wave propagation is meaningful to many fields. Considering the mechanical properties of the medium, wave velocity and the stresses distribution are mostly concerned about, which provides references in material sciences. Meanwhile, focusing on the influences of defects and interfaces on wave propagation is necessary in material sciences as well. Moreover, due to the underground structures and local terrains exist commonly in practical engineering, investigation about influences of defects and interfaces on wave propagation is of great significance in earthquake engineering and civil engineering.

Wave scattering in homogeneous medium was a classical topic which was investigated by many scholars. For analytical analysis, wave function expansion method and complex function method were effective and utilized in most cases [1,2,3,4,5]. Moreover, with the aids of other methods, it is possible to solve complicated problems about wave propagation in homogeneous medium. By utilizing Green’s function method, the antiplane harmonic dynamics stress of an infinite isotropic wedge with a circular cavity was analyzed by [6]. Then the stress distribution around the cavity was calculated and discussed. As an efficient method, Green’s function method can be applied to solve problems of complex interfaces as well. By applying this method, linear cracks can be modeled. Meanwhile, contact conditions between different medium was able to be constructed by it validly [7, 8]. Aiming at wave scattering by defects or structures in half space or right-angled medium, image principle was mostly used to obtain the expression of scattering wave [9, 10]. By constructing one or more imaginary scattering sources, the scattering wave can satisfy the boundary condition at the surface of the half space or right-angled medium well. Furthermore, in order to investigate complicated defects (structures) or terrains, auxiliary boundary method was needed in most cases [9,10,11].

Except for analytical analysis, some semi-analytical and numerical methods are more appropriate in solving multi-scattering or complex terrain problem. Boundary element method and boundary integral equation method have advantages to research complex boundary value problems. Considering the scattering by multilayered embedded inclusion, the corresponding integral equations were derived in terms of the unknown boundary displacements and tractions. Subsequently, the wave fields and the stress fields in the background medium and the inclusion can be obtained [12,13,14]. Based on extensions to these methods, it was effective to investigate scattering by lined tunnel underground as well [15, 16]. Some researchers paid their attention to study wave scattering by applying numerical methods or hybrid methods. For solving wave scattering by trapezoidal terrain and dike, finite element method (FEM) had a high efficiency than many other analytical methods [17, 18]. Moreover, different kinds of degenerated models can be simulated to verify the validity of the calculation.

Since most media in the nature are not homogeneous, wave propagation in inhomogeneous medium have attracted lots of attention. Basic solutions of SH wave propagation in inhomogeneous anisotropic medium can be derived by analytical method directly [19]. Considering the inhomogeneity and anisotropy of the medium, the wave front was shown in the calculations. As a simplified condition, dividing continuous inhomogeneous medium to be multi-layered medium was a feasible way as well. Let the multi-layered medium be composed of periodically repeated fundamental laminae with a small thickness to achieve the wave velocity in the inhomogeneous medium [20]. Moreover, analyses of wave propagation in closed inhomogeneous region was helpful for material science and earthquake engineering. Considering the deposition of soils, the inhomogeneity of the soil layer was assumed to be radial inhomogeneous [21]. Then, based on the wave function expansion method, the surface motion was calculated with different conditions of inhomogeneity. Investigation of elastic wave scattered by an inhomogeneous circular tube was of vital importance in material science [22]. To assume the tube was linear inhomogeneous, Finite Fourier Transform was utilized to solve the governing equation. Furthermore, this research provided a feasible way to investigate SH wave scattered by inhomogeneous lined tunnel underground. Obviously, research of wave propagation in infinite inhomogeneous medium is also meaningful but with more difficulties. Generally, two or more methods were needed together in solving these problems. With the help of auxiliary function method, researches about wave motion in inhomogeneous medium with a constant velocity was conducted analytically [23,24,25]. Then, wave fields, stress distribution and far-field behavior were discussed. By applying conformal mapping method, the closed-form solution of SH wave propagation in inhomogeneous medium with a variable velocity was studied [26, 27]. Through normalized the governing equation, dynamic stress concentration around the inclusions was analyzed.

Since the lack of researches about body wave propagation in inhomogeneous half space with wave velocity variation, SH wave scattering in vertically inhomogeneous half space is investigated in this work. The mass density is assumed to be vertically inhomogeneous by applying the similar method in Refs.[26, 27]. Considering the effect of the horizontal surface, image principle is used to solve the scattering wave. Then, wave fields and stresses in the half space was obtained analytically. Ultimately, dynamic stress around the cylindrical cavity was calculated and discussed.

Fig. 1
figure 1

Scattering model of a cylindrical cavity

Full size image

2 Description of the problem

2.1 Model description

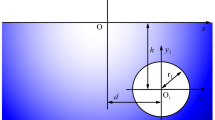
Scattering model of a cylindrical cavity in vertically inhomogeneous half space is shown in Fig. 1. The mass density of the half space is exponentially inhomogeneous while the shear modulus is a constant. The radius of the cavity is R and the buried depth is h. The surface of the half space locates at \({{y}_{1}}=0\) and the origin of the polar coordinate is coincident with the center of the cylindrical cavity. Considering the symmetry of the half space, the SH wave is assumed to be vertically incidence. Based on the transformation between two polar coordinates, xoy and \({{x}_{1}}{{o}_{1}}{{y}_{1}}\) have the relation of \(x={{x}_{1}}\), \(y={{y}_{1}}-h\).

The mass density of the half space is inhomogeneous and changes with the depth exponentially. Hence, the form of the mass density can be expressed as

$$\begin{aligned} \rho \left( y \right) ={{\rho }_{0}}{{\beta }^{2}}\exp \left( 2\beta y \right) \end{aligned}$$
(1)

where \({{\rho }_{0}}\) is a constant which is defined as the reference mass density, \(\beta\) is the inhomogeneous parameter of the half space. Since the shear modulus is a constant, the wave velocity in the half space has the form of

$$\begin{aligned} c\left( y \right) =\frac{{{c}_{0}}}{\beta }\exp \left( -\beta y \right) \end{aligned}$$
(2)

where \({{c}_{0}}=\sqrt{{\mu }/{{{\rho }_{0}}}\;}\) is the reference wave velocity, \(\mu\) is the shear modulus of the half space.

2.2 Basic equations

Considering harmonic response and ignoring the body force, the governing equation of wave motion in vertically inhomogeneous half space is

$$\begin{aligned} \frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}w}{\partial {{y}^{2}}}+k_{0}^{2}{{\beta }^{2}}\exp \left( 2\beta y \right) w=0 \end{aligned}$$
(3)

Based on complex function method, a pair of complex variables are introduced

$$\begin{aligned} z=x+{\text {i}}y,\quad \bar{z}=x-{\text {i}}y \end{aligned}$$
(4)

Then, the governing equation in complex coordinates is

$$\begin{aligned} \frac{{{\partial }^{2}}w}{\partial z\partial \bar{z}}+\frac{1}{4}k_{0}^{2}{{\beta }^{2}}\exp \left( 2\beta {\text {Im}}z \right) w=0 \end{aligned}$$
(5)

where \(w=w\left( x,y \right)\) is the displacement, \({{k}_{0}}={\omega }/{{{c}_{0}}}\;\) is the reference wave number and \(\omega\) is the circular frequency.

Since the equations like Eq. (5) is too difficult to solve, a pair of transformation is utilized on basis of conformal mapping method in order to normalize the governing equation

$$\begin{aligned} \chi =\exp \left( -{\text {i}}\beta z \right) ,\quad \bar{\chi }=\exp \left( {\text {i}}\beta \bar{z} \right) \end{aligned}$$
(6)

Substituting Eq. (6) into Eq. (5), the governing equation becomes

$$\begin{aligned} \frac{{{\partial }^{2}}w}{\partial \chi \partial \bar{\chi }}+\frac{1}{4}k_{0}^{2}w=0 \end{aligned}$$
(7)

Hence, the governing equation is normalized into a Helmholtz equation with constant coefficients.

3 Wave fields and corresponding stresses

3.1 Wave fields in half space

On the basis of the normalized governing equation, the vertical incident wave can be expressed as

$$\begin{aligned} {{w}^{\left( i \right) }}={{w}_{0}}\exp \left[ \frac{{{k}_{0}}}{2}\left( {{\chi }_{1}}-{{{\bar{\chi }}}_{1}} \right) \right] \end{aligned}$$
(8)

where \({{w}_{0}}\) is the displacement amplitude of incident wave.

Because of the surface of the half space, the incident wave will be reflected vertically

$$\begin{aligned} {{w}^{\left( r \right) }}={{w}_{0}}\exp \left[ \frac{{{k}_{0}}}{2}\left( {{{\bar{\chi }}}_{1}}-{{\chi }_{1}} \right) \right] \end{aligned}$$
(9)

Considering the Sommerfeld radiation condition at infinity and the zero-stress boundary condition at the surface, the scattering wave in the half space which is induced by the cylindrical cavity obeys

$$\begin{aligned} {{w}^{\left( s \right) }}=\sum \limits _{n=-\infty }^{\infty }{{{A}_{n}}\left\{ H_{n}^{\left( 1 \right) }\left( {{k}_{0}}\left| \chi \right| \right) {{\left\{ \frac{\chi }{\left| \chi \right| } \right\} }^{n}}+H_{n}^{\left( 1 \right) }\left( {{k}_{0}}\left| {{\chi }_{2}} \right| \right) {{\left\{ \frac{{{\chi }_{2}}}{\left| {{\chi }_{2}} \right| } \right\} }^{-n}} \right\} } \end{aligned}$$
(10)

where \({{A}_{n}}\) are undetermined coefficients need to be solved. Moreover, \({{\chi }_{2}}=\exp \left[ -{\text {i}}\beta \left( z+2h{\text {i}} \right) \right]\).

Hence, the whole wave field in the half space should be the superposition of the incident wave, the reflected wave and the scattering wave

$$\begin{aligned} {{w}^{\left( f \right) }}={{w}^{\left( i \right) }}+{{w}^{\left( r \right) }}+{{w}^{\left( s \right) }} \end{aligned}$$
(11)

3.2 Expression of stress components

Based on the constitutive relations between wave fields and corresponding stresses, the stress components in Cartesian coordinate system have the form of

$$\begin{aligned} {{\tau }_{xz}}=\mu \frac{\partial w}{\partial x},\,\,{{\tau }_{yz}}=\mu \frac{\partial w}{\partial y} \end{aligned}$$
(12)

In complex coordinate system, the constitutive relations become

$$\begin{aligned} {{\tau }_{rz}}= \mu \left( \frac{\partial w}{\partial z}{{{\text {e}}}^{\text {i}\theta }}+\frac{\partial w}{\partial \bar{z}}{{\text {e}}^{-{\text {i}}\theta }} \right) \end{aligned}$$
(13)
$$\begin{aligned} {{\tau }_{\theta z}}= {\text {i}}\mu \left( \frac{\partial w}{\partial z}{{\text {e}}^{{\text {i}}\theta }}-\frac{\partial w}{\partial \bar{z}}{{\text {e}}^{-{\text {i}}\theta }} \right) \end{aligned}$$
(14)

It can be inferred that in complex plane \(\left( \chi ,\bar{\chi } \right)\), the stress components can be written as

$$\begin{aligned} {{\tau }_{rz}}= \mu \left( \frac{\partial w}{\partial \chi }\frac{{\text {d}}\chi }{{\text {d}}z}{{\text {e}}^{{\text {i}}\theta }}+\frac{\partial w}{\partial \bar{\chi }}\frac{{\text {d}}\bar{\chi }}{{\text {d}}\bar{z}}{{\text {e}}^{-{\text {i}}\theta }} \right) \end{aligned}$$
(15)
$$\begin{aligned} {{\tau }_{\theta z}}= {\text {i}}\mu \left( \frac{\partial w}{\partial \chi }\frac{\text {d}\chi }{\text {d}z}{{\text {e}}^{{\text {i}}\theta }}-\frac{\partial w}{\partial \bar{\chi }}\frac{\text {d}\bar{\chi }}{\text {d}\bar{z}}{{\text {e}}^{-{\text {i}}\theta }} \right) \end{aligned}$$
(16)

Substituting the incident wave, the reflected wave and the scattering wave into Eqs. (12)–(15), the detailed expression of corresponding stress components can be obtained.

4 Boundary condition and dynamic stress concentration factor

4.1 Boundary condition at the cavity

In order to solve the undetermined coefficients in whole wave field, the boundary condition at the surface of the cavity need to be used. The boundary condition of the cylindrical cavity is zero-stress condition of radial stresses, which can be formulated as

$$\begin{aligned} \tau _{rz}^{\left( f \right) }=\tau _{rz}^{\left( i \right) }+\tau _{rz}^{\left( r \right) }+\tau _{rz}^{\left( s \right) }=0,\begin{matrix} {} &{} r=R \\ \end{matrix} \end{aligned}$$
(17)

Substituting the stress components into Eq. (17), the boundary condition can be simplified to

$$\begin{aligned} \sum \limits _{n=-\infty }^{\infty }{{{A}_{n}}}{{\xi }_{n}}=\xi \end{aligned}$$
(18)

where

$$\begin{aligned} {{\xi }_{n}}&= \left\{ H_{n-1}^{\left( 1 \right) }\left( {{k}_{0}}\left| \chi \right| \right) {{\left[ \frac{\chi }{\left| \chi \right| } \right] }^{n-1}}\cdot {\chi }'+H_{n-1}^{\left( 1 \right) }\left( {{k}_{0}}\left| {{\chi }_{2}} \right| \right) {{\left[ \frac{{{\chi }_{2}}}{\left| {{\chi }_{2}} \right| } \right] }^{-n+1}}\cdot {{{{\chi }'}}_{2}} \right\} {{\text {e}}^{{\text {i}}\theta }}\nonumber \\&\quad-\left\{ H_{n+1}^{\left( 1 \right) }\left( {{k}_{0}}\left| \chi \right| \right) {{\left[ \frac{\chi }{\left| \chi \right| } \right] }^{n+1}}\cdot {\bar{\chi }}'+H_{n+1}^{\left( 1 \right) }\left( {{k}_{0}}\left| {{\chi }_{2}} \right| \right) {{\left[ \frac{{{\chi }_{2}}}{\left| {{\chi }_{2}} \right| } \right] }^{-n-1}}\cdot {{{\bar{{\chi }'}}}_{2}} \right\} {{\text {e}}^{-{\text {i}}\theta }} \end{aligned}$$
(19)
$$\begin{aligned} \xi= -{{w}_{0}}\left( {{{{\chi }'}}_{1}}{{\text {e}}^{{\text {i}}\theta }}-{{{\bar{{\chi }'}}}_{1}}{{\text {e}}^{-{\text {i}}\theta }} \right) \left\{ \exp \left[ \frac{{{k}_{0}}}{2}\left( {{\chi }_{1}}-{{{\bar{\chi }}}_{1}} \right) \right] -\exp \left[ \frac{{{k}_{0}}}{2}\left( {{{\bar{\chi }}}_{1}}-{{\chi }_{1}} \right) \right] \right\} \end{aligned}$$
(20)

Applying orthogonal function expansion technique, we multiply \({{\text {e}}^{-{\text {i}}m\theta }}\) by both sides of Eq. (18) and make integration on the interval \(\left( -\pi ,\pi \right)\) to solve undetermined coefficients \({{A}_{n}}\)

$$\begin{aligned} \sum \limits _{n=-\infty }^{\infty }{{{A}_{n}}{{\xi }_{mn}}}={{\xi }_{m}},\begin{matrix} {} &{} m=n=0,\pm 1,\pm 2,\ldots \\ \end{matrix} \end{aligned}$$
(21)

where

$$\begin{aligned} {{\xi }_{mn}} & =\frac{1}{2\pi }\int \limits _{-\pi }^{\pi }{{{\xi }_{n}}{{\text {e}}^{-{\text {i}}m\theta }}\text {d}\theta },\\{{\xi }_{m}} &=\frac{1}{2\pi }\int \limits _{-\pi }^{\pi }{\xi {{\text {e}}^{-{\text {i}}m\theta }}\text {d}\theta } \end{aligned}$$
(22)

4.2 Dynamic stress concentration factor (DSCF)

In order to analyze the dynamic stress around the cylindrical cavity, dynamic stress concentration factor is defined, which has the form of

$$\begin{aligned} \tau _{\theta z}^{*}=\left| {\tau _{\theta z}^{\left( \centerdot \right) }}/{{{\tau }_{0}}}\; \right| \end{aligned}$$
(23)

where \(\tau _{\theta z}^{\left( \centerdot \right) }=\tau _{\theta z}^{\left( i \right) }+\tau _{\theta z}^{\left( r \right) }+\tau _{\theta z}^{\left( s \right) }\) which can be obtained by Eq. (16) and \({{\tau }_{0}}=\mu \beta {{k}_{0}}{{w}_{0}}\) is the stress amplitude of incident wave.

Fig. 2
figure 2

Distribution of DSCF with different wave number (\(\beta =0.1\))

Full size image
Fig. 3
figure 3

Distribution of DSCF with different wave number (\(\beta =0.3\))

Full size image
Fig. 4
figure 4

Distribution of DSCF with different wave number (\(\beta =0.5\))

Full size image
Fig. 5
figure 5

Distribution of DSCF with different wave number (\(\beta =0.8\))

Full size image
Fig. 6
figure 6

Distribution of DSCF with different wave number (\(\beta =1.0\))

Full size image
Fig. 7
figure 7

Distribution of DSCF with different wave number (\(\beta =1.2\))

Full size image

5 Numerical results and discussion

In order to investigate the influence of wave frequency on stress distribution around the cavity, DSCF under different reference wave number are shown in Figs. 2, 3, 4, 5, 6 and 7. In the numerical results, the reference wave number is named as \({{k}_{0}}=k\). Then, the dimensionless reference wave number is 0.5, 1.0, 1.5 and 2.0, and the depth of the cavity is \({h}/{R}\;=2.0\). Because of the symmetry of the model, the DSCF are symmetric distributed in the results. When the inhomogeneous parameter is small (\(\beta <0.5\)), the distribution of DSCF is simple, and the value of DSCF are small under different wave numbers. Specially, when \(\beta =0.1\), the distribution of DSCF is similar with each other under different reference wave number. In Figs. 2, 3 and 4, the maximum of DSCF mostly occurs from \(\theta =0\) to \(\theta =\pi\) due to the amplification of mass density at the lower half part of the cavity is much larger than the one at the upper half part. However, when the inhomogeneous parameter increases (\(\beta \ge 0.5\)), the mass density of the half space becomes larger, the distribution of DSCF becomes complicated, and the dynamic stresses around the cavity enhance at the same time. Moreover, the maximum of DSCF has a tendency to move towards the direction of surface of the half space when the inhomogeneous parameter becomes larger. That may because the interaction of the scattering wave and the surface to raise the dynamic stress. Hence, it can be inferred that this kind of interaction have a bigger impact on the maximum of DSCF than the changes of mass density.

Fig. 8
figure 8

Distribution of DSCF with different depth (\(kR=0.5\))

Full size image
Fig. 9
figure 9

Distribution of DSCF with different depth (\(kR=1.0\))

Full size image
Fig. 10
figure 10

Distribution of DSCF with different depth (\(kR=1.5\))

Full size image
Fig. 11
figure 11

Distribution of DSCF with different depth (\(kR=2.0\))

Full size image

Figures 8, 9, 10 and 11 demonstrate the influence of depth of the cavity with different reference wave number on distribution of DSCF. The inhomogeneous parameter is \(\beta =1.0\), Alike the condition of the half space is homogeneous, the value of DSCF decreases with the depth increasing. Since the density difference between the upper and the lower parts are stable, the DSCF with different depth is mainly affected by the interaction between the scattering wave (induced by the cavity) and the surface. When the reference wave number is small (in Figs. 8 and 9), the maximum of DSCF is similar when the depth of the cavity increases. That may because the condition is similar to the static state. Even the reference equals to 1.0 (In Fig. 9), the maximum of DSCF decreases no more than 25% when the depth raises from 2.0 to 3.0. When the reference wave number turns bigger (in Figs. 10 and 11), the effect of the depth becomes evident. With the condition of \(kR=1.5\) and \(kR=2.0\), the maximum of DSCF decreases more than 50% even more than 100% with the depth increasing. That indicates when the depth of the cavity increases, the higher the wave frequency is, the bigger the interaction (between the cavity and the surface) decline is.

Fig. 12
figure 12

Distribution of DSCF with different inhomogeneous parameter (\(kR=0.5\))

Full size image
Fig. 13
figure 13

Distribution of DSCF with different inhomogeneous parameter (\(kR=1.0\))

Full size image
Fig. 14
figure 14

Distribution of DSCF with different inhomogeneous parameter (\(kR=1.5\))

Full size image
Fig. 15
figure 15

Distribution of DSCF with different inhomogeneous parameter (\(kR=2.0\))

Full size image

Since the half space is vertically inhomogeneous, the influences of the inhomogeneity on the distribution of DSCF need to be investigated. Figures 12, 13, 14 and 15 demonstrate the distribution of DSCF around the cavity with different inhomogeneous parameters under incident SH wave. The dimensionless wave numbers equal to 0.5, 1.0, 1.5 and 2.0, respectively. Generally speaking, the inhomogeneous parameter mainly play its role in changing the value of DSCF. That because the mass density of the half space varies with the inhomogeneous parameter. Moreover, it affects the distribution of DSCF as well. When the reference wave number equals to 0.5, the changing of inhomogeneous parameter can hardly influence the distribution of DSCF. However, when the reference wave number becomes larger, both influences on the distribution and maximum of DSCF by the inhomogeneous parameter are significant.

Fig. 16
figure 16

Variation of DSCF with increasing inhomogeneous parameters (\({h}/{R}\;=2.0\), \(\theta =0\))

Full size image
Fig. 17
figure 17

Variation of DSCF with increasing reference wave numbers (\({h}/{R}\;=2.0\), \(\theta =0\))

Full size image

Variation of DSCF around the cavity with increasing inhomogeneous parameters under different reference wave number is presented in Fig. 16. The location chosen of the cavity is at \(\theta =0\). With the inhomogeneous parameter augments, the value of DSCF tends to increase when \(\beta <1.0\). After that, the DSCF fluctuates when the inhomogeneous parameter increases. That may be caused by the complicated interaction between the scattering wave and the surface. Especially, in the range of \(0.3<\beta <0.7\) (marked by dotted box), the value of DSCF varies little with inhomogeneous parameter with four different reference wave numbers. Besides, if the reference wave number is big, the DSCF usually fluctuates more evidently than the condition of a small reference wave number.

Figure 17 presents the variation of DSCF when the reference wave number increases from 0.1 to 6. Three different inhomogeneous parameters (\(\beta =0.8,\text { }0.9{\text { and }}1.0\)) are considered. The variations of DSCF are absolutely opposite between \(0.1<kR<2.0\) and \(2.0<kR<4.0\). When reference wave number bigger than 4.0, the DSCF begins to fluctuate with the wave number increasing because of the same reason in Fig. 16. With the condition of \(0.1<kR<2.0\), a bigger inhomogeneous parameter has a faster increasing tendency of DSCF. Similarly, the decreasing slope of the curve has positive correlation with inhomogeneous parameter as well with the condition of \(2.0<kR<4.0\).

6 Conclusions

Based on complex function method and multi-polar coordinates system, dynamic stress concentration factor (DSCF) around a cylindrical cavity in inhomogeneous half space is investigated. In order to solve the governing equation with variable coefficients, the conformal mapping method is applied. Then, by utilizing the boundary condition at the cavity, wave fields and corresponding stresses are solved. Finally, DSCF around the cavity is obtained and discussed, and some conclusions are summarized:

  1. (1)

    The distribution of DSCF is mainly influenced by reference wave number and inhomogeneous parameter. The increase of kR and \(\beta\) causes the distribution of DSCF to be complicated and may change the position of maximum of DSCF. Moreover, the distribution of DSCF is influenced by depth of the cavity as well.

  2. (2)

    The enhancement on DSCF by the interaction between the scattering wave and the surface surpasses the one by the increase of mass density of the half space.

  3. (3)

    The decline of the interaction (between the scattering wave and the surface) grows with the wave frequency.

  4. (4)

    The influence of the interaction (between the scattering wave and the surface) on DSCF becomes complicated with high mass density (\(\beta >1\)) and wave frequency (\(kR>4\)).