1 Introduction

The theory of elastic wave scattering has been established for a long time. The problem of elastic wave propagation in homogeneous media has been introduced in detail in reference [1]. Considering the bond between inclusion and the embedding matrix is damaged in the circumferential direction, the wave scattering characteristics of homogeneous inclusions are analyzed by [2].

In many Engineering fields, materials with inhomogeneous properties are widely used. To satisfy the requirements of the Engineering, a variety of artificial materials are designed. To investigate the propagation characteristics of waves in inhomogeneous medium, an adequate study is necessary. Hence, a variety of inhomogeneous forms have been studied. Based on the theory of complex variable functions, Liu et al. studied the scattering problems of SH waves with one-dimensional variations in both shear modulus and density [3, 4]. Yang et al. have carried out a series of studies on the scattering of SH waves in density inhomogeneous media [5, 6]. The boundary integral equation method is also an effective tool in solving the problem of wave propagation in inhomogeneous media, which is described in detail in [7].

Earlier, the propagation dispersion characteristics and displacement distributions of various surface waves were studied by Vrettos in which the shear modulus varies according to an exponential function polynomial [8, 9]. Subsequently, combined with the transfer matrix method, Vrettos studied the dynamic response of SH wave in the vertical inhomogeneous medium [10]. So far, there are many proven methods and results for the problem of wave propagation in inhomogeneous media. However, there are relatively few studies of inhomogeneous media where the shear modulus and shear wave velocity are variable. Therefore, in this work, the complex function method [11] and the conformal mapping technique are used to solve the scattering problem caused by SH wave in the modulus inhomogeneous medium. Conformal mapping technology is an effective method to deal with the problem of variable wave velocity [12].

2 Calculation model and Governing equations

2.1 Calculation model

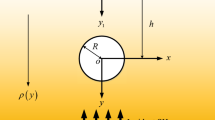
The scattering model of SH waves in inhomogeneous half space has been established in Fig. 1. The inhomogeneity of the medium is reflected in that the shear modulus is a function of the (x,y). xoy and x1y1z1 are coordinate systems of the horizontal surface and circular cavity respectively. The position of the circular cavity can be determined by h and d. The form of shear modulus is expressed as

$$\mu \left( {x,y} \right) = \mu_{0} \left( {\beta^{2} \left( {x^{2} + y^{2} } \right) + 2\gamma \beta x + \gamma^{2} } \right)$$
(1)

where β and γ are inhomogeneous parameters. If γ  = 1 and β is infinitesimal, the form of medium is similar to the homogeneous medium.

Fig. 1
figure 1

Calculation model of scattering problem

Full size image
Fig. 2
figure 2

Comparison of DSCF around circular cavity

Full size image

2.2 Governing equations

For anti-plane shear problems, the equation in the following form is obtained according to the equation of motion and the constitutive relation

$$\frac{{\partial \left( {\mu (x,y)\frac{\partial w}{{\partial x}}} \right)}}{\partial x} + \frac{{\partial \left( {\mu (x,y)\frac{\partial w}{{\partial y}}} \right)}}{\partial y} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }}$$
(2)

To simplify the equation, displacement auxiliary functions are introduced

$$Aux\left( {x,y} \right) = \sqrt {\left( {\beta^{2} x^{2} + \beta^{2} y^{2} + 2\gamma \beta x + \gamma^{2} } \right)^{ - 1} }$$
(3)
$$w(x,y) = \varphi (x,y)Aux\left( {x,y} \right)$$
(4)

Based on the complex function theory and conformal mapping technology, a new pair of variables are introduced

$$\zeta = \ln \left( {\beta z + \gamma } \right),\overline{\zeta } = \ln \left( {\beta \overline{z} + \gamma } \right)$$
(5)

For a steady state problem, the governing equation can be expressed as

$$\frac{{\partial^{2} \varphi }}{{\partial \zeta \partial \overline{\zeta }}} + \frac{1}{4}k_{T}^{2} \varphi = 0$$
(6)

where kT2 = k02/β2 − 1 and k0 is the reference wave number.

3 Displacement fields and stresses

There are incident waves, reflected waves generated by horizontal surface and scattering waves generated by circular cavity in half space.

$$w^{i} = \varphi_{0} Aux\left( {\zeta ,\overline{\zeta }} \right)\exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta e^{ - i\alpha } + \overline{\zeta }e^{i\alpha } } \right)} \right]$$
(7)
$$w^{r} = \varphi_{0} Aux\left( {\zeta ,\overline{\zeta }} \right)\exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta e^{i\alpha } + \overline{\zeta }e^{ - i\alpha } } \right)} \right]$$
(8)
$$\begin{aligned} w^{s} & = Aux\left( {\zeta ,\overline{\zeta }} \right)\sum\limits_{n = - \infty }^{\infty } {A_{n} } \left[ {H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{1} } \right|} \right)\left( {\frac{{\zeta_{1} }}{{\left| {\zeta_{1} } \right|}}} \right)^{n} } \right. \\ & \quad \left. { +\, H_{n}^{(1)} \left( {k_{T} \left| {\zeta_{2} } \right|} \right)\left( {\frac{{\zeta_{2} }}{{\left| {\zeta_{2} } \right|}}} \right)^{ - n} } \right] \\ \end{aligned}$$
(9)

where the superscripts i, r and s correspond to incident wave, reflected wave and scattering wave respectively. An are undetermined coefficients and Hn(1) is the first type of Hankel function of order n.

To solve the unknown coefficient An conveniently, the stress expressions are given in polar coordinates (Eqs. (14) and (15) in Ref. [5]).

4 Boundary conditions and dynamic stress concentration factor (DSCF)

The unknown coefficients in the scattering waves can be solved by boundary conditions. The radial stress on the circular cavity should be zero. Therefore, the boundary condition can be expressed as

$$\tau_{rz}^{i} + \tau_{rz}^{r} + \tau_{rz}^{s} = 0,r_{1} = R$$
(10)

Stress concentration is an important index to describe structural stability. The expression of surface displacement amplitude and dynamic stress concentration factor can be expressed as

$$w = w^{i} + w^{r} + w^{s} = \left| w \right|e^{i\omega \psi }$$
(11)
$$\tau_{\theta z}^{*} = \left| {\left( {\tau_{\theta z}^{i} + \tau_{\theta z}^{r} + \tau_{\theta z}^{s} } \right)/\tau_{0} } \right|$$
(12)

where τ0 is the stress amplitude of incident wave and \(\left| w \right|\) is the displacement amplitude.

5 Numerical example and discuss

The comparison of DSCF between this paper and homogeneous medium is shown in Fig. 1. when β = 10–6, the DSCF of this work has a good consistency with the homogeneous situation (Fig. 2). However, when β = 10–5, there are some differences between DSCF due to the inhomogeneity of the medium. Therefore, a conclusion for reference can be concluded that this working inhomogeneous medium can be recovered to the homogeneous medium when the β is smaller than 10–6.

Dependence of the surface displacement amplitude on η and h is shown in Fig. 3. According to Fig. 3a, the influence of η on the displacement amplitude is mainly reflected in the fluctuation of the displacement amplitude. At high frequency, obvious fluctuation occurs on the projection side and the extreme value of displacement amplitude decreases gradually. According to Fig. 3b, the distribution of displacement amplitude mainly presents a downward trend. The buried depth of the circular cavity mainly affects the value of displacement amplitude.

Fig. 3
figure 3

Distribution of surface displacement amplitude

Full size image

Dependence of the DSCF on β and k0R is shown in Fig. 4. The amplitude of DSCF is changed by changing the parameters β, but the distribution of DSCF is basically the same. The reason for this situation is that the inhomogeneity of the medium will be more obvious if the β is increased. The stress concentration around the circular cavity is more likely to occur at the position with small shear modulus. According to Fig. 4b, in the [0°, 90°], the extreme points of DSCF will gradually decrease with the increase of k0R, and the distribution is also different. Meanwhile, in the [90°,360°], the distribution trend of the DSCF is roughly similar at different k0R. This indicates that the variation of the reference wave number has a large effect on the shadow side.

Fig. 4
figure 4

Distribution of DSCF around circular cavity

Full size image

6 Conclusions

In this work, the scattering problem of SH wave caused by circular cavity in shear modulus inhomogeneous medium is solved by using complex function theory and conformal mapping technique. In order to analyze the importance of parameters, the distribution of surface displacement amplitude and dynamic stress concentration factor (DSCF) are discussed. The following conclusions are obtained for the reference.

  1. 1.

    Different wave numbers η can cause different fluctuations in displacement amplitude. At high frequency, the distribution of displacement amplitude will appear in the situation of increasing extreme points and obvious fluctuation phenomena. The buried depth mainly affects the value of displacement amplitude.

  2. 2.

    The influence of inhomogeneous parameters on DSCF is more obvious than that of reference wave number. The maximum value of the DSCF appears on the project side. This shows that the projection side of circular cavity is more susceptible affected by the stress concentration in the inhomogeneous medium of this study.