Frequency domain approach for probabilistic flutter analysis using stochastic finite elements

Abstract

In this work, a stochastic finite element method based on first order perturbation approach is developed for the probabilistic flutter analysis of aircraft wing in frequency domain. Here, both bending and torsional stiffness parameters of the wing are treated as Gaussian random fields and represented by a truncated Karhunen–Loeve expansion. The aerodynamic load on the wing is modeled using Theodorsen’s unsteady aerodynamics based strip theory. In this approach, Theodorsen’s function, which is a complex function of reduced frequency, is also treated as a random field. The applicability of the present method is demonstrated by studying the probabilistic flutter of cantilever wing with stiffness uncertainties. The present method is also validated by comparing results with Monte Carlo simulation (MCS). From the analysis, it is observed that torsional stiffness uncertainty has significant effect on the damping ratio and frequency of the flutter mode as compared to bending stiffness uncertainty. The probability density functions of damping ratio and frequency using perturbation technique and MCS are also discussed at various free stream velocities due to stiffness uncertainties. Furthermore, the flutter probability of the cantilever wing is studied by defining implicit limit state function in conditional sense on flow velocity for the flutter mode. Both perturbation and MCS are considered to study the flutter probability of the wing. From the cumulative distribution functions of flutter velocity, it is noticed that the presence of uncertainty in torsional rigidity lowers the predicted flutter velocity in comparison to uncertainty in bending rigidity.

1 Introduction

Aeroelasticity is the study of the effect of aerodynamic forces on elastic structures. The critical aeroelastic phenomena which have major concern in the design of air vehicles are Divergence and Flutter. Divergence is a steady state aeroelastic phenomenon related to the lift redistribution on lifting surfaces in which, excessive elastic deformation leads to unstable wing. Flutter is a dynamic aeroelastic instability phenomenon due to interaction of unsteady aerodynamic, inertial, and elastic forces which results in unstable self excited oscillations of lifting components (Fung [13]). Here, the power pumped into the aeroelastic system by interaction of aerodynamic loads is not completely dissipated by the system dissipative mechanisms which often leads to catastrophic structural failure of lifting components. The power balance between aerodynamic and dissipative system leads to constant amplitude harmonic oscillation for one of the aeroelastic modes. The velocity at which this balance occurs is called the flutter velocity and the frequency corresponding to its harmonic oscillation is called the flutter frequency.

Every phenomena observed in nature is essentially uncertain. The most acceptable classification of uncertainty was described by Melcher [27]: aleatory or irreducible uncertainty, the most common example for which is uncertainty in system’s parameter and epistemic uncertainty, which is related to lack of the knowledge about physical phenomena being observed, and uncertainty due to human error. In general aleatory uncertainty is handled by probabilistic description of the system parameters. Traditionally, deterministic flutter analysis is carried out for single aircraft which represents a set of aircraft of same series. However, it doesn’t capture the flutter behavior of the whole series of aircraft because of variation in aircraft weight, inertia, stiffness etc. [30]. In order to address the effect of system’s parameter uncertainty on the response of aeroelastic system, probabilistic aeroelastic analysis must be carried out. Pettit [29] addressed the importance and challenges of uncertainty quantification in aeroelasticity viz. LCO of airfoils and panels subjected to parametric uncertainty. The aeroelastic analysis by considering structural uncertainty was carried out by many researchers [5, 26, 36]. Castravete and Ibrahim [7] investigated the influence of bending and torsional stiffness parameters uncertainty modeled as Gaussian random fields on the flutter of cantilever wing in time domain. Kurdi et al. [24] modeled the aircraft wing as box type structure consisting of 3 spars and 11 ribs. The thickness of each upper and lower wing skins, spars, ribs, and area of posts, spars, and ribs caps were modeled as Gaussian random variables. The probabilistic flutter analysis using MSC-Nastran, ZONA 6 module for flutter, and MCS, showed that wing with tip store mass was highly sensitive in transonic regime, and indicated  trimodal probability density function (pdf) of flutter velocity. Khodaparast et al. [22] considered same aircraft wing discussed in [24] and carried out both probabilistic based perturbation method and non probabilistic based interval and fuzzy logic methods for determining flutter velocity pdf and bounds of flutter velocity respectively. Danowsky et al. [10] used a reduced order model based on high fidelity combined CFD–FEM nonlinear aeroelastic model to carryout aeroelastic uncertainty analysis of AGARD 445.6 wing subjected to structural and aerodynamic uncertainty using MCS, Response surface, and $\mu$ methods in subsonic and transonic flow regimes. Beran et al. [3] addressed the limit cycle oscillation of rigid airfoil supported by pitch and plunge structural coupling, with nonlinearities in pitch component. The uncertainty in the system was introduced through cubic torsional stiffness coefficient and initial pitch angle. The stochastic response was obtained using Weiner Hermite based intrusive, and Haar wavelet and B-Spline based non-intrusive methods. Desai and Sarkar [11] studied the bifurcation behavior of pitch plunge airfoil subjected to parametric uncertainties in cubic spring and viscous damping using polynomial chaos expansion (PCE) based on both intrusive and non-intrusive techniques. They observed that due to uncertain damping, bifurcation point was shifted towards lower value. Dai and Yang [9] gave comprehensive idea about both probabilistic and non-probabilistic aeroelasticity with greater emphasis on the robust aeroelastic study based on structured singular value ($\mu$-method). Riley et al. [34] presented a methodology for the quantification of modeling uncertainty using adjustment factor approach and Bayesian model averaging method. The mean and standard deviation of flutter velocity obtained from Bayesian model averaging approach is better than average adjustment factor approach as, it can accommodate experimental datasets. Riley and Grandhi [33] developed an approach for quantification of modeling induced uncertainty and parametric uncertainties using Bayesian model averaging approach. The developed approach provides a greater insight to designer to address the uncertain system response arising from model, parametric, and predictive uncertainties. Wu and Livne [40] presented two approaches to aerodynamic modeling uncertainty. In the first approach, uncertainty modeling was based on difference between Aerodynamic Influence coefficients (AICs) obtained from CFD and linear aerodynamic theory. In the second approach aerodynamic uncertainty was based on Rational functional approximation matrices. Both approaches were demonstrated by analyzing AGARD 445.6 wing in subsonic and transonic regimes. It was observed that largest uncertainty in flutter velocity and frequency prediction occurred in transonic regime. Recently, Beran et al. [2] reviewed the published articles on uncertainty quantification of aeroelastic system based on both traditional and computational aeroelastic techniques to study various phenomena such as flutter, LCO, bifurcation etc.

In the field of aeroelasticity, several authors carried out the aeroelastic reliability study. Cheng and Xiao [8] proposed a hybrid method based on Response surface method (RSM), FEM, and MCS to carryout the probabilistic free vibration and flutter analysis of suspension bridges. Borello et al. [4] studied the effect of structural uncertainty (as Gaussian RVs) on classical wing flutter, and results were presented in terms of Cumulative distribution function (CDF) of flutter speed. The interval based nonprobabilistic reliability method was developed by Wang and Qiu [39] for wing flutter reliability assessment based on flutter wind speed and natural wind speed interference model. Verhoosel et al. [38] proposed perturbation and importance sampling based methods to carryout aeroelastic uncertainty analysis of panel, where the elastic modulus of panel was represented by one dimensional Lognormal field. Canor et al. [6] investigated the flutter probability of long span bridge using various numerical techniques such as perturbation, collocation, and Galerkin approaches and indicated the advantages and limitation of each method. Recently, Pourazarm et al. [31] carried out the reliability analysis of wind turbine blade failure due to flutter having uncertainty in sectional lift coefficient and torsional natural frequency with Uniform and Gaussian distributions. For the reliability analysis First order reliability method (FORM), Second order reliability method (SORM), FORM-C and proposed Weighted average reliability method (WARM) were used. Among them, WARM was found to be the most accurate. It is noted that in these methods, the expansion of eigenvalue was carried out about the mean value of random parameters. The reliability sensitivity analysis of axially moving beam and a plate interacting with stochastic axial flow were carried out by Yao and Zhang [41] and Yao et al. [42] respectively using Mean value first order second moment (MVFOSM) method for divergence type instability. The reliability sensitivity analysis was carried out by taking derivative of reliability function with respect to mean and standard deviation of random variables separately.

From the literature survey presented above, it is noticed that studies carried out in the area of probabilistic aeroelasticity and reliability analysis of structures are limited to uncertain parameters modeled as random variables. It is also noted that uncertain parameter modeling as random fields has taken little consideration from aeroelastic analysis point of view, especially in frequency domain. This has motivated the authors to develop frequency domain approach by treating stiffness parameters as random fields to carryout probabilistic flutter analysis and extend it to reliability analysis.

In this paper, a novel approach based on stochastic finite element method (SFEM) for the probabilistic flutter analysis of wing is proposed. The uncertain stiffness parameters such as bending and torsional rigidities are modeled as second order Gaussian random fields with exponential isotropic covariance function. These random fields are expressed using truncated Karhunen–Loeve (K–L) expansion, based on spectral decomposition of covariance function, for their accurate representation with better convergence properties. The unsteady aerodynamic load on the wing is modeled by Theodorsen’s aerodynamics based strip theory, which is a complex function of reduced frequency. A first order perturbation approach is applied to study the probabilistic flutter characteristics of cantilever wing. The effect of bending and torsional stiffness uncertainties on the statistics of frequency and damping ratio of various modes of cantilever wing is studied and compared with Monte Carlo simulations. Furthermore, the flutter probability of the cantilever wing is studied using perturbation and MCS approaches by defining implicit limit state function in conditional sense on flow velocity for the flutter mode.

2 Mathematical modeling

Fig. 1

Schematic representation of a generic cantilever wing

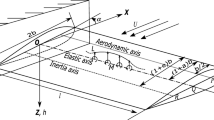
A uniform cross section straight cantilever wing [16] with random stiffness characteristics is shown in Fig. 1. Here, the wing is modeled as a 1-D beam where the geometric coupling in the beam arises due to non-coincidence of elastic and inertia axes. In this figure, point O represents the origin of the axes system and points F, G, and H denote the locations of aerodynamic center, center of gravity, and shear center of cross-section respectively. The span of wing is represented by l and the distances of inertia and elastic axes from the leading edge of the wing are $(1+e)b$ and $(1+a)b$ respectively, where a and e are dimensionless parameters ranging from − 1 to 1 and b is semi-chord length. h and $\alpha$ represent the heave and pitch displacements of the wing respectively. L and M are the aerodynamic lift and moment acting on the wing respectively.

The kinetic energy of the wing can be written as:

$$\begin{aligned} T=\frac{1}{2}\int _0^l{I_p\dot{\alpha }^2dy}+\frac{1}{2}\int _0^l{m\dot{h}^2 dy}+\int _0^l{mx_{\alpha }b\dot{h}\dot{\alpha }dy} \end{aligned}$$

(1)

where $I_p$, m, and $x_\alpha (=e-a)$ are mass moment of inertia per unit span about elastic axis, mass per unit span, and dimensionless static unbalance respectively and the dot ($\dot{}$) denotes time derivatives.

The potential energy of the wing can be written as:

$$\begin{aligned} V=\frac{1}{2}\int _0^l{EI\left( \frac{\partial ^2h}{\partial y^2}\right) ^2dy} +\frac{1}{2}\int _{0}^{l}{{GJ\left( \frac{\partial \alpha }{\partial y}\right) ^{2}dy}} \end{aligned}$$

(2)

where EI and GJ are bending and torsional rigidities respectively.

The external virtual work done by the aerodynamic lift (L) and moment (M) can be expressed as:

$$\begin{aligned} \delta {W_{ext}}=-\int _{0}^{l}{Ldy\delta {h}}+\int _{0}^{l}{Mdy\delta \alpha } \end{aligned}$$

(3)

where $M=M_{1/4}+L(1/2+a)b$ about elastic axis and $M_{1/4}$ is the moment per unit span at quarter chord. Now using Hamilton’s principle:

$$\begin{aligned} \int _{t_1}^{t_2}{[\delta {(T-V)}+\delta {W_{ext}}]dt=0} \end{aligned}$$

(4)

After substituting Eqs. (1–3) in Eq. (4) and performing integration by parts, the governing equation of aeroelastic system can be expressed as:

$$\begin{aligned} m\ddot{h}+mx_{\alpha }b\ddot{\alpha }+\frac{\partial ^2}{\partial y^2}\left( EI\frac{\partial ^2h}{\partial y^2}\right) +L= \,& {} 0 \end{aligned}$$

(5)

$$\begin{aligned} I_p\ddot{\alpha }+mx_{\alpha }b\ddot{h}-\frac{\partial }{\partial y}\left( GJ\frac{\partial \alpha }{\partial y}\right) -M= \,& {} 0 \end{aligned}$$

(6)

According to Theodorsen’s unsteady aerodynamics based strip theory [35], the lift and moment (per unit span) at the aerodynamic center which is located at quarter chord of the section can be written as:

$$\begin{aligned} L= \,& {} 2\pi \rho _{\infty }bUC(k)\left( U\alpha +\dot{h}+b\left( \frac{1}{2}-a\right) \dot{\alpha }\right) \nonumber \\&+\,\pi \rho _{\infty }b^2\left( \ddot{h}+U\dot{\alpha }-ba\ddot{\alpha }\right) \end{aligned}$$

(7)

$$\begin{aligned} M_{1/4}= \,& {} -\pi \rho _{\infty }b^3\left( \frac{1}{2}\ddot{h}+U\dot{\alpha }+b\left( \frac{1}{8}-\frac{a}{2}\right) \ddot{\alpha }\right) \end{aligned}$$

(8)

where $\rho _{\infty }$, U, and C(k) are free stream density, free stream velocity, and Theodorsen’s function (Complex function of reduced frequency) [35] respectively. After obtaining weak form of governing differential Eqs. (5) and (6), and substituting suitable finite element approximation for heave (h) and pitch $(\alpha )$ displacements, the finite element equations for $i^{th}$ element can be expressed as:

$$\begin{aligned}&\left[ M_{SB}\right] \{\ddot{w}_e\}+\left[ M_{AB}\right] \{\ddot{w}_e\}+\left[ M_{SC}\right] \{\ddot{\alpha }_e\}+\left[ M_{AC}\right] \{\ddot{\alpha }_e\}\nonumber \\&\qquad +\,\left[ C_{AB}\right] \{\dot{w}_e\}+\left[ C_{AC}^{12}\right] \{\dot{\alpha }_e\}+\left[ K_{AC}\right] \{\alpha _e\}+\left[ K_{SB}\right] \{w_e\}\nonumber \\&\quad =\{F_i\} \end{aligned}$$

(9)

$$\begin{aligned}&\left[ M_{ST}\right] \{\ddot{\alpha }_e\}+\left[ M_{AT}\right] \{ \ddot{\alpha }_e\}+\left[ M_{SC}\right] \{\ddot{w}_e\}+\left[ M_{AC}\right] \{\ddot{w}_e\}\nonumber \\&\qquad +\,\left[ C_{AT}\right] \{\dot{\alpha }_e\}+\left[ C_{AC}^{21}\right] \{\dot{w}_e\}+\left[ K_{AT}\right] \{\alpha _e\}+\left[ K_{ST}\right] \{\alpha _e\}\nonumber \\&\quad =\{\tau _i\} \end{aligned}$$

(10)

where $[M_{SB}]$, $[M_{SC}]$, and $[M_{ST}]$ are elemental structural bending, bending-torsional structural coupled, and torsional inertia matrices respectively; $[M_{AB}]$, $[M_{AC}]$, and $[M_{AT}]$ are aerodynamic bending, bending-torsional aerodynamic coupled, and aerodynamic torsional inertia matrices respectively. Similarly, $[K_{SB}]$ and $[K_{ST}]$ are elemental structural bending and torsional stiffness matrices respectively; $[K_{AC}]$ and $[K_{AT}]$ are aerodynamic bending-torsion coupled and aerodynamic torsional stiffness matrices respectively. Furthermore, $[C_{AB}]$ and $[C_{AT}]$ are elemental aerodynamic bending and torsional damping matrices respectively, and $[C_{AC}^{12}]$ is aerodynamic bending-torsion coupled damping matrix. Here, $\{F_i\}$ and $\{\tau _i\}$ are the internal load vectors, which vanish completely after assembly of elemental equations and application of boundary conditions. The elemental bending and torsional degrees of freedom for $i^{th}$ element are denoted as $\{w_e\}=\lfloor h_i, \frac{\partial {h_i}}{\partial {y}}, h_{i+1}, \frac{\partial {h_{i+1}}}{\partial {y}} \rfloor ^T$ and $\{\alpha _e\}=\lfloor \alpha _i, \alpha _{i+1} \rfloor ^T$ respectively. The detailed formulation and the expression for each term in Eqs. (9) and (10) are given in “Appendix”.

3 Stochastic modeling

The aleatory uncertainties present in the structural systems such as bending stiffness (EI) and torsional stiffness (GJ) are considered as random parameters, and modeled by second order stationary Gaussian random process. The stochastic bending and torsional stiffness parameters can be represented as:

$$\begin{aligned} EI(y,\theta )= \,& {} \overline{EI} + \widehat{EI}(y,\theta ) \end{aligned}$$

(11)

$$\begin{aligned} GJ(y,\theta )= \,& {} \overline{GJ}+\widehat{GJ}(y,\theta ) \end{aligned}$$

(12)

where $\overline{EI}$ and $\overline{GJ}$ are the mean values of the bending and torsional stiffness parameters respectively. $\widehat{EI}(y,\theta )$ and $\widehat{GJ}(y,\theta )$ are zero mean Gaussian random processes with same covariance kernel as EI and GJ. The isotropic exponential covariance function $(\kappa )$ considered for random process can be expressed as:

$$\begin{aligned} \kappa (y,y_1)=\bar{\sigma }^2e^{c |y-y_1| } \end{aligned}$$

(13)

where $\bar{\sigma }$ is the standard deviation of the process and c is the reciprocal of correlation length ($l_{cor}$). Here, correlation length is considered as wing span length (l). The random process with known covariance kernel can be expressed by the truncated Karhunen–Loeve expansion [19] in N dimensional space as:

$$\begin{aligned} \chi \left( y,\theta \right) =\overline{\chi }+\sum _{n=1}^{N}\sqrt{\lambda _{n}}\xi _{n}(\theta )f_n(y) \end{aligned}$$

(14)

where $\overline{\chi }$ is the mean of the process $\chi (y,\theta )$, and $\lambda _{n}$ and $f_n(y)$ are the $n^{th}$ eigenvalue and eigenfunction of the process. $\xi _{n}(\theta )$ are zero mean $(E(\xi _{n}(\theta ))=0)$ and orthonormal random variables $E(\xi _{m}(\theta ),\xi _{n}(\theta ))=\delta _{mn}$ with respect to Gaussian basis, where $\delta _{mn} =1$ when $(m=n)$ and $=0$ when $(m\ne {n})$. The eigenvalues and eigenfunctions of the process can be obtained by solving the fredholm integral of equation of second kind [37] represented in kernel form as:

$$\begin{aligned} \int _{l}\kappa (y,y_1)f_n(y_1)dy_1=\lambda _{n}f_n(y) \end{aligned}$$

(15)

The eigenfunctions show the condition of orthonormality as follows:

$$\begin{aligned} \int _{l}f_m(y)f_n(y)dy=\delta _{mn} \end{aligned}$$

(16)

Equation (15) can be solved for eigenvalues and eigenfunctions both analytically (for limited covariance kernel) and numerically. Here, in the present case, analytical procedure is adopted for obtaining eigenvalues and eigenfunctions of the covariance function [15, 37]. The eigenfunction obtained from the kernel Eq. (15) is optimal in the sense of mean square error resulting from finite representation of the process [15]. The expression for eigenvalue can be written as [15, 37]:

$$\begin{aligned} \lambda _{n}=\frac{2\bar{\sigma }^2c}{c^2+\varpi _n^2} \end{aligned}$$

(17)

where $\varpi _n$ is a parameter obtained by solving Eqs. (18) and (19) for odd and even values of n respectively.

$$\begin{aligned} \tan (\varpi _n\frac{l}{2})-\frac{c}{\varpi _n}= \,& {} 0 \end{aligned}$$

(18)

$$\begin{aligned} \tan (\varpi _n\frac{l}{2})+\frac{\varpi _n}{c}= \,& {} 0 \end{aligned}$$

(19)

The eigenfunctions corresponding to the odd and even values of subscript n can be written as:

$$\begin{aligned} f_n(y)= \,& {} \frac{\cos (\varpi _ny)}{\frac{l}{2}+\frac{\sin (\varpi _nl)}{2\varpi _n}} \end{aligned}$$

(20)

$$\begin{aligned} f_n(y)= \,& {} \frac{\sin (\varpi _ny)}{\frac{l}{2}-\frac{\sin (\varpi _nl)}{2\varpi _n}} \end{aligned}$$

(21)

It is important to note that eigenvalues are in descending order with increasing n. Having obtained eigenvalues and eigenfunctions of covariance function, and substituting the spectral representation of EI and GJ in elemental stiffness matrices $\left[ K_{SB}\right]$ and $\left[ K_{ST}\right]$ in Eqs. (50) and (51), the elemental structural stiffness matrices can be expressed as:

$$\begin{aligned} \left[ K_{SB}\right]= \,& {} \overline{EI}\int _{y_i}^{y_{i+1}}{\lfloor N_w^{''}\rfloor ^T\lfloor N_w^{''}\rfloor dy}\nonumber \\&+\,\sum _{n=1}^{N}\sqrt{\lambda _{n}}\xi _{n}\left( \theta \right) \int _{y_i}^{y_{i+1}}{f_n(y){\lfloor N_w^{''}\rfloor ^T\lfloor N_w^{''}\rfloor dy}} \end{aligned}$$

(22)

$$\begin{aligned} \left[ K_{ST}\right]= \,& {} \overline{GJ}\int _{y_i}^{y_{i+1}}{\lfloor N_\alpha ^{'}\rfloor ^T\lfloor N_\alpha ^{'}\rfloor dy}\nonumber \\&+\,\sum _{n=1}^{N}\sqrt{\lambda _{n}}\xi _{n}\left( \theta \right) \int _{y_i}^{y_{i+1}}{f_n(y){\lfloor N_\alpha ^{'}\rfloor ^T\lfloor N_\alpha ^{'}\rfloor dy}} \end{aligned}$$

(23)

where $[K_{SB}]$ and $[K_{ST}]$ are stochastic elemental stiffness matrices due to uncertain bending and torsional rigidity respectively. Here, the above expressions can be rewritten as $[K_{SB}]= [\bar{K}_{B}^e] +\sum _{n=1}^{N}[K_{B,n}^e]\xi _{n}(\theta )$ and $[K_{ST}]=[\bar{K}_{T}^e] +\sum _{n=1}^{N}[K_{T,n}^e]\xi _{n}(\theta )$, where the first term represents the mean and the second term is random term by virtue of K–L expansion. Now assembling the elemental Eqs. (9) and (10), and using Eqs. (22) and (23) we can get the assembled form of stochastic finite element equations as:

$$\begin{aligned}&\left( [M_S]+[M_A]\right) \{\ddot{q}\}+\left( U[C_A]+UC(k)[C_{A\omega }]\right) \{\dot{q}\}\nonumber \\&\quad +\,([\bar{K}_B]+\sum _{n=1}^{N}\xi _{n}\left( \theta \right) [K_{B,n}]+[\bar{K}_T]+\sum _{n=1}^{N}\xi _{n}\left( \theta \right) [K_{T,n}]\nonumber \\&\quad +\,U^2C(k)[K_{A\omega }])\{q\}=\{0\} \end{aligned}$$

(24)

where $[M_S]$ and $[M_A]$ are the structural and aerodynamic inertia matrices respectively. $U[C_{A}]$ is the aerodynamic damping matrix, and $(UC(k)[C_{A\omega }])$ and $(U^2C(k)[K_{A\omega }])$ are the frequency dependent aerodynamic damping and stiffness matrices respectively. $[\bar{K}_B]$ and $[\bar{K}_T]$ are the mean structural bending and torsional stiffness matrices respectively, and $\sum _{n=1}^{N}\xi _{n}(\theta )[K_{B,n}]$ and $\sum _{n=1}^{N}\xi _{n}(\theta )[K_{T,n}]$ are random structural bending and torsional stiffness matrices respectively. $\{q\}$ is the generalized displacement vector containing three DOFs ($h, \frac{\partial {h}}{\partial {y}}$ and $\alpha$) at each node. Now, substituting $\{q\}=\{{q_o}\}\exp {(\gamma t)}$ in Eq. (24), we get second order random eigenvalue problem as:

$$\begin{aligned}&(\gamma ^2\left( [M_S]+[M_A]\right) +\gamma \left( U[C_A]+UC(k)[C_{A\omega }]\right) \nonumber \\&\quad +\, ([\bar{K}_B]+\sum _{n=1}^{N}\xi _{n}\left( \theta \right) [K_{B,n}]+[\bar{K}_T]+\sum _{n=1}^{N}\xi _{n}\left( \theta \right) [K_{T,n}]\nonumber \\&\quad +\,U^2C(k)[K_{A\omega }]))\{{q_o}\}=\{0\} \end{aligned}$$

(25)

where $\gamma =-\zeta \omega +i\omega$, $\zeta$ and $\omega$ are the damping ratio and frequency of the aeroelastic system. The above equation will be solved using perturbation approach in the next section.

4 Perturbation approach

There are various techniques available for uncertainty propagation through aeroelastic model such as random perturbation approach [23], stochastic collocation technique [25], and PCE based Galerkin methods [14, 15]. In this study, perturbation approach is used because of its relative simplicity to the mathematical formulation and low computational cost compared to other methods [6]. For small dispersion, the first order Taylor series is a good approximation where all random response quantities are expanded about their mean values [23]. Since the bending and torsional stiffness are treated as random parameters, the response quantities such as eigenvalues, eigenvectors, and Theodorsen’s function of the aeroelastic system must be random. Hence, the random response quantities of the $j^{th}$ mode expanded via Taylor series retaining only first order term can be expressed as:

$$\begin{aligned} \gamma _j= \,& {} \bar{\gamma }_j+\sum _{n=1}^{N}{\left( \frac{\partial {\gamma }_j}{\partial {\xi _n}(\theta )}\right) _{\xi _n(\theta )=0}\xi _n(\theta )} \end{aligned}$$

(26)

$$\begin{aligned} \{{q_o}\}_j= \,& {} \{\bar{q}_o\}_j+\sum _{n=1}^{N}{\left( \frac{\partial \{{q_o}\}_j}{\partial {\xi _{n}(\theta )}}\right) _{\xi _n(\theta )=0}\xi _n(\theta )}\end{aligned}$$

(27)

$$\begin{aligned} C(k_j)= \,& {} C(\bar{k}_j)+\frac{b}{U}\sum _{n=1}^{N}{\left( \frac{\partial {C(k_j)}}{\partial {k_j}}\frac{\partial {Im(\gamma _j)}}{\partial {\xi _n}(\theta )}\right) _{\xi _n(\theta )=0}\xi _n(\theta )} \end{aligned}$$

(28)

where $\bar{\gamma _j}$, $\{\bar{q}_o\}_j$, and $C(\bar{k}_j)$ are the mean values of eigenvalue, eigenvector, and Theodorsen’s function of the $j^{th}$ mode respectively, $k_j=bIm(\gamma _j)/U$ is the reduced frequency of the mode and its derivative $\frac{\partial {k_j}}{\partial {\xi _{n}}}=\frac{b}{U}\frac{\partial {Im{(\gamma _j)}}}{\partial {\xi _{n}}}$. Here, $\xi _{n}$ are the same random variables as obtained by K–L expansion. Now, substituting Eqs. (26)–(28) in Eq. (25) and separating zeroth and first order terms, we get zeroth and first order equations as:

Zeroth order:

$$\begin{aligned}&(\bar{\gamma _j}^2\left( [M_S]+[M_A]\right) +\bar{\gamma _j}\left( U[C_A]+UC(\bar{k}_j)[C_{A\omega }]\right) \nonumber \\&\quad +\,([\bar{K}_B]+[\bar{K}_T]+U^2C(\bar{k}_j)[K_{A\omega }]))\{\bar{q}_o\}_j=\{0\} \end{aligned}$$

(29)

First order:

$$\begin{aligned}&(\bar{\gamma _j}^2\left( [M_S]+[M_A]\right) +\bar{\gamma _j}\left( U[C_A]+UC(\bar{k}_j)[C_{A\omega }]\right) \nonumber \\&\quad +\,([\bar{K}_B]+[\bar{K}_T]+U^2C(\bar{k}_j)[K_{A\omega }]))\frac{\partial \{{q_o}\}_j}{\partial {\xi _{n}}}+\frac{\partial {\gamma _j}}{\partial {\xi _n}}\nonumber \\&\qquad \left( 2\bar{\gamma _j}\left( [M_S]+[M_A]\right) +\left( U[C_A]+UC(\bar{k}_j)[C_{A\omega }]\right) \right) \{\bar{q}_o\}_j\nonumber \\&\quad +\,\frac{\partial {Im(\gamma _j)}}{\partial {\xi _n}}\big (\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k_j}}\bar{\gamma _j}U[C_{A\omega }]+\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k_j}}U^2[K_{A\omega }]\big )\nonumber \\&\qquad \{\bar{q}_o\}_j=-\,\left( [K_{B,n}]+[K_{T,n}]\right) \{\bar{q}_o\}_j \end{aligned}$$

(30)

The zeroth order is a mean flutter equation which is solved by pk method [18, 21] to obtain the mean flutter velocity and frequency of the aeroelastic system. To obtain the statistics of the frequency and damping ratio, we premultiply both sides of Eq. (30) by mean adjoint vector or transpose of the left eigenvector of $j^{th}$ mode $\{\bar{q}_{l}\}^T$ [1, 12, 17, 28] obtained from coefficient matrix of Eq. (29) as:

$$\begin{aligned}&\{\bar{q}_{l}\}_j^T(\bar{\gamma _j}^2\left( [M_S]+[M_A]\right) +\bar{\gamma _j}\left( U[C_A]+UC(\bar{k}_j)[C_{A\omega }]\right) \nonumber \\&\quad +\, ([\bar{K}_B]+[\bar{K}_T]+U^2C(\bar{k}_j)[K_{A\omega }]))\frac{\partial \{{q_o}\}_j}{\partial {\xi _{n}}}+\frac{\partial {\gamma _j}}{\partial {\xi _n}}\{\bar{q}_{l}\}_j^T\nonumber \\&\qquad \left( 2\bar{\gamma _j}\left( [M_S]+[M_A]\right) +\left( U[C_A]+UC(\bar{k}_j)[C_{A\omega }]\right) \right) \{\bar{q}_o\}_j\nonumber \\&\quad +\,\frac{\partial {Im(\gamma _j)}}{\partial {\xi _n}}\{\bar{q}_{l}\}_j^T\big (\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k_j}}\bar{\gamma _j}U[C_{A\omega }]+\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k}_j}U^2[K_{A\omega }]\big )\nonumber \\&\qquad \{\bar{q}_o\}_j=-\{\bar{q}_{l}\}_j^T\left( [K_{B,n}]+[K_{T,n}]\right) \{\bar{q}_o\}_j \end{aligned}$$

(31)

Here, the first term of Eq. (31) becomes zero. Hence, Eq. (31) can be rewritten as:

$$\begin{aligned}&\frac{\partial {\gamma _j}}{\partial {\xi _n}}\{\bar{q}_{l}\}_j^T\left( 2\bar{\gamma _j}\left( [M_S]+[M_A]\right) +\left( U[C_A]+UC(\bar{k}_j)[C_{A\omega }]\right) \right) \nonumber \\&\quad \{\bar{q}_o\}_j+\frac{\partial {Im(\gamma _j)}}{\partial {\xi _n}}\{\bar{q}_{l}\}_j^T\big (\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k_j}}\bar{\gamma _j}U[C_{A\omega }]+\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k}_j}\nonumber \\&\quad U^2[K_{A\omega }]\big )\{\bar{q}_o\}_j=-\{\bar{q}_{l}\}_j^T\big ([K_{B,n}]+[K_{T,n}]\big )\{\bar{q}_o\}_j \end{aligned}$$

(32)

The various terms of Eq. (32) can be represented as:

$$\begin{aligned}&\{\bar{q}_{l}\}_j^T\left( 2\bar{\gamma _j}\left( [M_S]+[M_A]\right) +\left( U[C_A]+UC(\bar{k}_j)[C_{A\omega }]\right) \right) \nonumber \\&\quad \{\bar{q}_o\}_j=\varepsilon +i\beta \end{aligned}$$

(33)

$$\begin{aligned}&\{\bar{q}_{l}\}_j^T\big (\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k}_j}\bar{\gamma _j}U[C_{A\omega }]+\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k}_j}U^2[K_{A\omega }]\big )\nonumber \\&\quad \{\bar{q}_o\}_j=\psi +i\vartheta \end{aligned}$$

(34)

$$\begin{aligned}&-\,\{\bar{q}_{l}\}_j^T\left( [K_{B,n}]+[K_{T,n}]\right) \{\bar{q}_o\}_j=\eta +i\varphi \end{aligned}$$

(35)

Since $\gamma _j = Re(\gamma _j)+ i\, Im(\gamma _j)$ and substituting it in Eq. (32) with terms represented by Eqs. (33)–(35), we get the eigenvalue derivative as:

$$\begin{aligned} \frac{\partial Re(\gamma _j)}{\partial \xi _{n}}= \,& {} \frac{\varphi (\psi -\beta )-\eta (\vartheta +\varepsilon )}{\beta (\psi -\beta )-\varepsilon (\vartheta +\varepsilon )}\nonumber \\ \frac{\partial Im(\gamma _j)}{\partial \xi _{n}}= \,& {} \frac{\eta \beta -\varphi \varepsilon }{\beta (\psi -\beta )-\varepsilon (\vartheta +\varepsilon )} \end{aligned}$$

(36)

Since $\gamma _j=-\,\zeta _j\omega _j+i\omega _j$, where the damping ratio $(\zeta _j)$ is the stability parameter, its value equal to zero represents stability boundary. The derivative of damping ratio and frequency can be written as:

$$\begin{aligned} \frac{\partial \zeta _j}{\partial {\xi }_n}= \,& {} -\frac{1}{\bar{\omega _j}}\left( \frac{\partial Re(\gamma _j)}{\partial \xi _{n}}+\bar{\zeta _j}\frac{\partial Im(\gamma _j)}{\partial \xi _{n}}\right) \nonumber \\ \frac{\partial \omega _j}{\partial {\xi }_n}= \,& {} \frac{\partial Im(\gamma _j)}{\partial \xi _{n}} \end{aligned}$$

(37)

where $\bar{\zeta _j}$ and $\bar{\omega _j}$ are the mean values of the damping ratio and frequency of the $j^{th}$ mode. Now, the variance of damping ratio $(\zeta _j)$ and frequency $(\omega _j)$ can be written as:

$$\begin{aligned} Var(\zeta _j)= \,& {} \sum _{n=1}^{N}\left( \frac{\partial \zeta _j}{\partial {\xi }_n}\right) ^2\nonumber \\ Var(\omega _j)= \,& {} \sum _{n=1}^{N}\left( \frac{\partial \omega _j}{\partial {\xi }_n}\right) ^2 \end{aligned}$$

(38)

5 Flutter probability

The flutter velocity of aeroelastic system is defined as the flow velocity at which damping ratio of one of the modes (say $j^{th}$ mode) becomes zero. If the damping ratio $(\zeta _j>0)$, the aeroelastic system is stable. Hence, the probability of failure of the aeroelastic system due to flutter (or flutter probability) can be defined in conditional sense (on flow velocity) as [6, 31]:

$$\begin{aligned} Pr_{flutter}=Pr\left( \zeta _j({\xi _n})\le 0|_{U_{flutter}=U}\right) \end{aligned}$$

(39)

where ${\xi _n}$ are orthonormal random variables as defined in Sect. (3). The flutter probability can be calculated using perturbation approach by linearizing the limit state function $(\zeta _j({\xi _n})= 0|_{U_{flutter}=U})$ based on the first order Taylor’s series approximation as discussed in Sect. (4). Here, the flutter probability can be written as:

$$\begin{aligned} Pr_{flutter}=\varPhi \left( -\beta _R\right) \end{aligned}$$

(40)

where $\beta _R=\frac{\bar{\zeta _j}}{\sqrt{Var(\zeta _j)}}$ and $\varPhi$ is the standard normal cumulative distribution function. The flutter probability can also be calculated using MCS based on the number of samples $(n_s)$ satisfying the above conditional statement (Eq. (39)) at each flow velocity as:

$$\begin{aligned} Pr_{flutter}=\frac{n_s(\zeta _j \le 0)}{N_s} \end{aligned}$$

(41)

where $N_s$ is total number of samples.

6 Results and discussion

In this section, the effects of various uncertain stiffness parameters on the probabilistic flutter characteristics of cantilever wing are investigated. Here, the bending and torsional stiffness properties of the cantilever wing are considered as Gaussian random fields with the coefficient of variation (C.O.V) varying from 0.01 to 0.05. The efficiency of the proposed method is also demonstrated by comparing the present results with MCS. The wing with fixed-free boundary conditions is discretized into ten finite elements for the analysis. The mean flutter analysis is carried out using the numerical data given in Table 1 [20].

Table 1 Properties of Goland wing [20]

The Complex Theodorsen’s function [20] used in the present analysis can be written as:

$$\begin{aligned} C(k)= \,& {} 1+\frac{0.1757}{1+(\frac{1.099}{k})}-\frac{0.6724}{1+(\frac{0.243}{k})}\nonumber \\&+\,\left( \frac{2.41}{1+(\frac{0.214}{k})}-\frac{2.41}{1+(\frac{0.156}{k})}\right) i \end{aligned}$$

(42)

Fig. 2

Mean damping and frequency of cantilever wing at various free stream velocities

Fig. 3

First four eigenvalues and eigen functions of exponential covariance function

The variation in mean frequency and damping ratio for different modes (Mode 1—Bending, Mode 2—Torsional) of cantilever wing at various free stream velocities is shown in Fig. 2. From the figure, it is observed that the second eigen mode crosses zero damping line at free stream velocity of $(U)=137.38$ m/s leading to flutter and the corresponding eigen frequency is $82.53\,rad/s$. Henceforth, the second mode is called as the flutter mode. The present mean flutter velocity of cantilever wing is also compared with those given in [20] which matches well with each other.

Fig. 4

Convergence of SD of a damping ratio and b frequency with various K–L expansion terms for the flutter mode (Mode 2) of cantilever wing at $U = 125$ m/s due to 5% C.O.V in EI

Fig. 5

Convergence of SD of a damping ratio and b frequency with various K–L expansion terms for the flutter mode (Mode 2) of cantilever wing at $U = 125$ m/s due to 5% C.O.V in GJ

Table 2 Variation of mean and SD of damping ratio and frequency with free stream velocity for the flutter mode (Mode 2) of cantilever wing due to C.O.V in $EI = 5\%$

Fig. 6

C.O.V of a damping ratio and b frequency for the flutter mode (Mode 2) of cantilever wing obtained from Perturbation approach and MCS due to variation in EI at $U=135$ m/s

Table 3 Variation of mean and SD of damping ratio and frequency with free stream velocity for the flutter mode (Mode 2) of cantilever wing due to C.O.V in $GJ = 5\%$

Fig. 7

C.O.V of a damping ratio and b frequency for the flutter mode (Mode 2) of cantilever wing obtained from Perturbation approach and MCS due to variation in GJ at $U=135$ m/s

Furthermore, the eigenvalues and eigenfunctions of the exponential covariance function used to represent random processes are discussed. Figure 3 shows the first four eigenvalues and the corresponding eigenfunctions of the exponential covariance function obtained by solving Eq. (15).

The convergence of standard deviation (SD) of eigenvalues with various K–L expansion terms for the flutter mode (Mode 2) of wing with C.O.V of $EI(=5\%)$ and $GJ(=5\%)$ at flow velocity ($U=125 \,m/s$) are shown in Figs. 4 and 5 respectively. From the figures, it is observed that the SD of frequency and damping ratio of the flutter mode of the aeroelastic system converges well with four K–L expansion terms. Hence, based on this study, all subsequent stochastic analyses are performed using four K–L expansion terms.

Next, Table 2 shows the comparison of mean and SD of damping ratio and frequency obtained using perturbation approach and MCS at various free stream velocities. The SD of damping ratio and frequency computed using deterministic C(k) function are also shown in the table in bracket. It is observed that the mean and SD of damping ratio and frequency for flutter mode of wing match well with MCS due to $5\%$ C.O.V in EI. However, the SD of damping ratio and frequency obtained using deterministic C(k) show small deviations with MCS results (values shown in bracket).

Fig. 8

C.O.V of damping ratio and frequency of cantilever wing obtained from perturbation approach at various free stream velocities due to 5% C.O.V in a EI and b GJ

Furthermore, Fig. 6 shows the variation of C.O.V of eigenvalue of wing due to variation in EI at $U = 135\,m/s$ which matches well with MCS. Here, a small uncertainty in EI with 1% C.O.V induces about 2.5 % variation in the damping ratio of flutter mode (Mode 2).

Similarly, Table 3 shows the comparison of mean and SD of eigenvalues of cantilever wing due to variation in GJ at various free stream velocities. It is observed that the mean and SD of frequency and damping ratio for flutter mode of wing match well with MCS at lower velocity. However, at higher velocity, a small discrepancy in the mean and SD of eigenvalue between the two methods is observed. Furthermore, the discrepancy is found to be more when C(k) is treated as deterministic (values shown in bracket). Figure 7 shows the variation of C.O.V of eigenvalue of cantilever wing due to variation in GJ at $U = 135\,m/s$. It is observed that the C.O.V of eigenvalue obtained from perturbation approach matches well with MCS upto 3% C.O.V of GJ. Beyond this range, the 1st order perturbation approach shows deviations with MCS results indicating limitations of the present approach. Here, a small uncertainty in GJ with 1% C.O.V induces about 25 % variation in the damping ratio of flutter mode (Mode 2).

The C.O.V of damping ratio and frequency for various modes of wing at different free stream velocities due to 5% C.O.V in EI and GJ is presented in Fig. 8. It is observed that C.O.V of frequency is higher for Mode 1 as compared to Mode 2 due to variation in EI and follows similar trend as those of mean frequency. The C.O.V of damping ratio for Mode 2 is very small throughout and shows very high values (a spike) near the flutter point.

Fig. 9

Pdfs of damping ratio and frequency for the flutter mode (Mode 2) of cantilever wing obtained from MCS and Perturbation approach due to 5% C.O.V in EI at $U=100$ m/s

Fig. 10

Pdfs of damping ratio and frequency for the flutter mode (Mode 2) of cantilever wing obtained from MCS and Perturbation approach due to 5% C.O.V in GJ at $U=100$ m/s

Fig. 11

Pdfs of damping ratio and frequency for the flutter mode (Mode 2) of cantilever wing obtained from MCS and Perturbation approach due to 5% C.O.V in EI at $U=135$ m/s

Fig. 12

Pdfs of damping ratio and frequency for the flutter mode (Mode 2) of cantilever wing obtained from MCS and Perturbation approach due to 3% C.O.V in GJ at $U=135$ m/s

Fig. 13

Pdfs of damping ratio and frequency for the flutter mode (Mode 2) of cantilever wing obtained from MCS and Perturbation approach due to 5% C.O.V in GJ at $U=135$ m/s

Fig. 14

CDFs of flutter velocity of cantilever wing due to a 5% C.O.V in EI, b 3% C.O.V in GJ, c 5% C.O.V in GJ

This is due to the fact that the mean value of damping ratio is very small near (approaching zero) flutter point. It is also observed that the uncertainty in GJ has more influence on the damping ratio and frequency of flutter mode as compared to EI.

The probability density functions (pdfs) of damping ratio and frequency of flutter mode of cantilever wing obtained using perturbation approach and MCS are shown in Figs. 9, 10, 11, 12 and 13 for up to 5% C.O.V in EI and GJ at two different flow velocities. A suitable distribution model curve fit for MCS data are also shown in the figure. At $U=100$ m/s (away from flutter velocity), it is observed that the pdfs of damping ratio and frequency of flutter mode follow Gaussian distributions (Figs. 9 and 10) due to 5% variation in EI and GJ. Here, the skewness of each pdf obtained from MCS are also examined and found to be close to 0. Since, the pdf of damping ratio doesn’t become negative, there is a negligible chance of occurrence of flutter at this velocity due to uncertainty considered in bending and torsional rigidity.

At $U=135$ m/s with 5% C.O.V in EI, the pdfs of damping ratio and frequency of flutter mode follow Gaussian distributions (Fig. 11) with skewness value close to 0. Here, the pdf of damping ratio doesn’t become negative, indicating no chance of flutter at this velocity due to uncertainty in EI. However, due to 3% variation in GJ, the pdfs of damping ratio and frequency of flutter mode (Mode 2) obtained from MCS, follow nearly Gaussian distribution (Fig. 12) with small skewness values − 0.55 and 0.21 respectively. Furthermore, some region of the pdf of damping ratio of flutter mode (Mode 2) becomes negative which indicates that there is a chance of occurrence of flutter at this velocity due to uncertainty in GJ. Similar interpretation can be made for Fig. 13, when C.O.V in GJ is 5% at flow velocity $U=135$ m/s with skewness of damping ratio and frequency of flutter mode (Mode 2) − 0.74 and 0.30 respectively. It is also observed that pdf of damping ratio of flutter mode (Mode 2) shows wide band density function near mean flutter point as compared to pdf at lower velocity (away from mean flutter point).

Next, the flutter probability of the cantilever wing is discussed by calculating cumulative distribution function (CDF) of the flutter velocity as discussed in Sect. (5). Figure 14 shows the CDFs of flutter velocity obtained using perturbation approach and MCS due to dispersion in EI and GJ. From Fig. 14a, it is observed that the CDF of flutter velocity obtained using perturbation approach matches well with MCS due to 5% C.O.V in EI. Furthermore, with 3% C.O.V in GJ, CDF obtained from the perturbation approach shows good comparison with MCS results as the pdf of damping ratio shows nearly Gaussian characteristics. However, due to 5% C.O.V in GJ, a discrepancy in the tail region of the CDF between perturbation approach and MCS is observed. The above discrepancy in the flutter probability (with 5% C.O.V in GJ) can be reduced by considering second order perturbation approach and improved structural reliability methods. From the figures, it may be noted that the flutter velocity of wing is more sensitive to uncertainty in torsional rigidity as compared to bending rigidity which is similar to those observed in [4].

7 Conclusions

In this paper, a novel approach based on Stochastic Finite Element Method is proposed for the probabilistic flutter analysis of aircraft wing in frequency domain. Here, the uncertainty modeling of the input random parameters as random fields are based on truncated Karhunen–Loeve expansion. The uncertainty propagation is based on first order perturbation approach which efficiently handles the expansion of implicit frequency dependent Theodorsen’s function of the unsteady aerodynamics. The method is demonstrated by analyzing the probabilistic flutter characteristics of a cantilever wing having random stiffness properties and comparing results with MCS. Here, the bending and torsional stiffnesses of the wing are treated as second order Gaussian random fields. It is observed that the perturbation method is very accurate for all levels of bending stiffness uncertainty studied. However, the method loses its accuracy, when C.O.V in torsional rigidity is considered more than 3%. It is also observed that the uncertainty in torsional rigidity has greater influence on the damping ratio and frequency of flutter mode as compared to bending rigidity. It is also shown that the SD of damping ratio and frequency obtained using random C(k) function agree well with MCS results as compared to those obtained using deterministic C(k) function. Furthermore, the pdfs of damping ratio and frequency for flutter mode of cantilever wing show Gaussian characteristics at low flow velocity. However, at higher flow velocity, the pdfs show wide band variation in damping and frequency. The flutter probability of cantilever wing is also studied by defining limit state function in conditional sense on flow velocity. It is observed that the CDFs of flutter velocity using perturbation approach match well with MCS with 5% and 3% C.O.V in EI and GJ respectively. The lower prediction of flutter velocity in the presence of uncertainty in torsional rigidity shows that this is a more sensitive parameter in comparison of bending rigidity. This indicates that in the design of air vehicle, the dispersion in torsional rigidity should be controlled to avoid flutter conditions.

Appendix

The weak forms of the governing Eqs. (5) and (6) are obtained by multiplying weight functions $v_1$ and $v_2$ respectively and integrating over an $i^{th}$ element length as [32]:

$$\begin{aligned} \int _{y_i}^{y_{i+1}}v_1\left( m\ddot{h}+mx_{\alpha }b\ddot{\alpha }+\frac{\partial ^2}{\partial y^2}\left( EI\frac{\partial ^2h}{\partial y^2}\right) +L\right) dy= \,& {} 0 \end{aligned}$$

(43)

$$\begin{aligned} \int _{y_i}^{y_{i+1}}v_2\left( I_p\ddot{\alpha }+mx_{\alpha }b\ddot{h}-\frac{\partial }{\partial y}\left( GJ\frac{\partial \alpha }{\partial y}\right) -M\right) dy= \,& {} 0 \end{aligned}$$

(44)

Substituting the expressions for lift (L) and moment (M), and performing integration by parts, the above equations can be expressed as:

$$\begin{aligned}&\int _{y_i}^{y_{i+1}}v_1m\ddot{h}dy+\int _{y_i}^{y_{i+1}}v_1\pi \rho _{\infty }b^2\ddot{h}dy+\int _{y_i}^{y_{i+1}}v_1mx_{\alpha }b\ddot{\alpha }dy\nonumber \\&\quad -\,\int _{y_i}^{y_{i+1}}\pi \rho _{\infty }b^3a\ddot{\alpha }dy+\int _{y_i}^{y_{i+1}}v_1UC(k)2\pi \rho _{\infty }b\dot{h}dy\nonumber \\&\quad +\,\int _{y_i}^{y_{i+1}}v_1U\pi \rho _{\infty }b^2\dot{\alpha }dy+\int _{y_i}^{y_{i+1}}v_1UC(k)\pi \rho _{\infty }b^2(1-2a)\dot{\alpha }dy\nonumber \\&\quad +\,\int _{y_i}^{y_{i+1}}v_1U^2C(k)2\pi \rho _{\infty }b{\alpha }dy+\int _{y_i}^{y_{i+1}}\frac{\partial ^2v_1}{\partial y^2}\left( EI\frac{\partial ^2h}{\partial y^2}\right) dy\nonumber \\&\quad +\,\left( -v_1S^b-\frac{\partial {v_1}}{\partial {y}}M^b\right) \arrowvert _{y_i}^{y_{i+1}}=0 \end{aligned}$$

(45)

$$\begin{aligned}&\int _{y_i}^{y_{i+1}}v_2I_p\ddot{\alpha }dy+\int _{y_i}^{y_{i+1}}v_2\pi \rho _{\infty }b^4\left( \frac{1}{8}+a^2\right) \ddot{\alpha }dy\nonumber \\&\quad +\,\int _{y_i}^{y_{i+1}}v_2mx_{\alpha }b\ddot{h}dy-\int _{y_i}^{y_{i+1}}v_2\pi \rho _{\infty }b^3a\ddot{h}dy\nonumber \\&\quad -\,\int _{y_i}^{y_{i+1}}v_2U\pi \rho _{\infty }b^3\left( -\frac{1}{2}+a\right) \dot{\alpha }dy\nonumber \\&\quad -\,\int _{y_i}^{y_{i+1}}v_2UC(k)\pi \rho _{\infty }b^3\left( \frac{1}{2}+a\right) \left( 1-2a\right) \dot{\alpha }dy\nonumber \\&\quad -\,\int _{y_i}^{y_{i+1}}v_2UC(k)2\pi \rho _{\infty }b^2\left( \frac{1}{2}+a\right) \dot{h}dy\nonumber \\&\quad -\,\int _{y_i}^{y_{i+1}}v_2U^2C(k)2\pi \rho _{\infty }b^2\left( \frac{1}{2}+a\right) {\alpha }dy\nonumber \\&\quad +\,\int _{y_i}^{y_{i+1}}\frac{\partial {v_2}}{\partial {y}}\left( GJ\frac{\partial {\alpha }}{\partial {y}}\right) dy-v_2\tau \arrowvert _{y_i}^{y_{i+1}}=0 \end{aligned}$$

(46)

where $M^b$, $S^b$, and $\tau$ are bending moment, shear force, and torsional moment respectively and can be written as:

$$\begin{aligned} M^b= \,& {} EI\frac{\partial ^2h}{\partial y^2}\\ S^b= \,& {} -\frac{\partial }{\partial {y}}\left( EI\frac{\partial ^2h}{\partial y^2}\right) \\ \tau= \,& {} GJ\frac{\partial {\alpha }}{\partial {y}} \end{aligned}$$

Now by using finite element approximation functions, the heave (h) and pitch $(\alpha )$ displacements can be expressed as:

$$\begin{aligned} h(y,t)= \,& {} \lfloor N_w\rfloor \{w_e(t)\}\nonumber \\ \alpha (y,t)= \,& {} \lfloor N_\alpha \rfloor \{\alpha _e(t)\} \end{aligned}$$

(47)

where $\lfloor N_w\rfloor =\lfloor N_1, N_2, N_3, N_4\rfloor$ and $\lfloor N_\alpha \rfloor =\lfloor \bar{N}_1,\bar{N}_2\rfloor$ are Hermite and Lagrange shape functions [32] respectively and $\{w_e\}$ and $\{\alpha _e\}$ are the bending and torsional degrees of freedom respectively. The weight functions $v_1$ and $v_2$ can be also written as $v_1= \lfloor N_w\rfloor ^T$ and $v_2=\lfloor N_\alpha \rfloor ^T$ respectively. On substitution of the above approximation functions and weight functions, the elemental equations can be written in notational form as:

$$\begin{aligned}&\left[ M_{SB}\right] \{\ddot{w}_e\}+\left[ M_{AB}\right] \{\ddot{w}_e\}+\left[ M_{SC}\right] \{\ddot{\alpha }_e\}+\left[ M_{AC}\right] \{\ddot{\alpha }_e\}\nonumber \\&\qquad +\,\left[ C_{AB}\right] \{\dot{w}_e\}+\left[ C_{AC}^{12}\right] \{\dot{\alpha }_e\}+\left[ K_{AC}\right] \{\alpha _e\}+\left[ K_{SB}\right] \{w_e\}\nonumber \\&\quad =\{F_i\} \end{aligned}$$

(48)

$$\begin{aligned}&\left[ M_{ST}\right] \{\ddot{\alpha }_e\}+\left[ M_{AT}\right] \{ \ddot{\alpha }_e\}+\left[ M_{SC}\right] \{\ddot{w}_e\}+\left[ M_{AC}\right] \{\ddot{w}_e\}\nonumber \\&\qquad +\,\left[ C_{AT}\right] \{\dot{\alpha }_e\}+\left[ C_{AC}^{21}\right] \{\dot{w}_e\}+\left[ K_{AT}\right] \{\alpha _e\}+\left[ K_{ST}\right] \{\alpha _e\}\nonumber \\&\quad =\{\tau _i\} \end{aligned}$$

(49)

where $\{F_i\}=\lfloor -S_{y_{i}}^{b}, -M_{y_{i}}^{b}, S_{y_{i+1}}^{b}, M_{y_{i+1}}^{b}\rfloor ^T$ and $\{\tau _i\}=\lfloor -\tau _{y_i},\tau _{y_{i+1}}\rfloor ^T$. The terms involved in Eq. (48) are:

$$\begin{aligned} \left[ M_{SB}\right]= \,& {} m\int _{y_i}^{y_{i+1}}{\lfloor {N_w}\rfloor ^T\lfloor N_w\rfloor dy}\nonumber \\ \left[ M_{AB}\right]=\, & {} \pi \rho _{\infty }b^2\int _{y_i}^{y_{i+1}}{\lfloor {N_w}\rfloor ^T\lfloor N_w\rfloor dy}\nonumber \\ \left[ M_{SC}\right]=\, & {} mx_{\alpha }b\int _{y_i}^{y_{i+1}}{\lfloor {N_w}\rfloor ^T\lfloor N_\alpha \rfloor dy}\nonumber \\ \left[ M_{AC}\right]=\, & {} -\pi \rho _{\infty }b^3a\int _{y_i}^{y_{i+1}}{\lfloor {N_w}\rfloor ^T\lfloor N_\alpha \rfloor dy}\nonumber \\ \left[ C_{AB}\right]=\, & {} UC(k)2\pi \rho _{\infty }b\int _{y_i}^{y_{i+1}}{\lfloor {N_w}\rfloor ^T\lfloor N_w\rfloor dy}\nonumber \\ \left[ C_{AC}^{12}\right]= \,& {} U\pi \rho _{\infty }b^2\int _{y_i}^{y_{i+1}}{\lfloor {N_w}\rfloor ^T\lfloor N_\alpha \rfloor dy}\nonumber \\&+\,UC(k)\pi \rho _{\infty }b^2(1-2a)\int _{y_i}^{y_{i+1}}{\lfloor {N_w}\rfloor ^T\lfloor N_\alpha \rfloor dy}\nonumber \\ \left[ K_{AC}\right]= \,& {} U^2C(k)2\pi \rho _{\infty }b\int _{y_i}^{y_{i+1}}{\lfloor {N_w}\rfloor ^T\lfloor N_\alpha \rfloor dy}\nonumber \\ \left[ K_{SB}\right]=\, & {} \int _{y_i}^{y_{i+1}}{EI\lfloor {N_w^{''}}\rfloor ^T\lfloor N_w^{''}\rfloor dy} \end{aligned}$$

(50)

and the terms in Eq. (49) can be written as:

$$\begin{aligned} \left[ M_{ST}\right]= \,& {} I_p\int _{y_i}^{y_{i+1}}{\lfloor {N_\alpha }\rfloor ^T\lfloor N_\alpha \rfloor dy}\nonumber \\ \left[ M_{AT}\right]= \,& {} \pi \rho _{\infty }b^4\left( a^2+\frac{1}{8}\right) \int _{y_i}^{y_{i+1}}{\lfloor {N_\alpha }\rfloor ^T\lfloor N_\alpha \rfloor dy}\nonumber \\ \left[ M_{SC}\right]= \,& {} mx_{\alpha }b\int _{y_i}^{y_{i+1}}{\lfloor {N_\alpha }\rfloor ^T\lfloor N_w\rfloor dy}\nonumber \\ \left[ M_{AC}\right]= \,& {} -\pi \rho _{\infty }b^3a\int _{y_i}^{y_{i+1}}{\lfloor {N_\alpha }\rfloor ^T\lfloor N_w\rfloor dy}\nonumber \\ \left[ C_{AT}\right]= \,& {} -U\pi \rho _{\infty }b^3(-0.5+a)\int _{y_i}^{y_{i+1}}{\lfloor {N_\alpha }\rfloor ^T\lfloor N_\alpha \rfloor dy}\nonumber \\&-\,UC(k)\pi \rho _{\infty }b^3(0.5+a)(1-2a)\int _{y_i}^{y_{i+1}}{\lfloor {N_\alpha }\rfloor ^T\lfloor N_\alpha \rfloor dy}\nonumber \\ \left[ C_{AC}^{21}\right]= \,& {} -UC(k)2\pi \rho _{\infty }b^2(0.5+a)\int _{y_i}^{y_{i+1}}{\lfloor {N_\alpha }\rfloor ^T\lfloor N_w\rfloor dy}\nonumber \\ \left[ K_{AT}\right]= \,& {} -U^2C(k)2\pi \rho _{\infty }b^2(0.5+a)\int _{y_i}^{y_{i+1}}{\lfloor {N_\alpha }\rfloor ^T\lfloor N_\alpha \rfloor dy}\nonumber \\ \left[ K_{ST}\right]= \,& {} \int _{y_i}^{y_{i+1}}{GJ\lfloor {N_\alpha ^{'}}\rfloor ^T\lfloor N_\alpha ^{'}\rfloor dy} \end{aligned}$$

(51)