A study on stochastic aeroelastic stability and flutter reliability of a wing

Abstract

In this work, the stochastic aeroelastic stability and flutter reliability of a wing are investigated using the stochastic finite element method in conjunction with the first order reliability method (FORM). Three stability conditions are proposed for estimating flutter onset in aeroelastic systems in the presence of uncertainties. Here, stability conditions are represented as limit state functions and defined in conditional sense on flow velocity for flutter reliability studies. Due to various representation of limit states, a lack of invariance in reliability estimates is observed using the conventional flutter reliability approach such as the first order second moment method. In this paper, a general FORM is proposed, which is suitable for all the limit state functions considered and shows invariance in reliability estimates. The proposed approach is applied to a wing having uncertain stiffness parameters, modeled by either random variables or random fields. Random fields are represented by a Karhunen–Loeve expansion, and the effect of correlation length on the flutter reliability of the wing is discussed. The computational efficiency of the FORM algorithm for various limit states in comparison of MCS is also discussed.

1 Introduction

In aircraft design, two aeroelastic instability phenomena are considered: divergence and flutter. Divergence is a steady state aeroelastic phenomenon that occurs at a flow velocity at which the moment generated by aerodynamic load overcomes the resisting moment by structural stiffness, leading to structural failure [1]. Flutter is a dynamic aeroelastic phenomenon, in which structures extract energy from air-stream, which leads to setup of self-excited sustained oscillation resulting in destruction of structures [2]. The velocity at which the aeroelastic system exhibits sustained oscillation is the flutter velocity, and the frequency which shows the characteristics of sustained oscillation is called the flutter frequency. Traditionally, a factor of safety is considered in the aeroelastic design [3, 4] to avoid flutter onset within the operational envelope.

In general, uncertainty is always present in aeroelastic systems in the form of aleatory uncertainty (inherent uncertainty) and epistemic uncertainty (comes from lack of knowledge and data) [5]. The aleatory uncertainty, which is irreducible in nature, is modeled by random variables/random fields; it is propagated through the mathematical model to quantify the response quantity [6, 7]. Lindsley et al. [8] carried out limit cycle oscillation (LCO) analysis of a panel in supersonic flow by modeling elastic modulus as a Gaussian random field and uncertain boundary condition as a random variable using Monte Carlo simulation (MCS). Early review article appeared in uncertainty quantification (UQ) in aeroelasticity [9], discussed the importance and challenges associated with UQ in aeroelasticity and emphasized the use of reliability based design optimization for industrial design application. Castravete and Ibrahim [10] investigated the effect of spatial distribution of stiffness parameters (bending and torsional rigidities) on the flutter behavior of a cantilever wing in the time domain using both perturbation and MCS approaches. Danowsky et al. [11] compared three uncertainty quantification methods namely the Monte Carlo method, the design of experiment (DOE)/response surface method (RSM), and the non-probabilistic $\mu$-analysis method for a reduced order model of a wing in transonic flow in the presence of structural and atmospheric uncertainties. The DOE/RSM results of flutter altitude were identical to full baseline Monte Carlo analysis. Verhoosel et al. [12] proposed perturbation (mean, median, and mode centered) and importance sampling based methods to carryout uncertain aeroelastic response analysis of a panel in supersonic flow. The panel elastic modulus was represented by one-dimensional lognormal field. Anton et al. [13] proposed a method based on the stochastic normal form to predict the effect of uncertainties in structural stiffness terms and flow speed on the stability of nonlinear aeroelastic system near the Hopf bifurcation point. The analysis revealed that for a two degrees of freedom (dofs) airfoil aeroelastic system in the presence of uncertainty in flow velocity, shifted the bifurcation point below the deterministic flutter velocity. Adamson et al. [14] developed a receptance based experimental approach to carryout flutter analysis of aeroelastic systems due to variability in manufacturing tolerances, damage, and degradation. Onkar [15] developed a successive robust flutter prediction technique by coupling nominal analysis, ground vibration test, wind tunnel test, uncertainty model updation, and the $\mu$-analysis method to predict the worst flutter boundary of a swept back wing in transonic flow regime in the presence of structural and aerodynamics uncertainties. A good estimate of transonic flutter boundary (transonic dip) was found by successively updating the aerodynamic uncertainty bounds using wind tunnel data. Recently, Beran et al. [16] reviewed published articles in the area of UQ in aeroelasticity based on the pk method [17] and Schur method based eigenvalue analysis. The authors addressed the difficulty, that the perturbation method was not able to predict bi-modal probability density function (PDF), which was encountered in mode switching and transonic aeroelastic cases.

Due to decrement of onset of flutter velocity [10, 12, 13] in the presence of parametric uncertainty, there is a need to carry out aeroelastic reliability analysis to ensure that aeroelastic systems are free from flutter instability. Ge et al. [18] studied the flutter reliability of a cable-stayed bridge using the first order reliability method based on mean point, design point, and extended design point (for non-normal random variables) approaches by defining limit state function as the difference between critical flutter speed and extreme wind speed. Zhang et al. [19] carried out flutter reliability analysis of a long cable stayed bridge by combining Latin hypercube sampling and check-point approach, where the limit state function was defined as the difference between the critical flutter wind speed and the design wind speed. Cheng et al. [20] proposed a flutter reliability analysis method for a suspension bridge based on the RSM, the finite element method (FEM), the first order reliability method (FORM), and the importance sampling method. In this method, RSM was used to approximate the limit state function; FEM was used to carryout deterministic flutter analysis, and finally probability of failure was evaluated using the combination of FORM and importance sampling method. Liaw and Yang [21] studied the flutter reliability of a laminated curved shell in supersonic flow using the mean centered second order perturbation approach subjected to independent parametric variation. Further, the authors [22] extended the reliability study to laminated plates, which had parametric variations in material and geometric properties. Results of such study indicted that correlation among the plies lowers the reliability of the aeroelastic system in comparison of no correlation among the plies. Shufang et al. [23] conducted flutter reliability analysis of 2-dofs and 3-dofs (with flap) wing sections in transonic flow using improved line sampling technique (directional sampling) to reduce the computational cost. Borello et al. [24] carried out flutter reliability analysis of (1) 2-dimensional equivalent airfoil section model and (2) composite wing for load-resistance type limit states using various reliability methods such as MCS, FORM, second order reliability method (based on analytical expression), response surface coupled with FORM and MCS in subsonic flow. The cumulative distribution function (CDF) of flutter velocity revealed that the higher order response surface coupled with MCS and FORM gave the best prediction of flutter onset velocity. Wu and Livne [25] developed a simulation tool on MCS for aeroelastic reliability analysis of a typical advanced fighter aircraft in the presence of control component uncertainty under roll control. The failure of notch filter was observed in the presence of physical control component uncertainty. Recently, Swain et al. [4] performed flutter reliability analysis of a laminated plate in subsonic flow using perturbation based FORM and polynomial neural network (PNN) based reliability algorithms in the presence of structural uncertainties. The perturbation based FORM method was very efficient than PNN. Pourazaram et al. [26] proposed a reliability framework using the mean value based perturbation approach to carryout flutter reliability analysis of a wind turbine blade. A new weighted average reliability method was proposed, which was based on the weighted sum of CDF of flutter velocity corresponding to altered design point. In this, the performance function was represented in terms of real part of eigenvalues imposing a condition on rotor speed. Wang and Qiu [27] developed a non-probabilistic interval method for reliability assessment of aircraft flutter based on flutter wind speed and natural wind speed interference model, where the non-probabilistic reliability was defined by the ratio of volume of safe region to the total volume bounded by interval variables. Zheng and Qiu [28] proposed a novel numerical method based on interval bounds on real part of eigenvalues to study the flutter reliability of aeroelastic systems in the presence of parametric uncertainties. Rezaei et al. [29] developed a fuzzy reliability method to study the aeroelastic reliability of an aircraft wing subjected to uncertainty in structural parameters and airspeed. In this method, a performance function was defined on the basis of interference area in three-dimensional fuzzy pyramid shape of stability region bounded by fuzzy flutter speed and airspeed. The reliability index was defined in a similar way as given in [27]. The method was employed to a wing section and a typical cantilever wing model.

The consequences associated with aeroelastic instability demand accurate and efficient reliability algorithms development due to chances of decrement of flutter velocity in the presence of uncertainties. From the literature, it can be observed that uncertainty quantification and reliability estimation of aeroelastic systems are mainly based on methods like MCS, mean centered reliability methods, RSM conjunction with FORM; where limit state functions are represented in a typical load-resistance type or a response surface form. The MCS method is computationally expensive, while RSM is accurate in the range of design parameters used to approximate the response surface. In this work, the authors have proposed three different types of stability conditions/limit state functions based on intuition and engineering judgment. A general FORM based flutter reliability algorithm is proposed for various limit state functions and demonstrated on a cantilever wing in subsonic flow. The stochastic stiffness parameters are considered as Gaussian random variables as well as random fields. Here, random fields are discretized using the spectral decomposition method based on a truncated Karhunen–Loeve (K–L) expansion. Numerical results on the stochastic aeroelastic stability of a cantilever wing are discussed for various stability conditions. The invariance characteristics of FORM algorithms are shown for various limit state functions irrespective of uncertainty modeling approaches. Further, the effect of correlation length of random fields on the flutter reliability of the wing is discussed. The computational efficiency of the FORM algorithm for various limit states in comparison of MCS is also discussed.

2 Stability conditions

In aeroelastic studies, the flutter phenomenon due to coalescence of bending and torsional modes has been widely reported [2, 24, 30, 31]. In mode coalescence, generally, frequencies of two modes approach each other, and their corresponding phase becomes zero [32]. Here, stability of an aeroelastic system is obtained from eigenvalues, which are in general complex in nature due to the presence of unsteady aerodynamics or damping or both. Assume that jth and kth are the two coalescence modes which participate in the mechanism of flutter, and the corresponding complex eigenvalues are $\gamma _{j}$ and $\gamma _{k}$ respectively. Since the eigenvalues are complex in nature, and contain real part $\beta$ (decay rate) and imaginary part $\omega$ (frequency), the real part of eigenvalue can be expressed in terms of damping ratio and frequency as $\beta =-\zeta \omega$. For the jth and kth modes, the complex eigenvalues are $\beta _{j}+i\omega _{j}$ and $\beta _{k}+i\omega _{k}$ respectively. On the basis of participating modes in flutter onset, the characteristic equation representing aeroelastic system stability can be written as:

$$\begin{aligned} \left( \gamma -\gamma _{j}\right) \left( \gamma -\gamma _{k}\right) =0 \end{aligned}$$

(1)

Substituting the complex form of eigenvalues $\gamma _{j}$ and $\gamma _{k}$ in Eq. (1), the characteristic equation can be written as:

$$\begin{aligned} (\gamma -(\beta _{j}+i\omega _{j}))(\gamma -(\beta _{k}+i\omega _{k}))=0 \end{aligned}$$

(2)

The above characteristic equation [Eq. (2)] representing system stability contains complex coefficients. In order to make the characteristic equation coefficients real, there is a requirement of multiplying the equation having conjugate of eigenvalues of the jth and kth modes [33]. Consequently, the characteristic equation representing system stability can be written as:

$$\begin{aligned} (\gamma -(\beta _{j}+i\omega _{j}))(\gamma -(\beta _{k}+i\omega _{k}))(\gamma -(\beta _{j}-i\omega _{j}))(\gamma -(\beta _{k}-i\omega _{k}))=0 \end{aligned}$$

(3)

Equation (3) can be written in symbolic notation in quartic polynomial form as:

$$\begin{aligned} \gamma ^{4}+A_{3}\gamma ^{3}+A_{2}\gamma ^{2}+A_{1}\gamma +A_{o}=0 \end{aligned}$$

(4)

On simplification of Eq. (3) and comparing with Eq. (4), the real coefficients $A's$ of characteristic equation can be written as:

$$\begin{aligned} A_{3}= & {} -2\left( \beta _{j}+\beta _{k}\right) \nonumber \\ A_{2}= & {} \left( \left( \beta _{j}^2+\omega _{j}^2\right) +\left( \beta _{k}^2+\omega _{k}^{2}\right) +4\beta _{j}\beta _{k}\right) \nonumber \\ A_{1}= & {} -2\left( \beta _{j}\left( \beta _{k}^2+\omega _{k}^2\right) +\beta _{k}\left( \beta _{j}^2+\omega _{j}^{2}\right) \right) \nonumber \\ A_{o}= & {} \left( \beta _{j}^{2}+\omega _{j}^{2}\right) \left( \beta _{k}^{2}+\omega _{k}^{2}\right) \end{aligned}$$

(5)

The characteristic roots of Eq. (4) are called eigenvalues, and in the Laplace domain, these are known as poles. For describing the system’s absolute stability in the Laplace domain often called s-domain, the Routh’s stability criterion is used [34]. According to the Routh-Hurwitz stability criteria, the number of sign change in the second column of Routh table (Table 1), gives the number of poles/eigenvalues indicating instability. Since the roots of quartic characteristic polynomial with real coefficients are complex conjugate in nature, a pair of eigenvalues shows instability and one of them representing the actual root determines stability of the system [33].

Table 1 Routh table

For stability of a system, the real part of all the roots of Eq. (4) should be negative. The stability condition, where all polynomial coefficients have positive sign and second column of Table 1 corresponding to $\gamma ^{1}$ gives another condition $(F_{m})$ which should also have positive sign, can be expressed as:

$$\begin{aligned} F_{m}=-A_{o}+\frac{A_{1}}{A_{3}}A_{2}-\left( \frac{A_{1}}{A_{3}}\right) ^2 \end{aligned}$$

(6)

where $F_{m}$ is a stability parameter referred as flutter margin. Inspecting the table, if $F_{m} < 0$, there are two changes of sign, so a pair of eigenvalues is unstable (positive real roots), and in reality only one root belongs to the aeroelastic system characteristic equation represented by Eq. (2) [33]. If $F_{m}>0$, there is no change of sign, so the system is stable. If $F_{m}=0$, the system is marginally stable, i.e., the flutter onset condition for the aeroelastic system. Adding and subtracting $\frac{A_{2}^{2}}{4}$ on the right hand side of Eq. (6), on rearrangement, it can be written as:

$$\begin{aligned} F_{m}=\left( \left( \frac{A_{2}}{2}\right) ^2-A_{o}\right) -\left( \frac{A_{2}}{2}-\frac{A_{1}}{A_{3}}\right) ^2 \end{aligned}$$

(7)

On substitution of $A_{o},\ldots ,A_{3}$ from Eq. (5) into Eq. (7), the flutter margin expression in terms of coalescence modes decay rate and frequency is given as [35]:

$$\begin{aligned} F_{m}= & {} \left( \frac{\omega _{k}^{2}-\omega _{j}^{2}}{2}+\frac{\beta _{k}^{2}-\beta _{j}^{2}}{2}\right) ^{2}+4\beta _{j}\beta _{k}\left( \frac{\omega _{k}^{2}+\omega _{j}^{2}}{2}+2\left( \frac{\beta _{j}+\beta _{k}}{2}\right) ^2\right) \nonumber \\{} & {} -\left( \left( \frac{\beta _{k}-\beta _{j}}{\beta _{k}+\beta _{j}}\right) \left( \frac{\omega _{k}^{2}-\omega _{j}^{2}}{2}\right) +2\left( \frac{\beta _{j}+\beta _{k}}{2}\right) ^{2}\right) ^{2} \end{aligned}$$

(8)

On inspection, if $\beta _{j}$ or $\beta _{k}$ on the right hand side of Eq. (8) is zero, it leads to $F_{m} = 0$, indicating the flutter onset condition. The above expression of flutter margin can be viewed as a better representation of flutter prediction over conventional damping ratio based prediction, as it takes care of mode switching phenomenon due to parametric variation of system parameters. In terms of $F_{m}$, three conditions exist regarding stability of an aeroelastic system (1) $F_{m}<0$, unstable (2) $F_{m}=0$, stability (flutter onset) boundary (3) $F_{m}>0$, stable.

In coalescence modes flutter, the real part of one of the eigenvalue (decay rate) changes its sign (becomes unstable), while other eigenvalue remains stable. So, stability conditions similar to flutter margin can exist and are written in the form of product of decay rate $(\beta _{j}\beta _{k})$ of coalescence modes as: (1) $\beta _{j}\beta _{k}<0$, unstable (2) $\beta _{j}\beta _{k}=0$, stability (flutter onset) boundary (3) $\beta _{j}\beta _{k}>0$, stable. By inspecting the term $\beta _{j}\beta _{k}$, if the real part of any eigenvalue becomes zero, the flutter onset condition is encountered. This expression of stability also takes care of mode switching phenomenon due to parametric variation of system parameters [36].

Conventionally, for flutter onset prediction, damping ratio of various modes are traced with respect to flow velocities [17, 31, 37, 38], and say damping ratio of the jth mode becomes zero at a particular flow velocity, indicating flutter onset in the system. In terms of damping ratio, the stability condition can be written as: (1) $\zeta _{j}<0$, unstable (2) $\zeta _{j}=0$, stability (flutter onset) boundary, and (3) $\zeta _{j}>0$, stable.

3 Mathematical and stochastic modeling of an aeroelastic system

In this section, first the mathematical model of an aeroelastic system is presented for assessing system stability. Then, the stochastic model of various system parameters to account inherent uncertainty is discussed for assessing system reliability. Both random variables and random fields approaches are discussed for modeling uncertainty in system parameters.

Fig. 1

Cantilever wing model

3.1 Mathematical modeling

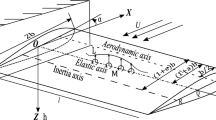
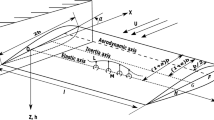
In order to examine the various forms of stability criteria, a typical straight cantilever wing with finite span is considered in Fig. 1. Here, P, Q, and R are the locations of aerodynamic, elastic, and inertia axes respectively. The aerodynamic axis is located at the quarter chord, i.e., b/2 distance from the leading edge; the location of elastic and inertia axes are controlled by the dimensionless parameters a and e respectively. The dimensionless parameters lie in the range (− 1, + 1). The span of the wing is l, and O is the origin of elastic axis. The governing differential equations of the wing are expressed as [39, 40]:

$$\begin{aligned}{} & {} m\ddot{h}(y,t)+mx_{\alpha }b\ddot{\alpha }(y,t)+\frac{\partial ^2}{\partial y^2}\left( EI\frac{\partial ^2h(y,t)}{\partial y^2}\right) +L(y,t)=0 \end{aligned}$$

(9)

$$\begin{aligned}{} & {} I_Q\ddot{\alpha }(y,t)+mx_{\alpha }b\ddot{h}(y,t)-\frac{\partial }{\partial y}\left( GJ\frac{\partial \alpha (y,t)}{\partial y}\right) -M(y,t)=0 \end{aligned}$$

(10)

where m is the mass per unit span, $I_{Q}$ is the mass moment of inertial per unit span, and $x_{\alpha } =(e-a)$ is the dimensionless static unbalance. EI and GJ are the bending and torsional stiffnesses of the wing respectively. L and $M= M_{1/4}+L(1/2+a)b$ are the distributed lift and moment on the elastic axis respectively. h(y, t) and $\alpha (y,t)$ are heave and pitch displacements respectively. The aerodynamic load on the cantilever wing is modeled using Theodorsen’s unsteady aerodynamics based strip theory [41]. According to the strip theory, the distributed lift and moment at the quarter chord are expressed as:

$$\begin{aligned} L= & {} 2\pi \rho _{\infty }bUC(k)\left( U\alpha +\dot{h}+b\left( \frac{1}{2}-a\right) {\dot{\alpha }}\right) +\pi \rho _{\infty }b^2\left( \ddot{h}+U{\dot{\alpha }}-ba\ddot{\alpha }\right) \end{aligned}$$

(11)

$$\begin{aligned} M_{1/4}= & {} -\pi \rho _{\infty }b^3\left( \frac{1}{2}\ddot{h}+U{\dot{\alpha }}+b\left( \frac{1}{8}-\frac{a}{2}\right) \ddot{\alpha }\right) \end{aligned}$$

(12)

where $\rho _{\infty }$ and U are the free stream density and flow velocity respectively. C(k) is a complex valued function of reduced frequency $k(=b\omega /U$, $\omega$ is aeroelastic system frequency), known as Theodorsen’s function.

The global form of finite element equations can be obtained using weak formulation and suitable approximation for heave and pitch displacements, as [40, 42]:

$$\begin{aligned} \left( \textbf{M}_\textbf{S}+\textbf{M}_\textbf{A}\right) {\ddot{{\textbf {q}}}}+\left( U\textbf{C}_\textbf{A}+UC(k){\textbf{C}}_{\textbf{A}\varvec{\omega }}\right) {\dot{{\textbf {q}}}}+\left( \textbf{K}_\textbf{B}+\textbf{K}_\textbf{T}+U^2C(k)\textbf{K}_{\textbf{A}\varvec{\omega }}\right) \textbf{q}=\textbf{0} \end{aligned}$$

(13)

where $\textbf{M}_\textbf{S}$, $\textbf{K}_\textbf{B}$, and $\textbf{K}_\textbf{T}$ are the structural mass, bending stiffness, and torsional stiffness matrices respectively. $\textbf{M}_\textbf{A}$, $U\textbf{C}_\textbf{A}$, $UC(k)\textbf{C}_{\textbf{A}\varvec{\omega }}$, and $U^2C(k)\textbf{K}_{\textbf{A}\varvec{\omega }}$ are the aerodynamic inertia, aerodynamic damping, frequency-dependent aerodynamic damping, and frequency-dependent aerodynamic stiffness matrices respectively, and $\textbf{q}$ is the generalized displacement vector. On substitution of $\textbf{q}={\bar{\textbf{q}}}\exp {(\gamma {t})}$ in Eq. (13), the second order eigenvalue equation can be obtained as:

$$\begin{aligned} \left( \gamma ^2\left( \textbf{M}_\textbf{S}+\textbf{M}_\textbf{A}\right) +\gamma \left( U\textbf{C}_\textbf{A}+UC(k)\textbf{C}_{\textbf{A}\varvec{\omega }}\right) +\left( \textbf{K}_\textbf{B}+\textbf{K}_\textbf{T}+U^2C(k)\textbf{K}_{\textbf{A}\varvec{\omega }}\right) \right) {\bar{\textbf{q}}}=\textbf{0} \end{aligned}$$

(14)

Here, $\gamma = -\zeta \omega +i\omega = \beta +i\omega = Re(\gamma )+i{}Im(\gamma )$ is the complex eigenvalue, and ${\bar{\textbf{q}}}$ is the eigenvector of the aeroelastic system.

3.2 Stochastic modeling

In order to model inherent uncertainty in the aeroelastic system, uncertainty modeling of system parameters is carried out. Uncertainty in system parameters can be modeled as random variables or random fields. The variability across the samples is represented by random variable, whereas variability in both physical space and samples are represented by random fields [43]. In this study, the bending and torsional stiffnesses of the wing are considered as stochastic parameters.

3.2.1 Random variables

In the stochastic modeling of system parameters as random variables, the uncertain terms can be expanded using a first-order Taylor series expansion about the design point ($\textbf{r}^*$, containing N random variables). The random input terms in Eq. (14) due to uncertain stiffness parameters are expressed as:

$$\begin{aligned} \textbf{K}_\textbf{B}=\textbf{K}_\textbf{B}^\mathbf {*}+\sum _{n=1}^{N}\frac{\partial {\textbf{K}_\textbf{B}}}{\partial {r_n}}|_{\textbf{r}^*}\delta {r_n}; \hspace{2pt} \textbf{K}_\textbf{T}=\textbf{K}_\textbf{T}^\mathbf {*}+\sum _{n=1}^{N}\frac{\partial {\textbf{K}_\textbf{T}}}{\partial {r_n}}|_{\textbf{r}^*}\delta {r_n} \end{aligned}$$

(15)

where $\delta {r_n}=r_n-r_n^*$ and $r_{n}$ is the nth random variable and $(.)^{*}$ denotes the term evaluated at the design point. Since the input parameters are random, so the response parameters are also random in nature [6]. The response quantities such as eigenvalue and eigenvector of the jth mode, as well as frequency dependent Theodorsen’s function can be expanded using the first-order Taylor series expansion as:

$$\begin{aligned} \gamma _{j}= & {} \gamma _{j}^*+\sum _{n=1}^{N}\frac{\partial \gamma _{j}}{\partial {r_n}}|_{\textbf{r}^*}\delta {r_n}; \hspace{5pt} {\bar{\textbf{q}}}_j={\bar{\textbf{q}}}^{*}_{j}+\sum _{n=1}^{N}\frac{\partial {{\bar{\textbf{q}}}_j}}{\partial {r_n}}|_{\textbf{r}^*}\delta {r_n}\nonumber \\ C\left( k_j\right)= & {} C(k_{j}^*)+\frac{b}{U}\sum _{n=1}^{N}\frac{\partial {C\left( k_j\right) }}{\partial {k_j}}\frac{\partial {Im\left( \gamma _{j}\right) }}{\partial {r_n}}|_{\textbf{r}^*}\delta {r_n} \end{aligned}$$

(16)

where, $k_{j}$ is the reduced frequency of the jth mode. On substituting the random terms from Eqs. (15) and (16) into Eq. (14) for the jth mode, and separating the zeroth and first order terms, the zeroth and first order equations can be written as:

Zeroth order:

$$\begin{aligned}{} & {} \left( {\gamma _{j}^*}^2\left( \textbf{M}_\textbf{S}+\textbf{M}_\textbf{A}\right) +{\gamma _{j}^*}\left( U\textbf{C}_\textbf{A}+UC(k_{j}^*)\textbf{C}_{\textbf{A}\varvec{\omega }}^*\right) \right. \nonumber \\ {}{} & {} \left. +\left( \textbf{K}_\textbf{B}^\mathbf {*}+\textbf{K}_\textbf{T}^\mathbf {*}+U^2C(k_{j}^*)\textbf{K}_{\textbf{A}\varvec{\omega }}\right) \right) {\bar{\textbf{q}}}^\mathbf {*}_j=\textbf{0} \end{aligned}$$

(17)

First order:

$$\begin{aligned}{} & {} \bigg ({\gamma _{j}^*}^2\left( \textbf{M}_\textbf{S}+\textbf{M}_\textbf{A}\right) +{\gamma _{j}^*}\left( U\textbf{C}_\textbf{A}+UC(k_{j}^*)\textbf{C}_{\textbf{A}\varvec{\omega }}\right) +\left( \textbf{K}_\textbf{B}^\mathbf {*}+\textbf{K}_\textbf{T}^\mathbf {*}+U^2C(k_{j}^*)\textbf{K}_{\textbf{A}\varvec{\omega }}\right) \bigg )\frac{\partial {{\bar{\textbf{q}}}}_j}{\partial {r_n}}\nonumber \\{} & {} \quad +\frac{\partial \gamma _{j}}{\partial {r_n}}\bigg (2\gamma _{j}^*\left( \textbf{M}_\textbf{S}+\textbf{M}_\textbf{A}\right) +U\textbf{C}_\textbf{A}+UC(k_{j}^*)\textbf{C}_{\textbf{A}\varvec{\omega }}\bigg ){\bar{\textbf{q}}}^\mathbf {*}_j+\frac{\partial {Im\left( \gamma _{j}\right) }}{\partial {r_n}}\bigg ({\gamma _{j}^*}U\frac{b}{U}\frac{\partial {C\left( k_{j}\right) }}{\partial {k_{j}}}\textbf{C}_{\textbf{A}\varvec{\omega }}\nonumber \\{} & {} \quad +U^2\frac{b}{U}\frac{\partial {C\left( k_{j}\right) }}{\partial {k_{j}}}\textbf{K}_{\textbf{A}\varvec{\omega }}\bigg ){\bar{\textbf{q}}}^\mathbf {*}_j=-\left( \frac{\partial {\textbf{K}_\textbf{B}}}{\partial {r_n}}+\frac{\partial {\textbf{K}_\textbf{T}}}{\partial {r_n}}\right) {\bar{\textbf{q}}}^\mathbf {*}_j \end{aligned}$$

(18)

Multiplying the first order equation by left eigenvector transpose $({^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T)$ [44, 45], the coefficient matrix of eigenvector derivative becomes null row vector, the above equation can be written as:

$$\begin{aligned}{} & {} \frac{\partial \gamma _{j}}{\partial {r_n}}{^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\bigg (2\gamma _{j}^*\left( \textbf{M}_\textbf{S}+\textbf{M}_\textbf{A}\right) +U\textbf{C}_\textbf{A}+UC(k_{j}^*)\textbf{C}_{\textbf{A}\varvec{\omega }}\bigg ){\bar{\textbf{q}}}^\mathbf {*}_j+\frac{\partial {Im\left( \gamma _{j}\right) }}{\partial {r_n}}{^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\bigg ({\gamma _{j}^*}U\frac{b}{U}\frac{\partial {C\left( k_{j}\right) }}{\partial {k_{j}}}\textbf{C}_{\textbf{A}\varvec{\omega }}\nonumber \\{} & {} \quad +U^2\frac{b}{U}\frac{\partial {C\left( k_{j}\right) }}{\partial {k_{j}}}\textbf{K}_{\textbf{A}\varvec{\omega }}\bigg ){\bar{\textbf{q}}}^\mathbf {*}_j=-{^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\left( \frac{\partial {\textbf{K}_\textbf{B}}}{\partial {r_n}}+\frac{\partial {\textbf{K}_\textbf{T}}}{\partial {r_n}}\right) {\bar{\textbf{q}}}^\mathbf {*}_j \end{aligned}$$

(19)

Various terms of Eq. (19) can be represented for obtaining eigenvalue derivatives as [40]:

$$\begin{aligned}{} & {} {^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\bigg (2\gamma _{j}^*\left( \textbf{M}_\textbf{S}+\textbf{M}_\textbf{A}\right) +U\textbf{C}_\textbf{A}+UC(k_{j}^*)\textbf{C}_{\textbf{A}\varvec{\omega }}\bigg ){\bar{\textbf{q}}}^{*}_j=\varepsilon +i\varrho \end{aligned}$$

(20)

$$\begin{aligned}{} & {} {^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\bigg ({\gamma _{j}^*}U\frac{b}{U}\frac{\partial {C\left( k_{j}\right) }}{\partial {k_{j}}}\textbf{C}_{\textbf{A}\varvec{\omega }}+U^2\frac{b}{U}\frac{\partial {C\left( k_{j}\right) }}{\partial {k_{j}}}\textbf{K}_{\textbf{A}\varvec{\omega }}\bigg ){\bar{\textbf{q}}}^\mathbf {*}_j=\psi +i\vartheta \end{aligned}$$

(21)

$$\begin{aligned}{} & {} -{^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\left( \frac{\partial {\textbf{K}_\textbf{B}}}{\partial {r_n}}+\frac{\partial {\textbf{K}_\textbf{T}}}{\partial {r_n}}\right) {\bar{\textbf{q}}}^\mathbf {*}_j=\eta +i\varphi \end{aligned}$$

(22)

Since $\gamma _j = Re(\gamma _j)+$ i $Im(\gamma _j) = \beta _j+i \omega _{j}$ and substituting it in Eq. (19) with terms represented by Eqs. (20)–(22), the first order eigenvalue derivatives can be written at the design point as:

$$\begin{aligned} \frac{\partial Re(\gamma _j)}{\partial {r}_{n}}= & {} \frac{\partial \beta _j}{\partial {r}_{n}}=\frac{\varphi (\psi -\varrho )-\eta (\vartheta +\varepsilon )}{\varrho (\psi -\varrho )-\varepsilon (\vartheta +\varepsilon )}\nonumber \\ \frac{\partial Im(\gamma _j)}{\partial {r}_{n}}= & {} \frac{\partial \omega _j}{\partial {r}_{n}}=\frac{\eta \varrho -\varphi \varepsilon }{\varrho (\psi -\varrho )-\varepsilon (\vartheta +\varepsilon )} \end{aligned}$$

(23)

The eigenvalue of the jth mode can also be written as $\gamma {_j}=-\zeta _j\omega _j+i{}\omega _j$. Hence, the first derivative of damping ratio of the jth mode at the design point can be expressed as:

$$\begin{aligned} \frac{\partial {\zeta _j}}{\partial {r_n}}=-\frac{1}{\omega _j^*}\left( \frac{\partial {Re\left( \gamma _{j}\right) }}{\partial {r_n}}+\zeta _j^*\frac{\partial {Im\left( \gamma _{j}\right) }}{\partial {r_n}}\right) \end{aligned}$$

(24)

3.2.2 Random fields

In the present analysis, stiffness parameters are considered as uncertain structural parameters because variability in stiffness parameters takes care of variation in shape as well as variability in material properties [42]. The aleatory uncertainty present in random stiffness terms (EI) and (GJ) are considered as second order stationary Gaussian random fields, and represented by their mean and covariance function. A truncated Karhunen–Loeve expansion is employed for the decomposition of random fields with a known covariance function $(\kappa )$. According to the truncated K–L expansion, the random field $\chi \left( y,\theta \right)$ is represented in terms of finite series having orthonormal random variables in N dimensional space as [46]:

$$\begin{aligned} \chi \left( y,\theta \right) ={\overline{\chi }}+\sum _{n=1}^{N}\sqrt{\lambda _{n}}\xi _{n}(\theta )f_n(y) \end{aligned}$$

(25)

where ${\overline{\chi }}$ is the mean of the random field, $\lambda _{n}$ and $f_n(y)$ are the nth eigenvalue and eigenfunction respectively of the covariance kernel represented by Eq. (27). $\xi _{n}$ is the standard normal random variable showing the orthonormal condition with respect to Gaussian measure as $E[\xi _m,\xi _n]=\delta _{mn}$, where E[ ] and $\delta _{mn}$ are the mathematical expectation operator and Kronecker delta function respectively. In this study, the exponential covariance kernel is adopted because eigenvalues and eigenfunctions of the covariance kernel can be obtained analytically [6]. The exponential covariance function for the random field can be written as:

$$\begin{aligned} \kappa (y,y_1)={\sigma }^2e^{c |y-y_1| } \end{aligned}$$

(26)

where ${\sigma }$ is the standard deviation (SD) of the process and c is the reciprocal of correlation length $(l_{cor})$ equal to the span of the wing (l). The eigenvalue and eigenfunction presented in Eq. (25) can be obtained by solving Fredholm integral of second kind [47] and is represented in kernel form as:

$$\begin{aligned} \int _{l}\kappa (y,y_1)f_n(y_1)dy_1=\lambda _{n}f_n(y) \end{aligned}$$

(27)

By following the procedure for obtaining eigenvalue and eigenfunction of exponential covariance function given in [6, 47], the eigenvalue can be obtained as:

$$\begin{aligned} \lambda _{n}=\frac{2{\sigma }^2c}{c^2+\varpi _n^2} \end{aligned}$$

(28)

where $\varpi _n$ is a parameter obtained by solving Eqs. (29) and (30) for odd and even values of subscript respectively; and the corresponding eigenfunctions are defined by Eqs. (31) and (32) respectively.

$$\begin{aligned}{} & {} \tan \left( \varpi _n\frac{l}{2}\right) -\frac{c}{\varpi _n}=0 \end{aligned}$$

(29)

$$\begin{aligned}{} & {} \tan \left( \varpi _n\frac{l}{2}\right) +\frac{\varpi _n}{c}=0 \end{aligned}$$

(30)

$$\begin{aligned}{} & {} f_n(y)=\frac{\cos (\varpi _ny)}{\sqrt{\frac{l}{2}+\frac{\sin (\varpi _nl)}{2\varpi _n}}} \end{aligned}$$

(31)

$$\begin{aligned}{} & {} f_n(y)=\frac{\sin (\varpi _ny)}{\sqrt{\frac{l}{2}-\frac{\sin (\varpi _nl)}{2\varpi _n}}} \end{aligned}$$

(32)

It is important to note that the eigenvalues are arranged in descending order with increasing n. Since bending and torsional stiffnesses are treated as random field parameters, the global bending and torsional stiffness matrices in Eq. (13) can be written as [39, 42]:

$$\begin{aligned}{} & {} \textbf{K}_\textbf{B}=\bar{\textbf{K}}_\textbf{B}+\sum _{n=1}^{N}\xi _{n}\left( \theta \right) {\textbf{K}_\textbf{B}}_{,n} \end{aligned}$$

(33)

$$\begin{aligned}{} & {} \textbf{K}_\textbf{T}=\bar{\textbf{K}}_\textbf{T}+\sum _{n=1}^{N}\xi _{n}\left( \theta \right) {\textbf{K}_\textbf{T}}_{,n} \end{aligned}$$

(34)

where $\bar{\textbf{K}}_\textbf{B}$ and $\bar{\textbf{K}}_\textbf{T}$ are the mean structural bending and torsional stiffness matrices respectively; $\sum _{n=1}^{N}\xi _{n}(\theta ){\textbf{K}_\textbf{B}}_{,n}$ and $\sum _{n=1}^{N}\xi _{n}(\theta ){\textbf{K}_\textbf{T}}_{,n}$ are the random structural bending and torsional stiffness matrices respectively. Consequently, the stochastic finite element equations (Eq. (13)) for random field problem can be written as:

$$\begin{aligned}{} & {} \left( \textbf{M}_\textbf{S}+\textbf{M}_\textbf{A}\right) {\ddot{{\textbf {q}}}}+\left( U\textbf{C}_\textbf{A}+UC(k)\textbf{C}_{\textbf{A}\varvec{\omega }}\right) {\dot{{\textbf {q}}}}+ \bigg (\bar{\textbf{K}}_\textbf{B}+\sum _{n=1}^{N}\xi _{n}\left( \theta \right) {\textbf{K}_\textbf{B}}_{,n}\nonumber \\{} & {} \quad +\;\bar{\textbf{K}}_\textbf{T}+\sum _{n=1}^{N}\xi _{n}\left( \theta \right) {\textbf{K}_\textbf{T}}_{,n}+U^2C(k)\textbf{K}_{\textbf{A}\varvec{\omega }}\bigg )\textbf{q}=\textbf{0} \end{aligned}$$

(35)

Substituting $\textbf{q}={\bar{\textbf{q}}}\exp {(\gamma t)}$ in Eq. (35), the second-order random eigenvalue equation can be written for random field problem as:

$$\begin{aligned}{} & {} \bigg (\gamma ^2\left( \textbf{M}_\textbf{S}+\textbf{M}_\textbf{A}\right) +\gamma \left( U\textbf{C}_\textbf{A}+UC(k)\textbf{C}_{\textbf{A}\varvec{\omega }}\right) + \bigg (\bar{\textbf{K}}_\textbf{B}+\sum _{n=1}^{N}\xi _{n}\left( \theta \right) {\textbf{K}_\textbf{B}}_{,n}\nonumber \\{} & {} \quad +\;\bar{\textbf{K}}_\textbf{T}+\sum _{n=1}^{N}\xi _{n}\left( \theta \right) {\textbf{K}_{\textbf{T}}}_{,n}+U^2C(k) \textbf{K}_{\textbf{A}\varvec{\omega }}\bigg )\bigg ){\bar{\textbf{q}}}=\textbf{0} \end{aligned}$$

(36)

Express $\xi _{n}\left( \theta \right)$ = $\xi _{n}^{*}\left( \theta \right) +\delta \xi _{n}(\theta )$ and substitute random response terms from Eq. (16) into Eq. (36) for the jth mode by modifying notational representation of nth random variable as $r_n=\xi _{n}$, and random vector at design points $\textbf{r}^*=\varvec{\xi }^{*}$. After separating zeroth order and first order terms, the zeroth and first order equations can be written as:

Zeroth order:

$$\begin{aligned}{} & {} \left( {\gamma ^*_j}^2\left( \textbf{M}_{\textbf{S}}+\textbf{M}_{\textbf{A}}\right) +{\gamma ^*_j}\left( U\textbf{C}_{\textbf{A}}+UC(k^*_j)\textbf{C}_{\textbf{A}\varvec{\omega }}\right) + \bigg (\bar{\textbf{K}}_{\textbf{B}}+\sum _{n=1}^{N}\xi _{n}^*\left( \theta \right) {\textbf{K}_{\textbf{B}}}_{,n}\right. \nonumber \\{} & {} \left. \quad +\bar{\textbf{K}}_{\textbf{T}}+\sum _{n=1}^{N}\xi _{n}^*\left( \theta \right) {\textbf{K}_{\textbf{T}}}_{,n}+U^2C(k^*_j)\textbf{K}_{\textbf{A}\varvec{\omega }}\bigg )\right) {\bar{\textbf{q}}}^\mathbf {*}_j=\textbf{0} \end{aligned}$$

(37)

First order:

(38)

Multiplying Eq. (38) by left eigenvector transpose ${^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T$ [44, 45], the coefficient matrix of eigenvector derivatives becomes zero vector. Equation (38) can be written as:

$$\begin{aligned}{} & {} \frac{\partial {\gamma _j}}{\partial {\xi _n}}{^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\left( 2{\gamma ^*_j}\left( \textbf{M}_\textbf{S}+\textbf{M}_\textbf{A}\right) +\left( U\textbf{C}_\textbf{A}+UC(k^*_j)\textbf{C}_{\textbf{A}\varvec{\omega }}\right) \right) {\bar{\textbf{q}}}^\mathbf {*}_j+\frac{\partial {Im(\gamma _j)}}{\partial {\xi _n}}{^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\bigg ({\gamma ^*_j}U\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k_j}}\textbf{C}_{\textbf{A}\varvec{\omega }}\nonumber \\{} & {} \quad +U^2\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k_j}}\textbf{K}_{\textbf{A}\varvec{\omega }}\bigg ){\bar{\textbf{q}}}^\mathbf {*}_j=-{^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\left( {\textbf{K}_\textbf{B}}_{,n}+{\textbf{K}_\textbf{T}}_{,n}\right) {\bar{\textbf{q}}}^\mathbf {*}_j \end{aligned}$$

(39)

Various terms of Eq. (39) can be represented similar to Eqs. (20)–(22) for obtaining eigenvalue derivatives as:

$$\begin{aligned}{} & {} {^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\left( 2{\gamma ^*_j}\left( \textbf{M}_\textbf{S}+\textbf{M}_\textbf{A}\right) +\left( U\textbf{C}_\textbf{A}+UC(k^*_j)\textbf{C}_{\textbf{A}\varvec{\omega }}\right) \right) {\bar{\textbf{q}}}^\mathbf {*}_j=\varepsilon +i\varrho \end{aligned}$$

(40)

$$\begin{aligned}{} & {} {^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\left( {\gamma ^*_j}U\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k_j}}\textbf{C}_{\textbf{A}\varvec{\omega }}+U^2\frac{b}{U}\frac{\partial {C(k_j)}}{\partial {k_j}}\textbf{K}_{\textbf{A}\varvec{\omega }}\right) {\bar{\textbf{q}}}^\mathbf {*}_j=\psi +i\vartheta \end{aligned}$$

(41)

$$\begin{aligned}{} & {} -{^l{\bar{\textbf{q}}}^\mathbf {*}_j}^T\left( {\textbf{K}_{\textbf{B}}}_{,n}+{\textbf{K}_{\textbf{T}}}_{,n}\right) {\bar{\textbf{q}}}^\mathbf {*}_j=\eta +i\varphi \end{aligned}$$

(42)

Simplifying Eq. (39) using symbolic terms appeared in Eqs. (40)–(42), the eigenvalue derivatives can be obtained using Eqs. (23) and (24).

4 Aeroelastic reliability methods

In Sect. 3, the mathematical and stochastic models of a wing were discussed, and parameters were modeled as random variables as well as random fields. The process of obtaining eigenvalue derivatives was also discussed, which is required for aeroelastic reliability analysis. Reliability refers to a system performing its intended function over a given period of time under the operating conditions [48]. The aeroelastic instability phenomenon is obtained from stability conditions (discussed in Sect. 2), hence the limit state function $g({\textbf {r}})$, which is a boundary between safe and unsafe regions, can be written in implicit form by defining it in conditional sense as [26, 42, 49]:

$$\begin{aligned} g(\textbf{r})= & {} \zeta _{k}(\textbf{r})|_{U_{flutter}=U}=0\nonumber \\= & {} \beta _{j}(\textbf{r})\beta _{k}(\textbf{r})|_{U_{flutter}=U}=0 \nonumber \\= & {} F_{m}(\textbf{r})|_{U_{flutter}=U}=0 \end{aligned}$$

(43)

where the indices j and k are equal to 1 and 2 respectively. The probability of failure due to dynamic aeroelastic instability can be written as:

$$\begin{aligned} P_{flutter} = P\left[ g(\textbf{r})\le 0 \right] \end{aligned}$$

(44)

There are various methods for obtaining $P_{flutter}$ such as MCS, FOSM, and FORM. The reliability methods: MCS, FOSM, and FORM are discussed in the following sections.

4.1 Monte Carlo simulation

The Monte Carlo simulation method is a random sampling technique [50] in which a large number of simulations is required to obtain the desired response with required accuracy level [51]. MCS is used to quantify uncertainty in response of systems where approximate methods fail to capture it accurately. It is also used for the validation of approximate methods. The probability of failure ($P_{f}$) due to flutter can be obtained using the number of samples $(n_{s})$ satisfying Eq. (44), out of total samples $(N_{s})$ at various flow velocities. At a given flow velocity (U), the probability of failure can be written as:

$$\begin{aligned} P_{flutter}=\frac{n_{s}}{N_{s}} \end{aligned}$$

(45)

4.2 First order second moment method

In the FOSM method, the limit state function represented in Eq. (43) is expanded via Taylor’s series expansion about the mean value of random variables $(\textbf{r}^\textbf{o})$ truncated to the first order terms at a given flow velocity as [43, 52]:

$$\begin{aligned} g(\textbf{r})= g(\textbf{r}^\textbf{o})+\sum _{n=1}^{N}\frac{\partial {g(\textbf{r})}}{\partial {r_{n}}}|_{\textbf{r}^\textbf{o}}(r_{n}-r_n^{o}) \end{aligned}$$

(46)

where $r_n^{o}$ is the mean value of random variable, $r_{n}$. Taking the mathematical expectation of Eq. (46), the mean and variance of the limit state function can be written as:

$$\begin{aligned} E\left[ g(\textbf{r})\right] = g(\textbf{r}^\textbf{o});\hspace{5pt} \sigma ^2_{g(\textbf{r})}= \sum _{n=1}^{N}\left( \frac{\partial {g(\textbf{r})}}{\partial {r_{n}}}|_{\textbf{r}^\textbf{o}}\right) ^2\sigma _{r_{n}}^2 \end{aligned}$$

(47)

where $\sigma _{r_{n}}$ is the standard deviation of input random parameter. The reliability index $(\beta _{R})$ and the corresponding probability of failure due to flutter can be written as:

$$\begin{aligned} \beta _{R}= \frac{E\left[ g(\textbf{r})\right] }{\sigma _{g(\textbf{r})}}; \hspace{5pt} P_{flutter} = \Phi \left( -\beta _{R}\right) \end{aligned}$$

(48)

where $\Phi$ is the standard normal CDF function.

4.3 First order reliability method

The first order reliability method is an improvement over the FOSM method, in which performance function is expanded about a design point $({\textbf{r}^\mathbf {*}})$ using Taylor’s series expansion. Since the limit state function given in Eq. (43) is represented in implicit form, a Newton–Raphson based recursive algorithm proposed by Rackwitz and Fiessler [53] is used. In order to get faster convergence, the algorithm should be defined in the reduced co-ordinate system ($\textbf{r}{'}$), (zero mean and unit variance) and the limit state function can be written as:

$$\begin{aligned} g(\textbf{r}{'})=0 \end{aligned}$$

(49)

The limit state function can be linearized using the first-order Taylor series expansion as:

$$\begin{aligned} g( \textbf{r}^{\varvec{\prime {^*}}}_{k+1})= g( \textbf{r}^{\varvec{\prime {^*}}}_{k})+\pmb {\triangledown }g( \textbf{r}^{\varvec{\prime {^*}}}_{k})^T\left( \textbf{r}^{\varvec{\prime {^*}}}_{k+1}- \textbf{r}^{\varvec{\prime {^*}}}_{k}\right) \end{aligned}$$

(50)

where $\pmb {\triangledown }g(\textbf{r}^{\varvec{\prime {^*}}}_{k})$ is the gradient vector of the limit state function at the kth iteration point $\textbf{r}^{\varvec{\prime {^*}}}_{k}$. The limit state function becomes zero, if the $({k+1})$th design point satisfies the limit state, i.e., $g(\textbf{r}^{\varvec{\prime {^*}}}_{k+1})=0$. By rearranging the terms of Eq. (50), the $({k+1})$th design point can be obtained as:

$$\begin{aligned} \textbf{r}^{\varvec{\prime {^*}}}_{k+1}=\frac{1}{\arrowvert \pmb {\triangledown }g(\textbf{r}^{\varvec{\prime {^*}}}_{k}) \arrowvert ^2}\left[ \pmb {\triangledown }g( \textbf{r}^{\varvec{\prime {^*}}}_{k})^T\textbf{r}^{\varvec{\prime {^*}}}_{k}-g(\textbf{r}^{\varvec{\prime {^*}}}_{k})\right] \pmb {\triangledown }g( \textbf{r}^{\varvec{\prime {^*}}}_{k}) \end{aligned}$$

(51)

Since the value of the term $g(\textbf{r}^{\varvec{\prime {^*}}}_{k})$ is independent of coordinate system, the term in original coordinate system is $g(\textbf{r}^{\varvec{*}}_{k})$, Eq. (51) can be written in modified form as:

$$\begin{aligned} \textbf{r}^{\varvec{\prime {^*}}}_{k+1}=\frac{1}{\arrowvert \pmb {\triangledown }g(\textbf{r}^{\varvec{\prime {^*}}}_{k}) \arrowvert ^2}\left[ \pmb {\triangledown }g( \textbf{r}^{\varvec{\prime {^*}}}_{k})^T\textbf{r}^{\varvec{\prime {^*}}}_{k}-g(\textbf{r}^{\varvec{*}}_{k})\right] \pmb {\triangledown }g( \textbf{r}^{\varvec{\prime {^*}}}_{k}) \end{aligned}$$

(52)

The criteria for obtaining convergent design points are described below. In this algorithm, two convergence criteria are used [42].

• (a) If a design point lies beyond the limit set by the user, then the reliability index should be calculated by using FOSM and the converged design point is the mean value of design point. Here, in the present case $\mu \pm 6\sigma$ is the limit.

• (b) If a design point lies within the prescribed limit set by the user, then the reliability index is computed using FORM and it runs till convergence on $|\triangle \beta _{R}|$ and $|\triangle {g}|$ are satisfied. The convergence criteria depend on limit state functions as:

  • For limit state functions,

    $$\begin{aligned} \zeta _{k}(\textbf{r})|_{U_{flutter}=U}= & {} 0\\ \beta _{j}(\textbf{r})\beta _{k}(\textbf{r})|_{U_{flutter}=U}= & {} 0 \quad |\triangle \beta _{R}|\le 0.001 \hspace{2pt}\text {and}\hspace{2pt} |\triangle {g}|\le 0.0001 \end{aligned}$$

  • For limit state function, $F_{m}(\textbf{r})|_{U_{flutter}=U}=0$, $|\triangle \beta _{R}|\le 0.001$ and $|\triangle {g}|\le 0.01$.

The steps of the FORM algorithm to calculate the reliability index are given below.

• 1. Consider a limit state function from Eq. (43) at a given flow velocity (U).

• 2. Calculate the mean and standard deviation of limit state functions considering design points as mean value of random variables $(\textbf{r}^\textbf{o})$, hence the reliability index using Eq. (48).

• 3. Assume initial design point $(\textbf{r}^\mathbf {*})$ at $\textbf{r}_{\mu -3.5\sigma }$ of random variables if $U < U_{f}$ else mean value of random variables $(\textbf{r}^\textbf{o})$, where $U_{f}$ is the mean flutter velocity.

• 4. Compute the mean $(\mu _{{r}_{n,k}}^{Norm})$ and standard deviation $(\sigma _{{r}_{n,k}}^{Norm})$ of design point $(\textbf{r}^{\varvec{*}})$ at kth iteration in the equivalent normal space using equivalent normal transformations [54].

• 5. Compute the gradient of limit state function $\pmb {\triangledown }g(\textbf{r})$ at kth iteration design point $(\textbf{r} =\textbf{r}^{\varvec{*}}_{k})$.

• 6. Compute the gradient of limit state function at kth iteration design point in the reduced co-ordinate system as: $\pmb {\triangledown }g( \textbf{r}^{\varvec{\prime {^*}}}_{k})$=$\pmb {\triangledown }g(\textbf{r}^{\varvec{*}_{k}}).*\varvec{\sigma }$, where $.*$ and $\varvec{\sigma }$ are element wise multiplication and a vector of equivalent normal standard deviation of random parameters.

• 7. Compute the design point $(\textbf{r}_{k+1}^{\varvec{\prime {^*}}})$ using Eq. (52).

• 8. Compute the reliability index (distance from the origin to limit state in the reduced coordinate system) as

  $$\begin{aligned} \beta _{R_{k+1}}=\sqrt{(\textbf{r}^{\varvec{\prime {^*}}}_{k+1})^{T}(\textbf{r}^{\varvec{\prime {^*}}}_{k+1}}) \end{aligned}$$

  and check the condition, if $U>U_{f}$ or alternatively $P_{flutter}\ge 0.5$ evaluated from Eq. (48), then $\beta _{R_{k+1}} = -\beta _{R_{k+1}}$.

• 9. Compute the new design point in original space as

  $$\begin{aligned} {r}_{n,k+1}^*=\mu _{{r}_{n,k}}^{Norm}+\sigma _{{r}_{n,k}}^{Norm}{r}^{'{^*}}_{n,k+1} \end{aligned}$$

  and the limit state function $g(\textbf{r}^{\varvec{^*}}_{k+1})$ corresponding to the new design point $\textbf{r}_{k+1}$ in the original coordinate system.

• 10. Check convergence condition (a). If satisfied, save the value of reliability index and design point computed in step 2 and go to step 12, else (if $k = 1$, go to step 4 ) go to the next step.

• 11. Check convergence condition (b). If satisfied, go to the next step else go to step 4.

• 12. Save the converged value of reliability index and the corresponding probability of failure using Eq. (48) for a given flow velocity (U).

To obtain the CDF (reliability) of flutter velocity, all the above steps are repeated for a range of flow velocities of interest. It is important to note that for handling random field problem, $r_{n}$, $\textbf{r}$ and $\sigma _{{r}_{n}}$ are replaced by $\xi _{n}$, $\varvec{\xi }$, and 1 (due to property of random variable $\xi _{n}$) respectively.

5 Results and discussion

In this section, stochastic aeroelastic stability and flutter reliability analyses of a cantilever wing using various limit state functions are discussed. Here, the stiffness parameters, EI and GJ are modeled as random variables and random fields as two separate cases and discussed in Sects. 5.1 and 5.2 respectively.

Table 2 Mean properties of cantilever wing [55]

Fig. 2

Variation of mean stability parameters a damping ratios $(\overline{\zeta _{i}})$, b product of decay rates $\overline{\beta _{1}\beta _{2}}$, and c flutter margin $(\overline{F_{m}})$ with flow velocities

The mean properties of the wing are given in Table 2. The approximate Theodorsen’s function is taken from Sazesh and Irani [55]. Figure 2 shows the variation of various mean stability parameters with flow velocities obtained from the perturbation approach. From Fig. 2a, it is observed that the mean damping ratio ($\overline{\zeta _2}$) of mode 2, changes its sign and becomes zero at flow velocity 137.38 m/s (hence mean flutter velocity) while for mode 1, the mean damping ratio $(\overline{\zeta _{1}})$ is always positive. The same mean flutter velocity is observed for other stability parameters ($\overline{\beta _{1}\beta _{2}}$ and $\overline{F_{m}}$) as shown in Fig. 2b, c. The present mean flutter velocity of the wing exactly matches with those reported in [55]. From these figures, it can also be noted that the mean damping ratio $(\overline{\zeta _{2}})$ and mean decay rates $(\overline{\beta _{1}\beta _{2}})$ increase initially with flow velocities. After 127 m/s, their values decrease rapidly with flow velocities and reach the flutter point immediately without giving sufficient margin. However, the mean $F_{m}$ values decrease gradually with flow velocities and provides a better flutter estimation approach compared to other stability parameters.

5.1 Random variables

Table 3 Variation in COVs of stability parameters with flow velocities for 5% COV in EI

Table 4 Variation in COVs of stability parameters with flow velocities for 5% COV in GJ

In this section, the effect of random variable modeling of stiffness parameters: EI and GJ on the aeroelastic stability and flutter reliability of the cantilever wing is studied. The coefficient of variations (COVs) of stiffness parameters are considered to be 5%. Table 3 shows the variation in stability parameters at various flow velocities in the presence of 5% COV in EI obtained from the perturbation approach (with C(k) considered as deterministic and random quantity in the vicinity of parametric uncertainty) and MCS with 20,000 samples. From the table, it is observed that the COVs of stability parameters at various flow velocities obtained from the perturbation approach do not agree with MCS, when C(k) is considered as deterministic. However, the COVs of stability parameters at various flow velocities obtained from the perturbation approach, when C(k) is considered as random, agree well with MCS. Table 4 shows the COVs of stability parameters at various flow velocities in the presence of 5% COV in GJ. From the table, it is observed that at flow velocity U = 100 m/s, the COVs of stability parameters obtained from perturbation agree well with MCS, when C(k) is considered as random and do not agree with when C(k) is considered as deterministic. At flow velocity 125 m/s, there are some discrepancy in the COVs of stability parameters obtained from the perturbation approach with C(k) as a random quantity compared with MCS due to change in probabilistic distribution of stability parameters as shown in Fig. 6. At flow velocity 135 m/s, the COVs of stability parameters obtained from the perturbation approach agree reasonably well with MCS, when C(k) is a random quantity in comparison of C(k) considered as a deterministic quantity. Hence, for all further studies, C(k) is considered as a random quantity in the vicinity of parametric uncertainty present in the aeroelastic system.

Figures 3 and 4 show the variation in COVs of stability parameters with flow velocities for 5% COV in EI and GJ respectively.

Fig. 3

Variation in COVs of stability parameters a $\zeta _{2}$, b $\beta _{1}\beta _{2}$, and c $F_{m}$ with flow velocities for 5% COV in EI

Fig. 4

Variation in COVs of stability parameters a $\zeta _{2}$, b $\beta _{1}\beta _{2}$, and c $F_{m}$ with flow velocities for 5% COV in GJ

From Fig. 3, it is observed that the COVs of stability parameters increase as flow velocity approaches the mean flutter velocity, and starts decreasing as flow velocity crosses the mean flutter velocity. It is also observed that the COVs of stability parameters obtained from the perturbation approach agree well with MCS. From Fig. 4, it is observed that the COVs of stability parameters increase up to the mean flutter velocity after that start decreasing. It is also noted that there is a slight difference in the mean flutter velocity prediction between the perturbation approach and MCS.

Next, the PDFs of stability parameters ($\zeta _{j}$, $\beta _{j}\beta _{k}$, and $F_{m}$) obtained using the perturbation approach and MCS along with a suitable model curve fit (parametric or non-parametric) are studied. In the case of perturbation approach, the first two moments (mean and standard deviation) of Gaussian density obtained from Eq. (47) are used to present the PDFs of stability parameters [52]. In the case of MCS, normalized histograms of the sampled data are used to present the PDFs of stability parameters [52]. Further, a parametric density model fit (Gaussian model curve fit) of the sampled data is also presented by using the first two moments of Gaussian density for each stability parameter. In the case of non-parametric density model fit (kernel model curve fit), the sampled data are processed in kernel density estimator having Gaussian kernel to present the PDF of each stability parameter [57].

Figures 5 and 6 show the PDFs of stability parameters in the presence of 5% COV in EI and GJ respectively using the perturbation approach and MCS at flow velocities 125 m/s (away from the mean flutter velocity) and 135 m/s (near to the mean flutter velocity).

Fig. 5

PDFs of stability parameters a $\zeta _{2}$ at 125 m/s, b $\zeta _{2}$ at 135 m/s, c $\beta _{1}\beta _{2}$ at 125 m/s, d $\beta _{1}\beta _{2}$ at 135 m/s, and e $F_{m}$ at 125 m/s, f $F_{m}$ at 135 m/s for 5% COV in EI

It is important to note that the skewness and kurtosis values of distribution indicate about the nature of probability distribution, i.e., symmetric and peakedness. Ideally for Gaussian distribution (a reference distribution), the skewness and kurtosis values are 0 and 3 (mesokurtic) respectively. According to Bulmer [56], if the skewness coefficient is less than $-$ 1 or greater than + 1, then the distribution is highly skewed. If skewness coefficient is in between $-$ 1 and $-$0.5 or between 0.5 and + 1, then the distribution is moderately skewed, and if skewness coefficient lies in between $-$ 0.5 to + 0.5, then the distribution is approximately symmetric.

The skewness and kurtosis values of the PDFs of stability parameters (as shown in Fig. 5) obtained from MCS at flow velocities 125 m/s and 135 m/s are given in Table 5.

Fig. 6

PDFs of stability parameters a $\zeta _{2}$ at 125 m/s, b $\zeta _{2}$ at 135 m/s, c $\beta _{1}\beta _{2}$ at 125 m/s, d $\beta _{1}\beta _{2}$ at 135 m/s, and e $F_{m}$ at 125 m/s, f $F_{m}$ at 135 m/s for 5% COV in GJ

Table 5 Skewness and Kurtosis values of stability parameters for 5% COV in EI using MCS

Table 6 Skewness and Kurtosis values of stability parameters for 5% COV in GJ using MCS

From the table, it can be observed that the skewness coefficients of stability parameters at both flow velocities lie between $-$ 0.5 to + 0.5 and kurtosis values are nearly 3. Hence, the distributions of stability parameters are Gaussian in nature, and the Gaussian distribution curve fit for MCS data on normalized histogram is shown in Fig. 5. It is also noted from the figure, there is no negative region bounded by stability parameters at 125 m/s and 135 m/s, so there is non-occurrence of flutter phenomenon at these two flow velocities due to 5% COV in EI.

Similarly, the skewness and kurtosis values of the PDFs of stability parameters (as shown in Fig. 6) obtained from MCS at flow velocities 125 m/s and 135 m/s are given in Table 6. Since the skewness values of stability parameters: $\zeta _{2}$ and $\beta _{1}\beta _{2}$ do not lie between $-$ 0.5 and + 0.5 at both flow velocities, hence the distributions are not symmetric and also kurtosis values are significantly away from 3.0 except at 135 m/s for the stability parameter $\zeta _{2}$, which is nearly 3. Hence, the Gaussian distribution curve fit is not suitable for parametric density curve fitting, and a non-parametric distribution curve fit (kernel density estimator having Gaussian kernel [57]) is considered for fitting MCS data at flow velocities 125 m/s and 135 m/s for stability parameters $\zeta _{2}$ and $\beta _{1}\beta _{2}$. However, for the stability parameter $F_{m}$, the skewness and kurtosis values are nearly close to the reference distribution (Gaussian), hence the Gaussian distribution is considered to fit MCS data. From Fig. 6, it can be seen that at flow velocity 125 m/s, there is no negative region bounded by abscissa of stability parameters. However, at 135 m/s, there are negative regions bounded by abscissa of stability parameters, so flutter phenomenon is encountered in the presence of uncertainty in GJ. From the figure, it is also observed that for stability parameters $\zeta _{2}$ and $\beta _{1}\beta _{2}$, the distribution characteristics changes with flow velocity, however in the case of stability parameter $F_{m}$ the distribution characteristics is invariant with flow velocity.

Fig. 7

CDFs of flutter velocity of cantilever wing for various limit states a $\zeta _{2} = 0$, b $\beta _{1}\beta _{2} = 0$, and c $F_{m} = 0$ for 5% COV in EI using FOSM, MCS and FORM methods: random variable modeling

Figures 7 and 8 show the CDFs of flutter velocity of the wing obtained from FOSM, FORM, and MCS for 5% COV in EI and GJ respectively for various limit state functions. From Fig. 7, it is observed that the CDFs of flutter velocity obtained from the FOSM method show small deviation in the lower tail region with MCS for all limit state representations in the presence of uncertainty in EI. However, the CDFs of flutter velocity obtained from FORM match well with MCS. The flutter velocities corresponding to CDF = 0.01 obtained from FOSM, MCS, and FORM for various limit states are given in Table 7. The predicted flutter velocity corresponding to CDF = 0.01 using the FOSM method depends on the form of limit state functions, so a lack of invariance with the FOSM method is observed.

Table 7 Flutter velocities corresponding to CDF = 0.01 for 5% COV in EI for various limit state functions

Fig. 8

CDFs of flutter velocity of cantilever wing for various limit states a $\zeta _{2} = 0$, b $\beta _{1}\beta _{2} = 0$, and c $F_{m} = 0$ for 5% COV in GJ using FOSM, MCS and FORM methods: random variable modeling

From Fig. 8 in the case of uncertainty in GJ, it is observed that the CDFs of flutter velocity obtained from the FOSM method do not agree with MCS for limit state functions $\zeta _{2} = 0$ and $\beta _{1}\beta _{2} = 0$ particularly in the lower tail region and agree with MCS for the limit state $F_m = 0$. However, the CDFs of flutter velocity obtained from FORM closely agree with MCS for all limit states. The flutter velocity corresponding to CDF = 0.01 obtained from FOSM, MCS, and FORM for various limit states are shown in Table 8. From the table it can be observed that the predicted flutter velocity corresponding to CDF = 0.01 using the FOSM method depends on the form of limit state functions, so a lack of invariance with the FOSM method is observed.

Table 8 Flutter velocities corresponding to CDF = 0.01 for 5% COV in GJ for various limit state functions

Figure 9 shows the CDFs of flutter velocity of the wing obtained from FORM for various limit state functions in the presence of uncertainty in EI and GJ. From these figures, it is observed that the CDFs of flutter velocity obtained from FORM agree well with each other as well as with MCS. At CDF = 0.01 for 5% COV in EI, the predicted flutter velocity obtained from FORM for all limit state functions is 136.85 m/s, and in the case of 5% COV in GJ, the predicted onset flutter velocity corresponding to CDF = 0.01 for all limit state functions is 128.59 m/s. Hence, the proposed FORM algorithm is able to overcome the lack of invariance problem in the prediction of flutter velocity. It is also noted that the computation time for the CDF of flutter velocity using the FORM algorithm for the EI case for various limit state functions $\zeta _{2}$, $\beta _{1}\beta _{2}$, and $F_{m}$ are 132, 141, and 252 s respectively with serial processor using Matlab 2017a on HP Z800 workstation with 24 GB RAM while MCS takes 8 h 17 min and 16 s with 4 cores parallel processor. Hence, the FORM algorithm works efficiently and effectively.

Fig. 9

CDFs of flutter velocity of cantilever wing for 5% COV in a EI, b GJ for various limit state functions using FORM and MCS: random variable modeling

5.2 Random fields

Fig. 10

a Eigenvalues, b eigenfunctions of covariance kernel

In the previous section, stochastic aeroelastic stability and flutter reliability analyses of a cantilever wing were performed by modeling stochastic parameters as random variables. In this section, reliability analysis of the wing is presented in which stiffness parameters are modeled as Gaussian random fields.

Figure 10 shows the eigenvalues and eigenfunctions of exponential covariance kernel, which are used for approximating Gaussian random fields. Figure 10a shows the eigenvalues of covariance kernel with various correlation lengths. From the figure, it is observed that, as correlation length increases, eigenvalues decay rapidly with increasing index, n. Figure 10b shows the first four eigenfunctions corresponding to $l_{cor} = l$. Figure 11 shows the variation in COVs of various stability parameters with number of K–L expansion terms at flow velocity 125 m/s for correlation length l. From the figure, it is observed that the COVs of various stability parameters converge from second terms onward. In further studies, the number of K–L expansion terms and correlation length considered are 4 and l respectively.

Fig. 11

Convergence of stability parameters due to 5% COV in a EI and b GJ with number of K–L expansion terms

Fig. 12

CDFs of flutter velocity of cantilever wing for various limit states a $\zeta _{2} = 0$, b $\beta _{1}\beta _{2} = 0$, and c $F_{m} = 0$ for 5% COV in EI using FOSM, MCS and FORM methods: random field modeling

Figures 12 and 13 show the CDFs of flutter velocity of the wing obtained from FOSM, FORM, and MCS for 5% COV in EI and GJ respectively, modeled as random fields for various limit state functions. From Fig. 12, it is observed that the CDFs of flutter velocity obtained using the FOSM method for all limit state functions show small deviation in the lower tail region with MCS in the presence of uncertainty in EI. However, the CDFs of flutter velocity obtained from FORM agree well with MCS. The flutter velocities corresponding to CDF = 0.01 obtained from FOSM, MCS, and FORM for various limit states are given in Table 9. The predicted flutter velocity corresponding to CDF = 0.01 using the FOSM method depends on the form of limit state functions, so a lack of invariance with the FOSM method is observed.

Table 9 Flutter velocities corresponding to CDF = 0.01 for 5% COV in EI for various limit state functions

Fig. 13

CDFs of flutter velocity of cantilever wing obtained for limit states a $\zeta _{2} = 0$, b $\beta _{1}\beta _{2} = 0$, and c $F_{m} = 0$ for 5% COV in GJ using FOSM, MCS and FORM methods: random field modeling

From Fig. 13 in the case of probabilistic uncertainty in GJ, it is observed that the CDFs of flutter velocity obtained from the FOSM method do not agree with MCS for limit state functions $\zeta _{2} = 0$ and $\beta _{1}\beta _{2} = 0$ particularly in the lower tail region, and agree for the limit state $F_{m}= 0$. However, the CDFs of flutter velocity obtained from FORM closely agree with MCS for all limit states. The flutter velocities corresponding to CDF = 0.01 obtained from FOSM, MCS, and FORM for various limit state functions are shown in Table 10. The onset of flutter velocity corresponding to CDF = 0.01 using the FOSM method depends on the form of limit state functions, so a lack of invariance in the prediction with the FOSM method is observed.

Table 10 Flutter velocities corresponding to CDF = 0.01 for 5% COV in GJ for various limit state functions

Fig. 14

CDFs of flutter velocity of cantilever wing for 5% COV in a EI, b GJ for various limit state functions using FORM and MCS: random field modeling

Figure 14 shows the CDFs of flutter velocity of the wing using FORM for various limit state functions in the presence of uncertainty in EI and GJ using random field model. From these figures, it is observed that the CDFs of flutter velocity obtained from FORM agree well with each other and also with MCS. At CDF = 0.01 for 5% COV in EI, the predicted onset flutter velocity obtained from FORM for all limit state functions is 136.90 m/s. Similarly, in the case of 5% COV in GJ, the predicted onset flutter velocity corresponding to CDF = 0.01 obtained from FORM for all limit state functions is 129.67 m/s. Hence, the proposed FORM algorithm is able to overcome the lack of invariance problem in the prediction of flutter velocity that was noticed using the FOSM method. It is also observed that the computation time for obtaining CDF data using the proposed FORM algorithm in the case of EI for limit state functions $\zeta _{2}$, $\beta _{1}\beta _{2}$, and $F_{m}$ are 239, 252, and 352 s respectively with serial processor using Matlab 2017a on HP Z800 workstation with 24 GB RAM while MCS takes 8 h 19 min and 3 s with 4 cores parallel processors for all three limit state functions handled together. Hence, the FORM algorithm works efficiently and effectively.

Fig. 15

Comparison of CDFs of flutter velocity of cantilever wing with parameters modeled as random variables and random fields for 5% COV in a EI, b GJ for various correlation lengths using FORM

Figure 15 shows the comparison of CDFs of flutter velocity of the wing using random variable and random field modeling approaches for various stiffness parameters. The effect of increasing correlation length (characteristic parameters) on the CDF of flutter velocity of the wing is also shown in the figure. It can be observed that, as the correlation length increases, the CDF of flutter velocity of the wing approaches random variable case. Here, the flutter onset velocity predicted using random variable model is lower than random field model in the lower tail region of CDF. Hence, a conservative estimate of flutter velocity is obtained using random variable modeling approach.

6 Conclusions

In this paper, the stochastic aeroelastic stability and flutter reliability of a wing are presented in the frequnecy domain. Various stability conditions are proposed for obtaining flutter onset in aeroelastic systems in the presence of uncertainties. The stability conditions are treated as limit state functions for flutter reliability analysis. A general FORM algorithm is developed for flutter reliability analysis of a cantilever wing having parametric uncertainties treated as either random variables or random fields. The developed FORM algorithm is computationally efficient in comparison to MCS and shows invariance characteristics in predicting the CDF of flutter velocity. Further, the CDFs of flutter velocity obtained with increasing correlation lengths of random field move towards random variable modeling case. It is also observed that the CDF value in the lower tail region using random field model is always less than random variable model at a given flow velocity. Among all the stability conditions, flutter margin shows the best representation of flutter onset condition from uncertainty quantification point of view, because its distribution characteristics (skewness and kurtosis values) don’t change significantly with flow velocities and random parameters.