1 Introduction

Piezoelectric materials are an important class of advanced materials so-called because of their tendency to deform when subjected to an electric field and to polarize when stressed. This intrinsic electromechanical coupling property has led to the use of piezoelectric materials in many modern devices such as electromechanical transducers, piezoelectric semiconductors, and MEMS/NEMS (micro/nanoelectromechanical systems). Theoretical studies involving Eshelby inclusions and inhomogeneities in piezoelectric materials have received considerable attention in the literature (see, for example, [1,2,3,4,5,6]). By constructing certain auxiliary functions and by confining his analysis to the physical (rather than the image) plane, Ru [4, 5] derived analytic solutions for Eshelby’s problem of an inclusion of arbitrary shape in a piezoelectric plane or half-plane or in one of two perfectly bonded dissimilar piezoelectric half-planes. The corresponding solutions in the case of an inclusion of arbitrary shape embedded in one of two imperfectly bonded piezoelectric half-planes were obtained by Wang and Pan [6].

In this paper, we are concerned with Eshelby’s problem of an arbitrarily shaped inclusion in a piezoelectric plane with a parabolic boundary. Our method proceeds as follows. The region below the parabola in the physical (z) plane is first mapped onto the lower half of the image (\( \xi_{\alpha } \)) plane using a succession of one-to-one mappings from [7]. The presence of the parabolic boundary in the physical z-plane makes it more convenient to analyze this problem in the image plane rather than in the physical plane (as in [4, 5]). Using analytic continuation and conformal mappings which further map the exterior of the region occupied by the (simply-connected) inclusion in the \( \xi_{\alpha } \)-plane onto the exterior of the unit circle, four auxiliary functions are constructed and their asymptotic behavior at infinity identified in terms of polynomial functions. Analytic solutions for a parabola with four types of electroelastic boundary conditions (namely, a traction-free and insulating parabola; a rigid and conducting parabola; a rigid and insulating parabola; a traction-free and conducting parabola) are then derived using these auxiliary functions. The practical importance of each of these sets of boundary conditions is discussed by Ru in [5]. In fact, it is expected that the analytic solutions obtained here will find a variety of applications including in the design of strained semiconductor devices in which residual electroelastic fields induced by built-in electric field and lattice mismatch between buried active components and surrounding materials play a crucial role in electronic performance including the prediction of conditions leading to failure and degradation (see [4, 5] and the references therein for more details). We mention in addition that these problems are also significant in the study of fracture of advanced materials. For example, the parabola can be used to represent a crack (or anti-crack) with a blunt crack tip and the inclusion perhaps a transformation strain spot of arbitrary shape. In this way, the corresponding model could be used to study the shielding or anti-shielding effect of the transformation strain spot on a nearby crack.

2 The Stroh octet formalism

In a fixed rectangular coordinate system \( x_{i} \, (i = 1,2,3) \), the governing equations for an anisotropic piezoelectric solid are given by Suo et al. [8]:

$$ \sigma_{ij} = C_{ijkl} u_{k,l} + e_{kij} \phi_{,k} ,\quad D_{k} = e_{kij} u_{i,j} - \in_{kl} \phi_{,l} ,\quad \sigma_{ij,j} = 0,\quad D_{i,i} = 0, $$
(1)

where j, k, l, m = 1, 2, 3; we sum over repeated indices; a comma in the subscript denotes differentiation; \( \sigma_{ij} \) and \( D_{i} \) are the stress components and electric displacements, respectively; \( u_{i} \) and ϕ are the displacement components and electric potential, respectively; \( C_{ijkl} \), \( e_{kij} \) and \( \in_{ij} \) are, respectively, the elastic, piezoelectric and dielectric constants.

For two-dimensional problems in which all quantities depend on \( x_{1} \) and \( x_{2} \) only, the general solution of Eq. (1) can be expressed as [2, 8,9,10]:

$$ \begin{aligned} {\mathbf{u}} & = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & {u_{3} } & \phi \\ \end{array} } \right]^{T} = {\mathbf{Af}}(z) + {\bar{\mathbf{A}}}\overline{{{\mathbf{f}}(z)}} , \\ \boldsymbol{\upvarphi}& = \left[ {\begin{array}{*{20}c} {\varphi_{1} } & {\varphi_{2} } & {\varphi_{3} } & {\varphi_{4} } \\ \end{array} } \right]^{T} = {\mathbf{Bf}}(z) + {\bar{\mathbf{B}}}\overline{{{\mathbf{f}}(z)}} , \\ \end{aligned} $$
(2)

where

$$ \begin{aligned} & {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {{\mathbf{a}}_{1} } & {{\mathbf{a}}_{2} } & {{\mathbf{a}}_{3} } & {{\mathbf{a}}_{4} } \\ \end{array} } \right],\quad {\mathbf{B}} = \left[ {\begin{array}{*{20}c} {{\mathbf{b}}_{1} } & {{\mathbf{b}}_{2} } & {{\mathbf{b}}_{3} } & {{\mathbf{b}}_{4} } \\ \end{array} } \right], \\ & {\mathbf{f}}(z) = \left[ {\begin{array}{*{20}c} {f_{1} (z_{1} )} & {f_{2} (z_{2} )} & {f_{3} (z_{3} )} & {f_{4} (z_{4} )} \\ \end{array} } \right]^{T} , \\ & z_{i} = x_{1} + p_{i} x_{2} ,\quad \text{Im} \left\{ {p_{i} } \right\} > 0,\quad (i = 1,2,3,4), \\ \end{aligned} $$
(3)

with

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{N}}_{1} } & {{\mathbf{N}}_{2} } \\ {{\mathbf{N}}_{3} } & {{\mathbf{N}}_{1}^{T} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{a}}_{i} } \\ {{\mathbf{b}}_{i} } \\ \end{array} } \right] = p_{i} \left[ {\begin{array}{*{20}c} {{\mathbf{a}}_{i} } \\ {{\mathbf{b}}_{i} } \\ \end{array} } \right],\quad (i = 1,2,3,4) $$
(4)
$$ {\mathbf{N}}_{1} = - {\mathbf{T}}^{ - 1} {\mathbf{R}}^{T} , \, {\mathbf{N}}_{2} = {\mathbf{T}}^{ - 1} , \, {\mathbf{N}}_{3} = {\mathbf{RT}}^{ - 1} {\mathbf{R}}^{T} - {\mathbf{Q}}, $$
(5)

and

$$ {\mathbf{Q}} = \left[ {\begin{array}{*{20}c} {{\mathbf{Q}}^{E} } & {{\mathbf{e}}_{11} } \\ {{\mathbf{e}}_{11}^{T} } & { - \in_{11} } \\ \end{array} } \right],\quad \, {\mathbf{R}} = \left[ {\begin{array}{*{20}c} {{\mathbf{R}}^{E} } & {{\mathbf{e}}_{21} } \\ {{\mathbf{e}}_{12}^{T} } & { - \in_{12} } \\ \end{array} } \right],\quad {\mathbf{T}} = \left[ {\begin{array}{*{20}c} {{\mathbf{T}}^{E} } & {{\mathbf{e}}_{22} } \\ {{\mathbf{e}}_{22}^{T} } & { - \in_{22} } \\ \end{array} } \right], $$
(6)
$$ ({\mathbf{Q}}^{E} )_{ik} = C_{i1k1} ,\quad ({\mathbf{R}}^{E} )_{ik} = C_{i1k2} ,\quad ({\mathbf{T}}^{E} )_{ik} = C_{i2k2} ,\quad ({\mathbf{e}}_{ij} )_{m} = e_{ijm} . $$
(7)

In addition, the extended stress function vector \( {\mathbf{\varphi }} \) is defined in terms of the stresses and electric displacements as follows

$$ \begin{aligned} & \sigma_{i1} = - \varphi_{i,2} ,\quad \, \sigma_{i2} = \varphi_{i,1} ,\quad \, (i = 1,2,3) \\ & D_{1} = - \varphi_{4,2} ,\quad \, D_{2} = \varphi_{4,1} . \\ \end{aligned} $$
(8)

The two matrices A and B satisfy the following orthogonality relations

$$ \begin{aligned} & {\mathbf{B}}^{T} {\mathbf{A}} + {\mathbf{A}}^{T} {\mathbf{B}} = {\mathbf{I}} = {\bar{\mathbf{B}}}^{T} {\bar{\mathbf{A}}} + {\bar{\mathbf{A}}}^{T} {\bar{\mathbf{B}}}, \\ & {\mathbf{B}}^{T} {\bar{\mathbf{A}}} + {\mathbf{A}}^{T} {\bar{\mathbf{B}}} = {\mathbf{0}} = {\bar{\mathbf{B}}}^{T} {\mathbf{A}} + {\bar{\mathbf{A}}}^{T} {\mathbf{B}}. \\ \end{aligned} $$
(9)

Let t be the extended surface traction on a boundary Γ. If s is the arc-length measured along Γ such that the material remains on the right-hand side in the direction of increasing s, it can be shown that [10]

$$ {\mathbf{t}} = \frac{d}{ds}{\mathbf{\varphi }}. $$
(10)

3 A piezoelectric inclusion in a region with a parabolic boundary

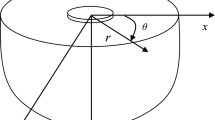
Consider an anisotropic piezoelectric material that occupies the region

$$ x_{2} \le bx_{1}^{2} ,\quad b \ge 0, $$
(11)

the traction-free and charge-free surface of which is a parabola described by

$$ x_{2} = bx_{1}^{2} . $$
(12)

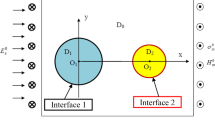
The parabola degenerates to a semi-infinite crack when b → ∞ and to a straight (plane) boundary when \( b = 0 \). The piezoelectric plane with the parabolic boundary contains a subdomain (inclusion) which has the same elastic, piezoelectric and dielectric constants as its exterior region and which undergoes uniform eigenstrains \( (\varepsilon_{11}^{ * } , \, \varepsilon_{22}^{ * } , \, \varepsilon_{12}^{ * } , \, \varepsilon_{13}^{ * } , \, \varepsilon_{23}^{ * } ) \) and eigenelectric fields \( (E_{1}^{ * } , \, E_{2}^{ * } ) \). Let \( S_{2} \) and \( S_{1} \) denote the subdomain and its exterior region with parabolic boundary, respectively and Γ the perfectly bonded interface separating \( S_{2} \) and \( S_{1} \) (see Fig. 1). Throughout the paper, the quantities in \( S_{1} \) and \( S_{2} \) will be identified by the subscripts 1 and 2, respectively.

Fig. 1
figure 1

An Eshelby inclusion of arbitrary shape in a piezoelectric plane with a parabolic boundary

Full size image

The boundary value problem takes the following form

$$ \begin{aligned} & {\mathbf{Af}}_{1} (z) + {\bar{\mathbf{A}}}\overline{{{\mathbf{f}}_{1} (z)}} = {\mathbf{Af}}_{2} (z) + {\bar{\mathbf{A}}}\overline{{{\mathbf{f}}_{2} (z)}} + {\mathbf{u}}^{ * } , \\ & {\mathbf{Bf}}_{1} (z) + {\bar{\mathbf{B}}}\overline{{{\mathbf{f}}_{1} (z)}} = {\mathbf{Bf}}_{2} (z) + {\bar{\mathbf{B}}}\overline{{{\mathbf{f}}_{2} (z)}} ,\quad z \equiv x_{1} + {\text{i}}x_{2} \in \varGamma ; \\ \end{aligned} $$
(13)
$$ {\mathbf{Bf}}_{1} (z) + {\bar{\mathbf{B}}}\overline{{{\mathbf{f}}_{1} (z)}} = {\mathbf{0}},\quad x_{2} = bx_{1}^{2} ; $$
(14)
$$ {\mathbf{f}}_{1} (z) \cong O(1),\quad \left| z \right| \to \infty , $$
(15)

where \( {\mathbf{u}}^{ * } \) given by

$$ {\mathbf{u}}^{ * } = \left[ {\begin{array}{*{20}c} {\varepsilon_{11}^{ * } x_{1} + \varepsilon_{12}^{ * } x_{2} } \\ {\varepsilon_{12}^{ * } x_{1} + \varepsilon_{22}^{ * } x_{2} } \\ {2(\varepsilon_{13}^{ * } x_{1} + \varepsilon_{23}^{ * } x_{2} )} \\ { - E_{1}^{ * } x_{1} - E_{2}^{ * } x_{2} } \\ \end{array} } \right],\quad z \in S_{2} . $$
(16)

is the vector of additional displacements and electric potential within the inclusion arising from uniform eigenstrains and eigenelectric fields. Pre-multiplying the two interface conditions in Eq. (13) by \( {\mathbf{B}}^{T} \) and \( {\mathbf{A}}^{T} \), adding the resulting equations, and making use of the orthogonality relations in Eq. (9), we find the following decoupled form for the interface conditions in Eq. (13)

$$ {\mathbf{f}}_{1} (z) = {\mathbf{f}}_{2} (z) + < z_{\alpha } > {\mathbf{c}} + < \bar{z}_{\alpha } > {\mathbf{d}},\quad z \in \varGamma , $$
(17)

where \( < * > \) is a \( 4 \times 4 \) diagonal matrix in which each component varies with the index α (from 1 to 4), and

$$ \begin{aligned} {\mathbf{c}} & = < \frac{{\bar{p}_{\alpha } }}{{\bar{p}_{\alpha } - p_{\alpha } }} > {\mathbf{B}}^{T} \left[ {\begin{array}{*{20}c} {\varepsilon_{11}^{ * } } \\ {\varepsilon_{12}^{ * } } \\ {2\varepsilon_{13}^{ * } } \\ { - E_{1}^{ * } } \\ \end{array} } \right] - < \frac{1}{{\bar{p}_{\alpha } - p_{\alpha } }} > {\mathbf{B}}^{T} \left[ {\begin{array}{*{20}c} {\varepsilon_{12}^{ * } } \\ {\varepsilon_{22}^{ * } } \\ {2\varepsilon_{23}^{ * } } \\ { - E_{2}^{ * } } \\ \end{array} } \right], \\ {\mathbf{d}} & = < \frac{1}{{\bar{p}_{\alpha } - p_{\alpha } }} > {\mathbf{B}}^{T} \left[ {\begin{array}{*{20}c} {\varepsilon_{12}^{ * } } \\ {\varepsilon_{22}^{ * } } \\ {2\varepsilon_{23}^{ * } } \\ { - E_{2}^{ * } } \\ \end{array} } \right] - < \frac{{p_{\alpha } }}{{\bar{p}_{\alpha } - p_{\alpha } }} > {\mathbf{B}}^{T} \left[ {\begin{array}{*{20}c} {\varepsilon_{11}^{ * } } \\ {\varepsilon_{12}^{ * } } \\ {2\varepsilon_{13}^{ * } } \\ { - E_{1}^{ * } } \\ \end{array} } \right]. \\ \end{aligned} $$
(18)

We now consider the following one-to-one mapping functions [7]

$$ z_{\alpha } = \omega_{\alpha } (\xi_{\alpha } ) = \xi_{\alpha } + bp_{\alpha } \xi_{\alpha }^{2} , \, \xi_{\alpha } = \frac{{\sqrt {1 + 4bp_{\alpha } z_{\alpha } } - 1}}{{2bp_{\alpha } }},\quad \text{Im} \left\{ {\xi_{\alpha } } \right\} \le 0,\quad \alpha = 1,2,3,4. $$
(19)

The parabola is mapped onto the real axis in the \( \xi_{\alpha } \)-plane and the region below the parabola is mapped onto the lower half \( \xi_{\alpha } \)-plane. Furthermore, the inclusion \( z_{\alpha } \in S_{2\alpha } \) is mapped onto \( \xi_{\alpha } \in \varOmega_{2\alpha } \); the matrix \( z_{\alpha } \in S_{1\alpha } \) is mapped onto \( \xi_{\alpha } \in \varOmega_{1\alpha } \); the interface \( z_{\alpha } \in \varGamma_{\alpha } \) is mapped onto \( \xi_{\alpha } \in L_{\alpha } \).

Equation (17) can be further expressed in a decoupled form in the \( \xi_{\alpha } \)-plane as

$$ {\mathbf{f}}_{1} (\xi ) = {\mathbf{f}}_{2} (\xi ) + < \omega_{\alpha } (\xi_{\alpha } ) > {\mathbf{c}} + < \overline{{\omega_{\alpha } (\xi_{\alpha } )}} > {\mathbf{d}},\quad \xi_{\alpha } \in L_{\alpha } , $$
(20)

where the following notation has been adopted:

$$ \begin{aligned} {\mathbf{f}}(\xi ) & = \left[ {\begin{array}{*{20}c} {f_{1} (\xi_{1} )} & {f_{2} (\xi_{2} )} & {f_{3} (\xi_{3} )} & {f_{4} (\xi_{4} )} \\ \end{array} } \right]^{T} \\ \, & = \left[ {\begin{array}{*{20}c} {f_{1} (\omega_{1} (\xi_{1} ))} & {f_{2} (\omega_{2} (\xi_{2} ))} & {f_{3} (\omega_{3} (\xi_{3} ))} & {f_{4} (\omega_{4} (\xi_{4} ))} \\ \end{array} } \right]^{T} . \\ \end{aligned} $$
(21)

If \( z \in S_{2} \) is simply-connected, \( z_{\alpha } \in S_{2\alpha } \) is also simply-connected. As a result, \( \xi_{\alpha } \in \varOmega_{2\alpha } \) is simply-connected. Consequently, there exists a conformal mapping \( \xi_{\alpha } = w_{\alpha } (\eta_{\alpha } ) \) that maps the exterior of \( \varOmega_{2\alpha } \) in the \( \xi_{\alpha } \)-plane onto the exterior of the unit circle in the \( \eta_{\alpha } \)-plane [10,11,12]. We can construct an auxiliary function \( D_{\alpha } (\xi_{\alpha } ) \) for each \( \xi_{\alpha } \in L_{\alpha } \) as

$$ \overline{{\omega_{\alpha } (\xi_{\alpha } )}} = \bar{\xi }_{\alpha } + b\bar{p}_{\alpha } \bar{\xi }_{\alpha }^{2} = \bar{w}_{\alpha } \left( {\frac{1}{{w_{\alpha }^{ - 1} (\xi_{\alpha } )}}} \right) + b\bar{p}_{\alpha } \left[ {\bar{w}_{\alpha } \left( {\frac{1}{{w_{\alpha }^{ - 1} (\xi_{\alpha } )}}} \right)} \right]^{2} = D_{\alpha } (\xi_{\alpha } ),\quad \xi_{\alpha } \in L_{\alpha } , $$
(22)

where \( w_{\alpha }^{ - 1} (\xi_{\alpha } ) \) is the inverse mapping of \( \xi_{\alpha } = w_{\alpha } (\eta_{\alpha } ) \).

In addition \( D_{\alpha } (\xi_{\alpha } ) \) is analytic in the exterior of \( \varOmega_{2\alpha } \) except at the point at infinity where it has a pole of finite degree determined by its asymptotic behavior

$$ D_{\alpha } (\xi_{\alpha } ) \cong P_{\alpha } (\xi_{\alpha } ) + O(\xi_{\alpha }^{ - 1} ),\quad \left| {\xi_{\alpha } } \right| \to \infty , $$
(23)

where \( P_{\alpha } (\xi_{\alpha } ) \) is a polynomial of order 2N in \( \xi_{\alpha } \) if \( \xi_{\alpha } = w_{\alpha } (\eta_{\alpha } ) \) is a polynomial of order N in \( {1 \mathord{\left/ {\vphantom {1 {\eta_{\alpha } }}} \right. \kern-0pt} {\eta_{\alpha } }} \).

We now introduce a new vector function \( {\mathbf{h}}(\xi ) = \left[ {\begin{array}{*{20}c} {h_{1} (\xi_{1} )} & {h_{2} (\xi_{2} )} & {h_{3} (\xi_{3} )} & {h_{4} (\xi_{4} )} \\ \end{array} } \right]^{T} \) defined by

$$ {\mathbf{h}}(\xi ) = \left\{ {\begin{array}{*{20}l} {{\mathbf{f}}_{1} (\xi ) - < D_{\alpha } (\xi_{\alpha } ) - P_{\alpha } (\xi_{\alpha } ) > {\mathbf{d}},} \hfill & {\xi_{\alpha } \in \varOmega_{1\alpha } ,} \hfill \\ {{\mathbf{f}}_{2} (\xi ) + < \omega_{\alpha } (\xi_{\alpha } ) > {\mathbf{c}} + < P_{\alpha } (\xi_{\alpha } ) > {\mathbf{d}},} \hfill & {\xi_{\alpha } \in \varOmega_{2\alpha } .} \hfill \\ \end{array} } \right. $$
(24)

It is seen from the above and Eq. (20) that \( {\mathbf{h}}(\xi ) \) is continuous across \( \xi_{\alpha } \in L_{\alpha } \) and is then analytic in the lower (\( \xi_{\alpha } \)) half-plane including at the point at infinity. For the convenience of the following analysis, we introduce a further conformal mapping:

$$ z = x_{1} + {\text{i}}x_{2} = \omega (\xi ) = \xi + {\text{i}}b\xi^{2} ,\quad \, \xi = \frac{{\sqrt {1 + 4{\text{i}}bz} - 1}}{{2{\text{i}}b}},\quad \text{Im} \left\{ \xi \right\} \le 0. $$
(25)

In view of the fact that \( \xi_{1} = \xi_{2} = \xi_{3} = \xi_{4} = \xi = x_{1} \) on the real axis, we can first replace \( \xi_{\alpha } \) by the same variable ξ. Once the analysis is complete, the complex variable ξ should be returned accordingly to the corresponding complex variables \( \xi_{\alpha } \).

The traction-free and charge-free boundary conditions on the parobola in Eq. (14) can be expressed in the ξ-plane as follows

$$ {\mathbf{Bf}}_{1} (\xi ) + {\bar{\mathbf{B}}}\overline{{{\mathbf{f}}_{1} (\xi )}} = {\mathbf{0}},\quad \text{Im} \left\{ \xi \right\} = 0^{ - } , $$
(26)

which can further be expressed in terms of \( {\mathbf{h}}(\xi ) \) and its analytic continuation as

$$ {\mathbf{Bh}}^{ - } (\xi ) + {\bar{\mathbf{B}}} < \bar{D}_{\alpha } (\xi ) - \bar{P}_{\alpha } (\xi ) > {\bar{\mathbf{d}}} = - {\mathbf{\bar{B}\bar{h}}}^{ + } (\xi ) - {\mathbf{B}} < D_{\alpha } (\xi ) - P_{\alpha } (\xi ) > {\mathbf{d}},\quad \text{Im} \left\{ \xi \right\} = 0, $$
(27)

where the superscripts ‘+’ and ‘−’ denote limiting values from the upper and lower half-planes, respectively. It is seen that the left- and right-hand sides of Eq. (27) are analytic in the lower and upper half-planes, respectively, including at the point at infinity. By applying Liouville’s theorem, the left- and right-hand sides of Eq. (27) should be identically zero. Consequently, we arrive at the following expression for \( {\mathbf{h}}(\xi ) \)

$$ {\mathbf{h}}(\xi ) = - {\mathbf{B}}^{ - 1} {\bar{\mathbf{B}}} < \bar{D}_{\alpha } (\xi ) - \bar{P}_{\alpha } (\xi ) > {\bar{\mathbf{d}}},\quad \text{Im} \left\{ \xi \right\} \le 0. $$
(28)

The above expression is valid only on the real axis of the \( \xi_{\alpha } \)-plane. The full-field expression can be conveniently expressed as

$$ {\mathbf{h}}(\xi ) = - \sum\limits_{j = 1}^{4} { < \bar{D}_{j} (\xi_{\alpha } ) - \bar{P}_{j} (\xi_{\alpha } ) > {\mathbf{B}}^{ - 1} {\bar{\mathbf{B}}\mathbf{I}}_{j} {\bar{\mathbf{d}}}} ,\quad \text{Im} \left\{ {\xi_{\alpha } } \right\} \le 0, $$
(29)

where

$$ \begin{aligned} & {\mathbf{I}}_{1} = {\text{diag}}\left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ \end{array} } \right],\quad \, {\mathbf{I}}_{2} = {\text{diag}}\left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ \end{array} } \right], \\ & {\mathbf{I}}_{3} = {\text{diag}}\left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ \end{array} } \right],\quad \, {\mathbf{I}}_{4} = {\text{diag}}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 1 \\ \end{array} } \right]. \\ \end{aligned} $$
(30)

The analytic vector functions inside and outside the Eshelby inclusion can be obtained from Eqs. (24) and (29) as

$$ \begin{aligned} & {\mathbf{f}}_{1} (\xi ) = < D_{\alpha } (\xi_{\alpha } ) - P_{\alpha } (\xi_{\alpha } ) > {\mathbf{d}} - \sum\limits_{j = 1}^{4} { < \bar{D}_{j} (\xi_{\alpha } ) - \bar{P}_{j} (\xi_{\alpha } ) > {\mathbf{B}}^{ - 1} {\bar{\mathbf{B}}\mathbf{I}}_{j} {\bar{\mathbf{d}}}} ,\quad \xi_{\alpha } \in \varOmega_{1\alpha } ; \\ & {\mathbf{f}}_{2} (\xi ) = - < \omega_{\alpha } (\xi_{\alpha } ) > {\mathbf{c}} - < P_{\alpha } (\xi_{\alpha } ) > {\mathbf{d}} - \sum\limits_{j = 1}^{4} { < \bar{D}_{j} (\xi_{\alpha } ) - \bar{P}_{j} (\xi_{\alpha } ) > {\mathbf{B}}^{ - 1} {\bar{\mathbf{B}}\mathbf{I}}_{j} {\bar{\mathbf{d}}}} ,\quad \xi_{\alpha } \in \varOmega_{2\alpha } . \\ \end{aligned} $$
(31)

It is seen that the structure of the solution in Eq. (31) for an anisotropic piezoelectric material is much simpler than that for an isotropic elastic material [13]. The underlying reason is that the isotropic elastic material belongs to the class of mathematically degenerate materials [10]. The electroelastic fields inside and outside the inclusion can be obtained by substituting Eq. (31) into Eq. (2). In particular, the extended hoop stress vector \( {\mathbf{t}}_{h} \) along the parabola acting on a surface perpendicular to the parabola can be derived from Eqs. (31) and (10) as

$$ {\mathbf{t}}_{h} = 4\cos \delta \text{Im} \left\{ {{\mathbf{B}} < \frac{{p_{\alpha } - \tan \delta }}{{1 + p_{\alpha } \tan \delta }} > {\mathbf{B}}^{ - 1} } \right\}\text{Im} \left\{ {{\mathbf{B}} < \left[ {D^{\prime}_{\alpha } (x_{1} ) - P^{\prime}_{\alpha } (x_{1} )} \right] > {\mathbf{d}}} \right\},\quad x_{2} = bx_{1}^{2} , $$
(32)

where \( \delta = \tan^{ - 1} (2bx_{1} ) \) is the angle the tangent to the parabola makes with the \( x_{1} \)-axis.

4 Other electroelastic boundary conditions on the parabola

In the previous section, we have considered the case in which the parabolic boundary is traction-free and charge-free. In this section, we will consider further electroelastic boundary conditions on the parabola. More specifically, we will address cases describing: (1) a rigid and conducting parabola; (2) a rigid and insulating parabola; (3) a traction-free and conducting parabola.

4.1 A rigid and conducting parabola

In this case, the boundary conditions on the parabola are

$$ u_{1} = u_{2} = u_{3} = 0,\quad \phi = 0,\quad x_{2} = bx_{1}^{2} , $$
(33)

or equivalently

$$ {\mathbf{Af}}_{1} (z) + {\bar{\mathbf{A}}}\overline{{{\mathbf{f}}_{1} (z)}} = {\mathbf{0}},\quad x_{2} = bx_{1}^{2} . $$
(34)

Using a method similar to that in Sect. 3, the analytic vector functions defined inside and outside the Eshelby inclusion can eventually be shown to be

$$ \begin{aligned} & {\mathbf{f}}_{1} (\xi ) = < D_{\alpha } (\xi_{\alpha } ) - P_{\alpha } (\xi_{\alpha } ) > {\mathbf{d}} - \sum\limits_{j = 1}^{4} { < \bar{D}_{j} (\xi_{\alpha } ) - \bar{P}_{j} (\xi_{\alpha } ) > {\mathbf{A}}^{ - 1} {\bar{\mathbf{A}}\mathbf{I}}_{j} {\bar{\mathbf{d}}}} ,\quad \xi_{\alpha } \in \varOmega_{1\alpha } ; \\ & {\mathbf{f}}_{2} (\xi ) = - < \omega_{\alpha } (\xi_{\alpha } ) > {\mathbf{c}} - < P_{\alpha } (\xi_{\alpha } ) > {\mathbf{d}} - \sum\limits_{j = 1}^{4} { < \bar{D}_{j} (\xi_{\alpha } ) - \bar{P}_{j} (\xi_{\alpha } ) > {\mathbf{A}}^{ - 1} {\bar{\mathbf{A}}\mathbf{I}}_{j} {\bar{\mathbf{d}}}} ,\quad \xi_{\alpha } \in \varOmega_{2\alpha } . \\ \end{aligned} $$
(35)

The extended hoop stress vector \( {\mathbf{t}}_{h} \) along the parabola can be determined as

$$ {\mathbf{t}}_{h} = 4\cos \delta \text{Im} \left\{ {{\mathbf{B}} < \frac{{p_{\alpha } - \tan \delta }}{{1 + p_{\alpha } \tan \delta }} > {\mathbf{A}}^{ - 1} } \right\}\text{Im} \left\{ {{\mathbf{A}} < \left[ {D^{\prime}_{\alpha } (x_{1} ) - P^{\prime}_{\alpha } (x_{1} )} \right] > {\mathbf{d}}} \right\},\quad x_{2} = bx_{1}^{2} . $$
(36)

4.2 A rigid and insulating parabola

In this case, the boundary conditions on the parabola are

$$ u_{1} = u_{2} = u_{3} = 0,\quad \varphi_{4} = 0,\quad x_{2} = bx_{1}^{2} , $$
(37)

or equivalently

$$ \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\mathbf{A}} + {\mathbf{I}}_{4} {\mathbf{B}}} \right]{\mathbf{f}}_{1} (z) + \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\bar{\mathbf{A}}} + {\mathbf{I}}_{4} {\bar{\mathbf{B}}}} \right]\overline{{{\mathbf{f}}_{1} (z)}} = {\mathbf{0}},\quad x_{2} = bx_{1}^{2} . $$
(38)

Using a method similar to that in Sect. 3, the analytic vector functions defined inside and outside the Eshelby inclusion are given by

$$ \begin{aligned} & {\mathbf{f}}_{1} (\xi ) = < D_{\alpha } (\xi_{\alpha } ) - P_{\alpha } (\xi_{\alpha } ) > {\mathbf{d}} \\ & \quad - \sum\limits_{j = 1}^{4} { < \bar{D}_{j} (\xi_{\alpha } ) - \bar{P}_{j} (\xi_{\alpha } ) > \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\mathbf{A}} + {\mathbf{I}}_{4} {\mathbf{B}}} \right]^{ - 1} \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\bar{\mathbf{A}}} + {\mathbf{I}}_{4} {\bar{\mathbf{B}}}} \right]{\mathbf{I}}_{j} {\bar{\mathbf{d}}}} ,\quad \xi_{\alpha } \in \varOmega_{1\alpha } ; \\ & {\mathbf{f}}_{2} (\xi ) = - < \omega_{\alpha } (\xi_{\alpha } ) > {\mathbf{c}} - < P_{\alpha } (\xi_{\alpha } ) > {\mathbf{d}} \\ & \quad - \sum\limits_{j = 1}^{4} { < \bar{D}_{j} (\xi_{\alpha } ) - \bar{P}_{j} (\xi_{\alpha } ) > \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\mathbf{A}} + {\mathbf{I}}_{4} {\mathbf{B}}} \right]^{ - 1} \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\bar{\mathbf{A}}} + {\mathbf{I}}_{4} {\bar{\mathbf{B}}}} \right]{\mathbf{I}}_{j} {\bar{\mathbf{d}}}} ,\quad \xi_{\alpha } \in \varOmega_{2\alpha } . \\ \end{aligned} $$
(39)

The extended hoop stress vector \( {\mathbf{t}}_{h} \) along the parabola can be determined as

$$ \begin{aligned} {\mathbf{t}}_{h} & = 4\cos \delta \text{Im} \left\{ {{\mathbf{B}} < \frac{{p_{\alpha } - \tan \delta }}{{1 + p_{\alpha } \tan \delta }} > \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\mathbf{A}} + {\mathbf{I}}_{4} {\mathbf{B}}} \right]^{ - 1} } \right\} \\ & \quad \times \text{Im} \left\{ {\left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\mathbf{A}} + {\mathbf{I}}_{4} {\mathbf{B}}} \right] < \left[ {D^{\prime}_{\alpha } (x_{1} ) - P^{\prime}_{\alpha } (x_{1} )} \right] > {\mathbf{d}}} \right\},\quad x_{2} = bx_{1}^{2} . \\ \end{aligned} $$
(40)

4.3 A traction-free and conducting parabola

In this case, the boundary conditions on the parabola are

$$ \varphi_{1} = \varphi_{2} = \varphi_{3} = 0, \, \phi = 0,\quad x_{2} = bx_{1}^{2} , $$
(41)

or equivalently

$$ \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\mathbf{B}} + {\mathbf{I}}_{4} {\mathbf{A}}} \right]{\mathbf{f}}_{1} (z) + \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\bar{\mathbf{B}}} + {\mathbf{I}}_{4} {\bar{\mathbf{A}}}} \right]\overline{{{\mathbf{f}}_{1} (z)}} = {\mathbf{0}},\quad x_{2} = bx_{1}^{2} . $$
(42)

Using a method similar to that in Sect. 3, the analytic vector functions inside and outside the Eshelby inclusion in this case are shown to be

$$ \begin{aligned} & {\mathbf{f}}_{1} (\xi ) = < D_{\alpha } (\xi_{\alpha } ) - P_{\alpha } (\xi_{\alpha } ) > {\mathbf{d}} \\ & \quad - \sum\limits_{j = 1}^{4} { < \bar{D}_{j} (\xi_{\alpha } ) - \bar{P}_{j} (\xi_{\alpha } ) > \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\mathbf{B}} + {\mathbf{I}}_{4} {\mathbf{A}}} \right]^{ - 1} \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\bar{\mathbf{B}}} + {\mathbf{I}}_{4} {\bar{\mathbf{A}}}} \right]{\mathbf{I}}_{j} {\bar{\mathbf{d}}}} ,\quad \xi_{\alpha } \in \varOmega_{1\alpha } ; \\ & {\mathbf{f}}_{2} (\xi ) = - < \omega_{\alpha } (\xi_{\alpha } ) > {\mathbf{c}} - < P_{\alpha } (\xi_{\alpha } ) > {\mathbf{d}} \\ & \quad - \sum\limits_{j = 1}^{4} { < \bar{D}_{j} (\xi_{\alpha } ) - \bar{P}_{j} (\xi_{\alpha } ) > \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\mathbf{B}} + {\mathbf{I}}_{4} {\mathbf{A}}} \right]^{ - 1} \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\bar{\mathbf{B}}} + {\mathbf{I}}_{4} {\bar{\mathbf{A}}}} \right]{\mathbf{I}}_{j} {\bar{\mathbf{d}}}} ,\quad \xi_{\alpha } \in \varOmega_{2\alpha } . \\ \end{aligned} $$
(43)

The extended hoop stress vector \( {\mathbf{t}}_{h} \) along the parabola can be determined as

$$ \begin{aligned} {\mathbf{t}}_{h} & = 4\cos \delta \text{Im} \left\{ {{\mathbf{B}} < \frac{{p_{\alpha } - \tan \delta }}{{1 + p_{\alpha } \tan \delta }} > \left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\mathbf{B}} + {\mathbf{I}}_{4} {\mathbf{A}}} \right]^{ - 1} } \right\} \\ & \quad \times \text{Im} \left\{ {\left[ {({\mathbf{I}} - {\mathbf{I}}_{4} ){\mathbf{B}} + {\mathbf{I}}_{4} {\mathbf{A}}} \right] < \left[ {D^{\prime}_{\alpha } (x_{1} ) - P^{\prime}_{\alpha } (x_{1} )} \right] > {\mathbf{d}}} \right\},\quad x_{2} = bx_{1}^{2} . \\ \end{aligned} $$
(44)

5 Discussion of a special case

In this section, we consider the special case of a hexagonal piezoelectric material exhibiting 6 mm symmetry with its poling direction along the \( x_{3} \)-axis. The subdomain \( z \in S_{2} \) undergoes only uniform anti-plane eigenstrains \( (\varepsilon_{13}^{ * } , \, \varepsilon_{23}^{ * } ) \) and eigenelectric fields \( (E_{1}^{ * } , \, E_{2}^{ * } ) \). In this case, the general solution can be expressed in terms of a two-dimensional analytic vector function \( {\mathbf{f}}(z) \) of the complex variable \( z = x_{1} + {\text{i}}x_{2} \) as follows

$$ \left[ {\begin{array}{*{20}c} {\sigma_{32} + {\text{i}}\sigma_{31} } \\ {D_{2} + {\text{i}}D_{1} } \\ \end{array} } \right] = {\mathbf{Cf^{\prime}}}(z),\quad \left[ {\begin{array}{*{20}c} {\varphi_{3} } \\ {\varphi_{4} } \\ \end{array} } \right] + {\text{i}}{\mathbf{C}}\left[ {\begin{array}{*{20}c} {u{}_{3}} \\ \phi \\ \end{array} } \right] = {\mathbf{Cf}}(z),\quad {\mathbf{C}} = {\mathbf{C}}^{T} = \left[ {\begin{array}{*{20}c} {C_{44} } & {e_{15} } \\ {e_{15} } & { - \in_{11} } \\ \end{array} } \right]. $$
(45)

We introduce the conformal mapping function in Eq. (25). By using this mapping function, the inclusion \( z \in S_{2} \) is mapped onto \( \xi \in \varOmega_{2} \), the matrix \( z \in S_{1} \) is mapped onto \( \xi \in \varOmega_{1} \), and the interface \( z \in \varGamma \) is mapped onto \( \xi \in L \). In addition, there is a conformal mapping \( \xi = w(\eta ) \) which maps the exterior of \( \varOmega_{2} \) in the ξ-plane onto the exterior of the unit circle in the η-plane for a simply-connected inclusion. As a result, we can construct the following auxiliary function \( D(\xi ) \):

$$ \overline{\omega (\xi )} = \bar{\xi } - {\text{i}}b\bar{\xi }^{2} = \bar{w}\left( {\frac{1}{{w^{ - 1} (\xi )}}} \right) - {\text{i}}b\left[ {\bar{w}\left( {\frac{1}{{w^{ - 1} (\xi )}}} \right)} \right]^{2} = D(\xi ),\quad \xi \in L. $$
(46)

In addition, \( D(\xi ) \) is analytic in the exterior of \( \varOmega_{2} \) except at the point at infinity, where it has a pole of finite degree, namely

$$ D(\xi ) \cong P(\xi ) + O(\xi^{ - 1} ),\quad \left| \xi \right| \to \infty , $$
(47)

where \( P(\xi ) \) is a polynomial of order 2 N in \( \xi \) if \( \xi = w(\eta ) \) is a polynomial of order N in \( {1 \mathord{\left/ {\vphantom {1 \eta }} \right. \kern-0pt} \eta } \).

In what follows, we derive analytic solutions for four types of boundary conditions on the parabola. For convenience and without loss of generality, we write \( {\mathbf{f}}_{i} (\xi ) = {\mathbf{f}}_{i} (\omega (\xi )), \, i = 1,2 \).

5.1 A traction-free and insulating parabola \( (\varphi_{3} = \varphi_{4} = 0) \)

In this case, the analytic vector functions inside and outside the inclusion are finally found to be

$$ \begin{aligned} {\mathbf{f}}_{1} (\xi ) & = - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } - {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } - {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {D(\xi ) - P(\xi )} \right] + \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {\bar{D}(\xi ) - \bar{P}(\xi )} \right],\quad \xi \in \varOmega_{1} ; \\ {\mathbf{f}}_{2} (\xi ) & = - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\omega (\xi ) + \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } - {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } - {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]P(\xi ) + \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {\bar{D}(\xi ) - \bar{P}(\xi )} \right],\quad \xi \in \varOmega_{2} . \\ \end{aligned} $$
(48)

5.2 A rigid and conducting parabola \( (u_{3} = \phi = 0) \)

In this case, the analytic vector functions inside and outside the inclusion are:

$$ \begin{aligned} {\mathbf{f}}_{1} (\xi ) & = - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } - {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } - {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {D(\xi ) - P(\xi )} \right] - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {\bar{D}(\xi ) - \bar{P}(\xi )} \right],\quad \xi \in \varOmega_{1} ; \\ {\mathbf{f}}_{2} (\xi ) & = - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\omega (\xi ) + \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } - {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } - {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]P(\xi ) - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {\bar{D}(\xi ) - \bar{P}(\xi )} \right],\quad \xi \in \varOmega_{2} . \\ \end{aligned} $$
(49)

5.3 A rigid and insulating parabola \( (u_{3} = \varphi_{4} = 0) \)

Here, the analytic vector functions inside and outside the inclusion are given by

$$ \begin{aligned} {\mathbf{f}}_{1} (\xi ) & = - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } - {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } - {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {D(\xi ) - P(\xi )} \right] - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } } \\ {\frac{{2e_{15} }}{{ \in_{11} }}(\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } ) + \tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {\bar{D}(\xi ) - \bar{P}(\xi )} \right],\quad \xi \in \varOmega_{1} ; \\ {\mathbf{f}}_{2} (\xi ) & = - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\omega (\xi ) + \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } - {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } - {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]P(\xi ) \\ \, & \quad - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } } \\ {\frac{{2e_{15} }}{{ \in_{11} }}(\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } ) + \tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {\bar{D}(\xi ) - \bar{P}(\xi )} \right],\quad \xi \in \varOmega_{2} . \\ \end{aligned} $$
(50)

5.4 A traction-free and conducting parabola \( (\varphi_{3} = \phi = 0) \)

In this case, the analytic vector functions inside and outside the inclusion are

$$ \begin{aligned} {\mathbf{f}}_{1} (\xi ) & = - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } - {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } - {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {D(\xi ) - P(\xi )} \right] + \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } - \frac{{e_{15} }}{{C_{44} }}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ {\tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {\bar{D}(\xi ) - \bar{P}(\xi )} \right],\quad \xi \in \varOmega_{1} ; \\ {\mathbf{f}}_{2} (\xi ) & = - \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\omega (\xi ) + \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } - {\text{i}}\varepsilon_{13}^{ * } } \\ { - \tfrac{1}{2}(E_{2}^{ * } - {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]P(\xi ) \\ & \quad + \left[ {\begin{array}{*{20}c} {\varepsilon_{23}^{ * } + {\text{i}}\varepsilon_{13}^{ * } - \frac{{e_{15} }}{{C_{44} }}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ {\tfrac{1}{2}(E_{2}^{ * } + {\text{i}}E_{1}^{ * } )} \\ \end{array} } \right]\left[ {\bar{D}(\xi ) - \bar{P}(\xi )} \right],\quad \xi \in \varOmega_{2} . \\ \end{aligned} $$
(51)

6 Conclusions

A general method is presented leading to analytic solutions of Eshelby’s problem of a two-dimensional inclusion of arbitrary shape in a piezoelectric plane with a parabolic boundary. The analytic vector functions inside and outside the inclusion are given in terms of auxiliary functions \( D_{\alpha } (\xi_{\beta } ), \, \alpha ,\beta = 1,2,3,4 \), the polynomials \( P_{\alpha } (\xi_{\beta } ), \, \alpha ,\beta = 1,2,3,4 \) and their analytic continuations. The electroelastic boundary conditions on the parabola can be: (1) traction-free and insulating (Sect. 3); (2) rigid and conducting (Sect. 4.1); (3) rigid and insulating (Sect. 4.2); (4) traction-free and conducting (Sect. 4.3). The special case of a transversely isotropic piezoelectric material is discussed in Sect. 5.