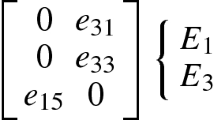1 Introduction

Quasicrystals form an unusual class of previously unencountered quasiperiodic metallic alloys that display non-classical rotational symmetry and quasiperiodic translational symmetry. Since Shechtman et al. [1] first widely revealed in 1984 their discovery, there has been a fascination with investigating both experimentally and theoretically the characteristics of their mechanically, electrically, thermally, magnetically and optically dependent behaviour. This interest is increasingly being motivated by the ever-expanding technological exploitation within, for example, the aerospace, automobile and nuclear fuel industries of their most desirable properties.

The novel modern transducers, sensors, attenuaters and transducers that are being developed in signal processing seek to advantageously incorporate the underlying coupling effects of piezoelectricity in quasicrystals.

As quasicrystals have been shown experimentally to be intrinsically quite brittle and thus prone to premature failure, it is important to study extensively the behaviour of cracks and flaws within them.

Quite shortly after quasicrystals were discovered, the basic mathematical equations governing the linear elasticity theory of quasicrystals became well established and analyses of boundary value problems in them, including various configurations of cracks, continue to be published. Convenient comprehensive reviews of, and references to, this literature have been given by Ding et al. [2], Fan [3, 4], Fan et al. [5], Guo et al. [6], Sladek et al. [7], Sladek et al. [8], Li [9], Tupholme [10], and Sladek et al. [11], for example. Yadav [12] provided a useful summary of the 56 presentations given at the 13th International Conference on Quasicrystals (ICQ13), which was held recently in Nepal.

The corresponding general three-dimensional fundamental mathematical equations of the piezoelectricity of quasicrystals were investigated in both differential and variationally invariant forms by Altay and Dökmeci [13]. Thereafter, increasingly attention has been devoted to the development of techniques for studying boundary value problems in piezoelectric quasicrystals.

Closed-form expressions for the components of the electroelastic fields created by a screw dislocation uniformly moving in a one-dimensional hexagonal piezoelectric quasicrystal with point group 6mm were derived by Wang and Pan [14] with the aid of the fundamental results of the study by Li and Liu [15] of the character formulae of the matrices representing the physical property tensors of one-dimensional quasicrystals with piezoelectric effects. Further, the elastic-electric fields of a straight stationary dislocation parallel to the periodicity axis of a one-dimensional piezoelectric quasicrystal were studied both analytically and numerically by Yang et al. [16] using the Stroh generalized formalism. Li et al. [17] rigorously applied operator theory and introduced two displacement functions to obtain a set of general three-dimensional solutions to facilitate the investigation of boundary value problems in hexagonal piezoelectric quasicrystals. The general solution of the governing equations of plane elasticity in one-dimensional orthorhombic piezoelectric quasicrystals was established by Zhang et al. [18] in terms of four potential functions. The fundamental equations of plane problems in the piezoelasticity of quasicrystals have been solved generally for all point groups by Yu et al. [19] using complex variable functions and operator techniques. An application of the semi-inverse method enabled them to then study the fields near the tip of a mode III uniformly-loaded motionless loaded Griffith crack in hexagonal piezoelectric quasicrystals. In addition, with the aid of a Stroh-type formalism and complex functions, Yu et al. [20] considered a remotely loaded anti-plane elliptical cavity in one-dimensional hexagonal piezoelectric quasicrystals. The internal and interfacial Green’s functions of quasicrystalline bi-materials with piezoelectric effects under the influence of line forces or dislocations were obtained by Zhang et al. [21].

Further papers involving one-dimensional hexagonal quasicrystals with piezoelectic effects appeared in 2016–2017. Yang and Li [22] presented analytical solutions for the field components created by a circular hole with an embedded straight crack by means of complex variable functions with conformal mappings and Fan et al. [23] established solutions for three-dimensional cracks in terms of unit point phonon and phason displacement and electric potential discontinuities and boundary integral equations for an arbitrarily-shaped planar crack were deduced. A composite matrix with an embedded elliptical inclusion was studied by Guo et al. [24] using complex variable and conformal mappings methods. Guo and Pan [25] proposed and analyzed a three-phase model of one-dimensional hexagonal piezoelectric quasicrystal composites. Expressions in closed-form for the mechanical and electric fields around an anti-plane non-uniformly loaded moving crack were given by Tupholme [26]. Most recently, Yang et al. [27] applied the methods of the Stroh-type formalism with conformal mappings in studying the antiplane problem of an ellipsoidal inclusion with two impermeable edge cracks.

Further demonstrations of the wider continuing interest in quasicrystal are provided by investigations of the behaviour of thermal effects within them. For example, Guo et al. [28] studied two-dimensional thermoelastic deformations of a conductive elliptical hole embedded within a two-dimensional decagonal quasicrystal and Fan et al. [29] used extended displacement discontinuities (EDD) with the EDD boundary integral equation method to analyze cracks in one-dimensional thermal hexagonal quasicrystals.

But no study at all by any technique has appeared of the physically interesting situation of a non-uniformly generally loaded anti-plane crack in a half-space of a piezoelectric quasicrystal. The objective of the current consideration is to give a brief explanation of how the basic technique of dislocation layers that was developed originally for classical isotropic elastic media can be extended in conjunction with a method of images to study the fields’ components of such a crack.

In Sect. 2, a summary is first presented of the underpinning general quasistatic three-dimensional equations governing the deformation of piezoelectric quasicrystals. The geometry and specification of the physical crack problem being studied here and the particular constitutive equations of one-dimensional hexagonal piezoelectric quasicrystals with point group 6mm are formulated. The underlying properties of a piezoelectric quasicrystal screw dislocation are then described in Sect. 3. The required extension of the original dislocation layer method together with a method of images is used in Sect. 4 to derive and solve the singular integral equations which govern the necessary density functions. From these, expressions are deduced and discussed in Sect. 5 for the components of the phonon and phason stresses and the electric displacement. Representative numerical results are presented graphically to illustrate the effects of the distance of the crack from the free surface. Finally, the main features of this investigation are summarized in the concluding Sect. 6.

2 Governing equations of a piezoelectric quasicrystal and specification of the crack problem

Within the framework of the linear theory of piezoelectric quasicrystals, Altay and Dökmeci [13] have presented and discussed in both differential and variational invariant forms the general three-dimensional equations which govern the deformation fields’ components. The general quasistatic equilibrium equations in the absence of any body forces or electric charge densities and the constitutive equations can be written concisely, respectively, in the forms

$$ \sigma_{ij,i} = 0,\,\,\,\,\,\,\,H_{ij,i} = 0,\,\,\,\,\,\,\,D_{i,i} {\kern 1pt} {\kern 1pt} = 0{\kern 1pt} {\kern 1pt} , $$
(1)
$$ \sigma_{ij} = c_{ijkl} (u_{k,l} + u_{l,k} )/2 + R_{ijkl} w_{k,l} - \,\,\,e_{kij} E_{k} , $$
(2)
$$ H_{ij} = R_{klij} (u_{k,l} + u_{l,k} )/2 + K_{ijkl} w_{k,l} - \,\,e'_{kij} E_{k} , $$
(3)
$$ D_{i} = e_{kij} (u_{j,k} + u_{k,j} )/2 + e'_{kij} w_{j,k} - \,\,\varepsilon_{ij} E_{j} , $$
(4)

relative to a fixed system of rectangular Cartesian coordinates \( (x_{1} ,x_{2} ,x_{3} ) \). Here the compact repeated summation convention over the suffices i, j, k, l = 1, 2, 3 is utilized and partial differentiation with respect to x p for p = i, j, k, l is indicated by a comma followed by p. The phonon stress and displacement, the phason stress and displacement and the electric displacement and field have components that are denoted by \( \sigma_{ij} \), \( u_{i} \), \( H_{ij} \), \( w_{i} \), \( D_{i} \) and \( E_{i} \), respectively, and the phonon elastic constants, the phonon-phason coupling constants, the phason elastic constants, the phonon and phason piezoelectric constants and the dielectric constants, respectively, are represented by \( c_{ijkl} \), \( R_{ijkl} \), \( K_{ijkl} \), \( e_{ijk} \), \( e'_{ijk} \) and \( \varepsilon_{ij}\).

Here the mode III fracture problem of a non-uniformly loaded strip crack of Griffith type which is embedded within a half-space of one-dimensional hexagonal piezoelectric quasicrystalline material with point group 6mm is considered. In its initial natural reference state, the homogeneous material is everywhere at rest and unstressed. Relative to a fixed system of rectangular Cartesian coordinates (x, y, z), the positive z-axis is in the direction of its quasiperiodicity and in the x–y plane it is periodic.

The stationary crack is assumed to be of width 2c and a distance l from the load-free surface \( y = 0 \) in the region \( L_{1} \) of the x-z plane defined by

$$ L_{1} = \left\{ {(x,y,z):\;\; - c\,<\,x < c,\;\;y = l,\;\; - \infty\,<\,z\,<\,\infty } \right\}, $$
(5)

as depicted in Fig. 1.

Fig. 1
figure 1

A loaded shear crack in a half-space of a piezoelectric quasicrystal

Full size image

The medium is subjected to an antiplane mode III deformation by applying symmetrically non-uniform phonon and phason mechanical and electrical loads to the two crack faces.

For such a hexagonal piezoelectric quasicrystal, the constitutive Eqs. (2)–(4) connecting the created components \( \sigma_{XY} \), \( \varepsilon_{XY} \) and \( u_{X} \) of the phonon stress and strain tensors and displacement vector, \( H_{zX} \), \( w_{zX} \) and \( w_{X} \) of the phason stress and strain tensors and displacement vector, and \( D_{X} \) and \( E_{X} \) of the electric displacement and field vectors, for X and Y = x, y or z, can be written in matrix form as

$$ \left[ {\begin{array}{c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{zz} } \\ {\sigma_{yz} } \\ {\sigma_{xz} } \\ {\sigma_{xy} } \\ {H_{zz} } \\ {H_{zx} } \\ {H_{zy} } \\ \end{array} } \right] = \left[ {\begin{array}{ccccccccc} {c_{11} } \hfill & {c_{12} } \hfill & {c_{13} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {R_{1} } \hfill & 0 \hfill & 0 \hfill \\ {c_{12} } \hfill & {c_{11} } \hfill & {c_{13} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {R_{1} } \hfill & 0 \hfill & 0 \hfill \\ {c_{13} } \hfill & {c_{13} } \hfill & {c_{33} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {R_{2} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {2c_{44} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {R_{3} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {2c_{44} } \hfill & 0 \hfill & 0 \hfill & {R_{3} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {c_{11} - c_{12} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {R_{1} } \hfill & {R_{1} } \hfill & {R_{2} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {K_{1} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {2R_{3} } \hfill & 0 \hfill & 0 \hfill & {K_{2} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {2R_{3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {K_{2} } \hfill \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{zz} } \\ {\varepsilon_{yz} } \\ {\varepsilon_{xz} } \\ {\varepsilon_{xy} } \\ {w_{zz} } \\ {w_{zx} } \\ {w_{zy} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {e_{31} } \hfill \\ 0 \hfill & 0 \hfill & {e_{31} } \hfill \\ 0 \hfill & 0 \hfill & {e_{33} } \hfill \\ 0 \hfill & {e_{15} } \hfill & 0 \hfill \\ {e_{15} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {e^{\prime}_{33} } \hfill \\ {e^{\prime}_{15} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {e^{\prime}_{15} } \hfill & 0 \hfill \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} {E_{x} } \\ {E_{y} } \\ {E_{z} } \\ \end{array} } \right],$$
(6)
$$ \left[ {\begin{array}{*{20}c} {D_{x} } \\ {D_{y} } \\ {D_{z} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {2e_{15} } \hfill & 0 \hfill & 0 \hfill & {e'_{15} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {2e_{15} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {e'_{15} } \hfill \\ {e_{31} } \hfill & {e_{31} } \hfill & {e_{33} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {e'_{33} } \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{zz} } \\ {\varepsilon_{yz} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{xz} } \\ {\varepsilon_{xy} } \\ \end{array} } \\ {w_{zz} } \\ \end{array} } \\ {\begin{array}{*{20}c} {w_{zx} } \\ {w_{zy} } \\ \end{array} } \\ \end{array} } \right] + \, \left[ {\begin{array}{*{20}l} {\varepsilon_{11} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {\varepsilon_{11} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\varepsilon_{33} } \hfill \\ \end{array} } \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}c} {E_{x} } \\ {E_{y} } \\ {E_{z} } \\ \end{array} } \right]. $$
(7)

with

$$ \varepsilon_{XY} = \frac{1}{2}\left( {\frac{{\partial u_{X} }}{\partial Y} + \frac{{\partial u_{Y} }}{\partial X}} \right),\,\,w_{zX} = \frac{{\partial w_{z} }}{\partial X}. $$
(8)

In the customary contracted notation of Voigt, the constants involved are the phonon elastic moduli, \( c_{ij} \), the phason elastic moduli, \( K_{i} \), the phonon-phason coupling elastic moduli, \( R_{i} \), the piezoelectric moduli, \( e_{ij} \) and \( e'_{ij} \), and the dielectric moduli, \( \varepsilon_{ij} \), with i and j taking integer values, and the electric field vector, E, can be expressed in terms of the electric potential, \( \phi \), with the relation

$$ \varvec{E} = - \nabla \phi . $$
(9)

The representative general boundary conditions considered here are that

$$ \sigma_{yz} (x,y) = { \mathsf{T}}(x),\quad H_{zy} (x,y) = {\mathsf{H}}(x),\,\,\,\,\,\,D_{y} (x,y) = {\mathsf{D}}(x)\quad {\text{on}}_{ } \;L_{1} $$
(10)

where \( { \mathsf{T}}(x) \), \( {\mathsf{H}}(x) \) and \( {\mathsf{D}}(x) \) are prescribed functions, with the plane surface \( y = 0 \) remaining free of stress and electrically insulated, so that

$$ \sigma_{yz} (x,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0) = 0,\quad \,\,\,H_{zy} (x,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0) = 0,\,\,\,\,\,\,\,\,\,\,D_{y} (x,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0) = 0. $$
(11)

Alternatively, an interested reader can develop the analyses corresponding to those below for analogous antiplane deformations when instead any desirable combinations of three of the components \( \sigma_{yz} ,\,\,\,\varepsilon_{yz} ,\,\,\,H_{zy} ,\,\,w_{zy} ,\,\,{\kern 1pt} D_{y} , \) or \( E_{y} \) are prescribed.

It is interesting to observe here that substantial exciting applications of quasicrystals are continually being developed, but as yet it is unclear how phason loads can be actually physically applied. For example, Sladek et al. [7] mentioned that “… a physical interpretation on these phason forces is still missing …”. Similarly Li [9] discussed this and observed that “Although no experiments have reported yet on how to impose the phason loads, within the theory of elasticity of QC …, however, traction in the phason field must exist on the boundary of a QC, from a theoretical point of view”.

All the field components are independent of z in these antiplane deformations. Therefore the components \( u_{z} \) and \( w_{z} \) of the phonon and phason displacements, respectively, are related to the relevant non-zero components of the phonon and phason strains by the expressions

$$ \varepsilon_{xz} = \frac{1}{2}\frac{{\partial u_{z} }}{\partial x}{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varepsilon_{yz} = \frac{1}{2}\frac{{\partial u_{z} }}{\partial y}{\kern 1pt} , $$
(12)
$$ w_{zx} = \frac{{\partial w_{z} }}{\partial x},\quad \,\,\,w_{zy} = \frac{{\partial w_{z} }}{\partial y}, $$
(13)

and, from Eqs. (6) and (7), the generalized Hooke’s laws that are required become

$$ {\kern 1pt} \sigma_{xz} = 2{\kern 1pt} {\kern 1pt} c_{44} {\kern 1pt} {\kern 1pt} \varepsilon_{xz} + R{\kern 1pt} {\kern 1pt} w_{zx} {\kern 1pt} - e_{15} E_{x} ,\,\,\,\,\,\,\,\,\,\,\sigma_{yz} {\kern 1pt} = 2{\kern 1pt} {\kern 1pt} c_{44} {\kern 1pt} {\kern 1pt} \varepsilon_{yz} + R{\kern 1pt} {\kern 1pt} w_{zy} - e_{15} E_{y} ,{\kern 1pt} $$
(14)
$$ {\kern 1pt} H_{zx} = 2{\kern 1pt} {\kern 1pt} R{\kern 1pt} {\kern 1pt} \varepsilon_{xz} + K{\kern 1pt} {\kern 1pt} w_{zx} {\kern 1pt} - e'_{15} E_{x} ,\,\,\,\,\,\,\,\,H_{zy} = 2{\kern 1pt} {\kern 1pt} R{\kern 1pt} {\kern 1pt} \varepsilon_{yz} + K{\kern 1pt} {\kern 1pt} w_{zy} - e'_{15} E_{y} , $$
(15)
$$ D_{x} = {\kern 1pt} 2e_{15} {\kern 1pt} {\kern 1pt} \varepsilon_{xz} + e'_{15} {\kern 1pt} {\kern 1pt} {\kern 1pt} w_{zx} {\kern 1pt} + \varepsilon_{11} E_{x} ,\,\,\,\,\,\,\,D_{y} = 2e_{15} {\kern 1pt} {\kern 1pt} \varepsilon_{yz} + e'_{15} {\kern 1pt} {\kern 1pt} w_{zy} + \varepsilon_{11} E_{y} , $$
(16)

where, here and henceforth, in the interests of brevity of presentation, R and K, are utilized as abbreviations for the constants R 3 and K 2.

3 A screw dislocation in a piezoelectric quasicrystal

As a preliminary, it is convenient to provide the foundations for analyzing this antiplane crack problem by outlining the main features of the fields created by a “piezoelectric quasicrystal screw dislocation” in an infinite piezoelectric quasicrystal.

The Burgers vector of the originally conceived screw dislocation of a purely linearly elastic solid is extended to a piezoelectric quasicrystalline material by incorporating a slip plane across which there are finite discontinuities of magnitudes b, d and \( b_{4} \) in the phonon displacement component, the phason displacement component and the electric potential; \( u_{z} \), \( w_{z} \) and \( \phi \), respectively.

It can be deduced from the more general results of Wang and Pan [14] for a moving dislocation of this type that the expressions for the phonon and phason displacement components and electric potential around a stationary straight dislocation which is situated at the origin parallel to the z-axis in an infinite region of a one-dimensional hexagonal piezoelectric quasicrystal with point group 6mm are

$$ u_{z}^{\text{III}} (x,y) = \frac{b}{2\pi }\tan^{ - 1} \left( {\frac{y}{x}} \right),\quad w_{z}^{\text{III}} (x,y) = \frac{d}{2\pi }\tan^{ - 1} \left( {\frac{y}{x}} \right),\,\,\,\,\,\,\,\phi^{\text{III}} (\xi , \, y) = \frac{{b_{4} }}{2\pi }\tan^{ - 1} \left( {\frac{y}{x}} \right), $$
(17)

with the field quantities related to a mode III deformation indicated by the III superscript, here and subsequently.

Consequently, by recalling Eqs. (14)–(16), it follows that the required non-zero phonon and phason stress and electric displacement components have the forms

$$ \sigma_{xz}^{\text{III}} (x,y) = - \frac{{c_{44} b + Rd + e_{15} b_{4} }}{2\pi }\frac{y}{{x^{2} + y^{2} }},\sigma_{yz}^{\text{III}} (x,y) = \frac{{c_{44} b + Rd + e_{15} b_{4} }}{2\pi }\frac{x}{{x^{2} + y^{2} }}, $$
(18)
$$ H_{zx}^{\text{III}} (x,y) = - \frac{{Rb + Kd + e'_{15} b_{4} }}{2\pi }\frac{y}{{x^{2} + y^{2} }}, H_{zy}^{\text{III}} (x,y) = \frac{{Rb + Kd + e'_{15} b_{4} }}{2\pi }\frac{x}{{x^{2} + y^{2} }}, $$
(19)
$$ D_{x}^{\text{III}} (x,y) = - \frac{{e_{15} b + e'_{15} d - \varepsilon_{11} b_{4} }}{2\pi }\frac{y}{{x^{2} + y^{2} }},D_{y}^{\text{III}} (x,y) = \frac{{e_{15} b + e'_{15} d - \varepsilon_{11} b_{4} }}{2\pi }\frac{x}{{x^{2} + y^{2} }}. $$
(20)

4 Analysis by extension of the dislocation layer technique and the solution of the governing singular integral equations

The underlying procedure of the ‘dislocation layer technique’ is based upon the original recognition for a solely elastic material that the field around a strip crack is equivalent to that of a suitable continuously-spread array of elastic dislocations, as conveniently described by, for example, Lardner [30] and Bilby and Eshelby [31]. This classical method is here extended using appropriate distributions of piezoelectric quasicrystal screw dislocations alongside the technique of images.

For the boundary conditions (11) to be maintained, it is necessary to distribute dislocations not only over the region \( L_{1} \) but also to consider a similar distribution over its image region \( L_{2} \) given by

$$ L_{2} = \left\{ {(x,y,z): \, - c\, <\, x\, <\, c, \, y = - l, \, - \infty\,<\,z\,<\,\infty } \right\}. $$
(21)

If the density functions of the appropriate discontinuities in the components of the phonon and phason displacements and the electric potential of the dislocations are taken to be \( f^{(i)} (x) \), \( g^{(i)} (x) \) and \( f_{4}^{(i)} (x) \) on \( L_{i} \), for i = 1, 2, then Eqs. (18)–(20) yield the corresponding components of their fields at a general point (x, y) as

$$ \sigma_{xz} (x,y) = - \frac{1}{2\pi }\left\{ {\int\limits_{{L_{1} }} {\frac{{\left[ {c_{44} bf^{(1)} (x^{\prime}) + Rdg^{(1)} (x^{\prime}) + e_{15} b_{4}\,\,f_{4}^{(1)} (x^{\prime})} \right]\;\;(y - l)}}{{(x - x^{\prime})^{2} + (y - l)^{2} }}dx^{\prime}} } \right.\left. { + \int\limits_{{L_{2} }} {\frac{{\left[ {c_{44} bf^{(2)} (x^{\prime}) + Rdg^{(2)} (x^{\prime}) + e_{15} b_{4}\,\, f_{4}^{(2)} (x^{\prime})} \right]\;\;(y + l)}}{{(x - x^{\prime})^{2} + (y + l)^{2} }}dx^{\prime}} } \right\}, $$
(22)
$$ \sigma_{yz} (x,y) = \frac{1}{2\pi }\left\{ {\;\int\limits_{{L_{1} }} {\frac{{\left[ {c_{44} bf^{(1)} (x^{\prime}) + Rdg^{(1)} (x^{\prime}) + e_{15} b_{4}\,\,f_{4}^{(1)} (x^{\prime})} \right]\;\;(x - x^{\prime})}}{{(x - x^{\prime})^{2} + (y - l)^{2} }}} } \right.dx^{\prime}\left. { + \int\limits_{{L_{2} }} {\frac{{\left[ {c_{44} bf^{(2)} (x^{\prime}) + Rdg^{(2)} (x^{\prime}) + e_{15} b_{4} \,\,f_{4}^{(2)} (x^{\prime})} \right]\;\;(x - x^{\prime})}}{{(x - x^{\prime})^{2} + (y + l)^{2} }}dx^{\prime}} } \right\}, $$
(23)
$$ H_{zx} (x,y) = - \frac{1}{2\pi }\left\{ {\int\limits_{{L_{1} }} {\frac{{\left[ {Rbf^{(1)} (x^{\prime}) + Kdg^{(1)} (x^{\prime}) + e'_{15} b_{4}\,\, f_{4}^{(1)} (x^{\prime})} \right]\;\;(y - l)}}{{(x - x^{\prime})^{2} + (y - l)^{2} }}} } \right.dx^{\prime}\left. { + \int\limits_{{L_{2} }} {\frac{{\left[ {Rbf^{(2)} (x^{\prime}) + Kdg^{(2)} (x^{\prime}) + e'_{15} b_{4}\,\, f_{4}^{(2)} (x^{\prime})} \right]\;\;(y + l)}}{{(x - x^{\prime})^{2} + (y + l)^{2} }}dx^{\prime}} } \right\}, $$
(24)
$$ H_{zy} (x,y) = \frac{1}{2\pi }\left\{ {\;\int\limits_{{L_{1} }} {\frac{{\left[ {Rbf^{(1)} (x^{\prime}) + Kdg^{(1)} (x^{\prime}) + e'_{15} b_{4} \,\,f_{4}^{(1)} (x^{\prime})} \right]\;\;(x - x^{\prime})}}{{(x - x^{\prime})^{2} + (y - l)^{2} }}} } \right.dx^{\prime}\left. { + \int\limits_{{L_{2} }} {\frac{{\left[ {Rbf^{(2)} (x^{\prime}) + Kdg^{(2)} (x^{\prime}) + e'_{15} b_{4} \,\,f_{4}^{(2)} (x^{\prime})} \right]\;\;(x - x^{\prime})}}{{(x - x^{\prime})^{2} + (y + l)^{2} }}dx^{\prime}} } \right\}, $$
(25)
$$ D_{x} (x,y) = - \frac{1}{2\pi }\left\{ {\;\int\limits_{{L_{1} }} {\frac{{\left[ {e_{15} bf^{(1)} (x^{\prime}) + e'_{15} dg^{(1)} (x^{\prime}) - \varepsilon_{11} b_{4}\,\, f_{4}^{(1)} (x^{\prime})} \right]\;\;(y - l)}}{{(x - x^{\prime})^{2} + (y - l)^{2} }}} } \right.dx^{\prime}\left. { + \int\limits_{{L_{2} }} {\frac{{\left[ {e_{15} bf^{(2)} (x^{\prime}) + e'_{15} dg^{(2)} (x^{\prime}) - \varepsilon_{11} b_{4}\,\,f_{4}^{(2)} (x^{\prime})} \right]\;\;(y + l)}}{{(x - x^{\prime})^{2} + (y + l)^{2} }}dx^{\prime}} } \right\}, $$
(26)
$$ D_{y} (x,y) = \frac{1}{2\pi }\left\{ {\;\int\limits_{{L_{1} }} {\frac{{\left[ {e_{15} bf^{(1)} (x^{\prime}) + e'_{15} dg^{(1)} (x^{\prime}) - \varepsilon_{11} b_{4}\,\, f_{4}^{(1)} (x^{\prime})} \right]\;\;(x - x^{\prime})}}{{(x - x^{\prime})^{2} + (y - l)^{2} }}} } \right.dx^{\prime}\left. { + \int\limits_{{L_{2} }} {\frac{{\left[ {e_{15} bf^{(2)} (x^{\prime}) + e'_{15} dg^{(2)} (x^{\prime}) - \varepsilon_{11} b_{4}\,\, f_{4}^{(2)} (x^{\prime})} \right]\;\;(x - x^{\prime})}}{{(x - x^{\prime})^{2} + (y + l)^{2} }}dx^{\prime}} } \right\}, $$
(27)

with the lines \( L_{1} \) and \( L_{2} \) integrated from \( x^{\prime} = - c \) to \( x^{\prime} = c \).

It can be seen from Eqs. (23), (25) and (27) that the boundary conditions (11) imposed on the surface \( y = 0 \) are met if

$$ f^{(1)} (x^{\prime}) = - f^{(2)} (x^{\prime}),\,g^{(1)} (x^{\prime}) = - g^{(2)} (x^{\prime}),\,f_{4}^{(1)} (x^{\prime}) = - f_{4}^{(2)} (x^{\prime}), $$
(28)

and clearly therefore, by observing Eqs. (10),

$$ \sigma_{yz} (x,y) = \,\,\,\, - { \mathsf{T}}(x), H_{zy} (x,y)= - {\mathsf{H}}(x),\,\,\,\,\,\,D_{y} (x,y)= - {\mathsf{D}}(x),{\text{ on}}\;L_{2} . $$
(29)

Expressions for appropriate complex combinations of the field components (22)–(27) can now be written most elegantly in terms of complex variables in the concise forms

$$ \Phi (\zeta ) = \frac{{bc_{44} }}{2\pi }\int\limits_{\mathsf{L}} {\frac{{f(\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}d\zeta^{\prime} + \frac{dR}{2\pi }\int\limits_{\mathsf{L}} {\frac{{g(\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}{\kern 1pt} {\kern 1pt} } } d\zeta^{\prime} + \frac{{b_{4} e_{15} }}{2\pi }\int\limits_{\mathsf{L}} {\frac{{f_{4} (\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}{\kern 1pt} {\kern 1pt} } , $$
(30)
$$ \Psi (\zeta ) = \frac{bR}{2\pi }\int\limits_{\mathsf{L}} {\frac{{f(\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}d\zeta^{\prime} + \frac{dK}{2\pi }\int\limits_{\mathsf{L}} {\frac{{g(\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}d\zeta^{\prime} + \frac{{b_{4} e'_{15} }}{2\pi }\int\limits_{\mathsf{L}} {\frac{{f_{4} (\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}{\kern 1pt} {\kern 1pt} } } } , $$
(31)
$$ \Phi_{4} (\zeta ) = \frac{{be_{15} }}{2\pi }\int\limits_{\mathsf{L}} {\frac{{f(\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}d\zeta^{\prime} + \frac{{de'_{15} }}{2\pi }\int\limits_{\mathsf{L}} {\frac{{g(\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}d\zeta^{\prime} - \frac{{b_{4} \varepsilon_{11} }}{2\pi }\int\limits_{\mathsf{L}} {\frac{{f_{4} (\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}{\kern 1pt} {\kern 1pt} } } } , $$
(32)

with \( {\mathsf{L}} = L_{1} \cup L_{2} \) and

$$ \Phi (\zeta ) = \left[ {\sigma_{yz} + i\sigma_{xz}^{{}} } \right]_{\,(\zeta = x + iy)}^{{}} ,\quad \varPsi (\zeta ) = \left[ {H_{zy} + i{\kern 1pt} H_{zx}^{{}} } \right]_{\,(\zeta = x + iy)}^{{}} ,\quad \Phi_{4} (\zeta ) = \left[ {D_{y} + i{\kern 1pt} D_{x}^{{}} } \right]_{\,(\zeta = x + iy)}^{{}} , $$
(33)

where

$$ \zeta^{\prime} = x + iy,\quad \zeta^{\prime} = \left\{ {\begin{array}{*{20}c} {x^\prime + \ell}& {{\text{on}}\;L_{1} ,} \\ {x^\prime - i\ell} & {{\text{on}}\;L_{2} ,} \\ \end{array} } \right. $$
(34)

and

$$ f(\zeta^{\prime}) = \left\{ {\begin{array}{*{20}c} {f^{(1)} (x^{\prime})} & {{\text{on}}\,L_{1} ,} \\ {f^{(2)} (x^{\prime})} & {{\text{on}}\,L_{2} ,} \\ \end{array}} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g(\zeta^{\prime}) = \left\{ {\begin{array}{*{20}c} {g^{(1)} (x^{\prime})} & {{\text{on}}\, \, L_{1} ,} \\ {g^{(2)} (x^{\prime})} & {{\text{on}}\,L_{2} ,} \\ \end{array}} \right.f_{4} (\zeta^{\prime}) = \left\{ {\begin{array}{*{20}c} {f_{4}^{(1)} (x^{\prime})} & {{\text{on }}L_{1} ,} \\ {f_{4}^{(2)} (x^{\prime})} & {{\text{on }}L_{2} .} \\ \end{array} } \right. $$
(35)

In accordance with the Plemelj formulae (see, for example, Plemelj [32], Muskhelishvili [33] and Lardner [30]), the improper integrals in Eqs. (30)–(32) need to be given their Cauchy principal value integral interpretations.

The system (30)–(32) of coupled equations can be solved to render ultimately three singular integral equations for the density functions \( f(\zeta ) \), \( g(\zeta ) \) and \( f_{4} (\zeta ) \) which after extensive manipulation and simplification become

$$ \frac{1}{2\pi }\int\limits_{\mathsf{L}} {\frac{{f(\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}d\zeta^{\prime} = \frac{1}{{b\varepsilon_{11} (\overline{c} {\kern 1pt}_{44} \overline{K} - \overline{R}^{2} )}}\left\{ {\varepsilon_{11} \overline{K} \Phi (\zeta ) - \varepsilon_{11} \overline{R} \varPsi (\zeta ) + (\overline{K} e_{15} - \overline{R} e'_{15} )\Phi_{4} (\zeta )} \right\},} $$
(36)
$$ \frac{1}{2\pi }\int\limits_{\mathsf{L}} {\frac{{g(\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}d\zeta^{\prime} = - \frac{1}{{d\varepsilon_{11} (\overline{c} {\kern 1pt}_{44} \overline{K} - \overline{R}^{2} )}}\left\{ {\varepsilon_{11} \overline{R} \Phi (\zeta ) - \varepsilon_{11} \overline{c} {\kern 1pt}_{44} \varPsi (\zeta ) - (\overline{c} {\kern 1pt}_{44} e'_{15} - \overline{R} e_{15} )\Phi_{4} (\zeta )} \right\}} , $$
(37)
$$ \frac{1}{2\pi }\int\limits_{\mathsf{L}} {\frac{{f_{4} (\zeta^{\prime})}}{{\zeta - \zeta^{\prime}}}d\zeta^{\prime} = \frac{1}{{b_{4} \varepsilon_{11} (\overline{c} {\kern 1pt}_{44} \overline{K} - \overline{R}^{2} )}}\times\left\{ {(\overline{K} e_{15} - \overline{R} e'_{15} )\Phi (\zeta ) + (\overline{c} {\kern 1pt}_{44} e'_{15} - \overline{R} e_{15} )\varPsi (\zeta )} \right.} \left. { - (c_{44} K - R^{2} )\Phi_{4} (\zeta )} \right\}, $$
(38)

with the piezoelectrically stiffened elastic constants in the phonon and phason fields, \( {\kern 1pt} {\kern 1pt} \overline{c}_{44} \quad \) and \( {\kern 1pt} {\kern 1pt} \overline{K} \quad \), and the piezoelectrically stiffened phonon-phason coupling elastic constant, \( {\kern 1pt} {\kern 1pt} \overline{R} \quad \), respectively, given by

$$ {\kern 1pt} \overline{c}_{44} = c_{44} + \frac{{e_{15}^{2} }}{{\varepsilon_{11} }}{\kern 1pt} , \overline{K} = K + \frac{{e_{15}^{'2} }}{{\varepsilon_{11} }},{\kern 1pt} \overline{R} = R + \frac{{e_{15}^{{}} \;e'_{15} }}{{\varepsilon_{11} }}. $$
(39)

The intricacies of the extensions of the underlying techniques of Gakhov [34], Mikhlin [35] and Muskhelishvili [33], as used by Tupholme [36] in the simpler analogous elastic isotropic situation, which are necessary to solve the governing Eqs. (36)–(38) are omitted here in the interest of conciseness. But it can be shown that with

$$ S^{ + } (\zeta ) = \left\{ {\begin{array}{*{20}c} \begin{aligned} - (c^{2} - x^{2} )^{{\frac{1}{2}}} \left\{ {c^{2} - (x + 2il)^{2} } \right\}^{{\frac{1}{2}}} , \hfill \\ \hfill \\ \end{aligned} & \quad {{\text{for}}\,\zeta \;{\text{on}}\, L_{1} } \\ {(c^{2} - x^{2} )^{{\frac{1}{2}}} \left\{ {c^{2} - (x - 2il)^{2} } \right\}^{{\frac{1}{2}}} ,} & \quad {{\text{for}}\,\zeta \,{\text{on}}\;L_{2} } \\ \end{array} } \right. $$
(40)

the solutions can be expressed as

$$ f(\zeta ) = \frac{2}{{\pi b\varepsilon_{11} (\overline{c} {\kern 1pt}_{44} \overline{K} - \overline{R}^{2} ){\kern 1pt} {\kern 1pt} S^{ + } (\zeta )}}\times\int\limits_{\mathsf{L}} {\frac{{S^{ + } (\zeta^{\prime})}}{{\zeta^{\prime} - \zeta }}\left\{ {\varepsilon_{11} \overline{K} { \mathsf{T}}(\zeta^{\prime}) - \varepsilon_{11} \overline{R} {\mathsf{H}}(\zeta^{\prime})} \right.} \left. { + (\overline{K} e_{15} - \overline{R} e'_{15} ){\mathsf{D}}(\zeta^{\prime})} \right\}\,\,d\zeta^{\prime}, $$
(41)
$$ g(\zeta ) = - \frac{2}{{\pi d\varepsilon_{11} (\overline{c} {\kern 1pt}_{44} \overline{K} - \overline{R}^{2} ){\kern 1pt} {\kern 1pt} S^{ + } (\zeta )}}\times\int\limits_{\mathsf{L}} {\frac{{S^{ + } (\zeta^{\prime})}}{{\zeta^{\prime} - \zeta }}\left\{ {\varepsilon_{11} \overline{R} { \mathsf{T}}(\zeta^{\prime}) - \varepsilon_{11} \overline{c} {\kern 1pt}_{44} {\mathsf{H}}(\zeta^{\prime})} \right.} \left. { - (\overline{c} {\kern 1pt}_{44} e'_{15} - \overline{R} e_{15} ){\mathsf{D}}(\zeta^{\prime})} \right\}\,\,d\zeta^{\prime}, $$
(42)
$$ f_{4} (\zeta )\quad = \quad \frac{2}{{\pi b_{4} \varepsilon_{11} (\overline{c} {\kern 1pt}_{44} \overline{K} - \overline{R}^{2} ){\kern 1pt} {\kern 1pt} S^{ + } (\zeta )}}\times\int\limits_{\mathsf{L}} {\frac{{S^{ + } (\zeta^{\prime})}}{{\zeta^{\prime} - \zeta }}\left\{ {(\overline{K} e_{15} - \overline{R} e'_{15} ){ \mathsf{T}}(\zeta^{\prime}) + (\overline{c} {\kern 1pt}_{44} e'_{15} - \overline{R} e_{15} ){ \mathsf{T}}(\zeta^{\prime})} \right.} \left. { - (c_{44} K - R^{2} ){\mathsf{H}}(\zeta^{\prime})} \right\}\,\,d\zeta^{\prime}. $$
(43)

5 Distributions of the phonon and phason stresses and the electric displacement

Having determine the necessary density functions, the expressions (41)–(43) can now be substituted into Eqs. (30)–(32) to yield closed-form representations for the complex combinations (33) of the phonon and phason stress and electric displacement components. The orders of integration of the resultant repeated integrals can be interchanged and, by using the residue theorem of Cauchy to evaluate the inner integrals, they reduce to the concise simplified forms

$$ \left[ {\sigma_{yz} + i\sigma_{xz} } \right]_{\;(\zeta = x + iy)}^{{}} = C({ \mathsf{T}}),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {H_{zy} + iH_{zx} } \right]_{\;(\zeta = x + iy)}^{{}} = C({\mathsf{H}}),\,\,\,\,\,\left[ {D_{y} + iD_{x} } \right]_{\;(\zeta = x + iy)}^{{}} = C({\mathsf{D}}) . $$
(44)

Here the function C is defined for \( {\mathsf{F}} = { \mathsf{T}}{\kern 1pt} ,{\kern 1pt} \,{\mathsf{H}} \) and \( {\mathsf{D}} \) by

$$\begin{aligned} C({\mathsf{F}}) & = - \frac{i}{{\pi \left[ {\left\{ {\zeta - ( - c + il)} \right\}\left\{ {\zeta - (c + il)} \right\}} \right]^{{\frac{1}{2}^{{^{{}} }} }} }}\\ & \times \frac{1}{\left[\{\zeta-(-c-il)\}\{\zeta-(c-il)\}\right]^\frac{1}{2}}\int_{-c}^{c}\left(c^{2}-x^{\prime 2}\right)^{\frac{1}{2}}{\mathsf{F}}(x^{\prime})\\ & \times \left[{\frac{{\left\{{c^{2} - (x^{\prime} + 2il)^{2} } \right\}^{{\frac{1}{2}}} }}{{x - x^{\prime} + i(y - l)}} + \frac{{\left\{ {c^{2} - (x^{\prime} - 2il)^{2} } \right\}^{{\frac{1}{2}}} }}{{x - x^{\prime} + i(y + l)}}}\right]dx^{\prime}, \end{aligned}$$
(45)

with all the square roots that occur interpreted when x or x′ is zero as having real and positive values. These explicit representations enable the general behaviour of the components to be studied.

However, it is particularly of interest practically to consider the variations of the components’ magnitudes with the distance ρ and the angle ψ near the tip of the crack which are related by

$$ \zeta \quad = \quad (c + il) + \rho {\kern 1pt} e^{i\psi } $$
(46)

with ρ ≪ c. It follows by the substitution of the relation (46) into the expression (45), with the branches selected appropriately, that as ρ → 0

$$ \left[ {C({\mathsf{F}})} \right]_{{({\text{near }}\,c + il)}} \approx - \frac{i}{2\pi }\frac{{e^{{{{ - i\psi } \mathord{\left/ {\vphantom {{ - i\psi } 2}} \right. \kern-0pt} 2}}} }}{{(2c\rho )^{{\frac{1}{2}}} (il)^{{\frac{1}{2}}} (c + il)^{{\frac{1}{2}}} }}\times\int_{ - c}^{c} {\left( {c^{2} - x^{\prime 2} } \right)^{{\frac{1}{2}}} {\mathsf{F}}(x^{\prime})} \times \left[ {\frac{{\left\{ {c^{2} - (x^{\prime} + 2il)^{2} } \right\}^{{\frac{1}{2}}} }}{{c - x^{\prime}}} + \frac{{\left\{ {c^{2} - (x^{\prime} - 2il)^{2} } \right\}^{{\frac{1}{2}}} }}{{c - x^{\prime} + 2il}}} \right]dx^{\prime}. $$
(47)

This demonstrates that all the field components are governed by a \( 1/\sqrt \rho \) crack-tip behaviour, as exhibited near the tip of a crack within an isotropic purely elastic medium. Moreover, it can be noted from Eqs. (41)–(43) that the density functions all depend not only upon the geometrical parameters, c and l, and the piezoelectric quasicrystal material constants but also upon the imposed loads \( {{\mathsf{T}(x)}} \),\( {\mathsf{H}}(x) \) and \( {\mathsf{D}}(x) \). However, in contrast, clearly from Eq. (45) the components in Eq. (44) of the phonon stress, phason stress and electric displacement are decoupled and depend solely on the respective loads \( {{\mathsf{T}(x)}} \),\( {\mathsf{H}}(x) \) and \( {\mathsf{D}}(x) \), as well as the geometric parameters, c and l, and not on the values of the material constants.

Further, taking the limit as l → ∞ of the expression (47) shows that then close to the crack tip at x = c

$$ \sigma_{yz} \sim\frac{{K_{ \mathsf{T}} }}{\sqrt \rho }\cos \left( {\frac{\psi }{2}} \right),\,\,\,\,\,\,\,\,\,\,\sigma_{xz} \sim - \frac{{K_{ \mathsf{T}} }}{\sqrt \rho }\sin \left( {\frac{\psi }{2}} \right), $$
(48)
$$ H_{zy} \sim\frac{{K_{\mathsf{H}} }}{\sqrt \rho }\cos \left( {\frac{\psi }{2}} \right),\,\,\,\,\,\,\,\,\,\,H_{zx} \sim - \frac{{K_{\mathsf{H}} }}{\sqrt \rho }\sin \left( {\frac{\psi }{2}} \right), $$
(49)
$$ D_{y} \sim\frac{{K_{\mathsf{D}} }}{\sqrt \rho }\cos \left( {\frac{\psi }{2}} \right),\,\,\,\,\,\,\,\,\,\,D_{x} \sim - \frac{{K_{\mathsf{D}} }}{\sqrt \rho }\sin \left( {\frac{\psi }{2}} \right), $$
(50)

as ρ → 0, where the phonon and phason stress and electric displacement intensity factors, \( K_{ \mathsf{T}} \), \( K_{\mathsf{H}} \) and \( K_{\mathsf{D}} \), are defined analogously to that at the tip of an isotropic elastic strip-like crack, for \( {\mathsf{F}} = { \mathsf{T}},{\kern 1pt} \,{\mathsf{H}} \) and \( {\mathsf{D}} \), by

$$ K_{\mathsf{F}} = - \frac{1}{{\pi \sqrt {2c} }}\int_{\,\, - c}^{\,\,c} {\left( {\frac{{c + x^{\prime}}}{{c - x^{\prime}}}} \right)^{{\frac{1}{2}}} {\mathsf{F}}(x^{\prime})dx^{\prime}} . $$
(51)

These do attain agreement, in the stationary limit, with the general results derived by Tupholme [26] for a moving shear crack in an infinite one-dimensional hexagonal piezoelectric quasicrystal.

The representations (44) with (47) are convenient for the evaluation numerically using mathematical computer software of the field components near the crack tip for specified forms of the loads \( { \mathsf{T}}(x) \),\( {\mathsf{H}}(x) \) and \( {\mathsf{D}}(x) \), as desired. But, for illustration, attention is restricted here to the situation normally considered in the literature of fracture in which \({ \mathsf{T}}(x) = { \mathsf{T}},\;{\mathsf{H}}(x) = {\mathsf{H}}\;{\text{and}}\;{\mathsf{D}}(x) = {\mathsf{D}} \) for constants \( { \mathsf{T}},\;{{{{\mathsf{H}}}}}\;{\text{and}}\;{\mathsf{D}} \). The non-dimensional variations with \( {x \mathord{\left/ {\vphantom {x c}} \right. \kern-0pt} c} \) of \( - {{\sigma_{yz} (x,l)} \mathord{\left/ {\vphantom {{\sigma_{yz} (x,l)} { \mathsf{T}}}} \right. \kern-0pt} { \mathsf{T}}} \) and \( {{ - \sigma_{xz} (x,l)} \mathord{\left/ {\vphantom {{ - \sigma_{xz} (x,l)} { \mathsf{T}}}} \right. \kern-0pt} { \mathsf{T}}} \) for a range of values of \( {l \mathord{\left/ {\vphantom {l c}} \right. \kern-0pt} c} \) are presented graphically in Figs. 2 and 3, respectively. Because of the previously-noted decoupling in Eqs. (44), the curves depicting the corresponding variations of \( - {{H_{zy} (x,l)} \mathord{\left/ {\vphantom {{H_{zy} (x,l)} { \mathsf{T}}}} \right. \kern-0pt} { \mathsf{T}}} \) and \( - D_{y} {{(x,l)} \mathord{\left/ {\vphantom {{(x,l)} {\mathsf{D}}}} \right. \kern-0pt} {\mathsf{D}}} \) are the same as those in Fig. 2, and likewise those of \( - \, H_{zx} {{(x,l)} \mathord{\left/ {\vphantom {{(x,l)} {\mathsf{H}}}} \right. \kern-0pt} {\mathsf{H}}} \) and \( - \, D_{x} {{(x,l)} \mathord{\left/ {\vphantom {{(x,l)} {\mathsf{D}}}} \right. \kern-0pt} {\mathsf{D}}} \) are as in Fig. 3.

Fig. 2
figure 2

Variation of \( {{ - \sigma_{yz} (x,l)} \mathord{\left/ {\vphantom {{ - \sigma_{yz} (x,l)} { \mathsf{T}}}} \right. \kern-0pt} { \mathsf{T}}} \) with \( {x \mathord{\left/ {\vphantom {x c}} \right. \kern-0pt} c} \) for a range of \( {l \mathord{\left/ {\vphantom {l c}} \right. \kern-0pt} c} \)

Full size image
Fig. 3
figure 3

Variation of \( {{ - \sigma_{xz} (x,l)} \mathord{\left/ {\vphantom {{ - \sigma_{xz} (x,l)} { \mathsf{T}}}} \right. \kern-0pt} { \mathsf{T}}} \) with \( {x \mathord{\left/ {\vphantom {x c}} \right. \kern-0pt} c} \) for a range of \( {l \mathord{\left/ {\vphantom {l c}} \right. \kern-0pt} c} \)

Full size image

For a fixed width, 2c, of the crack, it can be observed that \( \sigma_{yz} \) and \( \sigma_{xz} \) both have magnitudes which decrease as the distance l from the crack to the free surface is increased for a fixed value of x, and similarly for a fixed value of l as x is increased.

Finally, it is noteworthy that from Eqs. (32) and (33), it can be observed that the analysis above would not be valid if \( \overline{c} {\kern 1pt}_{44} \overline{K} - \overline{R}^{2} = 0 \). The data values reported for the piezoelectric quasicrystal material moduli are not yet fully reliable. But \( c_{44} = 5.0 \times 10{\kern 1pt}^{10} \;{\text{Nm}}^{ - 2} \), \( R = 1.2 \times 10{\kern 1pt}^{9} \;{\kern 1pt} {\text{Nm}}^{ - 2} \), \( K = 3.0 \times 10{\kern 1pt}^{8} \;{\text{Nm}}^{ - 2} \), \( e_{15} = - {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.138\;{\text{cm}}^{ - 2} \), \( e'_{15} = - {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.160\;{\text{cm}}^{ - 2} \) and \( \varepsilon_{11} = 82.6 \times 10^{ - 12} \;{\text{C}}^{2} {\text{N}}^{ - 1}{\text{m}}^{ - 2} \) are suggested by Li et al. [17] as being typical. With this, \( \overline{R}^{2} \) is thus much smaller than the product of \( \overline{c} {\kern 1pt}_{44} \) and \( \,\overline{K} \), so that \( \,\overline{c} {\kern 1pt}_{44} \overline{K} - \overline{R}^{2} \) is not zero.

6 Conclusions

In this paper the components of the deformed fields around a mode III, non-constantly loaded, Yoffe-type strip crack embedded within and parallel to the free of surface of a one-dimensional hexagonal quasicrystal are studied.

The analysis is fundamentally focussed upon adopting extensions and adaptations with a method of images of the traditional distribution of dislocations technique for modelling such a crack.

Solutions of the singular integral equations governing the density functions of the discontinuities in the appropriate piezoelectric quasicrystalline screw dislocations are derived explicitly. These yield closed-form expressions for the phonon and phason stress and electric displacement components.

Illustrative graphs are presented of the non-dimensional variations of these components with distance ahead of the crack tip for a range of values of the distance from the crack to the free surface.

Quasicrystals are a class of quite recently discovered very modern solid materials that have far-reaching practical applications and have attracted the attention of researchers who are able to study them theoretically. Not only are the investigations of crack problems in them of interest individually, but they also develop a portfolio of explicit benchmark solutions that are of value in more complex physical practical situations for providing the necessary checks against the numerical/experimental results which have to be sought when exact solutions are not available.