Crack analysis in decagonal quasicrystals by the MLPG

Abstract

A meshless method based on the local Petrov-Galerkin approach is proposed to solve initial-boundary-value crack problems in decagonal quasicrystals. These quasicrystals belong to the class of two-dimensional (2-d) quasicrystals, where the atomic arrangement is quasiperiodic in a plane, and periodic in the perpendicular direction. The ten-fold symmetries occur in these quasicrystals. The 2-d crack problem is described by a coupling of phonon and phason displacements. Both stationary governing equations and dynamic equations represented by the Bak’s model with oscillations for phasons are analyzed here. Nodal points are spread on the analyzed domain, and each node is surrounded by a small circle for simplicity. The spatial variation of phonon and phason displacements is approximated by the moving least-squares scheme. After performing the spatial integrations, one obtains a system of ordinary differential equations for certain nodal unknowns. That system is solved numerically by the Houbolt finite-difference scheme as a time-stepping method.

1 Introduction

The decagonal quasicrystals frequently occur since almost one half of all observed quasicrystals belong to this category. So this kind of solid phases plays an important role. They have ten-fold rotation symmetries. Quasicrystals (QC) with these symmetries belong to the class of two-dimensional (2-d) quasicrystals, where the atomic arrangement is quasiperiodic in a plane, and periodic in the third direction. The problem can be decomposed into plane and anti-plane elasticity. Here, we consider only the plane elasticity, because the anti-plane elasticity is a classical one and independent of phason variables. An opposite case is valid for the one-dimensional quasicrystals, where the atom arrangement is quasi-periodic in one direction and periodic in the plane perpendicular to the quasi-periodic arrangement. The plane problem is there represented by the conventional classical elasticity equations.

Experimental observations (Hu et al. 1997) have shown that quasicrystals are brittle. Therefore, to understand the effect of cracks on the mechanical behaviour of a quasicrystal, the crack analysis of quasicrystals, including the determination of the stress intensity factors, the elastic field, the strain energy release rate and so on, is a prerequisite. Although a sufficiently large number of solutions associated with cracks have been obtained for various problems of theoretical and practical importance in conventional LEFM for crystals, very few investigations are known for quasicrystals (Li et al. 1999). Crack problems in quasicrystals are more complicated than those in conventional crystals owing to the introduction of the phason field. Many crack investigations in the QC are focused on Griffith cracks in an infinite body, where analytical solutions are available for one and two-dimensional quasicrystals (Fan and Mai 2004; Zhou and Fan 2001; Guo and Fan 2001; Li and Fan 2008a, b). Analytical solutions are available also for cracks in a finite strip with the mode III (out-plane) cracks (Li and Fan 2008a, b; Shen and Fan 2003), where governing equations are simpler than that for in-plane problems. Elastodynamics of quasicrystals brings some additional problems. A unique opinion on governing equations for phason fields is missing. According to Bak (1985) the phason describes particular structure disorders in quasicrystals, and it can be formulated in a six-dimensional space. Since there are six continuous symmetries, there exit six hydrodynamic vibration modes. Then, phonons and phasons play similar roles in the dynamics and both fields should be described by similar governing equations, namely the balance of momentum. Lubensky and his students (Lubensky et al. 1985) were thinking that the phason field should be described by a diffusion equation with a very large diffusion time. According to them, phasons are insensitive to spatial translations and phason modes represent the relative motion of the constituent density waves. Probably due to the simpler mathematical formulation, the Bak’s model is more frequently utilized for dynamic study of quasicrystals (Fan et al. 2009). Rochal and Lorman (2002) suggested the minimal model of the phonon-phason dynamics in quasicrystals to reconcile contradictions between Bak’s and Lubensky’s arguments. Yakhno and Yaslan (2011) derived the time-dependent Green’s function of three-dimensional (3-d) elastodynamic problems of quasicrystals described by the Bak’s model. Recently, Yaslan (2012) has presented the variational iteration method for time-fractional elastodynamics of 3-d quasicrystals. Applications of Bak’s model to crack problems are very seldom (Zhu and Fan 2008; Fan 2011).

The purpose of this paper is to develop a reliable computational method for general crack problems in quasicrystals with a finite size. Up to date we have practically only analytical solutions for simple boundary value problems of elasticity for quasicrystals. However, there are strong limitations on applications of analytical approaches for complicated boundary-value problems. The finite-difference method has been applied for elasto-hydrodynamic problems by Fan (2011). The basic equations for the finite element method (FEM) can be found in Fan’s book too. The FEM has been applied only to a hollow cylinder of the octagonal quasicrystal.

In recent years, meshless formulations are becoming popular due to their high adaptability and low costs to prepare input and output data in numerical analysis. The term “meshless” or “meshfree” stems from the ability of an approximation or interpolation scheme to be constructed entirely from a set of nodes without the need to connect them into elements. Meshless methods for solving partial differential equations (PDE) in physics and engineering sciences are a powerful new alternative to the traditional mesh-based techniques. Focusing only on nodes or points instead of elements used in the conventional FEM, meshless approaches have certain advantages. The continuity of the moving least-square (MLS) approximation is given by the minimum between the continuity of the basis functions and that of the weight function. So continuity can be tuned to a desired degree. Previous results showed excellent convergence and accuracy of meshless approaches applied to many engineering problems of classical elasticity (Atluri 2004; Atluri et al. 2000; Sladek et al. 2004). They can be derived either from a weak-form formulation on the global domain or a set of local subdomains. In the global formulation, background cells are required for the integration of the weak-form. In the methods based on the local weak-form formulation no background cells are required and therefore they are often referred to as truly meshless methods. The meshless local Petrov-Galerkin (MLPG) method is a fundamental base for the derivation of many meshless formulations, since trial and test functions can be chosen from different functional spaces. The MLPG method with a Heaviside step function as the test functions has been successfully applied to multi-field coupled and crack problems (Sladek et al. 2009; Sladek et al. 2010, 2).

In the present paper, the MLPG is applied to crack analysis in decagonal quasicrystals under static and transient dynamic loads. The MLPG formulation is developed for both Bak’s and elasto-hydrodynamic models. The coupled governing partial differential equations are satisfied in a weak-form on small fictitious subdomains. Nodal points are introduced and spread on the analyzed domain and each node is surrounded by a small circle for simplicity, but without loss of generality. If the shape of subdomains has a simple form, numerical integrations over them can be easily carried out. The local boundary-domain integral equations have a very simple nonsingular form. The spatial variations of the phonon and phason displacements are approximated by the MLS scheme (Zhu et al. 1998). After performing the spatial MLS approximation, a system of ordinary differential equations for certain nodal unknowns is obtained. Then, the system of the ordinary differential equations of the second order resulting from the equations of motion is solved by the Houbolt finite-difference scheme (Houbolt 1950) as a time-stepping method.

2 Local boundary-domain integral equations for decagonal quasicrystals

The decagonal quasicrystals can be defined as being generated by stacking planar quasi-periodic structures of ten-fold symmetries along the third axis (Fan 2011). The Landau density wave theory (Bak 1985; Levine et al. 1985; Lubensky 1988) can be considered as a base of elasticity theory of quasicrystals. In the theory of elasticity of crystals the displacement field (phonon displacement field $u_i (\mathbf{x}))$ represents the phenomenological field corresponding to translational motion of atoms in crystals. Due to quasi-periodic lattice structure in quasicrystals, additional degrees of freedom corresponding to atomic rearrangements are introduced in the phenomenological theory via phason displacements $w_i (\mathbf{x})$. In the classical theory of elasticity, the deformation of crystals is described by the gradients of (phonon) displacements $u_{i,j} (\mathbf{x})$, or by (phonon) strains $\varepsilon _{ij} (\mathbf{x})$, which represent the fields canonically conjugated with stresses $\sigma _{ij} (\mathbf{x})$ acting on surfaces in elastic medium. Naturally, in the theory of elasticity of quasicrystals, the phason strains $w_{ij} (\mathbf{x})$ and phason stresses $H_{ij} (\mathbf{x})$ as conjugated fields play a role beside the phonon fields $\varepsilon _{ij} (\mathbf{x})$ and $\sigma _{ij} (\mathbf{x})$. The generalized Hooke’s law for plane elasticity of decagonal QC is given as (Fan 2011)

$$\begin{aligned} \sigma _{11}&= c_{11} \varepsilon _{11} +c_{12} \varepsilon _{22} +R(w_{11} +w_{22} ),\nonumber \\ \sigma _{22}&= c_{12} \varepsilon _{11} +c_{22} \varepsilon _{22} -R(w_{11} +w_{22} ),\nonumber \\ \sigma _{12}&= \sigma _{21} =2c_{66} \varepsilon _{12} +R(w_{21} -w_{12} ),\nonumber \\ H_{11}&= K_1 w_{11} +K_2 w_{22} +R(\varepsilon _{11} -\varepsilon _{22} ),\nonumber \\ H_{22}&= K_1 w_{22} +K_2 w_{11} +R(\varepsilon _{11} -\varepsilon _{22} ),\nonumber \\ H_{12}&= K_1 w_{12} -K_2 w_{21} -2R\varepsilon _{12} ,\nonumber \\ H_{21}&= K_1 w_{21} -K_2 w_{12} +2R\varepsilon _{12} , \end{aligned}$$

(1)

where the phonon and phason strains are defined as

$$\begin{aligned}&\varepsilon _{ij} (\mathbf{x})=\frac{1}{2}\left( {u_{i,j} +u_{j,i} } \right) ,\end{aligned}$$

(2)

$$\begin{aligned}&w_{ij} (\mathbf{x})=w_{i,j} (\mathbf{x}), \end{aligned}$$

(3)

in which the phason strains $w_{ij} (\mathbf{x})$ are not necessarily to be a symmetric tensor in contrast to the phonon strains $\varepsilon _{ij} (\mathbf{x})$. The material coefficients $c_{ij}$, $R$ and $K_i$ denote the classical phonon elastic coefficients, the phonon-phason coupling parameter and the phason elastic coefficients, respectively.

2.1 Bak’s oscillation model

It is well-known that the quasi-periodicity leads to two different elementary excitations in the material: phonons $u_i$ and phasons $w_i$. The phonon modes may be understood as vibrations of the quasicrystal lattice, and lead to elastic wave propagation. For the phason modes, there are different points of view. According to Bak (1985) the phason structure disorders are realized by fluctuations in quasicrystals. The balance of momentum is valid for phonon deformation and similarly for phason oscillations with the same mass of density playing role in relaxation processes. Then, the model is described by following governing equations:

$$\begin{aligned}&\sigma _{ij,j} (\mathbf{x},\tau )+X_i (\mathbf{x},\tau )=\rho {\ddot{u}}_i (\mathbf{x},\tau ),\end{aligned}$$

(4)

$$\begin{aligned}&H_{ij,j} (\mathbf{x},\tau )+g_i (\mathbf{x},\tau )=\rho {\ddot{w}}_i (\mathbf{x},\tau ), \end{aligned}$$

(5)

where ${\ddot{u}}_i ,\ddot{w}_i , \rho ,X_i$ and $g_i$ denote the acceleration of the phonon and phason displacements, the mass density, and the body force vectors, respectively. Both governing equations have mathematically a similar structure.

The following essential and natural boundary conditions are assumed

$$\begin{aligned}&u_i (\mathbf{x})=\tilde{u}_i (\mathbf{x}),\quad w_i (\mathbf{x})=\tilde{w}_i (\mathbf{x}),\quad \text{ on }\quad \Gamma _u ,\end{aligned}$$

(6)

$$\begin{aligned}&t_i (\mathbf{x})=\sigma _{ij} n_j=\tilde{t}_i (\mathbf{x}), \quad h_i(\mathbf{x})=H_{ij} n_j=\tilde{h}_i (\mathbf{x}) \quad \text{ on }\quad \Gamma _t , \end{aligned}$$

(7)

where $\Gamma _u$ is the part of the global boundary with prescribed displacements, and on $\Gamma _t$ the tractions are prescribed, respectively.

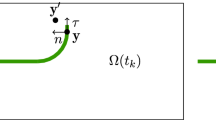
To solve the corresponding initial-boundary value problem, we apply the local boundary-domain integral equation method with meshless approximations. The MLPG method constructs a weak-form over the local subdomains such as $\Omega _s$, which is a small region taken around each node inside the global domain (Atluri 2004). The local subdomains could be of any geometrical shape and size. In the present paper, the local subdomains are taken to be of a circular shape for simplicity. The local weak-form of the governing equations (4) and (5) can be written as

$$\begin{aligned}&\mathop \int \limits _{\Omega _s } {\left[ {\sigma _{ij,j} (\mathbf{x},\tau )\!-\!\rho {\ddot{u}}_i (\mathbf{x},\tau )\!+\!X_i (\mathbf{x},\tau )} \right] u_{ik}^*(\mathbf{x}) d\Omega }=0,\end{aligned}$$

(8)

$$\begin{aligned}&\mathop \int \limits _{\Omega _s } {\left[ {H_{ij,j} (\mathbf{x},\tau )\!-\!\rho {\ddot{w}}_i (\mathbf{x},\tau )\!+\!g_i (\mathbf{x},\tau )} \right] u_{ik}^*(\mathbf{x}) d\Omega }=0, \end{aligned}$$

(9)

where $u_{ik}^*(\mathbf{x})$is a test function.

Applying the Gauss divergence theorem to the first domain integrals in both equations one gets

$$\begin{aligned}&\mathop \int \limits _{\partial \Omega _s } {\sigma _{ij} (\mathbf{x},t)n_j (\mathbf{x})u_{ik}^*(\mathbf{x})d\Gamma } -\mathop \int \limits _{\Omega _s } {\sigma _{ij} (\mathbf{x},t)u_{ik,j}^*(\mathbf{x})d\Omega }\nonumber \\&\qquad +\mathop \int \limits _{\Omega _s } {\left[ {-\rho {\ddot{u}}_i (\mathbf{x},t)+X_i (\mathbf{x},t)} \right] u_{ik}^*(\mathbf{x})d\Omega } =0,\end{aligned}$$

(10)

$$\begin{aligned}&\mathop \int \limits _{\partial \Omega _s } {H_{ij} (\mathbf{x},t)n_j (\mathbf{x})u_{ik}^*(\mathbf{x})d\Gamma } -\mathop \int \limits _{\Omega _s } {H_{ij} (\mathbf{x},t)u_{ik,j}^*(\mathbf{x})d\Omega }\nonumber \\&\qquad +\mathop \int \limits _{\Omega _s } {\left[ {-\rho {\ddot{w}}_i (\mathbf{x},t)+g_i (\mathbf{x},t)} \right] u_{ik}^*(\mathbf{x})d\Omega } =0, \end{aligned}$$

(11)

where $\partial \Omega _s$ is the boundary of the local subdomain which consists of three parts $\partial \Omega _s =L_s \cup \Gamma _{st} \cup \Gamma _{su}$ (Atluri 2004). Here, $L_s$ is the local boundary that is totally inside the global domain, $\Gamma _{st}$ is the part of the local boundary which coincides with the global traction boundary, i.e., $\Gamma _{st} =\partial \Omega _s \cap \Gamma _t$, and similarly $\Gamma _{su}$ is the part of the local boundary that coincides with the global displacement boundary, i.e., $\Gamma _{su} =\partial \Omega _s \cap \Gamma _u$. For simplicity, we assume that $\Gamma _{sw} =\Gamma _{su}$ and $\Gamma _{sh} =\Gamma _{st}$.

By choosing a Heaviside step function as the test function $u_{ik}^*(\mathbf{x})$ in each subdomain

$$\begin{aligned} u_{ik}^*(\mathbf{x})=\left\{ \begin{array}{l@{\quad }ll} \delta _{ik} &{} \text{ at } &{} \mathbf{x}\in \Omega _s \\ 0 &{} \text{ at } &{} \mathbf{x}\notin \Omega _s \\ \end{array}\right. , \end{aligned}$$

the local weak-forms (8) and (9) are converted into the following local boundary-domain integral equations

$$\begin{aligned}&\mathop \int \limits _{L_s +\Gamma _{su} } {t_i (\mathbf{x},\tau )d\Gamma } -\mathop \int \limits _{\Omega _s } {\rho {\ddot{u}}_i (\mathbf{x},\tau )d\Omega }\nonumber \\&\quad =-\mathop \int \limits _{\Gamma _{st} } {\tilde{t}_i (\mathbf{x},\tau )d\Gamma } -\mathop \int \limits _{\Omega _s } {X_i (\mathbf{x},\tau )d\Omega } ,\end{aligned}$$

(12)

$$\begin{aligned}&\mathop \int \limits _{L_s +\Gamma _{su} } {h_i (\mathbf{x},\tau )d\Gamma } -\mathop \int \limits _{\Omega _s } {\rho {\ddot{w}}_i (\mathbf{x},\tau )d\Omega }\nonumber \\&\quad =-\mathop \int \limits _{\Gamma _{st} } {\tilde{h}_i (\mathbf{x},\tau )d\Gamma } -\mathop \int \limits _{\Omega _s } {g_i (\mathbf{x},\tau )d\Omega }. \end{aligned}$$

(13)

Making use of the constitutive equations (1) and Eqs. (2) and (3), one can obtain the traction and the generalized traction vectors as

$$\begin{aligned} t_i (\mathbf{x},\tau )&= \sigma _{ij} (\mathbf{x},\tau )n_j (\mathbf{x}),\end{aligned}$$

(14)

$$\begin{aligned} h_i (\mathbf{x},\tau )&= H_{ij} (\mathbf{x},\tau )n_j (\mathbf{x}), \end{aligned}$$

(15)

expressed in terms of the phonon and phason displacement gradients $u_{i,j} (\mathbf{x},\tau )$, $w_{i,j} (\mathbf{x},\tau )$ with $n_j (\mathbf{x})$ being the outward unit normal vector to the boundary $\partial \Omega _s$.

In the MLPG method the test and the trial functions are not necessarily from the same functional spaces. For internal nodes, the test function is chosen as a unit step function with its support on the local subdomain. The trial functions, on the other hand, are chosen to be the MLS approximations by using a number of nodes spreading over the domain of influence. According to the MLS (Lancaster and Salkauskas 1981; Nayroles et al. 1992) method, the approximation of the displacement field can be given as

$$\begin{aligned} \mathbf{u}^{h}(\mathbf{x})=\sum _{i=1}^m {p_i (\mathbf{x})a_i (\mathbf{x})} =\mathbf{p}^{T}(\mathbf{x})\mathbf{a}(\mathbf{x}), \end{aligned}$$

(16)

where $\mathbf{p}^{T}(\mathbf{x})=\left\{ {p_1 (\mathbf{x}),p_2 (\mathbf{x}),\ldots ,p_m (\mathbf{x})} \right\}$ is a vector of complete basis functions of order $m$ and $\mathbf{a}(\mathbf{x})=\left\{ {a_1 (\mathbf{x}),a_2 (\mathbf{x}),\ldots ,a_m (\mathbf{x})} \right\}$ is a vector of unknown parameters which depend on x. For example, in 2-d problems

$$\begin{aligned} \mathbf{p}^{T}(\mathbf{x})=\left\{ {1,x_1 ,x_2 } \right\} \quad \text{ for } \text{ m }=3 \end{aligned}$$

and

$$\begin{aligned} \mathbf{p}^{T}(\mathbf{x})=\left\{ {1,x_1 ,x_2 ,x_1^2 ,x_1 x_2 ,x_2^2 } \right\} \quad \text{ for } \text{ m }=6 \end{aligned}$$

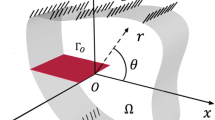
are linear and quadratic basis functions, respectively. The basis functions are not necessary to be polynomials. It is convenient to introduce $r^{-1/2}$—singularity for secondary fields at the crack-tip vicinity for modelling of fracture problems (Fleming et al. 1997). Then, the basis functions can be considered to have the following form

$$\begin{aligned}&\mathbf{p}^{T}(\mathbf{x})=\left\{ {1,x_1 ,x_2 ,\sqrt{r}\cos (\theta /2),\sqrt{r}\sin (\theta /2),}\right. \nonumber \\&\quad \left. {\sqrt{r}\sin (\theta /2)\sin \theta ,\sqrt{r}\cos (\theta /2)\sin \theta } \right\} \quad \text{ for } \text{ m }=\text{7 }, \end{aligned}$$

where $r$ and $\theta$ are polar coordinates with the origin at the crack-tip. The above given enriched basis functions represent all terms occurring in the asymptotic expansion of the displacements at the crack-tip vicinity. Then, the density of the node distribution in such a case can be lower than in the case of pure polynomial basis functions in order to receive the same accuracy of the numerical results.

The approximated functions for the phonon and phason displacements can be written as

$$\begin{aligned} \begin{aligned}&\mathbf{u}^{h}(\mathbf{x},\tau )\!=\!{\varvec{\Phi }}^{T}(\mathbf{x})\cdot \hat{{\mathbf{u}}}\!=\!\sum _{a\!=\!1}^n {\phi ^{a}(\mathbf{x})\hat{\mathbf{u}}^{a}(\tau )}, \\&\mathbf{w}^{h}(\mathbf{x},\tau )\!=\!\sum _{a\!=\!1}^n {\phi ^{a}(\mathbf{x})\hat{\mathbf{w}}^{a}(\tau )} \end{aligned} \end{aligned}$$

(17)

(Atluri 2004), where the nodal values $\hat{\mathbf{u}}^{a}(\tau )=( {\hat{{u}}_1^a (\tau )}, {\hat{{u}}_2^a (\tau )})^{T}$ and $\hat{\mathbf{w}}^{a}(\tau )=( {\hat{{w}}_1^a (\tau ), \hat{{w}}_2^a (\tau )} )^{T}$ are fictitious parameters for the phonon and phason displacements, respectively, and $\phi ^{a}(\mathbf{x})$ is the shape function associated with the node $a$. The number of nodes $n$ used for the approximation is determined by the weight function. A 4$\mathrm{th}$ order spline-type weight function is applied in the present work

$$\begin{aligned} \!\!\!\!&m^{a}(\mathbf{x})\nonumber \\ \!\!\!\!&\quad \!=\!\left\{ {{\begin{array}{ll} 1-6\left( {\frac{d^{a}}{r^{a}}} \right) ^{2}\!+\!8\left( {\frac{d^{a}}{r^{a}}} \right) ^{3}\!-\!3\left( {\frac{d^{a}}{r^{a}}} \right) ^{4}, &{} \quad 0\le d^{a}\le r^{a} \\ 0, &{} \quad d^{a}\ge r^{a} \\ \end{array} }} \right. ,\qquad \nonumber \\ \end{aligned}$$

(18)

where $d^{a}=\left\| {\mathbf{x}-\mathbf{x}^{a}} \right\|$ and $r^{a}$ is the size of the support domain. It is seen that the $C^{1}-$continuity is ensured over the entire domain, and therefore the continuity conditions of both phonon and phason stresses are satisfied. In the MLS approximation the rates of the convergence of the solution may depend upon the nodal distance as well as the size of the support domain (Wen and Aliabadi 2007, 2008; Wen et al. 2008). It should be noted that a smaller size of the subdomains may induce larger oscillations in the nodal shape functions (Atluri 2004). A necessary condition for a regular MLS approximation is that at least $m$ weight functions are non-zero (i.e. $n\ge m )$ for each sample point $\mathbf{x}\in \Omega$. This condition determines the size of the support domain.

Then, the traction vector $t_i (\mathbf{x},\tau )$ at a boundary point $\mathbf{x}\in \partial \Omega _s$ is approximated in terms of the same nodal values $\hat{\mathbf{u}}^{a}(\tau )$and $\hat{\mathbf{w}}^{a}(\tau )$ as

$$\begin{aligned} \mathbf{t}^{h}(\mathbf{x},\tau )&= \mathbf{N}(\mathbf{x})\mathbf{C}\sum _{a=1}^n {\mathbf{B}^{a}(\mathbf{x})\hat{\mathbf{u}}^{a}(\tau ) }\nonumber \\&+\,\mathbf{N}(\mathbf{x})\mathbf{R}\sum _{a=1}^n {\mathbf{B}_w^a (\mathbf{x})\hat{\mathbf{w}}^{a}(\tau )} , \end{aligned}$$

(19)

where N(x) is related to the normal vector n(x) on $\partial \Omega _s$ by

$$\begin{aligned} \mathbf{N}(\mathbf{x})=\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {n_1 }&{} 0&{} {n_2 } \\ 0&{} {n_2 }&{} {n_1 } \\ \end{array} }} \right] , \end{aligned}$$

the matrices $\mathbf{B}^{a}$ and $\mathbf{B}_w^a$ are represented by the gradients of the shape functions as

$$\begin{aligned} \mathbf{B}^{a}(\mathbf{x})=\left[ {{\begin{array}{c@{\quad }c} {\phi _{,1}^a } &{} 0 \\ 0 &{} {\phi _{,2}^a } \\ {\phi _{,2}^a } &{} {\phi _{,1}^a } \\ \end{array} }} \right] , \quad \mathbf{B}_w^a (\mathbf{x})=\left[ {{\begin{array}{c@{\quad }c} {\phi _{,1}^a } &{} 0 \\ 0 &{} {\phi _{,2}^a }\\ {\phi _{,2}^a } &{} {-\phi _{,1}^a } \\ \end{array} }} \right] , \end{aligned}$$

and the material matrices C and R are given by

$$\begin{aligned} \mathbf{C}=\left[ {{\begin{array}{c@{\quad }cc} {c_{11} }&{} {c_{12} }&{} 0 \\ {c_{12} }&{} {c_{22} }&{} 0 \\ 0&{} 0&{} {c_{66} } \\ \end{array} }} \right] ,\quad \mathbf{R}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c} R&{} R&{} 0 \\ {-R}&{} {-R}&{} 0 \\ 0&{} 0&{} {-R} \\ \end{array} }} \right] . \end{aligned}$$

Similarly the generalized traction vector $h_i (\mathbf{x},\tau )$ can be approximated by

$$\begin{aligned} \mathbf{h}^{h}(\mathbf{x},\tau )&= \mathbf{N}_h (\mathbf{x})\mathbf{R}_h \sum _{a=1}^n {\mathbf{B}^{a}(\mathbf{x})\hat{\mathbf{u}}^{a}(\tau ) }\nonumber \\&+\,\mathbf{N}_h (\mathbf{x})\mathbf{K}\sum _{a=1}^n {\mathbf{B}_{hw}^a (\mathbf{x})\hat{\mathbf{w}}^{a}(\tau )}, \end{aligned}$$

(20)

where

$$\begin{aligned}&\mathbf{N}_h (\mathbf{x})=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {n_1 }&{} 0&{} {n_2 }&{} 0 \\ 0&{} {n_2 }&{} 0&{} {n_1 } \\ \end{array} }} \right] ,\\&\quad \mathbf{K}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {K_1 }&{} {K_2 }&{} 0&{} 0 \\ {K_2 }&{} {K_1 }&{} 0&{} 0 \\ 0&{} 0&{} {K_1 }&{} {-K_2 } \\ 0&{} 0&{} {-K_2 }&{} {K_1 } \\ \end{array} }} \right] ,\quad \mathbf{B}_{hw}^a (\mathbf{x})=\left[ {{\begin{array}{c@{\quad }c} {\phi _{,1}^a }&{} 0 \\ 0&{} {\phi _{,2}^a } \\ {\phi _{,2}^a }&{} 0 \\ 0&{} {\phi _{,1}^a } \\ \end{array} }} \right] ,\nonumber \\&R_h =\left[ {{\begin{array}{c@{\quad }c@{\quad }c} R&{} {-R}&{} 0 \\ R&{} {-R}&{} 0 \\ 0&{} 0&{} {-R} \\ 0&{} 0&{} R \\ \end{array} }} \right] . \end{aligned}$$

Satisfying the essential boundary conditions and making use of the approximation formulae (17), one obtains the discretized form of these boundary conditions as

$$\begin{aligned}&\sum _{a=1}^n {\phi ^{a}(\mathbf{\zeta })\hat{\mathbf{u}}^{a}(\tau )} =\tilde{\mathbf{u}}(\mathbf{\zeta },\tau ),\nonumber \\&\sum _{a=1}^n {\phi ^{a}(\mathbf{\zeta })\mathbf{w}^{a}} (\tau )={\tilde{\mathbf{w}}}(\mathbf{\zeta },\tau )\quad \text{ for }\; \mathbf{\zeta }\in \Gamma _u. \end{aligned}$$

(21)

Furthermore, in view of the MLS-approximations (19) and (20) for the unknown quantities in the local boundary-domain integral equations (12) and (13), we obtain their discretized forms as

$$\begin{aligned}&\sum _{a=1}^n \left[ \left( {\mathop \int \limits _{L_s +\Gamma _{st} } {\mathbf{N}(\mathbf{x})\mathbf{C}} \mathbf{B}^{a}(\mathbf{x})d\Gamma } \right) \hat{\mathbf{u}}^{a}(\tau )\right. \nonumber \\&\quad \quad \left. -\left( {\mathop \int \limits _{\Omega _s } {\rho (\mathbf{x})\phi ^{a}d\Omega } } \right) {{\ddot{\hat{\mathbf{u}}}}}^{a}(\tau ) \right] \nonumber \\&\quad \quad +\sum _{a=1}^n {\left( {\mathop \int \limits _{L_s +\Gamma _{st} } {\mathbf{N}(\mathbf{x})\mathbf{R}} \mathbf{B}_w^a (\mathbf{x})d\Gamma } \right) \hat{\mathbf{w}}^{a}(\tau ) }\nonumber \\&\quad = -\mathop \int \limits _{\Gamma _{st} } {{\tilde{\mathbf{t}}}(\mathbf{x},\tau )d\Gamma } -\mathop \int \limits _{\Omega _s } {\mathbf{X}(\mathbf{x},\tau )d\Omega } , \end{aligned}$$

(22)

$$\begin{aligned}&\sum _{a=1}^n {\left( {\mathop \int \limits _{L_s +\Gamma _{st} } {\mathbf{N}_h (\mathbf{x})\mathbf{R}_h } \mathbf{B}^{a}(\mathbf{x})d\Gamma } \right) \hat{\mathbf{u}}^{a}(\tau ) }\nonumber \\&\quad \quad -\sum _{a=1}^n {\left( {\mathop \int \limits _{L_s +\Gamma _{st} } {\mathbf{N}_h (\mathbf{x})\mathbf{K}} \mathbf{B}_{hw}^a (\mathbf{x})d\Gamma } \right) \hat{\mathbf{w}}^{a}(\tau )} \nonumber \\&\quad \quad -\sum _{a=1}^n {\left( {\mathop \int \limits _{\Omega _s } {\rho (\mathbf{x})\phi ^{a}d\Omega } } \right) {{\ddot{\hat{\mathbf{w}}}}}^{a}(\tau )}\nonumber \\&\quad =-\mathop \int \limits _{\Gamma _{st} } {\tilde{\mathbf{h}}(\mathbf{x},\tau )d\Gamma } +\mathop \int \limits _{\Omega _s } {\mathbf{g}(\mathbf{x},\tau )d\Omega } , \end{aligned}$$

(23)

which are considered on the sub-domains adjacent to the interior nodes as well as to the boundary nodes on $\Gamma _{st}$.

Collecting the discretized local boundary-domain integral equations together with the discretized boundary conditions for the phonon and phason displacements results in a complete system of ordinary differential equations which can be rearranged in such a way that all known quantities are on the right-hand side (r.h.s). Thus, in matrix form the system becomes

$$\begin{aligned} \mathbf{A}{{\ddot{\mathbf{x}}}}+\mathbf{Cx}=\mathbf{Y}. \end{aligned}$$

(24)

There are many time integration procedures for the solution of this system of ordinary differential equations. In the present work, the Houbolt method is applied. In the Houbolt finite-difference scheme (Houbolt 1950), the “acceleration” is expressed as

$$\begin{aligned} {{\ddot{\mathbf{x}}}}_{\tau +\Delta \tau } =\frac{2\mathbf{x}_{\tau +\Delta \tau } -5\mathbf{x}_\tau +4\mathbf{x}_{\tau -\Delta \tau } -\mathbf{x}_{\tau -2\Delta \tau } }{\Delta \tau ^{2}} , \end{aligned}$$

(25)

where $\Delta \tau$ is the time-step.

Substituting Eq. (25) into (24), we get the following system of algebraic equations for the unknowns $\mathbf{x}_{\tau +\Delta \tau }$

$$\begin{aligned}&\left[ {\frac{2}{\Delta \tau ^{2}}\mathbf{A}+\mathbf{C}} \right] \mathbf{x}_{\tau +\Delta \tau }\nonumber \\&\quad =\frac{5\mathbf{A}}{\Delta \tau ^{2}}\mathbf{x}_\tau +\mathbf{A}\frac{1}{\Delta \tau ^{2}}\left\{ {-4\mathbf{x}_{\tau -\Delta \tau } +\mathbf{x}_{\tau -2\Delta \tau } } \right\} +\mathbf{Y}.\nonumber \\ \end{aligned}$$

(26)

2.2 Elasto-hydrodynamic model

Lubensky et al. (1985) pointed out that the phonon and phason fields play different roles in the hydrodynamics of quasicrystals, because phason displacements are insensitive to spatial translations. Furthermore, the relaxation of the phason strain is diffusive and is much slower than rapid relaxation of conventional phonon strains. Recently, the elasto-hydrodynamic model has been introduced by Fan et al. (2009). It is a combination of elastodynamics originating from Bak’s arguments and the hydrodynamics of Lubensky et al. (1985). Rochal and Lorman (2002) published a similar model, although they called it as the minimal model. The corresponding governing equations in this case have the following forms

$$\begin{aligned} \sigma _{ij,j} (\mathbf{x},\tau )+X_i (\mathbf{x},\tau )=\rho {\ddot{u}}_i (\mathbf{x},\tau ),\end{aligned}$$

(27)

$$\begin{aligned} H_{ij,j} (\mathbf{x},\tau )+g_i (\mathbf{x},\tau )=D\dot{w}_i (\mathbf{x},\tau ), \end{aligned}$$

(28)

where $D=1/\Gamma _w$, and $\Gamma _w$ denotes the kinematic coefficient of phason field of the material defined by Lubensky et al. (1985).

A solution of the governing equations (27) and (28) is more complicated than for either pure wave equations or pure diffusion equations. The present case belongs to a complicated dynamic coupling between wave propagation and diffusion propagation. The solution must describe the behaviour of waves, diffusion and their interactions. The MLPG method is again applied to solve the above given governing equations. The local boundary-domain integral equations are similar to the previous Bak’s model

$$\begin{aligned}&\mathop \int \limits _{L_s +\Gamma _{su} } {t_i (\mathbf{x},\tau )d\Gamma } -\mathop \int \limits _{\Omega _s } {\rho {\ddot{u}}_i (\mathbf{x},\tau )d\Omega }\nonumber \\&\quad =-\mathop \int \limits _{\Gamma _{st} } {\tilde{t}_i (\mathbf{x},\tau )d\Gamma } -\mathop \int \limits _{\Omega _s } {X_i (\mathbf{x},\tau )d\Omega } ,\end{aligned}$$

(29)

$$\begin{aligned}&\mathop \int \limits _{L_s +\Gamma _{su} } {h_i (\mathbf{x},\tau )d\Gamma } -\mathop \int \limits _{\Omega _s } {D\dot{w}_i (\mathbf{x},\tau )d\Omega }\nonumber \\&\quad =-\mathop \int \limits _{\Gamma _{st} } {\tilde{h}_i (\mathbf{x},\tau )d\Gamma } -\mathop \int \limits _{\Omega _s } {g_i (\mathbf{x},\tau )d\Omega }. \end{aligned}$$

(30)

If the MLS spatial approximation is applied for the unknown quantities in the local boundary-domain integral equations (29) and (30), we obtain their discretized forms as

$$\begin{aligned}&\sum _{a=1}^n \left[ \left( {\mathop \int \limits _{L_s +\Gamma _{st} } {\mathbf{N}(\mathbf{x})\mathbf{C}} \mathbf{B}^{a}(\mathbf{x})d\Gamma } \right) \hat{\mathbf{u}}^{a}(\tau )\right. \nonumber \\&\qquad \left. -\left( \mathop \int \limits _{\Omega _s } {\rho (\mathbf{x})\phi ^{a}d\Omega } \right) {{\ddot{\hat{\mathbf{u}}}}}^{a}(\tau ) \right] \nonumber \\&\qquad +\sum _{a=1}^n {\left( {\mathop \int \limits _{L_s +\Gamma _{st} } {\mathbf{N}(\mathbf{x})\mathbf{R}} \mathbf{B}_w^a (\mathbf{x})d\Gamma } \right) \hat{\mathbf{w}}^{a}(\tau ) }\nonumber \\&\quad = -\mathop \int \limits _{\Gamma _{st} } {\tilde{\mathbf{t}}}(\mathbf{x},\tau )d\Gamma -\mathop \int \limits _{\Omega _s } {\mathbf{X}(\mathbf{x},\tau )d\Omega } , \end{aligned}$$

(31)

$$\begin{aligned}&\sum _{a=1}^n {\left( {\mathop \int \limits _{L_s +\Gamma _{st} } {\mathbf{N}_h (\mathbf{x})\mathbf{R}_h } \mathbf{B}^{a}(\mathbf{x})d\Gamma } \right) \hat{\mathbf{u}}^{a}(\tau ) }\nonumber \\&\qquad -\sum _{a=1}^n {\left( {\mathop \int \limits _{L_s +\Gamma _{st} } {\mathbf{N}_h (\mathbf{x})\mathbf{K}} \mathbf{B}_{hw}^a (\mathbf{x})d\Gamma } \right) \hat{\mathbf{w}}^{a}(\tau )} \nonumber \\&\qquad -\sum _{a=1}^n {\left( {\mathop \int \limits _{\Omega _s } {D(\mathbf{x})\phi ^{a}d\Omega } } \right) {\dot{\hat{\mathbf{w}}}}^{a}(\tau )}\nonumber \\&\quad =-\mathop \int \limits _{\Gamma _{st} } {\tilde{\mathbf{h}}}(\mathbf{x},\tau )d\Gamma +\mathop \int \limits _{\Omega _s } {\mathbf{g}(\mathbf{x},\tau )d\Omega }. \end{aligned}$$

(32)

The discretized equations can be written in the matrix form with unknown vector x as

$$\begin{aligned} \mathbf{A}{{\ddot{\mathbf{x}}}}+\mathbf{B}{\dot{\mathbf{x}}}+\mathbf{Cx}=\mathbf{Y}. \end{aligned}$$

(33)

The Houbolt finite-difference scheme is applied for the acceleration

$$\begin{aligned} {{\ddot{\mathbf{x}}}}_{\tau +\Delta \tau } =\frac{2\mathbf{x}_{\tau +\Delta \tau } -5\mathbf{x}_\tau +4\mathbf{x}_{\tau -\Delta \tau } -\mathbf{x}_{\tau -2\Delta \tau } }{\Delta \tau ^{2}} , \end{aligned}$$

(34)

and the backward difference method for the diffusion term

$$\begin{aligned} {\dot{\mathbf{x}}}_{\tau +\Delta \tau } =\frac{\mathbf{x}_{\tau +\Delta \tau } -\mathbf{x}_\tau }{\Delta \tau }. \end{aligned}$$

(35)

Substituting Eqs. (34) and (35) into (33), we get the system of linear algebraic equations for the unknowns $\mathbf{x}_{\tau +\Delta \tau }$.

3 Computation of stress intensity factors

In practice, the distribution of the stresses near the crack-tip is of particular interest. Li et al. (1999) found an analytical solution for a Griffith crack in decagonal quasicrystals. It can be observed that both phonon and phason stresses exhibit the singularity $r^{-1/2}$, where $r$ is the radial coordinate with origin at the crack-tip. Neglecting higher-order infinitesimal terms in the analytical solution, one can obtain the asymptotic expression of stresses at the crack-tip vicinity proportional to $r^{-1/2}$. The asymptotic crack-tip field is the same for both the Bak’s and the elasto-hydrodynamic models. For the mode-I crack under a pure phonon load we have the following asymptotic stresses in polar coordinate system (Fan et al. 2012):

$$\begin{aligned} \sigma _{11} (r,\theta )&= \frac{K_I^{||} }{\sqrt{2\pi r}}\cos \frac{1}{2}\theta \left( {1\!-\!\sin \frac{1}{2}\theta \sin \frac{3}{2}\theta } \right) , \nonumber \\ \sigma _{22} (r,\theta )&= \frac{K_I^{||} }{\sqrt{2\pi r}}\cos \frac{1}{2}\theta \left( {1\!+\!\sin \frac{1}{2}\theta \sin \frac{3}{2}\theta } \right) , \nonumber \\ \sigma _{12} (r,\theta )&= \sigma _{21} (r,\theta )\!=\!\frac{K_I^{||} }{\sqrt{2\pi r}}\cos \frac{1}{2}\theta \cos \frac{3}{2}\theta , \end{aligned}$$

(36)

$$\begin{aligned} H_{11} (r,\theta )&= -\!\frac{d_{21} K_I^{||} }{\sqrt{2\pi r}}\sin \theta \left( {2\sin \frac{3}{2}\theta \!+\!\frac{3}{2}\sin \theta \cos \frac{5}{2}\theta } \right) , \nonumber \\ H_{22} (r,\theta )&= \frac{d_{21} K_I^{||} }{\sqrt{2\pi r}}\frac{3}{2}\sin ^{2}\theta \cos \frac{5}{2}\theta , \nonumber \\ H_{12} (r,\theta )&= \!-\!\frac{d_{21} K_I^{||} }{\sqrt{2\pi r}}\frac{3}{2}\sin ^{2}\theta \sin \frac{5}{2}\theta , \nonumber \\ H_{21} (r,\theta )&= \frac{d_{21} K_I^{||} }{\sqrt{2\pi r}}\sin \theta \left( {2\cos \frac{3}{2}\theta \!-\!\frac{3}{2}\sin \theta \sin \frac{5}{2}\theta } \right) , \end{aligned}$$

(37)

where

$$\begin{aligned} d_{21} =\frac{R\left( {K_1 -K_2 } \right) }{4\left( {MK_1 -R^{2}} \right) }, \end{aligned}$$

$$\begin{aligned} K_I^\parallel =\mathop {\lim }\limits _{r\rightarrow 0} \sqrt{2\pi r}\sigma _{22} (r,0), \end{aligned}$$

(38)

in which $M=(c_{11} -c_{12} )/2.$

However, the phason stress field arises due to the coupling relationship between the phonon and the phason fields despite a pure phonon load. For the Griffith crack with the length 2$a$ under a uniform phonon tension $p$, the stress ahead of the crack-tip is given as

$$\begin{aligned} \sigma _{22} (x_1 ,0)=p\left( {\frac{x_1 }{\sqrt{x_1^2 -a^{2}}}-1} \right) . \end{aligned}$$

Substituting the Griffith stress into the definition of the phonon stress intensity factor (38), one arrives at

$$\begin{aligned} K_I^\parallel =p\sqrt{\pi a}. \end{aligned}$$

(39)

The generalized stresses $H_{ij}$ have not been considered so far. Therefore, we are not able to prescribe a finite value of these quantities. However, it has been shown by Fan (2011) that the singularity of generalized stresses around the crack-tip also exhibits the square-root if the considered cracked body is under a pure phason load. Therefore, one can define in a similar manner the stress intensity factor for phason stresses as

$$\begin{aligned} K_I^\bot =\mathop {\lim }\limits _{r\rightarrow 0} \sqrt{2\pi r}H_{22} (r,0). \end{aligned}$$

(40)

The phonon stress intensity factor for the Griffith crack is identical with the stress intensity factor for crystals and it follows from Eq. (39) that is independent on material parameters. Also the phonon stresses (36) are independent on material parameters. However, the phason stresses (37) are dependent on the material parameters expressed by $d_{21}$. The phonon displacement field at the crack-tip vicinity is strongly related to the material parameters, like in conventional linear elastic fracture mechanics for crystals. Li et al. (1999) derived the phonon displacement on the faces of the Griffith crack as

$$\begin{aligned} u_2 (x_1 ,0)\!=\!\frac{p}{2}\left( {\frac{K_1 }{MK_1 \!-\!R^{2}}\!+\!\frac{1}{L\!+\!M}} \right) \sqrt{a^{2}\!-\!x_1^2 }, \end{aligned}$$

(41)

where $L=c_{12}.$

Similarly, the strain energy and the energy release rate are dependent on all material parameters related to the quasicrystal as it has been shown by Fan et al. (2012) for the Griffith crack. Therefore, strictly speaking, the quantitative conclusions in LEFM (without any phason material characteristics) cannot be directly applied to quasicrystal linear elastic fracture mechanics (QLEFM). Of course, if the coupling constant $R$ is so small that it can be ignored, the above results reduce to the well known results in LEFM.

4 Numerical examples

4.1 A central crack in a finite strip

In the first example a straight central crack in a finite quasicrystal strip under a pure phonon load is analyzed (Fig. 1). The strip is subjected to a stationary or impact mechanical load with Heaviside time variation and the intensity $\sigma _0 =1\,\mathrm{Pa}$ on the top-side of the strip. The material coefficients of the strip correspond to Al–Ni–Co quasicrystal and they are given by

$$\begin{aligned}&c_{11}\!=\!L\!+\!2M\!=\!23.43\!\times \!10^{10}\,\mathrm{Nm}^{\!-\!2} ,\\&c_{12}\!=\!L\!=\!5.74\!\times \!10^{10}\,\mathrm{Nm}^{\!-\!2} ,\quad K_1\!=\!12.2\!\times \!10^{10}\,\mathrm{Nm}^{-2} , \\&K_2\!=\!2.4 \times 10^{10}\,\mathrm{Nm}^{\!-\!2} ,\quad M\!=\!(c_{11} \!-\!c_{12} )/2, \\&\rho \!=\!4180\,\mathrm{kg/m}^{3} ,\quad \Gamma _w\!=\!4.8\times 10^{-19}\,\mathrm{m}^{3}\,\mathrm{s/kg}. \\ \end{aligned}$$

The crack-length $2a=1.0\,\mathrm{m}$, crack-length to strip-width ratio $a/w=0.4$, and strip-height $h=1.2w$ are considered. Due to the symmetry of the problem with respect to the crack-line as well as vertical central line, only a quarter of the strip is numerically analyzed. Both phonon and phason displacements in the quarter of the strip are approximated by using 930 (31$\times$30) nodes equidistantly distributed. The local subdomains are considered to be circular with a radius $r_{loc} =0.033\,\mathrm{m}$.

Fig. 1

Central crack in a finite quasicrystal strip

Note that formally it is no problem to apply also phason loading, but we do not it because the measurement of such loads on body surfaces is still not solved successfully.

Numerical results for the phonon displacement $u_2$ along the crack-face for various coupling parameter $R$ are given in Fig. 2. For the case of vanishing coupling parameter, $R/M = 0$, we obtain phonon displacements corresponding to conventional elasticity. One can observe a good agreement between the FEM and present MLPG results for this special case. The results reveal that the phonon crack-opening-displacements increase with increasing value of the coupling parameter. The variation of the phason displacements along the crack is presented in Fig. 3. It shows that the phason displacements are strongly dependent on the coupling parameter if the strip is under a pure phonon load. For vanishing value of the coupling parameter, the phason displacement should be zero. The stress intensity factor is computed by using equation (38) and the extrapolation technique from stresses ahead of the crack-tip with a finite distance. Numerical results for different values of the coupling parameter are given in Table 1. The stress intensity factor is increasing with increasing value of the coupling parameter.

Fig. 2

Variations of the phonon displacement on the crack-face with the normalized coordinate $x_1 /2a$ for a pure phonon load $\sigma _0 =1\,\mathrm{Pa}$

Fig. 3

Variations of the phason displacement on the crack-face with the normalized coordinate $x_1 /2a$ for a pure phonon load $\sigma _0 =1\,\mathrm{Pa}$

Table 1 Influence of the coupling parameter on the stress intensity factor

Recently, the experimental measurement of the phonon-phason coupling parameter for decagonal quasicrystals has been achieved and the considered Al-Ni-Co material has the value R $=$ 1.1 GPa, and it corresponds to R/M $=$ 0.012 (Fan 2011). Then, for the considered Al-Ni-Co quasicrystal, the coupling effect can be neglected as can be seen from Table 1 and Fig. 2. However, recent technological progress in quasicrystals affords also larger values of the coupling parameter in new quasicrystals with different chemical composition. The determination of the quasicrystal’s coefficients is related to the symmetry of the quasicrystals, which can be done by the group representation theory (Fan et al. 2012). This offers a rather wide range of elastic coefficients for various quasicrystals. Therefore, we have considered also larger values of the ratio R/M in our performed numerical analyses to show the influence of the coupling parameter on the crack-opening-displacement and the stress intensity factor.

In the next example, we analyze the same cracked strip under an impact load with Heaviside time variation $\sigma _0 H(t-0)$. The normalized stress intensity factor corresponding to the Bak’s model is compared with the FEM results in Fig. 4 for conventional elasticity, i.e., $R/M = 0$. The time variable is normalized as $c_L \tau /h$, where $c_L =\sqrt{c_{11} /\rho }$ is the velocity of longitudinal wave. One can observe that the stress intensity factor for a finite value of the coupling parameter is only slightly larger than the corresponding factor in conventional elasticity. The peak value is shifted to larger time instants for cracks in quasicrystals. We have selected the time-step $\Delta \tau =0.25\times 10^{-4}\,\mathrm{s}$ in our numerical analyses.

Fig. 4

Temporal variation of the normalized SIF for the central crack in a strip under an impact load according to the Bak’s model

In order to investigate the effect of the slow relaxation of phason strains, we have applied also the elasto-hydrodynamic model and the numerical results for the normalized SIF calculated are presented in Fig. 5. Three different values of the diffusion coefficient $D$ are considered in our numerical analyses to investigate its influence on the time variation of the SIF. With the increasing value of the diffusion coefficient, the stress intensity factor is decreasing and the peak value is shifted to earlier time instants.

Fig. 5

Temporal variation of the normalized SIF for the central crack in a strip under an impact load according to the elasto-hydrodynamic model

The stress intensity factors computed according to the Bak’s and the elasto-hydrodynamic model are compared in Fig. 6. One can see that the peak values are slightly larger in the Bak’s model. The peak values in the elasto-hydrodynamic model are shifted to earlier time instants.

Fig. 6

Comparison of normalized SIFs for the central crack in a strip under an impact load computed by the Bak’s and the elasto-hydrodynamic model

4.2 An edge crack in a finite strip

An edge crack in a finite strip is analyzed in the second example. The following geometrical parameters are considered: $a=0.5, a/w=0.4$ and $h/w=1.2$. Due to the symmetry with respect to $x_1$ only a half of the strip is modeled. We have used 930 nodes equidistantly distributed for the MLS approximation of the physical fields. On the top of the strip a uniform impact tension $\sigma _0 =1\,\mathrm{Pa}$ is applied.

Numerical results for the phonon and phason displacements along the crack-face for various coupling parameter $R$ are given in Figs. 7 and 8. The phonon displacement for a finite value of the coupling parameter is larger than the corresponding displacement in conventional elasticity. The stress intensity factor normalized to that in conventional elasticity is equal to $K_I^\parallel /\sigma _0 \sqrt{\pi a}=2,108$.

Fig. 7

Variations of the phonon displacement on the edge crack with the normalized coordinate $x_1 /2a$ for a pure phonon load $\sigma _0 =1\,\mathrm{Pa}$

Fig. 8

Variations of the phason displacement on the edge crack with the normalized coordinate $x_1 /2a$ for a pure phonon load $\sigma _0 =1\,\mathrm{Pa}$

We have analyzed the same cracked strip also under an impact load with the Heaviside time variation $\sigma _0 H(t-0)$ (Fig. 9).

Fig. 9

Temporal variations of the normalized SIFs for the edge crack in a strip under an impact load

For a phonon mechanical load, we have obtained $K_I^{stat} =2.642\,\text{ Pa }\,\text{ m }^{1/2}$ in stationary case for the corresponding crystal with vanishing coupling parameter. Similarly to the central crack, the peak values for the quasicrystal exceed those for the corresponding crystal and they are shifted to later time instants. One can see a good agreement of the FEM and MLPG results for conventional elasticity. The dynamic stress intensity factor is about two times larger than the corresponding static SIF.

5 Conclusions

A reliable meshless computational method has been developed for general crack problems in finite-size quasicrystals. Both the static and transient dynamic boundary value problems are analyzed. The coupled governing partial differential equations are satisfied in a weak-form on small virtual subdomains. The Heaviside step function as the test function is applied to derive local boundary-domain integral equations. The subdomains are considered as circles centred at nodal points randomly distributed over the analyzed domain. After performing the spatial MLS approximation, a system of ordinary differential equations for certain nodal unknowns is obtained.

The present dynamic fracture study is based on the Bak’s and elasto-hydrodynamic models. The influences of the coupling parameter and diffusion constant in the elasto-hydrodynamic model on the temporal variation of the stress intensity factor have been shown. A similar behaviour of the normalized stress intensity factors has been observed for the central and edge crack problems. The stress intensity factors for the static loading case are the same in both the Bak’s and the elasto-hydrodynamic models. However, they are different for the dynamic loading case in both models.