1 Introduction

Composition of functionally graded materials (FGMs) varies from one surface to another. Because of low coefficients of thermal expansion and low thermal conductivity, FGMs have a high capability for applications with thermal and mechanical loads [1, 2].

The nonlinear dynamic analysis has been an interesting subject of research in solid mechanics. Several researches have been carried out on nonlinear analysis in shell, cylinder, annular plates etc. using numerical or analytical methods.

Alwar and Reddy [3] employed von Karman’s large deflection plate theory to obtain the non-linear static and dynamic response of isotropic and orthotropic annular plates. Analysis of the large deflection bending of annular plates with variable thickness is presented by Reddy and Huang [4] using von Karman theory and finite element method. Large deflection axisymmetric response analyses of cylindrically orthotropic thin annular plates resting on annular elastic foundations are presented by Dumir [5] using Hamilton’s principle and von Karman theory. Srinivasanan and Ramachandra [6] used the finite element method to solve the large deflection bending of annular and circular bimodulus plates using the method of minimizing potential energy, finite element and Newton–Raphson iterative procedure. Shiue [7, 8] employed boundary element method and sub-element technique to obtain the geometrically nonlinear displacement and stress of a thick cylinder. Woo and Meguid [9] analyzed large deflection of functionally graded plates and shells under transverse mechanical loads and a temperature field using von Karman theory and Fourier series solution. A geometrically nonlinear analysis of functionally graded shells was presented by Arciniega and Reddy [10, 11] using tensor-based finite element formulation with curvilinear coordinates and first-order shear deformation theory. Owatsiriwong and Park [12] presented boundary element method for dynamic elastic and elastoplastic analyses using Houbolt time integration scheme and Newton–Raphson method. Zhao and Liew [13] studied the nonlinear response of functionally graded ceramic–metal shell panels under mechanical and thermal loading. They considered a modified version of Sander’s nonlinear shell theory and von Karman relations. They employed arc-length method, combined with the modified Newton–Raphson method. Sepahi et al. [14] analyzed large deflection of annular FGM plates on nonlinear elastic foundation under thermo-mechanical load with nonlinear von Karman assumptions using differential quadrature method. Liao-Liang et al. [15] studied the nonlinear vibration of FG beams using Galerkin method. Zhang et al. [16] used the perturbation method to investigate the nonlinear dynamics of a FG plate. They employed the Hamilton’s principle and the Galerkin method in their analysis. Zhang et al. [17] presented an analysis on the nonlinear dynamics of a FGM circular cylindrical shell based on the first-order shear deformation shell theory and von Karman relations using finite element method. Large deformation of transversely isotropic elastic thin circular disk in rotation was analyzed by Akinola et al. [18]. Upadhyay and Shukla [19] studied geometrically nonlinear static and dynamic behavior of FG skew plates using von-Karman’s nonlinear relations, Chebyshev series and Houbolt’s method. Arefi [20] studied the nonlinear thermoelastic analysis of thick-walled functionally graded piezoelectric cylinder. He solved the governing nonlinear differential equations using an analytical method. Dong et al. [21] perused nonlinear vibration of the FG cylindrical shell based on Reddy’s third-order plates and shell theory using finite element method. The nonlinear free vibration behavior of a laminated composite spherical shell under uniform thermal loading was investigated by Panda and Mahapatra [22] based on Green–Lagrange relations, finite element model and Hamilton’s principle. Zhang et al. [23] used total Lagrangian particle method for the large deformation analyses of solids and curved shells. Borboni and Santis [24] investigated the large deflection of a non-linearelastic beam using a numerical algorithm and finite element method. The transient large deformation of a geometrically nonlinear rectangular plate subjected to a moving mass was analyzed by Enshaeian and Rofooei [25] using the von Karman plate theory and Lagrange method. Shegokar and Lal [26] obtained the large amplitude vibration of FG piezoelectric beams based on von-Karman nonlinear strain kinematics and finite element method.

Also some researchers investigated nonlinear analysis using meshless methods specially MLPG that proposed by Atluri and Zhu [27] at first. Recently, Sladek et al. [28] presented a nice review on the applications of the MLPG method in Engineering and Sciences problems including nonlinear analysis.

Xiong et al. [29] employed MLPG method to solve the geometrically nonlinear problem using an incremental and iterative solution procedure. MLPG method is examined by Xiong et al. [30] to solve the elasto-plasticity problem using the incremental tangent stiffness method. Zhang et al. [31] analyzed large deformation of hyperelastic and elasto-plastic solids based on the MLPG method. Soares et al. [32] proposed a time-domain MLPG formulation for the dynamic analysis of nonlinear porous media. They solved the governing equations using Newmark and Newton–Raphson techniques. In another work [33], they applied meshless local Petrov–Galerkin formulations considering a time-marching scheme based on implicit Green’s functions to solve linear and nonlinear dynamic 2D problems. Also MLPG method was applied by them [34] for the dynamic analysis of nonlinear problems considering elastic and elastoplastic materials. Wang and Sun [35] formulated a Galerkin mesh free approach for geometrically nonlinear analysis of plates with large deflection. Moosavi and Khelil [36] performed isogeometric meshless finite volume for three-dimensional large deformation analysis in nonlinear elasticity.

Recently, some papers have been published to solve a hyper-elastic FG thick hollow cylinder under a mechanical load using MLPG method. Ghadiri Rad et al. [37] analyzed the large deflection analysis of a functionally graded thick hollow cylinder with Rayleigh damping using MLPG method. They considered the hyper-elastic neo-Hookean model for the cylinder. Also in another research [38], they obtained the displacements and stresses in hyper-elastic FG thick hollow cylinder using MLPG method.

In the literature, most of the previous researches have considered the nonlinear transient analysis of thin cylinder or other structures such as plate and beam using numerical or analytical method such as finite element method, MLPG, etc.

In this research, linear and nonlinear transient analysis is investigated in a FG thick hollow infinite length cylinder that is subjected to an impact loading. The analysis is conducted for a plane strain condition where a one dimensional grading patterns is assumed. The meshless local Petrov–Galerkin method and considering the Heaviside step function as the test function are employed. The total Lagrangian formulation is used as well. Also moving least square shape functions are used for the approximation of the displacement field in the weak form of the equation of motion. The mechanical properties of FG cylinder are assumed to be variable in the radial direction in terms of the volume fraction as power function. The time history of the nonlinear radial displacement and stress are discussed in details for various values of the power law exponent and different radius. Also, the effects of thickness value, loading types and the duration of loading on the dynamic behaviors of displacement and stress fields are obtained and discussed in details.

2 Meshless local Petrov–Galerkin method formulation and governing equations

In MLPG method formulation, \( {}^{t}\varOmega \), \( \partial \varOmega \), n and V are the domain of quadrature, internal boundary of the quadrature domain, unit outward normal vector on the boundary in the current configuration and weight or test function, respectively. Also \( {}^{t}\varGamma_{qi} \) is the internal boundary of the domain, \( {}^{t}\varGamma_{qu} \) is the part of the natural boundary that intersects the quadrature domain, and \( {}^{t}\varGamma_{q\tau } \) is the part of the essential boundary that intersects the quadrature domain [39].

Approximation of the displacement field in the sub-domain can be interpolated, at point r as:

$$ \begin{aligned} {\text{u}}_{\text{r}} ({\text{r}},{\text{t}}) & = {\upvarphi }({\text{r}}){\hat{\text{u}}}_{\text{r}} ({\text{t}}) = \sum\limits_{{{\text{a}} = 1}}^{\text{N}} {{\upvarphi }^{\text{a}} ({\text{r}})} {\hat{\text{u}}}_{\text{r}}^{\text{a}} ({\text{t}}) \\\updelta{\text{u}}_{\text{r}} ({\text{r}},{\text{t}}) & = {\upvarphi }({\text{r}})\updelta\,{\hat{\text{u}}}_{\text{r}} ({\text{t}}) = \sum\limits_{{{\text{a}} = 1}}^{\text{N}} {{\upvarphi }^{\text{a}} ({\text{r}})\,\updelta} {\hat{\text{u}}}_{\text{r}}^{\text{a}} ({\text{t}}) \\ \end{aligned} $$
(1)

where

$$ \begin{aligned} {\hat{\text{u}}}_{\text{r}}^{\text{T}} ({\text{t}}) & = \left[ {\begin{array}{*{20}c} {{\text{u}}_{\text{r}}^{2} ({\text{t}})} & {{\text{u}}_{\text{r}}^{2} ({\text{t}})} & \ldots & {{\text{u}}_{\text{r}}^{\text{N}} ({\text{t}})} \\ \end{array} } \right] \\\updelta{\hat{\text{u}}}_{\text{r}}^{\text{T}} ({\text{t}}) & = \left[ {\begin{array}{*{20}c} {\updelta{\text{u}}_{\text{r}}^{1} ({\text{t}})} & {\updelta{\text{u}}_{\text{r}}^{2} ({\text{t}})} & \ldots & {\updelta{\text{u}}_{\text{r}}^{\text{N}} ({\text{t}})} \\ \end{array} } \right] \\ \end{aligned} $$
(2)

Equations (1) can be rewritten as:

$$ \begin{aligned} {\text{U}}({\text{r}}) & = \{ {\hat{\text{u}}}_{\text{r}} ({\text{r}},{\text{t}})\}^{\text{T}} \\\updelta{\text{U}}({\text{r}}) & = \{\updelta{\hat{\text{u}}}_{\text{r}} ({\text{r}},{\text{t}})\}^{\text{T}} \\ \end{aligned} $$
(3)

where N denotes the total number of nodes in the support domain \( \varOmega_{s} \) that is independent of the quadrature domain. \( \varphi^{a} \) is the MLS shape function for node “a” that is created in the support domain \( \varOmega_{s} \) of point r, \( {\hat{\text{u}}}^{a} \) are the nodal parameters of displacement components in the r direction.

The shape function and the set of the radial basis functions are defined as:

$$ \begin{aligned}\upphi^{\text{T}} ({\text{r}}) & = {\text{R}}^{\text{T}} ({\text{r}}){\text{R}}_{\text{O}}^{ - 1} \\ \left| {\text{r}} \right|^{2} & = \left| {{\text{r}} - {\text{r}}_{\text{I}} } \right|^{2} \\ {\text{R}}^{\text{T}} ({\text{r}}) & = \left[ {\begin{array}{*{20}c} {{\text{R}}_{1} ({\text{r}})} & {{\text{R}}_{2} ({\text{r}})} & \ldots & {{\text{R}}_{\text{N}} ({\text{r}})} \\ \end{array} } \right] \\ \end{aligned} $$
(4)

where

$$ \begin{aligned} {\text{R}}_{\text{O}} & = \left[ {\begin{array}{*{20}c} {{\text{R}}_{1} ({\text{r}}_{1} )} & {{\text{R}}_{2} ({\text{r}}_{1} )} & \ldots & {{\text{R}}_{\text{N}} ({\text{r}}_{1} )} \\ {{\text{R}}_{1} ({\text{r}}_{2} )} & {{\text{R}}_{2} ({\text{r}}_{2} )} & \ldots & {{\text{R}}_{\text{N}} ({\text{r}}_{2} )} \\ \ldots & \ldots & \ldots & \ldots \\ {{\text{R}}_{1} ({\text{r}}_{\text{N}} )} & {{\text{R}}_{2} ({\text{r}}_{\text{N}} )} & \ldots & {{\text{R}}_{\text{N}} ({\text{r}}_{\text{N}} )} \\ \end{array} } \right] \\ {\text{R}}_{\text{I}} ({\text{r}}) & = \left( {|{\text{r}} - {\text{r}}_{{_{\text{I}} }} |^{2} - {\text{c}}^{2} } \right)^{{\frac{\text{m}}{2}}} ,\quad {\text{I}} = 1,2,3, \ldots ,{\text{N}} \\ \end{aligned} $$
(5)

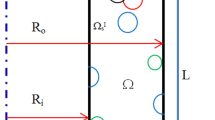
The motion of the cylinder is shown in Fig. 1. To obtain the displacements, the equation of motion in polar system is described as:

$$ \upsigma_{{{\text{r}},{\text{r}}}} + \frac{1}{\text{r}}(\upsigma_{\text{r}} -\upsigma_{\uptheta} ) + {\text{X}}_{\text{r}} =\uprho{\ddot{\text{u}}}_{\text{r}} $$
(6)

where \( {\ddot{{u}}}_{r} \) is the acceleration vector.

Fig. 1
figure 1

Motion of the cylinder

Full size image

To solve the governing Eqs. (6) in the axisymmetric cylinder we consider the local weak form of those equations in the current configuration \( {}^{t}\varOmega \) over intersecting sub-domains which is expressed by the following relations [40]:

$$ \int_{{{}^{\text{t}}\Omega }}^{{}} {\left[ {\upsigma_{{{\text{r}},{\text{r}}}} + \frac{1}{\text{r}}(\upsigma_{\text{r}} -\upsigma_{\uptheta} ) -\uprho{\ddot{\text{u}}}_{\text{r}} } \right]{\text{V}}_{\text{r}} {\text{d}}\Omega } = 0 $$
(7)

where V r is the test or weight function.

Considering axisymmetric problems, the sub-domains are:

$$ {\text{d}}\Omega = 2\uppi{\text{r}}\,{\text{d}}\Omega_{\text{q}} $$
(8)

Therefore

$$ \int_{{{}^{\text{t}}\Omega }}^{{}} {{\text{r}}\left[ {\upsigma_{{{\text{r}},{\text{r}}}} + \frac{1}{\text{r}}(\upsigma_{\text{r}} -\upsigma_{\uptheta} ) -\uprho{\ddot{\text{u}}}_{\text{r}} } \right]{\text{V}}_{\text{r}} {\text{d}}\Omega_{\text{q}} } = 0 $$
(9)

Essential and natural boundary conditions are:

$$ \left\{ {\begin{array}{*{20}l} {{\text{u}} = {\text{u}}_{\text{r}}^{*} } \hfill & {{\text{r}} \in {}^{\text{t}}\Gamma_{\text{u}} } \hfill \\ {\uptau = \upsigma_{\text{ij}} \,{\text{n}}_{\text{j}} =\uptau_{\text{r}}^{*} } \hfill & {{\text{r}} \in {}^{\text{t}}\Gamma_{\uptau} } \hfill \\ \end{array} } \right. $$
(10)

Because the problem is axisymmetric, each physical field depends on the radial and axial coordinate. Applying Gauss divergence theorem to Eq. (9) we have:

$$ \begin{aligned} \int_{{{}^{\text{t}}\Gamma_{\text{qu}} }}^{{}} {{\text{r}}\upsigma_{\text{r}} \,{\text{n}}_{\text{r}} {\text{V}}_{\text{r}} {\text{d}}\Gamma } + \int_{{{}^{\text{t}}\Gamma_{\text{qi}} }}^{{}} {{\text{r}}\upsigma_{\text{r}} \,{\text{n}}_{\text{r}} {\text{V}}_{\text{r}} {\text{d}}\Gamma } - \int_{{{}^{\text{t}}\Omega_{\text{q}} }}^{{}} {\left[ {{\text{r}}\upsigma_{\text{r}} {\text{V}}_{{{\text{r}},{\text{r}}}} +\upsigma_{\uptheta} {\text{V}}_{\text{r}} } \right]{\text{d}}\Omega } \hfill \\ \quad - \int_{{{}^{\text{t}}\Omega_{\text{q}} }}^{{}} {\uprho{\text{r}}{\ddot{\text{u}}}_{\text{r}} \,{\text{V}}_{\text{r}} {\text{d}}\Omega } + \int_{{{}^{\text{t}}\Gamma_{{{\text{q}}\uptau}} }}^{{}} {{\text{r}}\uptau_{\text{r}}^{*} {\text{V}}_{\text{r}} {\text{d}}\Gamma } = 0 \hfill \\ \end{aligned} $$
(11)

The governing Eq. (11) in matrix form can be given as:

$$ \int_{{{}^{\text{t}}\Gamma_{\text{qu}} }}^{{}} {{\text{rVn}}\upsigma{\text{d}}\Gamma } + \int_{{{}^{\text{t}}\Gamma_{\text{qi}} }}^{{}} {{\text{rVn}}\upsigma{\text{d}}\Gamma } - \int_{{{}^{\text{t}}\Omega_{\text{q}} }}^{{}} {{\text{W}}\upsigma{\text{d}}\Omega } - \int_{{{}^{\text{t}}\Omega_{\text{q}} }}^{{}} {{\text{rV}}\uprho{\ddot{\text{u}}}{\text{d}}\Omega } + \int_{{{}^{\text{t}}\Gamma_{{{\text{q}}\uptau }} }}^{{}} {{\text{rV}}\uptau^{*} {\text{d}}\Gamma } = 0 $$
(12)

where

$$ {\text{W}} = \left[ {{\text{rV}}_{{{\text{r}},{\text{r}}}} \quad {\text{V}}_{\text{r}} } \right],\quad {\text{V}} = \left[ {{\text{V}}_{\text{r}} \quad 0} \right],\quad {\text{n}} = \left[ \begin{aligned} {\text{n}}_{\text{r}} \quad 0 \hfill \\ 0\quad 0 \hfill \\ \end{aligned} \right],\quad\upsigma = \{\upsigma_{\text{r}} ,\upsigma{}_{\uptheta}\}^{\text{T}} ,\quad\uptau^{*} = \{\uptau_{\text{r}}^{*} \}^{\text{T}} $$
(13)

The Green-Lagrangian strain relations and the incremental strain components in polar system are defined as follows [41]:

$$ \begin{aligned}\upvarepsilon_{\text{r}} & = {\text{u}}_{{{\text{r}},{\text{r}}}} + \frac{1}{2}({\text{u}}_{{{\text{r}},{\text{r}}}} )^{2} \hfill \\\upvarepsilon_{\uptheta} & = \frac{1}{\text{r}}({\text{u}}_{\text{r}} ) + \frac{1}{{2{\text{r}}^{2} }}({\text{u}}_{\text{r}} )^{2} \hfill \\ \end{aligned} $$
(14)
$$ \begin{aligned} \updelta \upvarepsilon_{\text{r}} = (1 + {\text{u}}_{{\text{r}},{\text{r}}} )\updelta {\text{u}}_{{\text{r}},{\text{r}}} \hfill \\ \updelta \upvarepsilon_{\uptheta } = \frac{1}{{\text{r}}}\left(1 + \frac{{{\text{u}}_{{\text{r}}}}}{{\text{r}}}\right)\updelta {\text{u}}_{{\text{r}}} \hfill \\ \end{aligned} $$
(15)

Relation between the Cauchy stress σ and the second Piola–Kirchhoff stress S can be defined as:

$$ \upsigma = {\text{J}}^{ - 1} {\text{FSF}} $$
(16)

where J and F are the deformation gradient determinant and the deformation gradient respectively.

Equations (15) can be rewritten as [42]:

$$ \begin{aligned}\updelta \upvarepsilon _{\text{r}} = {\text{F}}_{11}\updelta{\text{u}}_{{{\text{r}},{\text{r}}}} \hfill \\\updelta \upvarepsilon _{\uptheta} = \frac{1}{\text{r}}{\text{F}}_{22}\updelta{\text{u}}_{\text{r}} \hfill \\ \end{aligned} $$
(17)

where

$$ {\text{F}} = \left[ {\begin{array}{*{20}l} {1 + {\text{u}}_{{{\text{r}},{\text{r}}}} } \hfill & 0 \hfill \\ 0 \hfill & {1 + \frac{{{\text{u}}_{\text{r}} }}{\text{r}}} \hfill \\ \end{array} } \right] $$
(18)

The following incremental relation represents stress vector in terms of strain vector:

$$ \updelta{\text{S}} = {\text{C}}\updelta \upvarepsilon $$
(19)

where C is the material response tensor:

$$ {\text{C}} = \frac{\text{E}}{{(1 +\upnu)(1 - 2\upnu)}}\left[ \begin{array}{ll} 1 -\upnu&\quad\upnu \hfill \\\upnu&\quad 1 -\upnu \hfill \\ \end{array} \right] $$
(20)

and

$$ \updelta \upvarepsilon = \{\updelta \upvarepsilon _{\text{r}} ,\updelta \upvarepsilon {}_{\uptheta}\}^{\text{T}} $$
(21)

Because the current configuration is unknown, the total Lagrangian formulation, which transfers the current configuration to the undeformed configuration, is used.

Moreover in the total Lagrangian formulation all variables are related to the initial configuration at time 0.

We have

$$ \upsigma{\text{n}}\,{\text{d}}{}^{\text{t}}\Gamma = {\text{FSN}}\,{\text{d}}{}^{0}\Gamma $$
(22)
$$ \uprho = {\text{J}}{}^{0}\uprho $$
(23)

where \( {}^{0}\varGamma \), N and \( {}^{0}\rho \) are, respectively, the boundary, unit outward normal vector on the boundary and the density in the initial configuration at time t = 0.

Therefore the equation of motion (12) can be rewritten as:

$$ \int_{{{}^{0}\Gamma_{\text{qu}} }}^{{}} {{\text{rVNFSd}}\Gamma } + \int_{{{}^{0}\Gamma_{\text{qi}} }}^{{}} {{\text{rVNFSd}}\Gamma } - \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{WFSd}}\Omega } - \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{rV}}{}^{0}\uprho{\ddot{\text{u}}}{\text{d}}\Omega } + \int_{{{}^{0}\Gamma_{{{\text{q}}\uptau}} }}^{{}} {{\text{rV}}{}^{0}\uptau_{{}}^{*} {\text{d}}\Gamma } = 0 $$
(24)

All variables at time \( t + \varDelta t \) are referred to the initial configuration at time 0 in the total Lagrangian formulation. Those variables are referred to the configuration at time t in the updated Lagrangian formulation [43].

Considering incremental relations for the problem geometric nonlinearity, we have:

$$ \begin{aligned} {}_{0}^{{{\text{t}} + \Delta {\text{t}}}} {\text{u}} = {}_{0}^{\text{t}} {\text{u}} +\updelta{\text{u}} \hfill \\ {}_{0}^{{{\text{t}} + \Delta {\text{t}}}} {\text{S}} = {}_{0}^{\text{t}} {\text{S}} +\updelta{\text{S}} \hfill \\ {}_{0}^{{{\text{t}} + \Delta {\text{t}}}} {\text{F}} = {}_{0}^{\text{t}} {\text{F}} +\updelta{\text{F}} \hfill \\ \end{aligned} $$
(25)

Substituting the incremental terms (25) into the local weak form of the equation of motion (24) leads to:

$$ \begin{aligned} \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{rV}}{}^{0}\uprho \updelta {\ddot{\text{u}}}{\text{d}}\Omega } - \int_{{({}^{0}\Gamma_{\text{qu}} + {}^{0}\Gamma_{\text{qi}} )}}^{{}} {{\text{rVNFC}}\updelta \upvarepsilon {\text{d}}\Gamma } + \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{WFC}}\updelta \upvarepsilon {\text{d}}\Omega } - \int_{{({}^{0}\Gamma_{\text{qu}} + {}^{0}\Gamma_{\text{qi}} )}}^{{}} {{\text{rVNS}}\updelta{\text{Fd}}\Gamma } + \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{WS}}\updelta{\text{Fd}}\Omega } \hfill \\ \quad = - \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{rV}}{}^{0}\uprho{\ddot{\text{u}}}{\text{d}}\Omega } + \int_{{({}^{0}\Gamma_{\text{qu}} + {}^{0}\Gamma_{\text{qi}} )}}^{{}} {{\text{rVNF}}{\bar{\text{S}}}{\text{d}}\Gamma } - \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{WF}}{\bar{\text{S}}}{\text{d}}\Omega } + \int_{{{}^{0}\Gamma_{{{\text{q}}\uptau}} }}^{{}} {{\text{rV}}{}^{0}\uptau_{{}}^{*} {\text{d}}\Gamma } \hfill \\ \end{aligned} $$
(26)

where

$$ {\bar{\text{S}}} = \{ {\text{S}}_{\text{r}} ,{\text{S}}{}_{\uptheta}\}^{\text{T}} $$
(27)

and \( {\bar{\text{S}}} \) is the 2nd Piola–Kirchhoff stress vector.

Substituting (1) in (26) we obtain the following system of non-linear equations:

$$ \begin{aligned} & \left( {\int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{rV}}{}^{0}{\uprho \upvarphi }{\text{d}}\Omega } } \right)\updelta{\ddot{\text{U}}} + \left( { - \int_{{({}^{0}\Gamma_{\text{qu}} + {}^{0}\Gamma_{\text{qi}} )}}^{{}} {{\text{rVNFCB}}^{\text{NL}} {\text{d}}\Gamma } + \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{WFCB}}^{\text{NL}} {\text{d}}\Omega } } \right. \\ & \left. {\quad - \int_{{({}^{0}\Gamma_{\text{qu}} + {}^{0}\Gamma_{\text{qi}} )}}^{{}} {{\text{rVNSB}}^{\text{L}} {\text{d}}\Gamma } + \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{WSB}}^{\text{L}} {\text{d}}\Omega } } \right)\updelta{\text{U}} = - \left( {\int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{rV}}{}^{0}{\uprho \upvarphi }{\text{d}}\Omega } } \right){\ddot{\text{U}}} \\ & \quad + \int_{{({}^{0}\Gamma_{\text{qu}} + {}^{0}\Gamma_{\text{qi}} )}}^{{}} {{\text{rVNF}}{\bar{\text{S}}}{\text{d}}\Gamma } - \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{WF}}{\bar{\text{S}}}{\text{d}}\Omega } + \int_{{{}^{0}\Gamma_{{{\text{q}}\uptau}} }}^{{}} {{\text{rV}}{}^{0}\uptau^{*} {\text{d}}\Gamma } \\ \end{aligned} $$
(28)

where

$$ {\text{B}}^{\text{NL}} = \left[ \begin{aligned} {\text{F}}_{11} {\upvarphi }_{{,{\text{r}}}} ({\text{r}}) \hfill \\ \frac{1}{\text{r}}{\text{F}}_{22} {\upvarphi }({\text{r}}) \hfill \\ \end{aligned} \right],\quad {\text{B}}^{\text{L}} = \left[ \begin{subarray}{l} {\upvarphi }_{{,{\text{r}}}} ({\text{r}}) \\ \frac{1}{\text{r}}{\upvarphi }({\text{r}}) \end{subarray} \right],\quad {\text{S}} = \left[ \begin{aligned} {\text{S}}_{\text{r}} \quad 0 \hfill \\ 0\quad {\text{S}}_{\uptheta} \hfill \\ \end{aligned} \right] $$
(29)

B L and B NL are linear and nonlinear strain–displacement transformation matrices, respectively.

The Heaviside unit step function is considered for test functions in each sub-domain:

$$ {\text{V}}({\text{r}},{\text{t}}) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{r}} \in \Omega_{\text{I}} } \hfill \\ 0 \hfill & {{\text{r}} \notin \Omega_{\text{I}} } \hfill \\ \end{array} } \right. $$
(30)

The nonlinear governing Eqs. (28) can be presented as Eq. (31) where M, K T and \( \bar{F} \) are the mass matrix, the tangent stiffness matrix and the external load vector, respectively [44]:

$$ {\text{M}}\updelta{\ddot{\text{U}}} + {\text{K}}^{\text{T}} \,\updelta{\text{U}} = {\bar{\text{F}}} $$
(31)

Also \( \delta{{U}} \) is the nodal incremental displacements vectors from time t to time \( t + \varDelta t \) and

$$ \begin{aligned} {\text{M}} & = \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{r}}{}^{0}{\uprho \upvarphi }{\text{d}}\Omega } \\ {\text{K}}^{\text{T}} & = - \int_{{({}^{0}\Gamma_{\text{qu}} + {}^{0}\Gamma_{\text{qi}} )}}^{{}} {{\text{rNFCB}}^{\text{NL}} {\text{d}}\Gamma } + \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{FCB}}^{\text{NL}} {\text{d}}\Omega } - \int_{{({}^{0}\Gamma_{\text{qu}} + {}^{0}\Gamma_{\text{qi}} )}}^{{}} {{\text{rNSB}}^{\text{L}} {\text{d}}\Gamma } + \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{SB}}^{\text{L}} {\text{d}}\Omega } \\ {\bar{\text{F}}} & = - \left( {\int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{rV}}{}^{0}{\uprho \upvarphi }{\text{d}}\Omega } } \right){{{\ddot{\text{U}}}}} + \int_{{({}^{0}\Gamma_{\text{qu}} + {}^{0}\Gamma_{\text{qi}} )}}^{{}} {{\text{rNF}}{\bar{\text{S}}}{\text{d}}\Gamma } - \int_{{{}^{0}\Omega_{\text{q}} }}^{{}} {{\text{F}}{\bar{\text{S}}}{\text{d}}\Omega } + \int_{{{}^{0}\Gamma_{{{\text{q}}\uptau }} }}^{{}} {{\text{r}}{}^{0}\uptau^{*} {\text{d}}\Gamma } \\ \end{aligned} $$
(32)

3 The Newmark and the Newton–Raphson iterations methods

The transient response of the system is calculated using the Newmark finite difference method [45].

We have:

$$ {\hat{\text{K}}}{}^{{{\text{t}} + \Delta {\text{t}}}}(\updelta{\text{U}}) = {}^{{{\text{t}} + \Delta {\text{t}}}}{\hat{\text{R}}} $$
(33)

where

$$ \begin{aligned} {\hat{\text{K}}} & = \left( {\frac{1}{{\upeta_{1} \Delta {\text{t}}^{2} }}} \right){\text{M}} + {\text{K}}^{\text{T}} \\ {}^{{{\text{t}} + \Delta {\text{t}}}}{\hat{\text{R}}} & = {}^{\text{t}}{\bar{\text{F}}} + {\text{M}}\left[ {\left( {\frac{1}{{\upeta_{1} \Delta {\text{t}}}}} \right){}^{\text{t}}({\dot{\text{U}}}) + \left( {\frac{1}{{2\upeta_{1} }} - 1} \right){}^{\text{t}}({{{\ddot{\text{U}}}}})} \right] \\ \end{aligned} $$
(34)

and the Newmark parameters, time step and the iterative variation are:

$$ \begin{aligned}\upeta_{2} & \ge 0.5 \\\upeta_{1} & \ge 0.25(0.5 +\upeta_{2} )^{2} \\ \Delta {\text{t}} & = {\text{t}}_{\text{N}} - {\text{t}}_{{{\text{N}} - 1}} \\ {}^{{{\text{t}} + \Delta {\text{t}}}}{\text{U}} & = {}^{\text{t}}{\text{U}} +\updelta{\text{U}} \\ \end{aligned} $$
(35)

The following relations are the new acceleration, velocity and displacement vectors at time \( t + \varDelta \,t \).

$$ \begin{aligned} {}^{{{\text{t}} + \Delta {\text{t}}}}(\updelta{{{\ddot{\text{U}}}}}) & = \left( {\frac{1}{{\upeta_{1} \Delta {\text{t}}^{2} }}} \right)(\updelta{\text{U}}) - \left( {\frac{1}{{\upeta_{1} \Delta {\text{t}}}}} \right){}^{\text{t}}({\dot{\text{U}}}) - \left( {\frac{1}{{2\upeta_{1} }} - 1} \right){}^{\text{t}}({{{\ddot{\text{U}}}}}) \\ {}^{{{\text{t}} + \Delta {\text{t}}}}({\dot{\text{U}}}) & = {}^{\text{t}}({\dot{\text{U}}}) + \Delta {\text{t}}(1 -\upeta_{2} ){}^{\text{t}}({{{\ddot{\text{U}}}}}) + (\upeta_{2} \Delta {\text{t}}){}^{{{\text{t}} + \Delta {\text{t}}}}({{{\ddot{\text{U}}}}}) \\ {}^{{{\text{t}} + \Delta {\text{t}}}}({\text{U}}) & = {}^{\text{t}}({\text{U}}) +\updelta{\text{U}} \\ \end{aligned} $$
(36)

The term \( \delta U \) is the incremental displacements vector at time t.

The nonlinear Eq. (33) can be solved by an incremental iterative procedure. In this research, the Newton–Raphson iterations [44] are applied at each time step. Therefore, incremental displacement from Eq. (33) is substituted into Eq. (31) at each time step. The residual force is not zero and must be corrected. Hence the iterations are continued until the incremental displacement vanishes.

We can suppose for (k + 1)th iteration:

$$ \begin{aligned} {}^{t + \Delta {\rm t}}U^{(k + 1)} = {}^{t + \Delta {\rm t}}U^{(k)} + {}^{t + \Delta {\rm t}}\Delta \updelta U^{(k + 1)} \hfill \\ {}^{t + \Delta {\rm t}}\updelta U^{(k + 1)} = {}^{t + \Delta {\rm t}}\updelta U^{(k)} + \Delta \updelta U^{(k + 1)} \hfill \\ \end{aligned} $$
(37)

Then the nonlinear Eq. (33) is rewritten and the responses at each iterative step may be computed.

We have:

$$ \begin{aligned} (\Delta\updelta{\text{U}})^{{({\text{k}} + 1)}} & = \left[ {({\hat{\text{K}}})^{{({\text{k}})}} } \right]^{ - 1} {\hat{\text{R}}}^{{({\text{k}})}} \\ {\hat{\text{R}}}^{{({\text{k}})}} & = {}^{\text{t}}{\bar{\text{F}}} - {\text{M}}\left[ {\left( {\frac{1}{{\upeta_{1} \Delta {\text{t}}^{2} }}} \right)\updelta{\text{U}}^{{({\text{k}})}} - \left( {\frac{1}{{\upeta_{1} \Delta {\text{t}}}}} \right){}^{\text{t}}{\dot{\text{U}}} - \left( {\frac{1}{{2\upeta_{1} }} - 1} \right){}^{\text{t}}{{{\ddot{\text{U}}}}}} \right] \\ \end{aligned} $$
(38)

where \( \varDelta\delta{{U}} \) is the correction to the displacement increment.

4 FG material properties and Boundary conditions

In the present analysis, the mechanical properties vary through the radial direction as follows [46]:

$$ {\text{P}} = ({\text{P}}_{\text{out}} - {\text{P}}_{\text{in}} )\left( {\frac{{{\text{r}} - {\text{r}}_{\text{in}} }}{{{\text{r}}_{\text{out}} - {\text{r}}_{\text{in}} }}} \right)^{\text{m}} +\, {\text{P}}_{\text{in}} $$
(39)

where P in , P out and m are mechanical properties such as elasticity modulus and mass density of inner and outer surfaces and power law exponent, respectively.

Poisson’s ratio is assumed to be constant. The cylinder is assumed to be made from a mixture of ceramic and metals and the material composition is continuously varied such that the inner surface of the cylinder is ceramic, whereas the outer surface is metal. As boundary conditions, the outer bounding surface of FG cylinder is assumed to be traction free and a dynamic pressure is considered to be applied on the inner bounding surface.

5 Results and discussions

The linear problem of expansion of a thick cylinder due to an internal pressure is solved by Owatsiriwong and Park [12] and Shariyat et al. [47]. To check the accuracy of linear simulation of the present study the similar conditions as employed by them are considered. Figure 2 shows a comparison of the time history of the linear radial displacement at the inner point with that of Ref. [12]. Also Fig. 3 shows a comparison of the time history of the linear radial stress at the middle point with that of Ref. [47]. A good agreement between these results is observed.

Fig. 2
figure 2

Time history of the linear radial displacement at the inner point of the thick hollow cylinder under uniform loading

Full size image
Fig. 3
figure 3

Time history of the linear radial stress at the middle point of the thickness of the FGM thick hollow cylinder under ramp loading

Full size image

For verifying the nonlinear results, first, the internal pressure is expressed as:

$$ \upsigma_{\text{r}} =\upsigma_{0} [1 - \exp ( - {\text{Ct}})] $$
(40)

where t is the time, σ 0 and C are 0.5 Psi and 106 1/s, respectively.

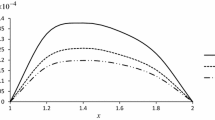
Equation (40) implies that the value of radial stress converges to a certain value in long time. It means that the behavior of displacement and stress fields should be converges to steady state values in both displacement and stress fields. The obtained results are compared with the data resulted from analysis of an geometrically nonlinear thick cylinder that was solved by Shiue [7, 8]. Figures 4 and 5 show the nonlinear radial displacement and stress along the radial direction, respectively. A good agreement can be found in these figures.

Fig. 4
figure 4

The nonlinear radial displacement along the radial direction

Full size image
Fig. 5
figure 5

The nonlinear radial stress along the radial direction

Full size image

As a next step, a functionally graded thick hollow cylinder is considered for nonlinear analysis with infinite length. The grading patterns are expressed as a nonlinear power law function. Inner and outer radii of FG cylinder are considered to be equal to r i  = 0.2 m and r o  = 0.4 m, respectively.

The cylinder is subjected to an sinusoidal internal pressure [48] expressed by:

$$ \upsigma_{\text{r}} = \left\{ {\begin{array}{*{20}l} {\upsigma_{0} \sin \left( {\frac{{\uppi{\text{t}}}}{{{\text{t}}_{0} }}} \right)} \hfill & {{\text{t}} \le {\text{t}}_{0} } \hfill \\ 0 \hfill & {{\text{t}} > {\text{t}}_{0} } \hfill \\ \end{array} } \right. $$
(41)

where σ 0 and t 0 are 10 MPa and 0.00015 s, respectively.

Elasticity modulus and density of inner and outer bounding surfaces are 380 GPa, 3800 kg/m3, 70 GPa and 2707 kg/m3, respectively. The proper time increment is assumed as \( \varDelta {\text{t}} = 10^{6} \,{\text{s}} \).

The time history of radial displacement and stress for the certain power law exponent (m = 0.1) at the midpoint of the cylinder (r = 0.3 m) are shown in Figs. 6, 7 and 8, respectively. In these figures numerical results obtained from the present study are compared for linear and nonlinear responses.

Fig. 6
figure 6

Time history of the linear and nonlinear radial displacement at the middle point before unloading for m = 0.1

Full size image
Fig. 7
figure 7

Time history of the linear and nonlinear radial displacement at the middle point after unloading for m = 0.1

Full size image
Fig. 8
figure 8

Time history of the linear and nonlinear radial stress at the middle point for m = 0.1

Full size image

The time history of the nonlinear radial displacement and stress for several radii with certain power law exponent are shown in Figs. 9 and 10. Also the time history of the nonlinear radial displacement and stress of all points of the thickness of the cylinder is illustrated in Figs. 11 and 12 for a better visualization. As it can be seen in these figures, the vibration amplitude decreases by moving from the inside surface to the outside surface. Also, the ceramic surface has a greater vibration amplitude with respect to the metal surface.

Fig. 9
figure 9

Time history of the nonlinear radial displacement at various radii under sinusoidal loading

Full size image
Fig. 10
figure 10

Time history of the nonlinear radial stress at various radii under sinusoidal loading

Full size image
Fig. 11
figure 11

Time history of the nonlinear radial displacement at all points of the thickness of the cylinder for m = 0.1

Full size image
Fig. 12
figure 12

Time history of the nonlinear radial stress at all points of the thickness of the cylinder for m = 0.1

Full size image

The time histories of the radial displacement and stress for the different power law exponents are shown in Figs. 13 and 14. The amplitude of vibration in the radial displacement and stress fields are increased when the value of power law exponent are decreased. As it is shown in these figures, the wave propagation velocity depends on the amount of the power law exponent. The frequency of vibration in radial displacement and stress fields are increased by increasing the value of power law exponent.

Fig. 13
figure 13

Time history of the nonlinear radial displacement at the middle point for various values of the power law exponent under sinusoidal loading

Full size image
Fig. 14
figure 14

Time history of the nonlinear radial stress at the middle point for various values of the power law exponent under sinusoidal loading

Full size image

The effects of various thicknesses of FG cylinder on dynamic behaviors of displacement and stress fields have been obtained and illustrated in Figs. 6, 7, 8, 15 and 16. It can be seen that there is no any significant differences between linear and nonlinear results for bigger thicknesses. The difference between linear and nonlinear results is increased by decreasing the thickness of FG cylinder. It means that the nonlinear analysis is taken into consideration for thin FG cylinder. Figures 17 and 18 show the time histories of radial displacement based on the linear and nonlinear analysis, which are obtained for various values of loading intensity. Also, the effect of loading duration on the linear and nonlinear dynamic behaviors of radial displacement and stress fields can be studied using Figs. 19, 20, 21 and 22. The amplitude of radial displacement vibration is decreased when the value of t 0 is increased.

Fig. 15
figure 15

Time history of the linear and nonlinear radial displacement at the middle point for h = 0.175 m under sinusoidal loading

Full size image
Fig. 16
figure 16

Time history of the linear and nonlinear radial stress at the middle point for h = 0.175 m under sinusoidal loading

Full size image
Fig. 17
figure 17

Time history of the linear radial displacement at the middle point for various values of the sinusoidal loading intensity (σ 0)

Full size image
Fig. 18
figure 18

Time history of the nonlinear radial displacement at the middle point for various values of the sinusoidal loading intensity (σ 0)

Full size image
Fig. 19
figure 19

Time history of the linear radial displacement at the middle point for different duration of sinusoidal loading

Full size image
Fig. 20
figure 20

Time history of the nonlinear radial displacement at the middle point for different duration of sinusoidal loading

Full size image
Fig. 21
figure 21

Time history of the linear radial stress at the middle point for different duration of sinusoidal loading

Full size image
Fig. 22
figure 22

Time history of the nonlinear radial stress at the middle point for different duration of sinusoidal loading

Full size image

To show the capability of the presented method for nonlinear analysis, various commonly used loadings (see Refs. [19] and [49]) are considered as dynamic pressure applied on inner bounding surface of the cylinder, which can be found as follows:

Case a:

$$ \upsigma_{\text{r}} = \left\{ {\begin{array}{*{20}l} {\upsigma_{0} \left( {1 - \frac{\text{t}}{{{\text{t}}_{0} }}} \right)\exp \left( { - \frac{{2{\text{t}}}}{{{\text{t}}_{0} }}} \right)} \hfill & {{\text{t}} \le {\text{t}}_{0} } \hfill \\ 0 \hfill & {{\text{t}} > {\text{t}}_{0} } \hfill \\ \end{array} } \right. $$
(42)

Case b:

$$ \upsigma_{\text{r}} = \left\{ {\begin{array}{ll} \upsigma_{0} \left( 1 - \frac{{\text{t}}}{{\text{t}}_{0}} \right) \hfill &\quad {\text{t}} \le {\text{t}}_{0} \hfill \\ 0 \hfill &\quad {\text{t}} \le {\text{t}}_{0} \hfill \\ \end{array}} \right.$$
(43)

Case c:

$$ \upsigma_{\text{r}} = \left\{ {\begin{array}{*{20}l} {\upsigma_{0} } \hfill & {{\text{t}} \le {\text{t}}_{0} } \hfill \\ 0 \hfill & {{\text{t}} > {\text{t}}_{0} } \hfill \\ \end{array} } \right. $$
(44)

Case d:

$$ \upsigma_{\text{r}} =\upsigma_{0} $$
(45)

where σ 0 and t 0 are 10 MPa and 0.00015 s, respectively.

Relations (42) to (45) represent exponential, triangular, rectangular and step loading, respectively. The obtained time histories of radial displacement and stress fields base on the presented loadings in Eqs. (42)–(45) (as case a–d) are illustrated in Figs. 23, 24, 25 and 26. The similar behaviors can be observed in these figures comparing to ones obtained from sinusoidal loading. It means that the presented meshless approach has a high capability for nonlinear analysis of FG cylinder subjected to various transient and dynamic loadings.

Fig. 23
figure 23

Time history of the linear radial displacement at the middle point under different loading for m = 0.1

Full size image
Fig. 24
figure 24

Time history of the nonlinear radial displacement at the middle point under different loading for m = 0.1

Full size image
Fig. 25
figure 25

Time history of the linear radial stress at the middle point under different loading for m = 0.1

Full size image
Fig. 26
figure 26

Time history of the nonlinear radial stress at the middle point under different loading for m = 0.1

Full size image

6 Conclusion

In the current study, the geometrically nonlinear transient analysis of FG cylinder is investigated using MLPG method and total Lagrangian formulations. The derived nonlinear equations are solved using the Newmark finite difference and Newton–Raphson methods in the time domain. To derive the descritized equations, the axisymmetry and plane strain conditions are assumed in the problem. The results indicate that the grading patterns of FG, thickness of cylinder and intensity and type of loading have important roles on the transient and dynamic behaviors of radial displacement and stress fields in nonlinear analysis. The dynamic behaviors of radial displacement and stress fields are studied in details for various kinds of dynamic loadings. Also, the effects of various parameters (such as the grading patterns of FG, thickness of cylinder and intensity) on the results are assessed for each type of loadings. It can be concluded that the presented meshless approach has a high capability for both linear and nonlinear dynamic analysis of FG structures.