Stochastic finite element nonlinear free vibration analysis of piezoelectric functionally graded materials beam subjected to thermo-piezoelectric loadings with material uncertainties

Abstract

In this paper, second order statistics of large amplitude free flexural vibration of shear deformable functionally graded materials (FGMs) beams with surface-bonded piezoelectric layers subjected to thermopiezoelectric loadings with random material properties are studied. The material properties such as Young’s modulus, shear modulus, Poisson’s ratio and thermal expansion coefficients of FGMs and piezoelectric materials with volume fraction exponent are modeled as independent random variables. The temperature field considered is assumed to be uniform and non-uniform distribution over the plate thickness and electric field is assumed to be the transverse components E _z only. The mechanical properties are assumed to be temperature dependent (TD) and temperature independent (TID). The basic formulation is based on higher order shear deformation theory (HSDT) with von-Karman nonlinear strain kinematics. A C ⁰ nonlinear finite element method (FEM) based on direct iterative approach combined with mean centered first order perturbation technique (FOPT) is developed for the solution of random eigenvalue problem. Comparison studies have been carried out with those results available in the literature and Monte Carlo simulation (MCS) through normal Gaussian probability density function.

1 Introduction

The FGMs are microscopic inhomogeneous anatomy ceramic and metal to continuous changes in their microstructures by the variation in compositions and structures gradually over volume in a preferred direction. Now a days, functionally graded material (FGM) is increasingly used due to the advantage of eliminating the interface problems due to smooth and continuous change of material properties from one surface. Due to above characteristics, it fulfills the specific demand in different engineering applications specially for working high temperature environment applications of heat exchanger tubes, thermal barrier coating for turbine blades, thermoelectric generators, furnace linings, electrically insulated metal ceramic joints, space/aerospace industries, automotive applications, biomedical etc. [1–3].

In the recent research and development, FGM structures with surface bonded thin piezoelectric layers at top and bottom have promised new design opportunities for future high performance mechanical and structural due to its properties of inherent capability for accurate measurement of the traditional performance.

Large amplitude free flexural vibration (LAFFV) behavior of a beam arises in many engineering applications, particularly in the panels of aircraft using intelligent materials such as piezoelectric or shape memory alloy (SMA). When a structure is deflected substantially, i.e., half of its thickness, a considerable geometrical nonlinearity occurs, mostly due to the development of in-plane membrane. These membrane stresses are tensile in nature that stiffens the panel. This stiffening effect results in the rise of resonance frequencies and change of mode shapes as well. Thus, the linear model is not being capable to determine the behavior of the structures completely. Therefore, in the recent years, geometrically nonlinear flexural vibration of panels has received considerable attention for behavior of plates [4].

The manufacturing and processing of FGM with fully specified profile of material gradation is very difficult due to significant variability in their mechanical and structural properties. These variables are statistical in nature and will, in turn, be reflected in the scattering of the material properties, structural stiffness and micro-mechanical behavior and may affect the fundamental characteristics of structural response such as frequency response. Therefore, proper handling of the randomness in the material properties is required for accurate prediction of structural response for safe and reliable design. The stochastic analysis is a useful analytical tool to predict accurately the response of structures with random material properties by the theory of random fields.

A good number of literatures have been reported on the linear and nonlinear free vibration of FGM beam structures subjected to thermo-piezoelectric loadings acting simultaneously or individually with or without piezoelectric layers using deterministic approach.

In this direction, Kapania and Rachiti [5] provided a detail review of shear deformation theories for static, vibration and buckling analysis of thin and thick laminated beams and plates using analytical, numerical and experimental techniques. Ke et al. [6] obtained nonlinear free vibration response with of FGM beam with different end supports by using Euler Bernoulli beam theory with von Karman nonlinear strain-displacement. Shoostari and Rafiee [7] presented the nonlinear forced vibration response of a beam made of symmetrically functionally graded materials based on Euler-Bernoulli beam theory and von Karman geometric nonlinearity. Yang and Chen [8] investigated free vibration and buckling analysis of FGM beam with open crack at their edge by using Bernoulli-Euler beam theory and the rotation spring model. Xiang and Yang [9] used Timoshenko beam theory to study the free and forced vibration of laminated functionally graded beam under heat conduction using differential quadrature method (DQM). Kitipornchai et al. [10] derived the eigenvalue equation by using Ritz method via direct iterative method to obtain the nonlinear forced vibration of a cracked FGM beam with different end supports based on Timoshenko beam theory and von Karman geometric nonlinearity. Sina et al. [11] formulated the analytical solution for a free vibration of FGMs beam using first order shear deformation theory (FSDT). Pradhan and Chakraverty [12] investigated free vibration analysis of FGM beams based on Euler-Bernoulli and Timoshenko beam theory using Rayleigh–Ritz method. Vo et al. [13] developed refined shear deformation theory which does not require shear correction factor to obtain static and vibration response of FG beams. Aydogdu [14] used different higher order shear deformation theories and classical beam theories to obtain free vibration frequencies and mode shapes for different material properties and slenderness ratios. Simsek [15] has investigated the fundamental frequency of FGMs beam having various boundary conditions within the framework of classical, first order and different higher order shear deformation theories using Lagrange multiplier method. Thai and Vo [16] developed higher order shear deformation beam theories for bending and free vibration of FGM beam. Wattanasakulpong et al. [17] used an improved third order shear deformation theory to analyze linear thermal buckling and vibration of FG beam using Ritz method. Reddy [18] proposed a third order plate theory for static analysis of the FGMs plate subjected to thermal, mechanical and sinusoidal loadings using finite element models based on third order shear deformation theory. Huang and Shen [19] investigated the nonlinear vibration and dynamic response of FGM plate with surface bonded piezoelectric layer in thermal environment using semi analytical approach. Kapuria et al. [20] presented a bending response and natural frequency of FGM beam from efficient zigzag and theoretical models showing validation with experiments. Li et al. [21] investigated the response of free vibration of piezoelectric FGM beam under uniform electric field and nonuniform temperature rise using the Galerkin’s procedure and elliptical function. Fu et al. [22] analyzed the nonlinear free vibration and nonlinear dynamic stability of piezoelectric FGM beam using Galerkin’s technique, doffing equation and nonlinear Mathieu equation. Ying et al. [23] obtained the exact solutions for bending and free vibration of FGM beams resting on a Winkler-Pasternak elastic foundation based on the two dimensional elasticity theories. Fallah and Aghdam [24] presented approximate analytical expressions for geometrically nonlinear vibration analysis of FGMs beam on nonlinear foundation by using He’s variational method.

The above mentioned literatures are based on deterministic analysis. In the deterministic analysis, the mean value of material properties give only mean response and unaccounted deviation caused due to inherent material properties. However, the studies related to stochastic analyses are limited. Certain effort have been made in past by the researchers to predict the structural response of structures with random system properties. In this direction, Stefanou [25] provided a state-of-the-review of past and recent developments of stochastic FEM in computational stochastic mechanics indicating future directions to be examined by the computational mechanics community. Vanmarcke and Grigoriu [26] evaluated the second order statistics of deflection behavior of beam using random material properties and rigidity via correlation method. Kaminski [27] evaluated bending response using second-order perturbation and second order probabilistic moment method via stress-based finite element method (FEM). Locke [28] presented the thermally buckled and vibration analysis for large deflection response using iterative techniques and method of linearization. Chang and Chang [29] used the finite element method in conjunction with perturbation technique and Monte Carlo simulation to investigate the statistical dynamic responses of a nonuniform beam with stochastic Young’s modulus of elasticity. Raj et al. [30] obtained the static response of graphite-epoxy composite laminates with randomness in material properties subjected to deterministic loading using FSDT via FEM combined with FOPT. Singh et al. [31, 32] investigated the vibration of composite laminate plates using C ⁰ FEM based on HSDT in conjunction with FOPT. Onkar et al. [33] presented the generalized force nonlinear vibration of laminated composite plate with random material properties using classical plate theory (CLT) combined with FOPT. Kitipornchai et al. [34] studied the vibration composed by the third order shear deformation theory with random material effect using FOPT incorporating mixed type and semi-analytical approach to derive the standard eigenvalue problem. Shaker et al. [35, 36] presented the stochastic finite element method (SFEM) to investigate the natural frequency of composite laminated and functionally graded plates HSDT based on first order reliability method and second order reliability method. Lal et al. [37, 38] evaluated the linear and nonlinear free vibration response of laminated composite plates with and without supported with elastic foundation and thermal environment using HSDT based C ⁰ linear and nonlinear FEM combined with and without direct iterative method in conjunction with FOPT. Yang et al. [39] evaluated stochastic transverse central deflection of FGM plate subjected to thermomechanical loading with random material properties using first order shear deformation theory (FSDT) via FOPT. Jagtap et al. [40] examined the stochastic nonlinear free vibration response of FGM plate using HSDT with von-Karman kinematic nonlinear via direct iterative based stochastic finite element method.

It is evident from the available literatures mentioned above that the studies of stochastic nonlinear free flexural vibration analysis of FGM beam with surface bonded piezoelectric layers subjected to thermo-piezoelectric loadings using higher order shear deformation theory are not dealt by the researchers to the best of the authors’ knowledge. In the present work, an attempt is made to address this problem using probabilistic approach. The basic formulation of the present beam analysis is based on HSDT incorporating von-Karman nonlinear strain kinematics. A C ⁰ nonlinear finite element method based on direct iterative procedure combined with the mean centered FOPT i.e., direct iterative based stochastic finite element method (DISFEM) with reasonable accuracy is employed to handle the randomness in material properties of FGMs beam with surface bonded piezoelectric layers subjected to thermo-piezoelectric loadings. The proposed probabilistic DISFEM approach is valid for small random material properties as compared to mean values. This condition is satisfied by most of the engineering problems, including FGMs that fall in this category [34, 39].

The paper is organized as follow. Section 1 gives the brief introduction of the related problem with suitable justification and literature survey based on deterministic and probabilistic analysis. Section 2 provides brief description of geometric configuration, material properties of FGMs beam with surface bonded piezoelectric layers. Section 3 provides detail FEM mathematical formulation using C ⁰ continuity model of FGMs piezoelectric beam subjected to uniform and non-uniform temperature distribution with uniform piezoelectric loadings. The governing equation of the problem is presented in Sect. 4. Section 5 provides the solution methodology of deterministic and probabilistic approach. Section 6 explains the results and discussion followed by validation studied with respect to various parameters via numerical examples. Section 7 accomplishes the conclusion based on the observation.

2 Geometric configuration and material properties

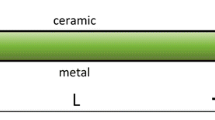
A piezoelectric laminated FGM rectangular beam of length L, thickness h with its coordinate definition and material direction of typical lamina in (x,z) coordinate system is shown in Fig. 1. The FGM beam is attached with surface bonded piezoelectric layers in different conditions of top-bottom, top and bottom layers with thickness of h _p. The thickness of FGM beam and total thickness of structures including piezoelectric layers acting top and bottom are assumed as h and H, respectively. It is assumed that a perfect bonding exists between FGM and surface bonded piezoelectric layers so that no slippage can occurs at the interface and the strain experienced by the FGM and piezoelectric material are equal. It is also assumed that FGM behaves like heterogeneous composite materials and the effects of constituent’s materials are detected separately using power index law. The properties of the FGM beam are assumed to be vary through the thickness of the plate only, such that the top surface z=h/2 is ceramic-rich and the bottom surface z=−h/2 is metal-rich.

Fig. 1

Geometry of FGM beam with surface bonded piezoelectric layers

The elastic material properties vary through the plate thickness according to the volume fractions of the constituents using power law distribution (as shown in Fig. 2) which is expressed as [19]

$$ P(z) = (P_{c} - P_{m})V_{c} + P_{m} $$

(1)

with

$$\begin{aligned} V_{C} ( z ) = \biggl( \frac{z}{h} + \frac{1}{2} \biggr)^{n},\quad - h/2 \le z \le h/2, 0 \le n \prec\infty \end{aligned}$$

(2)

where, P denotes the effective material property, P _m and P _c represents the properties of metal and ceramic, respectively. The parameters V _c and n represents the volume fraction of the ceramic and volume fraction exponent, respectively. From Eq. (1), it is clear that the beam is fully ceramic with n=0 and fully metal with n=∞. The above power-law theory estimates a simple rule of mixtures which is used to find the effective material properties of the ceramic-metal graded beam and this rule of mixtures applied in the thickness direction only.

Fig. 2

Variation of Young’s modulus and Poisson’s ratio of SUS304-Si₃N₄ FGM beam along the thickness for various power law indexes

It is evident that from Fig. 2 that an increase in power law index, n, results in an increase in Young’s modulus and the bending rigidity of the FGM beam.

3 Theoretical formulations

3.1 Displacement field model

In the present study, the assumed displacement field model based on the higher order shear deformation theory (HSDT) is used in the present analysis [41]. The in-plane and transverse displacement field components of an arbitrary points within the beam along x and z directions based on based on above displacement field is expressed as

$$\begin{aligned} \begin{aligned}[c] &\bar {u}(x,z) = u_{0}(x) + z\psi_{x} - \frac{4}{3h^{2}}z^{3}(\psi_{x} + \partial w / \partial x) \\ &\bar {w}(x,z) = w_{0}(x) \end{aligned} \end{aligned}$$

(3)

where u ₀, w ₀, Ψ _x and ∂w/∂x are the mid-plane axial displacement, transverse displacement, rotation of normal to the mid-plane along y-axis and slope along x-axis, respectively.

The C ⁰ continuous element permits easy isoparametric finite element formulation and consequently, can be applied for non-rectangular geometry as well. In modified form of C ⁰ continuity, the derivative of out-of-plane displacement (i.e., φ=∂w/∂x) is themselves considered as separate degree of freedom (DOFs) [35]. Thus, 3 DOFs given in Eq. (3) as u ₀, w ₀ and Ψ _x with C ¹ continuity are transformed into 4 DOFs as u ₀, w ₀, Ψ _x and ϕ _x with C ⁰ continuity due to conformity with HSDT. In this change, the artificial constraints are imposed, which can be enforced variationally through a penalty approach, in order to satisfy the constraint emphasized. However, the literature [35] demonstrates that without enforcing these constraints the accurate results using C ⁰ continuity can be obtained.

The modified displacement field components along x- and z-direction for an arbitrary FGM beam is now written as

$$\begin{aligned} \begin{aligned}[c] &\bar{u}(x,z) = u_{0}(x) + f_{1}(z)\psi_{x} + f_{2}(z)\varphi_{x};\\ & \bar{w}(x,z) = w_{0}(x) \end{aligned} \end{aligned}$$

(4)

where f ₁(z) and f ₂(z), given in Eq. (4) can be written as

$$\begin{aligned} \begin{aligned}[b] &f_{1}(z) = C_{1}z - C_{2}z^{3}\quad \text{and}\quad f_{2}(z) = - C_{4}z^{3}\\ & \quad\text{where}\ C_{1} =1\ \text{and}\ C_{2} =C_{4} =4/3h^{2} \end{aligned} \end{aligned}$$

(5)

The displacement vector for the modified C ⁰ continuous model is denoted as

$$ \{ \varLambda\} = \begin{bmatrix} u & w & \varphi_{x} & \psi_{x} \end{bmatrix} ^{T} $$

(6)

3.2 Strain displacement relation

For the FGM beam considered here, the relevant strain vector consisting of linear strain (in terms of mid plane deformation, rotation of normal and higher order terms), non-linear strain (von-Karman type), thermal and piezoelectric strains vectors associate with the displacement are expressed as

$$\begin{aligned} \{ \bar{\varepsilon} \} = \bigl\{ \bar{\varepsilon}^{L} \bigr\} + \bigl\{ \bar{\varepsilon}^{NL} \bigr\} - \bigl\{ \bar{ \varepsilon}^{T} \bigr\} - \bigl\{ \bar{\varepsilon}^{V} \bigr\} \end{aligned}$$

(7)

where $\{ \bar{\varepsilon}^{L} \}$, $\{ \bar{\varepsilon}^{NL} \}$, $\{ \bar{\varepsilon}^{T} \}$ and $\{ \bar{\varepsilon}^{V} \}$ are the linear, non-linear, thermal and piezoelectric strain vectors, respectively.

From Eq. (7), the linear strain tensor using HSDT can be written as

$$\begin{aligned} \bar{\varepsilon}^{L} = [B]\{ q\} \end{aligned}$$

(8)

where B and {q} are geometrical matrix and displacement field vector for the two node beam element, respectively [42].

Assuming that the strains are much smaller than the rotations (in the von-Karman sense), one can rewrite nonlinear strain vector $\{ \bar{\varepsilon}^{NL} \}$ given in Eq. (7) is represented as [40]

$$ \begin{aligned}[b] &\bar {\varepsilon}^{NL} = \frac{1}{2} [ A_{nl} ] \{ \varphi_{nl} \}\quad\mbox{with}\ \{ A_{nl}\} = \frac{1}{2} [ w_{,x} ]\\ &\quad\mbox{and}\ \{ \varphi_{nl} \} = \{ w_{,x} \} \end{aligned} $$

(9)

The thermal strain vector $\{ \bar{\varepsilon}^{T} \}$ given in Eq. (7) is expressed as

$$\begin{aligned} \bigl\{ \bar{\varepsilon}^{T} \bigr\} = \{ \alpha\}\Delta T \end{aligned}$$

(10)

where α is coefficients of thermal expansion along the x direction, and ΔT denotes the uniform or non-uniform change in temperature in the beam attached with surface bonded piezoelectric layer.

The temperature field is assumed to be varying in the thickness direction only and temperature field is uniform and non-uniform distributed in the x direction of the beam. In such a case, the temperature distribution along the thickness can be obtained by solving a steady-state heat transfer equation [43]

$$\begin{aligned} - \frac{d}{dz} \biggl[ k(z)\frac{dT}{dz} \biggr] = 0 \end{aligned}$$

(11)

where, k(z) is thermal conductivity of the piezoelectric FGM beam with surface bonded piezoelectric layers.

The temperature field for uniform or non-uniform temperature change for FGM beam is expressed as [42]

$$ \Delta T = T(z) - T_{0} $$

(12)

In case of the non-uniform temperature distribution along z direction, T(z) and for uniform temperature change it is expressed as [42]

$$\begin{aligned} T(z) = T_{0} + (T_{U} - T_{L}) \end{aligned}$$

(13)

where, T ₀ is the uniform temperature rise at room temperature and assumed to be 300 K.

The electric field vector $\{ \bar{\varepsilon}^{V} \}$ as given in Eq. (7) can be represented as

$$ \bigl\{ \bar{\varepsilon}^{V} \bigr\} = \frac{V_{p}}{h_{p}} \{ d_{31} \} $$

(14)

where d ₃₁,V _p and h _p are the piezoelectric strain constants in the x-direction, applied voltage to the actuators in the thickness direction and thickness of piezoelectric layer in the FGM beam subjected with uniform electric field rise, respectively.

3.3 Stress-strain relation

The constitutive law of thermo-piezoelectric-elastic constitutive relationship for material under consideration relates the stresses with strains in a in-plane stress state is given as [22]

$$\begin{aligned} \bar{\sigma} = [ Q ] ( \bar{\varepsilon} - \alpha\Delta T ) - [ e ]E_{z} \end{aligned}$$

(15)

where, [Q],[e] and E _z are transform reduced elastic constant matrix of beam material, matrix of piezoelectric stress constant and electric field vectors, respectively [42].

The electric displacement vector of the piezoelectric layer is given by [44]

$$ D = [ e ] \bigl( \bar{\varepsilon}^{L} + \bar{\varepsilon}^{NL} \bigr) + \xi E_{z} + P\Delta T $$

(16)

where ξ and P are the dielectric coefficient matrix and the pyroelectric constants vector, respectively.

Using the linear Lagrangian interpolation function, the electric potential corresponding to each piezoelectric layer φ can be written as

$$ \varphi= [ N_{\varphi} ]\varepsilon_{z}^{\varphi} $$

(17)

where, [N _ϕ ] is shape function matrix of piezoelectric layer.

The electrical field vector E is defined as negative gradient of electric potential as below

$$ E = - \nabla\varphi $$

(18)

where ∇ is the gradient operator.

From Eq. (18), the electric field vector E _z is calculated based on the gradient of the electric potential ϕ _p can be written as [22]

$$\begin{aligned} E_{z} = - \nabla\varphi= B_{\varphi} \varepsilon_{z}^{\varphi} \end{aligned}$$

(19)

where,

$$\begin{aligned} B_{\varphi} = - \nabla[ N_{\varphi} ] \end{aligned}$$

(20)

$\varepsilon_{z}^{\varphi}$ is electric potential degree of freedom vector is considered as

$$\begin{aligned} \varepsilon_{z}^{\varphi} = \left\{ \begin{matrix} \varphi_{L} & \varphi_{U} \end{matrix} \right \}^{T} \end{aligned}$$

(21)

where,ϕ _L and ϕ _U are the electric potential corresponding to lower and upper piezoelectric layers, respectively.

3.4 Strain energy of piezoelectric FGM beam

The total strain energy of the system consisting of linear, nonlinear and piezoelectric strain energy of the FGM beam with surface bonded piezoelectric layers can be expressed as

$$ \varPi_{1} = \varPi_{a} - \varPi_{b} $$

(22)

where Π _a and Π _b are the strain energy of FGM beam and surface bonded piezoelectric layer piezoelectric layer, respectively.

From Eq. (22), the strain energy (Π _f ) of the FGM beam can be expressed as

$$\begin{aligned} \varPi_{a} = U_{L} + U_{NL} \end{aligned}$$

(23)

From Eq. (23) the linear stain energy (U _L ) of the FGM beam is given by

$$\begin{aligned} U_{L} &= \int_{\varOmega} \frac{1}{2} \bigl\{ \bar{ \varepsilon}^{L} \bigr\} [ Q ] \bigl\{ \bar{\varepsilon}^{L} \bigr\} ^{T}d\varOmega \\ &= \int_{\Delta} \frac{1}{2} \bigl\{ \bar{\varepsilon}^{L} \bigr\} [ D_{mn} ] \bigl\{ \bar{ \varepsilon}^{L} \bigr\} ^{T}d\Delta \end{aligned}$$

(24)

where [D _mn ] is the elastic stiffness matrix [42].

From Eq. (23) the nonlinear strain energy (U _NL ) of the FGM beam can be rewritten as

$$\begin{aligned} U_{NL} &= \int_{\varOmega} \frac{1}{2} \bigl\{ \bar {\varepsilon}^{L} \bigr\} [ D_{3} ] \bigl\{ \bar {\varepsilon}^{NL} \bigr\} ^{T}d\varOmega \\ &\quad + \frac{1}{2}\int_{\varOmega} \bigl\{ \bar { \varepsilon}^{NL} \bigr\} [ D_{4} ] \bigl\{ \bar { \varepsilon}^{L} \bigr\} ^{T}d\varOmega \\ &\quad + \frac{1}{2}\int _{\varOmega} \bigl\{ \bar {\varepsilon}^{NL} \bigr\} [ D_{5} ] \bigl\{ \bar {\varepsilon}^{L} \bigr\} ^{T}d\varOmega \end{aligned}$$

(25)

where Ω, $\bar{\varepsilon}^{L}$ and $\bar{\varepsilon}^{NL}$ denotes undeformed configuration of FGM beam, linear and nonlinear strain tensors, respectively.

Using Eq. (9), Eq. (25) can be expressed as

$$\begin{aligned} U_{NL} &= \frac{1}{2}\int_{\varOmega} [ A_{nl} ] \{ \varphi_{nl} \} [ D_{3} ] \bigl\{ \bar {\varepsilon}^{L} \bigr\} d\varOmega \\ &\quad + \frac{1}{2}\int _{\varOmega} \bigl\{ \bar {\varepsilon}^{L} \bigr\} [ D_{4} ] [ A_{nl} ] \{ \varphi_{nl} \}d\varOmega \\ &\quad + \frac{1}{2}\int_{\varOmega} [ A_{nl} ] \{ \varphi_{nl} \} [ D_{5} ] [ A_{nl} ]^{T} \{ \varphi_{nl} \}^{T}d\varOmega \end{aligned}$$

(26)

where D ₃, D ₄ and D ₅ are the stiffness matrices of the FGM beam [42].

Similarly from Eq. (22) the strain energy (Π _b ) due to surface bonded piezoelectric layers can be rewritten as

$$ \varPi_{b} = U_{\varphi L} + U_{\varphi NL} $$

(27)

where U _ϕL and U _ϕNL are the linear and nonlinear strain energy of surface bonded piezoelectric layers. From Eq. (24), the linear strain energy (U _ϕL ) due to surface bonded piezoelectric layer can be expressed as,

$$\begin{aligned} U_{\varphi L} &= \int_{\varOmega} \bigl\{ \varepsilon^{L} \bigr\} [ e ]^{T} \bigl\{ E^{\varphi} \bigr\} d\varOmega \\ &\quad + \int _{\varOmega} \frac{1}{2} \bigl\{ E^{\varphi} \bigr\} [ \xi] \bigl\{ E^{\varphi} \bigr\} ^{T}d\varOmega \\ &\quad + \int _{\varOmega} \bigl\{ E^{\varphi} \bigr\} P\Delta Td\varOmega \end{aligned}$$

(28)

From Eq. (27), the nonlinear strain energy (U _ϕNL ) due to surface bonded piezoelectric layer can be expressed as,

$$\begin{aligned} U_{\varphi NL} = \int_{\varOmega} \{ \varphi_{p} \}^{T}\{ A_{nl}\}^{T} [ e ] E^{\varphi} d\varOmega \end{aligned}$$

(29)

3.5 Work done due to thermo-piezoelectric loadings

The potential energy (Π ₂) storage due to thermo-piezoelectric loadings (uniform and non-uniform change in temperature and uniform change in electrical potential) is written as

$$\begin{aligned} \varPi_{2} = \frac{1}{2}\int_{A} N_{xTE}(w_{,x})^{2}dA \end{aligned}$$

(30)

where N _xTE is the prebuckling thermoelectrical stress with $N_{xTE} = \bar{N}_{0}^{T} + \bar{N}_{0}^{V}$, the $\bar{N}_{0}^{T}$ and $\bar{N}_{0}^{V}$ are in-plane thermal and electrical loadings, respectively and defined in the Appendix (56) and (57), respectively.

3.6 Kinetic energy of the FGM beam

The kinetic energy (Π ₃) of the vibrating FGM beam can be expressed as [38]

$$\begin{aligned} \varPi_{3} = \frac{1}{2}\int_{v} \rho\{ \hat{u} \}^{T} \{ \hat{u} \}dv \end{aligned}$$

(31)

where ρ and $\{ \dot{\hat{u}} \} = \{ \dot{\bar{u}} \ \dot{\bar{w}} \}$ are the density and velocity vector of the FGM beam, respectively.

Equation (31) can be rewritten for 2-D beam as

$$\begin{aligned} \varPi_{3}& = \frac{1}{2}\int_{0}^{l} \int_{ - h/2}^{h/2} \rho(z) \bigl[ \bigl( \dot{\bar{u}} \bigr)^{2} + \bigl( \dot{\bar{w}} \bigr)^{2} \bigr]dzdx \\ &= \frac{1}{2}\int_{0}^{l} \int _{ - h/2}^{h/2} \rho(z)N^{T}Ndzdx \end{aligned}$$

(32)

where N is inertia matrix (58).

3.7 Finite element model

In the present study, a C ⁰ one-dimensional Hermitian beam element with 4 degree of freedom (DOF) per node is employed. For this type of element, the displacement vector and the element geometry can be expressed as [42]

$$\begin{aligned} \{ q \} = \sum_{i = 1}^{NN} N_{i} \{ q \}_{i};\qquad x = \sum_{i = 1}^{NN} N_{i} x_{i}; \end{aligned}$$

(33)

where N _i and {q} _i are the interpolation function for the ith node and the vector of unknown displacements for the ith node, NN is the number of nodes per element and x _i is the Cartesian coordinate of the ith node.

For the present analysis, linear interpolation functions are chosen for axial displacement and rotation of normal while, Hermite cubic interpolation functions for transverse deflection and slope.

The linear mid-plane strain vector as given in Eq. (8) can be expressed in terms of mid plane displacement field and then the energy is computed for each element and then summed over all the elements to get the total strain energy.

Following this and using finite element model as given in Eq. (33), Eq. (23) after summed over all the elements can be written as

$$\begin{aligned} \varPi_{a} = \sum_{e = 1}^{\mathit{NE}} \varPi_{a}^{ ( e )} = \sum_{e = 1}^{\mathit{NE}} \bigl( U_{L}^{(e)} + U_{NL}^{(e)} \bigr) \end{aligned}$$

(34)

where, NE is the number of elements and $\varPi_{a}^{ ( e )}$ is the elemental potential energy of the beam.

Substituting Eqs. (24) and (26), Eq. (34) can be further expressed as

$$\begin{aligned} \varPi_{a} &= \sum_{e = 1}^{\mathit{NE}} \bigl[ \{ q \}^{T ( e )} \bigl[ K_{l} + K_{nl} ( q ) \bigr]^{^{ ( e )}} \{ q \}^{ ( e )} \bigr] \\ & = \{ q \}^{T} \bigl[ K_{l} + K_{nl} ( q ) \bigr] \{ q \} \end{aligned}$$

(35)

where $[ K_{nl} ] = \frac{1}{2} [ K_{nl_{1}} ] + [ K_{nl_{2}} ] + \frac{1}{2} [ K_{nl_{3}} ]$ where [K _l ], [K _nl ] and {q} are defined as global linear, nonlinear stiffness matrices and global displacement vector, respectively.

Using finite element model equation (33), Eq. (27) after summing over the entire element can be written a

$$\begin{aligned} \varPi_{b} = \sum_{e = 1}^{\mathit{NE}} \varPi_{b}^{ ( e )} = \sum_{e = 1}^{\mathit{NE}} \bigl( U_{\varphi L}^{(e)} + U_{\varphi NL}^{(e)} \bigr) \end{aligned}$$

(36)

where $\varPi_{b}^{ ( e )} ( \varPi_{bl}^{ ( e )} + \varPi_{bnl}^{ ( e )} )$ is the elemental linear and nonlinear potential energy of the surface bonded piezoelectric layers.

Using and Eq. (28) and Eq. (36) for linear potential energy for surface bonded piezoelectric layer can be expressed as

$$\begin{aligned} \varPi_{bl} &= \sum_{e = 1}^{\mathit{NE}} \bigl( \{ q \}^{(e)T} [ K_{1lp} ]^{(e)} \{ q_{\varphi} \}^{ ( e )} \\ &\quad + \{ q_{\varphi} \}^{(e)T} [ K_{2lp} ]^{(e)} \{ q_{\varphi} \}^{ ( e )} + \{ q_{\varphi} \}^{(e)T} [ K_{3lp} ]^{(e)} \bigr) \\ &= \{ q \}^{T} [ K_{1lp} ] \{ q_{\varphi} \} + \{ q_{\varphi} \}^{T} [ K_{2lp} ] \{ q_{\varphi} \} \\ &\quad + \{ q_{\varphi} \}^{T} [ K_{3lp} ] \end{aligned}$$

(37)

Similarly, using and Eq. (29) and Eq. (36) for nonlinear potential energy for surface bonded piezoelectric layer can be expressed as

$$\begin{aligned} \varPi_{bnl} &= \frac{1}{2}\sum_{e = 1}^{\mathit{NE}} \bigl( \{ q \}^{(e)T} [ K_{1nlp} ]^{(e)} \{ q_{\varphi} \}^{ ( e )} \bigr) \\ &= \{ q \}^{T} [ K_{1nllp} ] \{ q_{\varphi} \} \end{aligned}$$

(38)

where [K _1lp ], [K _1nllp ] and {q _φ } are defined as global linear coupling matrix between elastic mechanical and electrical effects, nonlinear coupling matrices between elastic mechanical and electrical effects and global electric field vector, respectively.

Using finite element model equation (33), Eq. (30) after summing over the entire element can be written as [35]

$$\begin{aligned} \varPi_{2} &= \sum_{e = 1}^{\mathit{NE}} \varPi_{2}^{ ( e )} = \frac{1}{2}\sum _{e = 1}^{\mathit{NE}} \{ q \}^{T ( e )}\lambda[ K_{ ( G )} ]^{ ( e )} \{ q \}^{ ( e )} \\ &= \frac{1}{2} \lambda\{ q \}^{T} [ K_{ ( G )} ] \{ q \} \end{aligned}$$

(39)

where, λ and [K _(G)] are defined as the thermo-piezoelectric buckling load parameters and the global geometric stiffness matrix (arises due to thermo-piezoelectric loadings), respectively.

Using finite element model equation (33), Eq. (32) may be written as

$$\begin{aligned} \varPi_{3} = \sum_{e = 1}^{\mathit{NE}} \varPi_{^{3}}^{ ( e )} \end{aligned}$$

(40)

where

$$\begin{aligned} \varPi_{3}^{ ( e )} = \sum_{e = 1}^{\mathit{NE}} \{ \dot{\varLambda} \}^{ ( e )T} [m] \{ \dot{\varLambda} \}^{ ( e )} dA \end{aligned}$$

(41)

Using finite element model equation (33), Eq. (41) after summing over the entire element can be written as

$$ \varPi_{3} = \{ \dot{q} \}^{T}[M] \{ \dot{q} \} $$

(42)

Where, [M] is the global consistent mass matrix defined in the Appendix (59).

4 Governing equation

The governing equation for the nonlinear free vibration analysis can be derived using Hamilton principle, which is generalization of the principle of virtual displacement [38, 45]. The Lagrange equation for the conservative system can be written as

$$\begin{aligned} &\frac{\partial}{\partial t} \biggl( \frac{\partial T}{\partial \dot{q}} \biggr) + \frac{\partial ( \varPi_{a} + \varPi _{bl} + \varPi_{bnl} )}{\partial q} - \frac{\partial ( \varPi_{2} + \varPi_{3} )}{\partial q} \\ &\quad = 0 \end{aligned}$$

(43)

By substituting Eqs. (35), (37), (38), (39) and (42) in Eq. (43), ones obtain as in the form of nonlinear generalized eigenvalue problem as

$$\begin{aligned}{} [ K ] \{ q \} + [M] \{ \ddot{q} \} = 0 \end{aligned}$$

(44)

where, [K]={[K _L ]+[K _NL ]−λ _T [K _(G)]} with $[ K_{L} ] = \frac{1}{2} [ K_{l1} ] - \frac{1}{2} [ K_{lp_{1}} ]$ and $[ K_{NL} ] = \frac{1}{2} [ K_{nl1} ] + [ K_{nl2} ] + \frac{1}{2} [ K_{nl3} ] - \frac{1}{2} [ K_{1nlp} ]$ λ _T is the critical thermopiezoelectric buckling.

The above Eq. (44) is the nonlinear free vibration equation that can be solved literately as a linear eigenvalue problem assuming that the beam is vibrating in its principal mode in each iteration. For each iteration, Eq. (44) can be expressed as generalized eigenvalue problem as

$$ [K] \{ q \} = \lambda[ M ] \{ q \} $$

(45)

where, λ=ω ² with ω is the natural frequency of the beam.

Equation (45) is the nonlinear free vibration problem which is random in nature, being dependent on the system properties. Consequently, the natural frequency and mode shapes are random in nature. In deterministic environment, Eq. (45) is evaluated using eigenvalue formulation and solved employing a direct iterative methods, Newton-Raphson methods, incremental methods etc. However, in random environment, it is not possible to solve the problem using the above mentioned methods without changing the nature of the equation. For this purpose, the direct iterative method based on nonlinear finite element method combined with mean centered FOPT i.e., direct iterative based stochastic finite element method (DISFEM), with a reasonable accuracy is used to obtain the second order statistics of nonlinear natural frequency response. The overview of present outlined probabilistic approach is shown in Fig. 3.

Fig. 3

Schematic diagram of present outlined probabilistic approach

5 Solution approach

5.1 Solution approach—a DISFEM for nonlinear free vibration problem

The nonlinear eigenvalue problem as given in Eq. (45) is solved by employing a direct iterative based C ⁰ nonlinear finite element method in conjunction with perturbation technique (DISFEM) assuming that the random changes in eigenvector during iterations does not affect much the nonlinear stiffness matrix with the following steps [38].

Step 1.:

The nonlinear stiffness matrices in the first step neglecting using amplitude ratios as zero, the linear eigenvalue problem [[K _l ]{q}=λ[M]{q}] is obtained from Eq. (45) by assuming that the system vibrates in its principal mode. Then the random linear eigenvalue problem is broken into zeroth and first-order equation using perturbation technique and neglecting the higher order equations. Then the eigenvalue (λ=ω ²) and eigenvector {q} is obtained from any standard deterministic method using zeroth order perturbation equation. The mean centered first order perturbation technique is then employed to obtain the standard deviation of the nonlinear fundamental frequency using the first-order perturbation equation.

Step 2.:

The mean mode shape of the desired nonlinear mode is normalized with respect to given amplitude at the point of maximum deflection.

Step 3.:

Using the normalized mode shape, the nonlinear random stiffness matrix is computed. Again, the zeroth and the first order eigen equations are obtained using perturbation technique.

Step 4.:

The zeroth and the first order equations are then solved to obtain new eigenvalue and corresponding eigenvectors and standard deviation using updated zeroth and first order equations, respectively.

Step 5.:

Steps (2)–(4) are repeated until convergence is attained for {q}_max,ω ² and the standard deviation (SD) and corresponding to the converged mode shape, the mean and standard deviation are computed.

The detail analysis of stochastic (perturbation technique) nonlinear free vibration analysis of FGM beam is shown in Fig. 4.

Fig. 4

Schematic flow chart procedure of stochastic nonlinear free vibration analysis using DISFEM

5.2 Solution approach: perturbation technique

The fabrication and manufacturing of the FGMs are complicated process due to involvement of large number of uncertainties as stated earlier. In the present analysis, the elastic constants such as Young’s modulus and Poisson’s ratio of FGM and surface bonded piezoelectric material along with volume fraction exponent are treated as independent random variables. A class of problem considered where the zero mean random variation is very small when compared to the mean part of random system properties. Further it is quite logical to assume that the dispersions in the derived quantities such as [K], q, λ, etc. are also small with respect to their mean values.

In general, without any loss of generality, any arbitrary random variable can be represented as the sum of its mean and a zero mean random variable, expressed by superscripts ‘d’ and ‘r’, respectively [31, 32, 37, 38],

$$\begin{aligned} K = K^{d} + K^{r}, \qquad \lambda_{i} = \lambda_{i}^{d} + \lambda_{i}^{r},\qquad q_{i} = q_{i}^{d} + q_{i}^{r} \end{aligned}$$

(46)

where, $\lambda_{2i}^{d} = \omega_{i}^{d^{2}},\lambda_{i}^{2} = 2\omega_{i}^{d}\omega_{i}^{r} + \omega_{i}^{r^{2}}$, i=1,2,…,p.

The parameter p indicates the size of eigen problem.

For sake of simplicity, the mass matrix is taken as constant in the present analysis.

Using Taylor series and neglecting the second and higher-order terms since the first order approximation is sufficient to yield desired accuracy with low variability as in the case of the sensitive applications [46].

Substituting Eq. (46) in Eq. (45) and collecting same order of the magnitude term one obtains as [37]

Zeroth order perturbation equation:

$$\begin{aligned} \bigl[ K^{d} \bigr] \bigl\{ q_{i}^{d} \bigr\} = \lambda_{i}^{d} [ M ] \bigl\{ q_{i}^{d} \bigr\} \end{aligned}$$

(47)

First order perturbation equation:

$$\begin{aligned} &\bigl[ K^{d} \bigr] \bigl\{ q_{i}^{r} \bigr\} + \bigl[ K^{r} \bigr] \bigl\{ q_{i}^{d} \bigr\} = \lambda_{i}^{d} [ M ] \bigl\{ q_{i}^{r} \bigr\} + \lambda_{i}^{r} [ M ] \bigl\{ q_{i}^{d} \bigr\} \end{aligned}$$

(48)

The zeroth order perturbation Eq. (47) is the deterministic equation relating to the mean eigenvalues and corresponding mean eigenvectors, which can be determined using conventional eigensolution algorithms. Equation (48) is the first order random perturbation equation defining the stochastic nature of the free vibration which cannot solve using conventional method [31, 32].

According to the orthogonality properties, the normalized eigenvector meet the following conditions.

$$\begin{aligned} &\bigl\{ q_{i}^{d} \bigr\} ^{T} [ M ] \bigl\{ q_{i}^{d} \bigr\} = \delta_{ij} \end{aligned}$$

(49)

$$\begin{aligned} &\bigl\{ q_{i}^{d} \bigr\} ^{T} \bigl[ K^{d} \bigr] \bigl\{ q_{i}^{d} \bigr\} = \delta_{ij}\lambda_{i}^{d},\quad (i, j = 1, 2,\ldots ,p) \end{aligned}$$

(50)

where δ _ij is the Kronecker delta.

The eigen vectors, after being properly normalized, form a complete orthogonal set and any vector in the space can be expressed as their linear combination of these eigenvectors.

Hence, the ith random part of the eigenvectors can be expressed as

$$\begin{aligned} &\bigl\{ q_{i}^{r}\bigr\} = \sum _{j = 1}^{p} C_{ij}^{r}\bigl\{ q_{i}^{d}\bigr\} , \\ &\quad \bigl(i \ne j, C_{ii}^{r} = 0,\ i = 1, 2,\ldots,\bigr) \end{aligned}$$

(51)

where $C_{ii}^{r}$ are random coefficients to be determined.

Substituting Eq. (51), in Eq. (47), premultiplying, the first by $\{q_{i}^{d}\}^{T}$ and then by {q _j }^T (j≠i), respectively and making use of orthogonality condition, Eq. (50) can be rewritten as

$$\begin{aligned} \bigl\{ q_{i}^{d} \bigr\} ^{T} \bigl[ K^{r} \bigr] \bigl\{ q_{i}^{d} \bigr\} = \lambda_{i}^{r} \end{aligned}$$

(52)

For the present case, as discussed earlier, the derived quantities are random because of the randomness in the system properties. Let b ₁,b ₂,…,b _n denote system properties. Following Eq. (46), the random variables (b _i ) can also be expressed as

$$\begin{aligned} b_{i} = b_{i}^{d} + b_{i}^{r},\quad i = 1, 2,\ldots,n \end{aligned}$$

(53)

The FEM in conjunction with the FOPT has been found to be accurate and efficient [31, 32, 37, 38, 46]. According to this method, the random variables are expressed by Taylor’s series. Keeping the first-order terms and neglecting the second- and higher-order terms, Eq. (46) can be expressed as

$$ \begin{aligned}[c] &\lambda_{i}^{r} = \sum_{j = 1}^{q} \lambda_{i,j}^{d} b_{j}^{r}; \qquad \bigl\{ q_{i}^{r} \bigr\} = \sum_{j = 1}^{p} q_{i,j}^{d} b_{j}^{r}; \\ & \bigl[ K^{r} \bigr] = \sum_{j = 1}^{q} \bigl[ K_{,j}^{d} \bigr] b_{i}^{r}; \end{aligned} $$

(54)

Using the above and decoupled equations, the expressions for $\lambda_{i,j}^{d}$ is obtained.

Using Eq. (54), the variances of the eigenvalues can now be expressed as [37, 38]

$$\begin{aligned} \operatorname{Var} ( \lambda_{i} ) = \sum_{j = 1}^{p} \sum_{k = 1}^{p} \lambda_{i,j}^{d} \lambda_{i,k}^{d}\operatorname{Cov} \bigl( b_{j}^{r},b_{k}^{r} \bigr) \end{aligned}$$

(55)

where, $\operatorname{Cov} ( b_{j}^{r},b_{k}^{r} )$ is the cross variance between $b_{j}^{r}$ and $b_{k}^{r}$. The standard deviation (SD) is obtained by the square root of the variance.

5.3 Monte Carlo simulation (MCS)

The Monte Carlo simulation (MCS) is the one of the most general approach being used to quantify the structural response uncertainties on the basis of direct use of computer and simulate experiments by a set of random number generations of material properties. In such simulated experiments, a set of random number of random material parameter is generated first to represent the statistical uncertainties in the structural parameters by satisfactory convergence of results. These random numbers are substituted into the response equation (48) to obtain again, a set of random number which reflects the uncertainties in structural response [46]. A sufficient set of random number is to be generated for mean and standard deviation of structural response based on the convergence of results [45, 47]. However, MCS approach is costly since, it needs tremendous repeated computations for all different types of samples, particularly when nonlinear finite element analysis is adopted and sometimes suffers from computational inefficiency [39]. Keeping in mind the drawback of MCS, it is used for validation purpose in the present analysis. The detail computation analysis of material randomness using MCS is presented with the help of flow chart as shown in Fig. 5.

Fig. 5

Schematic flow chart procedure of stochastic nonlinear vibration using independent MCS

6 Results and discussion

The second order statistics of nonlinear free vibration analysis of FGM beam with surface bonded piezoelectric layers having random material properties subjected to thermo-piezoelectric loadings is computed using the proposed direct iterative based stochastic finite element method (DISFEM). A computer algorithm has been developed in MATLAB 12.5.2 environment for computation of the numerical results. The validation and efficacy of the proposed algorithm is examined by comparing the results with available literature and MCS.

A C ⁰ one dimensional Hermitian two node beam element with 8 DOFs per element is developed and implemented for the present problem. Convergence and validation studies have been carried out through numerical examples to demonstrate the accuracy of the present formulation. Based on convergence study conducted as presented below, a 30 element (as shown in Table 3) has been used for numerical calculation in the present analysis.

The effect of combination of multiple random variables varying simultaneously and individually with volume fraction exponents, slenderness ratios, thermo-piezoelectric loadings, piezoelectric layers acting at top and/or bottom of FGM beam, material properties, various mode of temperature change, applied voltage, vibration mode shape and different combination of boundary conditions on the linear and nonlinear natural frequency of rectangular FGM beam with surface bonded piezoelectric layers have been examined and conclusions are noted in the analysis through tabular form. The mean and standard deviation of the nonlinear natural frequency square referred as natural frequency in the following texts are obtained. The probability density function of dimensionless linear and nonlinear fundamental frequency with respect to random input variable by changing volume fraction exponent.

The present outlined DISFEM is divided into two parts. In the first parts, one set of mean vibration problem is examined and in second parts set of random vibration problem is evaluated with respect to various random parameters. These two parts are solved sequentially to determine the mean and COV (=SD/mean), where, SD and mean indicate the standard deviation and dimensional natural frequency of the beam, respectively. Due to linear nature of variation of COV as mentioned earlier and passing through the origin, the COV results are presented by taking coefficient of correlation (COC) of the system properties equal to 0.1 i.e., 10 % variation of material properties from their mean values. However, the present COV results can be explored for COC value up to 20 %, keeping in mind the limitation of FOPT.

The basic random variable (b _i ) such as E _c ,ν _c ,E _m ,ν _m ,n,ρ _c ,ρ _m ,E _p ,ν _p ,ρ _p ,α _c , and α _m are sequenced and defined as b ₁=E _c ,b ₂=ν _c ,b ₃=E _m ,b ₄=ν _m ,b ₅=n,b ₆=ρ _c ,b ₇=ρ _m ,b ₈=E _p ,b ₉=ν _p ,b ₁₀=ρ _p ,b ₁₁=α _c , and b ₁₂=α _m .

In the present analysis, various combinations of boundary edge support conditions are as follows:

Both edges are simply supported (SS):

$$\begin{aligned} u=w=0; \quad \text{at}\ x=0, a \end{aligned}$$

Both edges are clamped (CC)

$$\begin{aligned} u=w=\theta_{x} = \psi_{x} = 0;\quad \text{at}\ x=0, a \end{aligned}$$

One end simply supported and other is clamped (CS)

$$\begin{aligned} &u=w=\theta_{x} = \psi_{x} = 0;\quad \mbox{at}\ x= a\quad \text{and}\\ &u=w=0;\quad \mbox{at}\ x=a \end{aligned}$$

For the convergence and validation study, the aluminum (Al; E _m =70 GPa, ρ _m =2702 kg/m³, υ _m =0.3) and alumina (Al₂O₃; E _c =380 GPa, ρ _c =3960 kg/m³, υ _c =0.3) material properties are used (unless otherwise stated).

The dimensionless mean natural frequency is used for validation purpose and defined as (unless otherwise stated)

$$\begin{aligned} \varpi= \omega\bigl(L^{2}/h\bigr)\sqrt{\rho_{m} \bigl(1 - \upsilon_{m}^{2}\bigr)/E_{m}} \end{aligned}$$

where, ω, ρ _m , υ _m and E _m indicate the dimensional mean natural frequency, density Poisson’s ratio and Young’s modulus of the metal, respectively. It is to be noted that the for the computation of numerical results for mean and COV, dimensionless mean natural (ϖ) is taken in the analysis while, for the COV results, SD/mean, ω ² is taken in the analysis.

The following TD material properties of FGM beam is given by [40]

$$\begin{aligned} P=P_{0} \bigl(P_{-1} T^{-1} + 1+P_{1} T+ P_{2} T^{2} + P_{3} T^{3}\bigr) \end{aligned}$$

where P ₀, P ₋₁, P ₁, P ₂ and P ₃ are given in Table 1.

Table 1 The following FGMs properties subjected to TID and TD properties are used for computation. Jagtap et al. [40]

The value of temperature T given in above expression is taken as 300 K for whole of the analysis.

For temperature independent (TID), the values of P ₋₁,P ₁,P ₂ and P ₃ are assumed as zero.

The material properties of surface bonded piezoelectric layer are expressed in Table 2.

Table 2 The following piezoelectric (PZT-5) material properties are used for computation. Fu et al. [22]

6.1 Convergence and validation study of deterministic and probabilistic approach

To make certain, the accuracy and proficiency of the present FEM formulation, six test examples have been examined for linear and nonlinear deterministic and random free vibration response of the FGM beam with and without surface bonded piezoelectric layers.

Example 1

The convergence study of present finite element formulation is performed with various number of terms of displacement functions for rectangular Al/Al₂O₃ clamped-clamped supported beam of slenderness ratio (L/h)=5 and volume fraction exponent (n)=1. The present results using C ⁰ FEM with HSDT is compared with those given by Simsek [15] using higher shear deformation beam theory as shown in Table 3. It is evident from the table that the present finite element result is converged for total element number 30. Therefore, 30 element numbers are used for further computation of the results as mentioned earlier. It is observed that present results are in good agreements with the available results in terms of accuracy.

Table 3 Convergence and validation study of different number of terms for Al-Alumina, rectangular FGM beam for clamped–clamped boundary condition having L/h=5 & n=1

Example 2

The first three dimensionless frequencies of functionally graded (FG) beam by various theories for different value of volume fraction exponent (n), length to thickness ratios (L/h) have been examined in Table 4 and compared with Thai and Vo [16] and Nguyen et al. [48]. It can be seen that all the shear deformation beam theories give the approximate same frequency but CBT give low frequencies due to the effect of shear deformation and rotary inertia. Again good agreements between the results are accomplished for different L/h ratios and n. The results are also compared with Nguyen et al. [48] by taking the effect of with and without poison’s ratio. It is observed that the effect of poison’s ratio tends to increase the fundamental frequency.

Table 4 Validation study for effect of length to thickness ratio (L/h) with volume fraction index (n) on the first three nondimensional fundamental frequencies ϖ of the simply supported Al-Alumina FGM beam

The first four mode of linear free vibration of FGM beam with different L/h ratios and n are plotted and shown in Fig. 6.

Fig. 6

Schematic diagram of first four natural frequency mode shape of FGM beam

Example 3

The dimensionless natural frequencies for FG beam with n=0.3 in different boundary conditions (BC) with different length to thickness ratio (L/h) are compared with Sina et al. [11], Simsek [15] and Wattanasakulpong et al. [17] and shown in Table 5. It is observed that the present fundamental frequency results are in good agreement with the published results for various boundary conditions and length to thickness ratio (L/h). The deviation in the results can be occurred due to the higher order terms used in present analysis.

Table 5 Validation study for effect of different boundary condition (BC) with length to thickness ratio (L/h) on dimensionless fundamental frequency $\varpi = \omega L^{2}\sqrt{\frac{I_{0}}{h^{2}\int_{ - h/2}^{h/2} E(z)d_{z}}}$ of Al/Al₂O₃ FGM beam with n=0.3

Example 4

Table 6 presents the effect of vibration amplitude, $i=W_{\max}/\sqrt{ I}/A$ (where I is the moment of inertia and A is the area of cross section) on the nonlinear frequency ratio (ω _nl /ω _l ) of isotropic homogenous clamped-clamped FGM beam with n=0, L/h=20 and h=100 mm. It is observed that the present results are in good agreement with the published results of Fu and Wang [22], Ke et al. [6], and Shooshtari and Rafiee [7]. The percentage difference is within the range of 2 % when compared with published literature of Ke et al. [6].

Table 6 Validation study for effect of vibration amplitude (W _max/h) on the nonlinear frequency ratio (ω _nl /ω _l ) of isotropic homogenous clamped-clamped FGM beam with different initial condition having n=0, L/h=20 and h=100 mm

Example 5

In this example, the effects of temperature on the top surface (T _t ) and applied voltage (V) with volume fraction (n) on the dimensionless fundamental frequency of CC supported SUS304-Si₃N₄ FGM beam with surface bonded piezoelectric layers subjected to thermo-piezoelectric loads with TID and TD material properties are presented in Table 7 and compared with Fu et al [22]. It can be observed that the dimensionless mean fundamental frequency with TD material properties is small than TID material properties. It means that TID material properties overestimate the stiffness of structure. It is also concluded that dimensionless frequency of piezoelectric FGM beam decreases as temperature of top surface temperature increases. The mean fundamental frequency decreases when positive applied voltage and increases when negative applied voltage. It is due to fact that axial compressive and tensile force would be generated in the beam by the positive and negative voltage.

Table 7 Validation study for effects of temperature on the top surface (T _t ) and applied voltage (V) with volume fraction exponent (n) on the dimensionless mean fundamental frequency of the clamped-clamped SUS304-Si₃N₄ FGM beam with surface bonded piezoelectric layers subjected to thermo-piezoelectric load with TID/TD material properties

Example 6

The validation study of COV of nonlinear free vibration response of CC SUS304/Si₃N₄ FGM beam for different L/h ratios with random material properties, b _i (i=1,…,7) varying from 0 to 20 % from their mean values are compared with independent MCS due to not availability of probabilistic results in the literature as shown in Fig. 7. For the MCS approach, the sample values are generated in MATLAB environment to fit the desired mean and SD of the response using Gaussian probabilistic distribution function (GPDF). The convergence of MCS results are examined by generating the different sets of random number generation to represent the material uncertainties which are given as input to the present deterministic and statistic of response are calculated by collecting again a sets of random number generation which shows the statistic of sample of response. From the convergence study, it is experience that 8,000 samples are sufficient to simulate the results of desired response. From the figure, it is observed that the present results using DISFEM are very good agreement with the independence MCS approach for different L/h ratios. The percentage difference between the DISFEM and independent MCS is up to 5 %. However, MCS is more general approach, but it requires more computation times and sometime suffers from computation inefficiency. Keeping in mind the limitation of MCS, it is used for validation purpose. These four comparison studies with different (L/h) ratios show that the present DISFEM result matches very well with the independent MCS approach.

Fig. 7

Validation study of present DISFEM results from independent MCS for nonlinear free vibration response of piezoelectric FGM beam with CC support condition for random change in material properties {b _i , (i=1–7)} keeping others as deterministic

In the present parametric study, the material properties of FGM beam and surface bonded piezoelectric layers has shown in Tables 1 and 2 and the dimensionless linear and nonlinear natural frequency is defined as $\varpi= \omega_{nl}L\sqrt{\rho_{c} / E_{c}(300\ \text{K})}$ (unless otherwise stated).

6.2 Parametric study for second order statistic of nonlinear free vibration response

Table 8 examines the effect of individual random variables {b _i , (i=1 to 12)=0.10}, volume fraction exponent (n), uniform and non-uniform temperature distribution on the dimensionless mean and COV of nonlinear fundamental frequency of the simply supported SUS304-Si₃N₄ piezoelectric FGM beam with TD and TID material properties, L/h=15, and ΔT=200 K. It is observed that nonlinear fundamental frequency are more affected by random change in material properties of E _c , E _m , ρ _m and n. The strict control of these random parameters is, therefore, required if high reliability of FGM beam is desired. It is also observed that TD material properties are more sensitive than TID properties with random change in E _c , E _m , n, E _p . It is because of temperature increments makes the stiffness of the beam lower. It is also examined that with increase the n, the COV of individual material properties decreases with random change in E _c , ν _c , α _c , ρ _c , ρ _p and n while increases in E _m , E _p α _m , ν _m , ν _p and ρ _m . It is because of more volume of metal portion is involved and affect the effective material properties of FGM beam. It can be also noticed that the dimensionless fundamental frequency of beam is less sensitive and COV of nonlinear fundamental frequency is more sensitive in non-uniform temperature distribution as compared to uniform temperature distribution subjected to TD and TID material properties.

Table 8 Effects of individual random variables {b _i , (i=1 to 12)=0.10}, volume fraction exponent, uniform and non-uniform temperature distribution on the dimensionless mean and COV of nonlinear fundamental frequency of the clamped–clamped SUS304-Si₃N₄ FGM beam with surface bonded piezoelectric layers with TD and TID material properties, L/h=15, ΔT=200 K, V=0, W _max/h=1

Table 9 examines the effect of slenderness ratio (L/h), volume fraction exponent (n) and effect of piezoelectric layer with random material properties {b _i , (i=(1,…,7) and (8,…,10))=0.1} on the dimensionless mean and COV of fundamental frequency of clamped-clamped SUS304-Si₃N₄ FGM beam with TID material properties. It is observed that the mean fundamental frequency and corresponding COV decreases with increasing the L/h ratio at the same volume fraction exponent and with and without considering piezoelectric layer. It is because of increasing the L/h ratio, the beam becomes thin and ultimately stiffness of the beam decreases. It is also observed that with the increase of n the mean fundamental frequency decreases. However, COV increases for n=0.5 and 2 and again increases when n is greater than 2. It is because of increasing the value of n, volume of metal part up to certain limit is increasing and ultimately stiffness of the beam decreasing. It is also interesting to note that when piezoelectric layer is attached at the top portion, bottom portion and both of the top and bottom portions of the beam, there are significant changed in dimensionless mean and COV of fundamental frequency. When the piezoelectric layers are attached top position, the fundamental frequency and corresponding COV {b _i , (i=(1,…,7))=0.1} is highest while COV is lowest when piezoelectric layer is attached at bottom and top and bottom of the beam. It is because of piezoelectric layer senses the mean response more accurately when it is placed at the top of the beam while more sensitive to response dispersion, when it attached at bottom or top and bottom of beam subjected to random change in material properties. It is also noticed that response dispersion is most sensitive with higher value of ‘n’ when the piezoelectric layer is attached at top of the beam.

Table 9 Effect of slenderness ratio (L/h), volume fraction exponent and effect of piezoelectric layer on the dimensionless mean and COV of linear fundamental frequency of clamped-clamped SUS304-Si₃N₄ FGM beam with TID material properties

The effect of material properties (SUS304/Si₃N₄ and ZrO₂/Ti–6Al–4V) with thermal loading (ΔT), volume fraction exponent (n), amplitude ratio (W _max/h) and non-uniform temperature distribution with variation of random material properties {b _i , (i=(1,…,10) and (11,12))=0.1} on the dimensionless mean and COV of nonlinear fundamental frequency of the CC piezoelectric FGM beam with TD and TID material properties, L/h=20 is presented in Table 10. It is observed that for the same n and ΔT, SUS304/Si₃N₄ materials beam shows higher dimensionless mean corresponding lower COV of fundamental frequency than ZrO₂/Ti–6Al–4V materials beam. The increase in the mean and decrease in COV of fundamental frequency is due to higher value of material stiffness are used. It is also observed that dimensionless mean and COV of nonlinear fundamental frequency is less sensitive for n and ΔT as compared to ZrO₂/Ti–6Al–4V. This is because of higher material properties is used which increases the stiffness of the plate.

Table 10 Effects of material properties (SUS304/Si₃N₄ and ZrO₂/Ti–6Al–4V) with thermal loading (ΔT), volume fraction index (n), amplitude ratio (W _max/h) and non-uniform temperature distribution with variation of random material properties {b _i , (i=(1,…,10) and (11,12))=0.1} on the dimensionless mean and COV of nonlinear fundamental frequency of the CC FGM beam with surface bonded piezoelectric layers with TD and TID material properties, L/h=20, V=0

Table 11 shows the effects of different random variables {b _i , (i=1 to 12)=0.10} changing simultaneously with volume fraction exponent (n) on the COV of the nonlinear frequency of the clamped FGM beam attached surface bonded piezoelectric layer subjected to thermal loading with TD and TID material properties, L/h=20, ΔT=200 K, W _max/h=1. It is observed that COV tends to be higher as more material properties parameter are taken to be random inputs and is the maximum when all the material properties varies simultaneously [34]. It is worthy of noting that response dispersion lowers when n is increasing. However, when more material properties changing simultaneously, the response dispersion increases with increase the n.

Table 11 Effects of different random variables {b _i , (i=1 to 12)=0.10} changing simultaneously and volume fraction exponent (n) on the dimensionless mean and COV of the nonlinear frequency of the clamped-clamped surface bonded piezoelectric FGM beam subjected to thermal loading with TD and TID material properties, L/h=20, ΔT=200 K, V=0, W _max/h=1

The effects of various support conditions (namely, SS, CC and CS), thermal loading (ΔT), volume fraction exponent (n), amplitude ratio (W _max/h) and temperature distribution with variation of random material properties {b _i , (i=(1,…,10) and (11,12))=0.1} on the dimensionless mean and COV of the nonlinear fundamental frequency of the FGM beam with surface bonded piezoelectric layers with TD and TID material properties, L/h=15 is examined in Table 12. It is observed that dimensionless mean fundamental frequency is highest for the beam supported with CS boundary condition while COV with random change in material properties b _i , (i=1…,10) and b _i , (i=11,12) is highest for the beam supported with SS boundary condition. It is because of increased boundary constraint increases the stiffness of the plate. Therefore, tight control of SS supported beam is required for high reliability of the FGM beam.

Table 12 Effects of support boundary condition (BC) with thermal loading (ΔT), volume fraction exponent (n), amplitude ratio (W _max/h) and non-uniform temperature distribution with variation of random material properties {b _i , (i=(1,…,10) and (11,12))=0.1} on the dimensionless mean and COV of the nonlinear fundamental frequency of the FGM beam with surface bonded piezoelectric layers with TD and TID material properties, L/h=15, V=0

Table 13 shows the effect of piezoelectric layers, applied voltage (V), volume fraction exponent (n) and frequency modes with variation of random material properties {b _i , (i=(1,…,10) and (11,12))=0.1} on the dimensionless mean and COV of the nonlinear natural frequency of the piezoelectric clamped SUS304/Si₃N₄ FGM beam subjected to uniform and nonuniform temperature distribution with TD material properties, L/h=15, W _max/h=1, ΔT=200 K. The three different positions of surface bonded piezoelectric layers on the FGM layer namely; (I) piezoelectric layer at top and bottom, (II) piezoelectric layer at top and (III) piezoelectric layer at bottom of the beam are considered. It is observed that among the different position of piezoelectric layers, the dimensionless mean natural frequency is highest while, corresponding COV is lowest with random change in material properties {b _i , (i=(1–10))} and random piezoelectric properties {b _i , (i=(11–12))} for piezoelectric layer attached as (I). It is because of piezoelectric layer increases the stiffness of the beam. It is also noticed that applied voltage decreases the dimensionless mean and increases the COV of natural frequency with random change in {b _i , (i=(1–10))} and {b _i , (i=(11–12))}. It is because of applied voltage makes the stiffness of beam lowers. It is also interesting that the dimensionless mean natural frequency increases with increase the frequency mode. However, no definite pattern observed for COV with random change in all material properties increases {b _i , (i=(1–10))} and {b _i , (i=(11–12))}. However, it is expected that the dimensionless mean natural frequency is higher and corresponding COV is lower for uniform temperature distribution as compared to non-uniform temperature distribution.

Table 13 Effect of piezoelectric layers (I), (II), (III), applied voltage (V), volume fraction exponent (n) and modes with variation of random material properties {b _i , (i=(1,…,10) and (11,12))=0.1} on the COV of the nonlinear dimensionless natural frequency of the clamped-clamped SUS304/Si₃N₄ FGM beam with surface bonded piezoelectric layers subjected to uniform and nonuniform temperature distribution with TD material properties, L/h=15, W _max/h=1. (I) piezolayer at top and bottom, (II) piezolayer at top and (III) piezolayer at bottom of the plate. ΔT=200 K

Figure 8 shows probability density function (PDF) of the linear and nonlinear dimensionless fundamental frequency with change in volume fraction exponents for a clamped–clamped SUS304-Si₃N₄ FGM beam with surface bonded piezoelectric layers having TID material properties, L/h=15, ΔT=200 K and COC=10 % of random input variables using Gaussian distribution for (a) Convergence study at various samples (b) Random change in E _c (c) Random change in E _m (d) Random change in ρ _m . The convergence study has been carried out for the probability density function with various samples size for random change in E _c using Monte Carlo sampling. On the basis of convergence study conducted, 10000 samples size is taken into consideration for the computation of results.

Fig. 8

Probability density function of the linear and nonlinear dimensionless fundamental frequency with change in volume fraction exponents for a clamped–clamped SUS304-Si₃N₄ FGM beam with surface bonded piezoelectric layers having TID material properties, L/h=15, ΔT=200 K and COC=10 % of random input variables for (a) Convergence study at various samples (b) Random change in E _c (c) Random change in E _m (d) Random change in ρ _m

It is observed from Fig. 8(b) that as the volume fraction exponent increases the dispersion in PDF of dimensionless fundamental frequency decreases with respect to random change in E _c . Also, it is observed from Fig. 8(c) and 8(d) that as the volume fraction exponent increases the dispersion in PDF of dimensionless fundamental frequency increases with respect to random change in E _m and ρ _m .

7 Conclusions

A C ⁰ nonlinear FEM using direct iterative procedure in conjunction with FOPT has been presented to obtain the dimensionless mean and COV of nonlinear natural frequency of rectangular FGMs beam with surface bonded piezoelectric layers subjected to thermo-piezoelectric loadings with random material properties in the framework of HSDT via von-Karman nonlinearity. From the limited study, the following conclusion can be drawn.

For a given boundary conditions and loadings, the dimensionless mean nonlinear fundamental frequency is lower and corresponding COV is higher for metal rich beam as compared to ceramic rich beam. The dimensionless mean fundamental frequency decreases as the volume fraction exponent increases. However, COV of nonlinear fundamental frequency does not follow the defined path. Among the different random system properties studied, the elastic modulus, volume fraction exponent, density of metal and ceramic have dominant effects on the COV of nonlinear fundamental frequency as compared to other system properties subjected to uniform and nonuniform change in temperature with TID and TD properties. The tight control of these parameters are required if high reliability of the FGM structure is desired. The mean fundamental frequency decreases with increasing the slenderness ratio for both of metal and ceramic rich beam. However, COV decreases with increasing the slenderness ratio for ceramic to metal rich beam. Similar trend is observed for the beam with surface bonded piezoelectric layers attached on top and bottom and top of beam. However, COV increases with increase the volume fraction exponent and length to thickness ratio for random change in random piezoelectric properties. It is also interesting to note that among the three cases considered, the mean fundamental frequency and corresponding COV is most sensitive for beam with surface bonded piezoelectric layer attached at top position. The CC supported beam shows highest dimensionless mean and lowest COV of fundamental nonlinear frequency as compared other supported beam. The mean fundamental frequency of FGM bean with surface bonded piezoelectric layers decreases and corresponding COV increases when positive applied piezoelectric voltage increases. The COV of fundamental frequency of beam subjected to thermal loading with TD and TID material properties increases with increase the random input parameters taking simultaneously. In general, an increase in frequency mode, the dimensionless mean natural frequency of FGM beam with surface bonded piezoelectric layers increases and corresponding COV decreases. The dispersion due thermal exponential coefficients, density of respective FGM beam and surface bonded piezoelectric layers is quite significant. It is not desirable to ignore the randomness in the system properties for a reliable design.

The efficacy of present approach has been verified using PDF assuming Gaussian and the results shown by probabilistic finite element method (perturbation technique) are in perfect agreement with the Monte Carlo sampling.

Appendix

$$\begin{aligned} & \begin{aligned}[b] N_{0}^{T} &= \begin{bmatrix} N_{x}^{T} & M_{x}^{T} & P_{x}^{T} \end{bmatrix} \\ & = \int _{ - h/2}^{h/2} \bigl(1,z,z^{3}\bigr) (Q_{11})\alpha\Delta Tdz \end{aligned} \end{aligned}$$

(56)

$$\begin{aligned} & \begin{aligned}[b] N_{0}^{V} &= \begin{bmatrix} N_{x}^{V} & M_{x}^{V} & P_{x}^{V} \end{bmatrix} \\ &= \sum _{k = 1}^{Na} \int_{Z_{k}}^{Z_{k + 1}} \bigl(1,z,z^{3}\bigr)d_{11}\bigl(Q_{11}^{a} \bigr)\frac{V_{p}}{h_{p}}dz \end{aligned} \end{aligned}$$

(57)

$$\begin{aligned} &[ N ] = \begin{bmatrix} N_{1} & 0 \\ - C_{2}z^{3}\frac{\partial N_{3}}{\partial x} & N_{3} \\ - C_{2}z^{3}\frac{\partial N_{4}}{\partial x} & N_{4} \\ (z - C_{2}z^{3})N_{1} & 0 \\ N_{2} & 0 \\ - C_{2}z^{3}\frac{\partial N_{5}}{\partial x} & N_{5} \\ - C_{2}z^{3}\frac{\partial N_{6}}{\partial x} & N_{6} \\ (z - C_{2}z^{3})N_{2} & 0 \end{bmatrix} \end{aligned}$$

(58)

$$\begin{aligned} &[ M ] = \begin{bmatrix} pe_{1} & q_{2}e_{2} & q_{2}e_{2} & q_{1}e_{1} \\ q_{2}e_{1} & I_{2}e_{3} + pe_{4} & I_{2}e_{3} + pe_{4} & I_{3}e_{2} \\ q_{2}e_{1} & I_{2}e_{3} + pe_{4} & I_{2}e_{3} + pe_{4} & I_{3}e_{2} \\ q_{1}e_{1} & I_{3}e_{2} & I_{3}e_{2} & I_{1}e_{1} \end{bmatrix} \\ &e_{1} = \int_{0}^{l} N^{T}N dx = \begin{bmatrix} l/3 & l/6 \\ l/6 & l/3 \end{bmatrix} \\ & e_{2} = \int_{0}^{l} N^{T} \bar{N}_{x} dx = \begin{bmatrix} - 1/2 & l/12 & 1/2 & - l/12 \\ - 1/2 & - l/12 & 1/2 & l/12 \end{bmatrix} \\ & e_{3} = \int_{0}^{l} \bar {N}_{x}^{T}\bar {N}_{x} dx \\ &\phantom{e_{3}} = \begin{bmatrix} 6/5l & 1/10 & - 6/5l & 1/10 \\ 1/10 & 2l/15 & - 1/10 & - l/30 \\ - 6/5l & - 1/10 & 6/5l & - 1/10 \\ 1/10 & - l/30 & - 1/10 & 2l/15 \end{bmatrix} \\ & \begin{aligned}[t] e_{4} &= \int_{0}^{l} \bar {N}^{T}\bar {N} dx \\ &= \begin{bmatrix} 13l/35 & 11l^{2}/210 & 9l/70 & - 13l^{2}/420 \\ 11l^{2}/210 & l^{3}/105 & 13l^{2}/420 & - l^{3}/140 \\ 9l/70 & 13l^{2}/420 & 13l/35 & - 11l^{2}/210 \\ - 13l^{2}/420 & - l^{3}/140 & - 11l^{2}/210 & l^{3}/105 \end{bmatrix} \end{aligned} \\ &N = \begin{bmatrix} N_{1} & N_{2} \end{bmatrix} \qquad\bar{N}_{x} = \begin{bmatrix} N_{3} & N_{4} & N_{5} & N_{6} \end{bmatrix} \\ &( p,q_{1},q_{2},I_{1},I_{2},I_{3} ) \\ &\quad = \int_{h/2}^{ - h/2} \bigl(\rho^{c} - \rho^{m}\bigr) \bigl(1,f_{1}(z),f_{2}(z),f_{1}^{2}(z), \\ &\qquad f_{2}^{2}(z),f_{1}(z)*f_{2}(z) \bigr) dz \\ &p = h \biggl( \rho^{m} + \bigl(\rho^{c} - \rho^{m}\bigr) \biggl[ \frac{1}{n + 1} \biggr] \biggr) \\ & \begin{aligned}[t] q_{1} &= h^{2}C_{1}\bigl(\rho^{c} - \rho^{m}\bigr) \biggl[ \frac{1}{n + 2} - \frac{1}{2(n + 1)} \biggr] \\ &\quad - C_{2}h^{4}\bigl(\rho^{c} - \rho^{m} \bigr) \biggl[ \frac{1}{n + 4} - \frac{3}{2(n + 3)} \\ &\quad + \frac{3}{4(n + 2)} - \frac{1}{8(n + 1)} \biggr] \end{aligned} \\ & \begin{aligned}[b] q_{2} &= - C_{4}h^{4}\bigl(\rho^{c} - \rho^{m}\bigr) \biggl[ \frac{1}{n + 4} - \frac{3}{2(n + 3)} \\ &\quad + \frac{3}{4(n + 2)} - \frac{1}{8(n + 1)} \biggr] \end{aligned} \\ & I_{1} = C_{1}^{2}h^{3} \biggl\{ \bigl( \rho^{c} - \rho^{m}\bigr) \biggl[ \frac{1}{n + 3} - \frac{1}{n + 2} + \frac{1}{4(n + 1)} \biggr] \biggr\} \\ &\qquad + \frac {C_{1}^{2}\rho^{m}h^{3}}{12} + C_{2}^{2}h^{7} \biggl\{ \bigl( \rho^{c} - \rho^{m}\bigr) \biggl[ \frac{1}{n + 7} - \frac{3}{n + 6} \\ &\qquad + \frac{15}{4(n + 5)}- \frac{5}{2(n + 4)} + \frac{15}{16(n + 3)} \\ &\qquad - \frac{3}{16(n + 2)} + \frac{1}{64(n + 1)} \biggr] \biggr\} + \frac{C_{2}^{2}h^{7}\rho^{m}}{448} \\ &\qquad - 2C_{1}C_{2}h^{5} \biggl\{ \bigl(\rho^{c} - \rho^{m}\bigr) \biggl[ \frac{1}{n + 5} - \frac{2}{(n + 4)} \\ &\qquad + \frac{3}{2(n + 3)} - \frac{1}{2(n + 2)} + \frac {1}{16(n + 1)} \biggr] \biggr\} \\ &\qquad - \frac{C_{1}C_{2}h^{5}\rho^{m}}{40} \\ & \begin{aligned}[t] I_{2} &= - C_{2}h^{7} \biggl\{ \bigl( \rho^{c} - \rho^{m}\bigr) \biggl[ \frac{1}{n + 7} - \frac{3}{n + 6} \\ &\quad + \frac{15}{4(n + 5)} - \frac{5}{2(n + 4)} + \frac{15}{16(n + 3)}\\ &\quad - \frac{3}{16(n + 2)} + \frac{1}{64(n + 1)} \biggr] \biggr\} - \frac{C^{2}_{2}h^{7}\rho^{m}}{448} \end{aligned} \\ & \begin{aligned}[t] I_{3} &= C_{2}^{2}h^{7}\bigl( \rho^{c} - \rho^{m}\bigr) \biggl[ \frac{1}{n + 7} - \frac{3}{n + 6} + \frac{15}{4(n + 5)} \\ &\quad - \frac{5}{2(n + 4)} + \frac{15}{16(n + 3)} - \frac{3}{16(n + 2)}\\ &\quad + \frac{1}{64(n + 1)} \biggr] + \frac{C_{2}^{2}\rho^{m}h^{7}}{448} \\ &\quad - C_{1}C_{2}h^{5}\bigl( \rho^{c} - \rho^{m}\bigr) \biggl[ \frac{1}{n + 5} - \frac{2}{(n + 4)} \\ &\quad + \frac{3}{2(n + 3)} - \frac{1}{2(n + 2)} + \frac {1}{16(n + 1)} \biggr] \\ &\quad - \frac{C_{1}C_{2}h^{5}\rho^{m}}{80} \end{aligned} \end{aligned}$$

(59)